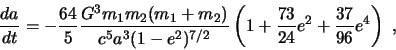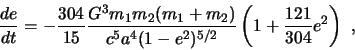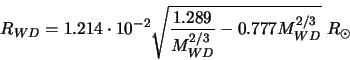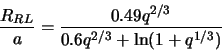|
Астронет: В. Б. Игнатьев/ГАИШ Гравитационно-волновое излучение от галактических
компактных двойных звезд на эллиптических орбитах http://www.astronet.ru/db/msg/1174691/node3.html |
<< 1. Введение | Оглавление | 3. ГВ от компактных >>
- 2.1 Моделирование начальных условии методом популяционного синтеза
- 2.2 Стационарная функция распределения компактных двойных звезд в Галактике
2. Стационарная функция распределения компактных двойных звезд в галактике
2.1 Моделирование начальных условии методом популяционного синтеза
Существование двойных нейтронных звезд являются закономерным следствием эволюции массивных двойных звезд. Известно шесть НЗ в двойных системах, вторым компонентом которых является НЗ.
| Двойные Пульсары в парах с НЗ | |||
| Системы | Период (дни) | эксцентриситет, |
|
| B1913+16 | 0.323 | 0.617 |
|
| B1534+12 | 0.420 | 0.274 |
|
| B2721+11c | 0.335 | 0.681 |
|
| B2303+46 | 12.340 | 0.658 |
|
| J1518+4904 | 8.634 | 0.249 |
|
| B1820-11 |
357.762 | 0.795 |
|
|
|
|||
Три из этих систем достаточно тесные для того, чтобы слиться из-за
испускания гравитационных волн за время меньше Хаббловского ![]() .
Теоретическая оценка темпа слияния двойных нейтронных звезд в Галактике
.
Теоретическая оценка темпа слияния двойных нейтронных звезд в Галактике ![]() события в год (см. Грищук и др., 2001).
события в год (см. Грищук и др., 2001).
Двойные системы образуются с различными начальными параметрами
(массы компонент, большая полуось, эксцентриситет).
На эволюцию двойной системы также оказывают сильное влияние такие параметры, как
дополнительная скорость ![]() (скорость «отдачи»),
приобретаемая молодой НЗ во время вспышки сверхновой,
эффективность уноса углового момента на стадии общей оболочки
(скорость «отдачи»),
приобретаемая молодой НЗ во время вспышки сверхновой,
эффективность уноса углового момента на стадии общей оболочки ![]() и др.
и др.
При помощи метода популяционного синтеза ("Машина сценариев", Липунов и др. 1996) проводились
расчеты большого числа эволюционных треков ![]() с различными начальными параметрами.
Часть этих треков приводила к образованию двойных нейтронных звезд.
При этом, в системе дважды происходила вспышка сверхновой типа II или Ib/с (если водородная
оболочка была потеряна в ходе обмена массами).
с различными начальными параметрами.
Часть этих треков приводила к образованию двойных нейтронных звезд.
При этом, в системе дважды происходила вспышка сверхновой типа II или Ib/с (если водородная
оболочка была потеряна в ходе обмена массами).
При мгновенном сферически-симметричном сбросе массы одной из компонент двойной
системы на круговой орбите новая орбита становится эллиптичной с эксцентриситетом ![]() (Блаау 1961),
где
(Блаау 1961),
где ![]() - сброшенная масса,
- сброшенная масса, ![]() - полная масса системы после вспышки сверхновой.
Если существует асимметрия коллапса, которая характеризуется дополнительной
пространственной скоростью, то
эксцентриситеты орбит образующихся НЗ в среднем становятся больше.
- полная масса системы после вспышки сверхновой.
Если существует асимметрия коллапса, которая характеризуется дополнительной
пространственной скоростью, то
эксцентриситеты орбит образующихся НЗ в среднем становятся больше.
Как уже говорилось выше, дополнительная скорость,
которую приобретает молодая НЗ, влияет на эволюцию двойной системы
(распад системы, изменение эксцентриситета, распределение пространственных скоростей).
Наблюдательные данные по радиопульсарам показывают, что распределение дополнительных
скоростей имеет среднее значение порядка 200 - 400 км/с и обладает широкой формой
с высокоскоростным хвостом, тянущимся до скоростей порядка 1500 км/с
(Лайн и Лоример 1994, Арзуманян и др. 2001).
Предполагаем, что распределение скорости «отдачи» имеет Максвелловскую форму
Пространственное распределение двойных нейтронных звезд в Галактике
является весьма чувствительным
к амплитуде скорости «отдачи» ![]() . До вспышки сверхновой двойная система
находится в тонком галактическом диске, где рождаются звезды.
После двух (или одной в случае систем БК+НЗ)
вспышек сверхновой центр масс двойной системы приобретает значительную пространственную
скорость, если система не распалась в результате взрыва.
Из-за этого образовавшаяся система НЗ+НЗ (БК+НЗ)
может уйти на большие расстояния от плоскости галактики. Этот эффект рассматривался
в работе Булик и др. 1999. Было показано, что пространственное распределение
двойных нейтронных звезд перед слиянием имеет почти сферический вид и для
. До вспышки сверхновой двойная система
находится в тонком галактическом диске, где рождаются звезды.
После двух (или одной в случае систем БК+НЗ)
вспышек сверхновой центр масс двойной системы приобретает значительную пространственную
скорость, если система не распалась в результате взрыва.
Из-за этого образовавшаяся система НЗ+НЗ (БК+НЗ)
может уйти на большие расстояния от плоскости галактики. Этот эффект рассматривался
в работе Булик и др. 1999. Было показано, что пространственное распределение
двойных нейтронных звезд перед слиянием имеет почти сферический вид и для ![]() км/с
тянется до
км/с
тянется до ![]() кпк. Для нахождения обратного среднего расстояния до компактных
двойных звезд в Галактике мы воспользовались результатами этой работы.
кпк. Для нахождения обратного среднего расстояния до компактных
двойных звезд в Галактике мы воспользовались результатами этой работы.
Так как интересующие нас детекторы будут находиться в окрестности Солнца
(т.е. на расстоянии ![]() кпк от центра Галактики), то необходимо знать
пространственное распределение двойных НЗ относительно Солнца.
кпк от центра Галактики), то необходимо знать
пространственное распределение двойных НЗ относительно Солнца.
Можно свернуть амплитуду гравитационной волны регистрируемой детектором, которая
обратно пропорциональна расстоянию до источника, с функцией распределения расстояний
от Солнца до сливающихся систем.
Предполагается, что все источники имеют одинаковые массы,
в случае НЗ
![]() (Прохоров и Постнов 2001); по всем орбитальным углам проводим усреднение.
Тогда операцию свертки можем заменить определением
(Прохоров и Постнов 2001); по всем орбитальным углам проводим усреднение.
Тогда операцию свертки можем заменить определением
![]() , и именно
эту величину подставить вместо неизвестного нам расстояния до источника.
Также можно ввести эффективное расстояние
, и именно
эту величину подставить вместо неизвестного нам расстояния до источника.
Также можно ввести эффективное расстояние
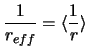 -
соответствующее среднему по ансамблю обратных расстояний до компактных двойных звезд.
В случае двойных нейтронных звезд
-
соответствующее среднему по ансамблю обратных расстояний до компактных двойных звезд.
В случае двойных нейтронных звезд ![]() кпк.
В системе массивный БК+НЗ происходит только одна вспышка сверхновой и в среднем
пространственная скорость центра масс системы меньше. Оценим
кпк.
В системе массивный БК+НЗ происходит только одна вспышка сверхновой и в среднем
пространственная скорость центра масс системы меньше. Оценим ![]() из следующих соображении: верхний предел - это
из следующих соображении: верхний предел - это
![]() кпк, а нижний предел -
это расстояние до центра Галактики. В качестве оценки возьмем
кпк, а нижний предел -
это расстояние до центра Галактики. В качестве оценки возьмем
![]() кпк.
кпк.
Двойные компактные звезды формируются в широком интервале орбитальных параметров:
большой полуоси ![]() и эксцентриситета
и эксцентриситета ![]() . При помощи программы расчета
эволюции двойных звезд «Машина Сценариев»
мы получили начальные функции распределения двойных нейтронных звезд сразу после
второй вспышки сверхновой и систем состоящих из массивного белого карлика и
только что образованной НЗ по
. При помощи программы расчета
эволюции двойных звезд «Машина Сценариев»
мы получили начальные функции распределения двойных нейтронных звезд сразу после
второй вспышки сверхновой и систем состоящих из массивного белого карлика и
только что образованной НЗ по ![]() .
Именно эти параметры определяют потери энергии и углового момента в виде ГВ
в двойной системе.
.
Именно эти параметры определяют потери энергии и углового момента в виде ГВ
в двойной системе.
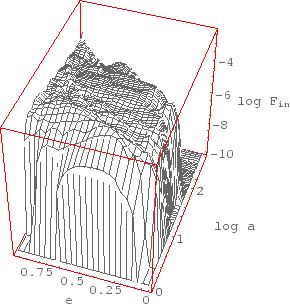 |
| Рис. 2.1
Начальная функция распределения двойных НЗ |
Рассмотрим характерные особенности начальной функции распределения
систем БК+БК.
Главное отличие от двойных нейтронных звезд состоит в том, что
орбита системы состоящих из двух белых карликов является почти
круговой, что является следствием прохождения этих систем
стадии общей оболочки.
Темп слияния таких систем
![]() год
год![]() .
.
Более интересными в этом плане представляются системы типа БК+НЗ,
в которой первичная компонента в результате своей эволюции образует белый
карлик, а вторичная компонента вследствие перетекания вещества с первой
звезды набирает необходимую массу и взрывается как сверхновая.
Подробный анализ образования двойных систем, включающих
старый белый карлик и молодую НЗ, представителями
которых могут быть радиопульсары на эксцентричных орбитах
PSR B2303+46 и PSR J1141-6545, проводился в работе
Таурис и Сеннелс (2000), см. также Портегис Цварт и Юнгельсон 1999
и Браун и др. 2001.
Такая система также будет обладать
отличным от нуля эксцентриситетом. Но среднее значение эксцентриситета орбит
невелико ![]() . Темп слияния
. Темп слияния
![]() год
год![]() .
Таким образом, хотя темп слияния систем БК+НЗ сопоставим с темпом
слияния НЗ+НЗ, эти системы имеют в среднем меньшие эксцентриситеты
и мы не будем их рассматривать при анализе широкополосных
импульсов ГВ от сливающихся компактных двойных звезд (см. раздел 3.3).
.
Таким образом, хотя темп слияния систем БК+НЗ сопоставим с темпом
слияния НЗ+НЗ, эти системы имеют в среднем меньшие эксцентриситеты
и мы не будем их рассматривать при анализе широкополосных
импульсов ГВ от сливающихся компактных двойных звезд (см. раздел 3.3).
2.2 Стационарная функция распределения компактных двойных звезд в Галактике
2.2.1 Построение стационарной функции распределения
После образования двойной НЗ дальнейшая эволюция системы в основном определяется излучением ГВ. Это хорошее приближение для достаточно разреженных звездных полей. В случае плотных звездных скоплении следует учитывать процессы динамического взаимодействия. На последних стадиях слияния (последние «3 минуты»), а также в системах типа БК+НЗ необходимо учитывать приливные взаимодействия.
Будем предполагать, что эволюция системы определяется только
одним механизмом, а именно излучением ГВ, которые уносят из системы энергию
и момент импульса. Также предполагаем, что темп рождения таких систем в Галактике постоянен
(разумное предположение для последних нескольких миллиардов лет). При
таких предположениях можно найти стационарную функцию распределения
двойных НЗ по орбитальным параметрам ![]() в Галактике. Для
такой функции
в Галактике. Для
такой функции
![]() . Это выполняется, если
характерное время слияния двойной системы больше характерного
времени изменения параметров начальной функции распределения.
. Это выполняется, если
характерное время слияния двойной системы больше характерного
времени изменения параметров начальной функции распределения.
Вследствие излучения ГВ большая полуось ![]() и эксцентриситет
и эксцентриситет ![]() системы
будут уменьшаться с течением времени (Питерз и Матьюз 1963).
системы
будут уменьшаться с течением времени (Питерз и Матьюз 1963).
На плоскости ![]() система будет эволюционировать, двигаясь по
эволюционному треку (см. рисунок 2.2)
система будет эволюционировать, двигаясь по
эволюционному треку (см. рисунок 2.2)
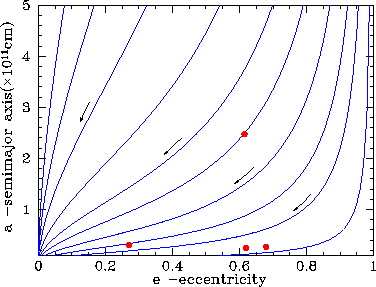 |
| Рис. 2.2
Эволюционные треки двойных систем на фазовой плоскости |
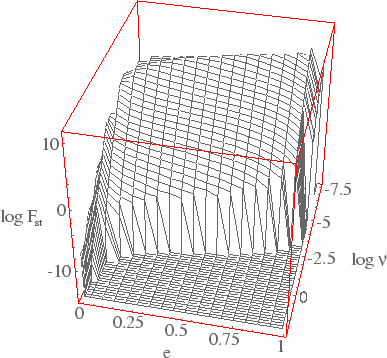 |
| Рис. 2.3 Стационарная функция распределения двойных НЗ на эллиптических орбитах сливающихся под действием излучения ГВ, рассчитанная для начальной функции распределения из рисунка 2.1. |
Тогда, если известна начальная функция распределения, то можно построить
стационарную функцию распределения
(см. Буитраго и др. 1994, Пиерро и Пинто 1996)
2.2.2 Особенности стационарной функции распределения для двойных систем с белым карликом
Подобным образом можно построить стационарную функцию и для других типов компактных систем, зная начальную функцию распределения и предполагая, что эволюция системы происходит только из-за излучения ГВ.
В отличие от двойных НЗ, которые рождаются на орбитах с большим эксцентриситетом,
двойные БК рождаются на круговых орбитах. Это значительно упрощает расчет
стационарной функции распределения, поскольку в этом случае имеется
лишь одна независимая переменная ![]() .
Тогда
.
Тогда
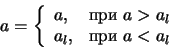
так как при
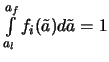 вследствие
выбранной нормировки.
В случае круговых орбит можно построить стационарную функцию распределения
двойных компактных звезд в области
вследствие
выбранной нормировки.
В случае круговых орбит можно построить стационарную функцию распределения
двойных компактных звезд в области Для систем, хотя бы одна из компонент которых белый карлик, появляется еще одно ограничение, связанное с тем, что в некоторый момент сближения основным процессом, определяющим эволюцию системы, становятся приливные взаимодействия.
Оценим эту границу следующим образом. Будем считать, что этот эффект
становится важен, когда белый карлик близок к заполнению своей полости Роша,
т.е. полость Роша для белого карлика в периастре будет порядка 3 - 5
радиусов звезды.
где
где
Таким образом, из условия (2.7) мы получаем условие на минимальное
значение большой полуоси, как функцию эксцентриситета и массы белого
карлика.
<< 1. Введение | Оглавление | 3. ГВ от компактных >>