Астронет > Механика сплошных сред

Астронет: В. А. Алешкевич, Л. Г. Деденко, В. А. Караваев, Научная Сеть/Физический факультет МГУ Механика сплошных сред
http://variable-stars.ru/db/msg/1173645/lect4-3.html

Механика сплошных сред

О турбулентности атмосферы.

При описании атмосферы мы отмечали, что в нижнем (приземном) слое происходит интенсивное конвективное перемешивание воздуха. Скорость воздушных потоков в каждой точке является случайной функцией времени. Это подтверждается, например, оптическим явлением мерцания звезд, свет от которых рассеивается на случайных областях с повышенной и пониженной плотностью атмосферы. Это явление аналогично дрожанию и искажению объектов, наблюдаемых через пространство с с сильным испарением воды после дождя в теплую погоду или бензина на автозаправочных станциях. Вариации скорости в потоках атмосферы также являются турбулентными, поэтому описание движения атмосферы требует статистического подхода. Осуществить в полном объеме такое описание невозможно. Очень плодотворным является представление турбулентных потоков в виде совокупности вихрей от величины $\ell_0\sim 1$ мм до величины L₀~1 м. Эти величины носят название внутреннего и внешнего масштабов турбулентности, причем оба масштаба возрастают при удалении от поверхности Земли. Внутренний масштаб возникает как результат последовательного распада больших, но неустойчивых вихрей на более мелкие, которые, в свою очередь распадаются дольше вплоть до вихрей размером порядка нескольких миллиметров. Оценку величины внутреннего масштаба можно получить из следующих простых соображений. Если в потоке, движущемся со скоростью v имеется неоднородность с линейным размером $\sim\ell$ , то кинетическая энергия переносимая неоднородностью

$E_k=\frac{mv^2}{2}\sim \rho\ell^3 v^2.$

(4.29)

Из-за наличия вязкости часть этой энергии диссипирует в тепло. Если неоднородность смещается на расстояние $\sim\ell$ , то количество тепла Q равно работе сил вязкого трения

$Q=F_{тр}\cdot \ell \sim \mu \frac{ v}{\ell}S\ell\sim \mu v \ell^2.$

(4.30)

Здесь учтено, что $\frac{dv}{d\ell}\sim \frac{v}{\ell};\; S\sim \ell^2$ - площадь поверхности неоднородности, к которой приложена сила вязкости. Отношение кинетической энергии к количеству теплоты приблизительно равно числу Рейнольдса:

$\frac{E_k}{Q}\cong \frac{\rho v\ell}{\mu}= {\rm Re}.$

(4.31)

Если E_k>Q (Re>1), то силы инерции превосходят силы вязкости. В таком интервале скоростей, называемым инерционным интервалом, вихри распадаются на более мелкие, у которых число Рейнольдса Re~1. При скоростях течения v~1 см/с такому числу Рейнольдса соответствует $\ell$ ~1 мм, что по порядку величины совпадает со внутренним масштабом турбулентности.

Рис. 4.15.

Исходя из такого представления, А.Н. Колмогоров рассмотрел изменение во времени разности скоростей в двух точках пространства, разнесенных на расстояние $\ell$ (рис. 4.15). Он установил, что средний квадрат разности скоростей $\left\lt [ v(r+\ell) -v(r)]^2 \right\gt$ можно описать универсальной зависимостью в инерционном интервале $\ell_0 < |\ell|< L_0$ . Для компонент вектора скорости, направленных вдоль $\ell$

$D_{\ell\ell}= \left\lt [ v_{\ell}(r+\ell) -v_{\ell}(r)]^2 \right\gt= C_v^2 \ell^{2/3}.$

(4.32)

Функция $D_{\ell\ell}$ называется структурной функцией пульсаций скорости и описывается универсальной зависимостью $\ell^{2/3}$ . Она не зависит от r вследствие статистической однородности пульсаций скорости, и не зависит от направления разноса точек, а только от величины $\ell$ . Последнее является результатом статистической изотропности турбулентности. Структурная функция для поперечных компонент v_t $D_{tt}= \left\lt [ v_{t}(r+\ell) -v_{t}(r)]^2 \right\gt$ с учетом несжимаемости атмосферы (div v=0) выражается через $D_{\ell\ell}$ следующим образом:

$D_{tt}=\frac{1}{2\ell}\frac{d}{d\ell}\left( \ell^2 D_{\ell\ell} \right).$

(4.33)

C_v² называется структурная постоянная скорости и характеризует общее количество энергии турбулентности. Структурная функция скоростей $D_{\ell\ell}$ позволяет рассчитать структурную функцию флуктуаций температуры, подчиняющейся также закону "2/3":

$D_{TT}=\left\lt [ T(r+\ell) -T(r)]^2 \right\gt=C^2_T\ell^{2/3}.$

(4.34)

Вывод этой формулы может быть выполнен на основе усреднения решений уравнений гидродинамики и теплопереноса при учете (4.32), что выходит за рамки нашего курса. Структурная постоянная температуры C_T² может быть рассчитана, если измерить микропульсации температуры с помощью чувствительных, разнесенных на расстояние $\ell$ , датчиков и усреднить результаты за длительный (порядка 1 часа) отрезок времени. Такие датчики устанавливаются на мачтах, шарах-зондах и самолетах. В настоящее время широкое применение получили методы акустической локации, позволяющие изучать высотную зависимость C_T² вплоть до высот ~1 км. Эти методы основаны на том, что участки атмосферы с интенсивными флуктуациями температуры (и, следовательно, плотности) сильнее отражают акустические импульсы, чем участки со слабыми температурными флуктуациями. Высотная зависимость C_T², полученная акустическим методом, изображена на рис. 4.16. Хотя флуктуации температуры составляют сотые (и даже меньше) доли градуса, тем не менее они приводят к флуктуациям показателя преломления n. Структурная функция n получается из материального уравнения n=n(p, T) (p и T - равновесные значения давления и температуры) и также подчиняется универсальному закону "2/3":

$D_{nn}=\left\lt [ n(r+\ell) -n(r)]^2 \right\gt=C^2_n\ell^{2/3}.$

(4.35)

Величина C_n² называется структурной постоянной показателя преломления и лежит в пределах 10^-15м^-2/3<C_n²<10^-14 м^-2/3. Она легко подсчитывается из уравнения n=n(p, T), если известна C_T².

Рис. 4.16.

Формула (4.35) играет фундаментальную роль в задачах распространения световых волн через атмосферу, выделенных в самостоятельную науку - атмосферную оптику. На рис. 4.17 (а) приведены результаты компьютерного моделирования мгновенного изображения здания Московского университета, рассматриваемого через турбулентную атмосферу в подзорную трубу с расстояния в несколько километров. С течением времени это изображение, разумеется, будет хаотически меняться. Однако при известном распределении флуктуаций показателя преломления с помощью компьютерных методов обработки изображений можно устранить турбулентные искажения (рис. 4.17 б).

Рис. 4.17.

Взаимодействие тела с потоком идеальной жидкости.

Одной из важнейших проблем гидро и аэродинамики является всестороннее исследование и установление основных закономерностей воздействия потоков жидкости и газа на обтекаемые ими тела. Эта область знаний приобрела исключительное значение при проектировании гидроэлектростанций, ветряных двигателей, в турбиностроении, развитии авиации и др. Еще И. Ньютоном была сформулирована ударная теория, базирующаяся на представлении воздуха в виде отдельных не связанных друг с другом материальных частиц. 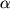Согласно его теории сила давления воздушного потока на площадку S, подставленную под углом $\alpha$ (углом атаки) к направлению потока равна

$F=\rho S v^2 \sin^2 \alpha.$

(4.36)

Эта формула легко получается, если посчитать импульс, передаваемый площадке в единицу времени неупруго взаимодействующей с ней струей (рис. 4.18). Опытная проверка этой формулы показала, что она неверно описывает зависимость силы F от угла атаки. (И только при скоростях потока, значительно больших скорости звука в этой жидкости, формула Ньютона оказывается справедливой, что подтверждается опытным путем). На самом деле величина этой силы пропорциональна $\sin\alpha$ . Если бы формула (4.36) была бы верна, то это означало бы невозможность полетов на аппаратах тяжелее воздуха. Все это говорит о том, что модель жидкости как совокупности дискретных частиц является неверной. Реальные же силы могут быть посчитаны на основе гидродинамического подхода, учитывающего обтекание тела движущимся потоком континуальной среды.

Рис. 4.18.

Проиллюстрируем сказанное на простейшем примере. Пусть в движущемся со скоростью v₀ потоке помещены диск и шар одинакового радиуса r (рис. 4.19).

Рис. 4.19.

В центре диска в точке K, называемой критической, поток останавливается (v=0), и давление, согласно уравнению Бернулли

$p_k=p_0+\frac{\rho v_0^2 }{2}.$

(4.37)

Это давление больше статического давления в потоке p₀ на величину $\frac{\rho v_0^2}{2}$ , получившую ранее название динамического давления, или динамического напора. Из-за поворота трубок тока на 90 $^\circ$ давление в других точках на поверхности диска будет таким же, как и в точке К. Поэтому, если позади диска давление равно p₀, то поток действует на диск с силой

$F_\parallel = (p_k-p_0) \pi r^2 =\frac{1}{2} \rho v_0^2 S.$

(4.38)

Гидродинамическая сила $F_\parallel$ , которая может трактоваться как сила лобового сопротивления при движении диска со скоростью v₀ в жидкости, и вдвое меньше силы, вычисляемой на основе ударной теории (см. (4.36) при $\sin\alpha$ ). Если теперь в поток поместить шар, то по ударной теории на него будет действовать та же сила, что и на диск. При гидродинамическом подходе эта сила будет отсутствовать вовсе. Действительно, при симметричном потоке относительно сечения О₁О₂ давление в произвольной т.М и симметричной т.M' будут одинаковы, поскольку одинаковы скорости потока в этих точках. Равенство нулю результирующей силы при плавном (безотрывном) обтекании идеальной жидкостью шара, цилиндра и др. Называется парадоксом Даламбера. Давление в любой точке потока вблизи поверхности шара можно рассчитать, пользуясь уравнением Бернулли:

$p=p_0 + \frac{\rho v_0^2 }{2} - \frac{\rho v^2 }{2}.$

(4.39)

На рис. 4.20 изображено распределение избыточных сил давления $\sigma_p=p-p_0$ , действующих нормально на единицу площади поверхности шара. При этом сила направлена к поверхности, если p>p₀, и от поверхности при p<p₀. Отсутствие силы в т.А и т.A' есть результат равенства скоростей в этих точках исходной скорости потока: v_A=v'_A=v₀.

Рис. 4.20.

Назад | Вперед