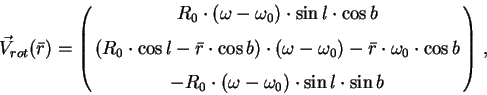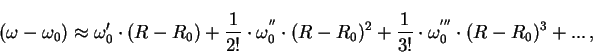 |
Астронет: А. С. Расторгуев/ГАИШ Определение кривой вращения и шкалы расстояний в Галактике http://variable-stars.ru/db/msg/1172553/node5.html |
<< 3. Системы координат | Оглавление | 5. Основные формулы метода >>
4. Кинематическая модель: движение Солнца, дифференциальное вращение
выборки и "космическая" дисперсия
Рассмотрим простейшую кинематическую модель подсистемы,
включающую три компонента: локальное движение выборки относительно
Солнца, глобальное систематическое движение в форме
дифференциального вращения и случайное движение, описываемое
трехосным эллипсоидальным распределением остаточных скоростей
(Шварцшильдовским). Рассеяние остаточных скоростей относительно
центроида часто называют "космической" дисперсией, подчеркивая их
отличие от влияния ошибок наблюдений (см. далее). Для простоты
будем считать дифференциальное вращение баротропным,
т.е. не зависящим от 
- координаты (хотя в принципе легко
обобщить модель на случай зависимости угловой скорости не только
от 
, но и от ). Такая модель хорошо представляет кинематику
большинства плоских галактических подсистем. Модель может быть
усложнена путем введения некруговых движений, вызванных, например,
возмущающим влиянием спиральных рукавов [12]. Оно
особенно существенно для подсистем с малой дисперсией скоростей,
т.е. молодых объектов - классических цефеид, рассеянных
скоплений, ОВ-ассоциаций и ОВ-звезд. Так, наблюдения газовых
дисков других спиральных галактиках показывают, что величина
возмущений скорости может достигать 20 - 30 км/с, что заметно
больше "космической" дисперсии скоростей газа. Модель некруговых
движений сложна, она зависит от способа описания волны плотности,
и требует отдельного обсуждения. Что касается эллипсоида
скоростей, условимся для простоты считать его форму и размеры его
осей одинаковыми во всей изучаемой области Галактики, хотя, как
показывают внегалактические наблюдения, дисперсии скоростей в
дисках спиральных галактик убывают по мере удаления от центра
галактик и уменьшения поверхностной плотности диска.
На рисунке
- спроектированное на
плоскость Галактики среднее (т.е. уточненное) расстояние до
центроида 
, 
и 
- соответственно лучевая скорость и
тангенциальная скорость по галактической долготе (вектор
тангенциальной скорости по галактической широте, разумеется, не
показан). Будем выражать собственные движения в "/год, линейные
(в том числе лучевые) скорости в км/с, расстояния в кпк, а
угловые скорости в единицах км/с/кпк. Для удобства введем
коэффициент
(км/с/кпк)("/год)
,
переводящий расстояния и собственные движения в линейные
скорости, например, в формуле
, где
- компонент тангенциальной скорости (по галактической
долготе или широте).
Обозначим местный (околосолнечный) центроид объектов как 
.
Пусть при этом скорость местной выборки относительно Солнца равна
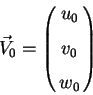
, где компоненты скорости записаны в галактической прямоугольной системе координат (ось
которой направлена в центр Галактики,
ось 
- в сторону галактического вращения, - к северному
полюсу Галактики). Рассматривая треугольник и применив к
расстояниям теорему косинусов, легко вычислим расстояние
центроида от оси вращения Галактики по гелиоцентрическому
расстоянию 
и его галактическим координатам по формуле
Проще всего рассматривать распределение скоростей объектов в локальной системе координат, привязанной к направлению на объект и галактическим координатам
; в этой системе координат
компоненты скорости нам либо известны из измерений (лучевая
скорость), либо могут быть легко вычислены по расстоянию и
компонентам собственного движения (тангенциальные скорости по
галактической долготе и широте). Поскольку тангенциальные
скорости вычисляются через принятое расстояние 
, вектор
наблюдаемой скорости в этой системе координат можно записать в
виде
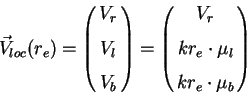
Легко показать, что вклад дифференциального вращения Галактики в наблюдаемую скорость описывается формулами Боттлингера [1], которые могут быть переписаны с использованием среднего расстояния
в локальной системе
координат в векторном виде
где
и
- угловые
скорости исследуемого центроида на расстоянии и на расстоянии
Солнца 
соответственно. Для решения обычно разлагают разность
угловых скоростей в ряд Тейлора
ограничиваясь, как правило, вторым или третьим порядком. Такое разложение дает хорошие результаты даже для расстояний 5 - 6 кпк от Солнца. Наконец, обозначим через
истинную
остаточную скорость звезды относительно центроида ,
обусловленную "космической" дисперсией.
<< 3. Системы координат | Оглавление | 5. Основные формулы метода >>