Астронет > Вакуумный конденсат

Астронет: "Физическая Энциклопедия"/Phys.Web.Ru Вакуумный конденсат
http://variable-stars.ru/db/msg/1172514

Вакуумный конденсат
11.10.2001 0:00 | "Физическая Энциклопедия"/Phys.Web.Ru

Ненулевое вакуумное среднее какого-либо локального оператора поля. Представление о вакуумном конденсате - одно из центральных в современных теориях электрослабого взаимодействия и сильного взаимодействия - квантовой хромодинамике (КХД). Употребление слова "конденсат" связано с картиной, согласно которой вакуумное, или низшее по энергии, состояние следует представлять не в виде "пустого" пространства, а как своеобразную среду флуктуирующих с большой амплитудой полей. Часто обсуждают, например, такие отличные от нуля вакуумные средние:

$\lt 0 \mid \varphi\mid 0\gt$ , $\lt 0 \mid\bar{u} u \mid 0 \gt$ , $\lt 0 \mid\bar{d} d \mid 0 \gt$ , $\lt 0 \mid G_{\mu\nu}^{a} G_{\mu\nu}^{a}\mid 0 \gt$ , (1)

где $\varphi$ - скалярное поле (Хиггса поле), u и d - поля u и d-кварков (черта над u, d означает дираковское сопряжение; см. Дирака поле), $G_{\mu\nu}^{a}$ - тензор напряженности калибровочного векторного глюонного поля в КХД ( $\mu, \nu$ =0, 1, 2, 3 - лоренцовы индексы, a = 1, ..., 8 - цветовой индекс; по дважды встречающимся индексам производится суммирование). Соответственно говорят о вакуумном конденсате скалярного поля, кварковом и глюонном вакуумном конденсате. Первый обсуждается в теории электрослабого взаимодействия, последние - в КХД.

С теоретической точки зрения особый интерес представляет случай спонтанного нарушения симметрии, когда симметрия вакуумного конденсата ниже, чем симметрия исходного лагранжиана. В этом случае спектр наблюдаемых частиц не обладает полной симметрией исходного лагранжиана. Например, лагранжиан электрослабого взаимодействия обладает симметрией относительно поворотов в изотопическом пространстве. Волновые функции фотона и промежуточного векторного бозона переходят друг в друга при таких поворотах. Однако массы этих частиц сильно различаются. Причиной служит отличное от нуля вакуумное среднее хиггсовского поля, которое и выделяет определенное направление в изотопическом пространстве. Ввиду того что поля описываются размерными величинами, вакуумные конденсаты вносят определенные массовые масштабы. Симметрия исходного лагранжиана восстанавливается в наблюдаемых амплитудах процессов только при энергиях (точнее, переданных 4-импульсах), много больших этого масштаба.

Феноменологические следствия из существования вакуумных конденсатов наиболее подробно изучены в КХД. В пределе нулевых масс u- и d-кварков исходный лагранжиан в КХД инвариантен относительно изотопических вращений с изменением четности:

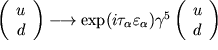$\left( \begin{array}{c}u \\ d \end{array} \right) \longrightarrow\exp(i\tau_\alpha\varepsilon_\alpha) \gamma^{5} \left( \begin{array}{c}u \\ d \end{array}\right)$ (2)

где $\tau_\alpha$ - Паули матрицы, действующие в изотопическом пространстве u- d-кварков, $\varepsilon_\alpha$ - параметры поворота ( $\alpha$ =-1, 2, 3), $\gamma^{5}$ - Дирака матрица в спиновом пространстве. Однако экспериментально вырождения по четности масс низших, невозбужденных резонансов (в которых составляющие кварки находятся в S-состоянии) не наблюдается. Причина этого - существование кваркового вакуумного конденсата, $\lt\ 0 \mid\bar{u} u + \bar{d} d\mid 0 \gt \neq 0$ , который не инвариантен относительно вращений (2). Один из результатов такого ле равных нулю масс кварков. Поэтому свойства пиона связаны нарушения симметрии - появление $\pi$ - мезона, масса которого исчезает в пределе равных нулю масс кварков. Поэтому свойства пиона связаны со свойствами вакуумного конденсата. В частности,

$(m_u+m_d)\lt 0 \mid \bar{u} u + \bar{d} d \mid 0 \gt = -m_\pi^{2} f_\pi ^{2}$ (3)

где $f_\pi$ - константа $\pi \longrightarrow \mu\nu_\mu$ -распада, определяющая вероятность (ширину $\Gamma$ ) распада:

$\Gamma(\pi\longrightarrow\mu\nu_\mu)={\displaystyle {1} \over \displaystyle {8\pi}} {G}_F^{2}\cos^2\vartheta_C{f}_\pi^{2}m_\mu^{2}m_\pi \left[ 1- {\displaystyle {m_\mu^{2}} \over \displaystyle{m_\pi^{2}}} \right]^2$ (4)

$f\pi\approx$ 93 МэВ), m_u, m_d - массы u- и d-кварков, $m_\pi$ - масса пиона, $m_\mu$ - масса мюона, G_F - фермиевская константа слабого взаимодействия, $\vartheta_C$ - Кабиббо угол.

Хотя представление о вакуумном конденсате стало неотъемлемой частью современной теории, существуют основания полагать, что включение в рассмотрение гравитации приводит к серьезной проблеме. Согласно принципу эквивалентности, энергия вакуума гравитирует и входит поэтому в уравнения общей теории относительности. Ограничение же на плотность энергии вакуума, которое получается из опыта, оказывается на много порядков (примерно в 10⁴⁶ раз) меньше энергии, связанной, например, с глюонным конденсатом. Механизм уменьшения плотности энергии вакуума неизвестен.

Глоссарий Astronet.ru