Astronet Астронет: А. Н. Петров/ГАИШ Законы сохранения в ОТО и их приложения
http://www.astronet.ru/db/msg/1170672/node15.html
<< 3.2 Конформные векторы Киллинга для ... | Оглавление | 3.4 Новые интегральные соотношения >>

Разделы

3.3 Законы сохранения и интегральные величины для возмущенной фридмановской модели

Квази-локальные, или глобально сохраняющиеся величины весьма интересны в космологии, и обычно расчитываются внутри сферы на сечениях постоянного времени $\eta $. Чтобы их получить обычно используется дифференциальный закон сохранения типа (2.24) в лекции 2: $\hat {\cal I}^\mu=\partial_\nu\hat{\cal I}^{\mu\nu}$, который здесь (в линейном приближении по возмущениям) мы используем, точнее, его нулевую компоненту:

\begin{displaymath} \hat {\cal I}^0=\partial_l\hat{\cal I}^{0l}. \end{displaymath} (3.16)

3.3.1 Возмущенное фридмановское решение и линейные приближения

Обозначим возмущенную метрику (3.1) как это более принято $g_{\mu\nu}=a^2(e_{\mu\nu}+{\tilde h}_{\mu\nu})$. Таким образом имеем

\begin{displaymath} ds^2= a^2(e_{\mu\nu}+{\tilde h}_{\mu\nu})dx^\mu dx^\nu. \end{displaymath} (3.17)

Кроме того, мы используем 3-мерные компоненты: ${\tilde h}_{00}, {\tilde h}_{0l}, {\tilde h}_{kl}$, индексы которых поднимаются и опускаются с помощью fkl:
\begin{displaymath} {\tilde h}^m_l=f^{mk}{\tilde h}_{kl},   {\tilde h}^{mn}=f^{mk}f^{nl}{\tilde h}_{kl},    {\tilde h}^m_0=f^{ml}{\tilde h}_{0l}. \end{displaymath} (3.18)

В модели, развитой в лекции 2 используются возмущения $\hat l^{\mu\nu} = \hat g^{\mu\nu} -\bar {\hat g^{\mu\nu}}$. Как было отмечено, преимущество этого в том, что модель, в принципе, может быть легко просчитана до любого порядка по возмущениям, поскольку в терминах $\hat l^{\mu\nu}$ мы представляем точные уравнения и точный, хотя и в линейной форме суперпотенциал. Здесь мы ограничиваемся лишь линейными приближениями и используем более популярную форму возмущений ${\tilde h}_{\mu\nu}$. Поэтому здесь формулы лекции 2 мы пересчитываем в терминах ${\tilde h}_{\mu\nu}$ с помощью справедливого в линейном приближении соотношения
   
  $\displaystyle \hat l^{\mu\nu}=a^2\sqrt{-\bar g}(-\bar g^{\mu\rho}\bar g^{\nu\si... ...}+{{\textstyle{\frac{1}{2}}}}e^{\mu\nu}e^{\rho\sigma}) {\tilde h}_{\rho\sigma}.$  

Определим 3-тензоры:

\begin{displaymath} q^m_l = {\tilde h}^m_l-\delta^m_l{\tilde h}^n_n,    Q^m_l =... ..._{0n})\delta^m_l+\nabla^m {\tilde h}_{0l}- \partial_0 {q^m_l}. \end{displaymath} (3.19)

Кроме того, символом $\cal Q$ обозначим возмущенный след внешней кривизны гиперповерхности $\eta=const$. Если $n^\mu$ является единичным вектором нормали к этой гиперповерхности, то
\begin{displaymath} {\cal Q}\equiv-D_\mu n^\mu-(-\overline{D_\mu n^\mu}) = {\tex... ...}{2}}}}\partial_0 {{\tilde h}}^{n}_n- \nabla_n {\tilde h}_0^n. \end{displaymath} (3.20)

Тогда для конформных киллинговых векторов, удовлетворяющих (3.8), расчет по формуле (24) лекции 2: $\hat {\cal I}^{\mu} = \hat {\cal T}^\mu_\nu\xi^\nu + \hat {\cal Z}^\mu$ с


$\hat {\cal T}^{\mu\nu} = (\hat T^{(\mu}_\rho\overline g^{\nu)\rho} -\overline {... ...rline g^{\mu\nu} + {1\over \kappa} {\hat l}^{\lambda[\mu} \bar R^{\nu]}_\lambda$


и


$2\kappa \hat {\cal Z}^\mu = 2\left(\bar z^{\rho\sigma}\overline D_\rho \hat l^... ...l^{\mu\nu}\overline D_\nu \bar z - \bar z\overline D_\nu \hat l^{\mu\nu}\right)$,


(где $\bar z_{\rho\sigma} = \overline D_{(\rho} \xi_{\sigma)}$), и с использованием обозначения (3.20) дает:

\begin{displaymath} \kappa\hat{\cal I}^0 = \kappa a^4\sqrt{f}\delta T^0_\mu \xi^... ...n_n+\nabla_n(\textstyle{1\over 4}\bar z{\tilde h}^n_0)\right], \end{displaymath} (3.21)

где $\textstyle{1\over 4}\bar z=\dot a \xi^0+{\textstyle{1\over 3}}\nabla_k\xi^k$, $\bar y= \nabla^2 {\xi^0}+3k \xi^0$ и $\nabla^2=f^{kl}\nabla_k\nabla_l$.

Расчет по формуле (26) лекции 2:

   
  $\displaystyle \hat {\cal I}^{\mu\nu} ={1 \over \kappa} \hat l^{\rho[\mu}\overline D_\rho\xi^{\nu]} + \hat {\cal P}^{\mu\nu}{_\lambda} \xi^\lambda,$  

где
   
  $\displaystyle \hat {\cal P}^{\mu\nu\rho} = {1 \over 2\kappa} \overline D_\sigma... ...\bar g^{\sigma\mu} \hat l^{\nu\rho}+\bar g^{\sigma\nu} \hat l^{\mu\rho}\right),$  

и с использованием обозначений (3.19), дает:
\begin{displaymath} \kappa\hat{\cal I}^{0l}= {\textstyle{1 \over 2}} a^2 \sqrt{f... ...{\xi^0}+Q^l_k\xi^k+ {\tilde h}_{0k}\nabla^{[k}\xi^{l]}\right]. \end{displaymath} (3.22)

3.3.2 Интегральные величины и их связи

Теперь мы имеем все необходимое, чтобы проинтегрировать уравнение (3.16) по сферическому объему V с границей S в фиксированное время $\eta $. Определим

\begin{displaymath} F({\bf\xi}) \equiv \int_V \hat {\cal I}^0 d^3x = \oint_S \hat {\cal I}^{0l}{\textstyle{\frac{1}{2}}}\epsilon_{lmn}dx^mdx^n. \end{displaymath} (3.23)

Если этот интеграл (проще анализировать поверхностный интеграл, который зависит только от возмущений метрики) не зависит от $\eta $, то F является интегралом движения. Фактически мы имеем 15 величин F, по одному на каждый конформный вектор Киллинга ${\bf\xi}_A (A=1,2,...,15)$. Можно составить линейные комбинации из F с временизависимыми коэффициентами, скажем $c^A(\eta)F(\xi_A)$. Поскольку выражения и (3.21), и (3.22) линейно зависят от $\xi^\mu$ и только их пространственных производных, то $c^AF(\xi_A)=F(c^A\xi_A)$. Вообще говоря, $c^A\xi_A$ c $c^A = c^A(\eta)$ уже не являются конформными векторами Киллинга, но как мы сейчас увидим некоторые такие комбинации оказываются крайне простыми и имеют физическую интерпретацию в подходящей каллибровке. Давайте представим эти удобные комбинации.

Семь из определенных выше конформных киллинговых векторов мы оставляем без изменения, их компоненты определяются как

\begin{displaymath} {\bf t} =(1,0),    {\bf s}_a =(0, \delta^k_a r'),     {\bf r}_a = (0, \epsilon_{kal}x^l), \end{displaymath} (3.24)

где $r=\sin \chi, \chi$ или $\sinh \chi $ в зависимости от k=1,  0 или -1; и r' -- производная по $\chi$. Следующие 8 линейных комбинаций, обозначенные векторами с крестами, составлены с помощью временизависимых коэффициентов. В этих формулах используются обозначения $\alpha = \sin \eta$ для k = 1 (или $\sinh \eta$ для k= -1); где $\alpha'$ есть производная $\alpha$ по $\eta $. Следующие 4 вектора не имеют пространственных компонент:


$\displaystyle {\bf l}^\dagger_a$ = $\displaystyle \left.\left( \alpha'{\bf l}_a- \alpha {\bf b}_a\right)\right\vert... ...1} = \left.\left({\bf l}_a - \eta {\bf s}_a\right)\right\vert _{k=0}= (x^a, 0),$  
$\displaystyle \left.{\bf a}^\dagger\right\vert _{k=\pm 1}$ = $\displaystyle \left.\left( \alpha'{\bf a}+ k\alpha{\bf d}\right)\right\vert _{k = \pm 1}= (r',0),$  
$\displaystyle \left.{\bf a}^\dagger\right\vert _{k=0}$ = $\displaystyle \left.\left({\textstyle{\frac{1}{2}}} {\bf a}- \eta{\bf d}+{\text... ...{2}}} \eta^2{\bf t}\right)\right\vert _{k=0}=({\textstyle{\frac{1}{2}}} r^2,0).$ (3.25)

Оставшиеся 4 комбинации не имеют временных компонент и представляют конформные киллинговы векторы на сечениях: $\eta={\rm const}$:
$\displaystyle {\bf d}^\dagger$ = $\displaystyle \left.\left(\alpha'{\bf d} - \alpha{\bf a}\right)\right\vert _{k=\pm 1}= \left.\left({\bf d}-\eta{\bf t}\right)\right\vert _{k=0}=(0,x^k r'),$  
$\displaystyle \left.{\bf b}^\dagger_{a}\right\vert _{k=\pm 1}$ = $\displaystyle \left.\left( \alpha' {\bf b}_a+ k\alpha{\bf l}_a\right)\right\vert _{k = \pm1}= (0, f^{ak}),$  
$\displaystyle \left.{\bf b}^\dagger_{a}\right\vert _{k=0}$ = $\displaystyle \left.\left(-{\textstyle{\frac{1}{2}}}{\bf b}_a+\eta{\bf l}_a- {\... ...ight)\right\vert _{k=0} =(0, \delta^{ak} {\textstyle{\frac{1}{2}}} r^2-x^ax^k).$ (3.26)

Как видно, комбинации подобраны так, что все компоненты всех векторов не зависят от времени.

Подставляя в (3.21) и (3.22) векторы с компонентами (3.24), (3.25) и (3.26), получим интегральные соотношения (3.23), соответствующие каждой группе векторов (3.24) - (3.26). В качестве элементов интегрирования следует считать $dV=a^3\sqrt{f}d^3x$ и $dS_l= a^2\sqrt{f}{\textstyle{\frac{1}{2}}} \epsilon_{lmn}dx^m dx^n$, используется также обычное определение постоянной Хаббла: $H=\dot a/a$. Таким образом для векторов (3.24) имеем

$\displaystyle \kappa F({\bf t})$ - $\displaystyle aH\oint_S{\tilde h}_0^l dS_l = \int_V [(a\kappa\delta T^0_0+2H{\c... ...over a}{\tilde h}^m_m]dV =-{\textstyle{\frac{1}{2}}}\oint_S \nabla_kq^{kl}dS_l,$  
$\displaystyle \kappa F({\bf s}_a)$ = $\displaystyle \int_V a\kappa\delta T^0_a r'dV =\oint_S ({\textstyle{\frac{1}{2}}} Q^l{_k}s^k_a- k{\tilde h}_{0k}x^{[k}s_a^{l]})dS_l,$  
$\displaystyle \kappa F({\bf r}_a)$ = $\displaystyle \int_V a\kappa\delta T^0_k\epsilon_{kal}x^ldV =\oint_S ({\textsty... ...k}x^{[k}r_a^{l]}+ {\textstyle{\frac{1}{2}}} {\tilde h}_{0k}\epsilon_{kal})dS_l.$ (3.27)

Соответственно для (3.25):
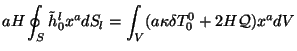
$\displaystyle \kappa F({\bf l}^\dagger_a)$ - $\displaystyle aH \oint_S {\tilde h}_0^l x^a dS_l = \int_V (a\kappa\delta T^0_0+2H{\cal Q})x^adV$  
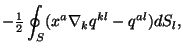
  = $\displaystyle - {\textstyle{\frac{1}{2}}}\oint_S (x^a\nabla_k q^{kl}-q^{al})dS_l,$  
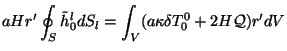
$\displaystyle \left.\kappa F({\bf a}^\dagger)\right\vert _{k=\pm 1}$ - $\displaystyle aHr'\oint_S{\tilde h}_0^l dS_l = \int_V (a\kappa \delta T^0_0+2H {\cal Q})r'dV$  
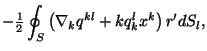
  = $\displaystyle - {\textstyle{\frac{1}{2}}} \oint_S \left( \nabla_k q^{kl} + k q^l_kx^k\right) r'dS_l,$  
$\displaystyle \left.\kappa F({\bf a}^\dagger)\right\vert _{k=0}$ - $\displaystyle {\textstyle{\frac{1}{2}}} aH\oint_S {\tilde h}_0^lr^2 dS_l = \int... ...le{\frac{1}{2}}} a\kappa \delta T^0_0+H{\cal Q})r^2-{1\over a}{\tilde h}^m_m]dV$  
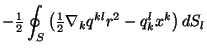
  = $\displaystyle -{\textstyle{\frac{1}{2}}} \oint_S \left( {\textstyle{\frac{1}{2}}} \nabla_k q^{kl} r^2 - q^l_k x^k\right)dS_l$ (3.28)

и для (3.26):
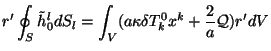
$\displaystyle \kappa F({\bf d}^\dagger)$ - $\displaystyle r'\oint_S{\tilde h}_0^l dS_l = \int_V (a\kappa \delta T^0_k x^k+{2\over a}{\cal Q}) r'dV$  
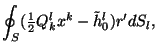
  = $\displaystyle \oint_S ({\textstyle{\frac{1}{2}}} Q^l_k x^k-{\tilde h}^l_0)r'dS_l,$  
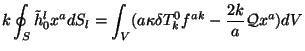
$\displaystyle \left.\kappa F({\bf b}^\dagger_a)\right\vert _{k=\pm 1}$ + $\displaystyle k\oint_S {\tilde h}_0^l x^a dS_l = \int_V (a\kappa \delta T^0_kf^{ak}-{2k\over a}{\cal Q}x^a)dV$  
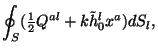
  = $\displaystyle \oint_S ({\textstyle{\frac{1}{2}}} Q^{al}+k{\tilde h}^l_0 x^a)dS_l,$  
$\displaystyle \left.\kappa F({\bf b}^\dagger_a)\right\vert _{k=0}$ + $\displaystyle \oint_S {\tilde h}_0^l x^a dS_l = \int_V [a\kappa \delta T^0_k(\delta^{ak}{\textstyle{\frac{1}{2}}} r^2-x^ax^k)-{2\over a}{\cal Q}x^a]dV$  
  = $\displaystyle \oint_S [{\textstyle{\frac{1}{2}}} kQ^l_k(\delta^{ak}{\textstyle{... ...}{2}}} r^2-x^ax^k)+{\tilde h}^l_0 x^a +{\tilde h}_{0k}x^{[k}\delta^{l]}_a]dS_l.$ (3.29)

Интегральные величины для настоящих конформных киллинговых векторов фридмановской геометрии легко восстанавливаются из (3.28) и (3.29) с помощью обратных линейных комбинаций с временизависимыми коэффициентами.


<< 3.2 Конформные векторы Киллинга для ... | Оглавление | 3.4 Новые интегральные соотношения >>

Rambler's Top100 Яндекс цитирования