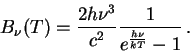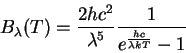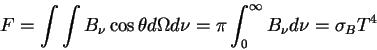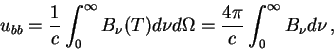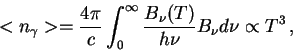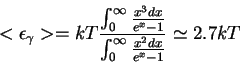|
Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков http://www.astronet.ru/db/msg/1170612/node12.html |
<< 2.2 Уравнение переноса | Оглавление | 2.4 Характеристические темп... >>
2.3 Тепловое излучение
Тепловое излучение порождается веществом, находящимся в тепловом равновесии.
2.3.1 Абсолютно черное тело
Важнейший пример теплового излучения представляет собой
излучения абсолютно черного тела (АЧТ).
Излучение АЧТ находится в полном термодинамическом равновесии.
Напомним кратко сновные свойства излучения АЧТ.
1). Спектр АЧТ (Планковский спектр:
![]() - функция Планка)
зависит только от температуры
- функция Планка)
зависит только от температуры ![]() , поле равновесного излучения
строго изотропно (т.е. полный поток через произвольно
ориентированную площадку строго равен нулю),
неполяризовано.
2). Закон Кирхгофа (справедлив для любого теплового излучения)
, поле равновесного излучения
строго изотропно (т.е. полный поток через произвольно
ориентированную площадку строго равен нулю),
неполяризовано.
2). Закон Кирхгофа (справедлив для любого теплового излучения)
Излучение, для которого функция источника отличается от функции Планка, называется нетепловым (примеры нетеплового излучения - синхротронное излучение релятивистских электронов в магнитном поле, обратное комптоноваское рассеяние, черенковское излучение и т.д.)
Важный вывод, следующий из уравнения переноса: любое тепловое излучение превращается в излучение АЧТ в пределе больших оптических толщин.
2.3.2 Закон Планка для АЧТ
Функция Планка для равновесного излучения
может быть записана в виде удельной интенсивности
в единичном интервале частот ([эрг/см![]() /c/Гц/стер])
/c/Гц/стер])
Чтобы перейти к удельной интенсивности в
единичном интервалу длин волн, воспользуемся законом сохранения
энергии
![]() и связью
и связью ![]() . Находим
. Находим
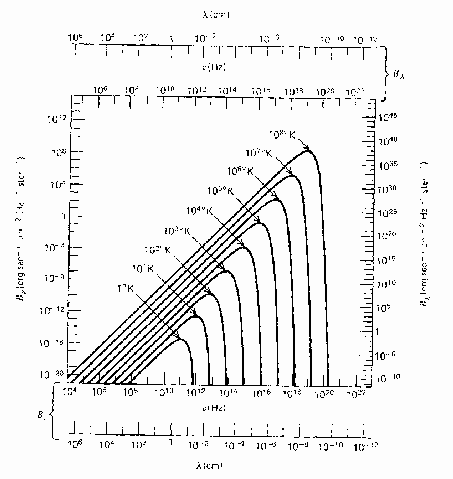
Функция Планка приведена на Рис. (2.4)
2.3.2.1 Предельные случаи и свойства функции Планка
- Закон Рэлея-Джинса,
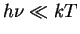 ,
,
Обратим внимание, что в выражение для интенсивности в этом случае не вошла постоянная Планка, т.е. в этом пределе формула описывает чисто классическое излучение. Попытка экстраполировать закон Рэлея-Джинса в область более высоких частот приводит к расходимости,
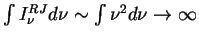 ("ультрафиолетовая катастрофа")
("ультрафиолетовая катастрофа")
- Закон Вина,
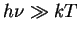
- Монотонное изменение с температурой:
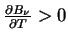 на всех
на всех 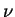 . Это означает, что кривые функции
Планка для разных температур нигде не пересекаются друг с другом,
поанковская кривая с температурой
. Это означает, что кривые функции
Планка для разных температур нигде не пересекаются друг с другом,
поанковская кривая с температурой 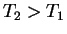 целиком лежит выше кривой
с температурой
целиком лежит выше кривой
с температурой 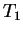 .
.
- Закон смещения Вина
Определим максимум в спектре АЧТ. Начнем с удельной интенсивности на единичный интервал частот
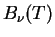 .
.
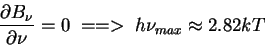
Максимум функции
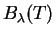 :
:
Подчеркнем, что
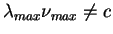 !!!
!!!
- Закон Стефана-Больцмана
Полный поток энергии с площадки, излучающей как АЧТ, пропорционален четвертой степени температуры.
где
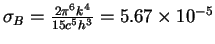 эрг/см
эрг/см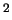 /c/град -
постоянная Стефана-Больцмана.
/c/град -
постоянная Стефана-Больцмана.
- Плотность энергии и давление равновесного излучения
Плотность энергии АЧТ
или пользуясь результатом (2.31)
где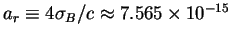 [эрг/см
[эрг/см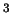 /град
/град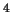 ] - постоянная плотности излучения. Давление
равновесного излучения
(2.10) при этом равно
] - постоянная плотности излучения. Давление
равновесного излучения
(2.10) при этом равно
- Средняя энергия чернотельного фотона
По определению, это величина
Делая замену переменных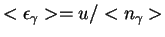 , где
, где
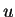 - плотность энергии,
- плотность энергии, 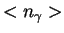 - плотность числа квантов.
Для АЧТ плотность энергии есть (2.32),
- плотность числа квантов.
Для АЧТ плотность энергии есть (2.32),
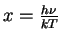 в интегралах приходим к
в интегралах приходим к
Фермиевские интегралы в числителе и знаменателе сводятся к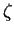 -функции
Римана
-функции
Римана
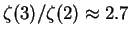 ,
в приближении Вина это просто гамма-функции
,
в приближении Вина это просто гамма-функции
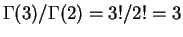 .
.
Очень полезное приближение для плотности числа фотонов чернотельного
излучения получается с использованием приближения Вина:
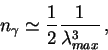
где
<< 2.2 Уравнение переноса | Оглавление | 2.4 Характеристические темп... >>