Астронет > 2.1 Уравнение переноса

Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков
http://variable-stars.ru/db/msg/1170612/node10.html

Лекции по Общей Астрофизике для Физиков

<< 2. Излучение | Оглавление | 2.2 Уравнение переноса >>

Разделы

2.1 Уравнение переноса излучения

Для количественного понимания процессов, происходящих в астрофизических источниках, нам понадобится знакомство с макроскопической теорией переноса электромагнитного излучения в среде.

2.1.1 Основные определения

Напомним основные определения. В электродинамическом (классическом) описании излучение описывается плоскими электромагнитными волнами, которые распространяются в пустоте со скоростью света . Частота монохроматической электромагнитной волны связана с длиной волны соотношением .

С точки зрения квантовой физики излучение можно описывать потоком безмассовых векторных частиц - фотонов, распространяющихся в пустоте со скоростью света. Импульс фотона связан с волновым вектором , ( - единичный вектор, касательный траектории движения фотона) как . Поскольку энергия релятивистской безмассовой частицы (каковой является фотон) связана с ее импульсом соотношением , то энергия фотона может быть выражена через частоту излучения

(2.1)

где

эрг с - постоянная Планка.

Для теплового излучения среды с температурой по порядку величины характерные фотоны имеют энергию , где эрг/К - постоянная Больцмана. Поэтому часто удобно бывает характеризовать излучение энергией квантов (выраженной в электрон-вольтах) или "температурой излучения" ^2.1 (выраженной в Кельвинах). Например, оптические кванты имеют энергию около 1 эВ, рентгеновские - порядка 1-10 кэВ. В энергетических единицах температура в 1 эВ соответствует физической температуре K. С другой стороны, для низкочастотного излучения (например, в радиодиапазоне) удобнее пользоваться частотой излучения, выраженной Гц. 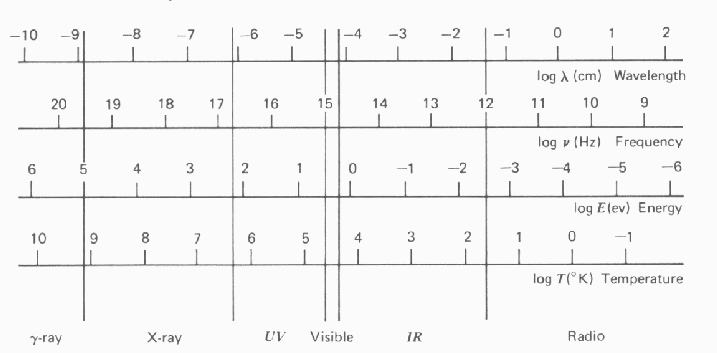Шкала электромагнитных волн представлена на Рис. 2.1.

Рис. 2.1 Электромагнитный спектр

Очень полезная оценка: характерная энергия квантов, излучаемых оптически толстым телом (например, фотосферой звезды) с температурой , по порядку величины есть эта температура, выраженная в энергетических единицах. Обратное утверждение неверно: по энергии квантов (не зная формы спектра) не всегда можно сделать верный вывод о температуре излучающей области.

2.1.2 Макроскопические характеристики излучения

Основные макроскопические характеристики поля излучения следующие.

2.1.2.1 Поток энергии излучения F

Определяется как количество энергии , протекающей через площадку единичного сечения за единицу времени со всех направлений

(2.2)

Размерность потока: [В/м] (СИ) или [эрг/см/c] (СГС).

Из закона сохранения энергии для изотропного источника немедленно получаем откуда

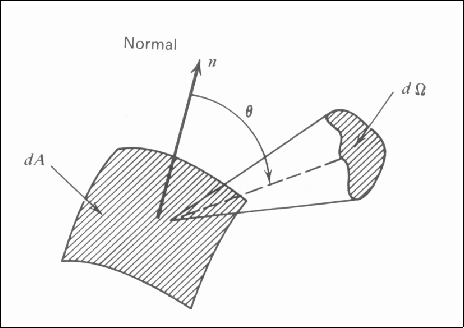
2.1.2.2 Удельная интенсивность (или яркость)

Поток зависит от ориентации площадки в пространстве и таким образом не является функцией только лишь координат наблюдателя в поле излучения. Более фундаментально с точки зрения физики описание поля излучения в терминах функции распределения фотонов - число световых квантов в спектральном интервале от до , находящихся в момент в элементе объема в точке и имеющих направление движения в элементе телесного угла около единичного вектора (далее для краткости мы будем говорить "направление ").

Каждый квант обладает энергией и движется со скоростью , так что величина

(2.3)

есть количество лучистой энергии в спектральном интервале

, протекающей в 1 сек через площадку в 1 см

, помещенную в точке

перпендикулярно к направлениям распространения энергии (лучам), которые лежат в элементе телесного угла

около вектора

. Величину

называют удельной интенсивностью излучения. Задание величины

или

полностью определяет поле излучения.

Опуская векторные обозначения и временную зависимость, пишем

(2.4)

Размерность : [эрг/см/с/Гц/Стер]

2.1.2.3 Полный поток излучения и поток импульса через площадку

Рассмотрим поле излучение (лучи идут со всех направлений). Тогда поток энергии через площадку из элементарного телесного угла (иногда говорят "удельный поток излучения")

(2.5)

здесь

- угол между нормалью к площадке и направлением

. Угловой фактор учитывает уменьшение видимой площади площадки

из направления

. (Рис. 2.2).

Рис. 2.2 К определнию полного потока через площадку

Интегрируя по всем направлениям, получаем выражение для потока через интенсивность

(2.6)

Замечание: Если поле излучения изотропно, не зависит от направления, то полный поток через площадку со всех направлений равен нулю. Такая ситуация реализуется в поле равновесного излучения (с большой точностью внутри звезды). И обратно, чем более неизотропно поле излучения, тем дальше от равновесного состояния оно находится (например, поле излучения вблизи границы фотосферы звезды).

Поток импульса в единицу времени через единичную площадку определяет давление, оказываемое на площадку. Импульс фотона , откуда

[поток импульса через площадку из направления ] =

А т.к. давление - нормальная к поверхности площадки компонента потока импульса, то возникает дополнительный фактор :

(2.7)

2.1.2.4 Плотность энергии излучения

Вспоминая связь удельной интенсивности с функцией распредeления фотонов (2.3), сразу можно записать выражение для спектральной плотности энергии излучения (энергия в единичном объеме в единичном интервале частот с размерностью [эрг/см/Гц] ):

(2.8)

где

- средняя интенсивность. Для изотропного поля излучения, очевидно,

ПРИМЕР: давление излучения в изотропном поле (например, равновесное излучение внутри звезды или на радиационно-доминированной стадии в ранней Вселенной)

Возьмем сферическую полость с идеально отражающими стенками. Внутри устанавливается изотропное поле излучения. Каждый фотон при отражении от стенки передает свой импульс дважды:

(2.9)

Полное давление излучения c учетом изотропии :

(2.10)

Этот результат хорошо известен и может быть получен из термодинамики излучения или непосредственно из свойств тензора энергии-импульса электромагнитного поля (см. напр. Л.Д. Ландау, Е.М. Лифшиц, "Теория Поля".)

2.1.3 Постоянство удельной интенсивности вдоль луча в пустом пространстве

Если поток излучения падает с удалением от источника, то интенсивность остается постоянной вдоль луча зрения. Это важнейшее свойство следует из закона сохранения энергии. Рассмотрим две точки на луче зрения. Если на пути нет источников и стоков энергии (т.е. среда не поглощает и не излучает), то

и с учетом соотношений

получаем

(2.11)

Это свойство удельной интенсивности можно переформулировать иначе: вдоль луча, если нет источников дополнительного излучения и поглощения.

<< 2. Излучение | Оглавление | 2.2 Уравнение переноса >>