 |
Астронет: К. А. Постнов/ГАИШ Лекции по Общей Астрофизике для Физиков http://variable-stars.ru/db/msg/1170612/3lec/node6.html |
<< 3.4 Физические ограничения на | Оглавление | Литература >>
3.5 О точности измерений световых потоков
Основная задача любого астрономического наблюдения - не только зарегистрировать источник, но и измерить поток излучения. Для регистрации источника достаточно различить его на фоне шума, приняв за количественный критерий заданный уровень отношения сигнал/шум. Измерение какой-либо физической величины (потока, итенсивности) требует задания точности, с которой мых хотим эту величину измерить. Естественно, чем выше точность измерения, тем лучше. При астрономических наблюдениях энергия фотонов, собранных телескопом за время экспозиции, преобразуется детектором в иные формы энергии и в конечном счете выводится в цифровом виде (например, как число фотоэлектронов в секунду на фотоумножителе). Затем отсчеты калибруются и таким образом устанавливается однозначное соответствие между скоростью счета детектора и падающим потоком фотонов в данном диапазоне энергий.
Важность повышения точности измерения светового потока от астрономического
источника иллюстрируется следующим примером.
Существует многочисленный класс интенсивно
изучаемых астрофизических объектов - тесные двойные звезды, в которых одна
из звезд близка к пределу приливной устойчивости из-за близости другой
(говорят, близка к заполнению полости Роша), при этом под действием
приливных сил вещество с этой звезды может перетекать на другую. Форма
искаженной приливными силами звезды отличается от сферической, сила тяжести
на разных участках поверхности разная и выходящий поток излучения варьируется
в пределах 
в зависимости от того, под каким углом мы видим эту
звезду (т.н. эффект эллипсоидальности). Таким образом, при обращении звезды
вокруг общего центра тяжести принимаемый поток будет[5 промодулирован на
уровне из-за этого эффекта. Чтобы обнаружить эту модуляцию (и тем
самым измерить орбитальный период и другие физические характеристики
системы), наблюдения следует производить с точностью лучше 
. В конце
1999 г. методами высокоточной фотометрии уже обнаружены планеты вокруг
близких звезд.
За время экспозиции телескоп собирает фотоны, идущие как от
источника, так и фоновые фотоны (рассеяние света в атмосфере, свечение
атмосферы, фотоны из межзвездной
среды и т.д.). Фон неба за время экспозиции можно считать постоянным,
будем характеризовать его величиной 
[квантов/см
/c/стер]
Типичное значение в сине-зеленой (В) области -
21.5 звездная величина с кв. секунды дуги, что соответствует
кв./см/с/А/кв. сек. Фон неба увеличивается в красной области
из-за свечения атмосферных молекул ОН.
Возьмем идеальный (
) приемник. Пусть
- время экспозиции,
- угловой размер изображения (обычно атмосферное),
- апертура телескопа,
- яркость фона неба [квантов/cм/c/стер],
- поток от источника [квантов/cм/c].
Количество фоновых квантов, попавших на детектор за время экспозиции
от источника+фон:
Будем считать, что за время экспозиции фон не меняется и флюктуации числа квантов носят Пуассоновский характер, т.е. дисперсия отсчетов есть
. Точность измерения характеризуется относительной
флюктуацией числа отсчетов, т.е. величиной
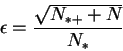
Различаются два разных случая:
А) Случай яркой звезды, 
. Тогда
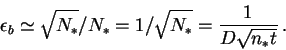
Чем больше диаметр телескопа, тем при меньших экспозициях достигается требуемая точность измерения.
Пример: Какая звездная величина может наблюдаться
электрофотометром (квантовый выход 
) на 6-м
телескопе за время экспозиции 
cек с точностью 1
?
Ответ:
c, 
см, откуда
кв/см/c,
а учитывая 
кв/см/c, получаем
B) Случай слабого объекта 
. Имеем
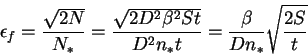
Обратите внимание на зависимость от качества изображения
и фона неба.
Пример:
Определить предельную звездную величину в Москве
при наблюдениях на 1-м телескопе.
Для предельной видимости полагаем относительную
точность
. Фон неба в лучшие ночи
19
/кв. сек. из-за сильной засветки. 
м, , 
c,
(лучшие мартовские или сентябрьские ночи в новолунии).
Cначала находим фон неба в потоках:
кв/см/c, а потом определяем
кв/см/c, т.е.
.
Обратите внимание, что предельная звездная
величина значительно отличается
(примерно в 10 раз меньше по потоку) от фона неба!
Полученные сведения теперь легко помогут разобраться в вопросе о том, можно ли наблюдать звезды невооруженным глазом днем со дна глубокого колодца? Для ответа достаточно сообразить, что фон неба с единицы площади и разрешающая способность глаза3.5 не зависит от того, откуда мы проводим наблюдения. Изменится ли ответ, если взять телескоп?
<< 3.4 Физические ограничения на | Оглавление | Литература >>