Астронет > 4.2 Коэффициент теплопроводности. Росселандово среднее

Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд
http://variable-stars.ru/db/msg/1169513/node26.html

Физические основы строения и эволюции звезд

<< 4.1 Перенос излучения при ... | Оглавление | 4.3 Поведение плотности и ... >>

4.2 Коэффициент теплопроводности. Росселандово среднее

Займемся важной для теории звезд задачей -- определим коэффициент теплопроводности.

$F_{\nu\;\rm eq}$ является функцией только температуры. Пусть температура меняется вдоль координаты $z,\;T=T(z),\;x$ -- любая ось в пространстве, и $\Theta$ -- угол между осями $(z,\;x)$ . Тогда

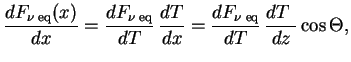
$\displaystyle {dF_{\nu\;\rm eq}(x)\over dx}={dF_{\nu\;\rm eq}\over dT}\,{dT\over dx} ={dF_{\nu\;\rm eq}\over dT}\,{dT\ \over dz}\cos \Theta,$

т.е. $dF_{\nu\;\rm eq}/dx$ зависит от угла $\Theta$ , и для интенсивности имеем соотношение

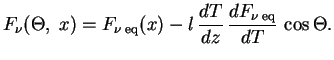
$\displaystyle F_\nu(\Theta,\;x)=F_{\nu\;\rm eq}(x)-l\,{dT\over dz}\, {dF_{\nu\;\rm eq}\over dT}\,\cos \Theta.$

Подсчитаем полный поток энергии, проинтегрированный по всем частотам. По соображениям симметрии поток направлен вдоль оси

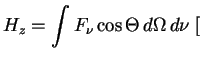$\displaystyle H_z=\int F_\nu\cos \Theta\, d\Omega\, d\nu\;[$ эрг/с см $\displaystyle ^2].$

Интеграл по $d \Omega$ берется по всем углам, т.е. полный поток есть разность потоков слева направо и справа налево. Подставим $F_\nu$ в выражение для

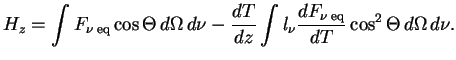
$\displaystyle H_z=\int F_{\nu\;\rm eq}\cos\Theta \,d\Omega\, d\nu-{dT\over dz}\int l_\nu{dF_{\nu\;\rm eq} \over dT}\cos^2\Theta \,d\Omega\, d\nu.$

Везде ниже будем писать $B_\nu$ , понимая под этим $F_{\nu\;\rm eq}$ . Первый член в правой части уравнения после интегрирования по $d \Omega$ обращается в ноль, а во втором зависимость $\cos^2\Theta$ даст $4\pi/3$ . В итоге полный поток равен

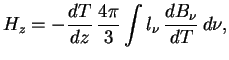
$\displaystyle H_z=-{dT\over dz}\,{4\pi\over 3}\int l_\nu\,{dB_\nu\over dT}\,d\nu,$

где величина ${4\pi\over 3}\int l_\nu\,{dB_\nu\over dT}\,d\nu$ называется коэффициентом лучистой теплопроводности (напомним, что в общем случае коэффициентом теплопроводности называется величина, стоящая при $\nabla T$ ). Запишем выражение для

в том же виде, что и в кинетической теории газов. Ранее мы определили плотность излучения в каждой точке как

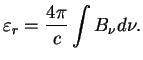
$\displaystyle \varepsilon_r={4\pi\over c}\int B_\nu d\nu.$

Следовательно,

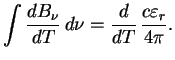
$\displaystyle \int {dB_\nu\over dT}\,d\nu={d\over dT}\,{c\varepsilon_r\over 4\pi}.$

Введем среднюю длину пробега

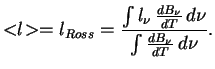
$\displaystyle <\!\!l\!>=l_{Ross}={\int l_\nu\,{dB_\nu\over dT}\,d\nu\over \int {dB_\nu\over dT}\,d\nu}.$

Эта величина называется росселандовым средним. Тогда

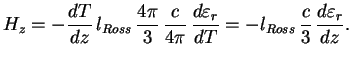
$\displaystyle H_z=-{dT\over dz}\,l_{Ross}\,{4\pi\over 3}\,{c\over 4\pi}\,{d\varepsilon_r\over dT}=-l_{Ross}\,{c\over 3}\,{d \varepsilon_r\over dz}.$

Итак, $\vec H=-D\nabla \varepsilon_r$ , где

-- коэффициент диффузии такой же, как в кинетической теории газов. Главный вклад в росселандово среднее дают кванты с энергией $h\nu\approx 4kT$ , т.е. основную роль в переносе энергии играют кванты с большой энергией.

В оптически толстом теле с источником тепла внутри возникает градиент температуры, и поток тепла определяется зонами прозрачности. Оптически тонкий горячий слой излучает (по закону Кирхгофа) то же, что он поглощал бы при внешнем облучении. Таким образом, больше всего такой слой излучает там, где велика непрозрачность, например в линиях.

П р и м е р ы. 1. Пусть имеется только томсоновское рассеяние, т.е. $l=1/ \varkappa_{\mbox{\sc t}}\rho$ . Чему равно $l_{Ross}$ ? Очевидно, $l_{Ross}=l$ , так как не зависит от $\nu$ .

Рис. 21.

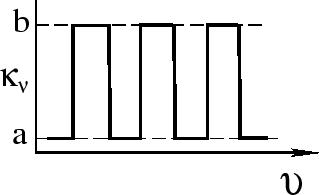
2. Пусть непрозрачность $\varkappa_\nu$ задана в виде гребенки (рис. 21) с длиной зубцов $b-a,\;b\gg a$ и шириной зубцов, равной расстоянию между ними. Тогда, очевидно, $l_{Ross}\simeq 1/2a\rho$ , т.е. в задачах переноса излучения весь поток поступает в ``окнах большей прозрачности'' (ответ не зависит от !). В задачах об излучении оптически тонкой плазмы все определяется верхушками гребенки, где велико поглощение и велико излучение.

В первом приближении такая гребенка (только с различной шириной зубцов и промежутков) может имитировать учет поглощения в линиях при переносе излучения.

3. Найдем $l_{Ross}$ для тормозного поглощения. Имеем

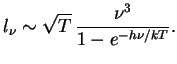
$\displaystyle l_\nu\sim\sqrt{T}\,{\nu^3\over {1-e^{-h\nu/kT}}}.$

Введем $x=h\nu/kT$ , тогда

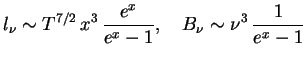
$\displaystyle l_\nu\sim T^{7/2}\,x^3\,{e^x\over {e^x-1}},\quad B_\nu\sim\nu^3\,{1\over {e^x-1}}$

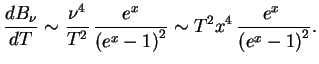
$\displaystyle {dB_\nu\over dT}\sim {\nu^4\over T^2}\,{e^x\over {(e^x-1)}^2}\sim T^2x^4\,{e^x\ \over {(e^x-1)}^2}.$

Интегрируя и выписывая численные коэффициенты, получим

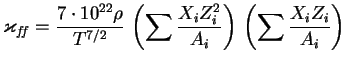
$\displaystyle \varkappa_{f\!f}={7\cdot 10^{22}\rho\over T^{7/2}}\,\left(\sum {X_iZ_i^2\over A_i} \right)\,\left(\sum {X_iZ_i\over A_i}\right)$

-- формула Крамерса.

Как и раньше,

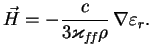
$\displaystyle \vec H=-{c\over 3\varkappa_{f\!f}\rho}\,\nabla \varepsilon_r.$

Оказывается, что $\varkappa_{f\!f}=\varkappa_\nu$ при $h\nu/kT=6$ , т.е. эффективный перенос тепла осуществляется квантами большой энергии. Это объясняется тем, что максимум весовой функции $dB_\nu/dT$ приходится на $x\approx 4$ , и, кроме того, тем, что усредняется $1/a'_\nu$ , а $a'_\nu$ убывает с частотой.

Заметим, что в формулу для непрозрачности входит отношение $\rho/T^{7/2}$ . С другой стороны, как мы показали ранее, $\rho/T^3\sim P_g/P_r$ , причем это отношение определяется массой звезды. Таким образом, в первом приближении, пренебрегая различием $T^{7/2}$ и , получим, что $\varkappa$ пропорциональна и тоже однозначно зависит от массы звезды.

Если в непрозрачности важны оба механизма, то $\varkappa_{Ross}\ne\varkappa_{f\!f}+\varkappa_{\mbox{\sc t}}$ (не забывайте, что усредняем $l_\nu=1/(\varkappa_\nu+\varkappa_{\mbox{\sc t}})$ ). В качестве упражнения подсчитайте в этом случае $\varkappa_{Ross}$ . Можно показать, что

$\displaystyle \varkappa_{Ross}=\varkappa_{\mbox{\sc t}}\,f(\rho/T^{7/2}).$

Не надо преувеличивать точность всех этих расчетов. Все, что мы говорили, справедливо для водородной плазмы, но для реального звездного вещества существенна роль тяжелых элементов. Например, для железа энергия связи последних -электронов порядка 9 кэВ и степень ионизации его меняется с глубиной. Все оказывается гораздо сложней. Необходимо учитывать многие процессы: свободно-связанные, связанно-связанные (линии) и др. В этой книге дается лишь общая физическая картина, общее представление, а не точные методы расчета. Один вопрос о теплопроводности, рассматриваемый в современных статьях, может быть предметом целого курса. Настоящий курс позволит начать чтение оригинальных статей, но никак не заменит их.

<< 4.1 Перенос излучения при ... | Оглавление | 4.3 Поведение плотности и ... >>