Астронет > 3.5 Рассеяние излучения на свободных электронах

Астронет: Я. Б. Зельдович, С. И. Блинников, Н. И. Шакура Физические основы строения и эволюции звезд
http://variable-stars.ru/db/msg/1169513/node23.html

Физические основы строения и эволюции звезд

<< 3.4 Тормозное излучение зарядов | Оглавление | 4. Теория переноса (продолжение) >>

3.5 Рассеяние излучения на свободных электронах

Рассмотрим движение электрона в плоской электромагнитной волне: $E_x=E_0\,\cos \omega t$ , распространяющейся вдоль оси . Уравнение движения электрона:

$\displaystyle m\ddot x=eE_0\,\cos \omega t,$

и энергия, излучаемая таким электроном,

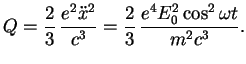
$\displaystyle Q={2\over 3}\,{e^2{\ddot x}^2\over c^3}={2\over 3}\,{e^4E_0^2\cos^2\omega t\over m^2c^3}.$

Своих источников энергии у электрона нет. Фактически он переизлучает (рассеивает) энергию падающей электромагнитной волны в других направлениях, так что

$\displaystyle Q=W\sigma_T\;[$ эрг $\displaystyle /$ с $\displaystyle ],$

где $W\;[$ эрг

см

-- поток падающей энергии:

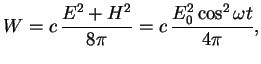
$\displaystyle W=c\,{{E^2+H^2}\over 8\pi}=c\,{E_0^2\cos^2\omega t\over 4\pi},$

и сечение рассеяния

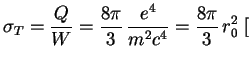$\displaystyle \sigma_T={Q\over W}={8\pi\over 3}\,{e^4\over m^2c^4}={8\pi\over 3}\,r_0^2\;[$ см $\displaystyle ^2]$

знаменитая формула Томсона. Величина

$\displaystyle r_0=e^2/mc^2=2,8\cdot 10^{-13}\;$ см $\displaystyle$

называется классическим радиусом электрона.

При преобладающей роли электронного рассеяния (процессы поглощения излучения несущественны) изменение интенсивности $F_\nu$ в монохроматическом пучке фотонов, очевидно, равно

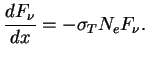
$\displaystyle {dF_\nu\over dx}=-\sigma_TN_eF_\nu.$

Можно ввести коэффициент ``поглощения'' при томсоновском рассеянии (хотя реально поглощения энергии и нет):

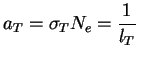$\displaystyle a_T=\sigma_TN_e={1\over l_T}\;$ см $\displaystyle ^{-1},$

где длина пробега

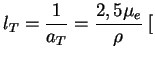$\displaystyle l_T={1\over a_T}={2,5\mu_e\over \rho}\;[$ см $\displaystyle ].$

Интегрируя уравнение для $F_\nu$ , получаем

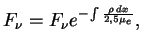
$\displaystyle F_\nu=F_\nu e^{-\int {\rho\,dx\over 2,5\mu_e}},$

т.е. $2,5\;$ г/см

водородной плазмы ( $\mu_e=1$ ) уменьшают $F_\nu$ в

раз за счет электронного рассеяния.

В астрофизике обычно пользуются не коэффициентом поглощения $a_T,\;a_\nu$ , а так называемой непрозрачностью

$\displaystyle \kappa_\nu=a_\nu/\rho\;[$ см $\displaystyle ^2/$ г $\displaystyle ].$

Таким образом, непрозрачность за счет рассеяния

$\displaystyle \kappa_T=0,4\mu_e\;[$ см $\displaystyle ^2/$ г $\displaystyle ].$

З а д а ч и. 1. Дана водородная () плазма со значениями плотности $\rho=10^{-6},\;10^{-3},\;1\;$ гсм, температурой $T=10^8,\;3\cdot 10^6,\;10^5\;$ K. Для $x=h\nu/kT=10^{-2},\;10^{-1},\;1,\;5,\;20$ найти $\nu,\; \lambda,\;\kappa_{f\!f},\;\kappa_T$ . В переменных $\lg T-\lg \rho$ найти кривую, на которой $\kappa_{f\!f}=\kappa_T$ . Подсчитайте $J_\nu$ .

2. Пусть в каждой точке звезды плотность и температура связаны соотношением $\rho=$ const $\cdot T^3$ , где const заранее не известна. (Тогда $P\sim T^4\sim \rho^{4/3}$ , т.е. индекс политропы .) Для чисто водородных моделей звезд с массами $M=1,\;10,\;100_\odot$ и центральных плотностей $\rho_c=100,\;1$ и $10^{-2}\;$ $\mbox {г}/\mbox{см}^3$ найти радиус , температуру в центре и полную энергию ${\cal E}$ .

3. Пусть распределение плотности по звезде определяется зависимостью $\rho=\rho_c {[1-(r/R)^2]}^g$ , где $g=1,\;2,\;3$ . Найти гравитационную энергию звезды $U=-{GM^2 \over R}\,K_g$ , т.е. найти .

Пусть энергия единицы массы связана с $\rho$ соотношениями: a) $E=A\rho^{1/3}\,$ , b) $E=A\rho^{1/2}$ . (Какое при этом $P=P(\rho)$ ?)

При тех же распределениях плотности найти связь между и из условия минимума полной энергии ${\cal E}$ .

<< 3.4 Тормозное излучение зарядов | Оглавление | 4. Теория переноса (продолжение) >>