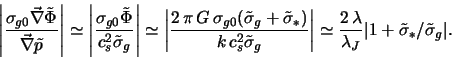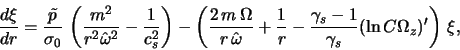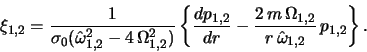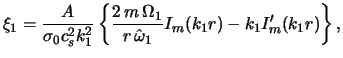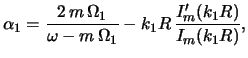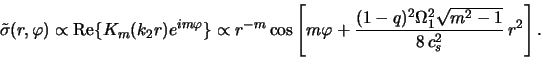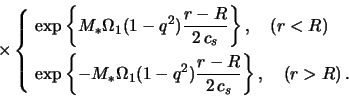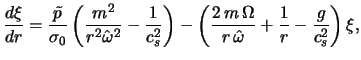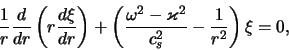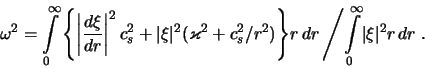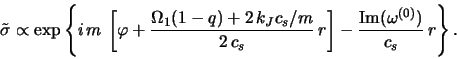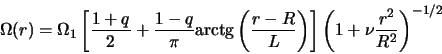|
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://www.astronet.ru/db/msg/1168623/node28.html |
<< 4.4 Диссипативные эффекты | Оглавление | 4.6 Неосесимметричный потенциал >>
- 4.5.1 Дисперсионное уравнение возмущений разрыва угловой скорости
- 4.5.2 Неустойчивость Кельвина-Гельмгольца
- 4.5.3 Центробежная неустойчивость
- 4.5.4 Неустойчивость скачка скорости вращения конечной ширины
- 4.5.5 Скачок плотности
- 4.5.6 Неоднородные газовые диски с двугорбыми кривыми вращения
- 4.5.7 Низкочастотная центробежная неустойчивость
4.5 Гидродинамические неустойчивости газового диска
В предыдущих разделах этой главы мы уже рассмотрели ряд гидродинамических неустойчивостей газового гравитирующего диска, имеющих, по-видимому, отношение к происхождению тех или иных наблюдаемых структур или налагающих ограничения на значения некоторых параметров галактических газовых подсистем. Это прежде всего гравитационная (или гравитационно-градиентная) неустойчивость, определяющая минимальную "температуру" диска, необходимую для предотвращения разбиения его на гравитационно связанные сгустки джинсовского масштаба. Другой класс неустойчивостей, обусловленных радиальной неоднородностью плотности и температуры диска, влияет на отношение радиальных градиентов указанных величин и, возможно, может приводить к возбуждению антициклонических вихревых структур типа солитонов Россби. Быстрая диссипативная неустойчивость может играть роль в решении проблемы турбулентной вязкости.
Однако среди перечисленных выше неустойчивостей нет
неустойчивости, обусловленной непосредственно дифференциальностью
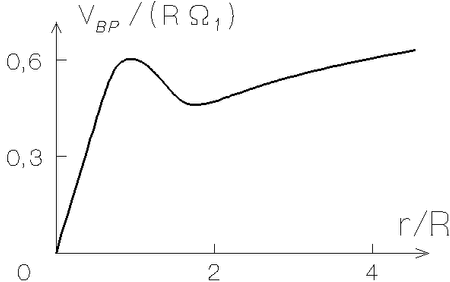
вращения диска. Неустойчивости такого типа могут возбуждаться в
тех частях диска, где степень дифференциальности вращения вещества
превышает некоторый предел -- например, в области резкого убывания
![]() снаружи от внутреннего горба
снаружи от внутреннего горба
![]() в галактиках
с двугорбыми кривыми вращения (см. рис. 1.1).
в галактиках
с двугорбыми кривыми вращения (см. рис. 1.1).
По крайней мере в нашей Галактике в этой же области (
![]() кпк) наблюдается заметная депрессия в поверхностной плотности
газового диска. Прямая оценка по данным наблюдений [70]
джинсовского масштаба в этой части газовой подсистемы Галактики
приводит к следующему результату:
кпк) наблюдается заметная депрессия в поверхностной плотности
газового диска. Прямая оценка по данным наблюдений [70]
джинсовского масштаба в этой части газовой подсистемы Галактики
приводит к следующему результату:
![]() кпк, что больше масштабов наблюдаемых
структур. Каковы же следствия этого результата?
кпк, что больше масштабов наблюдаемых
структур. Каковы же следствия этого результата?
Динамика возмущений в газовом диске определяется суммой двух
сил:
![]() , где
, где
![]() ,
, ![]() -- возмущенные давление и
гравитационный потенциал. Оценим их относительную интенсивность
-- возмущенные давление и
гравитационный потенциал. Оценим их относительную интенсивность
Оценки, проведенные в соответствии с результатами п. 4.1.2 по
данным наблюдений равновесных параметров звездной и газовой
плоских подсистем в рассматриваемой области Галактики, показывают,
что вклад звездного диска в возмущенный гравитационный потенциал
не превышает вклад газового (см. разд. 6.2). Поэтому если какая-либо гидродинамическая неустойчивость приводит к раскачке
возмущений с
![]() , то в уравнениях, описывающих динамику
газового диска, возмущенной гравитационной силой (
, то в уравнениях, описывающих динамику
газового диска, возмущенной гравитационной силой (
![]() )
в первом приближении можно пренебречь по сравнению с возмущенной
гидродинамической силой (
)
в первом приближении можно пренебречь по сравнению с возмущенной
гидродинамической силой (
![]() ). Этот вывод получил
обоснованное подтверждение в подробно описанных Фридманом и Поляченко
[2] работах [345-348]. Поэтому далее в этом разделе (кроме
п. 4.5.4) мы не будем учитывать вклад возмущенного гравитационного
потенциала в динамику возмущений газового диска. Подpобное обсуждение
этого вопpоса можно найти в pаботе [349].
). Этот вывод получил
обоснованное подтверждение в подробно описанных Фридманом и Поляченко
[2] работах [345-348]. Поэтому далее в этом разделе (кроме
п. 4.5.4) мы не будем учитывать вклад возмущенного гравитационного
потенциала в динамику возмущений газового диска. Подpобное обсуждение
этого вопpоса можно найти в pаботе [349].
4.5.1 Дисперсионное уравнение возмущений разрыва угловой скорости
Исследуем динамику возмущений в однородном газовом диске,
вращающемся с разрывом угловой скорости [предельная модель
двугорбой кривой вращения с узкой областью резкого убывания ![]() снаружи от внутреннего горба
снаружи от внутреннего горба
![]() ]:
]:
при
В рамках модели с непрерывным распределением ![]() из
линеаризованных уравнений газодинамики (4.2.14)
из
линеаризованных уравнений газодинамики (4.2.14) ![]() (4.2.17) для
возмущений типа (4.2.13) с учетом несущественности возмущений
гравитационного потенциала получаем систему уравнений
(4.2.17) для
возмущений типа (4.2.13) с учетом несущественности возмущений
гравитационного потенциала получаем систему уравнений
где
Переходя к модели разрыва ![]() (4.5.2), будем искать решения
системы (4.5.4), (4.5.5) отдельно по обе стороны от разрыва (
(4.5.2), будем искать решения
системы (4.5.4), (4.5.5) отдельно по обе стороны от разрыва (![]() ,
, ![]() ), полагая соответственно
), полагая соответственно
![]() . При
этом система уравнений (4.5.4), (4.5.5) сводится к одному для
. При
этом система уравнений (4.5.4), (4.5.5) сводится к одному для
![]() :
:
Решения этих уравнений должны быть сшиты на разрыве (при
Второе из этих граничных условий выглядит
необычным4.5. Поясним поэтому его физическую сущность. Радиальное
равновесие газовых галактических дисков обусловлено балансом градиента
давления, центробежной и гравитационной сил:
![]() , где штрих означает дифференцирование по радиальной координате.
Вклад градиента давления в это условие мал по сравнению с вкладом
гравитационной силы
, где штрих означает дифференцирование по радиальной координате.
Вклад градиента давления в это условие мал по сравнению с вкладом
гравитационной силы
![]() . Поэтому довольно резкий перепад
. Поэтому довольно резкий перепад ![]() в рассматриваемой
нами области диска обусловлен в основном в той же мере резким
градиентом
в рассматриваемой
нами области диска обусловлен в основном в той же мере резким
градиентом ![]() , создаваемым распределением вещества в массивной
звездной подсистеме. И в предельно идеализированной модели разрыва
, создаваемым распределением вещества в массивной
звездной подсистеме. И в предельно идеализированной модели разрыва
![]() величина
величина ![]() должна быть, очевидно, разрывной. В то же
время полное совокупное "давление"
должна быть, очевидно, разрывной. В то же
время полное совокупное "давление"
![]() должно быть
непрерывным на искривленной благодаря возмущениям
должно быть
непрерывным на искривленной благодаря возмущениям ![]() поверхности
разрыва, а равновесное
поверхности
разрыва, а равновесное
![]() -- непрерывным на
невозмущенном разрыве. Разложим эту величину в ряд по степеням амплитуды
возмущений, ограничиваясь линейными членами и пренебрегая в соответствии с
оценкой (4.5.1) возмущенным гравитационным потенциалом:
-- непрерывным на
невозмущенном разрыве. Разложим эту величину в ряд по степеням амплитуды
возмущений, ограничиваясь линейными членами и пренебрегая в соответствии с
оценкой (4.5.1) возмущенным гравитационным потенциалом:
откуда следует, что непрерывной на разрыве
Решения уравнений (4.5.6), (4.5.7) должны быть ограничены при
![]() и
и
![]() . С учетом этих граничных
условий они имеют вид
. С учетом этих граничных
условий они имеют вид
где
Сшивая затем решения (4.5.10)-(4.5.13) на разрыве ![]() согласно граничным условиям (4.5.8), (4.5.9), получаем искомое
дисперсионное уравнение [351]:
согласно граничным условиям (4.5.8), (4.5.9), получаем искомое
дисперсионное уравнение [351]:
Для наглядности представления результатов будем описывать
решения дисперсионного уравнения (4.5.15) с помощью двух
безразмерных параметров
![]() и
и
![]() .
.
4.5.2 Неустойчивость Кельвина-Гельмгольца
Получим решение дисперсионного уравнения (4.5.15) в пределе
"слабого" (![]() ) разрыва. Нетрудно видеть, что в этом случае
согласно (4.5.14)
) разрыва. Нетрудно видеть, что в этом случае
согласно (4.5.14)
![]() . Поэтому, используя
представления функций Бесселя в виде рядов по степеням их аргументов,
из (4.5.15) получаем (
. Поэтому, используя
представления функций Бесселя в виде рядов по степеням их аргументов,
из (4.5.15) получаем (![]() )
)
где
Поскольку в пренебрежении градиентами равновесных плотности и
давления газовой подсистемы возмущенные поверхностные плотность ![]() и давление
и давление ![]() связаны соотношением
связаны соотношением
![]() ,
нетрудно определить пространственную зависимость
,
нетрудно определить пространственную зависимость
![]() .
Например, в области
.
Например, в области ![]() при
при ![]() , используя результат
(4.5.18) и соотношение (4.5.14), учитывая, что физический смысл
имеют действительные части комплексных амплитуд, получаем
, используя результат
(4.5.18) и соотношение (4.5.14), учитывая, что физический смысл
имеют действительные части комплексных амплитуд, получаем
4.5.3 Центробежная неустойчивость
В спиральных галактиках, как правило, значение
![]() на
внутреннем горбе кривой вращения намного больше скорости звука в
газовой подсистеме и, таким образом, осуществляется другой
предельный случай:
на
внутреннем горбе кривой вращения намного больше скорости звука в
газовой подсистеме и, таким образом, осуществляется другой
предельный случай: ![]() . В этом пределе, используя
асимптотические представления функций Бесселя при
. В этом пределе, используя
асимптотические представления функций Бесселя при
![]() , из (4.5.15) в главном порядке указанных асимптотик получаем [351]
, из (4.5.15) в главном порядке указанных асимптотик получаем [351]
В рассмотренном пределе (![]() ) неустойчивость (4.5.21) уже
не похожа на неустойчивость тангенциального разрыва (4.5.18). Во-первых, потому, что она развивается только в том случае, когда
внутренняя часть диска вращается быстрее внешней:
) неустойчивость (4.5.21) уже
не похожа на неустойчивость тангенциального разрыва (4.5.18). Во-первых, потому, что она развивается только в том случае, когда
внутренняя часть диска вращается быстрее внешней: ![]() . Во-вторых, потому, что ее инкремент практически не зависит от
волнового числа
. Во-вторых, потому, что ее инкремент практически не зависит от
волнового числа
![]() [ср. с (4.5.18)]4.6. В-третьих, потому, что неустойчивость (4.5.21) в
противоположность классической неустойчивости тангенциального разрыва
не стабилизируется при
[ср. с (4.5.18)]4.6. В-третьих, потому, что неустойчивость (4.5.21) в
противоположность классической неустойчивости тангенциального разрыва
не стабилизируется при
![]() ,
а имеет место при сколь угодно большом
,
а имеет место при сколь угодно большом
![]() и более
того, инкремент неустойчивости (4.5.21) растет практически линейно с
ростом
и более
того, инкремент неустойчивости (4.5.21) растет практически линейно с
ростом ![]() [о стабилизации классической неустойчивости тангенциального
разрыва в двумерной газодинамике см. в книге Ландау и Лифшица [327];
этот эффект легко получить из формулы (5.3.18)].
[о стабилизации классической неустойчивости тангенциального
разрыва в двумерной газодинамике см. в книге Ландау и Лифшица [327];
этот эффект легко получить из формулы (5.3.18)].
Для выяснения природы неустойчивости (4.5.21) рассмотрим
динамику возмущения границы разрыва, имеющего, например, форму
выступа в область ![]() . Вещество, содержащееся в этом выступе,
продолжает вращаться с угловой скоростью
. Вещество, содержащееся в этом выступе,
продолжает вращаться с угловой скоростью ![]() и на него действует
(приходящая на единицу массы) центробежная сила
и на него действует
(приходящая на единицу массы) центробежная сила
![]() . Но этот выступ уже находится в области, где согласно условию
радиального равновесия гравитационная сила
. Но этот выступ уже находится в области, где согласно условию
радиального равновесия гравитационная сила
![]() (при
(при
![]() ).
Возникающая при этом направленная наружу сила
).
Возникающая при этом направленная наружу сила
![]() увеличивает амплитуду выступа
и тем самым приводит к неустойчивости. В случае
увеличивает амплитуду выступа
и тем самым приводит к неустойчивости. В случае
![]() возникающая сила направлена к центру диска и, следовательно,
стремится уменьшить амплитуду выступа -- это объясняет причину устойчивости
в случае
возникающая сила направлена к центру диска и, следовательно,
стремится уменьшить амплитуду выступа -- это объясняет причину устойчивости
в случае ![]() (
(
![]() ). Приведенные выше доводы корректны,
если вклад давления в условие радиального равновесия газового диска
пренебрежимо мал, а это может иметь место лишь в том случае, когда
). Приведенные выше доводы корректны,
если вклад давления в условие радиального равновесия газового диска
пренебрежимо мал, а это может иметь место лишь в том случае, когда
![]() (
(![]() ). Аналогичные рассуждения в случае
возмущения границы разрыва
). Аналогичные рассуждения в случае
возмущения границы разрыва ![]() , имеющей форму "вмятины" в область
, имеющей форму "вмятины" в область
![]() , также приводят к выводу о неустойчивости только при
, также приводят к выводу о неустойчивости только при
![]() (
(![]() ). Поэтому не является
удивительным тот факт, что инкремент неустойчивости (4.5.21)
пропорционален разрыву действующей на единицу массы центробежной
силы. В связи с этим неустойчивость (4.5.21) естественно называть
центробежной.
). Поэтому не является
удивительным тот факт, что инкремент неустойчивости (4.5.21)
пропорционален разрыву действующей на единицу массы центробежной
силы. В связи с этим неустойчивость (4.5.21) естественно называть
центробежной.
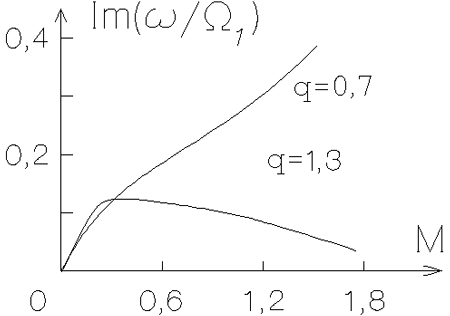 |
Рис. 4.8. Зависимость инкремента неустойчивости,
описываемой дисперсионным уравнением (4.5.15), от параметра
|
Различие между неустойчивостями Кельвина-Гельмгольца [НКГ --
(4.5.18)] и центробежной [ЦБН -- (4.5.21)] хорошо видно на рис. 4.8,
где изображена зависимость инкремента неустойчивости, описываемой
дисперсионным уравнением (4.5.15) при значениях параметра
![]() и
и ![]() для моды
для моды ![]() . Видно,
что при
. Видно,
что при ![]() инкременты в обоих случаях (
инкременты в обоих случаях (![]() ;
;
![]() ) близки друг к другу, но при
) близки друг к другу, но при
![]() их
различие оказывается весьма существенным: при
их
различие оказывается весьма существенным: при ![]() возбуждается
только НКГ, а при
возбуждается
только НКГ, а при ![]() основной вклад в инкремент
неустойчивости дает механизм ЦБН.
основной вклад в инкремент
неустойчивости дает механизм ЦБН.
Рассмотрим теперь вопрос о пространственной структуре
возмущений плотности, возбуждаемых центробежной неустойчивостью. С
учетом того, что эта неустойчивость имеет место при ![]() ,
используем в (4.5.10), (4.5.11) асимптотические представления
функций Бесселя. В результате получаем
,
используем в (4.5.10), (4.5.11) асимптотические представления
функций Бесселя. В результате получаем
Отсюда видно, что неустойчивые по (4.5.21) возмущения плотности имеют форму отстающих спиралей. Шаг такой спирали в радиальном направлении определяется соотношением
а угловая скорость ее вращения
В то же время амплитуда этих возмущений довольно быстро убывает с удалением от разрыва -- согласно (4.5.23) характерный масштаб убывания амплитуды
и при
Суммируем полученные результаты. Центробежная неустойчивость
характеризуется большим инкрементом и возбуждаемые ею возмущения
плотности представляют собой отстающие спирали. Последнее
обстоятельство выглядит весьма заманчивым с точки зрения
возможного решения проблемы происхождения спирального узора
галактик4.7. Однако в рамках рассмотренной нами идеализированной
модели разрыва ![]() центробежная неустойчивость генерирует слишком
короткие отрезки спиралей (
центробежная неустойчивость генерирует слишком
короткие отрезки спиралей (![]() ) и не выделяет по величине
инкремента какую-либо конкретную моду. В то же время ясно, что
исследование более реалистичных моделей с размазанным "разрывом"
) и не выделяет по величине
инкремента какую-либо конкретную моду. В то же время ясно, что
исследование более реалистичных моделей с размазанным "разрывом" ![]() выделит как наиболее неустойчивые низшие моды (высшие моды с
выделит как наиболее неустойчивые низшие моды (высшие моды с
![]() , где
, где ![]() -- ширина размазки "разрыва"
-- ширина размазки "разрыва" ![]() , не будут "воспринимать"
область резкого изменения
, не будут "воспринимать"
область резкого изменения ![]() как разрыв и, следовательно, не будут
возбуждаться). С другой стороны, общее уменьшение инкремента
неустойчивости с ростом ширины размазки "разрыва" должно увеличить
радиальную протяженность возбуждаемой структуры [см. (4.5.26)].
Поэтому подробное исследование центробежной неустойчивости на
более реалистичных моделях представляется весьма актуальным.
как разрыв и, следовательно, не будут
возбуждаться). С другой стороны, общее уменьшение инкремента
неустойчивости с ростом ширины размазки "разрыва" должно увеличить
радиальную протяженность возбуждаемой структуры [см. (4.5.26)].
Поэтому подробное исследование центробежной неустойчивости на
более реалистичных моделях представляется весьма актуальным.
4.5.4 Неустойчивость скачка скорости вращения конечной ширины
Определим влияние "размазки" разрыва угловой скорости ![]() на
полученные выше результаты. В первом приближении полагаем, что в
области
на
полученные выше результаты. В первом приближении полагаем, что в
области
![]() с достаточно малым
с достаточно малым
![]() осуществляется плавный переход от значения
осуществляется плавный переход от значения
![]() до
до
![]() . Используем также тот факт,
что в наиболее интересном для нас случае
. Используем также тот факт,
что в наиболее интересном для нас случае ![]() структура
неустойчивых возмущений в радиальном направлении является коротковолновой
[
структура
неустойчивых возмущений в радиальном направлении является коротковолновой
[
![]() ,
,
![]() ]. Для линейной
аппроксимации
]. Для линейной
аппроксимации ![]() в переходной области в главном порядке по малой
величине
в переходной области в главном порядке по малой
величине
где
Отсюда видно, что в приближении (4.5.27) величина
![]() ,
определяющая степень закрутки спиралей [см. (4.5.24)], не
изменяется. Однако инкремент неустойчивости
,
определяющая степень закрутки спиралей [см. (4.5.24)], не
изменяется. Однако инкремент неустойчивости
![]() уменьшается
довольно резко. Это приводит к двум важным следствиям. Во-первых,
возмущения с малым числом спиралей оказываются более
неустойчивыми, чем возмущения с
уменьшается
довольно резко. Это приводит к двум важным следствиям. Во-первых,
возмущения с малым числом спиралей оказываются более
неустойчивыми, чем возмущения с ![]() . Во-вторых, общее (и
основное из-за
. Во-вторых, общее (и
основное из-за ![]() ) уменьшение инкремента в соответствии с
(4.5.26) увеличивает характерный масштаб
) уменьшение инкремента в соответствии с
(4.5.26) увеличивает характерный масштаб ![]() убывания амплитуды возмущений в радиальном направлении, что
расширяет область локализации генерируемого спирального узора.
убывания амплитуды возмущений в радиальном направлении, что
расширяет область локализации генерируемого спирального узора.
В реальных спиральных галактиках с двугорбыми кривыми
вращения "размазка" разрыва ![]() заметно больше, чем допускает
условие (4.5.27). Поэтому, рассматривая полученные выше результаты
в модели со слабой "размазкой" с точки зрения определения
тенденции в изменении
заметно больше, чем допускает
условие (4.5.27). Поэтому, рассматривая полученные выше результаты
в модели со слабой "размазкой" с точки зрения определения
тенденции в изменении
![]() , следует все же вычислять последнюю
[как и
, следует все же вычислять последнюю
[как и
![]() ] на моделях с кривыми вращения, близкими к реальным.
В качестве такой модели используем кривую вращения (4.5.3),
обладающую тем свойством, что в пределе
] на моделях с кривыми вращения, близкими к реальным.
В качестве такой модели используем кривую вращения (4.5.3),
обладающую тем свойством, что в пределе
![]() эта функция
переходит в исследованный выше разрыв
эта функция
переходит в исследованный выше разрыв ![]() . С такой кривой вращения
систему уравнений (4.5.4), (4.5.5) можно решать численно на ЭВМ
как задачу типа Штурма-Лиувилля (определять собственные функции
. С такой кривой вращения
систему уравнений (4.5.4), (4.5.5) можно решать численно на ЭВМ
как задачу типа Штурма-Лиувилля (определять собственные функции ![]() ,
, ![]() и собственные значения
и собственные значения ![]() ) при граничных условиях
) при граничных условиях
Ясно, что, полагая радиальное смещение
Опишем кратко результаты в наиболее интересной с точки зрения
приложений области параметров
![]() ;
;
![]() [353,354,356].
[353,354,356].
- Высшие моды (
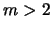 ) стабилизируются полностью при
) стабилизируются полностью при
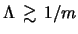 . Мода
. Мода 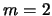 стабилизируется при
стабилизируется при
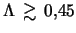 (в пределе
(в пределе
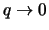 ). Этот результат нетрудно понять: во вращающейся
несжимаемой жидкости для раскачки возмущений с
). Этот результат нетрудно понять: во вращающейся
несжимаемой жидкости для раскачки возмущений с 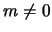 необходимо, чтобы
завихренность
необходимо, чтобы
завихренность
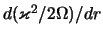 изменяла знак при конечном
изменяла знак при конечном
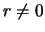 [357]. Для
[357]. Для 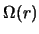 (4.5.3) точки изменения знака упомянутой
величины существуют при
(4.5.3) точки изменения знака упомянутой
величины существуют при
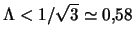 . Отклонение
границы устойчивости в нашем случае в меньшую сторону по параметру
. Отклонение
границы устойчивости в нашем случае в меньшую сторону по параметру
 обусловлено, по-видимому, стабилизирующим влиянием сжимаемости
среды.
обусловлено, по-видимому, стабилизирующим влиянием сжимаемости
среды.
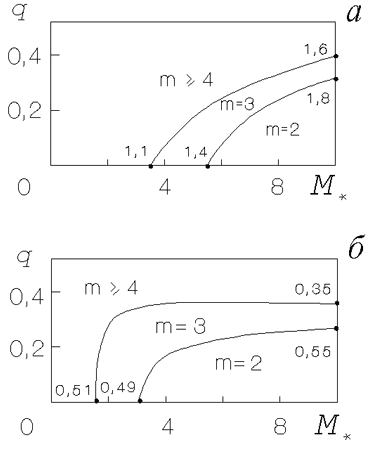
Рис. 4.9. Области доминирования различных мод (
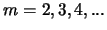 ) по
инкременту в плоскости
параметров
) по
инкременту в плоскости
параметров
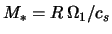 ;
;
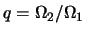 : a -- при
: a -- при
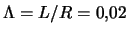 ; б -- при
; б -- при
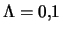 . Числа
в граничных точках кривых --
инкременты в единицах
. Числа
в граничных точках кривых --
инкременты в единицах 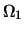 .
. - В области параметров
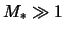 ,
, 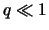 наиболее
неустойчивыми (без учета мод
наиболее
неустойчивыми (без учета мод 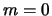 и
и 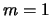 -- об этом см. ниже)
оказываются двухрукавные (
-- об этом см. ниже)
оказываются двухрукавные (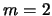 ) возмущения. Этот результат
иллюстрирует рис. 4.9, где в плоскости параметров
) возмущения. Этот результат
иллюстрирует рис. 4.9, где в плоскости параметров 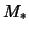 ,
, 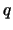 изображены
области доминирования по инкременту мод
изображены
области доминирования по инкременту мод 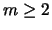 при
при
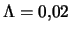 и
и
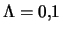 . Видно, что с ростом параметра
. Видно, что с ростом параметра 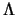 область
доминирования моды
область
доминирования моды 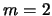 быстро расширяется.
быстро расширяется.
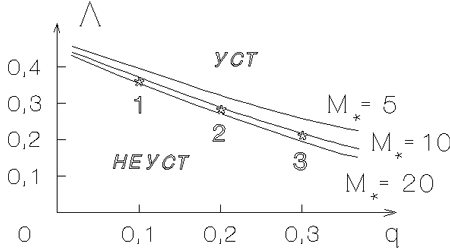
Рис. 4.10. Кривые маргинальной устойчивости моды
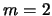 , каждая точка
которых [пара значений
(
, каждая точка
которых [пара значений
(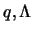 )] определяет профиль
кривой вращения (4.5.3),
для которого
)] определяет профиль
кривой вращения (4.5.3),
для которого
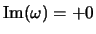 при
соответствующем значении
параметра
при
соответствующем значении
параметра 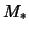 . Профили
. Профили
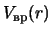 , соответствующие
точкам
, соответствующие
точкам 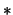 --
-- 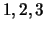 , -- см. рис. 4.11.
, -- см. рис. 4.11.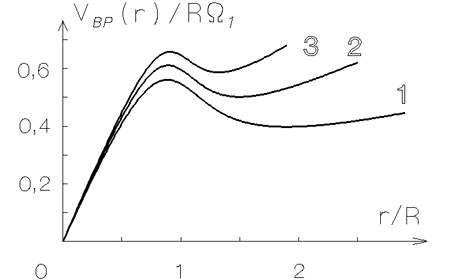
Рис. 4.11. Кривые вращения (окрестность внутреннего горба), допускающие возбуждение двухрукавного спирального узора с малым инкрементом (см. рис. 4.10) при
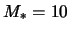 . Совокупность параметров
. Совокупность параметров
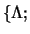

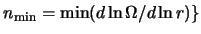 для
этих кривых имеет следующие значения:
1 --
для
этих кривых имеет следующие значения:
1 --
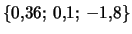 ;
2 --
;
2 --
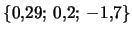 ;
3 --
;
3 --
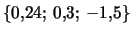 .
.
- Для двухрукавных возмущений область неустойчивости в
плоскости параметров
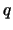 ,
, 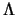 довольно велика (рис. 4.10) и ее размеры
слабо зависят от величины
довольно велика (рис. 4.10) и ее размеры
слабо зависят от величины 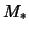 при
при 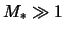 . На рис. 4.11 для примера
приведены три кривые вращения (4.5.3) (в окрестности внутреннего
горба), характеризуемые параметрами, обеспечивающими возбуждение
двухрукавной спирали в модели с
. На рис. 4.11 для примера
приведены три кривые вращения (4.5.3) (в окрестности внутреннего
горба), характеризуемые параметрами, обеспечивающими возбуждение
двухрукавной спирали в модели с 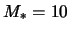 с малым инкрементом. Видно,
что для возбуждения спирального узора с помощью изучаемого нами
механизма плоской галактике достаточно обладать кривой вращения
даже со слабо выраженной двугорбостью. Такие кривые вращения
распространены довольно широко [29-31,45-48].
с малым инкрементом. Видно,
что для возбуждения спирального узора с помощью изучаемого нами
механизма плоской галактике достаточно обладать кривой вращения
даже со слабо выраженной двугорбостью. Такие кривые вращения
распространены довольно широко [29-31,45-48].
- С ростом параметра
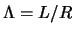 происходит некоторое уменьшение
происходит некоторое уменьшение
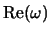 . При достаточно малом
. При достаточно малом
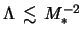 [см. условие (4.5.27)] отличие
[см. условие (4.5.27)] отличие
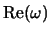 от значений (4.5.21)
не превышает 1% в соответствии с результатом (4.5.28). Но при конечных
от значений (4.5.21)
не превышает 1% в соответствии с результатом (4.5.28). Но при конечных
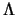 этот эффект становится заметным4.8и приводит к соответствующим росту шага спирали [см.(4.5.21)] и уменьшению
угловой скорости ее вращения
этот эффект становится заметным4.8и приводит к соответствующим росту шага спирали [см.(4.5.21)] и уменьшению
угловой скорости ее вращения
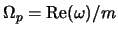 [см.(4.5.25)].
[см.(4.5.25)].
- Во всей исследованной области параметров
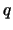 ,
, 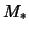 ,
, 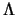 характерный масштаб убывания амплитуды возмущенной плотности
характерный масштаб убывания амплитуды возмущенной плотности 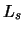 с
удалением от "разрыва" в область
с
удалением от "разрыва" в область 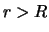 удовлетворительно
описывается соотношением [ср. с (4.5.26)]
удовлетворительно
описывается соотношением [ср. с (4.5.26)]
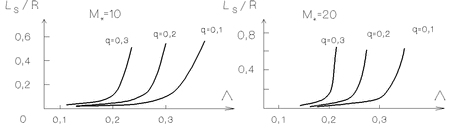 |
Рис. 4.12. Зависимость масштаба радиального убывания амплитуды
возмущенной плотности |
Таким образом, существенное уменьшение инкремента неустойчивости с
ростом параметра ![]() приводит к весьма заметному расширению области
локализации генерируемого спирального узора. Этот эффект
иллюстрирует рис. 4.12 [зависимость
приводит к весьма заметному расширению области
локализации генерируемого спирального узора. Этот эффект
иллюстрирует рис. 4.12 [зависимость ![]() ] и рис. 4.13, на котором
изображены примеры собственных функций возмущенной плотности
] и рис. 4.13, на котором
изображены примеры собственных функций возмущенной плотности
![]() .
.
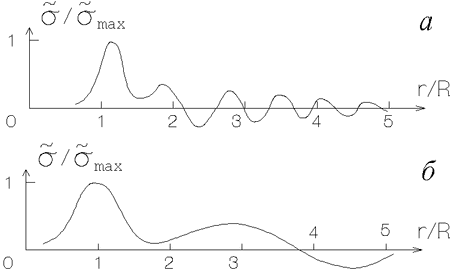 |
Рис. 4.13. Возмущенная
поверхностная
плотность
|
Важным также является вопрос о зависимости приведенных выше
результатов от характера кривой вращения за пределами зоны
"размазки" разрыва ![]() . Действительно, реальные кривые вращения
галактик в области
. Действительно, реальные кривые вращения
галактик в области ![]() обычно характеризуются законом вращения
обычно характеризуются законом вращения
![]() с
с ![]() , что существенно отличается от закона
вращения (4.5.3):
, что существенно отличается от закона
вращения (4.5.3):
![]() const при
const при ![]() . Да и
в области
. Да и
в области ![]() вращение реальных галактик заметно отличается от
твердотельного. С целью выяснения влияния этих факторов был проведен
сравнительный расчет устойчивости вращения газа в галактике M81 и в
модельной галактике с законом вращения (4.5.3) с практически совпадающими
участками
вращение реальных галактик заметно отличается от
твердотельного. С целью выяснения влияния этих факторов был проведен
сравнительный расчет устойчивости вращения газа в галактике M81 и в
модельной галактике с законом вращения (4.5.3) с практически совпадающими
участками
![]() между внутренним горбом и следующим за ним
минимумом
между внутренним горбом и следующим за ним
минимумом
![]() . Наблюдаемые части кривой вращения в областях
. Наблюдаемые части кривой вращения в областях ![]() кпк [41] и
кпк [41] и ![]() кпк [73] были сшиты полиномом третьей
степени в области
кпк [73] были сшиты полиномом третьей
степени в области
![]() . Распределение
. Распределение
![]() также бралось из наблюдений [73], а
также бралось из наблюдений [73], а ![]() полагалась монотонно
убывающей от
полагалась монотонно
убывающей от
![]() км/с до
км/с до
![]() км/с.
Вычисления были проведены для моды
км/с.
Вычисления были проведены для моды ![]() на основе уравнений, учитывающих
неоднородность
на основе уравнений, учитывающих
неоднородность ![]() и
и ![]() [ср. с (4.5.4),(4.5.5)]:
[ср. с (4.5.4),(4.5.5)]:
где
Рассмотрим теперь вопрос о возбуждении мод ![]() и
и ![]() .
Исключим из (4.5.4), (4.5.5) возмущенное давление, в результате для
.
Исключим из (4.5.4), (4.5.5) возмущенное давление, в результате для
![]() получим
получим
Отсюда видно, что неустойчивость моды ![]() (
(![]() ) может
иметь место только в том случае, если существует интервал
) может
иметь место только в том случае, если существует интервал
![]() , внутри которого (
, внутри которого (![]() ) величина
) величина
![]() отрицательна. Последнее может иметь место, если
отрицательна. Последнее может иметь место, если
Для большинства галактик с двугорбыми кривыми вращения ![]() и мода
и мода ![]() в них возбуждаться не может (в Галактике
в них возбуждаться не может (в Галактике
![]() по кривым вращения Хауда [35] и Клеменса [358]).
В то же время мода
по кривым вращения Хауда [35] и Клеменса [358]).
В то же время мода ![]() неустойчива и при
неустойчива и при ![]() , что показали
расчеты [352,353,356] (см. рис. 4.11).
, что показали
расчеты [352,353,356] (см. рис. 4.11).
Исследуя осесимметричный механизм возбуждения спиралей в
изолированной галактике, мы должны исключить из рассмотрения моду
![]() , поскольку раскачка таких возмущений сдвигает центр масс
газовой подсистемы относительно центра масс звездной [
, поскольку раскачка таких возмущений сдвигает центр масс
газовой подсистемы относительно центра масс звездной [
![]() ].
Последнее возможно, по-видимому, только при наличии внешних
воздействий на рассматриваемую систему.
].
Последнее возможно, по-видимому, только при наличии внешних
воздействий на рассматриваемую систему.
В заключение рассмотрим вопрос о влиянии возмущений
гравитационного потенциала на параметры генерируемой спиральной
структуры с учетом приведенной во введении к данному разделу
оценки: ![]() . Для этого в рамках рассмотренной выше модели
разрыва
. Для этого в рамках рассмотренной выше модели
разрыва ![]() (при
(при ![]() ) заменим возмущенное давление
) заменим возмущенное давление
![]() на
на
![]() , где
, где
![]() ,
а величину
,
а величину ![]() (4.5.30) на
(4.5.30) на ![]() , определяемую из соотношения
, определяемую из соотношения
![]()
![]() . Решая исправленное с учетом этой замены
дисперсионное уравнение (4.5.15) методом возмущений (
. Решая исправленное с учетом этой замены
дисперсионное уравнение (4.5.15) методом возмущений (
![]() ), находим [353]
), находим [353]
Отсюда видно, что, несмотря на дестабилизирующее влияние
(довольно слабое) возмущений гравитационного потенциала, масштаб
убывания амплитуды возмущенной плотности не изменяется. Это
связано с тем, что наряду с появлением поправки к
![]() (4.5.37) изменяется и определение
(4.5.37) изменяется и определение ![]() через частоту. В
результате оба эффекта взаимно компенсируются. Уменьшается лишь шаг
спирали [ср. с (4.5.24)]:
через частоту. В
результате оба эффекта взаимно компенсируются. Уменьшается лишь шаг
спирали [ср. с (4.5.24)]:
4.5.5 Скачок плотности
(Данный раздел написан совместно с В.В. Мусцевым.)
Исследуем теперь вопрос о влиянии резкого изменения плотности
газового диска в окрестности "разрыва" ![]() на параметры центробежной
неустойчивости и возбуждаемых структур. Прежде всего заметим, что
рассмотренные выше однородные модели с ТР угловой скорости были
изэнтропическими (
на параметры центробежной
неустойчивости и возбуждаемых структур. Прежде всего заметим, что
рассмотренные выше однородные модели с ТР угловой скорости были
изэнтропическими (
![]() ). При наличии скачка плотности
необходимо исходить из неизэнтропических
моделей. Действительно, для разрывной модели с (4.5.2) и
). При наличии скачка плотности
необходимо исходить из неизэнтропических
моделей. Действительно, для разрывной модели с (4.5.2) и
Запишем условия сшивки для возмущенных величин ![]() и
и ![]() ,
исходя из (4.5.32), (4.5.33):
,
исходя из (4.5.32), (4.5.33):
для
Ниже ограничимся случаем
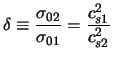 .
Действуя в духе п. 4.5.1, получим дисперсионное уравнение
.
Действуя в духе п. 4.5.1, получим дисперсионное уравнение
где
В пределе ![]() получаем
получаем
4.5.6 Неоднородные газовые диски с двугорбыми кривыми вращения
Выше мы рассмотрели предельный случай совмещенных разрывов в
распределениях
![]() и
и ![]() . Ясно, что предположения о
разрывности определяющих неустойчивость равновесных параметров и
совмещенности этих разрывов существенно идеализируют наблюдаемые
распределения. Кроме того, по крайней мере в Галактике не
выполняется условие
. Ясно, что предположения о
разрывности определяющих неустойчивость равновесных параметров и
совмещенности этих разрывов существенно идеализируют наблюдаемые
распределения. Кроме того, по крайней мере в Галактике не
выполняется условие ![]() const.
const.
Следует отметить еще одно обстоятельство. При численном
моделировании процесса возбуждения спирального узора в галактике с
двугорбой кривой вращения выяснилось, что в однородном (в
начальный момент) газовом диске раскачка неустойчивости приводит к
возникновению в окрестности внутреннего максимума
![]() резкого
градиента плотности, напоминающего наблюдаемый в Галактике4.9 [361]. Поэтому весьма актуально исследование влияния
скачка плотности на параметры возбуждаемого узора.
резкого
градиента плотности, напоминающего наблюдаемый в Галактике4.9 [361]. Поэтому весьма актуально исследование влияния
скачка плотности на параметры возбуждаемого узора.
Рассмотрим класс моделей, в котором распределения равновесных
термодинамических величин определены соотношением
Таким образом, по распределению
Выберем конкретное распределение ![]() в виде центрированной
на
в виде центрированной
на ![]() и "размазанной" на область шириной
и "размазанной" на область шириной
![]() ступеньки:
ступеньки:
обеспечивает выход на "плато" при достаточном удалении от центра (
Будем исходить из уравнений (4.5.32), (4.5.33). Данная
система должна служить для определения как собственных функций
![]() ,
, ![]() , так и собственного значения -- частоты
, так и собственного значения -- частоты
![]() . Простой анализ уравнений (4.5.32) и (4.5.33) в пределе
. Простой анализ уравнений (4.5.32) и (4.5.33) в пределе
![]() показывает, что
показывает, что
![]() ,
,
![]() . Асимптотика решений при
. Асимптотика решений при
![]() с учетом свойств нашей модели имеет вид
с учетом свойств нашей модели имеет вид
![]() . В этой
асимптотике выбор знака перед мнимой единицей в экспоненте
обеспечивает убывание амплитуды неустойчивых (
. В этой
асимптотике выбор знака перед мнимой единицей в экспоненте
обеспечивает убывание амплитуды неустойчивых (
![]() ) возмущений с удалением от области скачка
) возмущений с удалением от области скачка ![]() . Таким образом,
естественные граничные условия для системы (4.5.32), (4.5.33) в
случае возмущений с
. Таким образом,
естественные граничные условия для системы (4.5.32), (4.5.33) в
случае возмущений с ![]() имеют следующий вид:
имеют следующий вид:
Влияние вида кривой
![]() на параметры неустойчивости было
изучено в п. 4.5.4. Поэтому здесь зафиксируем кривую вращения:
на параметры неустойчивости было
изучено в п. 4.5.4. Поэтому здесь зафиксируем кривую вращения: ![]() ;
;
![]() ;
;
![]() [вид
[вид
![]() при
таких значениях параметров показан на рис. 4.14]. Число спиралей будем
полагать равным двум (
при
таких значениях параметров показан на рис. 4.14]. Число спиралей будем
полагать равным двум (![]() ). Сосредоточим наше внимание на параметрах
модели газового диска. К ним прежде всего относится величина
скачка поверхностной плотности газа
). Сосредоточим наше внимание на параметрах
модели газового диска. К ним прежде всего относится величина
скачка поверхностной плотности газа ![]() . В Галактике
. В Галактике
![]() [70]. Параметр
[70]. Параметр ![]() [см. (4.5.45)], определяющий
величину радиального градиента давления, относится, по-видимому,
к числу труднонаблюдаемых. Параметром
[см. (4.5.45)], определяющий
величину радиального градиента давления, относится, по-видимому,
к числу труднонаблюдаемых. Параметром
![]() удобно описывать
смещение центров скачков
удобно описывать
смещение центров скачков ![]() и
и ![]() . Для значений параметров
. Для значений параметров
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() численное решение поставленной выше задачи типа
Штурма-Лиувилля показывает, что при всех значениях рассматриваемых
параметров имеет место неустойчивость, приводящая к возбуждению
двухрукавной спирали [
численное решение поставленной выше задачи типа
Штурма-Лиувилля показывает, что при всех значениях рассматриваемых
параметров имеет место неустойчивость, приводящая к возбуждению
двухрукавной спирали [
![]() ] [356]. Такая растущая по
амплитуде пропорционально
] [356]. Такая растущая по
амплитуде пропорционально
![]() спираль вращается с
угловой скоростью
спираль вращается с
угловой скоростью
![]() . По поведению собственных
функций
. По поведению собственных
функций ![]() в принципе возможно определение длины волны
спирального узора
в принципе возможно определение длины волны
спирального узора ![]() на известном расстоянии от центра диска. Эта
величина, конечно, локальная. В случае однородного диска рассматриваемая
модель для
на известном расстоянии от центра диска. Эта
величина, конечно, локальная. В случае однородного диска рассматриваемая
модель для ![]() ,
, ![]() дает
дает
![]() . Отклонение
. Отклонение ![]() от величины
от величины
![]() почти на всей плоскости
почти на всей плоскости
![]() незначительно.
Только в области параметров газового диска
незначительно.
Только в области параметров газового диска ![]() ,
,
![]() возможно заметное увеличение угловой скорости вращения спирального узора
возможно заметное увеличение угловой скорости вращения спирального узора
![]() по сравнению с
по сравнению с
![]() . Расчеты показывают, что
величина
. Расчеты показывают, что
величина ![]() также слабо зависит от всех параметров модели, кроме
параметра
также слабо зависит от всех параметров модели, кроме
параметра ![]() :
:
![]() при
при ![]() и
и
![]() при
при ![]() .
.
Таким образом, учет реальных (конечной ширины) скачков
плотности в газовом диске не может в рамках линейной теории
привести к существенному изменению основного динамического
параметра спирального узора ![]() .
.
Могут ли какие-нибудь другие физические факторы привести к
заметному уменьшению величины ![]() ? Аналоговое моделирование
спирального узора (см. разд. 6.2) показывает различие между
предсказываемой линейной теорией величиной
? Аналоговое моделирование
спирального узора (см. разд. 6.2) показывает различие между
предсказываемой линейной теорией величиной
![]() и
ее экспериментальным значением
и
ее экспериментальным значением
![]() (
(
![]() )4.10. При этом ширины скачков угловой скорости
)4.10. При этом ширины скачков угловой скорости ![]() и
толщины слоя "мелкой воды"
и
толщины слоя "мелкой воды" ![]() -- аналога
-- аналога ![]() -- в экспериментах
были почти одинаковыми, а сами скачки -- практически совмещенными.
По-видимому, обсуждаемое различие между
-- в экспериментах
были почти одинаковыми, а сами скачки -- практически совмещенными.
По-видимому, обсуждаемое различие между
![]() и
и
![]() обусловлено нелинейностью эксперимента. Это подтверждается тем, что
высокомодовые возмущения (число спиралей
обусловлено нелинейностью эксперимента. Это подтверждается тем, что
высокомодовые возмущения (число спиралей ![]() ) обладают малой
амплитудой и для них различие экспериментального и теоретического
значений
) обладают малой
амплитудой и для них различие экспериментального и теоретического
значений ![]() существенно меньше, чем в случае возбуждения моды
существенно меньше, чем в случае возбуждения моды
![]() , обладающей сравнительно большей амплитудой. В связи с
вышесказанным особую роль в дальнейшем развитии гидродинамической
концепции происхождения спирального узора будут, вероятно, играть
совершенствование методики наблюдательного определения параметра
, обладающей сравнительно большей амплитудой. В связи с
вышесказанным особую роль в дальнейшем развитии гидродинамической
концепции происхождения спирального узора будут, вероятно, играть
совершенствование методики наблюдательного определения параметра
![]() и развитие численного эксперимента.
и развитие численного эксперимента.
4.5.7 Низкочастотная центробежная неустойчивость
Проведенное выше рассмотрение выявило одну неустойчивую моду,
поддерживаемую при
![]() центробежным механизмом, а при
центробежным механизмом, а при
![]() -- механизмом неустойчивости Кельвина-Гельмгольца. В то же
время существование наряду с основной неустойчивой модой и ее
высших гармоник в плоскопараллельных сверхзвуковых потоках газа --
хорошо известный факт (см. [364-367], п. 5.3.2). В
осесимметричных сверхзвуковых течениях с дифференциальным
вращением высшие неустойчивые гармоники были открыты не так давно
в системах со степенной зависимостью скорости вращения от радиуса
вида
-- механизмом неустойчивости Кельвина-Гельмгольца. В то же
время существование наряду с основной неустойчивой модой и ее
высших гармоник в плоскопараллельных сверхзвуковых потоках газа --
хорошо известный факт (см. [364-367], п. 5.3.2). В
осесимметричных сверхзвуковых течениях с дифференциальным
вращением высшие неустойчивые гармоники были открыты не так давно
в системах со степенной зависимостью скорости вращения от радиуса
вида
![]() ,
, ![]() (см. [368-370], п. 5.3.3).
(см. [368-370], п. 5.3.3).
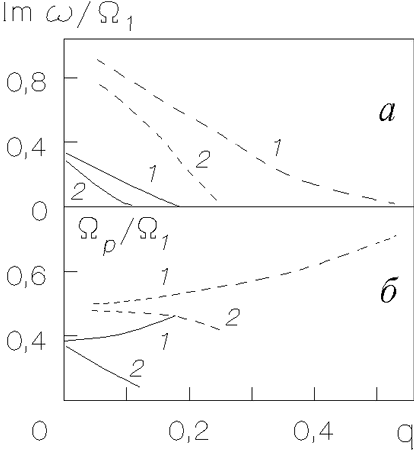 |
Рис. 4.15. Зависимости
безразмерного инкремента
|
В работе [371] в рамках модели, описываемой уравнениями
(4.5.32), (4.5.33), с кривой вращения (4.5.3), характерной для
газовых дисков галактик, было показано наличие второй неустойчивой
моды. Эта новая для нас мода отличается от рассмотренной выше
меньшими значениями как
![]() , так и
, так и
![]() (рис. 4.15).
(рис. 4.15).
В соответствии с этим основную моду центробежной
неустойчивости далее будем называть высокочастотной, а вторую --
низкочастотной. Кроме того, что высокочастотная мода обладает
большим инкрементом во всей рассмотренной области значений
параметров (см. рис. 4.15), возмущения этой моды могут нарастать в
тех диапазонах параметров, где низкочастотная мода
стабилизируется, а именно при меньшем скачке скорости вращения и
при малых числах Маха (
![]() ). Развитие возмущений обеих мод
приводит к генерации отстающих логарифмических спиральных волн. В
достаточно широкой области значений параметров зависимости
). Развитие возмущений обеих мод
приводит к генерации отстающих логарифмических спиральных волн. В
достаточно широкой области значений параметров зависимости
![]() и
и
![]() от
от ![]() для обеих мод приблизительно
параллельны, причем имеются участки, где различие не превышает 10
для обеих мод приблизительно
параллельны, причем имеются участки, где различие не превышает 10
![]() 30 % [371]. Таким образом, при определенных условиях возможно
их одновременное возбуждение.
30 % [371]. Таким образом, при определенных условиях возможно
их одновременное возбуждение.
Морозов и Мусцевой [372] высказали предположение о
существовании аналогичных высокочастотной и низкочастотной мод для
возмущений с ![]() для галактических кривых вращения вида (4.5.3),
(4.5.48) (по
крайней мере, в моделях со степенными зависимостями скорости
вращения от
для галактических кривых вращения вида (4.5.3),
(4.5.48) (по
крайней мере, в моделях со степенными зависимостями скорости
вращения от ![]() обнаруживается целый ряд неустойчивых отражательных
гармоник для различных
обнаруживается целый ряд неустойчивых отражательных
гармоник для различных ![]() (см. п. 5.3.3)).
(см. п. 5.3.3)).
Физический механизм раскачки низкочастотной моды носит
смешанный центробежно-резонансный характер, поэтому рассмотренный
случай имеет сходство со случаем моделей со степенным законом
вращения, где неустойчивость развивается из-за резонансного
излучения энергии на радиусе коротации (на котором имеется
синхронное вращение волнового узора с веществом диска) и
взаимодействия волн противоположных знаков энергии
(сверхотражения). Важность центробежных эффектов для поддержания
низкочастотной моды очевидна, так как она стабилизируется при
![]() . На резонансный характер этой моды указывает, в частности, ее
стабилизация при
. На резонансный характер этой моды указывает, в частности, ее
стабилизация при
![]() 4.11, поскольку для усиления из-за
резонансного взаимодействия волны с потоком необходимо наличие
критического слоя конечной толщины вблизи радиуса коротации, где
профиль скорости является монотонным. Другим доводом является ее
существенно сверхзвуковой характер -- низкочастотная мода
стабилизируется при уменьшении числа Маха до
4.11, поскольку для усиления из-за
резонансного взаимодействия волны с потоком необходимо наличие
критического слоя конечной толщины вблизи радиуса коротации, где
профиль скорости является монотонным. Другим доводом является ее
существенно сверхзвуковой характер -- низкочастотная мода
стабилизируется при уменьшении числа Маха до ![]() , что совпадает
с пороговым значением для сверхотражения, когда резонансное
усиление становится невозможным (см. рис. 4.15) [327,373,374] (см.
разд. 5.3).
, что совпадает
с пороговым значением для сверхотражения, когда резонансное
усиление становится невозможным (см. рис. 4.15) [327,373,374] (см.
разд. 5.3).
Следует отметить, что для раскачки низкочастотной моды
принципиально необходимо либо выполнение условия
![]() , но не
, но не
![]() , т.е. наличие конечной "размазки" скачка скорости,
либо при
, т.е. наличие конечной "размазки" скачка скорости,
либо при
![]() наличие внутренней относительно разрыва
скорости отражающей поверхности (твердой стенки или скачка плотности),
расположенной на таком радиусе
наличие внутренней относительно разрыва
скорости отражающей поверхности (твердой стенки или скачка плотности),
расположенной на таком радиусе ![]() , что не имеет места условие
, что не имеет места условие
![]() (выписанное здесь соотношение
(выписанное здесь соотношение
![]() аналогично
условию, при котором может быть неустойчив плоский слой сдвига:
аналогично
условию, при котором может быть неустойчив плоский слой сдвига:
![]() , где
, где ![]() -- волновое число возмущений вдоль слоя,
-- волновое число возмущений вдоль слоя, ![]() --
его характерная толщина; последнее утверждение очевидно, если учесть, что
величина
--
его характерная толщина; последнее утверждение очевидно, если учесть, что
величина ![]() имеет смысл азимутального волнового числа). Из сказанного
ясно, что спиральные узоры, обусловленные низкочастотной модой, не могли
наблюдаться в экспериментах с "мелкой водой" (гл. 6), поскольку в них,
вообще говоря, не выполнялось ни одно из указанных условий.
имеет смысл азимутального волнового числа). Из сказанного
ясно, что спиральные узоры, обусловленные низкочастотной модой, не могли
наблюдаться в экспериментах с "мелкой водой" (гл. 6), поскольку в них,
вообще говоря, не выполнялось ни одно из указанных условий.
<< 4.4 Диссипативные эффекты | Оглавление | 4.6 Неосесимметричный потенциал >>