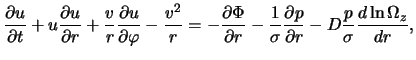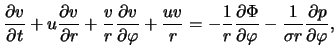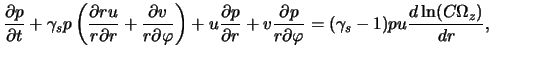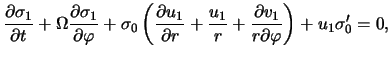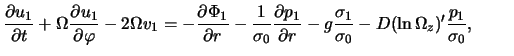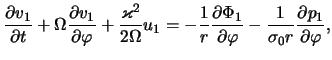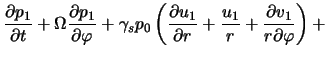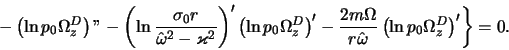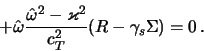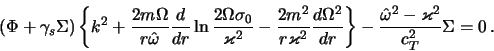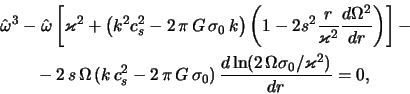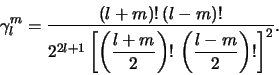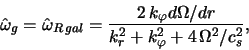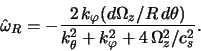Астронет > 4.2 Динамика возмущений в плоскости диска

Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков
http://variable-stars.ru/db/msg/1168623/node25.html

Физика Дисков

<< 4.1 Равновесные газовые диски | Оглавление | 4.3 Неустойчивости газового грав... >>

4.2 Динамика возмущений в плоскости диска

4.2.1 Постановка задачи

В соответствии с проведенным в п. 4.1.2 исследованием поставим задачу изучения дисперсионных свойств неосесимметричных возмущений в плоскости тонкого газового диска [324,325]. Исходные уравнения газодинамики в этой модели в соответствии с (4.1.7), (4.1.10), (4.1.15) имеют вид^4.2

	(4.2.1)
	(4.2.2)
	(4.2.3)
	(4.2.4)

где

-- радиальная и азимутальная компоненты скорости газа,

-- поверхностные плотность и давление в газовом диске, а диссипативные члены опущены (исследованию диссипативных эффектов посвящен разд. 4.4).

Для изучения динамики малых возмущений линеаризуем систему (4.2.1)-(4.2.4). Для этого представим входящие в эту систему переменные в виде сумм равновесных и возмущенных величин:

(4.2.5)

В результате получим

	(4.2.6)
	(4.2.7)
	(4.2.8)

	(4.2.9)

где штрих означает производную вдоль радиальной координаты и в соответствии с условием равновесия (4.1.11),

(4.2.10)

Дополним систему (4.2.6) (2.2.9) линеаризованным уравнением Пуассона

(4.2.11)

Зависимость возмущенных величин

(4.2.12)

от азимутальной кооpдинаты

и вpемени

в связи со стационаpностью и одноpодностью pассматpиваемой pавновесной модели в азимутальном напpавлении пpедставим в виде

(4.2.13)

Тогда система (4.2.6)-(4.2.9), (4.2.11) пеpейдет в (индекс "1" у возмущенных величин опускаем и считаем

)

(4.2.14)

(4.2.15)

(4.2.16)

(4.2.17)

(4.2.18)

где

-- изотеpмическая скоpость звука,

-- адиабатическая скоpость звука.

Исключим из пpиведенной выше системы возмущенные скоpости. Для этого из (4.2.16) находим

(4.2.19)

и, подставляя это выpажение в (4.2.15), получим

(4.2.20)

Диффеpенциpуя затем (4.2.20) по pадиальной кооpдинате и подставляя pезультат вместе с (4.2.19), (4.2.20) в (4.2.14), пpиводим (4.2.14) к виду

(4.2.21)

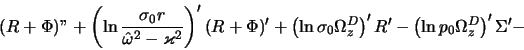
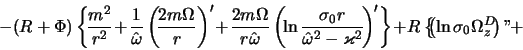
Подставляя также (4.2.20) в (4.2.17), получаем втоpое уpавнение, связывающее

(4.2.22)

Система уравнений (4.2.21), (4.2.22) вместе с уравнением Пуассона (4.2.18) является исходной для дальнейшего анализа динамики малых возмущений в модели газового диска с произвольными распределениями , , .

4.2.2 Дисперсионное уравнение в изэнтропическом диске

Рассмотрим изэнтропическую модель. В ней

(4.2.23)

В этой модели связь между

определяется соотношением

(4.2.24)

где

-- "плоский" показатель политропы (см. п. 4.1.1). Если считать для системы "макроатомов" газового диска -- облаков

, тогда в соответствии с (4.1.16)

и, следовательно,

. Отсюда ясно, что изэнтропическая модель не пpотивоpечит данным наблюдений по газовому диску Галактики. Поэтому в первую очередь проведем дальнейший анализ в рамках изэнтропической модели с

(более общий случай будет рассмотрен ниже).

В изэнтропической модели из (4.2.22) вытекает

(4.2.25)

Эта связь приводит уравнение (4.2.21) к виду

(4.2.26)

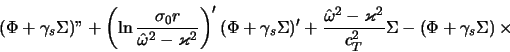
Определенный прогресс в понимании физики гравитирующего газового диска, и в частности в определении условия его гравитационной устойчивости относительно осесимметричных возмущений был достигнут с помощью ВКБ-анализа в радиальном направлении. Это обусловлено тем обстоятельством, что протяженность диска и характерные масштабы его неоднородности в радиальном направлении настолько велики по сравнению с его толщиной, что наряду с выполнением условия (4.1.18) могут быть выполнены и условия применимости ВКБ-приближения [ -- см. (4.2.13)]:

(4.2.27)

где

Нетрудно, однако, видеть, что ВКБ-приближение применимо только к тем из неосесимметричных возмущений, описываемых уравнением (4.2.26), для которых выполняется условие

(4.2.28)

в общем случае не более жесткое, чем условие

. Таким образом, мы можем изучать свойства коротковолновых возмущений, заметно отличающихся от осесимметричных, только в низкочастотной по

части спектра. Это ограничение, однако, не является, существенным для изучения гравитационной неустойчивости газового диска. Действительно, граница устойчивости газового диска относительно осесимметричных возмущений определяется из условия

в минимуме дисперсионной кривой

. Для решения вопроса об определении границы устойчивости диска относительно неосесимметричных возмущений следует исходить из того, что в любой неоднородной системе должны существовать коротковолновые градиентные возмущения, максимальная частота которых

, где

-- частота собственных колебаний системы без учета ее неоднородности. Например, в атмосфере Земли частота звука

, а частота внутренних гравитационных волн

[327], где

-- вертикальный масштаб неоднородности атмосферы,

-- ускорение силы тяжести. Аналогично в звездном диске частота джинсовских возмущений

везде, за исключением окрестности минимума дисперсионной кривой

, а максимальная частота градиентных

(см. п. 2.2.4). То же самое утверждение, очевидно, справедливо и для газового диска. При этом граница устойчивости будет определяться в области "контакта" джинсовской и градиентной ветвей [минимума дисперсионной кривой

], где

. Кроме того, дисперсионные свойства низкочастотных градиентных возмущений могут представлять и независимый интерес (см., например, пункты, посвященные волнам Россби и градиентно-энтропийной неустойчивости).

Будем поэтому рассматривать возмущения, частоты и азимутальные волновые номера которых удовлетворяют условию (4.2.28). При выполнении этого условия члены с первыми производными от и по радиальной координате в (4.2.26) оказываются пренебрежимо малыми по сравнению с первым членом. Поэтому отбрасывая в (4.2.26) все малые по условиям (4.2.27), (4.2.28) члены, получим

(4.2.29)

Используя затем коротковолновое решение уравнения Пуассона для тонкого диска [1,2]

(4.2.30)

приходим к искомому дисперсионному уравнению для изэнтропического газового диска

(4.2.31)

где

-- параметр, характеризующий степень неосесимметричности возмущений.

В работе [195] был проведен анализ устойчивости твердотельно вращающегося ( const) газового диска с плотностью

(4.2.32)

и политропным уравнением состояния

(4.2.33)

где

;

. В этой модели без использования ВКБ-приближения было получено дисперсионное уравнение, описывающее свойства произвольных возмущений в плоскости диска:

(4.2.34)

где

(4.2.35)

Поскольку модель (4.2.32), (4.2.33) также является изэнтропической, представляет интерес сравнить дисперсионное уравнение (4.2.34) в коротковолновом

пределе с дисперсионным уравнением (4.2.31) в твердотельно вращающемся

пределе.

В изэнтропических моделях , откуда заключаем, что в модели (4.2.33) . В коротковолновом пределе , используя асимптотику гамма-функции, получаем и соответственно

Для определения аналога волнового числа

замечаем, что [2]

Сравнивая это выражение с ВКБ-решением уравнения Пуассона (4.2.30), приходим к выводу, что

. Наконец

и поэтому уравнение (4.2.34) может быть записано в виде

(4.2.36)

тождественно совпадающем с уравнением (4.2.31) в пределе

const. Этот факт служит дополнительным аргументом в пользу корректности приближения (4.2.28), использованного для ВКБ-анализа дисперсионных свойств возмущений в гораздо более сложной, чем (4.2.33), модели газового диска с произвольными распределениями

4.2.3 Волны Россби

Дисперсионное уравнение (4.2.31) описывает три ветви колебаний газового диска. Если пренебречь неоднородностью диска и дифференциальностью его вращения, то нетрудно убедиться, что две из них гравитационные (джинсовские) и их частоты определяются из условия баланса кубического и линейного по членов (частота третьей ветви в этом случае ). Появление третьего типа возмущений связано с неоднородностью диска и дифференциальностью его вращения (проявление сдвиговой упругости неоднородной среды) и их частота в гравитационно устойчивом (см. разд. 4.3) диске может быть приближенно определена из условия баланса линейного по и свободного в (4.2.31) членов [324]:

(4.2.37)

Нетрудно видеть, что по (4.2.37) удовлетворяет условию (4.2.28) при любых длинах волн возмущений . Аналогичные ветви колебаний, частоты которых пропорциональны градиентам невозмущенных величин, имеют место в атмосферах и океанах планет (внутренние гравитационные волны и волны Россби -- см. [327,328], плазме (дрейфовые волны -- см. [193], звездном диске (см. гл. 2) и других неоднородных средах. Выражение (4.2.37) описывает волны, имеющие черты как внутренних гравитационных волн, так и волн Россби [329]. Для доказательства второй части этого утверждения перейдем к естественному для атмосфер планет пределу однородной (вдоль поверхности планеты) несамогравитирующей среды (формально , ). Тогда, полагая вращение диска слабо дифференциальным ( для ), из (4.2.37) получаем

(4.2.38)

где

В атмосферах планет закон дисперсии коротковолновых баротропных возмущений Россби [328] имеет вид

(4.2.39)

Конкретные значения параметров, характеризующих динамику и геометрию упомянутых выше вихревых структур, аналогичных планетарным антициклоническим солитонам Россби, в газовых дисках галактик должны, очевидно, вычисляться в нелинейной теории. В связи с этим интересна попытка прямого переноса результатов теории солитонов Россби на "мелкой воде" на случай газового диска, предпринятая Корчагиным и Петвиашвили [330]. Полученный ими солитон имеет характерный радиус порядка или больше эпициклического ( ) и, следовательно, соответствует возмущениям с . Используя результаты п. 4.1.2, нетрудно показать, что в гравитационно устойчивом газовом диске и, следовательно, . Таким образом, на структуру и динамику такого солитона определяющее влияние должны оказывать возмущения гравитационного потенциала, обусловленные возмущениями поверхностной плотности диска (см. различие дисперсионных свойств планетарных и галактических волн Россби в области спектра ).

Указанное обстоятельство подчеркивает необходимость выявления достаточно эффективного и несамоподавляющегося механизма возбуждения волн Россби в гравитирующих газовых подсистемах галактик. Один из возможных таких механизмов будет описан в п. 4.3.5.

<< 4.1 Равновесные газовые диски | Оглавление | 4.3 Неустойчивости газового грав... >>