 |
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://www.astronet.ru/db/msg/1168623/node18.html |
<< 3.1 Модели | Оглавление | 3.3 Гравитационная устойчивость ... >>
- 3.2.1 "Глобальный" критерий устойчивости
- 3.2.2 Устойчивость диска относительно возбуждения бар-моды
- 3.2.3 Центральная депрессия звездной плотности
- 3.2.4 Модели с "живым" гало
3.2 Крупномасштабная структура звездных дисков
3.2.1 "Глобальный"
критерий устойчивости
Рассмотрим результаты экспериментов со звездным диском без
гало (![]() ). В таких системах интересные
процессы протекают в центральной части диска. Проследим
эволюцию первоначально осесимметричной системы, находящейся в
основном на балансе
гравитационной и центробежной сил [
). В таких системах интересные
процессы протекают в центральной части диска. Проследим
эволюцию первоначально осесимметричной системы, находящейся в
основном на балансе
гравитационной и центробежной сил [
![]() , см. (3.1.3)]. Такая
система оказывается неустойчивой и ее развитие заключается в росте
дисперсии скоростей частиц. Одновременно происходит
перераспределение плотности вещества, скорости вращения и
искажение осесимметричной формы диска в бароподобную.
, см. (3.1.3)]. Такая
система оказывается неустойчивой и ее развитие заключается в росте
дисперсии скоростей частиц. Одновременно происходит
перераспределение плотности вещества, скорости вращения и
искажение осесимметричной формы диска в бароподобную.
По-видимому, первая экспериментальная попытка
охарактеризовать устойчивое стационарное состояние
бесстолкновительного гравитирующего диска одним "глобальным"
параметром была предпринята Острайкером и Пиблсом [216]. В
качестве такого параметра ими была выбрана величина, равная
половине доли кинетической энергии частиц системы, приходящейся на
их среднее (макроскопическое) движение. Поскольку для
гравитирующих систем справедлива теорема вириала в форме
![]() , где
, где ![]() -- кинетическая, а
-- кинетическая, а ![]() -- потенциальная энергия
системы, то упомянутый параметр можно записать в виде
-- потенциальная энергия
системы, то упомянутый параметр можно записать в виде
где
заметно отличающуюся от
Примерно за один-два оборота первоначально холодный диск
сильно разогревается, энергия вращательного движения переходит в
энергию случайного движения, что приводит к
Экспериментальное вычисление параметра ![]() , учитывающего
некруговые движения частиц в диске, дает [217]
, учитывающего
некруговые движения частиц в диске, дает [217]
Результат (3.2.4) требует некоторого уточнения, связанного с
тем, что теорема вириала для гравитирующих систем (![]() )
непосредственно к экспериментальным моделям не применима.
Действительно, ньютоновский потенциал -- однородная функция
)
непосредственно к экспериментальным моделям не применима.
Действительно, ньютоновский потенциал -- однородная функция ![]() (
(![]() ) степени координат [52]. Но используемый в
экспериментальных моделях потенциал с мягким "обрезанием"
гравитационного взаимодействия на малых расстояниях (см. п. 3.1.2)
при
) степени координат [52]. Но используемый в
экспериментальных моделях потенциал с мягким "обрезанием"
гравитационного взаимодействия на малых расстояниях (см. п. 3.1.2)
при ![]() (
(![]() -- радиус "обрезания") близок к квадратичному
потенциалу (
-- радиус "обрезания") близок к квадратичному
потенциалу (![]() ). С учетом того, что
). С учетом того, что ![]() (
(![]() -- радиус диска),
можно считать, что в среднем по диску
-- радиус диска),
можно считать, что в среднем по диску
![]() , где
, где
![]() . Тогда
. Тогда
![]() ,
,
![]() -- энергия системы. Сравнивая экспериментальные
значения величин
-- энергия системы. Сравнивая экспериментальные
значения величин ![]() и
и
![]() , можно
оценить
, можно
оценить ![]() . По результатам экспериментов [217,218]
. По результатам экспериментов [217,218]
![]() .
.
Представляет интерес вопрос о влиянии начального
распределения поверхностной плотности
![]() на устойчивость
бар-моды. Суммируя результаты многочисленных экспериментов, можно
сказать, что модели, для которых в начальный момент времени
характерна не очень высокая степень концентрации массы к центру
диска, укладываются по параметру
на устойчивость
бар-моды. Суммируя результаты многочисленных экспериментов, можно
сказать, что модели, для которых в начальный момент времени
характерна не очень высокая степень концентрации массы к центру
диска, укладываются по параметру ![]() в рамки, указанные
Острайкером и Пиблсом [см. (3.2.4)]. В моделях с более плотной
центральной частью диска величины
в рамки, указанные
Острайкером и Пиблсом [см. (3.2.4)]. В моделях с более плотной
центральной частью диска величины ![]() ,
,
![]() ,
, ![]() к концу
экспериментов оказываются меньшими. Этот эффект связан,
по-видимому, с большей интенсивностью релаксационных процессов в
более плотных системах. В экспериментах, стартующих из состояний с
начальной дисперсией радиальных скоростей
к концу
экспериментов оказываются меньшими. Этот эффект связан,
по-видимому, с большей интенсивностью релаксационных процессов в
более плотных системах. В экспериментах, стартующих из состояний с
начальной дисперсией радиальных скоростей
![]() [такой диск должен быть гравитационно устойчив
относительно мелкомасштабных возмущений (см. разд. 2.3)], конечное значение
параметра
[такой диск должен быть гравитационно устойчив
относительно мелкомасштабных возмущений (см. разд. 2.3)], конечное значение
параметра ![]() оказывается таким же, что и в экспериментах с
оказывается таким же, что и в экспериментах с
![]() 3.6. Но с увеличением
3.6. Но с увеличением ![]() степень бароподобного искажения
диска несколько уменьшается, а
степень бароподобного искажения
диска несколько уменьшается, а
![]() увеличивается примерно на
увеличивается примерно на
![]() .
.
Соотношения (3.2.4), (3.2.5) означают, что плоские гравитирующие системы без сфероидальных подсистем в стационарном состоянии должны быть достаточно "горячими" -- в пекулярных движениях звезд должно быть заключено более половины их кинетической энергии. В таких системах, как правило, возбуждается бар-мода, а дисперсия радиальных скоростей частиц даже на периферии диска не меньше половины величины круговой скорости вращения его вещества.
3.2.2 Устойчивость диска относительно возбуждения бар-моды
Начиная с классификации галактик Хаббла стало ясно, что плоские спиральные галактики можно разделить на две группы. Для одной из них (SB) характерно наличие яркой перемычки (бара) с прикрепленными к его концам (часто почти под прямым углом) спиралями. В другой группе плоских галактик (S) спирали отходят от образования, расположенного в центре галактики. Ясно, что исследование устойчивости гравитирующего диска (аналитическое и численно-экспериментальное) должно определить те факторы, которые препятствуют возбуждению бар-моды во многих плоских галактиках.
Поскольку бар-мода является крупномасштабным возмущением,
использованное в гл. 2 коротковолновое приближение для изучения его
устойчивости неприменимо. Таким образом, в этом случае необходимо
учитывать структуру диска в целом, что, естественно, накладывает
достаточно жесткие ограничения на свойства модели. Поэтому
детальное аналитическое исследование устойчивости бар-моды было
проведено лишь в моделях твердотельно вращающихся дисков
[50,223,238,266].
Эти исследования показали, что модели тонкого диска без учета
массы сферической подсистемы устойчивы относительно возбуждения
бар-моды только при
Более конструктивной оказалась постановка задачи, в которой
помимо конечной толщины диска учитывалось наличие и сфероидальной
подсистемы. Так, в модели, состоящей из однородного гало
(сфероидальной подсистемы) и однородного сплюснутого эллипсоида
вращения (диска) с большой полуосью ![]() и малой полуосью
и малой полуосью ![]() ,
было обнаружено [238], что в дисковом пределе (
,
было обнаружено [238], что в дисковом пределе (
![]() )
эллипсоид устойчив относительно возбуждения бар-моды при
)
эллипсоид устойчив относительно возбуждения бар-моды при
Как уже говорилось выше, аналитическое изучение устойчивости
бар-моды в дифференциально вращающихся неоднородных дисках
конечной толщины затруднительно. Это, очевидно, проще делать с
помощью численного эксперимента. Ранние эксперименты (см.,
например, [211,212,216,253]) подтвердили, что в недостаточно горячих
(
![]() ) тонких дисках без гало возбуждение
бар-моды неизбежно. Учет конечной массы гало показал, что с ростом массы
последнего бар-мода стабилизируется [268-272]. В то же
время в разных моделях границы устойчивости бар-моды по параметру
) тонких дисках без гало возбуждение
бар-моды неизбежно. Учет конечной массы гало показал, что с ростом массы
последнего бар-мода стабилизируется [268-272]. В то же
время в разных моделях границы устойчивости бар-моды по параметру
![]() заметно различаются, группируясь, однако, в окрестности
заметно различаются, группируясь, однако, в окрестности
![]() .
.
Результаты экспериментов удобно описывать с помощью параметра
![]() , характеризующего степень бароподобного искажения
диска для различных распределений объемной плотности гало
, характеризующего степень бароподобного искажения
диска для различных распределений объемной плотности гало ![]() [218].
В моделях без гало
[218].
В моделях без гало
![]() (рис. 3.1). С ростом
массы гало параметр
(рис. 3.1). С ростом
массы гало параметр ![]() уменьшается и при
уменьшается и при
![]() становится меньше уровня, на котором погрешность измерения величины
становится меньше уровня, на котором погрешность измерения величины ![]() в данных экспериментах делает ее различимой с
в данных экспериментах делает ее различимой с
![]() .
.
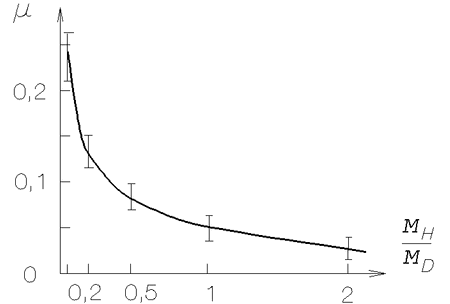 |
Рис. 3.1. Зависимость
|
В связи с приведенными выше результатами представляет интерес
и экспериментальный критерий [219], утверждающий, что для
устойчивости диска относительно возбуждения бар-моды должно
выполняться условие
![]() , где (
, где (
![]() -- максимальное значение
-- максимальное значение
![]() в диске. По результатам экспериментов [218] этот критерий
проверялся в конечных квазистационарных состояниях диска. Оказалось,
что величина
в диске. По результатам экспериментов [218] этот критерий
проверялся в конечных квазистационарных состояниях диска. Оказалось,
что величина ![]() изменяется от
изменяется от
![]() при
при ![]() до
до
![]() при
при ![]() . Таким образом, критерий [219]
выглядит слишком жестким. Причина состоит, по-видимому, в том, что
критерий был получен в экспериментах, в которых начальное
состояние диска было холодным (
. Таким образом, критерий [219]
выглядит слишком жестким. Причина состоит, по-видимому, в том, что
критерий был получен в экспериментах, в которых начальное
состояние диска было холодным (![]() ). В таком состоянии условия
возбуждения бар-моды наиболее благоприятны, а
). В таком состоянии условия
возбуждения бар-моды наиболее благоприятны, а
![]() (измеряемое
в начальный момент времени) -- больше, чем в горячем диске. Кроме
того, диски в экспериментах [219] двумерны, что также облегчает
возбуждение бар-моды. Поэтому неудивительно, что указанный
критерий приводит к необычайно низкой оценке отношения массы к
светимости (порядка единицы) для дисков Sc-галактик [250].
Исходя же из результатов экспериментов [218] следует считать, что
звездный диск устойчив относительно возбуждения бар-моды при
(измеряемое
в начальный момент времени) -- больше, чем в горячем диске. Кроме
того, диски в экспериментах [219] двумерны, что также облегчает
возбуждение бар-моды. Поэтому неудивительно, что указанный
критерий приводит к необычайно низкой оценке отношения массы к
светимости (порядка единицы) для дисков Sc-галактик [250].
Исходя же из результатов экспериментов [218] следует считать, что
звездный диск устойчив относительно возбуждения бар-моды при
![]() .
.
Численное моделирование процесса формирования бара остается весьма популярным. Но более поздние работы в основе своей подтверждают вышеизложенные результаты [273,274].
Суммируя сказанное выше, можно утверждать, что SB-галактики не должны иметь сферической подсистемы, масса которой сравнима с массой диска, а S-галактики имеют, по-видимому, сферическую подсистему с массой (в сфере радиуса видимого диска) большей или порядка массы диска. Косвенным подтверждением этого результата может служить тот факт, что вблизи центра скопления галактик в Волосах Вероники доля SB-галактик вдвое выше, чем на периферии скопления. Наиболее естественная причина этого -- в "сдувании" гало при взаимном сближении галактик и ослаблении вследствие этого устойчивости их дисков по отношению к возбуждению бар-моды [275]. Кроме того, фактором, способствующим формированию перемычки, может являться приливное взаимодействие со стороны массивного спутника [276]. Вопрос о влиянии газовой подсистемы на развитие бар-моды будет рассмотрен в разд. 3.4.
Следует сказать, что бар-мода не является единственным
механизмом формирования бара. В случае медленного вращения системы
(
![]() ) возникают условия для развития неустойчивости
радиальных орбит, которая непосредственно не связана с гравитацией
(см. [2]). Результатом развития этой неустойчивости могут
являться перемычки в галактиках с массивным балджем и мини-бары
размером несколько сотен парсек в центре ряда плоских галактик
[5,277].
) возникают условия для развития неустойчивости
радиальных орбит, которая непосредственно не связана с гравитацией
(см. [2]). Результатом развития этой неустойчивости могут
являться перемычки в галактиках с массивным балджем и мини-бары
размером несколько сотен парсек в центре ряда плоских галактик
[5,277].
3.2.3 Центральная депрессия звездной плотности
В гл. 1 упоминалось о таком локальном феномене, как депрессия ("дыра") в распределении поверхностной плотности в центральных частях звездных дисков галактик. Возникает естественный вопрос, почему центральная депрессия плотности звездного диска не исчезает под влиянием релаксационных процессов, обусловленных коллективными процессами. В рамках численного эксперимента эта проблема рассматривалась в работах [246,278,279].
Для описания динамической эволюции глубины депрессии удобна
величина
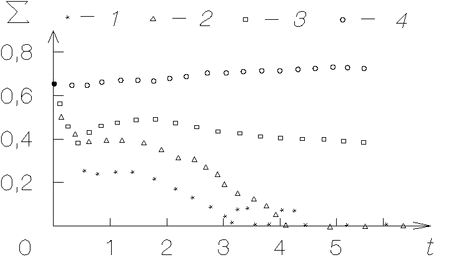 |
Рис. 3.2. Временная эволюция глубины депрессии |
Таким образом, из описанных выше экспериментов следует, что только галактики с массивной и/или достаточно концентрированной к центру сферической составляющей могут иметь депрессию звездной плотности. Фактически выживание депрессии в диске зависит от наличия массивного балджа, что согласуется с наблюдениями ряда реальных галактик (см. разд. 1.1). Заметим, что впервые на возможность существования "дефицита" поверхностной плотности во внутренней части плоской звездной подсистемы при определенных значениях параметров сферической подсистемы указывалось в работе [191], где этот вывод был сделан на основе расчетов равновесия вращающегося диска в поле гало.
В некоторых случаях наблюдения допускают наличие центральной депрессии плотности диска у галактик поздних морфологических типов, у которых балдж практически отсутствует, но имеется другая особенность -- перемычка. Поскольку бар вращается со скоростью, отличной от скорости вращения звездного диска, то это может приводить к перераспределению углового момента, что может сдерживать релаксацию центральной "дыры". По-видимому, в этом случае необходимо учитывать наряду со звездным диском и газовый. Причем бар не только может сдерживать релаксацию, но и быть ответственным за возникновение депрессии.
3.2.4 Модели с "живым" гало
Как мы видели, учет гало существен при построении
реалистичных моделей галактик. Как правило, считается, что
вещество гало почти не вращается и распределено симметрично.
Вопрос о применимости использования стационарного гало при
моделировании одиночных плоских галактик рассматривался Холом
[248], который рассчитывал динамическую модель диск![]() гало. Каждая из
подсистем состояла из
гало. Каждая из
подсистем состояла из ![]() одинаковых тел и, следовательно,
одинаковых тел и, следовательно,
![]() . После трех оборотов вращения "живое" гало оставалось
сферически симметричным, а в плоском диске без бара наблюдалась
спираль с двумя ветвями. В данном эксперименте обмен энергией
между гало и диском был мал.
. После трех оборотов вращения "живое" гало оставалось
сферически симметричным, а в плоском диске без бара наблюдалась
спираль с двумя ветвями. В данном эксперименте обмен энергией
между гало и диском был мал.
Селвуд [249], возвращаясь к этой проблеме, отмечает две
причины, по которым "живое" гало может отличаться от случая
неподвижной сферической подсистемы. Во-первых, возможна передача
углового момента диска к звездам гало, что приводит к устойчивости
без формирования бара (Марк [280] придавал важное значение обмену
угловым моментом между диском и гало в возникновении спиральных
волн в диске). Во-вторых, возмущения в распределении звезд в
дисках влияют через гало на динамику самого диска. Основные выводы
из проведенных Селвудом экспериментов заключаются в следующем.
Модели с неподвижным и "живым" гало дают вполне адекватные
результаты при исследовании глобальной устойчивости. Существенное
взаимодействие между двумя подсистемами возникает только после
формирования сильного бара. Хотя небольшой обмен угловым моментом
между диском и гало имеется даже в практически осесимметричных
системах, гипотеза Марка подтверждения не нашла. Для стабилизации
бар-моды необходимо, как и в случае стационарного гало,
сосредоточить
![]() от общей массы в сферической
подсистеме.
от общей массы в сферической
подсистеме.
В работе Литла и Карлберга [281] подробно анализируется
длительная эволюция системы, после того как процесс формирования
бара завершен. Наблюдаются медленные монотонные изменения
параметров бара, диска и гало: период бара вырастает за время
эксперимента (![]() лет) более чем в два раза, угловой момент
дисковой компоненты передается сфероидальной, причем в конце
эксперимента угловой момент гало всего в два раза меньше, чем у
диска.
лет) более чем в два раза, угловой момент
дисковой компоненты передается сфероидальной, причем в конце
эксперимента угловой момент гало всего в два раза меньше, чем у
диска.
Миллер [282] изучал динамику системы, в которой сферическая подсистема являлась сплющенной и оси симметрии диска и гало не совпадали. В такой ситуации центр дисковой подсистемы вращается вокруг некоторой точки.
В связи с обсуждаемым здесь вопросом о взаимодействии диска и
гало уместно упомянуть о работе [283], в которой предполагается,
что такое взаимодействие подсистем определяется потоком массы,
энергии, импульса и магнитного поля через так называемые "дымовые
трубы", образующиеся вспышками сверхновых II типа. Однако такого
рода модели в рамках задачи ![]() тел не рассматривались.
тел не рассматривались.
<< 3.1 Модели | Оглавление | 3.3 Гравитационная устойчивость ... >>
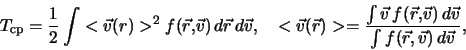
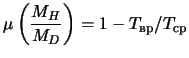 ,
характеризующая степень развития бар-моды. В
указанных на графике интервалах при каждом
значении
,
характеризующая степень развития бар-моды. В
указанных на графике интервалах при каждом
значении