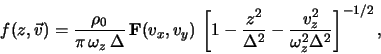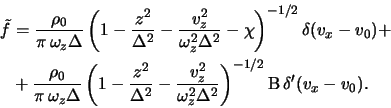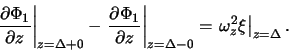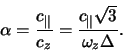|
Астронет: А. Г. Морозов, А. В. Хоперсков Физика Дисков http://www.astronet.ru/db/msg/1168623/node15.html |
<< 2.4 Условие грав. устойчивости | Оглавление | 3. Моделирование звездных дисков >>
- 2.5.1 Динамика изгибных возмущений
- 2.5.2 Какой должна быть величина
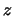 -дисперсии скоростей звезд?
-дисперсии скоростей звезд?
- 2.5.3 Динамика крупномасштабных изгибных возмущений диска, погруженного в массивное гало
2.5 Устойчивость диска относительно изгибных возмущений
2.5.1 Динамика изгибных возмущений
В предыдущих разделах были изучены динамика возмущений в плоскости звездного диска и вытекающие из требования устойчивости таких возмущений ограничения на параметры диска. В этом разделе мы остановимся на другом типе возмущений -- изгибающих плоскость звездного диска -- и соответственно найдем те ограничения на параметры диска и системы в целом, которые вытекают из условия устойчивости таких возмущений.
Впервые, по-видимому, динамика изгибных (мембранных)
колебаний в моделях холодных тонких дисков была рассмотрена в
работе Хантера и Тоомре [231]. Это исследование имело целью
объяснение наблюдаемого в ряде изолированных галактик
крупномасштабного искривления периферии их дисков. Еще одна
проблема, для решения которой необходимо изучение динамики
изгибных возмущений, связана с задачей объяснения существенного
различия толщин и ![]() -дисперсий скоростей объектов звездного и
газового дисков в плоских галактиках.
-дисперсий скоростей объектов звездного и
газового дисков в плоских галактиках.
Однако исследованные Хантером и Тоомре [231] модели холодных тонких дисков оказались устойчивыми относительно изгибных возмущений (подробное изложение теории этого вопроса см. в книге Фридмана и Поляченко [2]). В [232] было показано, что для решения упомянутых выше проблем необходимо изучать динамику изгибных возмущений в моделях дисков, горячих в их плоскости.
Очевидно, что такие локальные параметры, как ![]() -дисперсия
скоростей звезд и толщина диска, должны определяться из условия
устойчивости возмущений, масштабы которых малы по сравнению с его
толщиной. Соответствующее ВКБ-дисперсионное уравнение изгибных
возмущений в простейшей модели однородного тонкого невращающегося
звездного слоя можно записать в виде [233]
-дисперсия
скоростей звезд и толщина диска, должны определяться из условия
устойчивости возмущений, масштабы которых малы по сравнению с его
толщиной. Соответствующее ВКБ-дисперсионное уравнение изгибных
возмущений в простейшей модели однородного тонкого невращающегося
звездного слоя можно записать в виде [233]
С другой стороны, изгибные возмущения, масштабы которых малы по сравнению с толщиной диска, также должны быть устойчивыми [232]. Это означает, что существует минимально необходимая для устойчивости диска величина отношения
Динамика крупномасштабных изгибных возмущений, охватывающих весь диск, должна, очевидно, изучаться с учетом вращения и структуры диска в целом. Такое исследование для ряда моделей тонких дисков [234] показало, что наиболее крупномасштабные моды могут быть неустойчивыми, если равновесие дисков в радиальном направлении обеспечивается в основном давлением (а не вращением). С уменьшением вклада давления в условие равновесия наиболее крупномасштабные моды стабилизируются, а более коротковолновые остаются неустойчивыми. Этот результат вместе с дисперсионным уравнением (2.5.1) показывает, что неустойчивость изгибных возмущений диска в некотором смысле является дополнительной к гравитационной неустойчивости возмущений в плоскости диска. Действительно, гравитация дестабилизирует возмущения в плоскости диска и стабилизирует изгибные; давление оказывается стабилизирующим фактором для возмущений в плоскости диска и дестабилизирующим для изгибных. Поэтому можно было бы ожидать, что самые крупномасштабные изгибные моды будут, в отличие от возмущений в плоскости диска (см. гл. 3), дестабилизироваться достаточно массивной сфероидальной подсистемой. Обсуждению этого вопроса посвящен п. 2.5.3.
2.5.2 Какой должна быть величина -дисперсии скоростей звезд?
Определим, следуя Поляченко и Шухману [235], максимальную
анизотропию
![]() скоростей в звездном диске. Поскольку
вращение существенно только для возмущений, масштабы которых
сравнимы с радиусом диска, исходим из простой модели
бесстолкновительного невращающегося плоского слоя конечной толщины
[236], описываемой функцией распределения
скоростей в звездном диске. Поскольку
вращение существенно только для возмущений, масштабы которых
сравнимы с радиусом диска, исходим из простой модели
бесстолкновительного невращающегося плоского слоя конечной толщины
[236], описываемой функцией распределения
Считаем возмущения длинноволновыми в том смысле, что
характерный масштаб возмущения в плоскости слоя велик по сравнению
с его полутолщиной (![]() ). Однако параметр
). Однако параметр
![]() не предполагаем малым. Ориентируем ось
не предполагаем малым. Ориентируем ось ![]() вдоль
направления волнового вектора. Тогда зависимость
вдоль
направления волнового вектора. Тогда зависимость
![]() от
от ![]() в
невращающемся слое становится несущественной и задача сводится к
двумерной.
в
невращающемся слое становится несущественной и задача сводится к
двумерной.
Представим функцию распределения по ![]() в виде суперпозиции
потоков
в виде суперпозиции
потоков
Подстановка этого выражения в линеаризованное кинетическое уравнение приводит к следующим уравнениям для функций
где
Оценивая соотношение величин B и
где
Смещение границы слоя ![]() определяем из условия
определяем из условия
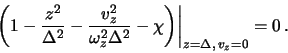
Отсюда следует
Вычислим теперь соответствующее (2.5.10) возмущение гравитационного потенциала. Для этого сошьем решения уравнения
при
Отсюда с точностью до членов порядка
Суммируя это выражение по всем потокам, приходим к искомому дисперсионному уравнению:
Для конкретных вычислений исходим из шварцшильдовской функции
распределения
![]() . В этом случае дисперсионное уравнение (2.5.14) приводится
к виду
. В этом случае дисперсионное уравнение (2.5.14) приводится
к виду
При
где
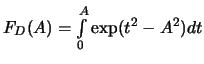 - интеграл Досона. Нетрудно видеть, что при
- интеграл Досона. Нетрудно видеть, что при
Данные наблюдений в околосолнечной окрестности Галактики не
противоречат оценке (2.5.18) -- согласно [53,56,57] в среднем по
не слишком молодым звездам
![]() . Таким образом, в
солнечной окрестности Галактики звездный диск устойчив
[согласно (2.5.18) -- с запасом] относительно изгибных возмущений
промежуточных масштабов
. Таким образом, в
солнечной окрестности Галактики звездный диск устойчив
[согласно (2.5.18) -- с запасом] относительно изгибных возмущений
промежуточных масштабов
![]() (
(![]() - радиус диска Галактики). То же самое можно, по-видимому,
утверждать и в отношении звездных дисков других плоских
галактик [64,65]. Обсуждение результатов численных экспериментов
можно найти в разд. 3.4.
- радиус диска Галактики). То же самое можно, по-видимому,
утверждать и в отношении звездных дисков других плоских
галактик [64,65]. Обсуждение результатов численных экспериментов
можно найти в разд. 3.4.
2.5.3 Динамика крупномасштабных изгибных возмущений диска, погруженного в массивное гало
Для изучения динамики захватывающих весь диск плоской галактики крупномасштабных изгибных мод необходимо, очевидно, учитывать структуру диска и окружающей его сферической подсистемы в целом. Аналитическое решение такой задачи возможно только на достаточно простых моделях, и в этом разделе мы опишем первые результаты такого типа исследований [238].
Представим модель галактики в виде двухосного твердотельно
вращающегося звездного эллипсоида однородной плотности с полуосями
![]() ,
, ![]()
![]() , погруженного в протяженное однородное сферическое
гало. Равновесный гравитационный потенциал внутри эллипсоида
(модели диска) равен
, погруженного в протяженное однородное сферическое
гало. Равновесный гравитационный потенциал внутри эллипсоида
(модели диска) равен
Ограничимся изучением динамики трех наиболее крупномасштабных мод:
а) ![]() ("купол")
("купол")
в)
где
Эти моды интересны прежде всего как наиболее крупномасштабные
и потому, как правило, самые опасные с точки зрения потери
устойчивости. Кроме того, следует ожидать, что поведение подобных
мод, захватывающих целиком всю систему, определяется небольшим
числом ее "глобальных" параметров. Это означает, что исследование
устойчивости рассматриваемой модели относительно возбуждения
перечисленных выше мод не потребует конкретизации функции
распределения -- достаточно лишь будет знать несколько главных ее
моментов. Для рассматриваемой модели однородного эллипсоида
выражения для линейных и квадратичных по скоростям моментов
определяются однозначно, если только предположить изотропию в
распределении скоростей в плоскости вращения. Упомянутые моменты
имеют вид
Метод исследования устойчивости стандартен [2,236]. Сначала
из уравнений для лагранжевых смещений ![]() эти величины
выражаются через возмущенный потенциал
эти величины
выражаются через возмущенный потенциал ![]() . Затем вычисляются
возмущения плотности и нормальное смещение границы эллипсоида.
Решая затем уравнение Пуассона и сравнивая получившийся потенциал
с исходным (2.5.20)-(2.5.22), приходим к системе линейных
алгебраических уравнений относительно коэффициентов, входящих в
выражение для возмущенного потенциала. Приравнивая, наконец, нулю
определитель такой системы, получаем искомое дисперсионное
уравнение.
. Затем вычисляются
возмущения плотности и нормальное смещение границы эллипсоида.
Решая затем уравнение Пуассона и сравнивая получившийся потенциал
с исходным (2.5.20)-(2.5.22), приходим к системе линейных
алгебраических уравнений относительно коэффициентов, входящих в
выражение для возмущенного потенциала. Приравнивая, наконец, нулю
определитель такой системы, получаем искомое дисперсионное
уравнение.
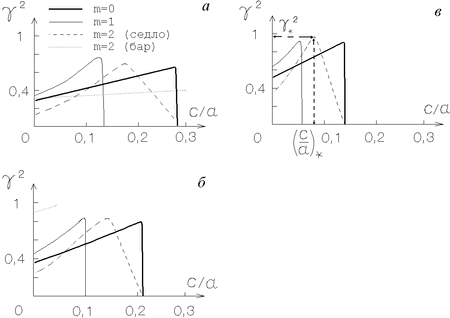 |
Рис. 2.10. Области неустойчивости изгибных мод (2.5.20)
|
Дисперсионные уравнения для указанных выше мод (2.5.20) ![]() (2.5.22) решались численно (они довольно громоздки и здесь не
приводятся). Результаты их решения приведены на рис. 2.10,а-в,
соответствующих различным значениям параметра
(2.5.22) решались численно (они довольно громоздки и здесь не
приводятся). Результаты их решения приведены на рис. 2.10,а-в,
соответствующих различным значениям параметра ![]() . Из этих
рисунков видно, что в дисковом пределе (
. Из этих
рисунков видно, что в дисковом пределе (
![]() ) каждая из мод
неустойчива при достаточно большой дисперсии скоростей звезд
(области под кривыми). С увеличением "толщины" эллипсоида область
неустойчивости по параметру
) каждая из мод
неустойчива при достаточно большой дисперсии скоростей звезд
(области под кривыми). С увеличением "толщины" эллипсоида область
неустойчивости по параметру ![]() сначала растет (т.е. неустойчивыми
становятся все более "холодные" системы), а затем довольно быстро
исчезает.
сначала растет (т.е. неустойчивыми
становятся все более "холодные" системы), а затем довольно быстро
исчезает.
Заметим, что резкий спад кривых -- границ областей
неустойчивости на рис. 2.10 происходит при такой сплюснутости
эллипсоида ![]() , для которой в используемой однородной модели
имеются резонансы между частотами колебаний звезд поперек
плоскости эллипсоида и в плоскости его вращения. Для мод
, для которой в используемой однородной модели
имеются резонансы между частотами колебаний звезд поперек
плоскости эллипсоида и в плоскости его вращения. Для мод ![]() и
и
![]() есть резонанс
есть резонанс
![]() , а для моды
, а для моды
![]() -- резонанс
-- резонанс
![]() .
Столь сильное влияние этих резонансов связано, очевидно, с
идеализацией модели. Для реальных дифференциально вращающихся
систем эти кривые будут иметь более гладкий вид.
.
Столь сильное влияние этих резонансов связано, очевидно, с
идеализацией модели. Для реальных дифференциально вращающихся
систем эти кривые будут иметь более гладкий вид.
Как видно из рис. 2.10, мода ![]() (седло) сравнительно мало
подвержена влиянию резонанса. Существенно, однако, что именно эта
мода обладает самой большой областью неустойчивости по
(седло) сравнительно мало
подвержена влиянию резонанса. Существенно, однако, что именно эта
мода обладает самой большой областью неустойчивости по ![]() при
при
![]() . Важно также отметить, что с увеличением массы гало
область неустойчивости по параметру сплюснутости эллипсоида
. Важно также отметить, что с увеличением массы гало
область неустойчивости по параметру сплюснутости эллипсоида
![]() сужается (неустойчивыми остаются только сильно сплюснутые
системы). Однако для моды
сужается (неустойчивыми остаются только сильно сплюснутые
системы). Однако для моды ![]() даже при очень больших значениях
массы гало (
даже при очень больших значениях
массы гало (
![]() ) эллипсоид неустойчив вплоть до
) эллипсоид неустойчив вплоть до
![]() , т.е. значений, характерных для плоских подсистем спиральных
галактик. Тем самым можно говорить о выделенности седлообразной
моды среди других мод изгибного типа. Заметим, что аналогичное
положение имеет место и для возмущений, не изгибающих плоскость
диска -- здесь тоже оказывается выделенной бароподобная мода
, т.е. значений, характерных для плоских подсистем спиральных
галактик. Тем самым можно говорить о выделенности седлообразной
моды среди других мод изгибного типа. Заметим, что аналогичное
положение имеет место и для возмущений, не изгибающих плоскость
диска -- здесь тоже оказывается выделенной бароподобная мода
![]() .
.
В целом наиболее важным результатом является обнаружение
зависимости положения границ областей неустойчивости от массы
гало: при достаточно большой массе гало неустойчивыми могут стать
системы с малой дисперсией скоростей в плоскости эллипсоида
[с малым (![]() )]. В этом и состоит дестабилизирующая роль гало.
)]. В этом и состоит дестабилизирующая роль гало.
В то же время с ростом массы гало необходимая для
гравитационной устойчивости диска дисперсия скоростей звезд в его
плоскости убывает:
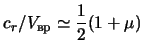 (см. гл. 3 и рис. 3.8). Поэтому может оказаться, что дестабилизирующая
(по отношению к крупномасштабным изгибным возмущениям) роль массивного гало не
проявится. Исследуем этот вопрос подробнее [239,240].
(см. гл. 3 и рис. 3.8). Поэтому может оказаться, что дестабилизирующая
(по отношению к крупномасштабным изгибным возмущениям) роль массивного гало не
проявится. Исследуем этот вопрос подробнее [239,240].
Предположим, что звездный диск обладает запасом гравитационной устойчивости
![]() , который мы определим как отношение наблюдаемой
, который мы определим как отношение наблюдаемой ![]() к получаемой
в численных экспериментах
к получаемой
в численных экспериментах ![]() [полагаем, что
[полагаем, что ![]() соответствует границе гравитационной устойчивости]. Тогда везде за пределами
центральной части диска
соответствует границе гравитационной устойчивости]. Тогда везде за пределами
центральной части диска
где
Состояние с
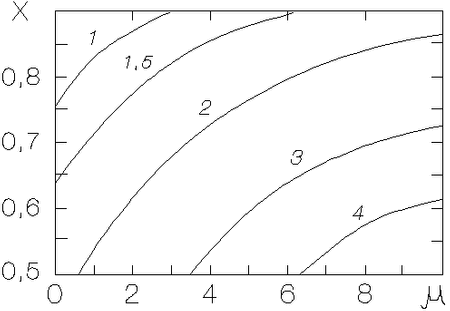 |
Рис. 2.11. Изолинии
параметра
|
Результаты вычислений величины
![]() приведены на
рис. 2.11 [заметим, что в рамках рассматриваемой модели параметр
приведены на
рис. 2.11 [заметим, что в рамках рассматриваемой модели параметр
![]() (см. рис. 2.10) выходит при
(см. рис. 2.10) выходит при ![]() на асимптотическое
значение
на асимптотическое
значение
![]() ]. Видно, что неустойчивыми оказываются только
периферийные области систем с малым
]. Видно, что неустойчивыми оказываются только
периферийные области систем с малым ![]() . В системах же с
. В системах же с
![]() крупномасштабные изгибные моды оказываются застабилизированными
[области, близкие к периферии эллипсоида (
крупномасштабные изгибные моды оказываются застабилизированными
[области, близкие к периферии эллипсоида (
![]() ), не изучались,
поскольку в рамках рассматриваемой модели в противоречие с данными
наблюдений они слишком холодны:
), не изучались,
поскольку в рамках рассматриваемой модели в противоречие с данными
наблюдений они слишком холодны: ![]() при
при
![]() ]. Таким
образом, следует ожидать, что в галактиках с достаточно массивным гало
неустойчивость крупномасштабных изгибных мод не будет проявляться.
]. Таким
образом, следует ожидать, что в галактиках с достаточно массивным гало
неустойчивость крупномасштабных изгибных мод не будет проявляться.
<< 2.4 Условие грав. устойчивости | Оглавление | 3. Моделирование звездных дисков >>