"Средь шумного бала ..."
27.03.2003 18:49 | С. Б. Попов/ГАИШ, Москва

Самые известные нейтронные звезды - пульсары. Самый известный пульсар - пульсар в Крабовидной туманности. Период вращения этой нейтронной звезды около 33 мс. Вспышка сверхновой наблюдалась в 1054 г. В статье авторы рассматривают изменения периода вращения по данным радионаблюдений. Кроме замедления периода, кроме второй производной, есть еще "шумовые" вариации (timing noise). Авторы детально исследуют этот "шум" (снова

Все чудеса в одной книге
26.03.2003 21:46 | С. Б. Попов/scientific.ru

В Архиве электронных препринтов появилась интересная и важная обзорная работа с юбилейным номером 0303500. В обзоре (книге!) популярно рассказывается об основных достижения Космического телескопа за 13 лет работы: от Солнечной системы до космологии. Автор начинает с падения кометы Шумейкеров-Леви на Юпитер, и заканчивает открытием ускорения расширения Вселенной. Благодаря столь широкому охвату читатель может

Кварковая модель не совсем верна?!
25.03.2003 19:08 | И. П. Иванов/scientific.ru

В январе 2003 года группа исследователей, работающая с установкой LEPS на японском накопителе SPring-8, опубликовала результаты поиска экзотической частицы Z+. Частица была найдена! И более того, она была найдена именно там, где ее предсказывали солитонные модели устройства барионов.

Интервью Артура Кларка
24.03.2003 23:26 | Astronet

Мэтр научной фантастики сэр Артур Кларк (Arthur C. Clarke) 24 марта 2003 года дал интервью "Обществу Планеты". Оно довольно интересное и, если вы владеете английским языком, я рекомендую вам послушать его: интервью (7.3M, формат wma). Дополнительную информацию и ссылки вы найдете здесь.

Весеннее равноденствие
21.03.2003 18:33 | Astronet

21 марта 2003 года весеннее равноденствие произошло в 01:00 UT.

Вселенная и Мы
21.03.2003 18:17 | Astronet

На нашем сайте появились матреиалы альманахов "Вселенная и Мы". Вселенная и Мы. N 4, 2001 Вселенная и Мы. N 3, 1997 Вселенная и Мы. N 2, 1994 Вселенная и Мы. N 1, 1993

Разрыв Вселенной
14.03.2003 19:57 | М. Е. Прохоров/ГАИШ, Москва

Статья Калдвелла, Камионковского и Вейнберга "Призрачная энергия и космический судный день" вызвала волну интереса в прессе. Здесь приведены достаточно подробные комментарии к этой статье.

Они танцуют на орбитах
12.03.2003 19:00 | М. Е. Прохоров/ГАИШ, Москва

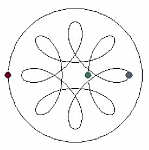
Классическая ньютоновская задача 3-тел еще не решена. Что уже говорить о более общей задаче n-тел в небесной механике. Одним из интересных и красивых направлений их исследования является поиск периодических решений - ситуаций, когда каждое из тел движется по замкнутой траектории и спустя некоторое время все они одновременно возвращаются в исходные точки.