Астронет > Полость Роша

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Полость Роша

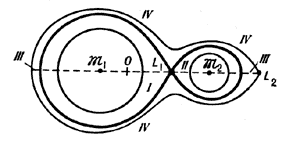
Критические эквипотенциальные поверхности
и полости Роша в двойной звёздной системе
с отношением масс компонентов 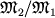${\mathfrak M}_2/{\mathfrak M}_1$ =0,215.

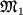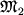- область вокруг звезды, внешней границей к-рой служит поверхность равного потенциала, содержащая т.н. первую точку Лагранжа. Положим, что массы звёзд ${\mathfrak M}_1$ и ${\mathfrak M}_2$ , вращающихся по круговым орбитам вокруг общего центра масс О, сосредоточены в их центрах (рис.). Периоды собств. вращения звёзд совпадают с орбитальным периодом. 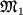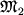В системе координат, вращающейся вместе с двойной системой, на каждую покоящуюся пробную частицу действуют три силы: силы притяжения со стороны ${\mathfrak M}_1$ и ${\mathfrak M}_2$ , возрастающие с приближением к гравитирующим массам, и центробежная, нарастающая при удалении от оси вращения. По соотношению действующих сил всё пространство можно разделить двумя поверхностями равного потенциала (внутр. критической и внеш. критической) на четыре области. Внутр. критич. поверхность, содержащая точку L₁ (т.н. 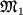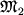первую точку Лагранжа), ограничивает две области, прилегающие к тяготеющим массам ${\mathfrak M}_1$ и ${\mathfrak M}_2$ . 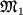В первой из этих областей (I) сила притяжения звезды ${\mathfrak M}_1$ превосходит как силу притяжения со стороны звезды-спутника, так и центробежную силу. 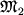Аналогично в полости II, прилегающей к ${\mathfrak M}_2$ , преобладает сила притяжения последней. В области III, заключённой между критич. 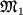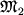поверхностями с точками L₁ и L₂ (второй точкой Лагранжа), суммарная сила гравитации масс ${\mathfrak M}_1$ и ${\mathfrak M}_2$ превосходит центробежную силу. В области IV (за внеш. критич. поверхностью с точкой L₂) действие центробежной силы преобладает и вещество системы, попадающее сюда, оказывается для нее утерянным. Полость, содержащая одну из гравитирующих масс и выделенная поверхностью с точкой L₁, наз. полостью Роша. При совпадении периодов собств. вращения звёзд с их орбитальным периодом размеры П.Р. и положение точек Лагранжа полностью определяются отношением масс звёзд-компонентов двойной системы. Если один из компонентов двойной звезды заполняет свою П.Р., то вещество его может свободно перетекать в полость звезды-спутника. При этом оно вытекает из окрестности точки L₁ в виде сравнительно тонкой струи. Если в ходе эволюции компонентов будут заполнены П.Р. обоих компонентов, то вокруг системы образуется общая оболочка, к-рая может заполнить полость, содержащую точку L₂. Вещество, покидающее эту точку даже с небольшой скоростью, как правило, уходит из системы, ускоряясь в переменном гравитац. поле двойной звезды. Существование П.Р. приводит к тому, что компонент, к-рый эволюционирует быстрее, первым заполняет П.Р. и начинает отдавать вещество второму компоненту. Перераспределение вещества в системе может очень сильно изменить её характеристики (см. Эволюция тесных двойных звезд).

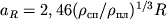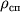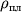При рассмотрении системы планета-спутник вводится понятие о пределе Роша - миним. радиусе круговой орбиты, на к-рой спутник не разрушается под действием притяжения центрального тела (приливных сил). Если масса спутника много меньше массы планеты, то предел Роша $a_R=2,46 (\rho_{сп}/\rho_{пл})^{1/3} R$ , где $\rho_{сп}$ и $\rho_{пл}$ - значения ср. плотности спутника и планеты, R - радиус планеты. Внутри сферы с радиусом a_R невозможна также гравитац. конденсация вещества с образованием единого тела. Такова, вероятно, причина образования колец Сатурна, Юпитера, Урана.

Лит.:
Белецкий В.В., Очерки о движении космических тел, 2 изд., М., 1977.

(А.В. Тутуков)

А. В. Тутуков, "Физика Космоса", 1986
Глоссарий Astronet.ru

L | R | А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я

Публикации с ключевыми словами: полость Роша - Тесные двойные системы - ограниченная задача трех тел
Публикации со словами: полость Роша - Тесные двойные системы - ограниченная задача трех тел

Карта смысловых связей для термина ПОЛОСТЬ РОША

См. также:

Двойная звезда φ Персея

Удивительная звезда Мира

Тесные двойные звезды на поздних стадиях эволюции

Эволюция тесных двойных звезд

Отдел Астрофизики Высоких Энергий ИКИ РАН

Очередной рентгеновский пульсар

Тесные двойные звезды на поздних стадиях эволюции

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати