Кеплера законы

1-й закон:
каждая планета движется по эллипсу, в одном из фокусов к-рого находится Солнце.
2-й закон:
каждая планета движется в плоскости, проходящей через центр Солнца, причём площадь сектора орбиты, описанная радиусом-вектором планеты, изменяется пропорционально времени. Часто 2-й закон формулируют как закон площадей: радиус-вектор планеты в равные промежутки времени описывает равные площади (рис.).
3-й закон:
квадраты периодов обращения планет вокруг Солнца относятся как кубы их ср. расстояний от Солнца. Если обозначить периоды обращения двух планет через T₁ и T₂, а их ср. расстояния от Солнца (большие полуоси их орбит) через a₁ и a₂, то 3-й К. з. можно записать в виде: . К. з. сыграли большую роль в установлении И. Ньютоном закона всемирного тяготения, они вошли в небесную механику в обобщённой и уточнённой форме, в этой форме они применяются при исследовании орбит, описываемых двумя гравитационно связанными небесными телами при отсутствии возмущений со стороны др. тел (в т.н. задаче двух тел). Под действием притяжения Солнца различные тела (планеты, астероиды, кометы, КА) в зависимости от своей скорости (точнее, полной механич. энергии) могут двигаться как по замкнутым траекториям (окружностям и эллипсам), так и по разомкнутым траекториям (параболам и гиперболам). Все перечисленные виды траекторий представляют собой т.н. конич. сечения.

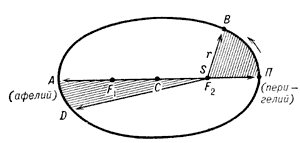
Орбита планеты Солнечной системы ПВАDП - эллипс; F1 и F2 - фокусы эллипса, в одном из фокусов находится Солнце S; СП=СА - большая полуось орбиты; r - радиус-вектор планеты; планета проходит отрезки траектории ПВ и AD за одинаковое время, площади секторов SПВ и SAD равны.

Обобщённая формулировка 1-го К. з. такова: траектория тела, движущегося в поле тяготения Солнца, представляет собой конич. сечение, в одном из фокусов к-рого находится Солнце. 2-й К. з. явл. следствием центрального характера сил тяготения, действующих между Солнцем и движущимся телом. В дифференциальные ур-ния относительного движения двух притягивающихся тел входит сумма их масс, и эта сумма появляется в уточнённой Ньютоном формулировке 2-го К. з.: квадраты периодов обращения тел вокруг Солнца, умноженные на сумму масс каждого тела и Солнца, относятся как кубы больших полуосей орбит: , где - масса Солнца, и - массы рассматриваемых тел (планет).

В первом приближении можно пренебречь массами планет (а тем более массами малых тел Солнечной системы) сравнительно с массой Солнца и тогда будет иметь место формулировка 3-го закона, данная Кеплером.

Условием движения тел по замкнутым эллиптич. траекториям вокруг Солнца явл. отрицат. значение полной механич. энергии тела в Солнечной системе; условием движения по разомкнутой траектории и, следовательно, разрыва динамич. связи тела с Солнцем - положит. значение механич. энергии тела. Гиперболич. движение может перейти в эллиптическое только в случае уменьшения по к.-л. причине (напр., влияния третьего тела) полной энергии движущегося тела до отрицательного значения (захват движущегося тела).