Черная дыра
(И. Д. Новиков, "Физика Космоса", 1986,
26.03.2003 19:16, 22.4 КБайт, ответов: 659)
Черная дыра - область пространства, в к-рой поле тяготения настолько сильно, что
вторая космич. скорость (параболическая
скорость)
для находящихся в этой области тел должна была бы превышать скорость света, т.е.
из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в природе ничто не
может
двигаться со скоростью, большей скорости света. Границу области, за к-рую не выходит
свет, наз. горизонтом Ч.д. Для того чтобы поле тяготения смогло "запереть" излучение,
создающее это поле масса  должна сжаться до объема с радиусом,
меньшим гравитационного радиуса
должна сжаться до объема с радиусом,
меньшим гравитационного радиуса 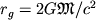 . Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу
. Гравитац. радиус чрезвычайно мал даже для больших масс (напр., для
Солнца, имеющего массу 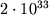 г,
г, 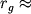 3 км).
3 км).
Поле тяготения Ч.д. описывается теорией тяготения Эйнштейна (см. Тяготение).
Согласно этой теории, вблизи Ч.д. геометрич. св-ва пространства
описываются неевклидовой (римановой) геометрией, а время течет медленнее, чем вдали,
вне сильного поля тяготения.
По совр. представлениям, массивные звезды (с массой в неск. 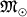 и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
и больше), заканчивая свою эволюцию, могут в конце концов сжаться (сколлапсировать)
и превратиться в Ч.д. (см. Эволюция звезд,
Гравитационный коллапс).
Если Ч.д. возникает при сжатии невращающегося незаряженного тела, то ее внеш. поле
тяготения оказывается строго сферическим и зависящим только от полной массы тела
 . Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
. Все отклонения от сферичности в граивтац. поле при образовании Ч.д. излучаются
в виде гравитац. волн (см. Гравитационное
излучение). Оставшееся поле не зависит от распределения массы внутри сжавшегося
тела. Т.о., хотя внутри Ч.д. может быть "спрятано" очень несимметрично сжимающееся
тело,
внеш. поле тяготения будет строго сферически-симметричным (т.н. поле Шварцшильда).
При образовании Ч.д. излучаются также все физ. поля, кроме статического электрического
поля (если коллапсирующее тело было электрически заряженным).
Если тело, образовавшее Ч.д., вращалось, то вокруг Ч.д. сохраняется "вихревое" гравитац.
поле, увлекающее все тела вблизи Ч.д. во вращательное движение вокруг нее. Это поле
определяется помимо массы Ч.д. только ее полным моментом импульса. Поле тяготения
вращающейся Ч.д. наз. полем Керра.
Движение тел в поле тяготения Шварцшильда обладает рядом особенностей. В теории Ньютона
движение по окружности вокруг тяготеющего центра возможно на любом расстоянии R
от него. В теории Эйнштейна это не так. Чем ближе к Ч.д., тем больше скорость кругового
движения. На окружности с R=1,5 rg скорость
движения достигает световой. Ближе к Ч.д. движение по окружности, очевидно, вообще
невозможно. В действительности же движение по окружности становится неустойчивым
на значительно
больших расстояниях, а именно: начиная с R=3 rg,
когда скорость движения составляет всего половину световой. Только на расстояниях,
превышающих 3rg, возможно устойчивое круговое движение.
На пределе устойчивости круговых орбит энергия
связи частицы 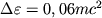 , где m - масса
частицы.
, где m - масса
частицы.
Особый интерес представляет возможность гравитац. захвата черной дырой тел, прилетающих
из бесконечности к тяготеющей массе, описывает около нее параболу или гиперболу и
(если
не испытывает соударения с тяготеющей массой) снова улетает в бесконечность. Гравитац.
захват в этой задаче невозможен.
|
|
Рис. 1.
|
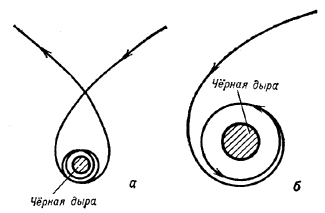
Иначе обстоит дело в поле тяготения Ч.д. Конечно, если тело движется на больших расстояниях
от Ч.д. (R>rg), где поле тяготения уже слабо и
справедлива с большой точностью теория Ньютона, то траектория движения почти точно
совпадает с параболой или гиперболой. В достаточной близости от Ч.д. траектория резко
отличается
от ньютоновской. Так, если скорость тела вдали от Ч.д. много меньшн световой и траектория
его движения подходит близко к окружности с R=2 rg,
то тело совершит много оборотов вокруг Ч.д., прежде чем снова улетит в космос (рис.
1, а).
Наконец, если тело подойдет вплотную к указанной окружности, то его орбита будет
неограниченно навиватсья на окружность. Тело окажется гравитационно захваченным Ч.д.
и никогда
снова не улетит в космос (рис. 1, б). Если же тело подлетит еще ближе к Ч.д., то
после неск. оборотов или даже не успев сделать ни одного оборота, оно упадет в Ч.д.
|
|
Рис. 2.
|
В поле тяготения Ч.д. выражение для параболической скорости записывается формально
так же, как и в теории Ньютона. Однако необходимо сделать следующее уточнение. Когда
тело
движется прямо по радису к Ч.д., то какую бы скорость тело не имело, в т.ч. и больше
параболической, оно упадет в Ч.д. Более того, если тело движется хотя и не прямо
по радиусу
к Ч.д., но траектория его достаточно близка к Ч.д., то оно тоже будет захвачено Ч.д.
Следовательно, для того чтобы вырваться из окрестностей Ч.д., мало иметь скорость,
превышающую
параболическую, надо еще, чтобы угол 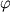 между направлением этой
скорости и направлением на Ч.д. превышал нек-рое критич. значение
между направлением этой
скорости и направлением на Ч.д. превышал нек-рое критич. значение 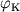 .
При
.
При 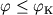 тело окажется захваченным Ч.д., при
тело окажется захваченным Ч.д., при 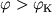 (и условии, что скорость больше или равна параболической) тело улетит
от Ч.д. Значение
(и условии, что скорость больше или равна параболической) тело улетит
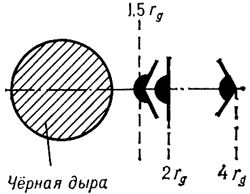
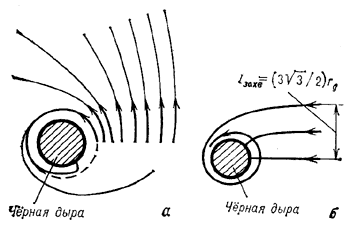
от Ч.д. Значение 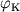 зависит от расстояния до Ч.д. На рис. 2 черным
цветом закрашен конус захвата: если вектор параболической скорости располагается
в этом
конусе, то тело будет захвачено Ч.д.
зависит от расстояния до Ч.д. На рис. 2 черным
цветом закрашен конус захвата: если вектор параболической скорости располагается
в этом
конусе, то тело будет захвачено Ч.д.
|
|
Рис. 3.
|
Поле тяготения Ч.д. искривляет траектории лучей света (и вообще любых ультрарелятивистских
частиц, к-рые движутся практически по тем же траекториям, что и фотоны). Чем ближе
к Ч.д. траектории, тем сильнее они искривлены. На рис. 3, а приведены траектории
лучей света, испущенных на разных расстояниях от Ч.д. перпендикулярно к радиальному
направлению.
Для лучей существует критич. окружность с R=1,5 rg.
По этой окружности может двигаться фотон, удерживаемый тяготением Ч.д. Однако это
движение неустойчиво. При малейшем возмущении фотон либо попадает в Ч.д., либо улетает
в космос.
Наличие критич. окружности ведет к тому, что все лучи с прицельным параметром на
бесконечности 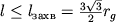 гравитационно захватываются
(рис. 3, б).
гравитационно захватываются
(рис. 3, б).
Около вращающейся Ч.д., как уже было сказано, должно существовать "вихревое" гравитац.
поле. Вдали от Ч.д. оно очень слабо, а вблизи возрастает настолько, что ведет к качественно
новым эффектам.
Так, в окрестности вращающейся Ч.д. возникает область, в к-рой все тела и фотоны
увлекатся в движение вокург Ч.д. Внеш. граница этой области наз. пределом статичности.
Однако
внутри предела статичности тела и фотоны совсем не обязательно должны падать к центру,
они могут и приближаться к Ч.д. и удаляться от нее, могут выходить за предел статичности.
Т.о., предел статичности не явл. границей Ч.д., ее горизонтом, из-под к-рого нельзя
выйти. Линейные размеры предела статичности по порядку величины равны rg.
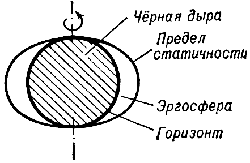
Горизонт Ч.д. расположен глубже, под пределом статичности. Пространство между горизонтом
и пределом статичности наз. эргосферой (рис. 4). Предел статичности касается горизонта
в полюсах вращающейся Ч.д.
При падении тела на вращающуюся Ч.д. оно сначала отклоняется в своем движении в сторону
вращения Ч.д., пересекает границу эргосферы и постепенно приближается к горизонту.
Для внеш. наблюдателя свет, испускаемый падающим телом, становится все более красным
и менее интенсивным, затем полностью затухает: тело, уйдя под горизонт, становится
невидимым
для внеш. наблюдателя. На горизонте все тела имеют одну ту же угловую скорость обращения,
в какое бы место горизонта ни попадало падающее тело.
Общая для всех падающих тел угловая скорость 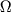 на горизонте Ч.д.
и есть скорость ее вращения:
на горизонте Ч.д.
и есть скорость ее вращения: 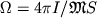 , где I
-
момент импульса тела, из к-рого возникла Ч.д.,
, где I
-
момент импульса тела, из к-рого возникла Ч.д.,  - масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и
- масса,
S - площадь горизонта Ч.д. Момент импульса Ч.д. заданной массы не может быть
сколь
угодно большим. Максимально возможные значения I и 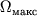 определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины
определяются тем, что при образовании Ч.д. линейная скорость вращения точек экватора
тела
не превышает скорости света. По порядку величины 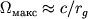 .
Для Ч.д. с массой, равной массе Солнца,
.
Для Ч.д. с массой, равной массе Солнца, 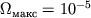 (1/с).
(1/с).
|
|
Рис. 4.
|
Гравитац. захват частиц Ч.д. с вращением несколько отличается от захвата невращающейся
Ч.д. Легче всего захватываются частицы, к-рые пролетают вблизи Ч.д. в сторону, противоположную
вращению, труднее захватываются частицы, летящие мимо Ч.д. в сторону вращения. Наглядно
можно себе представить, что вихревое гравитац. поле вокруг Ч.д. действует подобно
праще,
ускоряя, отбрасывая тем самым частицы, движущиеся мимо Ч.д. в ту же сторону, в к-рую
закручивается "вихрь" этого поля, и, наоборот, тормозя и захватывая частицы, движущиеся
против "вихря".
Рассмотрим для примера захват фотона, движущегося в плоскости экватора максимально
быстро вращающейся Ч.д.
Для фотона, движущегося в направлении вращения Ч.д., прицельный параметр lзахв,1=1/2
rg; для фотона, движущегося
против вращения, прицельный параметр намного больше: lзахв,2=4
rg. Изменяется ситуация и с круговыми орбитами.
Для Ч.д. без вращения последняя устойчивая круговая орбита имеет радиус 3rg;
частица, движущаяся по ней, имеет скорость c/2. И самое
важное: чтобы попасть на эту орбиту, частица с массой m должна отдать энергию
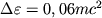 (энергию связи) в виде, напр., гравитационного
излучения.
(энергию связи) в виде, напр., гравитационного
излучения.
В случае максимально быстро вращающейся дыры последняя круговая орбита лежит в экваториальной
плоскости близко к горизонту, глубоко внутри эргосферы. Но здесь частица может
двигаться только в сторону вращения Ч.д. Энергия, к-рую выделяет частица, попавшая
на эту орбиту, гораздо больше и составляет 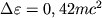 .
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию
.
В то
же время последняя устойчивая орбита частицы, обращающейся вокруг дыры в противоположном
направлении, лежит вне эргосферы и частица, попадающая в нее, выделяет энергию 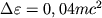 .
.
Полная масса вращающейся Ч.д. определяется как ее размерами (площадью S горизонта),
так и энергией вращения:
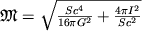 .
.
Если вращение отсутствует (I=0), то  определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
определяется
только размерами Ч.д. При максимально возможной скорости вращения Ч.д. второе слагаемое
под корнем равно первому.
В эргосфере Ч.д. возможны процессы, приводящие к уменьшению энергии вращения Ч.д.,
т.е., как оказывается, Ч.д. может терять энергию. В частности, когда в эргосферу
влетае
частица, имевшая вдали от Ч.д. энергию 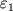 (включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
(включая энергию
покоя), и распадается на две частицы, то распад может произойти таким образом, что
одна
частица упадет на Ч.д., а другая, сравнительно немного увеличив свою скорость в момент
распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью.
Эта
скорость может намного превышать и первоначальную скорость подлета частицы к эргосфере,
и величину изменения скорости при распаде. В результате полная энергия вылетевшей
частицы
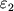 окажется больше
окажется больше 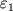 . Избыток энергии
. Избыток энергии
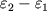 черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не меняется. Во всех других случаях площадь
горизонта несколько увеличивается за счет энергии частицы, упавшей в Ч.д. Оказывается,
что площадь горизонта Ч.д. не уменьшается ни при каких процессах вообще (за исключением
медленного самопроизвольного квантового испарения Ч.д., о к-ром говорится далее).
Напр., ч.д. могут столкнуться и слиться в одну. Часть их энергии будет унесена при
этом за
счет излучения гравитац. волн, но горизонт возникшей Ч.д. будет по площади больше,
чем сумма площадей горизонтов первоначальных дыр. Ни при каких воздействиях (приливных
и
других) Ч.д. не может разделиться на две или большее количество Ч.д.
черпается из энергии вращения Ч.д. Энергия
вращения Ч.д. может уменьшаться также при рассеянии эл.-магн. волн на Ч.д. Рассеянная
волна при определенных условиях может оказаться интенсивнее падающей. Потеря энергии
вращения Ч.д. при распаде частицы в эргосфере достигает максимума, когда распад происходит
на горизонте. При этом площадь горизонта не меняется. Во всех других случаях площадь
горизонта несколько увеличивается за счет энергии частицы, упавшей в Ч.д. Оказывается,
что площадь горизонта Ч.д. не уменьшается ни при каких процессах вообще (за исключением
медленного самопроизвольного квантового испарения Ч.д., о к-ром говорится далее).
Напр., ч.д. могут столкнуться и слиться в одну. Часть их энергии будет унесена при
этом за
счет излучения гравитац. волн, но горизонт возникшей Ч.д. будет по площади больше,
чем сумма площадей горизонтов первоначальных дыр. Ни при каких воздействиях (приливных
и
других) Ч.д. не может разделиться на две или большее количество Ч.д.
В эргосфере Ч.д. могут протекать квантовые процессы рождения частиц. В сильном поле
тяготения Ч.д. вакуум (представляет собой физ. поля в наинизшем энергетическом состоянии)
не устойчив и из него могут рождаться частицы и античастицы, в основном безмассовые:
фотоны, нейтрино, гравитоны.
Рожденные частицы, улетая из эргесферы на бесконечность, уносят энергию Ч.д. Характерная
частота 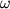 рождающихся фотонов по порядку величины равна
рождающихся фотонов по порядку величины равна 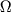 .
Скорость потери энергии вращения Ч.д. определяется соотношением:
.
Скорость потери энергии вращения Ч.д. определяется соотношением:
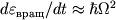 .
.
Чрезвычайно важно, что вакуум неустойчив в поле тяготения не только вращающейся Ч.д.,
но и невращающейся. Это означает, что за счет квантовых процессов невращающаяся Ч.д.
также теряет энергию, уменьшаются ее масса и размеры. Невращающаяся Ч.д. излучает
как абсолютно черное тело с темп-рой T=1011(1015/ ) К, полная мощность эл.-магн. излучения L=1010(1015/
) К, полная мощность эл.-магн. излучения L=1010(1015/ ) эрг/с, а время существенного
уменьшения массы Ч.д.
) эрг/с, а время существенного
уменьшения массы Ч.д. 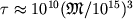 лет,
где
лет,
где  - значение массы Ч.д. в г. Приведенные соотношения
показыввают,
что квантовые процессы совершенно ничтожны для Ч.д., возникших из звезд с массами
- значение массы Ч.д. в г. Приведенные соотношения
показыввают,
что квантовые процессы совершенно ничтожны для Ч.д., возникших из звезд с массами
 >1034 г. Однако они существенны
для
маломассивных первичных Ч.д., к-рые могли возникать на ранних этапах расширения Вселенной.
>1034 г. Однако они существенны
для
маломассивных первичных Ч.д., к-рые могли возникать на ранних этапах расширения Вселенной.
По мере уменьшения массы Ч.д. мощность излучения должна расти, и в конце концов маленькая
Ч.д. породит мощную вспышку жесткого гамма-излучения (последние 109
г Ч.д. излучает за 0,1 с, что подобно взрыву миллиона мегатонных водородных бомб).
В реальных условиях Вселенной ч.д., к-рые могли возникнуть из звезд, все время увеличивают
свою массу за счет падения на них газа и излучения, в т.ч. и реликтового излучения
Вселенной. Увеличение массы Ч.д. при этом хотя обычно и мало, но существенно превышает
потери за счет квантового испарения.
Ч.д., возникшие в результате коллапса массивных звезд, могут вызывать своим сильным
гравитац. полем бурные процессы при падении в них газа. Такие газовые потоки могут
быть
особенно мощными, когда на Ч.д., входящую в состав тесной двойной звездной системы,
газ перетекает от звезды-гиганта. Газ, нагретый при падении в поле тяготения Ч.д.,
дает
рентг. излучение, и по этому излучению Ч.д. может быть обнаружена. Вероятно, одна
ч.д. уже обнаружена таким способом в рентг. источнике Лебедь Х-1 (см. Рентгеновская астрономия, Аккреционные
диски).
Возможно, что в центре ядер галактик и квазаров существуют сверхмассивные Ч.д., с
массой до 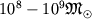 , в поле тяготения к-рых протекают
бурные
процессы, являющиеся причиной активности ядер галактик и квазаров.
, в поле тяготения к-рых протекают
бурные
процессы, являющиеся причиной активности ядер галактик и квазаров.
Лит.:
Зельдович Я.Б., Новиков И.Д., Теория тяготения и эволюция звезд, М., 1971; Мизнер
Ч., Торн К., Уилер Дж., Гравитация, т. 3, пер. с англ., М., 1977; Фролов В.П., Черные
дыры
и квантовые процессы в них, УФН, 1976, т. 118, в. 3, с. 473; Торн К., Поиски черных
дыр, пер. с англ., там же, с. 453.
(И.Д. Новиков)
- Re: Черная дыра
(oliya Korobeinikova,
11.12.2010 19:41, 362 Байт, ответов: 3)
Привет всем!Писала ,что в "черную дыру"сбрасывают планеты,звезды потом достают.Черная дыра есть во Вселенной,галактиках,в СС и на Земле.На Земле Бермудский треугольник.Он
находится рядом с Америкой,значит ЧД в СС находится рядом с Марсом.Стоит ли лететь на Марс?Там находится Олимп.На Земле в треугольники исчезают корабли,самолеты.Когда то появятся.
- Re[2]: Черная дыра
(с. а. вепрев,
16.12.2010 11:38, 738 Байт)
| Цитата: |
| Привет всем!Писала ,что в "черную дыру"сбрасывают планеты,звезды потом
достают.Черная дыра есть во Вселенной,галактиках,в СС и на Земле.На Земле Бермудский треугольник.Он
находится рядом с Америкой,значит ЧД в СС находится рядом с Марсом.Стоит ли лететь на Марс?Там находится
Олимп.На Земле в треугольники исчезают корабли,самолеты.Когда то появятся. |
Если на Земле она есть, тогда почему нас всех еще туда не засосало? Когда вещество попадает туда от
трения возникает излучение, почему оно в треугольнике не наблюдается?
- Re[2]: Черная дыра
(с. а. вепрев,
16.12.2010 11:38, 738 Байт)
| Цитата: |
| Привет всем!Писала ,что в "черную дыру"сбрасывают планеты,звезды потом
достают.Черная дыра есть во Вселенной,галактиках,в СС и на Земле.На Земле Бермудский треугольник.Он
находится рядом с Америкой,значит ЧД в СС находится рядом с Марсом.Стоит ли лететь на Марс?Там находится
Олимп.На Земле в треугольники исчезают корабли,самолеты.Когда то появятся. |
Если на Земле она есть, тогда почему нас всех еще туда не засосало? Когда вещество попадает туда от
трения возникает излучение, почему оно в треугольнике не наблюдается?
- Re[2]: Черная дыра
(Влад Логинов,
18.12.2010 20:58, 147 Байт)
А причем тут черная дыра и бермудский треугольник? И конечно, корабли и самолеты появятся, когда их со дна достанут. Похоже, сильно мистифицируете.
- Re: Черная дыра
(А. В. Рыков,
12.12.2010 14:34, 3.7 КБайт, ответов: 1)
Радиус чёрных дыр определяются по формуле Ньютона R(N)=sqrt(GM/g(max)) Минимальная дыра имеет
массу m(x)=1,859447219e9 кг. Её радиус совпадает с размером решетки среды (8). Приведенная формула резко отличается от формулы Шварцшильда,
найденная из решения ОТО: R(gr)=2*GM/c^2, что приводит к значительной разнице в оценках радиуса чёрных дыр. Шварцшильдовский радиус Солнца равен 3 км
R = 46 км по теории структуры среды), для Земли - 1 см79 мпо теории
структуры среды). Для чёрных дыр в центрах галактик плотность по Шварцшильду может быть на уровне плотности
воды, по структуре среды на 5-7 порядков больше. Среда равна структуре вакуума.
- Re[2]: Черная дыра
(В. В. Комогоров,
13.12.2010 19:38, 956 Байт)
Довольно странно, почему понятное триединство, существования энергии (Ек - Еп - Раб), воспринимается нами
закономерностью и вполне понятной. А вот триединство существования электричества, как ток - напряжение -
инуктивность (I - U - L), не можем даже помыслить. В этом мире все тройственно, как и наше появление на свет: от
желания отца и матери земных, по соизволению среды (одних желаний может быть мало). Действия порожденные одним
желанием приводят к мыслям о "черных дырах и темных энергиях". Вся беда в том, что мы законы видимого мира
применяем к миру "безвидному". "Черная дыра" - находится в научном мире, а не в идеально созденном для человека
мироздании, имя которому - Твердь Небесная. Хватит фантазий. Бедный Коперник даже не знал о дописанной нерадивым
учеником главы с математической моделью "вокруг Солнца". Он был уже парализован и, уединившись прекратил всякое общение
с внешним миром.
- Re: Черная дыра
(Г. В. Фивейский,
23.12.2010 14:19, 270 Байт)
Каждая черная дыра имеет свою звезду и они связаны неким тоннелем.Забирая из пространства все,что попадается в поле тяготения, черная дыра поставляетзвезде горючее.Если горючее
плохое или его мало,то звезда гаснет,если горючее слишком активное,звезда может взорваться.
- Re: Черная дыра
(Г. А. Зубков,
25.12.2010 0:36, 635 Байт)
товарищ Новиков
пишет,что при
приближении к
чёрной дыре
космонавтов
разорвёт из-за
приливных
сил,разности
ускорений.Почему
все забывают о
релятивистском
сокращении
размеров?Ведь при
влёте в чёрную
дыры вся
влетающая в неё
материя
сжимается,уменьшается
в размерах.Потому
разность ускорений
в уменьшемся теле
космонавта будет
небольшой.И сжатия
он также не
ощутит.На моём
сайте http://
genzubkov.narod.ru/
также есть статья
про чёрные дыры.
Правда мои
взгляды с недавних
пор
изменились:считаю
уже ,что свет не
подвержен
инерции,гравитации,ибо
не имеет массы
покоя.
- Re: Черная дыра
(А.П. Васи,
26.12.2010 14:31, 756 Байт, ответов: 1)
Г.А.Зубков
"Почему
все забывают о
релятивистском
сокращении
размеров?"
Мне приятно встретить толкового релятивиста,
который в практическом применении пользуется
релятивискими сокращениями в быту.
У меня вопрос, - космонавт в космическом корабле
держит в руках футбольный мяч, корабль разгоняется
до двукратного сокращения длинны, после чего
космонавт
с мячом в руках поворачивается на 90
градусов относительно направления движения,
со сплющенным мячом в руках, после чего корабль
начинает торможение, у космонавта
в руках
в итоге оказался сплющенный мяч для регби,
- вопрос какой внешний вид космонавта?
- Re[2]: Черная дыра
(А. В. Постников,
5.03.2016 13:41, 953 Байт)
| Цитата: |
Г.А.Зубков
"Почему
все забывают о
релятивистском
сокращении
размеров?"
Мне приятно встретить толкового релятивиста,
который в практическом применении пользуется
релятивискими сокращениями в быту.
У меня вопрос, - космонавт в космическом корабле
держит в руках футбольный мяч, корабль разгоняется
до двукратного сокращения длинны, после чего
космонавт
с мячом в руках поворачивается на 90
градусов относительно направления движения,
со сплющенным мячом в руках, после чего корабль
начинает торможение, у космонавта
в руках
в итоге оказался сплющенный мяч для регби,
- вопрос какой внешний вид космонавта?
|
- Re: Черная дыра
(А.П. Васи,
26.12.2010 14:43, 318 Байт)
Естественно вопрос возникает о единицах измерения,
связанных с сокращениями от скорости.
Так-же возникает вопрос - а скоро поступят в продажу
инструкции и
рекомендации по полетам на релятивиских
скоростях с целью проведения релятивиских
сокращений и растяжений вместо пластической хирургии?
- Re: Черная дыра
(Г. А. Зубков,
26.12.2010 20:48, 1.5 КБайт)
Чем ближе к
центру
гравитации,тем
теснее сходятся в
точку силовые
линии
гравитационного
поля.Так что мяч
будет плющить не
только вдоль,но и
поперёк-потому он
останется
круглым.Вообще
когда на тело
ничего кроме
гравитации не
действует,то оно
находится в
невесомости,и нет
никаких
перегрузок.Можно
связать систему
отсчёта с
космонавтом-он в
ней неподвижен,а
чёрная дыра на
него
надвигается.Чем
она ближе,тем она
больше,шире,разреженнее:возле
и внутри дыры
пространство
сильно сжато,так
что там может
поместиться целая
вселенная(в
принципе там и
находится целая
половина нашей
вселенной в
уменьшенном виде-
та,в которую
летим). Не мяч,а
вся круглая Чёрная
дыра станет
сплюснутой,плоской
и тонко-
эфемерной,как
блин. Благодаря
релятивистской
скорости
сближения время
внутри ракеты
течёт
медленнее,чем
снаружи.Потому
космонавт ''и
глазом моргнуть
не успеет'',как
пролёт сквозь
тоннель Чёрной
будет завершён.
Чёрная дыра тем и
отличается от
обычной или
нейтронной
звезды,что те
приходится
облетать, огибать,а
сквозь Чёрную
ДЫРУ можно
напрямик
скоротать путь и
время. Насчёт
радиуса
Шварцшильда есть
ещё такая
гипотеза,что он
должен быть в
четыре раза
меньше,чтобы
ракета и дыра
успели ускориться
до скорости 2с -
это относительная
скорость
сближения
фотонов.Так что
считать не по
формуле
R=2GM/(c^2),а так:
R=GM/(2c^2)
- Re: Черная дыра
(А.П. Васи,
27.12.2010 17:56, 1.5 КБайт, ответов: 1)
Г.А.Зубков
Я смотрю Вы не совсем полностью представляете
картину влияния и воздействия на некоторое тело,
в рамках
заявленных свойств Черной дыры.
В первую очередь тело под влиянием черной дыры,
находится под постоянным и увеличивающимся ускорением.
Второе -
черная дыра имеет заявленную большую массу, и
она не может в пространстве двигаться - она - якорь.
Третье - пространство сжиматься и разжиматься не может,
могут изменять свои размеры не качественные измерительные
инструменты, на основании чего делается вывод о сжатии или
разжатии пространства.
В связи
с тем что ускорение постоянно увеличивается,
то чем длиннее пробное тело, то его часть находящая ближе
к черной дыре - притягивается сильнее, и тело удлиняется,
так как увеличивающаяся гравитация, при приближении к дыре,
вызывает в длинном пробном теле растяжение на разрыв,
и уж никак пробное тело не находится в покое,
так как падение
в черную дыру - это не движение на орбите, и не свободное
падение - это принудительное падение с постоянно возрастающим
ускорением.
Черная дыра - не является тоннелем, по причине того что
у неё есть масса, и любой релятивист очень быстро и
доблестно разобъется в лепёшку о её поверхность,
так как её размер и радиус
Вам известен, - фильтруйте мысль, и иногда слегка попытайтесь
обосновать - перед тем как что-то утверждать.
- Re[2]: Черная дыра
(Г. А. Зубков,
28.12.2010 20:38, 2.1 КБайт)
Ой,не смешите
меня: чем это
свободное падение
отличается от
принудительного?
Если обрезать трос
лифта(или
выключить
двигатель
самолёта),то мы
будем падать
вместе с ним с
одной и той же
скоростью,таким же
ускорением
свободного
падения.Потому
относительно
лифта или
самолёта мы
будем в
невесомости.Это
если падать в
вакууме
конечно.Вот если
бы мы направили
самолёт вниз на
максимальной
тяге,это было бы
принудительное
падение,и мы
прилипли бы ''к
потолку''. По
Эйнштейну:
гравитация
реально искривляет
пространство,а не
только
приборы.Ускорение
измеряется в м/
с^2, а
секунды,время в
релятивистских
объектах текут по
другому.При
падении на Землю
ускорение тоже
растёт.И никого
ещё им не
''порвало'' и не
растянуло хоть на
микрон.В фотоне
скорость с , время
нулевое,замороженное,потому
ни фотон,ни что-
либо движущееся
со скоростью
света,разрушить
нельзя-никаким
ускорением или
столкновением.Закон
сохранения
энергии. Возьмём
например
аннигиляцию:электрон
и позитрон
разгоняются
встречно своими
полями до
скорости света и
превращаются в
два целёхоньких
фотона по
511кЭв.Без всяких
осколков,что было
бы при твёрдом
столкновении. Все
тела,и может даже
частицы состоят из
электронов и
позитронов.Так что
тела могут
например
аннигилировать
(перейти в
волновое
состояние) при
подлёте к чёрной
дыре,и
собираться,синтезироваться
заново на другом
конце дыры. Так же
как синтезируются
электрон и
позитрон при
пролёте фотона
1Мэв сквозь ядро
атома. Не всегда
можно понять:мы
двигаемся
навстречу
объекту,или он к
нам двигается.Вот
я и допустил,что
космонавт стоит на
месте,а дыра к
нему
притягивается.Не
важен источник
силы.Важна общая
относительная
скорость. Хотя по
теории
относительности
выходит,что если
частицу разогнать
до скорости
света,то её масса
станет
бесконечной.И
тогда частица
сможет целую
галактику к себе
притянуть.Абсурд.Так
что скорее всего
релятивистские
частицы наоборот
теряют массу до
нуля,а не тяжелеют.
- Re: Черная дыра
(А.П. Васи,
29.12.2010 23:24, 1019 Байт, ответов: 1)
Вы как и все астро физики, пишете о физических
свойствах чего либо в стиле -
"Так спимпздел что аж сам поверил".
И Вы просто не понимаете где Вы
врёте где другие
приврали да и не понимаете сам предмет о котором
рассуждаете.
Вы как лабух приплетаете Эйнштейна к черным дырам.
Вы я думаю даже
не знаете написанное на этом сайте
однозначное определение черной дыры - от автора.
А прочитали наверное околонаучной омосятины
на популярной механике о черных
дырах.
Они там и излучают и у них выбросы, и много прочих свойств.
Причем искривление пространства от Эйнштейна, к черным дырам?
Черные дыры придумал
- один автор.
Кривизну пространства придумал - другой автор.
Размер черной дыры - придумал третий.
Какое отношение имеет к черной дыре - аннигиляция?
"Так же как синтезируются электрон и позитрон при
пролёте фотона 1Мэв сквозь ядро атома."
---- это где Вы такую омосятину физическую прочитали?,
в какой книжке.
- Re[2]: Черная дыра
(Г. А. Зубков,
30.12.2010 8:34, 744 Байт)
Неприятно
общаться с такими
приблатнёнными
негативистами,как
вы. Нет,чтоб что-то
своё,конструктивное
добавить,занимаетесь
одним
критиканством. Ваш
уровень знаний по
некоторым
вопросам явно
ниже даже моего,а
вы наезжаете на
меня, как будто вы-
знатнейший
профессор.
Неважно,кто
автор.Всю теорию
Чёрных дыр можно
самому вывести из
формулы
гравитации F=GmM/
r^2 . Я больше сам
думаю,чем изучаю
чужие труды.Про
процесс,обратный
аннигиляции,написано
например в
''Элементарном
учебнике физики''
том 3 с.553
Г.С.Ландсберга:
''образование пары
электрон-позитрон
происходит в
результате
взаимодействия
гамма-кванта с
электрическим
полем одного из
атомных ядер
вещества.''
- Re: Черная дыра
(А.П. Васи,
30.12.2010 16:53, 1.8 КБайт)
Я Вам культурно всё время намекаю что Вы в
своих размышлениях то в облаках летаете,
то отбиваетесь от общепринятых утверждений,
то несёте в руках бред сивой
кобылы.
Если Вам это нравится - то это лично Ваш выбор,
могу Вас обрадовать, что таких мечтателей ниочем,
как Вы - делающих при этом наукоёмкий вид
и вырабатывая
мысли притендующем на аплодисменты, - так таких
среди астро-физиков практически абсолютное большинство.
А то что написано например на этом
сайте о черной дыре,
Вы я так понимаю взять за стандарт не хотите, и при этом
отбросить все выдумки. Определение достаточно простое,
- гравитация такая что
даже фотоны не могут покинуть -
здесь надо тогда признать врунами всех кто утверждает
что дыры излучают, - как по мне - надо так надо,
а Вам выбирать .
У черной дыры есть радиус следовательно есть поверхность,
и в этом случаи с моей точки зрения, - вруны те кто утверждает
что сквозь дыру есть тоннель,
- а Вам выбирать.
Я Вам вкратце пытаюсь объяснить что в физике если
автор предоставляет читателю право выбора - то это
уже говорит о том что это враньё
или необоснованная
выдумка изначально, и мне смешно и жаль Вас по
бессмысленно потраченному Вами времени в размышлениях
над черными дырами, если бы вы вникли
в базовые
авторские постановки задач и объяснений Вы бы сразу
поняли что это простая галиматья, не имеющая никакого
отношения к наблюдаемым объектам.
Я
Вам по дружески скажу почему на текущий момент
никто не обнаружил черной дыры, а слышны лишь утверждения
что она вот там должна быть, - потому что астро-физики
и сами не знают как она должна выглядеть, -
я думаю Вы догадываетесь, почему астрономию в школах
отменили.
- Re: Черная дыра
(А.П. Васи,
30.12.2010 17:13, 507 Байт)
В астрономии кризис очень большой - из за того что неудобно
ученикам пререкаться с преподавателем, и в лицо ему сказать
не могут - мол хватит нам бред сивой кобылы
в мозг заливать.
А со временем ученики на залитом в моск бреде и уверенности
в отсутствии критики - пишут такую галиматью, что уши
у одних заворачиваются,
а молодые воспринимают за "чистую монету",
и все идет по кругу - так называемый -
"авторитарный круговорот бреда сивой кобылы в астрономии".
- Re: Черная дыра
(А.П. Васи,
30.12.2010 17:29, 397 Байт)
Прочитайте 16 ответ, и другие ответы Самоучки
может поймёте другие ситуации, но как правило среднему
человеку дано понять одну теорию по теме, второй теорией
с другими идеями его обучать нет смысла,
ибо непойметс.
- Re: Черная дыра
(А.П. Васи,
30.12.2010 21:23, 911 Байт, ответов: 1)
Вы вот даже не знаете что лично Вы вот
являетесь физиком-теоретиком.
Это просто фантастическая анекдотическая история.
Было это давным давно -
заходит секретарь
цк кпсс, в лабораторию и спрашивает у своего
помощника - а на каком месте наша страна по
количеству физиков?
Не на первом, - отвечает
помощник.
Чтобы финансировать физика надо много денег на
оборудование.
секретарь: -А еще какие-то варианты есть?
помощник: -Да есть можно
при небольшом финансировании
выйти на первое место в мире если финансировать,
физико - математическое направление или теоретическую физику,
из всех приборов
и оборудования им достаточно письменного
стола карандаша и резинки.
секретарь: - Да?
помощник: - нет, ну если четно то стирательная резинка
теоретику не нужна, достаточно стола и карандаша,
- отоврётся если ошибется.
- Re[2]: Черная дыра
(Г. А. Зубков,
31.12.2010 17:32, 1.9 КБайт)
Сфера,радиус
чёрной дыры-
понятие
условное.Они могут
быть даже
нулевыми-тогда
Чёрная дыра станет
Чёрной
точкой.Любое тело
можно
рассматривать как
голое силовое
(гравитационное
или другое)
поле,условно
считать его
размеры
нулевыми,чтобы те
падать не мешали :-
D,ускоряться до
скорости света. До
скорости света
также разгоняются
(если верить теории
БВ) все галактики в
13 млрд.световых
лет от нас,так что
мы окружены некой
скорлупой-сферой
Шварцшильда
навыворот.А что за
ней?
Сверхсветовые
скорости или опять
же туннельные
перескоки,как в
Чёрной дыре? Вот
например,мы
разгонемся за год
до скорости
света,если наше
ускорение будет
равно земному -
10 м/с^2. Заметим
ли мы момент
сверхсвета?Вряд
ли. Ведь только
относительно
''покоящихся'' звёзд
и места старта мы
будем двигаться со
скоростью света, а
относительно
других звёзд
скорость будет
разной. И для
покоящихся звёзд
мы будем видеться
и являться
фотонами
(ничто,кроме
фотонов,не
движется со
скоростью света),а
для
других-ракетой.
Шмякнемся мы об
световой барьер?
Нет.Значит и об
сферу
Шварцшильда не
шмякнемся. Ведь
по эффекту
Допплера наша
частота,и частота
дыры будут
бесконечными.А
гамма-лучи сквозь
что угодно
пройдут. Неважно
как оно в
реальности.Главное
предвидеть
возможные
варианты,авось чья-
нибудь
модель,идея
выведет кого-
нибудь к новым
открытиям.Ведь
такая тоска
берёт,когда все
учёные,все
телеканалы подают
только один
вариант какого-
нибудь явления-
Разбегание
галактик,Чёрная
дыра и т.п. Почитал
я ответы товарища
Самоучки.Чтобы не
быть
посмешищем,ему
стоило бы перейти
на новую
терминологию.Эфир
заменить
нейтрино,гравитонами,частицами
с отрицательной
массой,микро-
чёрными дырами и
т.п. Эфирная
звезда-это по-
современному
Белая дыра,-
та,которая всё
отталкивает,отражает.
- Re: Черная дыра
(А.П. Васи,
31.12.2010 17:00, 571 Байт)
Да чуть не забыл что Вы просили высказать что-то конструктивное,
- да в науке были подобные времена когда наука в разных областях
не оправдывала вложенных денег,
и становилась непонятная для простых
людей, и объяснения ученных простым людям казались бредовыми
- практически аналогичная ситуация в физике и астрономии.
Так вот, лечилось это тем что на 50-100 лет рекомендовалось полностью
прекращать финансирование данных направлений в науке.
После чего финансирование возобновляется.
Поздравляю всех с наступающим Новым Годом!
- Re: Черная дыра
(А.П. Васи,
31.12.2010 18:31, 2.2 КБайт)
"(если верить теории
БВ)"
о - Вы делаете успехи.
Я эту теорию считаю ложной на 100%.
Черные дыры враньё 100% с моей точки зрения.
Теории Эйнштейна необоснованная
выдумка на 100%, - с
моей точки зрения.
Вы просто не понимаете что любая теория по большому счету выдумка.
Там где не объясняется теориями текущие
вопросы но делаются предсказания -
там Вас уже обманули.
"Главное
предвидеть
возможные
варианты,авось чья-
нибудь
модель,
идея
выведет кого-
нибудь к новым
открытиям"
Здесь Вы заблуждаетесь - в подтверждение тому сто лет
релятивиского шествия в никуда, и миллиарды людей на дифективных
теориях никогда
и низачто тратя любые деньги, ничего не добьются полезного.
Предвидеть как раз ничего не нужно, надо просто объяснить просто и понятно
то что наблюдается
сейчас.
"Чтобы не
быть
посмешищем,ему
стоило бы перейти
на новую
терминологию.Эфир
заменить
нейтрино,гравитонами,частицами
с отрицательной
массой,микро-
чёрными дырами и
т.п"
Расскажу я Вам одну историю, - давным давно все пользовались в физике эфиром,
в 1800 Т.Юнг, добился выдающихся успехов и на опытах обосновал световое
излучение
и интерференцию как колебания среды которые при воздействии создают в атомарной структуре
световое излучение, также для измерения количества колебаний
для сред был придуман
Доплером - эффект Доплера - и обоснован - для сред.
После чего Энштейн в молодости - заявляет что в пространстве пустота, и не опровергает
ни Юнга ни Доплера, а просто постулирует .
Вот собственно с этого момента вся физика пошла под откос, а астрономия
пошла под откос с ускорением, - вот
такая жестокая селяви.
Так что эфир по факту - остался, по причине отсутствия внятных опровержений,
которые по объяснительным возможностям превосходят объяснения
Юнга и Доплера,
а раз таковых за сто лет релятивисты не смогли обосновать то эфир лучше пустоты в пространстве.
- Re: Черная дыра
(А.П. Васи,
1.01.2011 15:22, 1.0 КБайт)
Вот яркий пример когда модераторы давят авторитетом и замолачивают
форум своими встряваниями не по теме.
На физ вопросах, обсуждают устройство компютера
и его мат обеспечение
при проэктировании.
Мне жаль Дмитрия Вибе .
Специально перенес его высказывание чтобы он не стер,
он очень полюбляет
поскандалить, а потом стереть где он
выглядел плохо, и где затевал скандал.
"Вы полагаете, что компьютер создавался без математической модели наблюдаемых
явлений?"
, совсем интеллектуально сдал, каждый его наезд
ярко видно его намеренья, встряёт с вопросами не по теме и провоцирует скандалы
своей
тупизной и непониманием, а второй модератор, встряет с очень строгим
подходом и хорошим пониманием того что ответы должны быть строго
по названию форума, вот и
получается один модератор тупит на его провокационные
вопросы если ответить то второй модератор забанит так как разговор не по теме.
http://www.astronomy.ru/forum/index.php/topic,79788.720.html
- Re: Черная дыра
(А.П. Васи,
1.01.2011 16:59, 1.2 КБайт)
""Вы полагаете, что компьютер создавался без математической модели наблюдаемых
явлений?"
Кстати вопрос не правильно поставлен, что
собственно говорит о том что задавший этот вопрос просто дилетант
в области основ компьютера.
Я более чем уверен что никто из здесь
присутствующих не знает ответа на этот вопрос.
А для меня этот вопрос проще лёгкого.
Так вот - за основу
при конструировании компьютера, было
взято некоторое логическое утверждение, что например есть некоторое
арифметическое - логическое устройство, которое может
одновременно выполнять команду,
устанавливать адресные данные, и по установленному адресу может производить
запись или чтение данных, (принимать или передавать
данные по
указанному адресу, при этом выполняет команду).
И начинает свою работу с установки нулей по адресу и по этому адресу делает чтение данных
и выполняет
команду записанную в нулевом адресе.
Как правило качестве источника заданий (программ) используется в младшем адресном пространстве
постоянная память (только
чтение) , в которой и записана программа, в старших адресах используется
оперативная память (запись и чтение).
- Re: Черная дыра
(А.П. Васи,
1.01.2011 19:23, 1.4 КБайт, ответов: 1)
ВибеВы полагаете, что компьютер создавался без математической
модели наблюдаемых явлений?
EVVНет. Я так не полагаю.
ВибеТо
есть, Вы признаёте, что для публикации текста о фантазийности
современной физики Вы используете одну (даже и не одну) из её фантазий?
В моё время тех кто задает вопросы , и перевирает слова и отвечает за оопонента и потом
за свой ответ за оппонента
упрекает - таких называли гнидами и чмошниками.
Вибе - совсем оборзел модератором.
Вот если там на форуме правду сказать
модератору, то Вас забанят,
Вы подобного никогда не делайте, они провокаторы и для них забанить кого
так это им в радость.
Я рад - хоть все видят методы
этого чмошника.
А это как он сам на свой вопрос о компютере ответил, я же точно говорил,
что этот чмошник не мог знать базовых основ компютеро строения,
а
вопрос задаёт.
"Цирк. Я не использую. Я только на кнопочки жму. И тот, кто создал
компьютер,
тоже не использовал. Он учил что-то где-то когда-то."
Понимание Вибе - о компьютере, явно детский лепет.
- Re[2]: Черная дыра
(Г. А. Зубков,
1.01.2011 20:21, 886 Байт)
Вас вообще наука
интересует?
Занимаетесь
мелкими
дрязгами,выяснением
отношений.
Забудьте об
эмоциях,личном и
вместе со всеми
ищите ответы на
ещё не
разрешённые
человечеством
вопросы.На
astronomy.ru
вообще-то ещё
даже терпимо,а вот
на dxdy.ru
модерация точно
жесточайшая и не
всегда
объективная.И
давайте не
уклоняться от
темы. Теория
Эйнштейна всё-
таки
подтверждается
экспериментами :
чем ближе
скорость частицы к
скорости света,тем
труднее её
ускорить .Спорными
могут быть лишь
детали:коэффициенты,релятивизм
массы;притяжение,давление
света и т.д. Я
недавно по тв
Дискавери видел
передачу Wormhole
- Сквозь
червоточину
,так там астрономы
целое видео
склепали из
фотографий
центра Млечного
пути,как там
звёзды вокруг
невидимой чёрной
дыры обращаются.
По расчётам так у
них выходит.
- Re: Черная дыра
(А.П. Васи,
1.01.2011 21:18, 1.3 КБайт)
Вы уж извините но в релятивиском ... я ковырятся не собираюсь,
ибо ценю своё время, и уважаю здравый смысл.
Так что вопросы на релятивиские темы не воспринимаю.
Рекомендую прочесть полностью, там есть все ответы
на типичные вопросы.
http://www.astronet.ru/db/forums/1244628?page=1
Если строго
разбираться с черными дырами, - то здесь
я считаю что Звезда Эфира более подходит на эту роль.
Дело в том что она решает ряд вопросов которые не может решить
черная дыра.
Я давно говорил, ещё до первых телескопов которые могут обнаруживать
холодные участки , что есть очень много звезд эфира с температурой ниже
160градусов
Цельсия.
http://znaniya-sila.narod.ru/
На этой странице написано что давече обнаружили и таких объектов
с температурой всего лишь на 10 градусов
больше абсолютного нуля,
только в нашей галактике больше миллиона.
И ещё до того как обнаружили хвосты у движущихся в пространстве звезд,
- Реактивные
Звезды Физиков, я говорил что у всех звезд которые движутся
не в рукавах а сами по себе с большой скоростью, то у них будет реактивный
выброс, и будет оставаться
след из пыли.
Так что у меня точные знания и достоверные в области астрономии.
И все просто и все сходится.
- Re: Черная дыра
(А.П. Васи,
2.01.2011 12:26, 189 Байт, ответов: 1)
Вот еще нашел "Предположение о звездах",
рекомендую прочесть просто для общего развития.
http://forum.membrana.ru/forum/alternative.html?parent=1053369627#1053369627
- Re[2]: Черная дыра
(Г. А. Зубков,
2.01.2011 23:08, 708 Байт)
По последней
ссылке прочитал
такое:чёрная дыра
поглощает
вещество и
излучает в
пространство
эфир.В другом
месте там же
написано:возможнно
эфир может
превращаться в
вещество.
Вот и выходит
тогда в сумме
такое:вещество
падает в чёрную
дыру,потом
превращается в
эфир,а потом
материализуется-
опять
превращается в
вещество. Только
вместо эфира
можно написать и
фотоны,и
нейтрино,и т.п.
Только по ссылке
выходит,что чёрная
дыра
отфутболивает
частицу
туда,откуда та
пришла(белая дыра
так и делает),а по
моему мнению
чёрная дыра
телепортирует
частицу сквозь
себя дальше-в том
же
направлении,куда
частица двигалась
(падала)раньше.
- Re: Черная дыра
(А.П. Васи,
3.01.2011 9:48, 2.8 КБайт)
Я не понимаю почему Вы всё время пытаетесь
найти что угодно вместо эфира.
Я понимаю что релятивисты отвергли эфир
более ста лет назад, и теперь эфир надо
вернуть на своё
место, и честно признаться что отказ от эфира был ошибкой.
И сто лет шествия релятивизма были бессмысленны.
Но это было видно сразу так как
отсутствовала методика
измерений и измерительные приборы на заявленные
релятивистами физические свойства.
Черная дыра излучающая эфир в пространство
- называется Звезда эфира.
Использование терминологии черная дыра, просто
для общения, и далее не применима, так как
черную дыру ничто не может
покинуть,
и в заявленных свойствах пространство вокруг черной дыры
пустое и она всё всасывает, звезда эфира наоборот - создает
большую плотность эфира вокруг
себя, и всё отталкивает.
Поглощает вещество звезда эфира которое больше
потери массы при излучении эфира в пространство ,
находясь внутри звезды Физики,
или внутри цыфеиды.
Я так понимаю что Вы не в курсе
того что альфа бета и гамма, это не колебания среды,
это частицы - так вот масса звезды эфира увеличивается
за счет этих частиц.
Радио волны и до фотонов- это колебания среды аналогичные
звуку, а альфа бета и гамма это частицы,
- дело в том что световое
излучение колебание
среды определяемое просто по отражению
от зеркала, оно отражается под углом падения, - значит
колебания среды, а альфа бета и гамма,
при столкновении
с зеркалом разлетаются куда угодно, и часть пролетает
сквозь зеркало.
Тоисть - фотоны это не частицы.
Очень рекомендую почитать
Вам работы Т.Юнга.
"чёрная дыра телепортирует частицу сквозь себя
дальше-в том же направлении,куда частица
двигалась (падала)раньше"
- это Ваше священное право так считать,
только Вам осталось выполнить священный долг физика
- обосновать своё утверждение
и привести практические
примеры, - а иначе
постулат без причины - признак дурачины.
Рекомендую сперва определится с -
пространством и его свойствами,
со свойствами черной
дыры, - и Вы должны
придумать ей другое название так как она
отличается от заявленных автором ЧД свойств,
так-же вопрос какие частицы,
могут ли быть
объекты и каких размеров,
может ли упасть в дыру портации - звезда,
планета или другая дыра портации.
Как выглядит дыра портации в телескоп?
И как
связанно это с тем что насмотрелись по
телевизору фантастики, или связанно с естественными
человеческими чувствами и желаниями халявы, и
связанного с этим
желанием перемещаться быстро
и бесплатно, в связи с чем можно строить коллайдер
новый для поиска дыры телепортации. С помощью которых
можно будет перемещаться
на халяву по всей планете.
Аферой попахивает.
- Re: Черная дыра
(А.П. Васи,
3.01.2011 10:52, 1.9 КБайт, ответов: 1)
Вы вот слишком узко смотрите на черную дыру,
и не можете обозреть мысленно всей глупости в
текущей астрономии.
Изначально черная дыра была придумана
для
утилизации избыточного излучения звезд.
До этого сделали первый радио телескоп, на шум этого
телескопа сбежалась стая жаждущих халявной славы,
и было придумано эхо большого взрыва, да и
сам большой взрыв придуман немногим раньше.
И релятивизм связывали с атомным оружием.
Хотя конструкция атомной
бомбы была опубликована в 1942
году в не секретном журнале. И релятивисты к этой публикации
не имели никакого отношения.
Большой взрыв подтверждался
шумом в радиотелескопе.
А то куда девается энергия от звезд, так и не получалось,
для этого придумали черные дыры, а так как кругом пустота
то дыра должна
притягивать и материальные объекты,
- вот здесь без эфира вся астрофизика пролетела намного
сильнее чем без черной дыры.
Потому что получалось что всё только
притягивается, звезды
притягивают звезды и черные дыры и планеты, а черные дыры
притягивают черные дыры звезды и планеты, - тоисть получается
что во вселенной
всё только притягивается, а если всё
притягивается значит не может всё разлетается после большого
взрыва, а может только всё сжиматься.
Пролет галактик одна
сквозь другую, на небольших скоростях,
то должно было вызвать стену огня и огромное количество
столкновений - чего не наблюдалось.
После этого срочно придумали
темную материю и темную
энергию , вместо эфира - заполняющую пространство, и
определили темной материи и темной энергии массу от
60 до 90 процентов, от общей
массы во вселенной, -
как говорится ручными постулатами, провели имитацию
эфира.
Так что Ваши поиски портала в черной дыре, - это ваше
время припровождение,
по причине того что ничего в
астрофизике не бывает просто так.
- Re[2]: Черная дыра
(Г. А. Зубков,
3.01.2011 15:36, 2.1 КБайт)
Вычислять
взаимодействия
между потоками
эфира намного
сложнее,чем -
между отдельными
объектами.Потому
эфир так
непопулярен.
Альфа-частицы-
это атомы(или
ядра) гелия,бета-
это
электроны,гамма-
это
суперпроникающие
электро-магнитные
волны (самый
высокочастотного
диапазон). Зеркало
не отражает
гамма-лучи,как
свет,лишь
потому,что
расстояние между
частицами зеркала
больше длины
волны гамма-
лучей.Чтобы
отражать гамма-
лучи,нужно зеркало
из суперплотного
проводящего
материала. Белая
дыра(Чёрная дыра
отрицательной
массы) отражает
любые лучи.
Примеры чёрных
дыр(ЧД)?
Электроны.Их масса
стабильна.Они
ведут себя и как
частицы,и как
волны.Их радиус
Шварцшильда-10^-57
м. Другие названия
ЧД-
Фотонизатор,Гравителепорт,Сквозная
масса,Сфера
прозрачной
Невидимости,Суперлинза.
В чёрную дыру
могут падать тела
любой массы.Если
на ЧД будет падать
другая ЧД,то они
не сольются,а
пройдут с
ускорением друг
сквозь друга.Если
масса планеты
намного больше
массы ЧД,то
планета останется
на месте,а ЧД
будет пролетать
сквозь
планету,выныривая
из неё ''то тут,то
там''. В телескоп
идеальная ЧД
будет выглядеть
как прозрачная
(гравитационная)
линза. Хотя многим
телам не хватает
инерционной
энергии,чтобы,пролетев
сквозь
дыру,навсегда
покинуть границы
её поля.Также не
все тела падают
строго по
направлению в
центр дыры.Потому
реальная ЧД-это
например центр
галактики,вокруг
которого кружится
уйма материи.
Также некоторые
области космоса
настолько
плотны,что их
можно считать
глобальной ЧД-они
и видны,как линзы
или фрагменты
линз .Когда
сталкиваются
галактики,их
центры встречно
телепортируются,а
остальная масса
звёзд слишком
рассеянна,чтобы
часто
сталкиваться.Куда
девается энергия
от звёзд?Почитайте
в поисковиках про
Фотонную
сферу.Все фотоны
типа тормозятся на
сфере
Метагалактики,и
потом эта
Фотонная сфера
гравитацией
расширяет наше
пространство.Я
сомневаюсь,что
сейчас реально
можно сжать
материю до
состояния ЧД.
- Re: Черная дыра
(А.П. Васи,
3.01.2011 16:25, 3.5 КБайт, ответов: 1)
"Вычислять
взаимодействия
между потоками
эфира намного
сложнее,чем -
между отдельными
объектами.Потому
эфир так
непопулярен."
Конечно выучить весь эфир за месяц и ли учится пять лет релятивизму,
понятно что для преподавателей астрономии
и физики эфир не привлекательный,
- негде губы надувать, и пальцы загибать.
По поводу собственно вычислений, так Ваши слова лживы, ибо компьютеру
глубоко до лампочки любые вычисления, он не устанет.
Вы может еще в ручную вычисляете, тогда я Вам рекомендую
использовать технические средства.
"Альфа-частицы-
это атомы(или
ядра) гелия,бета-
это
электроны,гамма-
это
суперпроникающие
электро-магнитные
волны (самый
высокочастотного
диапазон)."
Да Ваш уровень знания физики меня шокирует, а думаю что Вы еще намного выше
среднего, Вы хоть какие-то названия знаете.
Мне больше
всего понравилось
"бета-
это
электроны" - тоисть на каком излучении вырабатывают электричество
атомные станции у Вас сомнений нет. И эти электроны вылетают по проводам из
розетки и устают
когда компьютер гоняет их по процессору, смешно.
"Если
на ЧД будет падать
другая ЧД,то они
не сольются,а
пройдут с
ускорением
друг
сквозь друга"
Мне всё равно как Вы трактуете, но Вы выбирайте - или Вы идете в физике по
пути чмошников - только постулируя, или Вы как нормальный
физик -
обосновываете причины высказанных Вами явлений.
Вопрос почему черная дыра притягивает черную дыру, а их ядра пролетают мимо.
Вариант ответа,
- Мне так хочется - называется постулат.
"Когда
сталкиваются
галактики,их
центры встречно
телепортируются,а
остальная масса
звёзд
слишком
рассеянна,чтобы
часто
сталкиваться."
Здесь я Вам хочу сказать, что Вы иногда призадумывайтесь, над сказанным, Вы себе представьте
черную дыру массой в тысячу солнечных,
которая пролетает мимо другой,
и потом вся эта масса перемещается с мгновенной скоростью в другую точку пространства
не указанную Вами , Вы даже не догадываетесь
сколько энергии физической надо затратить,
и после выхода из тоннеля у черной дыры весом в тысячи масс солнца будет столько кинетической
энергии и такая скорость
движения, что пролетая она будет пробивать звезды, и лететь должна
со сверх световой скоростью.
Так что я думаю Вы не чмошник, и сможете объяснить от куда берётся
энергия для перемещения
тысячи масс солнца, и куда потом девается.
"Также некоторые
области космоса
настолько
плотны,что их
можно считать
глобальной ЧД-они
и видны,как линзы
или фрагменты
линз ."
Вы хоть понимаете что Вы в руках несёте - Вы хоть догадываетесь что в космосе
в рамках текущих теорий пустота, а у пустоты не может быть плотности.
Вы не понимаете, что текущая глобальная путаница и кризис в астрономии, как раз
из за того что пустоте приписывают свойства среды, и при этом среду отрицают.
"Все фотоны
типа тормозятся на
сфере
Метагалактики,и
потом эта
Фотонная
сфера
гравитацией
расширяет наше
пространство"
А слабо обосновать?
- Re[2]: Черная дыра
(Г. А. Зубков,
3.01.2011 22:16, 3.2 КБайт)
Насчёт электронов
я читал такое
официальное
объяснение:когда в
проводе течёт
ток,сами электроны
движутся
медленно-мм/
секунду,зато они
быстро передают
друг другу своими
отталкивающими
полями энергию
тока,заряд,и ток
движется почти со
скоростью света. Вы
вообще читали
статью про чёрные
дыры на моём
сайте http://
genzubkov.narod.ru/ ?
Я там всё логично
подробно
объяснил ,а до вас
никак не
''дойдёт'',сколько я
тут не пытаюсь
объяснить. ЧД
проходит сквозь
ЧД,так как они до
касания-
столкновения
успевают
разогнаться до
скорости с (или 2с).
При скорости с
внутреннее время
не идёт,потому
момент входа в
сферу ЧД и выхода
из неё для
космонавта
сольются в один
миг. Насчёт закона
сохранения
энергии:гравитация-
это вообще
сплошное его
нарушение.Планета
нас и предметы
притягивает,а
энергию на это не
тратит (если не
вникать в нюансы-
энергию связи).
Чем больше масса
ЧД,тем больше её
гравитация,ускорение,приобретённая
кинетическая
энергия. Куда
девается энергия?
Когда чёрные дыры
пролетят друг
сквозь
друга,своими
полями они друг
друга начнут
тормозить.Так что
сколько
гравитационной
энергии ушло на их
сближение,столько
же энергии уйдёт
на их торможение.
И получится в
итоге,что скорость
(кинетическая
энергия) галактик
не
изменится,просто
они перенесли друг
друга в
пространстве.Насчёт
гравитационных
линз: есть много
фотографий
космоса,на которых
видно искривление
света гравитацией
(а может быть это
просто
преломление-
имхо) ,видны как бы
части линз,серпы.
Формула радиуса
Шварцшильда
R=2GM/c^2.
Выведем
зависимость
радиуса
Шварцшильда от
плотности среды.
M=pV=p(4/3)ПИR^3 .
R=[2Gp(4/3)ПИR^3]/
c^2 .Сокращая
R,получаем: R=sqrt
[(3c^2)/(8GpПИ)]
.Отсюда видно,что
радиус ЧД обратно
пропорционален
квадратному корню
из плотности ЧД.
Значит,чем больше
радиус ЧД,тем
меньшей может
быть её плотность.
Наши учёные по
красному
смещению своими
методами
вычислили,что
плотность нашей
видимой Вселенной
(Метагалактики)
1.773298*10^-28
м.Если эту
плотность
подставить в
формулу выше,то
получим R=10^25
м,что совпадает с
реальным-
официально
принятым
радиусом
Метагалактики.Вот
и выходит,что наша
вселенная-
невидимая Чёрная
дыра,Гравителепорт
для наблюдателей
из других,внешних
Вселенных.Хотя по
моей теории
вещество внутри
ЧД не расширяется.
Про гравитацию
Фотонной
сферы,совпадающей
со сферой
Метагалактики,писал
на своём сайте
один учёный,позже
уточню.Смысл в
том,что
частицы,покидающие
нашу Вселенную,по
релятивистскому
закону,достигая
скорости света(а
фотоны-
увеличивая
частоту),становятся
бесконечно
тяжёлыми,а значит
обладают сильной
гравитацией,которая
и расширяет во все
стороны нашу
вселенную. Но есть
учёные(например
Гришаев http://
newfiz.narod.ru/ ),доказывающие,что
все поля также
имеют предел
скорости=с. Это
называется типа
Лоренцевское
преобразование
поля.Потому поля
релятивистских
частиц слабее,чем
покоящихся.Также
и поля потому не
поспевают за
релятивистскими
частицами.
- Re: Черная дыра
(Г. А. Зубков,
3.01.2011 23:12, 253 Байт)
Уточнение: про
Фотонную сферу
пишет Натанзон
Д.Д. на http://
www.sciteclibrary.ru/
rus/catalog/
pages/8894.html/ .
Товарищ пишет,что
всё,что вылетело из
нашей
Вселенной,превращается
в
спутники,кружащиеся
вокруг нашей
Вселенной.
- Re: Черная дыра
(Г. А. Зубков,
3.01.2011 23:15, 253 Байт)
Уточнение: про
Фотонную сферу
пишет Натанзон
Д.Д. на http://
www.sciteclibrary.ru/
rus/catalog/
pages/8894.html/ .
Товарищ пишет,что
всё,что вылетело из
нашей
Вселенной,превращается
в
спутники,кружащиеся
вокруг нашей
Вселенной.
- Re: Черная дыра
(Г. А. Зубков,
3.01.2011 23:16, 253 Байт)
Уточнение: про
Фотонную сферу
пишет Натанзон
Д.Д. на http://
www.sciteclibrary.ru/
rus/catalog/
pages/8894.html/ .
Товарищ пишет,что
всё,что вылетело из
нашей
Вселенной,превращается
в
спутники,кружащиеся
вокруг нашей
Вселенной.
- Re: Черная дыра
(А.П. Васи,
4.01.2011 0:08, 1.3 КБайт, ответов: 1)
Вы я смотрю недопонимаете,
- Вы берёте теоретическую черную дыру массой 1000
масс солнца, на которую движется другая такая-же теоретическая
черная дыра, по
условию о черных дырах, они уже друг
друга после сближения никогда не покинут.
Вы выводите дыру портации, и у Вас тысяча
солнечных масс не точно притягивает
другую тысячу,
- хотя задача черных дыр притягивать по самое дальше
некуда.
Вы возьмите два шарика для настольного тенниса,
намажьте резиновым клеем,
и положите в тарелку с водой
и толкните шарики друг на друга так чтобы они прилипли.
Я думаю что Вы поймете что если теоретические черные дыры
не сталкиваются,
а по определению они притягивают всё
с такой силой что ни то что материальные объекты имеющие
массу не могут его покинуть, а его не может покинуть
электромагнитное
излучение - это говорит о том что гравитация,
у дыры в ста метрах такая что пролетающую черную дыру просто
разорвет когда она будет мимо пролетать.
Ладно
не рвите сердце, обосновать Вы ничего не можете,
Вы можете прочитать написанное и пересказать его, а понять
в прочитанном что есть обоснование, где порожняк,
где выдумка, а где враньё - Вы пока не можете.
Желаю успехов в области астрофизики.
- Re[2]: Черная дыра
(Г. А. Зубков,
4.01.2011 6:14, 1.7 КБайт)
Гравитация и клей-
понятия слишком
разные.Гравитацию
обычно изображают
в виде
потенциальной
ямы.Пусть есть
некая не очень
глубокая ямка в
полу. И чтобы
шарику выкатиться
из ямки,его (вторая
космическая)
скорость на краю
ямки должна быть
не меньше 3 см/с
(аналог скорости
света). Пусть у нас
есть кий,которым
нам разрешено 1
раз сообщать
шарику скорость не
больше 3 см/сек .
Тогда если шарик
будет лежать на
дне,или ниже края
ямы(внутри сферы
Шварцшильда),то
импульсом в 3см/с
мы не сможем
вытолкнуть шарик
из ямы(потому и
свет не может
покинуть ЧД).Зато
если мы сообщим
скорость 3 см/с
шарику,находящемуся
на полу вне
ямы,то ,скатившись
в яму,шарик
благодаря
гравитации,на дне
ямы будет иметь
уже скорость 6см/
сек(в центре ЧД
относительная
скорость равна 2с).
И прокатившись по
инерции,шарик
выкатится с
другого края ямы
со скоростью 3см/
сек(это не меньше
второй
космической
скорости) и с этой
же скоростью
покатится дальше
по полу(вылетит
навсегда из ЧД).
Чёрную дыру
можно построить
например,если
собрать ртутью
(плотность 13600 кг/
м^3) заполнить
сферу радиусом
1.08*10^11м-( это
точно равно
радиусу орбиты
Венеры). Если взять
2 таких ртутных ЧД
и соединить их в
одну каплю,то
получится сфера
из ртути массой в
2 раза больше и
радиусом в (корень
кубический из
2)1.26 раз
больше,чем то же у
1 капли. Тогда эта
большая капля
перестанет быть
чёрной дырой,ибо
её радиус будет
меньше радиуса
Шварцшильда(при
удвоении ЧД её
радиус тоже
должен удвоиться).
А значит из этой
общей капли в
принципе не так
уж сложно будет
вырваться,и эта
капля будет менее
стабильна,чем 2
меньшие отдельные
капли(ЧД).
- Re: Черная дыра
(А.П. Васи,
4.01.2011 8:37, 1.4 КБайт)
Мне Ваши выдумки не интересны и не интересны
необоснованные с физической точки зрения
объяснения Ваших выдумок.
Вы одну выдумку объясняете другой выдумкой
-
в лучших традициях Эйнштейновского релятивизма.
Мне такая клоунада не понятна и не интересна.
У Вас нет стратегического понимания, вцепились за какую-то
мелкую ... и чахните над ней.
До лампочки всей астрофизике портирует или нет
черная дыра, которую ещё никто и не наблюдал, а только
рукой могут
указать на неё направление и сказать
- вот мол, она там где-то должна быть.
Тем более Вы не понимаете основных принципов, передачи
энергии другому телу
имеющему массу. Не понимая этого
и не определив как это обосновать простыми словами -
то всё остальное не имеет смысла.
"Насчёт закона сохранения
энергии:гравитация- это
вообще сплошное его нарушение."
Вы вот тысячу солнечных масс, разгоняли до двух световых,
и при гравитации пролетаете как
фанера над Парижем, мол есть
такая а как она гравитирует аж непонятно - так это
ответ чмошника. Если Вы занимаетесь дырой портала, то Вы
должны все вопросы
обосновать, и в первую очередь самые
трудные а не самые простые, мол перемещается ...
знает куда в портале, вот такой я молодец, просто "звёздные
врата"
разрегулированные получились у Вас.
- Re: Черная дыра
(А.П. Васи,
4.01.2011 9:27, 2.9 КБайт)
Я понимаю что можно докторскую защитить на
разборе падений в черную дыру.
При падении тело портируется - далеко или рядышком.
При падении в черную сжималку
тело сжимается.
При падении в черную разрушилку тело разрушается.
При падении в черную анигилилку тело анигилируется.
При падении в черную-расдвоилко-портало-анигилилку,
тело сперва раздваивается потом портируется после чего
доблестно анигилируется.
Видите сколько бессмысленных направлений и тем можно
высосать
из пальца за одну минуту, так я такой ерунды
могу придумывать без устали, только толку от этого
никакого. Но зато чмошных кандидатских и докторских можно
защитить
кучу и маленькую горку.
Рекомендую Вам чтобы вы если над чем-то думаете, то делать
это желательно так, что-бы второй раз ни Вы и ни другие над этим
вопросом
не напрягались, - если решаете то вопрос должен
быть решен и однозначно, если не решили значит зря потратили
время в данном направлении, значит надо искать причину
ошибки.
А потом вернутся к вопросу и решить его полностью.
"""Сформировавшиеся в предшествующее столетие корпускулярная
и волновая
концепция света в XIX веке продолжили ожесточенную
борьбу. Первая опиралась на авторитет Ньютона, вторая - на
авторитет Гука, Гюйгенса, Эйлера, Ломоносова. Сторонники
корпускулярной концепции надеялись объяснить с ее позиций
затруднения с объяснением явлений дифракции и интерференции.
Т.Юнг дал это объяснение с позиций
волновой концепции. Исходя
из высказанных им гипотез о существовании разреженного и упругого
светоносного эфира, заполняющего Вселенную, о возбуждении
волнообразных
движений в эфире при свечении тела, о зависимости
ощущения различных цветов от различной частоты колебаний,
возбуждаемых светом на сетчатке глаза, о притягивании
всеми
материальными телами эфирной среды, вследствие чего последняя
накапливается в веществе этих тел и на малом расстоянии вокруг
них в состоянии большей
плотности (но не большей упругости),
Юнг делает вывод о том, что излучаемый свет состоит из
волнообразных движений светоносного эфира. Это дало возможность
все разнообразие цветов свести к колебательным движениям эфира,
а различие цветов объяснить различием частот колебаний эфира,
а также сформулировать принцип
интерференции. """
http://pda.coolreferat.com/%D0%9E%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D1%8B%D0%B5_%D0%BA%D0%BE%D0%BD%D1%86%D0%B5%D0%BF%D1%86%D0%B8%D0%B8_%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B8_XIX_%D0%B2%D0%B5%D0%BA%D0%B0
Заметьте как Томас Юнг делал утверждения, - сперва находил некоторые
явления и разбирался в них а потом их формулировал.
А Вы как делаете, берете
необоснованный порожняк - ЧД,
придумываете для неё трассу с лифтом и габаритные огни.
- Re: Черная дыра
(А.П. Васи,
5.01.2011 13:35, 1.9 КБайт, ответов: 1)
http://www.astronomy.ru/forum/index.php/topic,79788.msg1436797.html#msg1436797
Вибе
продолжает тупить в полный рост,
этот чмошник сам не знает что
он хочет,
этот конь спорит с апgонентом на правах модератора,
этот конь педальный даже не может себе для спора другой ник
взять, тогда бы это ... узнало бы
что такое спор,
и как бы его ... за тупые вопросы другие
модераторы.
Он оборотень модераторский, защитник релятивизма,
и он думает что это
его предназначение.
Правилами форума на сколько я знаю не запрещено изобличать
модераторов чмошников с других форумов.
"Ох... Вы написали,
что сложность и многообразие методов
математики позволяет правдоподобно обосновать сомнительные
вещи в физике. Я попросил объяснить, как именно это должно
происходить.
Я нигде не утверждал (пока), что "результаты
расчетов, несовпадающие с наблюдениями, могут поставить
задачу пересмотра математических методов". Я всего
лишь
прошу Вас пояснить Ваши же утверждения. Пока Вы этого не
сделаете, я не могу даже быть уверен, что не согласен с ними."
"Проблема в том,
что у нас раздел -- физический.
Поэтому тут важно, чтобы утверждаемые положения
не противоречили бы физическим принципам. И вообще,
относились бы к физике."
"У меня общая просьба. Давайте всё-таки сузим обсуждение
до критериев истины в современной физике. Не в математике,
не в религии, не в жизни. В физике.
Понимая под критериями
истины критерии выбора той или иной физической модели или теории."
Этот чмошник ранее интересовался как устроен компьютер,
и наезжал с этим вопросом сам на него не зная ответа,
- теперь "белка хитрости" его пробила вести разговоры
строго в русле физики, для того чтобы это
... могло
стереть свои-же вопросы не по физике.
- Re[2]: Черная дыра
(Г. А. Зубков,
5.01.2011 18:34, 627 Байт)
К сожалению на
этом форуме
написанные ссылки
не кликабельны,а
вводить такую
большую ссылку
про Юнга вручную
мало кто захочет.
Объяснить что-то
теорией-это
''каждый дурак
может''. Теория
ещё должна быть
прикладнОй-
помогающей
изобретать что-
нибудь
полезное.Сможете
чё-нить из эфира
сварганить-
докажете больше
свою правоту! Я
вообще не только
теорию ЧД пытаюсь
развивать.Но
промежуточные
сырые результаты
на своём сайте
пока размещать
смысла не вижу.
Хотя в
физике,''мозговой
атаке'' чем больше
идей,тем
лучше:авось какая-
нибудь будет
верной или
пригодится.
- Re: Черная дыра
(А.П. Васи,
5.01.2011 19:55, 2.3 КБайт)
Вы в любом поисковике наберите Т. Юнг, интерференция,
самое смешное что длину световой волны он ещё в1800,
точно определил не используя никаких спец приборов
которые есть сейчас.
Я все-таки считаю что если любой астроном в рамках эфирной
теории сможет осмысленно и обоснованно ответить на любой
вопрос тому
кто не знает ничего о астрономии, и в рамках эфирной
теории ему будут просты и понятны причины внутри звездных
процессов, и причины формирования галактических
рукавов,
причины главной последовательно, понятны причины движений
звезд в пространстве, просты и понятны любые видимые
взрывы звезд и их причины, то у астрономов
будет осмысленный
взгляд на звёзды.
А сейчас они смотрят бессмысленно и все звездные теории
на текущий момент не взаимосвязаны, и высосаны из пальца.
Одно то что астрономы утверждают конечность вселенной,
и не замечают того что это уже длится не одну сотню лет,
и размер вселенной соответствует - тютелька
в тютельку
возможностям телескопов, это сравнимо с моей точки зрения
с глобальным позором всех астрономов.
Вы недопонимаете, у астрономов не так много
времени,
если они будут продолжать бред нести разрозненный то
вероятность полного прекращения финансирования достаточно
высока, по той причине что нет
смысла финансировать того
кто внятно и объяснит не может - зачем и что он ищет.
И гравитация - вот даже Вами трактуется на уровне чуда,
в эфирной
теории этот вопрос решается первым, и
проще простого, при этом решаются все вопросы
термодинамики, движения по орбитам, совпадает
на сто процентов с эффектом
Доплера, объясняет за одно
стационарность и бесконечность вселенной, и красное смещение.
Когда я слышу слова "мозговая атака", то у меня возникает
чувство что общаюсь с умственно неполноценным, по той причине
что этот термин удел тех кто экстренно хочет чего-то достичь.
В астрофизике экстренного ничего
не нужно, здесь достаточно
хорошо обоснованного. Вы посмотрите хоть на релятивистов -
сто лет читают одни и те-же книги, и их проповедуют,
и им что "мозговой
штурм", что "мозговая атака", что "мозговая оборона"
что "мозговое отступление" им это всё одинаково - пустой звук.
- Re: Черная дыра
(А.П. Васи,
8.01.2011 10:41, 1.8 КБайт)
"чем больше идей,тем лучше:авось какая- нибудь
будет верной или пригодится."
Когда сам подход к решению задач не правильный,
- то уже всё
равно сколько юзеров занимаются
решением и тем более всё равно сколько у них идей.
Вот яркий пример неправильного подхода,
аналогично портации черной
дырой.
В принципе полностью совпадает с Вашим подходом
только в данном случаи другой объект.
http://www.astronomy.ru/forum/index.php/topic,73751.msg1438840.html#msg1438840
"""Наша Вселенная почти наверняка ограничена по
объему и массе. Так говорит логика. Трудно
признать факт возникновения мгновенного
бесконечного
объема с бесконечной массой.
Теория инфляции говорит об этом своими моделями.
Но границ нет. Вселенная, по-видимому замкнута,
(пространство-время) при любой
геометрии - или
сфера, или куб,тор, многогранники и т.п..
Гомеоморфность "границ" """
В данном примере ярко видно
как не обоснованный
ответ и сплошные постулаты и требования к вселенной,
вступают в противоречие с текущей вселенной.
У данного ответа две технические
трудности ,
одна из них не способность понять бесконечность.
В тексте даже нет сомнения в возможности
существования бесконечности, и нет подхода
к
физическим методам определения данного вопроса,
вопрос решен постулированием.
Вторая тоже глобальная трудность - попытка обосновать
причину возникновения
вселенной, - собственно
там где это не нужно, в данном случаи надо
не обосновывать причину, а констатировать по
факту, так как любое обоснование причинности
в данном случаи - необоснованная выдумка,
- а это теории из пальца,
по той причине что отсутствует даже теоретическая
возможность подтверждения.
- Re: Черная дыра
(А.П. Васи,
16.01.2011 12:46, 1.5 КБайт)
По поводу того что я Вам рассказывал что за световым
излучением с повышением колебаний летят частицы, так я в этом вопросе
разобрался очень давно. Вот смотрю на
форуме как своими
силами пытаются разобраться астрономы, (я там как Вы поняли не
общаюсь, забанили, да и многие просили приходить когда-то потом - в будущем).
http://www.astronomy.ru/forum/index.php/topic,79500.msg1446226.html#msg1446226
И как всегда появляется чмошный модератор удивляющий своей тупизной,
и
его наезды носят требовательный характер, так как если тот к кому он
обратился с вопросом
"""
Модератор: Это откуда известно? """
Этот гнидёныш не утруждает себя доказательством того чтобы привести пример.
Да, так вот когда он обращается с подобным вопросом на который и он сам не
знает точного ответа, так это нормальное состояние модератора- гандольера.
Самое дикое возможно впереди - это когда модератор- гандольер, будет
требовать не отвечать
на другие вопросы до тех пор пока не ответят ему на этот,
после чего модератор - гандольер забанивает того с кем спорит.
http://bourabai.narod.ru/radio.htm
- Re: Черная дыра
(А.П. Васи,
16.01.2011 13:13, 656 Байт, ответов: 2)
Вот объяснить действия модератора-гандольера достаточно легко,
он написал некоторые свои высказывания от имени всех астрономов,
естественно он ведёт модерацию так
чтобы отвлекать и останавливать
развитие идей при общении других, которые выходят за пределы того
что он огласил самопроизвольно (как истинный гандольер), от имени
всех астрономов.
Я думаю что все астрономы обязаны сбросится деньгами на курсы
гандольеров в Венеции , для того чтобы у них был дипломированный
модератор
- гандольер.
http://elementy.ru/lib/430399
- Re[2]: Черная дыра
(С. В. Семенов,
7.01.2013 9:26, 1.1 КБайт, ответов: 1)
| Цитата: |
Вот объяснить действия модератора-гандольера достаточно легко,
он написал некоторые свои высказывания от имени всех астрономов,
естественно
он ведёт модерацию так
чтобы отвлекать и останавливать
развитие идей при общении других, которые выходят за пределы того
что он огласил самопроизвольно (как истинный гандольер), от имени
всех астрономов.
Я думаю что все астрономы обязаны сбросится деньгами на курсы
гандольеров в Венеции , для того чтобы у них был дипломированный
модератор
- гандольер.
http://elementy.ru/lib/430399 |
Я-новичок. Весело у вас, ребята! А.П.Васи, как я понял, дежурный клоун. Хамоватый (что клоунам прощают), но нахватавшийся терминов (что вселяет уважение у Митрофанушек и веселит
остальных). Так держать! Внесу этот сайт в Избранное.
- Re[3]: Черная дыра
(Ю. С. Решников,
7.01.2013 11:42, 583 Байт)
Физики,
что
религиозные
фанатики,
религия
которых
-
физика.
И
во
всём
видят
физику,
включая
астрономию.
Но
с
астрономией
такое
не
проходит
потому,
что
перед
тем,
как
сделать
"логические
построения"
физику
нужно
договориться
с
астрономом
об
астробъекте.
А
астроному
нужны
сотни
(а
может
тысячи
лет)
на
то,
чтобы
с
ним
определиться.
А
физик
ждать
не
может,
порождая
в
астрономии
массу
непроверяемых
гипотез,
сменяющих
одна
другую.
А
где
точная
наука ?
- Re: Черная дыра
(А.П. Васи,
16.01.2011 21:21, 1.7 КБайт)
Хоть я и увлекаюсь астрономией, но я ни разу не смотрел
в телескоп, да и мне совсем не интересно смотреть на
картинку.
Смотрел передачу про телескоп Хаббла,
так там сплошное
хвастовство и сводится к тому что мол стало лучше видно,
и постоянно меряются с другими телескопами (на линейках).
Я очень сочувствую астрономам
которые радуются
качественной неподвижной картинке звездного неба.
И даже не подозревают что ничего просто так не бывает,
и там на самом деле происходит
такая впечатляющая
динамика во всех процессах, от малого до большого.
Как по мне космос со звёздами на столько интересен в
динамике что если бы астрономы
могли в будущем представить
себе что во вселенной пространство заполнено эфиром,
то они сразу бы поняли что звездные фото - каменный век,
должна быть звездная
карта с указанием - массы и вектора каждой звезды,
и скорости, плотности эфира возле неё, и плотности эфира и температуры
в разных направлениях на расстоянии светового
года.
Естественно что для просмотра такой карты, желательно
использовать "3d". Также внутренняя часть звезды - имеет совсем
другую структуру и динамику
от общепринятой, и её если
сделать в разрезе с точки зрения увлекаемого эфира, то просто
за звёздами будет наблюдать на компьютере и проникать в них
интересно
любому, и посмотреть как они устроенны, - хотя
это идеи такого далёкого будущего, учитывая каменный век
текущей парадигмы, что я просто астрономам сочувствую
когда они смотрят в телескоп, не то что, на неподвижную картинку,
а на звезды - которые только и могут - что постоянно удаляться
от большого взрыва, и краснеть
.
- Re: Черная дыра как супер коллаедр
(L. L. luyko,
15.02.2011 13:47, 2.5 КБайт)
Начну с того что ЧД не сьедает материю, материя как у любой звезды стремится на разрыв, а увеличивающаяся
гравитация наest_enter_group,quest_add_left преобладает пока не достигнет ЧД равновессия сил,почему то все забывают о
теченнии времени,оно в центре замедляется,с нашей точки зрения оно вообще стоит, разность течения времён
создаёт непролазную для событий и вообще всего: материи и.т.д. стену.А внешняя схваченная материя
пускается в смертельный хоровод расщепления до частиц не имеющих заряда и массы.Если частица не имеет
массы и заряда она может принять любую форму.Схема диска вокруг ЧД похожа на воду в ванне после открытия
заглушки, примерно так: верняя половина плоскости диска вылетает огибая ЧД вниз нижняя огибая ЧД вверх,
чем больше ЧД (в чд супер гигантах)тем очевиднее это прявляется.Таким образом супер чд находящаяся в
центре галактик насыщает постранство невидимой материей и энергией, даже видимой энэргией из за этого они
разбегаются.Так что ЧД сидит глубоко на жёсткой диете,если и продерётся какой то квант света через стену
разновремения, то об этом ЧД узнает в далёёёёёёёёком будущем,она бедная как черепаха Тартила медленная до
нельзя,какие то гиганские звёзды мелькают перед глазами как мухи только сейчас была и уже нет.Вопреки
упрёкам всех в адрес ЧД,она просто так не растёт, внутри неё тишь да гладь как в глазу у Циклона.Её судьбу
может изменить только другая ЧД слившись с ней.Тогда она может слесть с диеты и начать обжорство .По
достижении равновесия внутренних сил устаканивания, опять сядет на диету. Около стены разности времени
есть область сжатого пространства, к примеру 1 мм равен растояния от земли до Сириуса{цифры не точны}
т.е.пространство тут какбы заменено разностью времени т.е.времени в точке Х много значит пространства
навалом.Простанство еще и сжато а время в добовок искривлено.Внутри ЧД огромное пространство,но оно не для
больших частиц которых можно без проблем регистрировать приборами.Коллаедр БАК в Церне ломается потому что
разгон частиц череват механическими послетствиями.Может неизвестные частицы взаимодействуют с холодильной
установкой БАКа.Частица при большой плотности протранства должна приобретать свойства волны,а форма может
быть любой,можо даже пофантазировать что карпускулярная частица раплющивается-удлиняется в струну и ей
теперь нужно минимум усилий-колебаний чтобы всё заходило ходуном в глобальном масштабе-во вселенной.Вопрос
номер-1 ОТО Эейнштейна работает или нет? Кажется я своей теорией снял множество вопосов,или может добавил
извените если что не так.
- Re: Черная дыра
(А.П. Васи,
16.04.2011 11:00, 968 Байт)
http://www.astronomy.ru/forum/index.php/topic,73830.msg1534675.html#msg1534675
Модератора на атрофоруме продолжает жестоко гандольерить с двойной силой, он
уже путает - своё мнение и обоснование которое вытекает из объяснения.
"Наблюдения
показали, что Луна удаляется от Земли на 3.6 - 3.8 см в год...
Посчитаем, на сколько эти объекты "удаляются" при измерении расстояний с
помощью светового сигнала при условии снижения скорости света...
видимое увеличение расстояния составит -- до Луны DR = 0.55 см за год...
Вычисленные значения на порядок отличаются от наблюдаемых... Для Луны
это отличие можно объяснить тем, что вычисленное значение только вклад в
наблюдаемое. Т.е. наряду с видимым увеличением расстояния имеется и
физическое увеличение за счет тех же приливных явлений."
Вибе аргументирует
- Есть ещё одно объяснение -- Ваши выводы об уменьшении скорости
света неверны.
- Re: Черная дыра
(s. s. pogosyan,
17.04.2011 9:15, 232 Байт)
www.armonpogosyan.com В современной науке установленно неверний режим возникновения и еволюции Первичных черных дыр.Об этом и о каркасе из ПЧД смотри в книге-Армоннайа
структура метавселенной.С уважением,С.Погосыан.Армениа.
- Re: Черная дыра
(L. L. Li,
24.05.2011 5:20, 2.5 КБайт)
Уважаемые коллеги теоретики давайте разберёмся с ЧД которая находится в центре галактик, потому что они
первые формируются. Когда она была звездой гигантом. При сжатии звезды гиганта под силой своего притяжения
в центре изменяется течение времени оно замедляет ход. Вся масса материи вокруг магнитной досягаемости
звезды начинает вращение как вода в ванне после открытия пробки, центробежная сила вращения газа, пыли,
и.т.д. прижимает всё в спиральный диск, ускоряющийся в центре. Но оно ускоряется в пределах дозволяющих
замедлённым временем т.е. скорость света не превышает свою же скорость, как и во всём космосе. Но есть в
космосе естественный способ обойти эту закономерность. Энергетические излучения из ЧД в центре галактики
могут исходить из двух источников. Первый из внешней оболочки, т.е. в скважину как в раковине, огибая но
не попадая в саму ЧД, как смерч уходя далеко от влияния диска. Второй из горизонта событий, из самой ЧД.
Если дисковой материи около ЧД становится очень много, масса диска начинает будоражить ЧД, при том
вращаться ЧД может со скоростью и направлением совершенно отличным от внешнего диска, если вообще она
вращается. Пустота или свободное пространство между ЧД и диском становится больше, вероятность
проникновения дисковой материи внутрь ЧД исключается вообще. Пустоты тем более здесь не может быть, она
заполнена тёмной материей, которая родилась из расщепления в диске, нормальной материи. Теперь она
ускоряясь удалятся от центра ЧД и достигает краёв галактики. Ускоряясь тёмная материя переходит в тёмную
волновую энергию проходящую через нас, мы воспринимаем её, не что иное как течение, ход Времени. В конце
пути на периферии в дальних рукавах галактики, тёмная энергия замедляется превращаясь в тёмную материю,
скапливается воздействуя на движение рукавов. Но ТМ может продолжить и обратный цикл, в силу того же
скопления оной на периферии, теперь уже к центру галактики. Это означает что время может течь обратно,
относительно нас, и с задержками. Похоже что ЧД за горизонтом событий живёт своей жизнью,в равновесном
состоянии не поглощает пока не встретит другую ЧД или др.супермассив материи. Выходит что ЧД является
свёрнутым в кокон времени, гигантским хранилищем материи который в своё время освободится из тяготения
ловушки. Как? В момент сжатия звезды, рождения ЧД задаются параметры на сколько далеко в будущее будет
действовать Кокон времени. В будущем астрофизики говорят останутся только холодный мрак и гигантские
чёрные дыры.
- Re: Черная дыра
(s. s. pogosyan,
24.05.2011 9:32, 1.2 КБайт)
Уважаемый Л.Л.Л.,Сверхмассивные ЧД возникают в процессе слияния ЧД с меньшими массами,до привращения этих обьектов в обычные галактики.Но самое главное у современной науки
не правильное представление о ЧД-х.Развиваемая нами космологическая модель вселенной с строго плоским прастранством исключает,заприщает существовоние абсолютного гравитационного
коллапса,абсолютных черных дыр.Плоское прастранство вселенной принуждает относительные ЧД ни коллапсировать,а обьединяясь увеличивать свои массы и размеры.Такие относительные
ЧД бывают двух видов: космологические-это Первичные ЧД,и метагалактические ЧД-их называем Д-телами в честь нашего соотечественника В.А.Амбарцумяна.Так вот Д-тела в процессе
космоэволюции,впроцессе расширения вселенной,обьединяясь увеличивают свю массу и размер,достегая некоторого предела.Все основные процессы квантово-гравитационной эволюции
материи происходят именно в Д-телах:нарушения симетрий Великого и электрослабого обьединений,кварк-глюонный фазовый переход,ядерный синтез,рекомбинация и т. д.В дольнейшем
Д-тела,сверхмассивные ЧД превращаються в скопления галактик,галактики...С уважением,Самвел Погосян. www.armonpogosyan.com
- Re: Черная дыра
(А.П. Васи,
25.05.2011 8:38, 1.3 КБайт, ответов: 2)
\давайте разберёмся с ЧД которая находится в центре галактик\
---никто не наблюдал ни одной черной дыры,
все они расчетные, так как математика
не сходится с реальностью.
\ЧД которая находится в центре галактик, потому что они
первые формируются\
--- первые формировались при большом взрыве, - который доказывается чем?,
реликтовым излучением, из чего делается вывод о том что было 14млрд
лет тому,
- это больше похоже на лохотрон, чем на научное обоснование.
А ваш вопрос объеденяет три лохотрона которые Вас прокатили.
1Большой взрыв
2черная
дыра
3формирование черных дыр при большом взрыве
\При сжатии звезды гиганта под силой своего притяжения
в центре изменяется течение времени оно замедляет ход\
- это тоже лохотрон на котором Вы катаетесь, по причине отсутствия
физической причины когда материальные
тела
при изменении своих свойств,
могут влиять на временные процессы в пространстве.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/#comments
прочтите все комментарии - Мимоходом,
полностью разгромлена вся мышиная возня вокруг черных дыр
- Re[2]: Черная дыра
(М. Ю. Якимов,
25.05.2011 9:56, 1.1 КБайт, ответов: 1)
Прежде чем трепать, дорогой господин Васи, подумайте, как отмываться-то будете. Или понятие чести у нас не в чести? Можно врать на каждом слове, и при этом даже не краснеть?
Если в центре нашей Галактики нет черной дыры, как же вы объясните, вокруг чего обращаются ближайшие к этому центру звезды, разгоняясь до 500 км/с и более http://www.astronet.ru/db/msg/1180936.
Как
объясните активность радиоисточника Стрелец А? Как объясните наличие характерных струй горячего газа вокруг объекта стрелец А? http://www.astronet.ru/db/msg/1227506
http://en.wikipedia.org/wiki/Sagittarius_A*
Как вы отмахнетесь от всего этого http://ru.wikipedia.org/wiki/%D0%A1%D1%82%D1%80%D0%B5%D0%BB%D0%B5%D1%86_A*?
Черная
дыра не просто говорит - вопиет о своем существовании! Отрицать этот факт (а это уже научный факт) по меньшей мере глупо.
- Re[3]: Черная дыра
(М. Ю. Якимов,
25.05.2011 10:05, 539 Байт)
Внимание!
К сожалению, приведенные в моем предыдущем сообщении ссылки отобразились неправильно - при переходе по ним нужно обязательно учитывать
звездочку в конце, которая почему-то игнорируется движком форума!
Прошу это учесть, и не переходить по этим ссылкам автоматически -
попадете не туда!!!
В свою очередь постараюсь связаться с администрацией форума, чтобы в очередной - который уже! - раз пожаловаться на систему.
Стоит
ли удивляться тому, что форум не популярен, несмотря на известность сайта.
- Re: Черная дыра
(А.П. Васи,
25.05.2011 21:22, 11.4 КБайт, ответов: 1)
М.Ю.Якимов
Вы за меня не переживайте,
Вы читали все посты мимоходом?
если нет то прочитайте.
А в центре галактики
большое количество
звезд у которых взаимная гравитация, и если бы вы посмотрели
видео то заметили бы что движения звезд вокруг явного центра
нет.
И
если Вы так резко возмущаетесь то если не сможете
дать четкой формулировки черной дыры и методики
её обнаружения то Вы просто недалёкий и не понимаете
предмета
разговора, - трепач.
А то что современная астрофизика не может прощитать
гравитацию для более двух тел - то это не значит
что там черная дыра.
Если
нет четкого однозначного предмета разговора с однозначными
характеристиками и однозначными определениями, то разговор
на этот предмет называется - болтовня.
Чтобы Вы были в курсе Земля летит по орбите 30км в секунду,
а солнечная система движется со скоростью 400км в секунду.
http://www.astronet.ru/db/msg/1244775/07.html
(Стоит сказать, что созвездию Кормы принадлежит еще один рекорд - самая
быстрая звезда - RX J0822-4300, двигающаяся со скоростью 1300 км/с)
Жду формулировку черной дыры и методы её обнаружения - успехов.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/2/
......Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
космогон
http://www.astronet.ru/db/msg/1188549
Полость Роша
Для создания акреционного диска, - полость Роша должна быть,
здесь практически полная невозможность существования данной полости у
звезды, учитывая тот же квадрат влияния гравитации, здесь вопрос о
удельной плотности звезды - у которой атмосфера содержит например 30%
массы звезды, и эта масса пополняется при её потере из недр звезды -
феерично.
Повторю - авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
Уважаемый Дмитрий Мамонтов
Моё -Падая на Черную Дыру вещество не может резко тормозится или резко ускорятся,
Ваше - Разогреваться может? А то, что нагретое вещество излучает,
знаете? Именно таков механизм излучения при аккреции. Там еще другие
процессы, но для Вас, боюсь, это будет слишком сложно.
Назовите пожалуйста физическую причину,
- или физические процессы, при которых разогреваются тела
в вакууме при свободном падении на другие тела ?
космогон
...При падении звезды (большего на меньшее) вещество будет перетекать по плотной спирали (аккреционный диск)...
Не хотел я затрагивать этот вопрос, блаженны верующие, Вам честно скажу -
не может вещество при ускоренном падении перетекать в диск , в первую
очередь - этот диск только предположение и компьютерное моделирование.
Невозможность объяснить
легко - Вы говорили о увеличении с квадратом расстояния - на практике
при изменении расстояния в 50 раз влияние гравитации возрастет в 2500
раз. Из чего есть физическая аналогия что черная дыра аналогична
пылесосу, в данном случаи пылесос является частью некоторого сектора
черной дыры, - так вот засосёт, точнее упадёт всё в черную дыру вместе с
акреционным диском и практически мгновенно. Ибо нет причины у тела при
падении отклоняться от прямолинейной траектории при падении и выходить
на круговую орбиту.
космогон
http://www.astronet.ru/db/msg/1186352
Рис. 1
У черной дыры большая гравитация, на расстоянии например
в 10 диаметров солнца, у черной дыры по сравнению со звездой по массе как Солнце гравитация например в 1000 раз больше.
А на рисунках рисуют не взирая на различную гравитацию, и одни и те-же
свойства, что для двойных звезд и тоже самое когда звезда и черная дыра.
- Re[2]: Черная дыра
(М. Ю. Якимов,
27.05.2011 7:00, 746 Байт)
А.П.Васи - ваше непонимание черной дыры происходит всего навсего из полного незнания или непониманияфизики - это совершенно очевидно из того, что тут у вас понаписано.
Один
перл насчет того, что вещество падает в черную дыру не ускоряясь, чего стоит. Возьмите орбитальную скорость, радиус и посчитайте хотя бы центростремительное ускорение. Но
я так понимаю, что что-то подсчитать для вас дело совершенно невозможное.
И теперь о форуме. Почему его так любят персонажи, подобные Васи? Все просто. На любом уважающем
себя форуме посты подобных авторов удаляют, а самих таких авторов отлучают от форума.
Чтобы на грядке росло что-то кроме сорняков, ее нужно пропалывать, господа администраторы
и модераторы!!!
- Re: Черная дыра
(А.П. Васи,
27.05.2011 8:27, 922 Байт)
М.Ю.Якимов
Вы или ответьте на вопрос
- формулировки черной дыры и методики
её обнаружения?
Если не можете, то Вы болтун, и пустортрёп,
и извинения в стиле - простить за некомпетентность - принимаются.
Еще раз Вам объясняю, есть авторское
изложение
Черных Дыр - это закон для астрофизиков.
И ни один астрофизик не имеет права излагать или трактовать
Черные Дыры как ему вздумается, по той причине
что то уже не Черные Дыры о которых говорил автор -
а что-то другое.
Вы когда будете астрофизику понимать а не знать,
тогда у Вас будет возможность
обосновать перед
модератором причину Вашей правоты. А на текущий момент,
Вы двух слов связать и обосновать не можете,
и не можете ответить на элементарный
вопрос, так что
Вас надо блокировать на форуме за некомпетентность.
- Re: Черная дыра
(А.П. Васи,
27.05.2011 9:11, 627 Байт)
М.Ю.Якимов
Вы определитесь зачем приходите на форум -
чтобы пообщаться с людьми у которых другая
точка зрения или
пообщаться с такими же как Вы,
- если первое, - то Вы должны
и задавать вопросы и отвечать обоснованно на вопросы оппонента,
а если
второе - то Вам проще перед зеркалом поговорить самим с собою.
На аттракционах весело кататься,
- там и не так много правил, - хвалить и дополнять аттракцион,
и хорошо отзываться о аттракционе, дополнениях, и хорошо отзываться о тех
кто на них катается.
- Re: Черная дыра
(А.П. Васи,
7.06.2011 19:14, 916 Байт)
http://www.astronomy.ru/forum/index.php/topic,85823.0.html
\\\
Дмитрий
Вибе Модератор
Тема закрыта.\\\
Модератор уже внятно обосновать причину
не может, совсем мозги потерял бедолага.
А автор темы то прав, что наука лохотрон
устроила,
с гравитацией, и на простые вопросы которые
в задачах для более чем двух тел - вся гравитация
яйца выеденного не стоит , и бессмысленность
формул видна даже не специалистам.
А модератор то формулам для двух тел - рукоплещет,
а задачу только заблокировать у него ума хватает,
а решить задачу
и внятно обосновать ответ - модератор не в состоянии,
мозгов не хватает.
- Re: Черная дыра
(А.П. Васи,
14.08.2011 10:47, 1.3 КБайт, ответов: 1)
http://www.astronomy.ru/forum/index.php/topic,76585.msg1641461.html#msg1641461
Дмитрий Вибе продолжает давить на линию обсуждения.
\\\augustina, вот
здесь
я уже просил Вас воздержаться от публикации новых смелых утверждений,
пока Вы не обоснуете уже сделанные. Там Вы писать перестали, и я закрыл
на это глаза. Но Вы решили продолжить генерацию гипотез, поэтому мне
приходится напомнить о том своём сообщении.
Остальным участникам
напоминаю, что эта тема посвящена возможности старения света. Прошу
ограничиться строго этой тематикой. Если вас волнуют иные или более
глобальные космологические проблемы, для их обсуждения можно найти уже
существующую или создать новую тему.\\\
Я объясню что происходит - этот клоун имеет свою точку зрения которая совпадает
с парадигмой перед которой он челом
бьет, но в физике Вибе не разбирается,
но он понимает что если сделают полномасштабный анализ всех взаимосвязей,
то накроется медным тазом вся парадигма, вот он
и запрещает проводить
причинный анализ, и требует говорить и обсуждать исключительно старение света,
а по правилам форума это можно делать только в рамках парадигмы.
- Re[2]: Черная дыра
(А.П. Васи,
14.08.2011 11:07, 3.1 КБайт)
Я лично вообще не понимаю того с каким усердием
все занимаются красным смещением.
Как глядя с точки зрения физика
вынули здравый смысл
и положили его на полку и пошли
заниматься третьестепенными задачами.
Даже с точки зрения физики эта задача решатся
через постановку опытов физических с аналогичной
аналогией - вот этого никто не делает.
А основные задачи никто старается не замечать, -
оно удобно положить здравый смысл на полку и
ждать когда
придут любители и на халяву
решат астрономам все трудности.
Вот основные задачи - куда девается тепло
и почему в космосе холодно?
Почему внутри
звезды нет водорода?
А все остальные вопросы пока нет ответа
на эти два это просто клоунада.
Повторю ещё про БВ.
\Если у предмета
обсуждения по физике,
нет однозначного общепринятого определения -
то рассуждения по этому предмету - болтовня бессмысленная.
Болтовня бессмысленная
- она из составляющих
непонятных и необоснованных теорий в физике.
Когда Вы соглашаетесь с подобными теориями
- будьте бдительны, Вам в этом случаи за Ваше
жито будут
вечно непонятно рассказывать о непонятном, и
при этом будете выглядеть глупо и не способным
понять гениальное.
Ладно что будете выглядеть всю
жизнь глупо,
так Вы ещё и бессмысленно потратите уйму времени,
а это не время, это Вы свою жизнь потратите
на то в чем не может быть результата.
Темная
энергия и темная материя изначально
были придуманы как подпорки парадигмы,
у которой энергия звезд непонятно куда девается в
пустой пустоте, по этой причине
когда в пустой
пустоте есть звезды, то поглощать тепловую энергию
могут только Черные Дыры, но для поглощения
энергии Черных Дыр оказалось недостаточно, точнее
их надо в тысячу раз больше чем звезд чтобы было,
а учитывая что официально не обнаружили не
одной дыры, по тем параметрам о которых говорил
автор, а потом
автор передумал и поменял решение,
а потом астрономы послали автора с его определениями
вдаль и стали искать и называть Черными Дырами
то что им нравится а
не то о чем говорил автор, вот
тогда и стало понятно что общество пошлет
в далёкую даль если сказать что черных
дыр в 1000 раз больше чем звёзд. И решили
утилизировать расширением вселенной,
а потом решили и ускоренной, только не учли
что и в этот лохотрон много тепла от звезд не поместится,
и потом на темную
энергию и темную материю решили
спросить всё тепло методом переброса массы,
и сказали что масса темной материи и темной
энергии столько то процентов. Но при
этом
опять не складывается - в большом взрыве то эта
масса не учтена, а если вся масса материи
при большом взрыве разогрета до миллиона градусов,
то охладиться
она может передав энергию
другим телам, а в вакууме - пустой
пустоте других тел нет, следовательно
если учитывать темную материю и темную энергию
при большом
взрыве то после взрыва вещество
не сможет в пустоте остыть и будет горячим вечно.\
- Re: Черная дыра
(А. П. Иванов,
2.09.2011 12:29, 290 Байт, ответов: 1)
Я думаю что никаких чёрных дыр нету.
Чёрные дыры существуют в сознании людей только из-за понятия гравитации.
При детальном рассмотрении этого понятия возникает
вопрос.
Как могут притягиваться два тела, без внешнего воздействия, если они уравновешены относительно друг друга?
- Re[2]: Черная дыра
(В. В. Комогоров,
5.09.2011 15:13, 554 Байт)
Вопрос имеет образ, но как быть с определениями? Что такое тело? Если тела
уравновешены, что является центром равновесия? Можно получить равновесие в
среде, но указать, что является средой. Математики и физики объединившись,
создали нечто третье, чего не существует в реальном мире. Физик, разглядывая
точку на фотопластинке, говорит: частица. Математик, ставя точку на листике,
говорит электрон. При этом понимают друг друга, несмотря на то, что один,
рисует вид, а другой пытается понять действие. Поток в сечении, тоже точкой
представляется.
- Re: Черная дыра
(А.П. Васи,
16.09.2011 23:37, 1.0 КБайт)
Гипотезы, теории создаются, когда нет удовлетворительного объяснения явлений в рамках действующей парадигмы.
Вибе
-Какое
именно явление не имеет удовлетворительного объяснения в рамках
действующей парадигмы и имеет удовлетворительное объяснение в рамках
Вашей "теории"?\\\
Модератора звездочета опять начинает гандольерить, оппонет говорит о парадигме
а модератор передергивает свою гандоллу и гандольерит
на конфликт.
Вибе должен сложить своё модераторство.
- Re: Черная дыра
(А.П. Васи,
17.09.2011 0:00, 544 Байт)
Парадигма даже причины скорости света не может
обосновать, и причины того что пустота выступает
линией задержки для электромагнитных колебаний
в том числе
и световых - у пространства то-исть пустоты
появилось свойство. Прям как в средах для сигналов.
Эффект Доплера для сред - вопрос почему его
можно применять
для сигналов в пустоте? А потому
что там среда, только релятивисты её никогда не признают,
а свойствами её пользуются с воплями - мол волновые свойства
фотонов
которые частицы.
- Re: Черная дыра
(А.П. Васи,
17.09.2011 17:42, 1.0 КБайт, ответов: 1)
http://www.astronomy.ru/forum/index.php/topic,88376.msg1675230.html#msg1675230
Ну и конечно, у меня есть претензии к самой парадигме в части пространства и времени.
Или это
не обсуждается?
Вибе -Что "это"? Ваши персональные претензии к пространству и времени?
Гоните этого Вибе из модераторов, по причине
того что этот модератор
совсем оборзел, и запрещает даже сомневаться на форуме в правильности парадигмы,
и этот модератор спорит с посетителями на правах модератора,
выберите модератора который не лижет парадигму,
который просто следит за культурой общения.
Этот упырь думает что на форуме только его студенты околачиваются,
- те методы которыми он студней воспитывает те он и на
форуме применяет - гнать в шею с модераторов.
- Re[2]: Черная дыра
(А. С. Вишневский,
19.09.2011 2:13, 1.2 КБайт)
<
tbody>| Цитата: |
http://www.astronomy.ru/forum/index.php/topic,88376.msg1675230.html#msg1675230
Ну и конечно, у меня есть претенз
ии к самой парадигме в части пространства и времени.
Или это
не обсуждается?
Вибе -Что "это"? Ваши персональные претензии к
пространству и времени?
Гоните этого Вибе из модераторов, по причине т
ого что этот модератор
совсем оборзел, и запрещает даже сомневаться на форуме в правильности п
арадигмы,
и этот модератор спорит с посетителями на правах модератора,
выберите модератора который не лижет парадигму,
который просто следит за культурой общ
ения.
Этот упырь думает что на форуме только его студенты околачиваются,
- те методы которыми он студней воспитывает те он и на
форуме применяет - гнать в шею с модер
аторов.
|
О, э
- Re: Черная дыра
(А.П. Васи,
19.09.2011 11:14, 4.7 КБайт)
Оно таки очень удобно для сторонников парадигмы
чтобы были именно такие правила на форуме как там есть,
сторонники парадигмы даже не напрягаются когда им говорят
что вот тот и вот это утверждение не верно.
Не напрягаются по причине того что не они это
придумали и по этому не им за это отвечать.
И в итоге появляется
желание у участников выглядеть
красиво и аргументированно и они предположительно
открывают кучу форумов на других сайтах по этой тематике
потом приходят
и "падают на колени" перед модератором
и как студенты ему отвечают, по причине того что модератор
не обоснованно поставил им задачу, - ничего не писать
пока не ответит на этот вопрос. В результате чего от трети
до половины форумов на мембране были аналогичные на звездочете.
Что меня удивляет, - так
это то что вся астрофизика красивая и пушистая,
и всё прекрасно.
Но это же не так, вот те-же черные дыры - это же
просто пипец - и что это никто не замечает
или никто не
понимает.
Хочу сразу спросить, Ваше мнение по
...Черная дыра...
http://www.astronet.ru/db/msg/1188232
Согласны ли Вы с этим?
Какие из перечисленных статей соответствуют стандартам Черной
Дыры?
1 Есть ли жизнь в черной дыре
http://www.popmech.ru/article/8822-est-li-zhizn-v-chernoy-dyire/
2[ссылка]
Установлена масса самой крупной из сверхмассивных черных дыр.
Такое нам и не снилось.
3[ссылка]
Мифология черных дыр.В нашей Галактике существуют миллионы черных дыр
массой в несколько солнечных
4http://www.popmech.ru/article/8140-raspad-dyiryi/
Распад дыры.
Взрыв сверхновой может заканчиваться образованием не одной, а сразу
нескольких черных дыр.
5[ссылка]
Детство черной дыры
Взрыв, зафиксированный в глубинах космоса 31 год назад, судя по всему,
знаменовал рождение черной дыры самой молодой из нам известных
6[ссылка]
Темный центр
Таинственный центр нашей галактики,
место обитания сверхмассивной черной дыры и источник мощнейших потоков излучения,
преподносит новые сюрпризы.
7[ссылка]
Небольшое замечание о природе гравитации приводит к следствиям
космического масштаба к выводам о рождении новых миров из черных дыр
8[ссылка]
Обычная по размерам черная дыра выбрасывает
колоссальные потоки излучения и частиц.
9[ссылка]
Астрофизики предложили способ (теоретически) уничтожить черную дыру
10[ссылка]
Из всех сверхмассивных черных дыр лишь около 1% выбрасывают
значительные количества энергии
11[ссылка]
Выживающие дыры
Пара редких экземпляров
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
каким-то чудом выживающих в соседстве с этим монстром.
12[ссылка]
Как живется внутри черной дыры? Вы и сами знаете,
как: если справедливы новые теоретические выкладки,
вся наша Вселенная может находиться внутри черной дыры,
расположенной в другой Вселенной. Эдакая матрешка мироздания.
13[ссылка]
Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину. Это дало цифру в 10103, тоже огромную, но все-таки на много
порядков ниже.
14[ссылка]
Если очень, очень быстрый космический корабль разогнать
почти до скорости света, превратится ли он в черную дыру?
15[ссылка]
Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
- Re: Черная дыра
(А.П. Васи,
19.09.2011 11:38, 28.3 КБайт)
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили,
что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в
электронных оболочках атомов или молекул. Оба эффекта используются в
рентгеновских трубках. Основными конструктивными элементами таких трубок
являются металлические катод и анод (ранее называвшийся также
антикатодом). В рентгеновских трубках электроны, испущенные катодом,
ускоряются под действием разности электрических потенциалов между анодом
и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных
частиц - необходим удар материи на скорости одной десятой и более
скорости света.
Из чего следует невозможное условие для излучения материи при падении в
черную дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей,
близких к с. В таком случае трения более чем достаточно для излучения
высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не
об что тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой
или одной третей скорости света, может прекрасно летать на орбите
вокруг Черной Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько
сильно, что вторая космич. скорость (параболическая скорость) для
находящихся в этой области тел должна была бы превышать скорость света,
т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в
природе ничто не может двигаться со скоростью, большей скорости света.
Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают
звезды, при этом излучают, и что в центре галактики в черных дырах
масса больше чем масса всех звезд в этой галактике, а с момента большого
взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в
черных дырах - этого никто не наблюдал, - не наблюдали и то как звезда
проходит через горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после
образования Н. з., её масса может со временем значительно увеличиться.
При ${mathfrak M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном
из нейтронов. Существование Н. з. было предсказано в 30-х гг. 20
в.,вскоре после открытия нейтрона. Однако только в 1967 г. они были
обнаружены в виде импульсных источников радиоизлучения - пульсаров.
Затем было установлено, что Н. з. проявляют себя также как рентгеновские
пульсары (1971 г.) и вспышечные источники рентг. излучения - барстеры
(1975 г.). Не исключено, что на одной из стадий существования Н. з. явл.
источниками гамма-всплесков. К 1984 г. открыто ок. 400 Н. з., из них
ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а остальные в
виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в
тесных двойных звёздных системах. Перетекание вещества со
звезды-компаньона на белый карлик постепенно увеличивает его массу, и,
когда она достигает ${mathfrak M}_Ч$, белый карлик превращается в Н. з. В
этом случае ${mathfrak M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие
собой вращающиеся нейтронные звезды с сильным магн. полем, излучающие за
счет аккреции (падения вещества на их поверхность). Магн. поля на
поверхности Р.п. ~ 1011-1014 Гс. Светимости большинства Р.п. от
1035-1039 эрг/с. Периоды следования импульсов P от 0,7 с до неск. тысяч
с. Р.п. входят в тесные двойные звездные системы, вторым компонентом
к-рых явл. нормальная (невырожденная) звезда, поставляющая вещество,
необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы
(этим компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная
звезда не проявляет себя как Р.п. Рентг. пульсары встречаются как в
массивных молодых двойных звездых системах, относящихся к населению I
Галактики и лежащих в ее плоскости, так и в маломассивных двойных
системах, относящихся к населению II и принадлежащих к сферич.
составляющей Галактики. Р.п. открыты также в Магеллановых Облаках. Всего
открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам
присваивались наименования по созвездиям, в к-рых они находятся. Напр.,
Геркулес X-1 означает первый по рентг. яркости объект в созвездии
Геркулеса, Кентавр Х-3 - третий по яркости в созвездии Кентавра. Р.п. в
Малом Магеллановом Облаке обозначается как SMC X-1, в Большом
Магеллановом Облаке - LMC X-4. Обнаружение со спутников большого числа
рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в
Крабе и Парусах, излучают и в рентг. диапазоне, см. Пульсары),
излучающих за счет энергии вращения замагниченной нейтронной звезды и
увеличиващих свой период со временем, Р.п., излучающие за счет аккреции,
ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял -не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую
подготовку в рамках хотя бы школы. У Вас такая подготовка, судя по
всему, хромает на обе ноги, поэтому Вы не понимаете большинство статей.
Для уточняющих вопросов есть комментарии, для базовой подготовки - школа
и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы
читать - то надо быть доктором наук, и в тоже самое время Вы лично не
можете ответить прямо на прямые вопросы, по этой статье. Вы меня в
принципе заинтриговали, я подумаю чтобы такой пузырь высосать из пальца в
рамках парадигмы, чтобы все вокруг аж зааплодировали за исключительно
высокохудожественный идиотизм в рамках бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы
доказательств которые позволяют определить какими были в первые моменты
большого взрыва звезды, черные дыры , температура и другие различные
свойства пространства и свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой
простой вопрос по обсуждаемой статье, то я не обязан верить написанному,
а скорее наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к
астрофизике, то они все в астрофизике - дилетанты, которые идеи
вбрасывали в астрофизику от случая к случаю, и серьёзно ей ни кто не
занимался. По этому вся астрофизика и состоит из разрозненных идей, -
озарялок, которые последователи пытаются состыковывать между собой по
причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей
разных, что могу делать выводы что высоска из пальца, а что и супер
грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы
водород выгорает. И астрофизики внятно ответить не могут причину по
которой самый легкий водород - преодолевает гравитацию становится
тяжелее всех металлов и летит в ядро звезды поучаствовать в ядерной
реакции. И В то что самый легкий водород преодолевает летит внутрь
звезды -я не верю, хоть в миллионе книжек это будет написано, и тысяче
учебников. Так как написанное не подтверждено физическими свойствами а
противоречит им.
- Re: Черная дыра
(А.П. Васи,
19.09.2011 14:51, 2.3 КБайт)
http://www.wikiznanie.ru/ru-wz/index.php/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BD-%D0%B2%D0%BE%D0%BB%D1%8C%D1%82
Электронвольт единица измерения энергии, равная энергии, необходимой для переноса электрона между разницей потенциалов
1В, широко
применяемая в атомной,
ядерной
физике и физике
элементарных частиц.
Для тех кто не понял - это еденица измерения переноса частицы в ускорителе,
указывающая какое ускоряющее напряжение приложено для ускорения частицы,
или аналогичное напряжение в результате тормозного излучения,
повылетают заряженные осколки.
"...
ученые получили значения масс верхнего кварка - 2,01 0,14
мегаэлектронвольта - и нижнего кварка - 4,79 0,16 мегаэлектронвольта.
Это составляет соответственно 0,214 и 0,510 процента от массы протона.
Таким образом, физики уменьшили погрешность в определении массы легких
кварков с 30 до 1,5 процентов. " http://lenta.ru/news/2010/04/05/quarks/
.
Ну при чем здесь масса к приложенному ускоряющему напряжению на ускорителе,
добавлю напруги бысрее полетят, и масса осколка увеличится - заряд увеличится,
точнее даже не заряд увеличится а энергия раскрутки осколка атома увеличится,
камера Вильсона тому подтверждение, так как с повышением
ускоряющего, при торможении
вылетают с определенного
напряжения - частицы которые отклоняются магнитным полем,
что говорит о том что осколок вращается с определенного напряжения ускоряющего.
- Re: Черная дыра
(А.П. Васи,
20.09.2011 9:05, 1.8 КБайт)
Ответ #4 : Сегодня в 06:44:07
Вибе - Нет уж, достаточно темы про старение света. Эту тему я закрываю.\\\
Гоните этого стар-пёра в смысле звездного
толкателя.
Я вот не понимаю какой умник додумался пустить козла в огород
http://elementy.ru/lib/430399
у Вибе есть своё виденье и ему глубоко ...
на мнение других,
ему важнее не обхезаться перед студьнями,
Вот его текст
\\\Такую возможность нам предоставляют
звездные скопления. (Звезды вних, конечно, образуются не совсем
одновременно, но вбольшинстве случаев разброс возрастов отдельных звезд
меньше среднего возраста скопления.) Теория звездной эволюции
предсказывает, что звезды различных масс эволюционируют по-разному чем
массивнее звезда, тем быстрее она заканчивает свой звездный путь.
Поэтому чем старше скопление, тем ниже опускается планка максимальной
массы населяющих его звезд. Например, вочень молодом звездном скоплении
Arches (Арки), расположенном вблизи центра Галактики, есть звезды
смассой вдесятки солнечных масс. Такие звезды живут не более
нескольких миллионов лет, стало быть, именно таков максимальный возраст
этого скопления. Авот вшаровых скоплениях наиболее тяжелые звезды
имеют массу не более 2масс Солнца. Это говорит отом, что возрасты
шаровых скоплений измеряются миллиардами лет.\\\
И надо быть дыб_илом, чтобы думать что Вибе будучи модератором
согласится с вечной вселенной. Овна в тачку,
всё что не
совпадает со статьёй написанной Вибе всё будет забанено.
- Re: Черная дыра
(А.П. Васи,
20.09.2011 9:19, 952 Байт, ответов: 1)
к Статической Вселенной можно ставить больше вопросов, чем к гипотезе старения света.
Вибе - Che, я думаю, что
открывать новую тему будет иметь смысл, когда у Вас будут ответы на эти вопросы.\\\
Гоните в шею Вибе из модераторов, в данном случаи он говорит посетителю,
чтобы тот со своей теорией шел к себе домой на кухню и там ей занимался,
а на форумах искать ответы и обсуждать и консультироваться с другими могут
только
те кто в парадигме - избранные и махровые релятивисты.
Вот теперь этот посетитель пойдет на скай тех или мембрану - и откроет
там обсуждения, чем собственно будет
замусоривать те сайты по причине
того что там до лампочки вопросы поднимаемые астрономами.
- Re[2]: Черная дыра
(А.П. Васи,
30.10.2011 13:01, 2.2 КБайт)
 С моей точки зрения основная трудность в физике
- наличие в ней гениев, по причине того что кроме
гениев в физике могут быть недоумки и дифективные,
и недогении.
Грубо говоря физики делятся на два основных класса
гении и недоумки, среднего не дано.
По скольку гениев единицы - то все воспитываются в стиле
недоумков, в принципе не способных своими словами ответить
на вопросы по физике, по скольку свои мысли считают
мыслями недоумков, и советуют почитать книжки
гениев с их точки зрения. При общении физиков то и происходит
взаимопосылание читать книжки.
Вот такая жестокая селяви.
С моей точки зрения основная трудность в физике
- наличие в ней гениев, по причине того что кроме
гениев в физике могут быть недоумки и дифективные,
и недогении.
Грубо говоря физики делятся на два основных класса
гении и недоумки, среднего не дано.
По скольку гениев единицы - то все воспитываются в стиле
недоумков, в принципе не способных своими словами ответить
на вопросы по физике, по скольку свои мысли считают
мыслями недоумков, и советуют почитать книжки
гениев с их точки зрения. При общении физиков то и происходит
взаимопосылание читать книжки.
Вот такая жестокая селяви.
http://www.astronomy.ru/forum/index.php/topic,79449.msg1722187.html#msg1722187
Вот Вибе например занимается гандольеризмом,
он вообще насаждает всем подряд единственно
правильную точку зрения, ибо как физик он не гений.
\\/Именно что по физике. А Поиск Истины -- это философия. На философском
форуме Вас, вероятно, приветили бы и с одуванчиками, и с апельсинами. А в
физике главное -- чтобы работало./\\
Совсем отупел уже - как работает замедление времени пусть расскажет, и как работает притяжение,
и кривизна пространства
- и какими измерительными инструментами это измеряется.
Этому не гению даже не понять что физике до лампочки чтобы работало,
- физике надо объяснить причину, и
измерить.
\\\Конечно. Но почему Вы решили, что занимаетесь физикой? У меня вот,
например, физическое образование, и по работе я, вроде как, физик. А
ничего, кроме упражнений в изящной словесности, я в Ваших текстах не
вижу. И у меня есть сильное подозрение (основанное на репликах других
участников), что я не одинок в таком их восприятии.\\\
Вот очередное желание пробиться в гении местного разлива, а понтов и пафоса как будто его
преподаватель
был Томас Юнг, а на самом деле проходило групповое чтение
книг по релятивизму с заучиванием наизусть.
\\\Это очень хорошо. Но почему Вы так стремитесь навязать
это объяснение другим?\\\
Только гандольер махровый не понимает что любая дискуссия, лекция, преподавание это навязывание
другой точки зрения кому либо.
- Re: Черная дыра
(А.П. Васи,
25.11.2011 22:58, 1.6 КБайт)
Шахсей-вахсей,
напишите, пожалуйста, здесь, зачем нужны Ваши изыскания. Укажите
конкретные эксперименты, которые Вы объясняете лучше, а также подробно
опишите новые эксперименты, которые позволят подтвердить или
опровергнуть Вашу точку зрения. До того как Вы это сделаете, прошу
другие сообщения в разделе не публиковать.
Шахсей-вахсей, поскольку Вы мои слова демонстративно игнорируете, я Вам закрываю возможность публикации
на неделю.\\\
\\\Тема закрывается до выхода автора из бана.\\\
У меня просто сегодня праздник,
гандольер вибе нарушил все права модератора,
он создал самовольно новые правила форума, -
принял на себя функции владельцев форума,
законотворчество не оговоренное правилами
форума - создал традиции,
после этого выступил в качестве потерпевшего
чмошника на вопрос которого не было ответа
(по неписанным правилам новых вибевских традиций),
после этого
выступил в качестве судьи от
имени возмущенного чмошника (егоже собственно) которому
не ответили на его разведывательный вопрос
который вынуждал отвечающего
расстаться со своими
авторским правами - в пользу какого-то гандольера.
После чего вибе совсем оборзел и закрыл форум,
на основании того , собственно
понятно чего, -
что все вокруг за бз дят ему как модератору перечить,
а кнопки пожаловаться на гандольера
модератора - хозяевам форума нет.
- Re: Черная дыра
(А.П. Васи,
26.11.2011 0:17, 1.1 КБайт)
Ответ #16 : 19.11.2011 [22:00:57]
lorein, ответьте,
пожалуйста, на традиционный вопрос. Зачем нужно то, что Вы пишете? Вы
лучше объясняете какие-то эксперименты? Может быть, предсказываете
результаты будущих экспериментов?
Яркий пример разведывательного традиционного вопроса чтобы шопнуть идею
и авторские права, ибо для того чтобы забрать права
есть основание -
и права могут уйти с формулировкой - наводящий вопрос,
ответ на который был дополнен формулой.
А ответ с формулой и ответ без формулы
- на сегодняшний день
это две разные весовые категории.
- Re: Черная дыра
(А.П. Васи,
30.11.2011 12:17, 3.4 КБайт)
Новая ситуация на форуме, участники обсуждения
приближаются к тому чтобы нагнуть релятивистов
и здесь появляется "вибёнок" и машет правилами
форума
и не даёт продолжатся дискуссии.
С другой точки зрения "вибенок" прост как кусок
..., ему надо чтобы автор поведал ему нюансы,
после этого можно
запустить поиск решения
методом "ансамбля", для этого надо иметь
ансамбль, а у "вибенка" он есть.
Так вот после того как автор рассказывает
о нюансах, "вибенок" на закрытом обсуждении
от других, раздаёт своим студентам задачи
с этими нюансами, после чего результаты
он будит сводить
по среднему, по лучшему варианту
он не сможет так как он не физик, после чего
пририсовывает формулы с помощью
программы "математика" и бежит потом
защищаться на новую степень.
------------------------------------------------------------
Да
могу, конечно, однако не вижу необходимости обрушивать сразу лавину
новых знаний на аудиторию, слабо знакомую со спецификой сплошной среды.
Зачем "гнать лошадей"?
"вибенок"
Затем, что таковы правила, принятые в разделе.
О разделе Горизонты науки о Вселенной.
Ввиду
серьёзности рассматриваемых мировоззренческих проблем, у меня большая
просьба к Вам, господин модератор: позволить дискуссии развиваться так,
как она и развивается. Неспешно, но в направлении корреляции с
Реальностью и законами классической физики.
"вибенок"
Вы специально для меня сразу
напишите, зачем нужна Ваша теория, как её можно проверить
экспериментально. Я на этом успокоюсь, и дискуссия сможет спокойно и
неспешно развиваться хоть в направлении реальности, хоть в направлении
классической физики.
-----------------------------------------------------------------------
Вибенок нарушает правила форума и даже сам не понимает
что именно нарушает
- маразм и стар перение берёт своё.
------------------------------
Дмитрий Вибе: То
есть, пока доказать нужность своей теории Вы не можете?
Читал где-то, что электродинамическая теория Максвелла получила
признание далеко не сразу. И главным возражением был тезис о том, что,
"может быть, математически и все верно - но это совершенно бесполезно, а потому и обсуждать физикам нечего..."
"вибенок"
Интересно, как Максвелл на это реагировал. Бродил по телеграфным форумам и ныл, что его никто не понимает?
-----------------------------------------------------
Правилами этого форума не запрещается
высказывать своё объективное мнение о модераторе с другого форума.
- Re: Черная дыра
(А.П. Васи,
30.11.2011 13:40, 3.8 КБайт)
\\\"вибёнок"
И это обсуждение тоже останется незавершённым. Потому что завершение
научной дискуссии -- это предложения по экспериментальной проверке. Так
что всё-таки: какие Вы видите преспективы по экспериментальной проверке
Ваших идей?\\\
Этому не гению даже не понять что физике до лампочки чтобы работало,
- физике надо объяснить причину, и
измерить.
Кстати хочу еще раз акцентировать
внимание на то что "вибёнок" гонит голимый
порожняк в своих утверждениях от имени всей
физики.
И все должны понимать что если гандольер
утверждает что мол физике главное чтобы работало -
то надо понимать - любая речь гандольера изначально
бесполезна для других и полезна для него лично.
----------------
Повторю так как актуально,
ибо все делают ошибки одни и те-же того не понимая.
С моей точки зрения основная трудность в физике
- наличие в ней гениев, по причине того что кроме
гениев в физике могут быть недоумки и дифективные,
и недогении.
Грубо говоря физики делятся на два основных класса
гении и недоумки, среднего не дано.
По скольку гениев единицы - то все воспитываются в стиле
недоумков, в принципе не способных своими словами ответить
на вопросы по физике, по скольку свои мысли считают
мыслями недоумков, и советуют почитать книжки
гениев с их точки зрения. При общении физиков то и происходит
взаимопосылание читать книжки.
Вот такая жестокая селяви.
http://www.astronomy.ru/forum/index.php/topic,79449.msg1722187.html#msg1722187
Вот Вибе например занимается гандольеризмом,
он вообще насаждает всем подряд единственно
правильную точку зрения, ибо как физик он не гений.
\\/Именно что по физике. А Поиск Истины -- это философия. На философском
форуме Вас, вероятно, приветили бы и с одуванчиками, и с апельсинами. А в
физике главное -- чтобы работало./\\
Совсем отупел уже - как работает замедление времени пусть расскажет, и как работает притяжение,
и кривизна пространства
- и какими измерительными инструментами это измеряется.
Этому не гению даже не понять что физике до лампочки чтобы работало,
- физике надо объяснить причину, и
измерить.
\\\Конечно. Но почему Вы решили, что занимаетесь физикой? У меня вот,
например, физическое образование, и по работе я, вроде как, физик. А
ничего, кроме упражнений в изящной словесности, я в Ваших текстах не
вижу. И у меня есть сильное подозрение (основанное на репликах других
участников), что я не одинок в таком их восприятии.\\\
Вот очередное желание пробиться в гении местного разлива, а понтов и пафоса как будто его
преподаватель
был Томас Юнг, а на самом деле проходило групповое чтение
книг по релятивизму с заучиванием наизусть.
\\\Это очень хорошо. Но почему Вы так стремитесь навязать
это объяснение другим?\\\
Только гандольер махровый не понимает что любая дискуссия, лекция, преподавание это навязывание
другой точки зрения кому либо.
"вибенок" продолжает свою серию наглых
разведывательных вопросов чтобы украсть чужие идеи,
он прекрасно понимает что завтра если он будет оставаться
"релятивистом махровым", его кормовая база будет
на скудном рационе, а влезьть в альтернативщики
он может только шопнув идеи альтов.
Re: Механика сплошной среды и Вселенная"вибенок"\\\\Ох...
Если Вы предлагаете новые взгляды, значит, старые Вас чем-то не
устраивают. Чем? Если Вы предлагаете новые взгляды, значит, они в чём-то
лучше старых. В чём?\\\\
- Re: Черная дыра
(А.П. Васи,
30.11.2011 14:20, 687 Байт)
 Посмотрел фильм понравился, как-бы
Посмотрел фильм понравился, как-бы
фильм
по астрофизике в художественном варианте.
В поисках галактики / Galaxy Quest (1999) [BDRip 720p]
http://www.ex.ua/view/2039278?r=2
 Посмотрел клип, и слегка обнаружил темную материю и темную энергию.
Посмотрел клип, и слегка обнаружил темную материю и темную энергию.
The Rasmus - October
and April (2009)
http://www.ex.ua/view/208350?r=1991
- Re: Черная дыра
(А.П. Васи,
30.11.2011 14:46, 1.7 КБайт)
"вибенок"
\\\Нет, конечно. Я и не прошу представить диссертацию или готовую
нобелевскую речь. У меня одна, всего одна, ма-а-аленькая просьба.
Написать о перспективах экспериментальной проверки.\\\
Гандольер продолжает разведку сам того не подозревая что требует
от каждого участника форума быть академиком.
А если не академик - то украсть у него идею и забанить.
Объясню что хочет этот гандольер.
Дело в следующем - чтобы разработать практический опыт,
надо знать все аналоги проводившихся опытов, после этого
надо понять что Физиков на планете было единицы, которые внятно
могли объяснить свои опыты. Следовательно
надо самостоятельно
переобъяснить все опыты и найти некоторую глобальную
ошибку для всех опытов.
После этого надо разделится на два пути поиска,
один
вариант придумать методику измерения глобальной ошибки,
или частной для какого-то опыта.
Второй вариант методику внешнего воздействия на данный опыт.
Бывает
так что надо будет задействовать и третий вариант,
поиск и анализ физ аналогов с целью провести опыт
на аналогии, а потом провести опыт по факту, или
для
доказательства аналогией.
После чего моделируется сам опыт.
Так вот тот кто сможет это всё сделать,
так тому "вибёнок" интеллектом в
пуп дышит.
Следовательно гандольер он потому и гандольер
что ставит невыполнимые требования и после
этого устраивает произвол.
Собственно
коню понятно что такие требования может
выполнить только группа физиков с финансированием
на уровне миллиона евро (каждому) в год как минимум,
а умственные
способности должны зашкаливать
и перед ними все должны приседать и делать два раза ку.
- Re: Черная дыра
(А.П. Васи,
30.11.2011 16:48, 1.7 КБайт)
Какие -то у Вас странные представления о Познании...
"вибёнок"
Уж какие есть. Что главное -- они совпадают
с представлениями владельцев форума и его администрации.\\\
Задавили интеллектом гандольера с силовыми полномочьями,
теперь он включает дурака кого-то зовёт
зовёт и на кого-то ссылается
и апелирует на несуществующие
требования владельцев форума к модераторам, о которых
никто кроме гандольера вибёнка не знает.
\\\
Вы
понимаете, что такое экспериментальная проверка? Вы можете написать
что-то в духе: "Для проверки моего подхода необходимо провести следующий
эксперимент..."?
Понимаете, какая беда: красивые речи про физический смысл, фундамент, Миропонимание, Познание меня совершенно не трогают...\\\
Вот
чем собственно отличается физик от гандольера.
Гандольер видит и любит себя (звания, оплата за каждый пук) в физике,
а физик любит физику внутри себя , и гандольеру
никогда не понять что физик занимается физикой потому
что она ему просто интересна, и может 99.99 %
никогда не смогут придумать эксперимента, но их в физике
интересуют
всяческие физические вопросы и трудности ,
и физикам приятно делать хоть маленькие но уверенные
шаги в осмыслении физических ситуаций.
Да и гандольер вибенок то и сам никогда не сможет предложить
никакого поверочного опыта, а от других требует.
- Re: Черная дыра
(А.П. Васи,
30.11.2011 19:08, 1.4 КБайт)
Мне жалко смотреть на то как мучаются юзеры с синхронизацией,
бьются как рыба об лёд.
Синхронизироваться можно и с "наблюдателями" только
надо
наблюдателям придать физического смысла, у "наблюдателей"
должна быть точка в пространстве - физическая,
у них должны в кармане лежать часы показывающее
глобальное время,
и у каждого наблюдателя в кармане 3 таймера.
Между наблюдателями известно расстояние, и скорость между ними,
известно расстояние и скорость
между каждым из наблюдателей и наблюдаемым
объектом.
В принципе если сделать "наблюдателей" физически грамотно
описанными, нет простора для
математических лохотронов,
а как для физического анализа "наблюдатели" физически
грамотно описанные и даром не нужны,
так как прямые измерения
будут аналогичны наблюдаемым.
Природа всегда преподносит неожиданные подарки,
по поводу того как в старину синхронизировали время,
- я вот читал что
давным давно собаке делали операцию, и вырезали у неё
то-ли кусочек какого-то органа то-ли брали какую-то
жидкость, точно не помню забыл где читал.
Так вот
потом эту собаку брали на корабль и плыли с ней
куда угодно, а там от куда вышел корабль брали
часть вещества нагревали его ровно в полдень, и собака
в любой
точке земли начинала гавкать.
Можно верить этому а можно и не верить.
- Re: Черная дыра
(А.П. Васи,
30.11.2011 23:42, 1.3 КБайт)
http://www.astronomy.ru/forum/index.php/topic,90464.msg1759427.html#msg1759427
Гришин С. Г.:
Вместо того, чтобы чернуху гнать,
посмотри в словаре, что такое "спекуляция".
Вроде на
"ты" не переходили.
Смотрим:
СПЕКУЛЯЦИЯ
(от лат. speculatio - выслеживание, высматривание),1) купля-продажа
ценностей (акций, товаров, валюты и т. д.) с целью получения прибыли от
разницы между покупной и продажной ценой (курсом).2) В переносном смысле
- расчет, умысел, направленный на использование чего-либо в корыстных
целях.
---------------------------------------------------------
Очередная модераторская технология, -
посетители на форуме устраивают скандал, после
чего модератор не скандалистов удаляет а форум закрывает.
После этого может быть ещё одна модераторская технология закрыть форум,
это когда два модератора
задают вопросы
на которые ответы будут взаимно противоречивы, в результате
тоже закроют форум.
- Re: Черная дыра
(А.П. Васи,
2.12.2011 9:29, 744 Байт)
Гандольер вибёнок за деньги которые ему постоянно платят
готов вечно
\\\Копить данные, проводить эксперименты, которые
бы постоянно проверяли
существующие теории на прочность.
Рано или поздно этот путь обязательно
приведёт к углублению познания Мира.\\\
Только гандольер не понимает что сколько бы он не смотрел в телескоп,
и не получал за это зарплату, то от этого
в дурной голове умный опыт не придумается,
его девиз - лохотрон, и он никогда
не сможет придумать опыт, и как
истинный гандольер он обещает
что когда-то,
но не говорит - когда.
- Re: Черная дыра
(А.П. Васи,
2.12.2011 9:42, 346 Байт)
Вибёнок - балласт науки.
Который только может кричать что он за новое,
а на деле он и такие-же как он стар-пёры
(звездные толкатели) блокируют всё новое,
есть причины как правило это то что вибенок
не переучится другой теории лучше чем его
студент, а в этом случаи преподаватель требует
немедленной замены.
- Re: Черная дыра
(А.П. Васи,
2.12.2011 19:45, 288 Байт)
Как и следовало ожидать закрыты оба форума.
В принципе понятно почему, не дать принять коллегиальных
решений, ибо коллегиальное решение 10 любителей,
с обоснованными высказываниями каждого,
не только нагибает гения но и делает коллегиальное
решение законом.
- Re: Черная дыра
(А.П. Васи,
3.12.2011 15:57, 4.1 КБайт)
Re: Действительно ли скорость света в вакууме - инвариант?
Аж понравилось как барышя интелектуально
нагнула релятивистов и отшмагала
интеллектуальным кнутом прямо по самое - асясяй.
И так крепко
ошмагала, что не видно даже в обозримом
будущем релятивиста который смог бы ответ держать,
и прикрыть своим умом чужие задницы.
\\\
Дробышев писал(а) Вчера :: 18:59:22:
Вот ваша ссылка. http://www.desy.de/user/projects/Physics/Relativity/SR/experiments.html.
Обещает "сотни опытов", доказывающих постулаты СТО.
При
внимательном рассмотрении этих опытов выясняется, что релятивисты
жульнически пытаются создать видимость наличия у них "множества
доказательств" постулатов СТО и под видом "доказательств" самым
мошенническим образом понатаскали здоровенную кучу посторонних опытов и
всевозможного хлама, чтобы создать видимость наличия доказательств и
чтобы все нормальные люди сломали ногу в этих псевдодоказательствах.
Если набраться терпения и разобрать весь этот хлам, то очень быстро и
легко обнаруживается, что никаких доказательств у релятивистов нет.
Давайте посмотрим повнимательнее на эту странную кучу. Чего здесь только нет!
Здесь
есть и Брэдли с его аберрацией света. И Физо с его определением
скорости света в движущейся воде. Здесь упоминается Микроволновое
Фоновое Космическое излучение. И множество прочих, совершенно
ПОСТОРОННИХ ОПЫТОВ, не имеющих ни малейшего отношения к доказательству
инвариантности скорости света! Зачем они сюда все это притащили? С целью
создать видимость моножества доказательств. 
Еще
целая серия опытов - опыты по доказательству "независимости скорости
света от скорости источника". Эти опыты релятивисты раз за разом
пытаются подсунуть под видом доказательства "инвариантности скорости
света". Уважаемые релятивисты! Мы умеем различать "инвариантность
скорости света" и "независимость скорости света от скорости источника".
"Независимость скорости света от скорости источника" инвариантности
скорости света не доказывает. Поэтому перестаньте мошенничать и жульническим образом подсовывать фальшивые доказательства. 
Про
многочисленные вариации опыта Майкельсона мы говорили уже тысячи раз -
Майкельсон неправильно изобразил траекторию поперечного луча (угол
отражения нарисовал неравным углу падения луча), откуда досадная ошибка в
его расчетах.
Лазеры - мазеры проверяют эффект Доплера и тоже подсунуты под видом доказательства "инвариантности скорости света".
И в таком
духе.
Ув.
Дробышев. Нам не нужны списки из сотен наименований всякого хлама.
Дайте нам всего лишь одну ссылку, но ссылку не на списки мусора
ненужного барахла, а ссылку на сам эксперимент, причем такой
эксперимент, который доказывает именно "инвариантность скорости света", а
не наличие эффекта Допплера, аберрации, фонового излучения,
независимости скорости света от скорости источника и прочих совершенно
посторонних вещей, понатасканных релятивистами от безысходности из-за
неимения настоящих доказательств.\\\
- Re: Черная дыра
(А.П. Васи,
3.12.2011 16:02, 72 Байт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1319091586/390#390
- Re: Черная дыра
(А.П. Васи,
14.12.2011 9:57, 1.4 КБайт)
 Эксперимент Александрова (и др.) по подтверждению независимости скорости света от движения источника
Эксперимент Александрова (и др.) по подтверждению независимости скорости света от движения источника
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?action=dereferer;url=http://ufn.ru/ufn11/ufn11_12/Russian/r1112l.pdf
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1323760148/0#0
Прочитал и взгрустнулось - как релятивисты физикой страдают,
но смогли хоть что-то
сделать при полном
непонимании то-го что сделали, ибо если-бы
понимали то о некоторых ньюансах бы не писали.
Итого что имеем - вылетают с кольца
синхрофазотрона одиночные разогнанные атомы металла,
изначально не сфокусированные, летят и ударяются об сапфир,
и происходит световая вспышка, в следующем варианте,
перед сапфиром ставят стекло, так как стекло ближе,
то на него попадает больше одиночно летяших атомов
металла и при их ударе о стекло вспышка естественно
будет ярче.
Вывод-
Заявленные в опыте задачи данное устройство решить не может.
- Re: Черная дыра
(А.П. Васи,
18.12.2011 19:12, 959 Байт)
Вот думал про опыт Александрова о том как его сделать с заявленными
возможностями.
Здесь что надо понимать, движутся одиночные атомы по кругу, и они
должны
излучать - для этого должна быть причина.
В опыте излучение за счет тормозного ускорения, или попросту говоря
световые вспышки происходят от ударов о препятствие,
то-ли это стекло или сапфир.
Изначально нет строгой физической причины для светового излучения.
Если добавить источник рентгеновского излучения в точку
потока,
то дополнительное воздействие возможно приведет к световому
излучению в потоке разогнанных частиц.
Возможно на поток воздействовать лазерным лучом,
чтобы отражение
луча было от частицы, хоть это не одно и то-же когда частица сама излучает,
но всё-таки ближе к заявленным свойствам.
Естественно все стенки
поверхностей надо покрыть чем-то поглощающим и
черного цвета, и внутри резьбу перед этим нарезать.
- Re: Черная дыра
(А.П. Васи,
25.12.2011 16:17, 2.6 КБайт)
На популярной кинематике меня забанили по новой,
не нравится там когда им правду говорят и всё называют
своими именами, вот если после лекции видео в обработке
- то это или лекция не удалась освистали лектора,
а второй вариант это жадность, ибо если будет видео
то кто-ж на платные лекции пойдет.
Потом
высказался по темной материи. У которой как все знают
нет определения, да и сама материя нужна группе математиков
страдающих физикой,
у которых другие теории
не сходятся с реалиями, и они
придумывают новые, чтобы старые сходились.
---------
Мои любимые ошибки парадигмы на которых она
покоится в колыбельке
глупости.
Водород самый легкий материал со временем
проходит сквозь любой металл, и вдруг с непонятного
желания астрофизиков он сорвал у себя башню
и полетел
в центры звёзд поучавствовать в горении.
А какая красота поговорить о том у чего даже нет определения,
темная материя и темная энергия - это
удел гигантов мысли,
разговор вечный и беcсмысленный, зато можно наговорится
и показать свой интеллект.
Вот взорвалась звезда и о чудо после взрыва водорода
не обнаружено - это не звезда без водородная оказалась
это все книжки по астрофизике ошибочные и бессмысленные.
А вот и виновница торжества из известного
опыта размером
со спичечный коробок - камера Вильсона, благодаря неправильной
интерпретации наблюдаемого сделали самую большую
и непонятную ошибку и её увековечили
и её не замечают -
электрон, - этим словом что только не называю.
Хотя электро потенциала в пространстве без носителя
не бывает, так вот - заряженный или раскрученный
атом
в пространстве, или осколки атомов стали от большого
ума называть электронами, как и то что внутри проводников
движется.
Я очень рад как
качественно физики и астрофизики загнали
себя в глухой угол.
=============
Потом почитал про гарпун для спутников чтобы кометы гарпунить.
На столько
недалёкие что даже не знают что практически у всех
спутников возле комет получились нештатные ситуации.
-------------
Детвора даже не понимает причины
необходимости
гарпуна, а она проста - кометы не притягивают,
им до лампочки книжки по физике.
Спутник подлетает по программе на 50 метров,
после чего
должен попасть под влияние гравитации
кометы, а влияния нет, спутник дрейфует куда попало,
но только не на комету.
Большая глупость распространить падающее
яблоко
на всю вселенную, вселенной до лампочки как яблоки
падают у вселенной для притяжения другие причины.
--------------
- Re: Черная дыра
(А.П. Васи,
17.01.2012 0:13, 2.0 КБайт)
Рассказ
Фантастический сон о городе физиков.
Приснился город физиков, он состоял из одной центральной улицы,
которая разделяла пустынные дикие просторы
классической физики,
и плодоносящие сады релятивистской физики.
По пустынным просторам классической физики скитались какие-то
голодранцы несколько было по
двое и по трое но в основном одиночки,
ходили что-то писали на песке, кое кто из альтернативщиков проводил
какие-то опыты на костре пока готовили еду.
Практически
все альтернативщики периодически и с разным успехом
участвовали в форумах
"скай-тюх" и "звездомер".
Эти участки дороги отличались разметкой
улицы, и наличием забора
со стороны релятивистов на "звездомере", забор на "звездомере" не
для того чтобы альты не лазили, а для того чтобы
сомневающиеся
релятивисты не смогли убежать от модераторской порки. Возле форумной
разметки с обеих сторон периодически стояли толпы зевак и приходили
ораторы
то с той а то с другой стороны.
На "скай-тюхе" демократии было побольше и все орали друг на друга и периодически
рвали на себе одежду и бросали через
дорогу, там в неё вышмаркивались и бросали
обратно.
На "звездомере" рерятивисты после меряний телескопами и после обеда в гос
столовой, пододвигались
и подкатывались на своих креслах к дороге,
чтобы лучше слышать.
По средине уличной разметки "звездомеровского" форума стоял - плёточных
шмаганий
мастер, - несравненный модератор Би-Бе. Он славился тем что от
прямых вопросов уходил своими ответами в интеллектуальное бегство.
От альтернативщиков он требовал
дать ему посмотреть тех паспорт на эфир,
и предоставить опыты за которые можно нобелевскую получить ещё вчера.
Естественно запрос на релятивистский тех-паспорт
на причину скорости света вызывает
шатание в креслах и бубнение релятивистов о том что в нем нет смысла,
а смысл есть в паспорте на эфир.
Так собственно
в непонимании и смотрели друг на друга.
- Re: Черная дыра
(А.П. Васи,
17.01.2012 0:43, 1.8 КБайт)
Продолжение
Рассказ
Фантастический сон о городе физиков.
Дальше у дороги релятивисты поставили трибу своих достижений
с трубными фанфарами.
На фанфарах
разные надписи, - без которых релятивизм
был бы невозможен.
Чтобы уйти от эфира придумали фанфары ---- "вакуум"
Чтобы уйти от света который был
в эфире, придумали фанфары --- "фотон"
Так как не смогли придумать
куда тепло девается от звезд,
придумали фанфары
- ---"большой взрыв",
тепла у звезд оказалось много
и чтобы поглощать ещё тепло
от звезд придумали фанфары -
--- "черная - дыра"
а энергии оказалось ещё больше,
придумали фанфары ---" ускоренное расширение",
и непонятно
чем притягивается
токмо по два тела придумали фанфары --- "гравитация".
А на против трибуны с фанфарами располагался зрительный зал
смеха
релятивистов, так как на трибуну с фанфарами периодически
забегали одичавшие альты, они прибегали с той стороны дороги,
со стороны классической физики. И когда
одичавшие альты в своих
возмущенных речах использовали слова исключительно для
релятивистов, и они совпадали с надписями на фанфарах, то вместо
слов они
дули в фанфары релятивистов.
Некоторые дикие альты целые релятивистские концерты
устраивали и выдували фуги , гораздо
лучше некоторых релятивистов. Релятивисты
особо сильно
смеялись когда дикие альты использовали все слова.
Вдруг зависли в воздухе удары плетью, мастер Би-Бе на "звездомере"
шмагал
всех подряд а чтобы уважали.
Собственно так и жили, классическая сторона - пустыня бедности,
и релятивистские фруктовые сады с шоколадными кабинетами.
По дороге то там то там пробегали бобры, их по дружески били
телескопами с любой стороны улицы.
Вот я и проснулся.
- Re: Черная дыра
(О. Е. Коробейникова,
24.01.2012 21:04, 1.1 КБайт)
Как писалГермес Трисменист:"То,что находится внизу,соответствует тому,что пребывает вверху, и то что пребывает вверху ,соответствует тому,что находится внизу,чтобы осуществить
чудеса единой вещи." Изумрудная скрижаль."Если черная дыра есть в центре Вселенной,. То и в Солнечной Системе есть,и на Земле,и у человека. В Солнечной Системе находится
от Пояса Койпера до Оьлака Оорта. На Земле от Уральских гор до Тихого океана. Черная дыра,как пылесос. Сибирь от слова "мести","подметать".Если положить
Созвездие Ориона на Землю. То его Пояс будет на Урале. Россия "сердце Ориона" Европа "верхняя половина тела,где правит голова,меч." Сибирь "чрево,нутро"
Америки ноги. В человеке правит сейчас"черная ненасытная дыра". Она постоянно просит пищи. Кинжал/вспомните созвездие/ тоже правит/Азия/. Чуть -что вонзят в спину,исподтишка.
Постоянно некоторым ударяет моча в голову. Голова там не правит. Заходите в мой дневник. Правда я там с января. hppt.//www/liveinternet/ru/users/4652061/profile Не знай правильно
набрала?
- Re: Черная дыра
(О. Е. Коробейникова,
4.02.2012 15:21, 31 Байт)
Спасибо!Что печатали мои посты.
- Re: Черная дыра
(А.П. Васи,
4.02.2012 17:59, 816 Байт)
Вы больны фактически и не понимаете этого,
заброс адреналина приводит к переходу организма в состояние атаки,
да так потом и остаётся организм в "атаке".
Лечится это очень дорого.
http://top.rbc.ru/health/03/02/2012/636178.shtml
\\\Сопротивляться желанию проверить обновления в социальных сетях, например
таких, как Facebook и Twitter, намного сложнее, чем отказаться от
алкоголя и сигарет. Такой вывод был сделан учеными из Высшей школы
бизнеса имени Бута Чикагского университета (University of Chicago Booth
School of Business, USA) на основе опроса 250 жителей США об их
повседневных желаниях, пишет The Telegraph.\\\
Читать полностью: http://top.rbc.ru/health/03/02/2012/636178.shtml
- Re: Черная дыра
(О. Е. Коробейникова,
5.02.2012 21:49, 111 Байт)
Мне все равно,что Вы про меня пишете.Вы показываете свое истинное лицо.Скажу знакомым,чтобы заглянули почитали.
- Re: Черная дыра
(А.П. Васи,
5.02.2012 23:34, 802 Байт)
http://www.psyclinic.ru/page_36.html
\\\Именно внезапность возникновения состояния страха или физиологического
дискомфорта является наиболее точным симптомом панической атаки. Наличие
конкретной причины, которой может быть вызван подобный эпизод совсем
необязательно. Однако, человеку свойственно искать повод для непонятного
явления в окружающих событиях или в самом себе. Единственная причина
панической атаки - выброс в кровь колоссального количества адреналина,
при котором наступает состояние передозировки этим биологически активным
веществом. Лечение панических атак
на начальной стадии направлено именно на регуляцию именно количества
адреналина в крови, а затем уже на сами симптомы и боязнь их повторения.\\\
- Re: Черная дыра
(А.П. Васи,
6.02.2012 21:27, 885 Байт)
Сегодня прочитал формулировку абсолютно противоречащую
авторскому от Доплера.
Пальму первенства глупости продолжают нести на плечах -
Кратко скажу
причину легкого идиотизма в разговоре товарищей
которые даже не понимают всей глупости расскажу кратко -
Эффект Доплера был придуман автором исключительно для сред,
и за долго до релятивизма, релятивисты от использования этого
эффекта отказаться не могли так как он имеет место быть,
а чтобы пролохотронить на околосветовых
скоростях они
начхав что эффект для сред в авторском изложении
придумали новый эффект для пустоты и назвали его
Релятивистский эффект Доплера - методы гандольеров.
Вот текст от недалёких
- Re: Черная дыра
(А.П. Васи,
6.02.2012 21:30, 2.2 КБайт)
Учитывая что модераторы там периодически глупость удаляют
Скопирую позор астрофизиков сюда.
Автор
замахнулся на самое святое - на интерпретацию космологического красного
смещения как на результат расширения пространства. Он полагает, что все
сводится к доплеру и гравитационному смещению. Соответственно, говорить
о третьем типе - некорректно.
Если у автора темы есть самое или не самое святое, то что он делает в "Горизонты науки"?
Есть же множество религиозный
форумов.
Ну и главное, Сергей Попов не мешало бы научиться читать, как минимум познакомиться, что такое Доплер эффект.
К сведению:
Эффе́кт
До́плера изменение частоты и длины волн, регистрируемых приёмником,
вызванное движением их источника и/или движением приёмника.
Так как
для распространения электромагнитных волн не требуется материальная
среда, можно рассматривать только относительную скорость источника и
наблюдателя.
То есть, никакого смещения спектров в следствие эффекта
Доплера для взаимно неподвижных источника и наблюдателя не будет. А если
автор (John Woodruff Simpson Fellow) упоминает о эффекте Доплера, то это
в любом разе означает движение источника света относительно
наблюдателя, то есть ни о каком "замахнулся на самое святое - на
интерпретацию космологического красного смещения как на результат
расширения пространства" речи и близко нет.
По самой статье:
рассматриваются тривиальные пространства с тривиальной метрикой и доказывается главное по мнению
автора:
Whats
interesting, of course, is that because the two sets of coordinates are
different (one inertial, the other not), the two decompositions are
generally not equal, but the final results are the same, as they should
be because the underlying physics is identical. Типа - безразлично, чем
обусловлено красное смещение, они оба приводят к одному результату
потому что основная физика идентична.
Примерно так у него и получается.\\\
- Re: Черная дыра
(А.П. Васи,
7.02.2012 1:47, 1.6 КБайт)
По черной дыре ещё
http://siteua.org/system_category/330344
\\\"До сих пор никто и никогда не фотографировал
черные
дыры, ввиду сложности этого мероприятия и экзотической природы самих
дыр", - говорит Димитриос Псалтис, астроном из Университета Аризоны и
один из координаторов проекта.\\\
Собираются первую фотографию черной дыры сделать, и всем до лампочки что без таковой,
уже тысячи статей о черной дыре написали.
Дело не в фотографии на самом деле, нет общей формулировки черной дыры -
каждый видит в своих изысканиях то что он хочет и называет это черной дырой
- и это
смешно, - классика жанра.
\\\.Материал
из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.... \\\
-----------------------------------
http://www.lenta.ru/news/2012/01/19/prize/
Астрономической награды удостоились Рейнхард
Генцель (Reinhard Genzel) и
Андреа Гез (Andrea Ghez). Премия была присуждена этим ученым за
обнаруженные ими и их сотрудниками весомые доказательства того, что в
центре Млечного Пути находится сверхмассивная черная дыра. Оба астронома
наблюдали звезды, обращающиеся вокруг центра Галактики и пришли к
одному и тому же выводу независимо друг от друга.\\\
- Re: Черная дыра
(А.П. Васи,
7.02.2012 16:42, 2.2 КБайт)
http://www.popmech.ru/article/10479-dyira-kak-vyiklyuchatel/page/4/
\\\Скорость рождения новых звезд в некоторых далеких галактиках так велика, что процесс этот называют
прямо вспышкой
звездообразования. Процесс этот, однако, лишь временный, и довольно скоро прекращается и судя по всему, виноваты в этом могут бытьсверхмассивные
черные дырыв центрах этих галактик.\\\
Вот тоже статья наполненная идиотизмом, и желанием
не съесть так по-надкусывать.
Это яркий пример того
до чего доводит сюсюканье
и потокательство. Вместо того чтобы открыто сказать
что мол - пшел вон дыбил с такой статьёй
в которой всё непонятно и отсутствует
смысловая
взаимосвязь, - так так никто не пишет в комментариях,
а автор думает что пипл хавает, и ему нравится -
и автор будет писать следующую статью с ещё
большим
идиотизмом и нескладушками.
А в нормальном и здравом виде статья бы выглядела
следующая -
обнаружили короткие и яркие вспышки, звездо-образование
или звездные вспышки неизвестно, под ни одну из теорий
не подходит, ни в какой из известных теорий подобный случай
не описывался.
Кстати о черных
дырах они тоже мямлили, понадкусывали
- в стиле мол, что если у какого-то следующего писателя будет
нешто подобное в припадке гениальности, так пусть он мол знает
в нашем припадке бессознательного идиотизма было впервые.
Это пипец, но пипл хавает астрономам нравится, мне смешно.
- Re: Черная дыра
(А.П. Васи,
12.02.2012 14:35, 2.7 КБайт)
Ответ #154 : Вчера в 16:04:25
А теперь Вы нам расскажите, как в законе Хаббла V=H*R проявляются квантовые
свойства фотона
полагаю - никак. В этом и проблема на мой взгляд.
А теперь Вы нам расскажите, как закон Хаббла важнее и выше каких-то там квантовых свойств
фотона.
Полагаю, закон Хаббла в рамках данной темы просто важнее и выше, каких-то там квантовых свойств фотона.
И
пока Вы не объясните, как в законе Хаббла проявляются квантовые
свойства фотона, здесь нет смысла говорить об этих квантовых свойствах.
Ответ #183 : Сегодня в 12:59:49
Станислав Кравченко, внятный
ответ дайте, пожалуйста. Не просто предложение со словами "фотон" и
"закон Хаббла", а внятный ответ. Прекрасный случай показать другим
пример адекватного физического подхода.
--------------------------
Модератору в моск ударило желание не выглядеть
идиотом, а самый грамотный релятивист, затупил по полной,
и в итоге
задали дилетанту вопрос суть которого в том
почему релятивисты когда хотят, а когда не хотят и в некоторых случаях
применяют одни физические свойства, а на другие
забивают,
а когда им надо для чего-то другого они на тоже самое
чихать хотели а акцентируются на другом.
Вот и требуют от дилетанта им объяснить почему
они иногда бывают
больные на всю голову, и просят их ввести в состояние здравомыслия,
точнее сказать вывести из состояния идиотизма.
Вот такая жестокая
селяви.
- Re: Черная дыра
(А.П. Васи,
12.02.2012 15:24, 2.3 КБайт)
Всё равно слово фотон с физической точки зрения
простым физическим опытом - сливается в канализацию физики,
а тот кто его применяет - будет
топтаться на месте
ибо не проводит физический анализ используемую
физическую сущность, а верят определениям,
сказал например один математик что свет состоит
из частиц,
так сразу лохи и зарукоплескали и поверили на слово,
математиками высосанным из пальца выдумкам ради
подтверждения своих теорий нужны, а лохи думают
что математики пальцем в небо попали, и что физика
такая как математики придумали, и потом начинают
соединять выдуманную математику с реальной физикой,
и не понимают почему они занимаются одним и тем-же
столетиями - да удел недалёких.
-------------
Как я ранее писал - фотон - не имеет физического смысла,
- обосновать это, - было легко.
Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а
говорится что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою скорость что
наблюдается например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица которая потеряла скорость, просто так взять и
при вылете из стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами. Так что фотон
как частица - выдумка чистой воды.
Вывод -
в пространстве распространяются колебания среды, и световое
излучение не движется а образуется от взаимодействия колебаний
среды и материала, как в 1800 году говорил
Томас Юнг.
Так что все что написано в астрофизике без учета среды - к
сожалению не правильно.
- Re: Черная дыра
(А.П. Васи,
12.02.2012 15:31, 469 Байт)
Из предыдущего следует что ни один релятивист
не может применять для красного смещения фотон
не учитывая то что он частица, и скорость полета
частицы определяет
скорость света, и не использовать
фотон как частицу - они не могут. Так как
только для среды задержка света в пространстве
может объясняться скоростью распространения
возмущения в среде. А у релятивистов среда
пустая, там нет ничего, и фотон летит как частица.
- Re: Черная дыра
(А.П. Васи,
12.02.2012 18:24, 2.9 КБайт)
\\\Полагаю, закон Хаббла в рамках данной темы просто важнее и выше, каких-то там квантовых свойств фотона.\\\
Расскажу правильный ответ на
этот вопрос, -
Изначально был общепринятый
эфир, на основании колебательных свойств света в
эфире аналогичных звуку в воздухе Томас Юнг объяснил
интерференцию света на двух очень близко расположенных
щелях. В связи с тем что например солнечный свет
проходил через щели, и было место где накладывалось
изображение солнца от двух близко расположенных щелей.
Опыт когда рисуют точечный источник света, а расстояние
между щелями больше диаметра источника
света - не корректный,
он только на рисунках, на практике он не возможен, так
как световые колебания не искривляются на щелях, свет
проходит сквозь щель
прямо. Этому подтверждение
школьный опыт по физике, когда делается маленькая дырка
и берется черный ящик без задней стенки и калька,
в черном ящике располагается
напротив дырки калька,
и изображение получается перевернутым,
и если сделать рядом еще одну дырку, получится
два изображения перевернутых, которые наложатся
друг
на друга - это и называется интерференция.
Так вот, после этого надо было сказать что объяснение интерференции
Томаса Юнга не корректно, и опровергнуть,
чего не было сделано.
Просто за-постулировали для пустоты что движутся световые
частицы. За-постулировали так за-постулировали, но появился
нюанс который
не решается для частиц, так как надо объяснить
интерференцию для солнца на двух щелях на расстоянии например
3мм между щелями. И что , и то что для фотонов надо
придумывать
дополнительные свойства, на уровне потенциала, то-есть фотоны
будут плюсовые и минусовые, при этом все пройдет.
Но здесь возникает следующий нюанс,
если частица со знаком
плюс или минус то они должны отклонятся
магнитным полем, - если поднести магнит к лучу,
например минусом то плюсовые фотоны должны
притягиваться
к магниту а минусовые отталкиваться, то-есть луч расширится,
- чего не наблюдается - вот такая жестокая селяви.
И что в итоге получаем
для красного смещения или закона Хаббла,
аж ничего, так как если расширяется, то должна уменьшаться
скорость фотонов - это невозможно так как это повлияет на
скорость света, а скорость света за-постулирована стабильной,
и не зависящей ни от чего. Что делать релятивистам? объяснять
то надо, остается через потерю напряженности
фотонов,
точнее электро-потенциалов, но дело в следующем в
этом случаи всё равно не может изменится частота, может
изменится только амплитуда разности, а
частота останется.
Вот и продолжают огород городить, и очень не хотят при расширении
считать что фотоны как частицы должны скорость менять,
- с моей точки
зрения - шикарный самозаклин от математиков.
- Re: Черная дыра
(А.П. Васи,
13.02.2012 1:12, 1.6 КБайт)
У модератора моск поплыл по полной, или старость
своё берет.
-------------------------------
Ответ #203 : Вчера в 17:24:20
Станислав Кравченко, я жду обоснования этого утверждения:
Вернемся к теме - интерпретация космологического красного смещения.
В
этом вопросе нельзя игнорировать тот экспериментальный факт, что фотон есть квант действия.
Не
его отдельных фрагментов, а целого утверждения, со всеми нюансами. В
частности, почему фотон -- квант действия, а не просто квант. Если
следующее Ваше сообщение не будет таким обоснованием, доступ на форум
Вам будет закрыт на какое-то время.
---------------------------------
Повторяю для обторможенных релятивистов - таки да, по Вашим
диффективным
теориям у Вас получается что фотон это квант действия,
по той причине что скорость фотона -константа, а сам фотон есть частица.
Фотон не может по релятивистским
теориям лететь медленно или стоять.
- Re: Черная дыра
(А.П. Васи,
13.02.2012 1:29, 409 Байт)
И модератор забанил посетителя за то что релятивисты тупят в физике,
особенно тормозит модератор.
Модератору надо почитать постулаты релятивизма, может
он
и поймет весь идиотизм релятивизма.
Вместо того
чтобы за релятивистские парадоксы посетителей банить
надо лучше физику учить, - хотя как мы видим на данном
скандале что моск математика физику не воспринимает в принципе.
- Re: Черная дыра
(А.П. Васи,
13.02.2012 15:46, 2.3 КБайт)
А теперь я посчитаю на сколько получается
разница при определении размеров звезд
методами красного смещения и Хаббла.
--------------------
Удалённость
Солнца от Земли, 149,6 млн км
диаметр Солнца = 1 391 000 километров.
А теперь посмотрим как недалёкие астрономы
даже обладая высококачественной
техникой
делают выводы о размере SN1987a c
большими перегибами, чувствуется что здравый
смысл они положили на полку, но зато в теории
вписались.
http://planetologia.ru/sverhnova/1332--qq-sn-1987a.html
\\\Располагаясь на расстоянии 168 тыс. световых лет от
Земли в галактике Большое Магеллановое
облако, сверхновая
SN 1987A дает ученым детальную информацию о том, как
доживают свои дни большие звезды. Звездой-предшественником
SN 1987A был голубой сверхгигант
Sanduleak -69 202 с массой
около 17 масс Солнца.\\\
\\\Они изучали взаимодействие образовавшихся от взрыва звезды
диаметром около 9,6 триллионов километров
колец газа,
окружающего сверхновую.\\\
Так вот, я думаю что размер предшествующей звезды был
два диаметра солнца(17 масс Солнца), после взрыва форма
звезды изменилось,
она приобрела дискообразный вид, диаметр диска с краёв
у которого происходят выбросы - после взрыва размер образовавшегося диска
с выбросами
по краям равен два с половиной диаметра солнца.
Диаметр диска с выбросами по фотографии в два раза меньше
диаметра колец и в трактовке современной парадигмы,
следовательно диаметр звезды в форме диска с выбросами
по краям от астрономов в парадигме равен 4.8 триллионов
километров.
Вот что у меня подучилось
"диаметр Солнца = 1 391 000 километров"
два с половиной диаметра солнца и равно 3.47 млн. км.
А у тех астрономов даже не 4.8 миллиардов километров,
- диаметр что в тысячу раз было бы больше моего анализа,
у них в миллион раз
размер больше не моего расчета - а в миллион раз больше
здравого смысла.
И смешно смотреть на эту клоунаду,
и о каких мелких вопросах вращения можно рассуждать
при ошибке на расстоянии 168 тыс.световых лет в - миллион- раз,
то
на сколько они могут ошибаться со своими зетами
для высосанных из пальца фотонов на больших расстояниях.
- Re: Черная дыра
(О. Е. Коробейникова,
14.02.2012 18:58, 53 Байт)
Я дала ссылку на Ваш сайт.Ничего. На тему Созвездия..
- Re: Черная дыра
(А.П. Васи,
15.02.2012 21:56, 460 Байт)
http://elementy.ru/lib/430551
Рисунок 1.
А вот за такие вещи я считаю что физиков фабрикующих
такие рисунки без опытов по которым они проводились
надо
лишать званий и запрещать пожизненно преподавательскую
деятельность, и работу в области физики.
Это ж надо до чего додумались, рисуют и им нас
рать что
это обычный лохотрон, они считают что это хорошо,
а пипл хавает оптики и астрофизики довольны, а мне смешно.
- Re: Черная дыра
(А.П. Васи,
15.02.2012 22:09, 804 Байт)
По большому счету астрофизику и физику проще
простого вылечить от идиотизма, лечится это при помощи
врачей , просто достаточно чтобы был закон по которому
физик или астрофизик обязан проходить реферирование
у психиатра своих статей, и если психиатр не понял
изысков физиков и астрофизиков - то это не незнание
и непонимание физики психиатром, а это скорее того
что физик или астрофизик взялся за задачу которая
превышает умственные способности автора,
или автор
заврался по самое дальше некуда,
или автор имеет отклонение.
А так что получается везде есть отбор, а в физике и астрофизике
кто напишет больше статей тот
и крассава, а то что статьи
переполненны идиотизмом и нестыковками так это норма,
ибо это ненаказуемо а наоборот поощряется.
- Re: Черная дыра
(А.П. Васи,
15.02.2012 22:18, 2.9 КБайт)
Ну ладно ... с ним как говорится отказались от
среды придумали фотон, а сколько ума надо чтобы
формулу фотона написать, и от формулы фотона
плясать, а не
хотро жо пить , мол хочу волновые
свойства эфира применяю, хочу эффект Доплера
(который изначально автором был для эфира придуман)
применяю, а хочу и корпускулярный
фотон применяю,
- я не могу понять цинизм ситуации, когда псевдо физики
сами выбирают и решают
что им применять и когда, как говорится а не сильно
ли
обнаглели, если сказали что скорость света константа,
так и держитесь за неё обеими руками, и скажите честно
что расширение пространства противоречит уже этой
ситуации, а то им на всё ..., вижу только желание
... мозги всем подряд и обвинять
в этом других.
|
|
Re: Черная дыра
|
12.02.201215:35 |
|
Ответ #154 : Вчера в 16:04:25
А теперь Вы нам расскажите, как в законе Хаббла V=H*R проявляются квантовые
свойства фотона полагаю - никак. В этом и проблема на мой взгляд.
А теперь Вы нам расскажите, как закон Хаббла важнее и выше каких-то там квантовых свойств
фотона.
Полагаю, закон Хаббла в рамках данной темы просто важнее и выше, каких-то там квантовых свойств фотона. И
пока Вы не объясните, как в законе Хаббла проявляются квантовые
свойства фотона, здесь нет смысла говорить об этих квантовых свойствах. | |
- Re: Черная дыра
(А.П. Васи,
18.02.2012 1:11, 1.6 КБайт)
Смотрю что в практических вопросах физики
модераторы оказались некомпетентны
и ведут себя тише воды, периодически вылазят
естественно позорятся, и затыкаются,
Вибе вообще
заткнулся - это ему не из-за спины с дубиной нападать
на правах модератора, и Вибе в силу своей некомпетентности
в физике чтобы не опозорится
никогда не высказывал
мнение по вопросам, так вот форумы набрали обороты с практическим
оттенком.
Что могу сказать с одной стороны хорошо, с другой
стороны - у неопределенного поиска не может
быть случайной цели,
она должна быть продуманна и спроектирована,
должна быть модель, а
ещё с третьей стороны - рекомендую вменяемым не тратить
своё бесценное время по той причине
что я на мембране
обсуждал эти вопросы 10 лет назад, и я из тех кто
проходит дорогу так - что по ней второй раз ходить
не надо, в отличие от релятивистов
- которые одни и те-же
вопросы решали сто лет и остались там-же - в начале пути.
Свет и пространство и о скорости света
Рекомендую - читать надо внимательно никуда не торопясь
от начала и
до конца, может показаться что там много лишнего,
на самом деле это не так - успехов.
- Re: Черная дыра
(А.П. Васи,
18.02.2012 1:15, 183 Байт)
http://www.astronet.ru/db/forums/1244628
"Свет и пространство и о скорости света."
В предыдущем посте переход не
правильный.
- Re: Черная дыра
(А.П. Васи,
18.02.2012 11:58, 1.4 КБайт)
http://www.astronomy.ru/forum/index.php/topic,92644.msg1861215.html#msg1861215
Вообще-то неплохо было бы разделять электромагнитное излучение по типу
происхождения.
Зачем?
----------------------------------
Я в принципе рад что не общаюсь на том форуме, это форум
с диктатом
гнид. ... они-же модераторы.
Модераторы там общяются как цари, и им все
посетители форума должны и обязаны как земля колхозу.
Я могу обосновать.
Вот гандольер Вибе задал вопрос, на нормальном форуме
его с таким вопросом послали бы на ....
На нормальном форуме впереди вопроса идет обоснование
вопроса.
Мол я вот считаю что то-то то-то разделять не логично, по причине
такой-то. А здесь что получается что дыбил в данном вопросе
тупит, и в данном
случаи требует у специалиста
провести ему бесплатную лекцию по тому вопросу в котором
он дыбил. Собственно эти вопросы от модераторов и тормозят
форум, по
той причине что человек думает над своими вопросами
а потом он должен отвлекаться и думать о том что на
сто восемьдесят градусов отличается от того чем он сейчас
занят,
специалист отвлекается и теряет настрой.
- Re: Черная дыра
(А.П. Васи,
19.02.2012 14:10, 1.3 КБайт)
Слесарь-сантехник
\\\Вот маятник - универсальный прибор связывающий понятия
массы, пространства и времени...\\\
Вибе \\\Не многовато чести маятнику? А если его пружиной заменить?\\\
Слесарь-сантехник
\\\
Получится пружинный маятник!
Колеблющийся то как маятник, то как груз на упругом подвесе...\\\
Вибе \\\...длина которого изменяется. Можно ли сказать,
что пружина "расширяется" в процессе её колебаний?\\\
Вибе \\\Слесарь-сантехник, я прошу аргументировать свои высказывания, а не выдавать их в виде аксиом.\\\
А
вот за такое незнание физики профессорских званий лишить Вибе просто необходимо,
я бы по крайней мере своему ребенку не разрешил бы у него учится в связи с проф непригодностью
профессора Вибе.
- Re: Черная дыра
(А.П. Васи,
19.02.2012 18:08, 817 Байт)
Ответ #233 : Сегодня в 17:34:02
На минусе батарейки накапливаются электроны,на плюсе-позитроны.
Кто там спрашивал, где искать антиматерию? Вот она -- в любой батарейке на плюсе.
---------------------------
И Вибе башню снесло не по детски.
- Re: Черная дыра
(А.П. Васи,
24.02.2012 3:41, 932 Байт)
ЖПС задействовали для точности, вот как
в душу гадят и не стесняются, думают что вокруг лохи
а они великие лохобои.
Для замера
расстояния между точками достаточно ВЧ кабеля
аналогичного для ТВ, чтобы узнать скорость в кабеле нужен
генератор импульсов, и осциллограф. С выхода генератора
импульсов,
который формирует короткие импульсы с большой скважностью,
подается импульс на один конец кабеля, и одновременно на вход
внешней синхронизации
осциллографа, и на осциллографе определяется
задержка кабеля.
И если есть источник событий и удалённый объект, то зная время задержки в
кабеле - производится
синхронизация.
- Re: Черная дыра
(А.П. Васи,
24.02.2012 22:40, 1.1 КБайт)
Эффект Вавилова Черенко́ва (излучение Вавилова Черенкова)
свечение, вызываемое в прозрачной среде заряженной частицей, которая
движется со скоростью, превышающей фазовую
скорость распространения света
в этой среде. Черенковское излучение широко используется в физике
высоких энергий для регистрации релятивистских частиц и определения их
скоростей.
--------------------
Вот ищут ответ на это излучение, а его искать не надо,
оно было всегда. И со скоростью превышающую
скорость света. Физики
физики не знают.
Надо просто взять и сказать мол извините повелись
на релятивистский лохотрон который науке ничего не дал,
даже нет методов и приборов для
измерения релятивистских
эффектов.
Я лично не вижу ничего зазорного, с кем не бывает
лучше спустя 100 лет чтобы моск осознал, чем вечно обещать что
все совпадает - только надо поставить очередной опыт чтобы определить
область применения.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 1:52, 1.4 КБайт)
Например,
закон всемирного тяготения Ньютона приемлем (но не адекватен для белее,
чем двух тел), поскольку позволяет решать почти все нужные задачи
"через ухо" теории возмущений.
Я
часто применяю закон тяготения Ньютона в задачах для непрерывной среды
(для бесконечного количества тел). И не использую при этом теорию
возмущений. Что я делаю неправильно?
-----------------------------
Вот как бывает, гандольер использует в расчетах свойства плотности эфира,
при этом его запрещает, а пропагандирует
пустоту, и при этом
спрашивает - почему когда он хитрит, то почему он при этом не
гандольер в его глазах, а другие когда говорят о среде - они дураки,
так
как среды в пространстве нет у релятивистов.
Цинизм у гандольера в данном случаи на качественно высоком уровне.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 10:27, 14.1 КБайт)
Ответ #84 : Сегодня в 09:13:42
Не следует ли из него, что абсолютно все наши приёмы являются искусственными?
Искусственность
чаще всего понимается не как модельность, а как подгонка под
необходимый результат. По крайней мере я его применил именно в этом
смысле. Например, в рассматриваемом мысленном эксперименте А-В, узнав,
что С по своим часам на полёт от А до В затратил 1 секунду, заявили:"Это
у него часы замедлили свой ход". Это не модель, отображающая
действительность, а искусственный прием, так как из физических
соображений ясно, что часы не могли замедлить свой ход от того, что
где-то кто-то летит с большой скоростью по отношению к этим часам.
-------------------------------------------
Ответ #85 : Сегодня в 09:22:30
из
физических соображений ясно, что часы не могли замедлить свой ход от
того, что где-то кто-то летит с большой скоростью по отношению к этим
часам.
Так они и не замедлили. С внимательно следил за ними; он подтвердит.
------------------------------------------------------
С одной точки зрения возможен цинизм.
А с другой точки зрения несчастный вибе, занимается физикой
и в физике он не полный ноль он в ней существо бестолковое.
---
Для решения данного вопроса для физика особо даже не
надо прилагать умственных затрат,
этот вопрос относится к вопросу или вопросам
носящим
общее название - синхронизация.
Рассматриваемый пример один из случаев синхронизации,
учитывая что задача изначально ставится не корректно,
она всё равно
решается однозначно.
---
Изначально
надо определится с названиями, - сравнения и измерение.
Сравнение
- когда я измеряю длину линейкой, я просто сравниваю размерность одного с
аналогичным.
Измерения
это когда из двух разных сущностей, но известных количественно определяется
третья сущность.
Например,
- напряжение через ток и сопротивление, скорость через длину и время.
Теперь о пространстве - получается два метода определения его величины, один
вариант - просто линейкой, второй скоростью света.
Линейкой
логично и просто.
Скоростью
света - получается что пытаемся приравнять измеряемую величину - зависящую
от времени, (и точности часов их считающих) линейки измеряющей расстояние (точнее
свойств линейки и её подверженности деформациям), и скоростью распространения
электромагнитного излучения.
Что
собственно получается - при измерению пространства, скоростью света по
сравнению с приравниванием пространства к линейке.
У
нас получается расстояние длинна,
только мы задействовали часы линейку, и электромагнитное излучение.
Для измерения у нас есть три сущности
скорость время и расстояние, и есть свойство пространства в котором распространение
электромагнитных колебаний равно некоторой скорости которую называют скоростью
света.
Здесь
надо понимать следующую ситуацию, - что с одной точки зрения можно сказать, -
что эта скорость быстрая но можно сказать что она медленная. Но в любом случаи
пространство для колебаний является линией задержки, в которой распространяется
сигнал. Вот, а здесь уже получается что пространство состоит из чего-то. Это
происходит потому что, пространство мы определили измерять в метрах.
Для
светового излучения пространство проявило ещё одно своё свойство - задержка
светового луча. Следовательно - пространство
заполнено веществом, которое задерживает световой сигнал, аналогично тому как в
воздухе или воде задерживается звук. Здесь можно немного поразмыслить о
скорости сигнала в средах, в воде звук во столько раз быстрее - чем в воздухе,
во столько на сколько ближе расстояние между молекулами в воде - чем в воздухе. Из чего следует - если
поделить скорость света на скорость звука в воздухе мы получим величину во
сколько раз ближе частички среды,
которым заполнено пространство по
сравнению с частицами воздуха.
На самом деле скоростью
света измерять пространство нельзя, потому что это не правильно, так как
скорость света за секунду не является мерой длинны.
Это
всё равно, что говорить, - что от Киева до Москвы три тысячи 75 секунд скорости
звука.
---
Сложение со скоростью света
и вычитание, при движении
объектов.
Есть объект, который относительно другого объекта может двигаться.
Есть скорость света, с которой
распространяется световое излучение в пространстве.
Получается - что нужно уйти от генератора излучения на исследуемом, а генератор
всё равно нужен.
Здесь принимаем волевое решение, генератор располагается на условно неподвижном
объекте.
На том объекте который движется будем располагать простое зеркало.
В качестве источника выбираем световой луч модулированный с частотой 300МГц,
что в пространстве будет из себя представлять одно колебание на метр длинны,
точнее один период на метр.
Устанавливаем на автомобиле зеркало , на взлётной полосе устанавливаем стенд с
световым генератором 300МГц с узко направленным лучом, и приёмник с
частотомером.
Первый опыт заключается в том что автомобиль расположен на расстоянии 1км, и
неподвижен, принимаемая отраженная частота будет равна передающей.
Опыт второй - автомобиль едет к стенду со скоростью 20метров в секунду, о чудо
частота увеличилась на 20Гц. Причина связана с тем что при движении к
источнику, машина проезжает на 20 метров ближе, а поскольку у нас в одном
метре один период колебания, то частота при приближении со скоростью 20 метров в секунду
увеличится на 20Гц.
Опыт второй машина удаляется от стенда со скоростью 30 метров в секунду, и частота
принимаемая от зеркала автомобиля ниже передающей на 30Гц.
Из чего следует, что свет проявляет свои свойства по отношению к пространству,
которое и задерживает свет.
Пространство для света является линией задержки.
Если есть в чем, - свету распространятся и задерживаться, то свет находится в
среде какой-то, аналогично звуку в воздухе.
По той причине что данное сложение и вычитание частоты можно повторить применив
вместо светового источника мощный динамик а на автомобиле установим частотомер
с микрофоном.
Берём частоту 300Гц, у нас получается при скорости звука 300метров в секунду,
одно колебание на метр.
Автомобиль приближается к динамику со скоростью 20метров в секунду, частота
принимаемого звука в автомобиле больше на 20Гц, после чего автомобиль движется
от стенда со скоростью 30метров в секунду и частота принимаемая в автомобиле,
ниже на 30Гц.
А звук точно движется в среде, - это воздух.
Вот я собственно и показал метод сложения скоростей в сравнении с аналогичным.
Могут быть некоторые неточности со скоростью света в воздухе, но это не
принципиально в данной задаче.
Естественно можно использовать данный метод с расположением зеркала под углом 45
градусов, при этом располагаются приёмник и генератор в разных местах, и
передвигается зеркало к и от приёмника, или к и от генератора.
Что я считаю недостатком данного опыта?, - особых технических недостатков не
вижу, так как опыт со световым лучом будет результативным и при около световых
скоростях.
Естественно данный опыт не рекомендую проводить самостоятельно без консультации
со специалистами по правилам соблюдения техники безопасности.
---
Общая идея предыдущих опытов в наглядности
того, что при
движении автомобиля к объекту или от него, частота принимаемая на автомобиле, и
отраженная им частота, будут одинаковыми, следовательно если автомобиль
посредине между двух генераторов, которые работают на одинаковой частоте, то
если автомобиль будет перемещаться между ними по прямой линии между
генераторами, то сумма частот делённая на 2 всегда будет равна исходной частоте
генератора.
---
Естественные выводы которые получились,-
если
пространство измерять в метрах, то у
пространства обнаруживается свойство по
задержке электромагнитных излучений.
---
Вот собственно используя базовые понятия о электромагнитном
излучении можно более детально перейти к световому излучению.
Световое излучение - колебание зарядов
в среде вокруг
друг друга примерно с частотой 100ТГц, при их движении
в среде со скоростью которая определяется плотностью среды.
Надо узнать сколько
колебаний в метре у света, поделим
100ТГц, на 300 тысяч км в секунду, и поделим ещё на 1000,
и узнаем количество в метре = 333 333.
Или - 333 колебания на
миллиметр.
Теперь надо понять что представляет из себя интерференция.
Здесь всё просто. Световой луч разделяется на два луча,
полу прозрачным стеклом,
внутри которого слой металла,
который пропускает часть лучей а другую часть отражает,
по причине того что заряды фотонов при взаимодействии вращаясь
летят,
и так как вращение их хаотичное, то подлетают к слою
по разному, часть ударяется одновременно плашмя, и отражается,
а часть проходит между атомами металла.
После чего из двух лучей с помощью зеркала и полупрозрачной
линзы востанавливается луч.
Здесь получаются кольцевые волны, о причине того что у нас
разная
длинна лучей, и фотоны имеют хаотичную раскрутку.
Если в одно плечо разделённого луча ввести сосуд с водой
- опыт Физо, и вода будет двигаться с некоторой
скоростью, то у нас
кольца начнут сходится и расходится.
Если я возьму фонарик и буду приближаться к стене,
со скоростью 10м/с, и при этом
буду
светить на стену, то частота принимаемых сигналов
на стене будет 333 333 умножить на 10, то есть на 3,333МГц,
больше чем в фонарике, если с такой-же скоростью буду
удаляться,
то на такую-же частоту сигнал будет меньше.
Здесь надо понимать причину, причина не в нарушении частоты генератора,
и частотомера, причина
в том что когда создаются
благоприятные условия для создания фотонов на нити спирали фонарика,
они вылетают в пространство, и движутся в нём,
а частота меняется
потому что последующие фотоны, вылетают
из фонарика в то время когда фонарик меняет своё расположение
в пространстве по отношению к стене, на которой частотомер.
---
Ещё раз внимательно ---
Частота
меняется по причине изменения расстояния между приёмником и передатчиком.
---
Вывод
- данная ситуация определяет единственно возможную физическую ситуацию
для электромагнитных колебаний в пространстве
- эффект Доплера для среды "Эфира".
В вышеизложенном тексте слово "фотон" - ошибка, вместо него
-"свет".
- Re: Черная дыра
(А.П. Васи,
26.02.2012 10:45, 972 Байт)
Естественно со смехом вспоминается опыт от дыбилов в физике,
- световые часы на орбите в которых луч вверх вниз под углом
движется.
Где здесь ошибка недалёких
математиков делающих бессмысленные
в своей беспощадности
шаги в физике.
Ошибка она в том что происходит перепривязка из одной системы координат
к другой в вопросах измерения длинны наклонного луча, так как к длине
луча добавляется длинна перемещения одной системы по отношению
к другой системе, - чего
на практике не то что не существует, а просто
невозможно. А в данном случае невозможное с физической точки
зрения выдаётся математиками за действительность.
В связи с чем релятивистов очень легко нагнуть, простым поворотом
светового генератора луча,
световой генератор достаточно повернуть на 90градусов,
и летит
вся наглядная агитация.
Точнее опыт нагибает ещё круче релятивистов, по той причине
что рулит эффект Доплера для среды.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 11:03, 1.2 КБайт)
Вспомнился ещё один опыт для математиков в физике,
опыт с поездом.
В разных вариациях муссируется эта ситуация.
Есть перрон, на перроне есть двое часов,
часы идут одинаково.
Часы поставили в центре перрона, на краю платформы,
одни часы поставили на высоте один метр, а вторые часы
на высоте два метра.
На
поезде есть два сачка, в первом вагоне сачок ловит на высоте
один метр, в последнем вагоне на высоте два метра.
Летит поезд груженный релятивистами вдоль
перрона,
и проезжая вдоль перрона первый вагон ловит сачком
часы - математики записывают показания первых часов,
потом сачком ловятся вторые часы и математики
записывают
показания вторых часов, зная длину между поездами
они определяют скорость.
Но суровые альты для релятивистов решили поставить
часы так как
релятивисты ставят наблюдателей,
и суровые альты разнесли часы на края платформы,
- и релятивисты оказались в шоке, поезд проезжал
со световой скоростью,
так как показания часов не
отличались.
А потом суровые альты часы поменяли местами,
и релятивисты сделали вывод математический
что движутся в обратную
сторону - вот такая жестокая
математическая селяви.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 11:20, 182 Байт)
http://physics.ru/courses/op25part2/content/chapter4/section/paragraph2/theory.html
- Re: Черная дыра
(А.П. Васи,
26.02.2012 11:59, 1.5 КБайт)
Ответ #559 : 05.09.2009 [19:31:35]
Что я такого сказал? Не удаляйте без обосновываний. Если я не прав, скажите в чем. Правила
форума я не нарушал.
Вы
нарушили правила раздела, опубликовав смелую гипотезу об эволюции
спирального узора и галактики в целом, не сопроводив ее
"обосновыванием".
---------------------
Вот я все понимаю, но не понимаю почему математический клоун всех лечит физикой,
и этот клоун
применяет разные физические случаи для среды и пользуется
ими, и не обосновывает причину того что он использует волновые свойства и свойства
среды, - хотя как
релятивист он этого не то что не имеет права делать,
и уж тем более не должен этим хвастаться, мол все вокруг дураки
а он мол забил на обоснование он просто пользуется,
ему клоуну математику так удобней.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 12:12, 1.0 КБайт)
Ответ #687 : 07.07.2010 [11:26:05]
\\\Вибе
"Вы видите картинку" -- это и есть современная физика
глазами альтов.
Человек видит картинку и начинает делать выводы. Скачает с сайта
фотографию спиральной галактики, помедитирует над ней и начинает писать,
что спиральные рукава явно вылетают из центра галактики. Для не-альта
картинка сама по себе несёт минимум информации.
Интерференция -- это не
полоски, а вполне определённая зависимость интенсивности света от
координаты.\\\
Вот крендель - даже не знает что кроме Томаса Юнга, который объяснил интерференцию
с точки зрения эфира как среды - никто кроме Томаса Юнга
ничего внятного
на планете Земля вот уже 200 лет сказать не может, моска не хватает.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 12:19, 2.5 КБайт)
А вот то что я искал, - избранность тех кто в парадигме,
кто пользуется пусть и неправильными трудами других
релятивистов, те кто за сто лет новой гайки не выточили
в релятивизме - а апломба как у первооткрывателей.
-----------------------------------------------------------------------------
\\\
Ответ #721 : 09.07.2010 [15:38:48]
Рискуя
быть удалённым с форума, выскажу своё мнение. Альт - участник данного
форума, взгляды которого на физические явления не совпадают с взглядами
Д.В.
\Вибе \-
Я об этом писал не один раз, и не только я. Альт -- это человек, который пренебрегает научной методологией.
Это пренебрежение может принимать разные формы, от глобальных ("Братья и
сестры! С научной точки зрения Вселенная есть Бог!") до частных
(например, выдача персональных умозаключений за установленный факт), но
смысл именно в этом. Важно, что это пренебрежение -- неосознанное. Альт
пренебрегает научной методолгией не потому, что она ему кажется
неправильной или он по натуре революционер, нет. Он пренебрегает научной
методолгией, потому что понятия не имеет о её существовании.
Возможно,
я не прав. Своё мнение основываю на недопустимости навешивания этого
неопределённого термина (ярлыка?) на тех, суждения и опыт которых
использован в науке Физика. А их суждения всегда были кому-то
альтернативными. Попасть в их компанию исходя из самооценки - верх
нескромности. Альтернативность суждений является необходимостью. Об этой
необходимости указал Ли Смолин в своей "Неприятности с физикой...".
Положительный эффект альтернативных суждений в их обоснованности. Свои
суждения основываю на признанных фактах, т.е. использую уже признанные
суждения. Даже при этом получаю тук-тук по темечку. Но если не имею
своих альт. суждений, а только сомневаюсь в некоторых уже принятых, то я
альт или не альт?\\\
- Re: Черная дыра
(А.П. Васи,
26.02.2012 12:21, 1.7 КБайт)
Ответ #724 : 09.07.2010 [16:10:04]
Альт
пренебрегает научной методолгией не потому, что она ему кажется
неправильной или он по натуре революционер, нет. Он пренебрегает научной
методолгией, потому что понятия не имеет о её существовании.
Если бы альты были такими тупыми, они бы так не раздражали.
\Вибе\-
Тупость
тут ни при чём. Просто когда я смотрю, например, на токаря у станка, я
понимаю, что у него есть определённые правила работы. Я не знаю этих
правил, но я знаю, что они есть, и понимаю: если мне хочется самому
встать к станку, я должен сначала усвоить эти правила. (Иначе будет в
лучшем случае: "Я технику безопасности как свои три пальца знаю!").
Подобные правила есть и в науке, но кто о них знает? Общественный образ
учёного -- это человек, который сидит в кресле и думает. Поэтому легко
поверить в то, что вот сам сел в кресло, подумал, и уже тоже стал
учёным.
- Re: Черная дыра
(А.П. Васи,
26.02.2012 12:24, 997 Байт)
Нет слов .
---------------------------------------------------------------

Ответ #726 : 09.07.2010 [16:13:01]
Альт - это просто ласковый намек на форумных графоманов.
\Вибе/-
Да нет, почему же. Я сам графоман, что я, не знаю?
- Re: Черная дыра
(А.П. Васи,
26.02.2012 12:53, 1.3 КБайт)
Смеялся, ибо математик занимающийся физикой
думает что он творит науку, а получается цирк на лопате.
---------------------------------------------------------------------
\\\
Ответ #1240 : 15.02.2011 [17:48:53]
Предвижу возражение, мол, воззрений-то как таковых нет. Есть "поток сознания", "литературное
произведения", "фантазия", наконец.
\Вибе\
В
большинстве случаев это так. Бывают, конечно, и исключения. Che,
например. Но в большинстве случаев -- да. И я действительно стараюсь это
подчёркивать, чтобы читатели (в том числе, и незримые) понимали, что
занятие наукой -- это работа, а не сочинение красивых текстов с умными словами.\\\
- Re: Черная дыра
(А.П. Васи,
28.02.2012 10:26, 598 Байт)
Вот это жестко астрономов сделали,
да уж какая парадигма, такое к ней и отношение.
---------------------------------------
\\\Дорогие друзья!
Честь имеем пригласить вас к участию во Всеукраинской научной конференции
Космология и Космонавтика: история и перспективы,
которая состоится в г. Киеве, в НТУУ КПИ18 мая 2012 года\\\
\\\Контакты:
г. Киев, пр. Победы 37, корпус 7, Факультет социологии и права\\\
- Re: Черная дыра
(Маша Ковалёва,
28.02.2012 11:05, 25 Байт)
Квазар - это Чёрная дыра?
- Re: Черная дыра
(А.П. Васи,
28.02.2012 19:55, 10.4 КБайт)
Квазар лично для меня звезда у которой есть
большой выброс или выбросы в пространство,
только луч направлен на нас.
А если луч направлен не на
нас, то это уже другая звезда,
-SS 433- например.
А у черной дыры в авторской трактовке -
излучение
А вот спектр квазаров
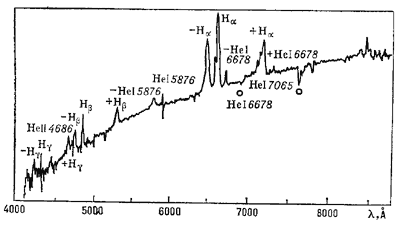
|
Рис. 1. Оптический спектр SS 433. Знаками плюс и минус
помечены подвижные эмиссионные линии Н , Н , Н , ,
Н , Hel. Кружками отмечены
линии, образующиеся , Hel. Кружками отмечены
линии, образующиеся
при поглощении излучения в земной атмосфере.
|
http://www.sdss.org/includes/sideimages/quasar_stack.html

И от себя добавлю, это из моего спора
с модератором поп механики.
----------------------------------
Re: Черная дыра
19.09.201112:38
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg

Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
- Re: Черная дыра
(А.П. Васи,
29.02.2012 11:18, 6.2 КБайт)
\\\Квазар - это Чёрная дыра?\\\
Учитывая нюансы текущей парадигмы которой
по большому счету до лампочки что есть черная дыра,
добавлю
что есть излучение.
Излучения - электромагнитные, это электромагнитные
колебания которые являются изменением плотности эфира
в пространстве аналогично звуку
в воздухе.
Но есть нюансы, если посмотреть ниже приведенную
таблицу то в ней не хватает нейтрино.
Что из таблицы сразу видно и понятно -
то что электро-манитное
излучение заканчивается на
ультрафиолетовом диапазоне, и этот диапазон является
переходным.
Последующие излучения - это уже не колебания среды,
это
осколки атомов, это летящие частицы с определённой
скоростью, а выражение \\\4 энергия фотона. \\\
следует понимать как напряжение которое прилагалось
для ускорения частиц атомов, с последующим разгоном
и ударом о мишень и в результате удара получились осколки
атома.
И нейтрино это осколки частиц
эфира.
-------------------------------------

Классификация диапазонов спектра электромагнитного излучения
по-английски. Колонки: 1 (чёрная) аббревиатуры обозначения диапазонов,
2 частота, 3 длина волны, 4 энергия фотона.
Материал из Википедии свободной энциклопедии
- Re: Черная дыра
(А.П. Васи,
29.02.2012 11:33, 916 Байт)
http://www.pravda.ru/science/eureka/hypotheses/29-02-2012/1109473-neitrino_falsh-0/
\\\Однако позже выяснилось, что сам по себе осциллятор не виноват. Дело в
том, что оптоволоконный кабель, подающий сигналы от GPS к нему,
оказывается, оба раза был просто неплотно вставлен. Возникшее
электрическое сопротивление в месте соединения приводило к задержке
сигнала. В результате время движения нейтрино, согласно расчетам,
уменьшалось, а его скорость, соответственно, увеличивалась. Проще
говоря, сенсационные результаты в экспериментах OPERA обеспечили
техники-разгильдяи, которые просто не удосужились проверить, всели в
порядке.\\\
Достаточно смешно, особенно -\\\Дело в
том, что оптоволоконный кабель, подающий сигналы от GPS к нему,
оказывается, оба раза был просто неплотно вставлен. Возникшее
электрическое сопротивление в месте соединения приводило к задержке
сигнала.\\\
- Re: Черная дыра
(А.П. Васи,
29.02.2012 13:10, 2.6 КБайт)
Вот если почитать что говорит звездо-бол по поводу
излучений - то из его текста следует что - читатель самостоятельно
должен во всём сам разобраться, и модель
себе построить.
Как мне не нравятся такие клоуны которые пишут
наукообразные статьи в которых полезная информация отсутствует,
и задача этих статей
- показать как автор статьи много
знает - но эти знания дутые, из разряда - надувательство.
------------------------------------------------------------------------------------
http://elementy.ru/lib/430399#radiowaves
От радиоволн до гамма-лучейПредставление
оединстве физических законов
позволяет сделать очень важное допущение. Пусть мы не можем, например,
проникнуть внедра звезды или вядро галактики, чтобы непосредственно
увидеть происходящие там процессы. Но мы можем логически вывести
эти процессы, наблюдая производимый ими результат. Результатом этим
вподавляющем большинстве случаев оказывается свет, точнее
электромагнитное излучение вочень широком диапазоне частот, которое мы
непосредственно и регистрируем. Всё остальное помимо излучения
представляет собою продукт теоретической интерпретации наблюдений, суть
которой заключена для астрономов впростой формуле ОС, тоесть
наблюдаемое (observed) минус вычисленное (computed). Чтобы понять природу какого-либо объекта, нужно построить его модель,
тоесть физико-математическое описание происходящих внём процессов,
азатем спомощью этой модели вычислить, какое излучение должно
рождаться вэтом объекте. Дальше остается сравнить предсказания модели с
результатами наблюдений и, если сравнение оказалось не вполне
убедительным, то либо изменить параметры имеющейся модели, либо
придумать новую, более удачную.
----------------------------
И этот математический клоун ещё лечит физиков.
За сто лет релятивисты не придумали
никакой модели, чего
они ждут, когда перестанут мечтать, хотя с другой точки зрения,
физические модели могут придумать физики, а математикам
естественно
такие модели не будут нравится, так как
математикам при адекватной физ модели вход в физику
будет закрыт на вечно.
- Re: Черная дыра
(А.П. Васи,
29.02.2012 20:17, 1.2 КБайт)
Ответ #486 : Сегодня в 18:54:20
Предложение
- открыть отдельную ветку - и там пусть все альтернативщики друг с
другом общаются и сами отвечают на собственные вопросы.
А как Вы их туда загоните

-------------------------------------------------
Вот модератор ..., как правило если открывается
такая ветка то всегда вопрос в другом, как
с альтернативной ветки выгнать релятивистов с их бредом.
- Re: Черная дыра
(А.П. Васи,
1.03.2012 13:12, 2.3 КБайт)
Ответ #511 : Сегодня в 11:12:13
то, что ото "рухнет" - вопрос времени, да и не лозунг это.
Прежде
чем говорить об этом, или даже думать-рекомендую ознакомиться пока вас не забанили с Экспериментальные проверки общей теории относительности: недавние успехи
и будущие направления исследований
http://www.mathnet.ru/php/getFT.phtml?jrnid=ufn&paperid=688&what=fullt&option_lang=rus
После ознакомления(а оно сразу отрезвляет) можно тогда и к делу, т.е. обсуждению перейти

-----------------------------------------------------------------------------------
Все эти теории яйца выеденного не стоят, опровергаются в несколько
минут.
1 Заявленное пустое пространство опровергается тем, что оно
обладает свойством, которое выступает линией задержки для света.
Что делает причину
для именно такой скорости света?, -
пространство пустое, то скорость не может быть ограниченна для частиц.
2 Заявленные фотоны как частицы - глупость, лечится легко
-
летит фотон со скоростью света, пролетает сквозь стекло
в стекле снижает скорость света в полтора раза, потом
вылетает из стекла и набирает скорость - так
вот
это не может быть свойством частиц, частицы могут замедляться,
но ускорятся они не могут, следовательно свет аналогичен
колебаниям звука в воздухе.
Вывод - и уже до лампочки все проверки и эксперименты,
так как ошибки глобальные.
Теории господствующей парадигмы -
бесполезный набор формул.
- Re: Черная дыра
(А.П. Васи,
1.03.2012 17:42, 1.9 КБайт)
Старый релятивист обхезался по полной,
перед барышней, - видно что что-то хочет сморозить,
но релятивистский моск привык искать ответы в книжках,
а когда
нет в принципе - на данные вопросы даже определений,
то что он может сказать, он может сделать только умный вид
а по факту выглядит глупее глупого.
Создает
видимость что он мол всё знает,
если бы знал то ответил бы по полной , а на поверку
его знания - голимый порожняк, и он об этом
догадывается.
-------------------------
Ответ #523 : Сегодня в 15:53:39
Нептун, нейтрино, позитрон и многое другое, включая гелиоцентризм, были
сначала только гипотезой на кончике пера теоретиков.
и не только это))
тема называется выше скорости света.
про гравитационное поле - ничего не
известно.
про черные дыры - тоже
про темную материю - тоже
про элементарные частицы- ничего
про зарождение вселенной- ничего
Увы,
это только подтвержает мой мягкий диагноз. 
Вам неизвестно
- согласен, но надо подписывать ИМХО.
- Re: Черная дыра
(А.П. Васи,
15.03.2012 4:12, 986 Байт)
Re: Что такое инерция материального тела?
Ответ #161 : Вчера в 19:48:50
Какова цель экспериментов? Какие возможны исходы и что они будут означать?
--------------------------
Модератор
тупит по полной, всем понятно что на любой теме
если предлагаются опыты, то для того чтобы разобраться
в физических вопросах данной темы.
Математику
не понятно зачем нужны опыты
ели у него и без них дважды два четыре.
Гоните стар пёра, в смысле звездного толкателя из модераторов,
по причине того
что он круче всех на форуме тупит,
если заметили, - все спокойно общаются и всем все понятно,
а модератор постоянно тупит и задаёт дыбильные вопросы.
- Re: Черная дыра
(А.П. Васи,
18.03.2012 14:13, 3.6 КБайт)


Ответ #12 : Сегодня в 13:00:41
А разве на основе планетарной модели можно моделировать многоэлектронные
молекулярные оболочки?
Можно. Но нужно учитывать кулоновское взимодействие электронов.
Структуру молекулы бензола смоделируете?
------------------------------------------------------------
Структуру молекулы бензола смоделируете?
Я
не имею ввиду техническую сторону вопроса - ведь и уравнение Шредингера
одночастичное. Может быть технически смоделировать молекулу бензола
очень трудно. Я хочу сказать, что принципиально учёт кулоновского
взаимодействия работает в планетарной модели. Вечером выложу расчёт для
атома гелия.
----------------------------------------
Ответ #14 : Сегодня в 13:44:27
Может быть технически смоделировать молекулу бензола очень трудно.
А может быть, вовсе невозможно?
-------------------------------------------------------
Я вот думаю что если профессор не понимает что если ему
что-то не дано, то это не значит что
это не дано другим,
для других это вопрос проще простого.
Я думаю что Вибе где не может свою математику применить
то думает что уже всё пипец - и это
невозможно.
Как я рад что я не на этом форуме с модератором
который профессор в математике и лабух в физических
задачах, и конь в пальто в моделировании.
С другой стороны я рад за релятивистов, такие
как Вибе держат это стадо в загоне, что альтов
избавляет от конкуренции.
И я рад что Вибе так релятивистов
строит - крассава.
- Re: Черная дыра
(А.П. Васи,
18.03.2012 20:06, 1.6 КБайт)
Ответ #227 : Сегодня в 14:45:39
Я прошу участников
сосредоточиться на обсуждаемой теме. Тексты с лозунгами и философскими
обобщениями далее будут удаляться без дополнительных комментариев.
---------------------------------------------------
Вот какой идиотизм на самом деле, а
модератор
профессор к этому идиотизму настоятельно серьёзно требует
относится.
---------
И все релятивисты сразу по-впрыгивали в машины времени,
и
нажали на ручник и дали полный задний интеллектуальный
тормоз, и их клинонуло после и понесло назад во времени.
Ждем возвращения, от тех кто побывал до большого
взрыва,
многие уже бывали в первые минуты в первые часы и в первые
секунды большого взрыва.
Здесь уместен девиз "не обманешь - не проживешь".
Совсем скоро лохобои должны вернутся из путешествия в прошлое,
от туда где материи ещё не было, а релятивисты там уже были,
и Дмитрий Вибе ждет возвращения
героев релятивистов
с докладом, на полном серьёзе.
А как я рад за релятивистов, молодцы - они так рискуют путешествуя
в прошлое, надо по нобелевской
премии каждому смельчаку за
такой героизм и самопожертвование давать.
- Re: Черная дыра
(А.П. Васи,
20.03.2012 14:56, 902 Байт)
http://www.computerra.ru/own/wiebe/660411/
\\\Солнечный ветер выдувает вокруг нашей планетной системы гигантский
пузырь - гелиосферу. Внутри неё - межпланетная среда, снаружи - уже
межзвёздная. Именно межзвёздная среда представляет собою тот компонент
Галактики, с которым Солнечная система контактирует непосредственно.\\\
-------------------
Этот релятивистский оборотень, всерьёз взялся писать о среде
в пространстве, - крассава.
Получается все релятивисты дураки что думают что космос пустой,
а релятивист Вибе самый умный, ему до лампочки что релятивисты
постулировали вакуум - пустоту, и отказались от среды.
Здесь есть один вариант Вибе должен на горизонтах
в заголовке создать тему и извинится перед
альтами,
в стиле " Простите отцы "зас ранца" "
- Re: Черная дыра
(А.П. Васи,
24.03.2012 16:55, 1.5 КБайт)
Редкий случай, адекватно рассуждающий человек
на релятивистском форуме, и не забаненный.
Как это модераторы прощёлкали.
------------------------------------------------------------

\Уверяю Вас, никто даже не заметил этой критики. Махисты (лучше,
неопозитивисты) похоронили материализм полностью примерно до 1930 года.
Почитайте внимательно Поппера и Куна они очень хорошие философы и
историки науки.
Современная теоретическая физика по своей
методологии неопозитивистская (Поппер называет ее то ли
технологической, то ли индустиральной, уже не помню, подразумевая, что
для современных теоретиков важно найти окончательные уравнения, но
совсем не важно, каким путем они получены). Не могу сказать, чтобы это
мне очень нравилось, но, во-первых, другого нет, а во-вторых, наука
добилась таких успехов на этом пути, что может быть прав был Фейнман,
что для науки это самая лучшая из методологий (надеюсь, Фейнмана Вы не
обвините в том, что он не знает, что говорит и делает). \-
--------------------------------------------
Так и получилось, формулы сами по себе, - не имеющие
не только физического
объяснения но и физического смысла.
- Re: Черная дыра
(А. И. Неживых,
31.03.2012 20:08, 407 Байт)
В формуле чёрной дыры нет никаких ограничений, которые могла бы принимать масса гравитирующего тела. Согласно этой формуле
наша Земля могла ба превратиться в чёрную дыру радиусом 8,84 мм, а вместо Солнца была бы чёрная дыра радиусом около 3-х км. Отсюда следует вывод, что таких чёрных дыр, которые
описывает так называемая теория, не существует!!!
- Re: Черная дыра
(А.П. Васи,
4.04.2012 18:16, 1014 Байт)
 [PDF] users.kpi.kharkov.ua/koef/Files/pr_c.files/Lab.../2.6_opt(Yung).pdf
[PDF] users.kpi.kharkov.ua/koef/Files/pr_c.files/Lab.../2.6_opt(Yung).pdf
----------------------
---------------------------
Обсуждают героически ботаники на форуме.
С какого-то улья приписали Томасу Юнгу опыт на трёх щелях, когда ясно
же написано что Томас Юнг проделал рядом две дырки иголкой в картоне
и поставил картонку перед солнечным светом.
А совсем недалёкие физики даже не понимают разницу
в разогнанных частицах
и светом - это пипец, - идиотизм в физике.
- Re: Черная дыра
(А.П. Васи,
4.04.2012 18:22, 256 Байт)
Я вообще не понимаю зачем писать то что не возможно,
и мне не понятно какой баран приписывает Томасу Юнгу опыт
на трёх щелях.
Так-же не понятно почему опыт
на двух щелях и солнечным светом
не проходят в школе. Уж опыт дешевле дешевого.
- Re: Черная дыра
(А.П. Васи,
4.04.2012 18:34, 764 Байт)
http://msk.edu.ua/ivk/Fizika/Tushev_Shizika/TUSHEV2/18-2.html
\\\Томас Юнг наблюдал интерференцию от двух источников, прокалывая
на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном
экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие
в другом непрозрачном экране.Интерференционная картина наблюдалась на экране, удаленном
на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т.
Юнг определил длины световых волн.\\\
Текст правильный а ресунок не соответствует тексту.
И здесь какой-то ботаник в физике пририсовал перед двумя щелями
ещё одну, я даже не понимаю
каким надо быть недалёким чтобы не понимать того что эта щель не нужна.
- Re: Черная дыра
(А.П. Васи,
4.04.2012 18:54, 456 Байт)
Итого опыт Томаса Юнга, - используются две проколотые иголкой
дырки в картоне на расстоянии 1мм друг от друга.
Для наведения солнечного луча на маленькие дырки,
проделывалась условно большая
дырка диаметром 5-10мм впереди для того чтобы интерференция наблюдалась
в определённом месте на экране устройства.
-------
Не знаю мне даже не хочется комментировать.
Скажу просто в опыте Томаса Юнга луч на щели не преломляется.
- Re: Черная дыра
(А.П. Васи,
5.04.2012 12:33, 1.0 КБайт)
Цитата Хартиков
Сергей: Если Вы установите детектор
фотонов (то есть такой детектор, который считает фотоны), то он будет
щелкать не во время каждого импульса лазера, а иногда.
Означает
ли это, что в однофотонном эксперименте далеко не каждый испущенный
источником одиночный фотон проникает в одну из щелей и участвует в
создании интерференционной картины?
-------------------------------
Это же надо быть такими недалёкими, это же надо так не понимать физику,
и в итоге
проповедовать вместо физики идиотизм.
---
Простыми словами -
Опыт Томаса Юнга на двух щелях аналогичен наложению двух фотографий
солнца одна на
другую, в результате чего появились темные полосы на фотографиях,
вместо ожидаемого повышения яркости в местах пересечения изображений солнца.
- Re: Черная дыра
(А.П. Васи,
5.04.2012 16:15, 2.4 КБайт)
и более идиотских и необоснованных утверждений при этом я давно
не
встречал.
Приходит некоторый "релятивист провокатор" и задвигает то чего не было
в авторском варианте, он сам придумал
Re: Master Theory (edition 3)\\\Хотя, почему-то
большинство ниспровергателей СТО от него отмахиваются и рисуют маловразумительные картинки без оси времени.\\\
Здесь имеется ввиду что у времени появляются свойства,
и оно может менять
свой темп и направление движения.
Так вот влазит этот релятивист провокатор со своим бредом, после
чего его развивает,
После этого
релятивист провокатор понимает что его маневр не прошел, и он не
может обосновать физическую сторону своих утверждений, и переходит на обсуждение
заговора релятивистов.
Здесь видим то как гандольерствующий модератор вместо того чтобы забанить
релятивиста провокатора за увод дискуссии в сторону он закрывает форум.
============
Ответ #99 : Сегодня в 15:21:05
Поскольку автору темы интересно обсуждать не свою "теорию", а заговоры, тема закрывается.
----



-

- Сообщений: 111
- Рейтинг: +3/-0
- Re: Черная дыра
(А.П. Васи,
6.04.2012 13:39, 1.5 КБайт)
Оттого
и возникает вопрос: действительно ли в однофотонных экспериментах
каждый фотон попадает в одну из щелей? А если да, то почему?
Ваша версия?
Фотон попадает только в одну из щелей, фотон проходит через обе щели,
фотон вообще через щели не проходит?
И рассмотрите лучше интерферрометр маха-цандера, там попроще будет решить,
где проходит фотон, так как расстояние между возможными
разными путями может
быть десяток метров.
А перекрытие одного из них приводит к тому же результату - пропаданию интерференции.
--------------------------------------------
Что собственно видно из этих обсуждений - видно то что с помощью
фотонов адекватно не получается описать интерференцию.
Дело в том что если использовать
фотоны они могут только увеличивать яркость
второго источника при наложении на первый, а если использовать эфир как
среду в пространстве, а свет получается - изменение
плотности эфира
аналогичные в воздухе - звуку, то получается простая и понятная картина.
- Re: Черная дыра
(А.П. Васи,
17.04.2012 15:33, 1.8 КБайт)
Рассмешил меня этот форум
А если Большой
взрыв - это заблуждение?
http://www.astronomy.ru/forum/index.php/topic,95394.0.html
видать светлая мысль ударила в пустоту моска
что можно же все книжки с идиотизмом переписать
на адекватные, ибо лучше адекватное от дураков
чем идиотизм от гениев.
И что наблюдается - а наблюдается
что в очередной
раз попали в обсуждении в небо пальцем, так как в итоге
обсуждения выяснилось что есть желание накрыть медным
тазом большой взрыв у большинства
присутствующих,
и при всём при том выяснилось что никто из присутствующих
не только модели строить не в состоянии, никто не
в состоянии и теории строить,
да и гипотезы тоже,
да и не в состоянии даже обосновывать что либо,
ибо это же своей головой думать надо, а до этого
только из книжек чужими идеями аргументировали.
Вот так и оказались у разбитого корыта - и не могут
обосновать причину того что большой взрыв полная ерунда,
- хотя это могут сделать радиоастрономы легко,
для этого достаточно смоделировать некоторую ситуацию,
- а модельеров то и нет чтобы ситуацию смоделировать.
Ладно с большим взрывом, а с черными дырами
что будут
делать, и с темной материей и темной энергией, минимум
год на опровержение каждой ерунды, а релятивизм опровергать,
тем кто его десятилетия защищал.
Но что-то мне подсказывает что поменяют модератора, и
вернутся обратно к истинному релятивизму.
По крайней мере хоть поймут как - качественно моделировать
-
тяжело на самом деле, и сколько читать, сравнивать и
думать надо по каждой мелкой мелочи чтобы не пришлось
думать по сто лет вместо того чтобы думать
один раз .
- Re: Черная дыра
(А.П. Васи,
20.04.2012 13:19, 2.4 КБайт)
Не понимаю
на сколько надо быть недалёкими чтобы не понимать
того что без строгого определения даже их
релятивистского пустого пространства, получается околонаучный стёб
вместо адекватного обсуждения.
Строго при этом надо определять отдельно пространство,
и отдельно пустоту, и время с пустотой, время в пространстве,
и тогда
сразу станет понятно что из себя стоит теория.
Дело в том что при заявленной пустоте и ей
недалекие ученные приписывают свойства сред такие
как - расширение,
сжатие, задержка волнового сигнала,
применение к пустоте волновых свойств(волны на границах
между сред), распространение полей в пустоте ( поля тоже
могут
быть только в средах по причине того что поля сплошные),
и применяют свойства для сред
даже не понимая того что они же от среды отказались, а какого-то
улья
свойства для сред применяют.
В пустоте могут передвигаться только и исключительно - частицы.
И все ситуации релятивистов могут быть исключительно из отдельных частиц.
А вот когда частиц так много что они создают поля или обретают
непосредственное взаимодействие в виде плотности,
это говорит о том что имеем дело со средой,
так как среды бывают
только сплошные. И если сжатие или расширение используется для
чего-то сплошного то значит процесс происходит в среде, так как
у пустоты
свойств не бывает, в пустоте только частицы отдельные друг
от друга.
И если например есть статическое поле - то это не отдельные частицы
это сконцентрировалась
некоторая сплошная среда.
Достаточно легко и однозначно накрывается весь релятивизм медным
тазом и сразу - эффект Доплера исключительно для сред, следовательно
можно отличить среду от пустоты - в пустоте эффект Доплера не работает.
А так как в солнечной системе эффект Доплера работает везде, - то солнечная
система
заполнена средой.
До адекватных обоснований ещё нет понимания необходимости таковых
и чтобы что-то обосновывать то надо иметь или способности или чтобы кто-то
обучил, или уметь понимать свои недостатки, - своих способностей нет, обучить некому
неадекватности своего мировоззрения не замечают - вот такая жестокая селяви.
И самое смешное что даже не понимают всю смехотворность уровня ошибок.
- Re: Черная дыра
(А.П. Васи,
24.04.2012 9:04, 2.1 КБайт)
Вот тоже яркий пример неадекватного разговора по причине
неадекватного понимания физики.
Что надо заметить что спорящие напрочь забывают что
фотоны
и их скорость не зависит от того в какой системе
отсчета находится наблюдатель.
С одной точки зрения применяют штатный теоретический постулат
о постоянстве
скорости а результат смотрят
по эффекту Доплера который для сред, и на полном ручнике не понимают
что и почему у них не сходится.
А когда у них не
сходится факт с идиотизмом теории
применяется следующий манёвр замедление времени
у движущегося объекта.
-------------------
Ответ #129 : Сегодня в 06:23:18
Вы знаете, что время идет по иному в движущейся СК? А ближе к скорости
света(например, в Звездолете будущего) очень заметно?
Вообще-то
оно ведёт себя так же. "Идёт" абсолютно одинаково, и по СТО, и по ОТО.
Часики тикают с такой же скоростью у космонавта на ракете, как такие же
тикают у того, кто за ним наблюдает в телескоп ...
Часики
у движущегося космонавта, если на них смотреть в телескоп, будут идти
медленнее. (за исключением встречного движения по одной прямой)
- Re: Черная дыра
(А.П. Васи,
24.04.2012 18:01, 2.6 КБайт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1334922693
 СТО - АЦКАЯ ЖЕСТЬ
СТО - АЦКАЯ ЖЕСТЬ
---------
Мне собственно не понятно почему данную тему переместил модератор
во флудильну,
но это вопрос модераторский ему важны посетители.
А с технической точки зрения вопрос поднимаемый автором актуальный,
но автор делает ошибку, по сколько это краеугольный
камень то надо быть
намного детально разбирать ситуации и писать вдумчиво обоснованно
и внятно чтобы самый недалёкий почувствовал себя обманутым
и заблудившимся
в двух соснах.
Собственно на качественном уровне не показан лохотрон летящих
частиц фотонов, для этой цели достаточно замедлить кратно все движущиеся
предметы и проанализировать ситуацию с разных сторон в пространстве.
Также надо раз и навсегда разобраться с лохотронящим наблюдателем,
который не меряет расстояние
от себя до объекта, и не синхронизирует свои часы
с событием, а если он будет это делать то он и даром не нужен.
---
А тема как раз актуальная, релятивисты
в данном вопросе в силу своей
доверчивости в правильность теорий проблемы вопиющей и не замечают.
Они даже не понимают почему у них летят частицы ихние запостулированные
ими же, из этих частиц у них получается нескладуха в теории
у них скорость с любой точки должна быть константа - это глупо естественно,
, но такой у них
постулат и при всём при этом их жмёт
ещё один постулат что при том что с любой точки зрения скорость константа,
то ещё и сама скорость "частиц фотонов"
в пустом пространстве тоже
константа - а вот это уже верх глупости, так как постулаты противоречат друг другу,
что собственно называется "парадокс" по
простому дефект в теории.
И выходят из этой ситуации следующим предположением, выводя следующий
постулат что у движущего объекта время внутри него замедляется.
Что собственно здесь смешно, смешно то совсем другое смешно как раз
то что собственно то тормозит "частицы фотоны" в "пустоте" именно
до такой скорости, скорости света?
- Re: Черная дыра
(А.П. Васи,
24.04.2012 18:16, 816 Байт)
С технической точки зрения с частицами как носителями
света пролёт по полной программе. Дело в том что
при стабильной скорости света не может быть
у фотонов
красного смещения в принципе.
Так как если фотоны летят пусть последовательными пакетами
синусоидальной плотности, то получается что при покраснении
увеличилось
расстояние между фотонами следовательно
объект излучающий удаляется следовательно скорость
фотонов при излучении была ниже относительно приёмника
что противоречит
постулату о постоянстве скорости.
Хотя естественно надо подумать прежде чем подобную
статью писать, может лучше пусть пасётся себе релятивизм
на лужайке,
все-же меньше конкуренция, да и релятивисты думают
что заняты полезным для общества делом а это уже не переубедить.
- Re: Черная дыра
(А.П. Васи,
25.04.2012 21:31, 5.7 КБайт)


 26032012119.jpg
(181.9 КБ, 900x675 - просмотрено 27 раз.)
26032012119.jpg
(181.9 КБ, 900x675 - просмотрено 27 раз.)

 26032012123.jpg
(172.31 КБ, 900x675 - п
26032012123.jpg
(172.31 КБ, 900x675 - п
----------------



-

- Сообщений: 171
- Рейтинг: +6/-0
- Мне нравится этот форум!
-
Ответ #380 : Вчера в 23:40:22
Наконец картинка поменялась.
--------------------------------

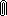 20042012234.jpg
(231.73 КБ, 900x675 - просмотрено 17 раз.)
20042012234.jpg
(231.73 КБ, 900x675 - просмотрено 17 раз.)

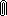 20042012235.jpg
(224.52 КБ, 900x675 - просмотрено 19 раз.)
20042012235.jpg
(224.52 КБ, 900x675 - просмотрено 19 раз.)
-------------------------------------------------------------------------
Не знаю как кому но мне это
напоминает танцы с бубном.
На много проще изменить конструкцию печки, по центру
просверлить дырку установить вал из жаропрочной нержавейки,
на этот вал и
устанавливается корыто в котором плавится стекло,
к валу надо сделать редуктор и привод с частотником, для поддержания
стабильной частоты вращения, и надо установить
контроллер для
нагрева поддержания и охлаждения.
И всё .
Итого надо насыпать в корыто стекла, выставить обороты вращения,
от оборотов будет зависеть фокусное
расстояние и включить контроллер
нагрева, немного подождать и вынуть изделие полностью готовое к напылению.
- Re: Черная дыра
(А.П. Васи,
26.04.2012 13:25, 3.1 КБайт)





-

- Сообщений: 2 684
- Рейтинг: +50/-16
- Suum сuiquе!
-
Ответ #135 : Сегодня в 01:38:26
Прямой ответ:
Эсли БВ - это заблуждение ? - То надо искать модель без БВ и то
такую ,чтоб крупномасштабная структура существовала на предельных
расстояниях и была подобной близкой - это основное ,но варианты и
подробности важны ............
Не видно оснований для утверждений
БВ - это заблуждение.
Если они (заблуждения) есть, то приведите их. Если доводы будут
достаточно убедительны то мы рассмотрим альтернативу для сравнения. Ну,
например,-голографический или экпиротический сценарии

Посмотрим
и сравним, что они могут объяснить чего нет в теории БВ.
-------------------------------------
Просто и красиво, этот случай показывает то что нельзя содержать
тысячи
физиков которые думают по придуманному в книжках, это балласт.
С другой точки зрения даже если тысячи книжкочитозубров поставить
задачу, то можно быть
спокойным в том что они не смогут её решить,
так как самостоятельно они никогда не решали а вычитывали ответы в книжках.
- Re: Черная дыра
(А.П. Васи,
26.04.2012 13:55, 2.0 КБайт)
Смешно,- большой взрыв важнее тепла от звезд
для ботаников таки да.
Хотя ответ на вопрос проще простого
достаточно понимать физические свойства.
При
заявленной пустоте пространства релятивистов
взрыв в пространстве у них не возможен по определению
ибо "взрыв" - это свойство непрерывной среды, а среды
нет.
Я в принципе не понимаю на сколько надо быть недалёкими
чтобы не понимать того что эта выдумка была придумана для того
чтобы деть энергию от звезд,
которая в итоге улетает
за горизонт событий. И надо понимать до тех пор
пока они не заметят свой основной
вопрос - куда девается тепло от звёзд то к астрономам
вряд-ли будет общественность адекватно общаться.
---
Еще раз - в каждом квадратном градусе звездного
неба 10 в шестой звезд, которые светят миллиарды
лет и выделяют триллионы гигаватт энергии - при этом
в космосе холодно и космос охлаждает землю.
---
Ясный и понятно что большой взрыв не спасает ситуации
по поглощению тепла от звезд тем ручным управлением что
тепло от звезд улетает а реликтовый фон от большого взрыва
никуда не может улететь и остаётся колбаситься
вечно,
но даже это не решает вопрос почему нет зарева звездного
неба и почему вокруг не тысячи градусов жары,
а наоборот космос холодный по самое дальше
некуда,
так как в космосе обязаны быть "холодильники",
которые не как черные дыры поглощают тепло а
ещё и круче охлаждают всё вокруг себя, я этот
вопрос решил - Звезда Эфира. Количество звезд эфира
у меня тоже может быть и больше количества звёзд,
по скольку звезда более менее вечная структура,
и звезды в процессе своей жизни конденсируют эфир внутри себя
и периодически его из себя выбрасывают по причинам
изменения плотности эфира в пространстве или
по физическим причинам внутри самой звезды
внутри которой звезда эфира. И звезда может
за время своей жизни сконденсировать
внутри себя хоть миллион
раз звезду эфира и избавится
от неё выбросив в космос.
- Re: Черная дыра
(А.П. Васи,
29.04.2012 11:22, 1.8 КБайт)
Теоретические воззрения должны указывать на возможность сохранения современной относительной распространённости элементов в модели вечной Вселенной,
а не на её невозможность. Как Вы, безусловно, знаете, утверждения в науке должны доказываться авторами, а не опровергаться оппонентами.
-----------------------------------------------
Модератор опять жжет.
Чё-то я не помню как обосновывалась именно
такая причина именно такой скорости света
в пустой пустоте летящих частиц-фотонов.
Да и не припомню как релятивисты на машине
времени летали в начало большого взрыва.
---
И что меня удивляет так это массовое отсутствие моска при анализе
состава звёзд. Ни до кого не доходит что их металичность в верхних
слоях звезды. А внутри звезды даже водорода нет ибо это и коню понятно
что водород самый
легкий и у него нет возможности физической и интеллектуальной
чтобы проникнуть в центр звезды.
Не знаю на сколько надо быть недалёкими чтобы не понимать что водород
по причине того что его удельная плотность ниже - он не может быть не
то что в центре звезды, он может быть исключительно в верхних
слоях, и как и кому это
можно доказать если моск вынут и положен на полку.
Итого - своим пацанам можно постулировать,
и их нельзя опровергать, так как некрасиво.
А чужим альтам
надо доказывать в космических
масштабах.
И как например физику объяснить математику что водород
не может быть внутри звезды, математику до лампочки по формулам
сходится,
а физику принципиально ибо это невозможно.
- Re: Черная дыра
(А.П. Васи,
29.04.2012 15:47, 2.3 КБайт)
А если есть в доступных публикациях толковое изложение, тогда как?
С чего бы им взяться если мэтры к единому мнению относительно ТБВ не могут прийти.
То
есть, Вы сами не интересовались, есть ли в доступных публикациях
толковое изложение? Вы почитали приведённую ссылку и на её основании
сделали вывод, что изложения нет?
-----------------------------------------------
Как говорится мечтать не вредно.
Модератор опять жжет.
Никто внятной причины не знает, и обоснования большого взрыва
тоже, и никто при большом взрыве не присутствовал
а зато сколько профессорами стало.
Если
бы было внятное и понятное обоснование -
то только по незнанию адекватного объяснения
задавали бы вопросы,
а вопросы задают массово, значит есть причина
- полное отсутствие адекватного обоснования.
---
Как по мне учитывая количество глупости то логично
за опровержение давать профессорские звания, ибо
релятивизм
восхвалять или большой взрыв моска не надо.
Хотя идиотизм ситуации то на поверхности, только недалёким
не понятно что 4.5 млрд лет,
это
переход урана из одного состояния в другое, но это же
не значит что уран до этого не существовал.
Буй с ним с тем ураном пусть он распадается до железа, -
железо
на земле есть - сколько тысяч миллиардов лет надо было железу
для этого времени?, да и от куда тогда уран взялся?
Как по мне с возрастом и методами определения
возраста Земли полный абзац,
а всё туда-же возраст вселенной от большого взрыва определять.
- Re: Черная дыра
(А.П. Васи,
29.04.2012 18:14, 13.0 КБайт)
Ответ #194 : Сегодня в 17:53:33
В
стационарной Вселенной есть проблема наблюдаемой одинаковой
распространённости химических элементов на масштабах, соответствующих
временным интервалам модели Большого взрыва порядка 10 млрд. лет. Но эта
же проблема имеет место и в модели Большого взрыва; в этой части модели
равноправны.
В модели Большого Взрыва этой проблемы нет. Она не предсказывает постепенное возрастание металличности.
--------------------------
Вот так звездят прохффесора.
Захотел и нет металличности, захотел и водород не
горит с преобразованием во всё
более тяжелые элементы,
и ясный конь что только гандольерствующий прохфесор не
знает что жизнь звезд в текущей парадигме заканчивается
или черной дырой или
железным ядром, так как при распаде
железа энергии больше поглощается чем выделяется.
Все астрофизики знают о металичности один модератор не
знает.
Гоните
в шею двуличного лохобоя.
---
Вот я в гуглях набрал
- железное ядро старые звезды-
---------------
---------------
---------------
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Астронет > Новые и сверхновые звезды >>
Глава XII ...
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
ОтменитьСообщений:
16-Авторов: 8-19 май 2010
... шаре, имеющем кору, мантию и железное ядро, которую мы заученно ...... В центре сферы на остатках
твердого ядра старой звезды ...
- Re: Черная дыра
(А.П. Васи,
30.04.2012 2:28, 1.4 КБайт)
А ларчик просто открывался кое кто на своей волне залип.
---------------------------------------
http://www.computerra.ru/own/wiebe/630833/
В результате
современный спектральный класс Солнца выглядит как G2V.
Он означает, что Солнце имеет цвет, соответствующий температуре порядка
6000К, внутри спектрального класса G оно расположено ближе к границе с
классом F, чем к границе с классом K, а цифра V говорит о принадлежности
к карликам, то есть звёздам с компактными плотными атмосферами. Двумя
словами - жёлтый карлик. Прочие параметры таковы: масса 21027 тонн, светимость (мощность излучения) 1026 ватт, диаметр около полутора миллионов километров.
Насколько эти параметры похожи или не похожи на параметры других
звёзд? Начнём с главного - с массы. Теория звёздной эволюции утверждает,
что именно этот параметр для звезды является определяющим. Вообще,
звёздные массы заключены в весьма широких пределах - от одной десятой
массы Солнца до сотни или даже сотен солнечных масс. Однако количество
звёзд разных масс существенно разное, и чем меньше масса звезды, тем
больше таких звёзд в Галактике. Скажем, на каждую звезду с массой
порядка сотни солнечных масс приходится несколько сотен звёзд с массой
порядка одной солнечной и около десяти тысяч звёзд, менее массивных, чем
Солнце.
- Re: Черная дыра
(А.П. Васи,
30.04.2012 12:41, 41.4 КБайт)
Ответ #186 : Сегодня в 08:21:20
В модели Большого Взрыва этой проблемы нет. Она не предсказывает постепенное
возрастание металличности.
Но предсказывает непостепенное (некоторое) ,или нет?
Строго
говоря, модель БВ несёт ответственность только за начальный
нуклеосинтез (Big Bang Nucleosynthesis, BBN). Остальное -- это вообще не
к ней, а к моделям звёздной эволюции и эволюции галактик.
-----------------------------------------------
Не знаю на кого рассчитаны такие отписки.
Не понимаю почему модератор думает что на его форуме
безмозглая скотина которая не знает космологии,
я думаю что он догадывается что они знают что он
их мозг трахает по полной и понимает что он модератор
и если кто-то оборзеет и укажет на его ошибку
то будет сразу забанен.
Набираю в гуглях - водород при большом взрыве-.
и иду по первой ссылке.
------------------
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
Отменить
Вы уже поставили +1 этой странице.
ОтменитьВы уже поставили +1 этой странице.
ОтменитьОтветов:
2-13 июл 2011
При Большом взрыве тяжелые элементы когда образовались в самом ... с остатками электронов, которые и образовали водород.
Вы уже поставили +1 этой странице.
Отменить
-----------
К далее написанному надо относится с пониманием того что для альтов
это высосано из пальца и украшено идиотизмом, а для релятивистов
это настольная книга по
которой они думали, думают и будут думать.
\\\К концу второго периода, то есть через 5
минут после Большого Взрыва, расширяющееся вещество состоит из ядер атома
водорода 70% и ядер гелия 30%. \\\
http://mrcnn.narod.ru/bigbang.htm
Из первичного состава следует что это не большой взрыв, а
"Железный Пипец".
Да рекомендую прочитать всё, не знаю как кому но как по мне
не в обиду автору (текст читается как раз легко),содержание содержит столько
необоснованных
выдумок смешанных с глупостью, содержат огромное
количество взаимных противоречий что это просто что-то с чем-то.
\\\Имеются
некоторые
естественные вехи, которые делят весь интервал времени после Взрыва (все время
жизни Вселенной, поскольку ее летоисчисление началось с Большого Взрыва) на
отдельные периоды. Первый такой период (возможно, состоящий из подпериодов) от
начала Взрыва продолжался всего 1 секунду. Но именно в этот период была
определена вся дальнейшая "судьба" Вселенной (ее строение, химический
состав, эволюция).\\\
Ясен конь, если в начале был водород и гелий то дорога эволюции одна - вперёд к железным
космическим болванкам.
-------------------
Вот нашел
------
http://mrcnn.narod.ru/bigbang.htm
\\\Эволюция
звезды определяется, главным образом, ее - массой. Естественно, чем
больше масса звезды, тем больше
.; энергия, которая может выделиться внутри звезды в процессе
термоядерных реакций. Другими словами, тем больше
' горючего содержится внутри такой звезды. Казалось бы, такая звезда
должна жить (светиться) дольше. Но это не так. Чем массивнее звезда, тем
больше она излучает энергии в космическое пространство. Так, если массу
звезды увеличить в три раза, то ее расход энергии на излучение
(светимость) увеличится в девять раз! Поэтому с увеличением массы звезды
продолжительность ее жизни резко уменьшается. Так. например, горючего
для ядерного реактора внутри Солнца хватит еще на десятки миллиардов
лет. Около пяти миллиардов лет это горючее уже расходуется. Но, если
масса звезды в 50 раз превышает массу Солнца, то ее горючего хватит
всего на несколько миллионов лет!
Когда
в процессе термоядерных реакций в ядре звезды израсходуется весь
водород (он превращается в гелий), то термоядерные реакции превращения
водорода в гелий начинают идти в слое вокруг ядра. Светимость звезды на
этом этапе
, увеличивается. Звезда как будто разбухает. Но температура
поверхностных слоев звезды уменьшается, поскольку размеры ее
увеличились, поэтому она начинает светиться не голубым, а красным
цветом. Такую звезду называют красным гигантом. Дальше звезда
эволюционирует следующим образом. Поскольку в ядре не идут термоядерные
реакции и не выделяетса тепло, она постепенно сжимается под действием
сил гравитации. В результате сжатия ядра увеличивается его температура.
Она достигает 100150 миллионов градусов. При столь высокой температуре
гелий становится источником тепла: идут термоядерные реакции, в
результате которых ядра гелия превращаются в ядра углерода. Давление
внутри ядра звезды увеличивается, поэтому сжатие прекращается.
Светимость звезды на этом этапе увеличивается, так как в нее вносит
вклад и выделение энергии из ядра. В результате увеличивается и
поверхностная температура звезды. Но когда-то кончается и гелий. Причем
значительно быстрее, чем кончился водород. Когда это происходит, звезда
теряет свои наружные слои. Они расширяются и отделяются от ядра звезды.
Эти слои впоследствии наблюдаются как планетарная туманность. Судьба
ядра звезды после этого зависит от ее массы. Если масса звезды меньше
1,2 массы Солнца, то вещество звезды под действием гравитационного
сжатия уплотняется таким образом, что его плотность достигает 10 тысяч
тонн в кубическом сантиметре. При такой огромной плотности атомы
разрушаются. После этого сжатие звезды прекращается, так как ему
начинает противодействовать сила упругости образованного очень плотного
газа. Образованная таким путем звезда (ее называют "мертвой") является
белым карликом. Таким образом, до того, как звезда превратится в белого
карлика, она на некоторое время становится красным гигантом. Затем белый
карлик в течение нескольких миллиардов лет остывает и превращается в
черного карлика, то есть тело не излучающее а поэтому и невидимое. И.С.
Шкловский назвал его "трупом" звезды. Если масса первоначальной
зашлакованной звезды превышает критическую величину в 1,2 массы Солнца,
то силы упругости сверхплотного (вырожденного) газа не в
состоянии справиться с силами гравитационного сжатия.\\\
---
Ладно запостулировали глупость что от массы так это не
значит что надо безмозло в телескоп смотреть и статьи писать неочём,
Надо сказать что истинна дороже и послать в даль то что не
соответствует наблюдениям, по той причине что не наблюдается
того что чем дальше звёзды и чем у них больше "Z" то тем
они более
массивные.
---
Итого
Большой взрыв на самом деле как раз и определяет металичность
ибо заданна начальная составляющая столько то водорода
и
столько-то гелия.
И заданна необратимость со временем превращения заданных
веществ в более тяжелые, и есть конец этого коленкора под
названием "Железный
Пипец", по причине того что всё должно
превратится в кучу железных болванок.
От массы тоже не может зависеть возраст звезд, так как
это противоречит
наблюдениям, - эта лапша на уши проходила
только при слабых телескопах, в которые нельзя было
рассмотреть далёкие галактики.
--------
У меня
такое чувство что вопросами астрономии вообще астрономы
не занимаются в принципе, им просто начхать на то правильная она
или неправильная.
- Re: Черная дыра
(А.П. Васи,
30.04.2012 13:44, 595 Байт)
Для тех кто не понял почему не может масса определять
возраст звезды.
В телескопы наблюдаются звёзды первый миллиард лет
от большого взрыва.
Следовательно
все звезды этого миллиарда должны быть
в основном из водорода и гелия - чего не наблюдается,
в них есть металлы.
Из этого получается что в начале большого
взрыва должны быть
металлы - что невозможно ибо это уже не большой
взрыв а другая теория, и второй вариант что большой
взрыв который придуман глядя на взрыв
водородной бомбы
просто не подходит для описания эволюции звезд.
- Re: Черная дыра
(А.П. Васи,
30.04.2012 13:57, 4.5 КБайт)
Эволюция звёзд это в принципе нечто смешное.
-----------------------------
Материал из Википедии свободной энциклопедии
\\\Звезда начинает свою жизнь как холодное разрежённое облако межзвёздного
газа, сжимающееся под действием собственного тяготения и постепенно принимающее форму шара. При сжатии энергия гравитации
переходит в тепло, и температура объекта возрастает. Когда температура в центре достигает 15-20 миллионов К,
начинаются термоядерные реакции
и сжатие прекращается. Объект становится полноценной звездой. Первая
стадия жизни звезды подобна солнечной в ней доминируют реакции
водородного цикла[1].
В таком состоянии он пребывает бо́льшую часть своей жизни, находясь на главной
последовательности диаграммы
Герцшпрунга Расселла, пока не закончатся запасы топлива в его ядре. Когда в центре звезды весь водород
превращается в гелий, образуется гелиевое ядро, а термоядерное горение водорода продолжается
на его периферии.

Эволюция звезды класса G на примере
Солнца
В этот период структура звезды начинает меняться. Её светимость
растёт, внешние слои расширяются, а температура поверхности снижается
звезда становится красным гигантом,
которые образуют ветвь на диаграмме Герцшпрунга-Рассела. На этой ветви
звезда проводит значительно меньше времени, чем на главной
последовательности. Когда накопленная масса гелиевого ядра становится
значительной, оно не выдерживает собственного веса и начинает сжиматься;
если звезда достаточно массивна, возрастающая при этом температура
может вызвать дальнейшее термоядерное превращение гелия в более тяжёлые
элементы (гелий в углерод, углерод
в кислород, кислород в кремний, и наконец кремний в железо).\\\
------------------
Ещё
вариант
http://4put.ru/view-max-picture.php?id=767124


- Re: Черная дыра
(А.П. Васи,
4.05.2012 21:00, 3.9 КБайт)
Модераторам задают однозначные вопросы а модераторы
вместо ответов дурака включают и дыбилируют, и стараются
сделать дурака из задающего вопросы.
Если
модератор не может ответить на вопрос, то он должен
об этом сказать а не выпендриваться.
Естественно задающие вопрос обязаны более строго и внятно
задавать
вопрос так как в данном случаи краткость
сестра идиотизма, и модератор будет показывать свой интеллект и будет
унижать задающего краткий и не корректный вопрос,
а если вопрос подробный и не дающий модератору
склеить дурака , то модератор будет нагнут тем что он
не сможет на него ответить в силу своего низкого
профессионализма.
Рекомендую коллекционировать вопросы и отсутствие на них ответов модераторов,
и отмазки которые модераторы использовали, этими неответами
их можно будет их подначивать и напоминать им вечно.
-------------------
A) Какую начальную массу имело Солнце в момент своего рождения?
B) И о динамике эволюции параметра
величины массы Солнца тоже. 
К сожалению, ответа не было.
--------------
Очень хотелось бы понять, стечение каких
уникальных условий послужило основанием для формирования Солнца в одиночестве.
А что в этом событии уникального

Одиночных звезд море в космосе.

--------------------------
Даже я в книжках читал что считается что 60% звезд зарождались двойными
по канонам текущей космологии.
Набираю
в гуглях - процент двойных звезд.
-------
Вы уже поставили +1 этой странице.
Отменить
---
Так что модератор в вопросах формирования звёзд просто недалёкий, а корчит из себя гиганта мысли.
- Re: Черная дыра
(А.П. Васи,
5.05.2012 2:11, 2.2 КБайт)
Собственно модератор хотел перехитрить и ответил
вопросом на вопрос, вместо того чтобы ответить на вопрос по сути.
В такой ситуации надо зазнавшегося ставить
на место,
и напомнить ему ещё раз вопрос и попросить ответить
ещё раз развёрнуто на заданный
ему вопрос по сути, и спросить
в чём трудность того что
он не может ответить на этот вопрос
а интересуется вот этим вопросом, и что собственно
даст ему если ему ответят на этот вопрос?
И спросить на всякий
случай если бы ему ответили вопросом на вопрос
то на сколько бы он забанил, как модератор, времени такого борзого посетителя,
или закрыл бы тему на правах модератора?
---
И очень рекомендую подобный случай запомнить,
и можно модератору смело отвечать вопросом на
вопрос ссылаясь на его же борзость.
------------------------------------------------------------------
------------------------------------------------------------------
------------------------------------------------------------------
Ответ #28 : Вчера в 20:41:18
Очень хотелось бы узнать мнение Дмитрия Вибе в отношении проблемы:
A)
Какую начальную массу имело Солнце в момент своего рождения?
B) И о динамике эволюции параметра величины массы Солнца тоже.

Чем Вас не устраивает
масса в одну массу Солнца, мало меняющаяся в ходе эволюции?
- Re: Черная дыра
(А.П. Васи,
5.05.2012 13:58, 480 Байт)
Вопросы таки надо ставить корректно.
Качественный вопрос.
Какие были физические обоснования для 1 определения
возраста солнца?, 2 определения
временного промежутка
между большим взрывом и началом термоядерных
реакций у солнца?
По каким физическим признакам определяется возраст
земли
от начала термоядерной реакции?
( Не задавайте вопрос про массу не страдайте ерундой
нет весов в космосе - ответ будет от фонаря однозначно)
- Re: Черная дыра
(А.П. Васи,
5.05.2012 15:35, 3.2 КБайт)
Модератор в очередной раз выглядит нелогично,
явно он не знает предмет вопроса на который даёт
глупый и бессмысленный совет,
дело в том что на текущий момент
ни в один из телескопов
не наблюдается у двойных две оптически раздельные
друг от друга звезды.
И это тот случай когда астрономам желательно затрачивать
больше
времени на размышления чем на наблюдения,
чтобы не выглядеть глупо в простых вопросах.
Его советы дважды глупы первый раз что двойные
не
наблюдаются даже в самый большой телескоп,
а второй раз совет не имеет смысла то что само определение
"двойной" тоже не доказано и не обосновано с физической
точки зрения, так что кто-то сам себе придумал
двойные и думает что он их наблюдает.
При всём при том что есть пятна на солнце, а моск
в рамках
парадигмы у релятивов не допускает простых
мыслей что могут быть пятна на пол звезды,
и аномально яркие участки на звёздах, если это предположить
то двойных
и даром не нужно, - но это уже
совсем другая история и для тех кто не закомплексован
текущими парадигмами.
-----------------------------------------------
Ответ #39 : Сегодня в 13:40:52
- Re: Черная дыра
(А.П. Васи,
10.05.2012 14:13, 3.9 КБайт)
\\\

Ответ #241 : Вчера в 19:18:05
Фотон , допустим, жёлтого цвета , испущенный из лампочки
или долетевший от Солнца , всегда имеет одну и ту же частоту , а стало быть и амплитуду.
Дальше читать не интересно, Вы путаете теплое
с мягким.

\\\
----------------------------------------------------------------------------
----------------------------------------------------------------------------
----------------------------------------------------------------------------
Ещё один модератор хочет пройти курсы в Венеции по
управлению водным транспортом.
Если модератор знает правильный ответ он обязан
сказать - что вот так-то и так-то и потому-что,
и обосновать причину физическую своего утверждения
а
в данном случаи просто наблюдается у модератора показать на сколько
он сильнее как модератор в возможности борзеть и
ещё более силён высокомерно необоснованно
отвечать,
и делать опломб что мол он перец
обладающий исключительными знаниями.
Так и охота сказать такому модератору если знаешь ответ и причину, - то
какого улья умалчиваешь?,
а отвечаешь на ответ борзостью наделенной модераторской должностью.
На самом деле модератор и не думал отвечать он боится, так как
если он хоть слово
напишет по сути вопроса то обхезается по полной и его будут вечно
окунать в этот ответ.
---
Ладно перейду от оборзевших модераторов
к вопросу по сути.
Что самое смешное так пусть даже если допустить у нефизичной частицы
- фотона будет "амплитуда" - которая может быть выражена
количеством фотонов.
Буй с ним даже если представить для фотона - частоту как
например вращение фотонов (спин) -
что собственно тогда противоречит тому
что фотон - частица,
по причине того что частота определяется изменением количества
испускаемых фотонов. Собственно получается что на частоту сигнала
может
влиять высокоскоростная количественная модуляция фотонов,
- будет меняться количество частиц, а ещё и второй случай меняется
раскрутка фотона как частицы.
С другой точки зрения -до лампочки все эти манёвры релятивистов
и всё равно как они красиво танцуют с бубном, так как нет причины
для изменения амплитуды - количества
фотонов, - фотоны в пустоте
не могут потеряться замедлится или ускорится, так-же и не
могут изменить скорость своего вращения как частицы в пустой
пустоте
ибо в пустой пустоте нет трения.
Фотоны могут только как частицы у релятивистов
лететь по непонятной причине с исключительно точным
поддержанием определённой
скорости в пустой пустоте,
и точно эта скорость всегда будет например в стекле у фотонов
скорость в полтора раза меньше.
А вот релятивисты не хотят
объяснить причину - почему именно со скоростью
в полтора раза больше чем в стекле скорость света больше в космосе
- там где пустая пустота, и не хотят сказать
что именно фотоны там может в пустой пустоте
тормозить именно до такой скорости, ссылаются на то что мол не они придумали
и не им объяснять.
- Re: Черная дыра
(А.П. Васи,
10.05.2012 14:27, 605 Байт)
Для тех кто не заметил как релятивисты двойными манёврами
с фотонами в споре и делают из опонента
лопуха и навешивают ему макароны на уши, -
это то что у
релятивистов частота фотонов может описываться двумя
методами - последовательными амплитудно модулированными
пакетами фотонов, а второй вариант вращением фотонов.
И если Вы будете говорить например что амплитудная модуляция
у частиц фотонов - вам скажут что Вы недалёкий ибо есть спин.
А если будете ссылаться на спин
вам скажут что Вы недалёкий
так как фотоны летят пачками с определённой частотой.
- Re: Черная дыра
(А.П. Васи,
16.05.2012 2:09, 3.9 КБайт)
Ответ #17 : Вчера в 23:50:40
Qw, давайте не будем фантазировать, кто во что не поверит. Докажите, что Ваша "гипотеза" обладает предсказательной силой.
-----------------------------------
Модератора мутит по полной, аж укачивает его
в гандолле.
Новые правила модератор придумал для форума
-
каждая гипотеза обязана обладать предсказательной силой.
Ничего и никакая гипотеза модератору не должна,
тем более она не должна ничего предсказывать.
---
\\\Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений (
примеров),\\\
---
\\\Материал из Википедии свободной энциклопедии
Гипо́теза (др.-греч.
ὑπόθεσις
предположение; от ὑπό
снизу, под + θέσις
тезис) предположение или догадка;
утверждение, предполагающее доказательство, в отличие от аксиом, постулатов, не требующих доказательств. Гипотеза считается научной,
если она фальсифицируема,
т.е. может быть опровергнута.
Также она может определяться как форма развитий знаний,
представляющая собою обоснованное предположение, выдвигаемое с целью
выяснения свойств и причин исследуемых явлений[1].
Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений (примеров),
и поэтому выглядит правдоподобно. Гипотезу впоследствии или доказывают, превращая её в установленный факт
(см. теорема, теория),
или же опровергают (например,
указывая контрпример), переводя в разряд
ложных утверждений.
Недоказанная и неопровергнутая гипотеза называется открытой проблемой.\\\
- Re: Черная дыра
(А.П. Васи,
16.05.2012 2:20, 353 Байт)
Для тех кто не понял, гипотеза не должна ничего
предсказывать она описывает как есть,
текущую ситуацию, основываясь на некоторых наблюдениях
размешанными
с авторским виденьем ситуации и авторской фантазией.
---
Я рад что релятивистов строит такой модератор, - крассава,
я за релятивистов спокоен, они в
красивой уздечке.
- Re: Черная дыра
(А.П. Васи,
25.05.2012 2:10, 2.0 КБайт)
Модератора гандольерит по самое дальше некуда,
он уже не знает до чего ещё придраться,
но нельзя же быть настолько звезданутым чтобы требовать
от
автора гипотезы подтверждения её истинности другим методом.
Дело в том что только безмозглый модер не знает того
что как раз вот этот вопрос автор может очень
легко решить в свою пользу, но это уже не будет гипотеза,
так как гипотеза по определению - должна быть опровергаемая.
А здесь получается что пустить
козла в огород,
попросить автора подтвердить правильность
его же гипотезы.
--------------------------------------------------

Ответ #61 : Вчера в 22:30:11
тайте
мне ДВА любых, угодных вам числа, характеризующие, на ваш взгляд,
внешнюю и внутреннюю границы гипотетического протопланетного диска. И я
берусь по ним (только по ним) рассчитать в этом диске (в строгом
соответствии с обсуждаемой схемой) все реальные резонансные орбиты.
Причем, это будет единственный возможный вариант их расположения.
Хотелось
бы помимо собственно расчёта увидеть убедительное доказательство того,
что "это будет единственный возможный вариант их расположения". До того
как Вы представите такое доказательство, прошу другие сообщения в
разделе не публиковать. Своё умение подгонать что-то под что-то Вы уже
продемонстрировали. Теперь обратимся к физике.
- Re: Черная дыра
(А.П. Васи,
25.05.2012 23:19, 4.0 КБайт)
Ну что я говорил то и произошло, альтернативщик порвал как
мавпа газету, релятивистов по их же безмозглой просьбе.
-------------
-------------
-------------
Ответ #63 : Сегодня в 22:13:27
Своё умение подгонать что-то под что-то Вы уже продемонстрировали. Теперь обратимся
к физике.
Для
начала прошу уточнить, где и в чем именно, по-вашему утверждению, я
занимался подгонкой. Лично у меня складывается впечатление, что за
ширмой моей подгонки вы просто прячете собственное нежелание видеть
очевидные вещи.
Постараюсь предельно популярно проиллюстрировать свою мысль на конкретном примере звезды HD-37124, расчет системы которой приведен
мною ранее (в ответе 60).
Я
утверждаю, что все планеты в регулярных системах формируются на
резонансных орбитах. Для расчета этих орбит служит уже известная вам
формула. И именно резонансные явления в протопланетном диске
перераспределяют его вещество (концентрируя массу) по указанным орбитам.\\\
-------------------
-------------------
-------------------
Объясню
физическую сторону того о чем идет речь.
Если взять кварц подключить к нему устройство широкополосной
авто-генерации и после этого посмотреть спектр излучаемый
этим генератором. Амплитудно частотную характеристику,
при изменении частоты возбуждения кварца - и что получается,
получается что амплитуды возбуждения
на разной кратности частот
будут разные. Будут выделятся вторые, третьи, пятые и десятые.
Заметьте амплитуды биения на определённых гармониках,
они
разные.
-------------------------------------
-------------------------------------
-------------------------------------
http://radioelpribori.ru/pribor-dlya-issledovaniya-amplitudno-chastotnyih-harakteristik-chetyirehpolyusnikov.html
\\\
Устройство калибровки оси частот (маркерное устройство) состоит из:
- кварцевого генератора;
- смесителя;
- фильтра нижних частот.
На один вход смесителя подается напряжение кварцевого генератора, основная частота которого равна F1, например F1
= 1МГц. Это напряжение характеризуется весьма широким спектром (содержит много высших гармоник), частоты соседних составляющих которого отличаются друг от друга на
величинуF1(1МГц). Ко второму входу смесителя подводится напряжение от генератора.
Каждый раз, когда качающаяся частота становится
близкой и равной частоте какой-либо гармоники кварцевого генератора, на
выходе смесителя появляются импульсы нулевых биений между напряжениями
гармоник кварцевого генератора и напряжением качающейся частоты.
Принцип получения частотных мерок на изображении амплитудно-частотной характеристики

Напряжение нулевых биений (точнее, низкой разностной частоты)
подается с выхода смесителя через фильтр нижних частот и усилитель на
вертикально отклоняющие пластины электронно-лучевой трубки. При качании
частоты от одного крайнего значения до другого на экране наблюдается
серия частотных меток (марок), отстоящих друг от друга по частоте на расстоянии F1 (1МГц).\\\
- Re: Черная дыра
(А.П. Васи,
25.05.2012 23:35, 74 Байт)
http://www.kit-e.ru/articles/measure/2010_07_169.php
рис.23
- Re: Черная дыра
(А.П. Васи,
26.05.2012 0:48, 2.0 КБайт)
Ответ #65 : Вчера в 23:56:43
Для начала прошу уточнить, где и в чем именно, по-вашему утверждению, я занимался
подгонкой.
Подгонка -- совершенно легальная и типичная процедура.
Я
утверждаю, что все планеты в регулярных системах формируются на
резонансных орбитах... Я берусь утверждать, что слабое гравитационное
влияние Юпитера было просто не в состоянии помешать сформироваться Фаэтону, поскольку более сильное (минимум в 3,3 раза) гравитационное
влияние планеты HD-37124d не помешало сформироваться планете HD-37124c.
Прекрасно. Докажите эти утверждения. До
того как Вы это сделаете, прошу другие сообщения в разделе не публиковать.
--------------------------
--------------------------
--------------------------
Да если нет стратегического мышления, то его и не появится.
Мне просто грустно смотреть как альтернативщик издевается над недалёким модером.
Модератор
думает что поставил крутой и трудный вопрос,
- этот вопрос - наживка которую съел модератор, и ответ
на него уже есть и был у альтернативщика, до того как модератор
задал вопрос.
- Re: Черная дыра
(А.П. Васи,
26.05.2012 8:39, 105 Байт)
Для тех кто не заметил старческий маразм модератора,
- в его вопросе уже есть ответ на его вопрос.
- Re: Черная дыра
(А.П. Васи,
26.05.2012 9:03, 1.2 КБайт)
Ответ #360 : Вчера в 19:36:00
МОЯ ЛИЧНАЯ ТОЧКА ЗРЕНИЯ
Первично расширение времени...
Не серьёзно. Эдак нам быстро тему прикроют.
------------------------------------------------
------------------------------------------------
------------------------------------------------
Даже если и прикроют, то физическое обоснование
для красного смещения релятивисты для
этой своей
выдумки будут искать до последнего
фаната релятивизма.
- Re: Черная дыра
(А.П. Васи,
27.05.2012 0:37, 5.3 КБайт)
Ответ #68 : Вчера в 21:07:22
Впрочем,
если и это вам ничего не доказывает, то имеет ли смысл приводить мне
расчет системы звезды HD-95128 (она же 47 Ursae Majoris), системы, в
которой резонанс Фаэтона (а1,2 = 3,6 а.е.) занимает планета HD-95128c?
Нет. Доказать утверждение вовсе не означает ещё
раз его повторить.
--------------------------------
Вот математику физику объяснять это глупо.
Автор гипотизы высказал свою идею обосновываясь
на наблюдениях
привел математический метод поиска наиболее устойчивых орбит
для планет, показал что есть физические аналогии
как в физическом резонансе
так и по совпадению устойчивых орбит
с его гипотезой.
Модера просто жаба давит что он профессор и в своей жизни ничего
не привнёс в астрономию, просто
как попугай повторяет
всё время чужие идеи.
А здесь альтернативщики которые не профессора по астрономии
выдвигают свои идеи которые намного лучше тех что
он знает,
и он упирается рогом и требует доказательств которые до него
не дошли в силу того что его жаба давит.
---
Лично с моей точки зрения автор
данной гипотезы не прав,
по скольку с моей точки зрения не может быть резонансного
влияния в пространстве без физической причины.
Я подобное видел в модели
атома водорода - которую а тоже не
разделяю. Но это как я понимаю.
Хотя при всем при том - данная гипотеза
тоже должна иметь право на существование.
Модератор естественно недалёкий, он не понимает что у него
должна быть граница выстебонов, и черта после которой он не задаёт вопросы автору гипотезы,
и модер
должен четко сказать - Ваша гипотеза имеет место быть,
а не выстёбываться до последнего чтобы в итоге забанить автора,
по той причине что это гипотеза по определению.
\\\Материал из Википедии свободной энциклопедии
Гипо́теза (др.-греч.
ὑπόθεσις
предположение; от ὑπό
снизу, под + θέσις
тезис) предположение или догадка;
утверждение, предполагающее доказательство, в отличие от аксиом, постулатов,
не требующих доказательств. Гипотеза считается научной,
если она фальсифицируема,
т.е. может быть опровергнута.
Также она может определяться как форма развитий знаний,
представляющая собою обоснованное предположение, выдвигаемое с целью
выяснения свойств и причин исследуемых явлений[1].
Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений (примеров),
и поэтому выглядит правдоподобно. Гипотезу впоследствии или доказывают, превращая её в установленный факт
(см. теорема, теория),
или же опровергают (например,
указывая контрпример), переводя в разряд
ложных утверждений.
Недоказанная и неопровергнутая гипотеза называется открытой проблемой.\\\
- Re: Черная дыра
(А.П. Васи,
31.05.2012 9:03, 2.5 КБайт)
Как я рад что не на форуме где модератор гандольер.
Пришел человек например на форум, чтобы высказать свою гипотезу
и с той целью чтобы ему помогли и подсказали
некоторые нюансы
в которых у него трудности.
Итогом нормального посетителя - написание небольшой итоговой статьи,
и не обязательно в реферируемый журнал.
Что на звездочёте творится - приходит посетитель, модератора от своей научной
неполноценности жаба давит, и он вступает в конфронтацию и не даёт возможности
по обсуждать посетителю свои вопросы, модератор включает "дурака" и требует
от посетителя сразу профессорского уровня подхода к данному вопросу,
и начинает придираться по каждой мелочи, с явной задачей забанить посетителя.
И гандольерствующий модератор в силу того что его жаба давит, он никогда не скажет
посетителю что его гипотеза имеет место быть, посетитель со своей любой гипотезой
будет в итоге забанен.
------------------------
Ответ #94 : Вчера в 22:46:37
Qw, перечитайте, пожалуйста, вот это моё сообщение:
Я
утверждаю, что все планеты в регулярных системах формируются на
резонансных орбитах... Я берусь утверждать, что слабое гравитационное
влияние Юпитера было просто не в состоянии помешать сформироваться Фаэтону, поскольку более сильное (минимум в 3,3 раза) гравитационное
влияние планеты HD-37124d не помешало сформироваться планете HD-37124c.
Прекрасно. Докажите эти утверждения. До
того как Вы это сделаете, прошу другие сообщения в разделе не публиковать.
- Re: Черная дыра
(А.П. Васи,
31.05.2012 22:57, 1.8 КБайт)
Чтобы были понятны мечты некоторого профессора -
финансировать другие направления не надо , и выделять
интеллектуальные ресурсы на другие направления тоже
не надо,
- надо лежать на печи и думать что всё должно
произойти само собой, через сто или тысячу лет.
И альты ещё очень мешают.
И о себе в науке думает
как о телеге с лошадью,
которую альты мешают толкать вперёд, и представляет себя лошадью
которая тащит телегу, но по факту больше напоминает - телегу или
лошадь лежащую в телеге. И винит всех альтов так как альты тормозят науку.
И по многим направлениям науки прямо перед тем как мысль пришла альты
её дискредитировали
тем что занимались самостоятельно данными вопросами.
Просто красапета.
------------------------------------
http://www.computerra.ru/own/wiebe/670110/
\\\Вот и теперь не нужно торопить физику.
Всё произойдёт само собой и в
своё время.
Если теории относительности или теории Большого Взрыва
суждено уйти в историю,
это произойдёт не потому, что они кому-то
надоели и ему хочется новую молодую жену взамен старой примелькавшейся.
Это произойдёт, когда и если они перестанут согласовываться с
наблюдениями
и экспериментами. Это может случиться через год, или через
сто лет, или через тысячу.
Надо будет- и случится. А попытки ускорить
движение лошади подталкиванием телеги
к добру не приводят. По сути,
многочисленные "спасители науки" тормозят её развитие.
С одной стороны, к
определённым тематикам сложно подступиться,
потому что они полностью
дискредитированы самодеятельными исследователями.
С другой стороны,
иногда кажется, что не очень... качественные работы по этим тематикам
просачиваются в научные журналы, потому что редакции опасаются обвинений
в догматизме.\\\
- Re: Черная дыра
(А.П. Васи,
27.06.2012 21:00, 2.3 КБайт)
\\\
 Re: Поле и эфир
Re: Поле и эфир
Ответ #1020 - Сегодня :: 19:50:01
riv123 писал(а) Сегодня :: 18:59:31:
Эфир не общая основа.
Поскольку есть силовое поле - оно вполне справляется с функциями эфира.
Копать глубже конечно можно из любопытства. Только желательно сначала
разобраться, что такое поле, свет, масса, вещество, материя, каким
бывают магнитные поля (что такое спин например и почему он так похож на
торсионное поле) Без этого структуру эфира, его модель не построить.
Вернее существует множество разных моделей, и все правильные.
Математически доказываются.\\\
---
Что с моей точки зрения здесь не логично, что грубо говоря нельзя ставить телегу впереди лошади,
и нельзя надеяться
слепить что-то из кусков чужих теорий.
Зачем эфиру спин, зачем эфиру электрон, напряженность эфира и есть поле,
достаточно изменение плотности эфира это уже
- эл маг колебания, осевая раскрутка
частиц эфира - магнитное поле.
К эфиру автор придумывает свойства какие он хочет и считает нужными.
А не берёт
всякий мусор из других теорий и начинает искать
у кого-то похожее описание эфира которое подходит под мусор из других
не стыкуемых между собой теорий,
которые
он знает.
Бывает так что модель эфира строить можно и по
другому, достаточно приписывать ему те свойства которые физик считает
нужными, а ботаник или
математик по причине отсутствия понимания физ процессов
борется с чем попало только он не понимает что его беспощадный
труд бессмысленный и бесполезный.
- Re: Черная дыра
(А.П. Васи,
11.07.2012 1:52, 3.7 КБайт)
Я опять на одном форуме был просто шокирован,
------------------------------------------------------------------
---------------------------------------------------------------------
---------------------------------------------------------------------
\\\
 Re: Поле и эфир
Re: Поле и эфир
Ответ #1407 - Сегодня :: 01:23:57
Цитата:
VIP 09.07.2012
в 17:02:07 Пост 1338
Мы пока с Вами договариваемся о том, что волны могут существовать только в среде, способной колебаться. Вы с этим согласны?
vpd44
09.07.2012 в 17:46:00 Пост 1343
Принципиально - согласен.
Вот только зачем оговаривать способность среды колебаться?
Разве есть среды в которых колебания невозможны?
VIP 09.07.2012 в 19:55:26 Пост 1354
Конечно,
таких сред нет. Но, для нас с Вами сейчас важно то, что волны есть
колебания среды, в которой эти волны распространяются. То есть волны и есть сама среда, но не вся, а только колеблющаяся её часть.
Уважаемый vpd44!
Пошли
вторые сутки, а реакции на эту фразу нет. За это время Вы
комментировали множество вопросов и доводов, но этот самый главный
обошли стороной.
Поэтому я вынужден повторить вопрос: Вы согласны
с тем, что волны есть колебания среды, в которой эти волны распространяются, то есть, волны и есть сама среда (или часть этой среды)?
Если согласны, то достаточно Вашего
да. \\\
---------------------------------------------------------------
----------------------------------------------------------------
---------------------------------------------------------------
- зачем они занимаются этим, я не понимаю,
ищут ответы друг у друга вместо того чтобы прочитать
определения.
Недалёкие и то знают
что распространение волны в среде
называется - возмущение среды.
Ибо слово волна по определению может быть - на границе между сред, - морская
между воздухом
и водой,
или в виде изменения плотности - звуковая волна,
радио волна - изменение плотности эфира,
а вот уже ударная волна - это возмущение среды,
и
скорость звука - это скорость возмущения воздуха,
скорость света это - скорость возмущения эфира -
я не понимаю как можно не оделять мух от ...,
и котлеты
от мух .
---
ru.wikipedia.org/wiki/Волна
Волна́ изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в
...
---
- Re: Черная дыра
(А.П. Васи,
23.07.2012 23:15, 2.4 КБайт)
Давече прочел очередную статью одного вчённого
который думает что он профессор.
На столько в отрыве от техники что уже термины придумывает
так как не
знает базовой терминологии.
---
http://www.computerra.ru/own/wiebe/695353/
\\\А вот в астрономии на них попадаешь постоянно. Одним из основных
компонентов космической пыли считаются минералы, содержащие кремний и
кислород. Основанием для такого вывода служат наблюдения в ИК-диапазоне:
колебания связи Si-O в теле пылинки эффективно излучают или поглощают
фотоны с длиной волны около 10 микрон. Соответственно если пылинка
излучает сама, в спектре на 10 микронах появляется горб; если она
поглощает фоновое излучение, в спектре на 10 микронах появляется провал.
В английском языке можно не заморачиваться конкретной ситуацией и
говорить просто про "10 micron feature". (Да-да, тоже в спектрах тоже
есть "фичи".) А как эти горбы-провалы назвать по-русски? Спектральная
особенность? Нет, это как-то не так. Получается, что 10-микронная "фича"
особенность, а бальмеровский скачок не особенность?\\\
---
А вот ответ
http://www.gelezo.com/electricity/540000/543000/543090/polosovoiy_filtr_i_rejektorniiy_filtr.html
\\\Полосовой фильтр
- это частотночувствительная схема, которая пропускает узкий диапазон. частот
в окрестности центральной резонансной частоты (fr)
Все другие частоты ниже
или выше узкой полосы пропускания значительно подавляются. Типичная характеристика
полосового фильтра показана на рисунке 24-1А.

Рис. 24-1.
Режекторный фильтр представляет
собой противоположность полосовому фильтру. Он подавляет или устраняет сигналы,
частоты которых попадают в узкий диапазон с центральной частотой fc.
Все частоты выше и ниже центральной частоты фильтр пропускает с минимальным
ослаблением (см. рис. 24-1 В). Режекторный фильтр иногда называют вырезающим
фильтром, поскольку этот фильтр используется для вырезания или режекции мешающего
сигнала одной частоты.\\\
- Re: Черная дыра
(А.П. Васи,
23.07.2012 23:23, 644 Байт)
\\\Соответственно если пылинка
излучает сама, в спектре на 10 микронах появляется горб;\\\
- Ясный конь что это называется полосовое свечение, или полосовое излучение - на
10 микронах.
\\\ если она
поглощает фоновое излучение, в спектре на 10 микронах появляется провал.\\\
и дважды ясный конь что это называется - режекторное поглощение, или режекторная фильтрация
- на 10 микронах.
Даже по два словосочетания есть.
- Re: Черная дыра
(А.П. Васи,
23.07.2012 23:32, 1.4 КБайт)
Но есть ещё и третье название подобной ситуации - резонансное излучение,
и резонансная фильтрация.
---
Перевод
РЕЗОНАНСНОЕ ИЗЛУЧЕНИЕ
(резонансная флуоресценция, резонансное рассеяние, резонансная люминесценция) - фотолюминесценция,
при к-рой частота возбуждающего излучения w0 практически совпадает с частотой фотолюминесценции атома  , где
, где  и
и  -
энергии верхнего возбуждённого и нижнего (обычно основного) уровней
энергии атома. Р. н. впервые обнаружено в 1904 Р. Вудом (R. Wood) в
парах натрия.
-
энергии верхнего возбуждённого и нижнего (обычно основного) уровней
энергии атома. Р. н. впервые обнаружено в 1904 Р. Вудом (R. Wood) в
парах натрия.
---
- Re: Черная дыра
(А.П. Васи,
23.07.2012 23:36, 168 Байт)
\\\РЕЗОНАНСНОЕ ИЗЛУЧЕНИЕ\\\
http://dic.academic.ru/dic.nsf/enc_physics/4516/%D0%A0%D0%95%D0%97%D0%9E%D0%9D%D0%90%D0%9D%D0%A1%D0%9D%D0%9E%D0%95
Ссылка.
- Re: Черная дыра
(А.П. Васи,
25.07.2012 1:28, 743 Байт)
http://www.astronomy.ru/forum/index.php/topic,98240.0.html
Смешна картина наблюдается барышня альтернативщица
явно с астрономическим образованием, релятивистам вопросы
задаёт по большому взрыву. Модераторы самоустранились,
их грамотность улетучилась, и чтобы не опозорится как щенки в углы
по-забивались, а те кто встал на защиту релятивизма лепечет
что-то невнятное и по сути
вопроса смысла в их словах
не наблюдается.
- Re: Черная дыра
(А.П. Васи,
25.07.2012 1:53, 447 Байт)
Я достаточно качественно анализировал о том какая вселенная вечная
или имеет стартовое время. Пришел к выводу что это зависит от текущей
господствующей модели
и умственных особенностей индивидуума.
Предполагаю что половина может представить бесконечное пространство,
а половина не может, а может только говорить что может.
И собственно нет смысла даже переубеждать
в противоположном кого-то так как это не имеет смысла.
- Re: Черная дыра
(А.П. Васи,
25.07.2012 9:09, 1.7 КБайт)
А что я наблюдаю, плывёт гандолла и на ней
модератор плывёт.
-----------------------------------
Ответ #46 : Сегодня в 04:28:18
Тема закрыта. Валенок, если
Вы и дальше будете в этом разделе вести обсуждения в подобном тоне, я
Вам на некоторое время закрою доступ на форум. Сейчас этого не делаю,
поскольку тема была зачем-то перенесена сюда из другого раздела.
-----------------------------------------------------------
Вот так и всегда когда у релятивистов отсутствует аргументация
они предпочитают замять
вопрос для ясности.
А откуда аргументации взяться если теория большого
взрыва это обычная ни на чём не обоснованная выдумка.
Просто не замечают что в
астрономии
временной звездёж стоит в полный рост.
Точнее сказать временная конспирология обещаний и
бесполезные теории использующие не проверяемые
события в прошлом и так-же в будущем во времени.
Прямо анекдот напрашивается на эту ситуацию.
---
Альт и релятивист смотрят в телескоп.
У каждого
из них спрашивают что они в телескоп видят.
Альт говорит что видит звёзды.
А релятивист говорит что видит большой взрыв, первые
минуты, и если присмотреться
то и первые секунды
большого взрыва.
---
- Re: Черная дыра
(А.П. Васи,
25.07.2012 21:30, 2.1 КБайт)
Забанили барышню за то что попросила ответить на свои
вопросы по сути вопроса, забанили за менторский тон данной
просьбы. И забанили нагло, так как правилами
форума не запрещено
открывать новый форум на аналогичный который модератор забанил,
собственно модератор оборзел и придумал от себя правила
по которым и
забанил барышню.
---------------------------------
Ответ #1 : Сегодня в 10:43:12

Комментарий
модератора раздела
Тема
закрыта как повторное открытие закрытой модераторами темы. Поскольку
это грубое нарушение, госпожа Валенок отправляется отдыхать на двое
суток.
----------------------------------
Я лично нигде не читал что если модератор по какой-то причине
закрыл тему то нельзя открывать аналогичную.
Вот если тему закрыли пять лет назад а кто-то
через пять лет задаст похожий вопрос и его
на шару забанят как бешеную собаку.
Будьте бдительны
открывая темы проверяйте
не были ли подобные закрыты модераторами термин
давности я так понимаю не ограничен.
Здесь просто видно как модераторы очень
сильно боятся данной темы.
Модераторы просто за собой не замечают что они
сами борзеют по полной требуя от автора ответить на их вопрос
по сути и не
писать никаких других сообщений, а то забанят.
Модераторы не замечают за собой что они как недалёкие
не могут ответить на релятивистские вопросы по сути, а
сливают
в стиле не я придумал не мне и отвечать, хотя уверенны в правильности
релятивизма а обосновать не могут свою уверенность.
- Re: Черная дыра
(А.П. Васи,
26.07.2012 8:16, 1.4 КБайт)
------------------------------------
Ответ #829 : Сегодня в 01:16:31
Придумал парадоксальный вопрос по СТО и эффекту Допплера(ЭД).
-------------------
-------------------
Вот
модератор подобный идиотизм не удаляет а аплодирует.
Ибо на фоне недалёких они выглядят грамотеями.
Чтобы был понятен весь идиотизм данной ситуации объясняю.
Релятивистские теории типа то и сто основаны на том что свет состоит
из фотонов которые есть частицы летящие в пустоте, а эффект
Доплера был открыт задолго
до релятивизма и в авторском изложении
он для сред, в которых распространяются волны аналогичные звуку.
Собственно получается - релятивисты отказались от
среды, а эффект
Доплера это исключительно для сред, в связи с чем подобный вопрос
не имеет смысла так как в нём есть взаимное исключение.
- Re: Черная дыра
(В. А. Аксёнова,
26.07.2012 20:06, 159 Байт)
Я-абсолютный новичок на форуме..Недавно прочитала в научно-популярной книге,что пространство может расширятся быстрее скорости света. Действительно ли это так?
- Re: Черная дыра
(А.П. Васи,
26.07.2012 20:39, 733 Байт)
Относитесь проще.
Астрономия и астрономы кишат необоснованными идеями
и утверждениями - это называется недоказуемые постулаты.
Есть много теорий без физического
обоснования - это
сказка.
В данном случаи у Вас необоснованная сказка.
Собственно в астрономы не отбирают самых адекватных,
и нет никакого наказания
и запретов писать статьи
с откровенным и недоказуемым бредом явным идиотизмом,
или просто по неграмотности.
Также процветает временная конспирология когда
например
говорят что миллиард лет тому или через миллиарды лет после
будет то-то и то-то.
Надо относиться спокойно, астрономы люди хорошие
просто они
заблудились в своих необоснованных сказках.
- Re: Черная дыра
(А.П. Васи,
26.07.2012 20:47, 424 Байт, ответов: 1)
Если есть время могу посоветовать из адекватного -
Свет и пространство и о скорости света.
http://www.astronet.ru/db/forums/1244628
Сам придумывал, всё выдумка, рекомендую открывать
ссылки особенно с фото, по тексту можете пропускать
что не нравится или непонятно,
там собственно всё хаотично расположено.
- Re[2]: Черная дыра
(В. А. Аксёнова,
26.07.2012 21:09, 28 Байт)
Да Вы прям Пелевин какой-то!
- Re: Черная дыра
(А.П. Васи,
26.07.2012 21:48, 408 Байт)
Не думаю что качество моих рассказов высокое,
так как я даже не стараюсь, я в молодости фантастикой
увлекался, и мне что-то написать не составляет труда.
У
некоторых моих рассказов есть совсем другой смысл, так
как авторство у писателей автоматически распространяется на 70лет,
то некоторыми короткими рассказами я
блокирую своим авторством
данные вопросы при моём приоритете.
- Re: Черная дыра
(В. А. Аксёнова,
27.07.2012 10:24, 564 Байт)
Дело не в качестве,а во взглядах.Он тоже критиковал большой взрыв и чёрные дыры.Но к теории большого взрыва приводит простейшее линейное уравнение движения. Отсюда определяют
и возраст. 13,8 млрд лет.Это самое простое решение. СТО гласит,что никакой сигнал не обгонит луч света. Но о пространстве речь не идёт.Объект А 1689-zD1 удаляется от нас в
8 раз быстрее скорости света (так в книге зарубежных правда астрономов написано) Но сама вселенная может расширятся с такой огромной скоростью.Просто нельзя использовать это
расширение ,чтобы обогнать луч света.
- Re: Черная дыра
(А.П. Васи,
27.07.2012 19:27, 28.3 КБайт)
Скажу Вам по секрету я черные дыры закрыл полностью,
только я статью по этому поводу писать не хочу.
--------------
Re: Черная дыра 19.09.2011 12:14
Что меня удивляет, - так это то что вся астрофизика красивая и пушистая,
и всё прекрасно.
Но это же не так, вот те-же черные дыры - это же
просто пипец - и что это никто не замечает или никто не
понимает.
Хочу сразу спросить, Ваше мнение по
...Черная дыра...
http://www.astronet.ru/db/msg/1188232
Согласны ли Вы с этим?
Какие из перечисленных статей соответствуют стандартам Черной
Дыры?
1 Есть ли жизнь в черной дыре
http://www.popmech.ru/article/8822-est-li-zhizn-v-chernoy-dyire/
2[ссылка]
Установлена масса самой крупной из сверхмассивных черных дыр.
Такое нам и не снилось.
3[ссылка]
Мифология черных дыр.В нашей Галактике существуют миллионы черных дыр
массой в несколько солнечных
4http://www.popmech.ru/article/8140-raspad-dyiryi/
Распад дыры.
Взрыв сверхновой может заканчиваться образованием не одной, а сразу
нескольких черных дыр.
5[ссылка]
Детство черной дыры
Взрыв, зафиксированный в глубинах космоса 31 год назад, судя по всему,
знаменовал рождение черной дыры самой молодой из нам известных
6[ссылка]
Темный центр
Таинственный центр нашей галактики,
место обитания сверхмассивной черной дыры и источник мощнейших потоков излучения,
преподносит новые сюрпризы.
7[ссылка]
Небольшое замечание о природе гравитации приводит к следствиям
космического масштаба к выводам о рождении новых миров из черных дыр
8[ссылка]
Обычная по размерам черная дыра выбрасывает
колоссальные потоки излучения и частиц.
9[ссылка]
Астрофизики предложили способ (теоретически) уничтожить черную дыру
10[ссылка]
Из всех сверхмассивных черных дыр лишь около 1% выбрасывают
значительные количества энергии
11[ссылка]
Выживающие дыры
Пара редких экземпляров
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
каким-то чудом выживающих в соседстве с этим монстром.
12[ссылка]
Как живется внутри черной дыры? Вы и сами знаете,
как: если справедливы новые теоретические выкладки,
вся наша Вселенная может находиться внутри черной дыры,
расположенной в другой Вселенной. Эдакая матрешка мироздания.
13[ссылка]
Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину. Это дало цифру в 10103, тоже огромную, но все-таки на много
порядков ниже.
14[ссылка]
Если очень, очень быстрый космический корабль разогнать
почти до скорости света, превратится ли он в черную дыру?
15[ссылка]
Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
---
---
---
Re: Черная дыра 19.09.2011 12:38
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2 В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика M87. В
ядре галактики, предположительно, находится чёрная дыра. На снимке видна
релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие магнитных
полей с аккреционным диском вокруг чёрной дыры или нейтронной звезды.
В статье на Элементах методом численного моделирования показано, что при слиянии
двух нейтронных звёзд образуется черная дыра, магнитное поле которой вытянуто
вдоль оси. Это наводит на мысли, что этот же процесс может формировать и
релятивистские струи. Тем не менее, в статье говорится, что предложенная
авторами научной работы математическая модель оказалась очень сложна, а
вычислительные возможности современных компьютеров оказались недостаточны, чтобы
с должной точностью провести все необходимые расчеты и убедительно доказать
формирование струй.
В другой статье на Элементах проводятся параллели между процессами в черных
дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат может
коллапсировать (слипаться) и при последующем его распаде тоже могут возникать
узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение: удивительно
большая доля компактных источников показывала сверхсветовое движение, в то время
как на основании простых геометрических доводов получалось, что только несколько
процентов таких объектов должно быть случайно ориентировано почти вдоль линии
зрения. Присутствие симметричных протяжённых радиокомпонент предполагало, что
они обеспечивались энергией от центрального источника двух симметричных лучей.
Но трудно сравнить светимость приближающейся и удаляющейся (или даже
стационарной) компонент. Это очевидное различие обычно обсуждается в контексте
модели с двойным истечением [4], когда излучение из ядра рассматривается как
стационарная точка, где приближающийся релятивистский поток становится
непрозрачным. Сверхсветовое движение наблюдается между этой стационарной точкой
в сопле и движущимися волновыми фронтами или другими неоднородностями в
выходящем релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное
излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких
энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил - зачем добру
пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной дыры будет ещё и
преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества. Излучение
Хокинга - другой процесс. Странно, что за 7 лет "увлечения астрофизикой" Вы
этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает
рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о Черных
Дырах говорит что излучение в основном из фотонов - а все другие говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а третий
говорит из гамма частиц - я должен слушать исключительно автора Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский
вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не хотят,
- так на неудобные вопросы отвечать должен будет автор, а при интерпретации
автора - писака например статьи с левыми идеями в области Черных Дыр,
прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и
не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее, разумеется,
не они сами, а аккрецирующее вещество. ЧД так и обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя как
рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная переменность
рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей черную
дыру с массой около десяти солнечных, в состоянии, когда рентгеновская
светимость понижена, а рентгеновский спектр жесткий и степенной, наблюдается
быстрая иррегулярная переменность рентгеновского потока на временах порядка
миллисекунды. Наблюдения, выполненные с бортов современных рентгеновских
обсерваторий, таких, как ГИНГА, МИР-КВАНТ, ГРАНАТ, АСКА, показали, что
рентгеновские спектры аккрецирующих черных дыр систематически более жесткие, чем
спектры аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя как
рентгеновский пульсар. Однако, если нейтронная звезда обладает слабым магнитным
полем (напряженностью менее 1010 Гс) или если ее ось вращения неудачно
ориентирована относительно земного наблюдателя, при аккреции на такую нейтронную
звезду могут не наблюдаться регулярные пульсации рентгеновского излучения.
Поэтому отсутствие строго периодических пульсаций рентгеновского излучения - это
лишь необходимый, но не достаточный признак черной дыры. В то же время при
слабом магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного вещества,
приводящие к явлению рентгеновского барстера I типа - коротким (длительностью
порядка 1-10 с) и мощным вспышкам интенсивности рентгеновского излучения, что
также является характерным признаком аккрецирующей нейтронной звезды, обладающей
твердой поверхностью. Поскольку черная дыра не обладает твердой поверхностью,
аккреция вещества на нее не должна приводить к феномену рентгеновского барстера
I типа. Разумеется, отсутствие этого феномена также является лишь необходимым
критерием наличия черной дыры. Таким образом, мы можем сформулировать важнейшие
признаки аккрецирующей черной дыры: это мощное рентгеновское излучение, большая
масса (более трех солнечных), отсутствие феноменов рентгеновского пульсара или
рентгеновского барстера I типа. При этом вопрос о надежном определении массы
релятивистского объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц (тормозное
излучение), либо при высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в рентгеновских трубках. Основными
конструктивными элементами таких трубок являются металлические катод и анод
(ранее называвшийся также антикатодом). В рентгеновских трубках электроны,
испущенные катодом, ускоряются под действием разности электрических потенциалов
между анодом и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных частиц
- необходим удар материи на скорости одной десятой и более скорости света.
Из чего следует невозможное условие для излучения материи при падении в черную
дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей, близких к
с. В таком случае трения более чем достаточно для излучения высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не
аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную
Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не об что
тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой или
одной третей скорости света, может прекрасно летать на орбите вокруг Черной
Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько сильно,
что вторая космич. скорость (параболическая скорость) для находящихся в этой
области тел должна была бы превышать скорость света, т.е. из Ч.д. ничто не может
вылететь - ни излучение, ни частицы, ибо в природе ничто не может двигаться со
скоростью, большей скорости света. Границу области, за к-рую не выходит свет,
наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают звезды,
при этом излучают, и что в центре галактики в черных дырах масса больше чем
масса всех звезд в этой галактике, а с момента большого взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в черных дырах
- этого никто не наблюдал, - не наблюдали и то как звезда проходит через
горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить
как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после образования Н. з.,
её масса может со временем значительно увеличиться. При ${mathfrak
M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет устойчивость и в результате
релятивистского гравитационного коллапса превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном из
нейтронов. Существование Н. з. было предсказано в 30-х гг. 20 в.,вскоре после
открытия нейтрона. Однако только в 1967 г. они были обнаружены в виде импульсных
источников радиоизлучения - пульсаров. Затем было установлено, что Н. з.
проявляют себя также как рентгеновские пульсары (1971 г.) и вспышечные источники
рентг. излучения - барстеры (1975 г.). Не исключено, что на одной из стадий
существования Н. з. явл. источниками гамма-всплесков. К 1984 г. открыто ок. 400
Н. з., из них ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а
остальные в виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в тесных
двойных звёздных системах. Перетекание вещества со звезды-компаньона на белый
карлик постепенно увеличивает его массу, и, когда она достигает ${mathfrak
M}_Ч$, белый карлик превращается в Н. з. В этом случае ${mathfrak
M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет устойчивость и в результате
релятивистского гравитационного коллапса превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие собой
вращающиеся нейтронные звезды с сильным магн. полем, излучающие за счет аккреции
(падения вещества на их поверхность). Магн. поля на поверхности Р.п. ~ 1011-1014
Гс. Светимости большинства Р.п. от 1035-1039 эрг/с. Периоды следования импульсов
P от 0,7 с до неск. тысяч с. Р.п. входят в тесные двойные звездные системы,
вторым компонентом к-рых явл. нормальная (невырожденная) звезда, поставляющая
вещество, необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы (этим
компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная звезда не
проявляет себя как Р.п. Рентг. пульсары встречаются как в массивных молодых
двойных звездых системах, относящихся к населению I Галактики и лежащих в ее
плоскости, так и в маломассивных двойных системах, относящихся к населению II и
принадлежащих к сферич. составляющей Галактики. Р.п. открыты также в
Магеллановых Облаках. Всего открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам присваивались
наименования по созвездиям, в к-рых они находятся. Напр., Геркулес X-1 означает
первый по рентг. яркости объект в созвездии Геркулеса, Кентавр Х-3 - третий по
яркости в созвездии Кентавра. Р.п. в Малом Магеллановом Облаке обозначается как
SMC X-1, в Большом Магеллановом Облаке - LMC X-4. Обнаружение со спутников
большого числа рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в Крабе и
Парусах, излучают и в рентг. диапазоне, см. Пульсары), излучающих за счет
энергии вращения замагниченной нейтронной звезды и увеличиващих свой период со
временем, Р.п., излучающие за счет аккреции, ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял
-не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую подготовку в
рамках хотя бы школы. У Вас такая подготовка, судя по всему, хромает на обе
ноги, поэтому Вы не понимаете большинство статей. Для уточняющих вопросов есть
комментарии, для базовой подготовки - школа и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы читать -
то надо быть доктором наук, и в тоже самое время Вы лично не можете ответить
прямо на прямые вопросы, по этой статье. Вы меня в принципе заинтриговали, я
подумаю чтобы такой пузырь высосать из пальца в рамках парадигмы, чтобы все
вокруг аж зааплодировали за исключительно высокохудожественный идиотизм в рамках
бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы доказательств
которые позволяют определить какими были в первые моменты большого взрыва
звезды, черные дыры , температура и другие различные свойства пространства и
свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой простой
вопрос по обсуждаемой статье, то я не обязан верить написанному, а скорее
наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к астрофизике, то
они все в астрофизике - дилетанты, которые идеи вбрасывали в астрофизику от
случая к случаю, и серьёзно ей ни кто не занимался. По этому вся астрофизика и
состоит из разрозненных идей, - озарялок, которые последователи пытаются
состыковывать между собой по причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей разных, что
могу делать выводы что высоска из пальца, а что и супер грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы водород
выгорает. И астрофизики внятно ответить не могут причину по которой самый легкий
водород - преодолевает гравитацию становится тяжелее всех металлов и летит в
ядро звезды поучаствовать в ядерной реакции. И В то что самый легкий водород
преодолевает летит внутрь звезды -я не верю, хоть в миллионе книжек это будет
написано, и тысяче учебников. Так как написанное не подтверждено физическими
свойствами а противоречит им.
---
- Re: Черная дыра
(А.П. Васи,
27.07.2012 19:32, 6.9 КБайт)
|
|
Re: Черная дыра
|
12.02.201214:35 |
|
Ответ #154 : Вчера в 16:04:25
А теперь Вы нам расскажите, как в законе Хаббла V=H*R проявляются квантовые
свойства фотона полагаю - никак. В этом и проблема на мой взгляд.
А теперь Вы нам расскажите, как закон Хаббла важнее и выше каких-то там квантовых свойств
фотона.
Полагаю, закон Хаббла в рамках данной темы просто важнее и выше, каких-то там квантовых свойств фотона. И
пока Вы не объясните, как в законе Хаббла проявляются квантовые
свойства фотона, здесь нет смысла говорить об этих квантовых свойствах.
Ответ #183 : Сегодня в 12:59:49
Станислав Кравченко, внятный
ответ дайте, пожалуйста. Не просто предложение со словами "фотон" и
"закон Хаббла", а внятный ответ. Прекрасный случай показать другим
пример адекватного физического подхода.
--------------------------
Модератору в моск ударило желание не выглядеть
идиотом, а самый грамотный релятивист, затупил по полной,
и в итоге
задали дилетанту вопрос суть которого в том
почему релятивисты когда хотят, а когда не хотят и в некоторых случаях
применяют одни физические свойства, а на другие
забивают,
а когда им надо для чего-то другого они на тоже самое
чихать хотели а акцентируются на другом.
Вот и требуют от дилетанта им объяснить почему
они иногда бывают
больные на всю голову, и просят их ввести в состояние здравомыслия,
точнее сказать вывести из состояния идиотизма.
Вот такая жестокая
селяви.
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Черная дыра
|
12.02.201215:24 |
|
Всё равно слово фотон с физической точки зрения
простым физическим опытом - сливается в канализацию физики,
а тот кто его применяет - будет
топтаться на месте
ибо не проводит физический анализ используемую
физическую сущность, а верят определениям,
сказал например один математик что свет состоит
из частиц,
так сразу лохи и зарукоплескали и поверили на слово,
математиками высосанным из пальца выдумкам ради
подтверждения своих теорий нужны, а лохи думают
что математики пальцем в небо попали, и что физика
такая как математики придумали, и потом начинают
соединять выдуманную математику с реальной физикой,
и не понимают почему они занимаются одним и тем-же
столетиями - да удел недалёких.
-------------
Как я ранее писал - фотон - не имеет физического смысла,
- обосновать это, - было легко.
Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а
говорится что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою скорость что
наблюдается например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица которая потеряла скорость, просто так взять и
при вылете из стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами. Так что фотон
как частица - выдумка чистой воды.
Вывод -
в пространстве распространяются колебания среды, и световое
излучение не движется а образуется от взаимодействия колебаний
среды и материала, как в 1800 году говорил
Томас Юнг.
Так что все что написано в астрофизике без учета среды - к
сожалению не правильно. | |
- Re: Черная дыра
(А.П. Васи,
27.07.2012 19:40, 5.3 КБайт)
Итого
что имеем - есть большой взрыв который предопределил
изначально состав водорода и гелия во вселенной, 70% и 30%.
\\\К концу второго периода, то есть через 5
минут после Большого Взрыва,
расширяющееся вещество состоит из ядер атома
водорода 70% и ядер гелия 30%. \\\
http://mrcnn.narod.ru/bigbang.htm
Заданна необратимость изменения материи всё должно превратится в железо.
Заданна нелинейность - чем больше концентрация тем быстрее идет
превращение
материи к железу.
Можно даже сказать по другому чем больше выделилось энергии из
звезды тем больше звезда переработала водорода и гелия.
---------------------------------------------
\\\

Эволюция звезды класса G на примере
Солнца
[]
Материал из Википедии свободной энциклопедии\\\
-------------------------------------------------------------------------------
http://4put.ru/view-max-picture.php?id=767124


Итого что точно известно - состав солнца по
спектру в верхнем слое солнца.
------------
И вот вопрос -
---------------------------------------
---------------------------------------
---------------------------------------
Ответ #28 : Вчера в 20:41:18
Очень хотелось бы узнать мнение Дмитрия Вибе в отношении проблемы:
A)
Какую начальную массу имело Солнце в момент своего рождения?
B) И о динамике эволюции параметра величины массы Солнца тоже.

Чем Вас не устраивает
масса в одну массу Солнца, мало меняющаяся в ходе эволюции?
------------------------------
------------------------------
------------------------------
Релятивисты своими же теориями и не могут обосновать причину возраста.
---
Учитывая как долго по одному вопросу страдают,
и из этого вопроса не переходят на следующий для
получения причинно следственной связи то это пипец логики.
Да я в своё время послал в даль и по полной
всю эту
лабуду.
Я естественно напомню про спектр, ширину, смещение
поглощения на спектре и пики в спектре, и напомню
то как используют спектр - хуже
не придумать
для определения расстояний до звёзд -
чем дальше тем краснее - для альтернативщиков
астрономы сделали подарок и сами релятивисты
никогда
не поймут как спектр использовать по другому и зачем,
а их ошибка -
она всегда на виду но чтобы её заметить надо отказаться от
релятивизма и модели звезд,
и идеи Хаббла.
Хотя ещё надо заметить что всё высосано из пальца что касается
космических дат и прошедшего времени жизни звезд.
Возраст земли - не обосновано
Возраст материи - не обосновано
Возраст между большим взрывом и началом солнца - не обосновано
Возраст солнца - не обосновано
- Re: Черная дыра
(А.П. Васи,
27.07.2012 19:44, 2.6 КБайт)
| Re: Спиральная галактика NGC 1672: вид в телескоп им.Хаббла
|
16.05.201211:44 |
|
\\\Не
лозунг,
а
пожелание.
Выскажетесь
по
теме.
Сводима
ли
астрономия
к
физике.
Информация
о
электромагнитных
полях
и
излучениях
(физика)
есть
источник
астрономических
знаний,
но
к
ним
не
сводятся
астрономические
объекты
(астрономия),
которые
имеют
своё
строение,
развитие,
несут
в
себе
свой
смысл.\\\
По теме так по теме.
Я для примера текущей неадекватности перемешанной с глупостью
планетарного масштаба возьму черные дыры.
Автор
придумал черные дыры, сказал что у этих дыр есть излучение в основном из фотонов.
После этого какие-то псевдо соавторы решают что источники рентгеновского излучения в
космосе
это тоже черные дыры.
Я вот не понимаю - некуда девать рентгеновские звезды - назовите рентгеновские
звезды от Васи Пупкина заодно и увековечили бы
себя в астрономии, а то решили
что это черные дыры.
После этого придумывают что у черной дыры нет поверхности и материя из звезд туда падает
вечно при этом
излучается рентгеновское излучение.
Что имеем по факту, возьмём цветной телевизор, внутри него разгоняются как в ускорителе
частицы, ударяются в итоге об маску
или люминофор экрана, со скоростью 0.3 скорости света,
при этом это частицы 27 кило электрон вольт, что собственно соответствует высокому
напряжению на маске кинескопа
- высокое так сказать.
При ударении частиц о маску или люминофор происходит незначительное рентгеновское излучение,
этот эффект называется - тормозное излучение,
так как при резком торможении частицы летящие разбиваются
на более мелкие, вот эта мелюзга и есть рентгеновское излучение.
То-есть получается что в первый
раз наплевали на авторский вариант излучения,
во втором случаи сказав что у черной дыры нет поверхности , наплевали на физику,
ибо чтобы с поверхности черной дыры
излучалось рентгеновское излучение,
то надо чтобы тормозное излучение было со скоростями большими чем в цветном
телевизоре, а это скорость больше 0.3С. Следовательно
падение на поверхность черной
дыры будет стремительное, и для излучения рентгеновского у черной дыры обязана быть поверхность.
|
- Re: Черная дыра
(А.П. Васи,
27.07.2012 19:46, 34.0 КБайт)
Более развёрнуто по черным дырам,
чтобы так сказать проникнутся в самую глубину абсурда ситуации.
------------------------------------------------------------------------------
http://www.astronet.ru/db/forums/1188232?page=7
---
Что меня удивляет, - так
это то что вся астрофизика красивая и пушистая,
и всё прекрасно.
Но это же не так, вот те-же черные дыры - это же
просто пипец - и что это никто не замечает
или никто не
понимает.
Хочу сразу спросить, Ваше мнение по
...Черная дыра...
http://www.astronet.ru/db/msg/1188232
Согласны ли Вы с этим?
Какие из перечисленных статей соответствуют стандартам Черной
Дыры?
1 Есть ли жизнь в черной дыре
http://www.popmech.ru/article/8822-est-li-zhizn-v-chernoy-dyire/
2[ссылка]
Установлена масса самой крупной из сверхмассивных черных дыр.
Такое нам и не снилось.
3[ссылка]
Мифология черных дыр.В нашей Галактике существуют миллионы черных дыр
массой в несколько солнечных
4http://www.popmech.ru/article/8140-raspad-dyiryi/
Распад дыры.
Взрыв сверхновой может заканчиваться образованием не одной, а сразу
нескольких черных дыр.
5[ссылка]
Детство черной дыры
Взрыв, зафиксированный в глубинах космоса 31 год назад, судя по всему,
знаменовал рождение черной дыры самой молодой из нам известных
6[ссылка]
Темный центр
Таинственный центр нашей галактики,
место обитания сверхмассивной черной дыры и источник мощнейших потоков излучения,
преподносит новые сюрпризы.
7[ссылка]
Небольшое замечание о природе гравитации приводит к следствиям
космического масштаба к выводам о рождении новых миров из черных дыр
8[ссылка]
Обычная по размерам черная дыра выбрасывает
колоссальные потоки излучения и частиц.
9[ссылка]
Астрофизики предложили способ (теоретически) уничтожить черную дыру
10[ссылка]
Из всех сверхмассивных черных дыр лишь около 1% выбрасывают
значительные количества энергии
11[ссылка]
Выживающие дыры
Пара редких экземпляров
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
каким-то чудом выживающих в соседстве с этим монстром.
12[ссылка]
Как живется внутри черной дыры? Вы и сами знаете,
как: если справедливы новые теоретические выкладки,
вся наша Вселенная может находиться внутри черной дыры,
расположенной в другой Вселенной. Эдакая матрешка мироздания.
13[ссылка]
Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину. Это дало цифру в 10103, тоже огромную, но все-таки на много
порядков ниже.
14[ссылка]
Если очень, очень быстрый космический корабль разогнать
почти до скорости света, превратится ли он в черную дыру?
15[ссылка]
Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
--------------------
Это из моего спора на форуме на популярной механике.
| Re: Черная дыра
|
19.09.201112:38 |
|
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили,
что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в
электронных оболочках атомов или молекул. Оба эффекта используются в
рентгеновских трубках. Основными конструктивными элементами таких трубок
являются металлические катод и анод (ранее называвшийся также
антикатодом). В рентгеновских трубках электроны, испущенные катодом,
ускоряются под действием разности электрических потенциалов между анодом
и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных
частиц - необходим удар материи на скорости одной десятой и более
скорости света.
Из чего следует невозможное условие для излучения материи при падении в
черную дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей,
близких к с. В таком случае трения более чем достаточно для излучения
высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не
об что тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой
или одной третей скорости света, может прекрасно летать на орбите
вокруг Черной Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько
сильно, что вторая космич. скорость (параболическая скорость) для
находящихся в этой области тел должна была бы превышать скорость света,
т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в
природе ничто не может двигаться со скоростью, большей скорости света.
Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают
звезды, при этом излучают, и что в центре галактики в черных дырах
масса больше чем масса всех звезд в этой галактике, а с момента большого
взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в
черных дырах - этого никто не наблюдал, - не наблюдали и то как звезда
проходит через горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после
образования Н. з., её масса может со временем значительно увеличиться.
При ${mathfrak M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном
из нейтронов. Существование Н. з. было предсказано в 30-х гг. 20
в.,вскоре после открытия нейтрона. Однако только в 1967 г. они были
обнаружены в виде импульсных источников радиоизлучения - пульсаров.
Затем было установлено, что Н. з. проявляют себя также как рентгеновские
пульсары (1971 г.) и вспышечные источники рентг. излучения - барстеры
(1975 г.). Не исключено, что на одной из стадий существования Н. з. явл.
источниками гамма-всплесков. К 1984 г. открыто ок. 400 Н. з., из них
ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а остальные в
виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в
тесных двойных звёздных системах. Перетекание вещества со
звезды-компаньона на белый карлик постепенно увеличивает его массу, и,
когда она достигает ${mathfrak M}_Ч$, белый карлик превращается в Н. з. В
этом случае ${mathfrak M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие
собой вращающиеся нейтронные звезды с сильным магн. полем, излучающие за
счет аккреции (падения вещества на их поверхность). Магн. поля на
поверхности Р.п. ~ 1011-1014 Гс. Светимости большинства Р.п. от
1035-1039 эрг/с. Периоды следования импульсов P от 0,7 с до неск. тысяч
с. Р.п. входят в тесные двойные звездные системы, вторым компонентом
к-рых явл. нормальная (невырожденная) звезда, поставляющая вещество,
необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы
(этим компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная
звезда не проявляет себя как Р.п. Рентг. пульсары встречаются как в
массивных молодых двойных звездых системах, относящихся к населению I
Галактики и лежащих в ее плоскости, так и в маломассивных двойных
системах, относящихся к населению II и принадлежащих к сферич.
составляющей Галактики. Р.п. открыты также в Магеллановых Облаках. Всего
открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам
присваивались наименования по созвездиям, в к-рых они находятся. Напр.,
Геркулес X-1 означает первый по рентг. яркости объект в созвездии
Геркулеса, Кентавр Х-3 - третий по яркости в созвездии Кентавра. Р.п. в
Малом Магеллановом Облаке обозначается как SMC X-1, в Большом
Магеллановом Облаке - LMC X-4. Обнаружение со спутников большого числа
рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в
Крабе и Парусах, излучают и в рентг. диапазоне, см. Пульсары),
излучающих за счет энергии вращения замагниченной нейтронной звезды и
увеличиващих свой период со временем, Р.п., излучающие за счет аккреции,
ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял -не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую
подготовку в рамках хотя бы школы. У Вас такая подготовка, судя по
всему, хромает на обе ноги, поэтому Вы не понимаете большинство статей.
Для уточняющих вопросов есть комментарии, для базовой подготовки - школа
и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы
читать - то надо быть доктором наук, и в тоже самое время Вы лично не
можете ответить прямо на прямые вопросы, по этой статье. Вы меня в
принципе заинтриговали, я подумаю чтобы такой пузырь высосать из пальца в
рамках парадигмы, чтобы все вокруг аж зааплодировали за исключительно
высокохудожественный идиотизм в рамках бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы
доказательств которые позволяют определить какими были в первые моменты
большого взрыва звезды, черные дыры , температура и другие различные
свойства пространства и свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой
простой вопрос по обсуждаемой статье, то я не обязан верить написанному,
а скорее наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к
астрофизике, то они все в астрофизике - дилетанты, которые идеи
вбрасывали в астрофизику от случая к случаю, и серьёзно ей ни кто не
занимался. По этому вся астрофизика и состоит из разрозненных идей, -
озарялок, которые последователи пытаются состыковывать между собой по
причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей
разных, что могу делать выводы что высоска из пальца, а что и супер
грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы
водород выгорает. И астрофизики внятно ответить не могут причину по
которой самый легкий водород - преодолевает гравитацию становится
тяжелее всех металлов и летит в ядро звезды поучаствовать в ядерной
реакции. И В то что самый легкий водород преодолевает летит внутрь
звезды -я не верю, хоть в миллионе книжек это будет написано, и тысяче
учебников. Так как написанное не подтверждено физическими свойствами а
противоречит им.
|
- Re: Черная дыра
(А.П. Васи,
27.07.2012 20:44, 1.4 КБайт)
Вот как бывает небольшое высказывание а как
нагнуло всех релятивистов.
---
 Re: Новое открытие в теории пространства-времени, закрывающее СТО
Re: Новое открытие в теории пространства-времени, закрывающее СТО
Ответ #48 - Сегодня :: 18:55:38
Patrice писал(а) Сегодня :: 10:25:25:Это к кому обращено?
Это в пустое пространство Пуанкаре. Даже эха не дождёшься.
---
Для тех кто не понял как сильно нагнули
релятивистов с большим
взрывом.
Что собственно в - \пустоте\ - \постоянно\ - \ отражает\- \реликтовое излучение\,
- это самый жестокий и беспощадный удар
по теории большого взрыва.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 12:25, 769 Байт)
В.А.Аксёнова
\\\Но к теории большого взрыва приводит простейшее линейное уравнение движения.\\\
Ну что заметили что весь фундамент из здания астрофизики
не имеет физического смысла,
и оно валится по полной, а здание то заполнено релятивистами.
Я в принципе удивлен как так получилось что труд тысяч ученных
на протяжении ста лет оказался бессмысленным и бесполезным.
Не понятно почему они рогом уперлись
в несколько направлений,
и не меняли модели каждые двадцать - тридцать лет.
Да и особого труда не составило чтобы
обосновать нелогичность физического смысла
у моделей,
так сказать порвать все книжки по астрофизике в клочья, как мавпа газету.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:42, 3.2 КБайт)
| Re: Черная дыра
|
12.02.201219:24 |
|
\\\Полагаю, закон Хаббла в рамках данной темы просто важнее и выше, каких-то там квантовых свойств фотона.\\\
Расскажу правильный ответ на
этот вопрос, -
Изначально был общепринятый
эфир, на основании колебательных свойств света в
эфире аналогичных звуку в воздухе Томас Юнг объяснил
интерференцию света на двух очень близко расположенных
щелях. В связи с тем что например солнечный свет
проходил через щели, и было место где накладывалось
изображение солнца от двух близко расположенных щелей.
Опыт когда рисуют точечный источник света, а расстояние
между щелями больше диаметра источника
света - не корректный,
он только на рисунках, на практике он не возможен, так
как световые колебания не искривляются на щелях, свет
проходит сквозь щель
прямо. Этому подтверждение
школьный опыт по физике, когда делается маленькая дырка
и берется черный ящик без задней стенки и калька,
в черном ящике располагается
напротив дырки калька,
и изображение получается перевернутым,
и если сделать рядом еще одну дырку, получится
два изображения перевернутых, которые наложатся
друг
на друга - это и называется интерференция.
Так вот, после этого надо было сказать что объяснение интерференции
Томаса Юнга не корректно, и опровергнуть,
чего не было сделано.
Просто за-постулировали для пустоты что движутся световые
частицы. За-постулировали так за-постулировали, но появился
нюанс который
не решается для частиц, так как надо объяснить
интерференцию для солнца на двух щелях на расстоянии например
3мм между щелями. И что , и то что для фотонов надо
придумывать
дополнительные свойства, на уровне потенциала, то-есть фотоны
будут плюсовые и минусовые, при этом все пройдет.
Но здесь возникает следующий нюанс,
если частица со знаком
плюс или минус то они должны отклонятся
магнитным полем, - если поднести магнит к лучу,
например минусом то плюсовые фотоны должны
притягиваться
к магниту а минусовые отталкиваться, то-есть луч расширится,
- чего не наблюдается - вот такая жестокая селяви.
И что в итоге получаем
для красного смещения или закона Хаббла,
аж ничего, так как если расширяется, то должна уменьшаться
скорость фотонов - это невозможно так как это повлияет на
скорость света, а скорость света за-постулирована стабильной,
и не зависящей ни от чего. Что делать релятивистам? объяснять
то надо, остается через потерю напряженности
фотонов,
точнее электро-потенциалов, но дело в следующем в
этом случаи всё равно не может изменится частота, может
изменится только амплитуда разности, а
частота останется.
Вот и продолжают огород городить, и очень не хотят при расширении
считать что фотоны как частицы должны скорость менять,
- с моей точки
зрения - шикарный самозаклин от математиков.
|
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:47, 2.9 КБайт)
| Re: Черная дыра
|
13.02.201216:46 |
|
А теперь я посчитаю на сколько получается
разница при определении размеров звезд
методами красного смещения и Хаббла.
--------------------
Удалённость
Солнца от Земли, 149,6 млн км
диаметр Солнца = 1 391 000 километров.
А теперь посмотрим как недалёкие астрономы
даже обладая высококачественной
техникой
делают выводы о размере SN1987a c
большими перегибами, чувствуется что здравый
смысл они положили на полку, но зато в теории
вписались.
---
http://astroprofspage.com/archives/744

---
http://planetologia.ru/sverhnova/1332--qq-sn-1987a.html
\\\Располагаясь на расстоянии 168 тыс.
световых лет от
Земли в галактике Большое Магеллановое
облако, сверхновая
SN 1987A дает ученым детальную информацию о том, как
доживают свои дни большие звезды. Звездой-предшественником
SN 1987A был голубой сверхгигант
Sanduleak -69 202 с массой
около 17 масс Солнца.\\\
\\\Они изучали взаимодействие образовавшихся от взрыва звезды
диаметром около 9,6 триллионов километров
колец газа,
окружающего сверхновую.\\\
Так вот, я думаю что размер предшествующей звезды был
два диаметра солнца(17 масс Солнца), после взрыва форма
звезды изменилось,
она приобрела дискообразный вид, диаметр диска с краёв
у которого происходят выбросы - после взрыва размер образовавшегося диска
с выбросами
по краям равен два с половиной диаметра солнца.
Диаметр диска с выбросами по фотографии в два раза меньше
диаметра колец и в трактовке современной парадигмы,
следовательно диаметр звезды в форме диска с выбросами
по краям от астрономов в парадигме равен 4.8 триллионов
километров.
Вот что у меня подучилось
"диаметр Солнца = 1 391 000 километров"
два с половиной диаметра солнца и равно 3.47 млн. км.
А у тех астрономов даже не 4.8 миллиардов километров,
- диаметр что в тысячу раз было бы больше моего анализа,
у них в миллион раз
размер больше не моего расчета - а в миллион раз больше
здравого смысла.
И смешно смотреть на эту клоунаду,
и о каких мелких вопросах вращения можно рассуждать
при ошибке на расстоянии 168 тыс.световых лет в - миллион- раз,
то
на сколько они могут ошибаться со своими зетами
для высосанных из пальца фотонов на больших расстояниях.
|
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:52, 635 Байт)
http://elementy.ru/lib/430551
Рисунок 1.

А вот за такие вещи я считаю что физиков фабрикующих
такие рисунки без опытов по которым они проводились
надо
лишать званий и запрещать пожизненно преподавательскую
деятельность, и работу в области физики.
Это ж надо до чего додумались, рисуют и им нас
рать что
это обычный лохотрон, они считают что это хорошо,
а пипл хавает оптики и астрофизики довольны, а мне смешно.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:57, 2.1 КБайт)
Рассказ
Фантастический сон о городе физиков.
Приснился город физиков, он состоял из одной центральной улицы,
которая разделяла
пустынные дикие просторы
классической физики,
и плодоносящие сады релятивистской физики.
По пустынным просторам классической физики скитались какие-то
голодранцы несколько было по
двое и по трое но в основном одиночки,
ходили что-то писали на песке, кое кто из альтернативщиков проводил
какие-то опыты на костре пока готовили еду.
Практически
все альтернативщики периодически и с разным успехом
участвовали в форумах
"скай-тюх" и "звездомер".
Эти участки дороги отличались разметкой
улицы, и наличием забора
со стороны релятивистов на "звездомере", забор на "звездомере" не
для того чтобы альты не лазили, а для того чтобы
сомневающиеся
релятивисты не смогли убежать от модераторской порки. Возле форумной
разметки с обеих сторон периодически стояли толпы зевак и приходили
ораторы
то с той а то с другой стороны.
На "скай-тюхе" демократии было побольше и все орали друг на друга и периодически
рвали на себе одежду и бросали через
дорогу, там в неё вышмаркивались и бросали
обратно.
На "звездомере" рерятивисты после меряний телескопами и после обеда в гос
столовой, пододвигались
и подкатывались на своих креслах к дороге,
чтобы лучше слышать.
По средине уличной разметки "звездомеровского" форума стоял - плёточных
шмаганий
мастер, - несравненный модератор Би-Бе. Он славился тем что от
прямых вопросов уходил своими ответами в интеллектуальное бегство.
От альтернативщиков он требовал
дать ему посмотреть тех паспорт на эфир,
и предоставить опыты за которые можно нобелевскую получить ещё вчера.
Естественно запрос на релятивистский тех-паспорт
на причину скорости света вызывает
шатание в креслах и бубнение релятивистов о том что в нем нет смысла,
а смысл есть в паспорте на эфир.
Так собственно
в непонимании и смотрели друг на друга.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:57, 2.1 КБайт)
Рассказ
Фантастический сон о городе физиков.
Приснился город физиков, он состоял из одной центральной улицы,
которая разделяла
пустынные дикие просторы
классической физики,
и плодоносящие сады релятивистской физики.
По пустынным просторам классической физики скитались какие-то
голодранцы несколько было по
двое и по трое но в основном одиночки,
ходили что-то писали на песке, кое кто из альтернативщиков проводил
какие-то опыты на костре пока готовили еду.
Практически
все альтернативщики периодически и с разным успехом
участвовали в форумах
"скай-тюх" и "звездомер".
Эти участки дороги отличались разметкой
улицы, и наличием забора
со стороны релятивистов на "звездомере", забор на "звездомере" не
для того чтобы альты не лазили, а для того чтобы
сомневающиеся
релятивисты не смогли убежать от модераторской порки. Возле форумной
разметки с обеих сторон периодически стояли толпы зевак и приходили
ораторы
то с той а то с другой стороны.
На "скай-тюхе" демократии было побольше и все орали друг на друга и периодически
рвали на себе одежду и бросали через
дорогу, там в неё вышмаркивались и бросали
обратно.
На "звездомере" рерятивисты после меряний телескопами и после обеда в гос
столовой, пододвигались
и подкатывались на своих креслах к дороге,
чтобы лучше слышать.
По средине уличной разметки "звездомеровского" форума стоял - плёточных
шмаганий
мастер, - несравненный модератор Би-Бе. Он славился тем что от
прямых вопросов уходил своими ответами в интеллектуальное бегство.
От альтернативщиков он требовал
дать ему посмотреть тех паспорт на эфир,
и предоставить опыты за которые можно нобелевскую получить ещё вчера.
Естественно запрос на релятивистский тех-паспорт
на причину скорости света вызывает
шатание в креслах и бубнение релятивистов о том что в нем нет смысла,
а смысл есть в паспорте на эфир.
Так собственно
в непонимании и смотрели друг на друга.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 17:58, 1.9 КБайт)
Продолжение
Рассказ
Фантастический сон о городе физиков.
Дальше у дороги релятивисты поставили трибу своих достижений
с трубными
фанфарами.
На фанфарах
разные надписи, - без которых релятивизм
был бы невозможен.
Чтобы уйти от эфира придумали фанфары ---- "вакуум"
Чтобы уйти от света который был
в эфире, придумали фанфары --- "фотон"
Так как не смогли придумать
куда тепло девается от звезд,
придумали фанфары
- ---"большой взрыв",
тепла у звезд оказалось много
и чтобы поглощать ещё тепло
от звезд придумали фанфары -
--- "черная - дыра"
а энергии оказалось ещё больше,
придумали фанфары ---" ускоренное расширение",
и непонятно
чем притягивается
токмо по два тела придумали фанфары --- "гравитация".
А на против трибуны с фанфарами располагался зрительный зал
смеха
релятивистов, так как на трибуну с фанфарами периодически
забегали одичавшие альты, они прибегали с той стороны дороги,
со стороны классической физики. И когда
одичавшие альты в своих
возмущенных речах использовали слова исключительно для
релятивистов, и они совпадали с надписями на фанфарах, то вместо
слов они
дули в фанфары релятивистов.
Некоторые дикие альты целые релятивистские концерты
устраивали и выдували фуги , гораздо
лучше некоторых релятивистов. Релятивисты
особо сильно
смеялись когда дикие альты использовали все слова.
Вдруг зависли в воздухе удары плетью, мастер Би-Бе на "звездомере"
шмагал
всех подряд а чтобы уважали.
Собственно так и жили, классическая сторона - пустыня бедности,
и релятивистские фруктовые сады с шоколадными кабинетами.
По дороге то там то там пробегали бобры, их по дружески били
телескопами с любой стороны улицы.
Вот я и проснулся.
- Re: Черная дыра
(В. А. Аксёнова,
28.07.2012 20:02, 256 Байт)
Черепащук говорил по телевидению,что чёрные дыры -это гипотетические объекты.Их называют кандидатами в чд. Так что астрономы понимают ,что их наука ,рассуждения о пространстве
граничат с эзотерикой.Но они не могут без этого. Забавный рассказ Вы сочинили.
- Re: Черная дыра
(А.П. Васи,
28.07.2012 22:25, 6.0 КБайт)
Чтобы вы были в курсе на сегодняшний день официально
не обнаружена ни одна черная дыра, догадались почему,
- собственно они и сами не знают как она должна выглядеть.
Но в тоже самое время столько премий вручили за черные дыры
и на достаточные суммы, вот наберите в гуглях премия за черные дыры.
---
http://ria.ru/science/20080118/97279705.html
Размер премии составляет 500 тысяч долларов. В этом году сумма была
поделена между двумя номинациями. Первая половина премии была присуждена
за достижения в области математики, вторая половина - за достижения в
области астрофизики Рашиду Сюняеву.
Максим Концевич (Институт высших научных исследований, Франция) и Эдвард
Уиттен (Институт высших исследований Принстона, США) получили свою
половину премии за исследования различных типов геометрических объектов
и, в частности, за решение ряда математических проблем, связанных с
развитием теории струн.
Присуждение премии Крафорда Сюняеву является признанием огромного вклада
ученого в исследование экстремальных процессов, происходящих во
Вселенной, - аккреции (падении) вещества на компактные объекты: черные
дыры и нейтронные звезды.
Читайте далее:
http://ria.ru/science/20080118/97279705.html#ixzz21wUMU4rh---
http://lenta.ru/news/2012/01/19/prize/
В Швеции объявлены лауреаты премии Крафорда, присуждающейся за открытия в
области астрономии, математики, а также биологии, наук о земле и
исследований методов лечения полиартрита. В 2012 году награда вручена и
астрономам и математикам. Основания присуждения премии указаны в
пресс-релизе
призового комитета Шведской королевской академии наук. Денежный
эквивалент премии составляет 4 миллиона шведских крон (около 400 тысяч
евро).
Астрономической награды удостоились Рейнхард Генцель (Reinhard Genzel) и
Андреа Гез (Andrea Ghez). Премия была присуждена этим ученым за
обнаруженные ими и их сотрудниками весомые доказательства того, что в
центре Млечного Пути находится сверхмассивная черная дыра. Оба астронома
наблюдали звезды, обращающиеся вокруг центра Галактики, и пришли к
одному и тому же выводу независимо друг от друга.
---
При всём при том что обнаружение черных дыр - ожидается, и нобелевская за открытие
черных дыр ещё никому не присуждена.
---
http://news.grimuar.info/%D0%BD%D0%B0%D0%B1%D0%BB%D1%8E%D0%B4%D0%B5%D0%BD%D0%B8%D1%8F-%D0%B7%D0%B0-%D1%87%D0%B5%D1%80%D0%BD%D0%BE%D0%B9-%D0%B4%D1%8B%D1%80%D0%BE%D0%B9-%D1%81-%D1%80%D0%B5%D0%BA%D0%BE%D1%80%D0%B4%D0%BD%D1%8B%D0%BC-%D1%80%D0%B0%D0%B7%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC-544.html
Астрономы
с обсерватории в Чили с телескопа APEX одновременно с астрономами с
телескопа расположенного на Гавайях (США) и с телескопа, расположенного в
штате Аризона (США) провели наблюдения и получили рекордное разрешение
снимков глубин космоса.
Провели они это наблюдение за ядром
удаленного квазавра 3C 279, чтобы получить снимки сверхмассивных черных
дыр. Снимки получились с рекордным разрешением, которое превышает
человеческое зрение в 2 миллиона раз. Этот квазар содержит в центре
огромную черную дыру, с массой примерно превышающую солнечную в миллиард
раз. Находится эта свермассивная черная дыра на расстоянии 5 миллиардов
лет от нас.

Об этом сообщили в пресс-релизе Европейской южной обсерватории,
которой принадлежит телескоп APEX. В этом пресс-релизе отмечается, что
эти снимки имеют рекордное разрешение, которое может сейчас быть
получено. Высокое разрешение было получено из-за того что наблюдение
было одновременно проведено сразу с трех телескопов и все эти три
инструмента образовали интерферометр, а так же наблюдение провели в
радиодиапазоне 1,3 мм, которое еще не использовали для таких наблюдений.
В результате получилось разрешение, которое может различать детали в 2
миллиона раз мельче, чем может различить человеческий глаз.
Это открыло новый этап на пути к исследованию недр глубокого космоса.
Теперь появился новый проект, по которому соединят большее число мощных
телескопов и создадут, так называемый, Телескоп горизонта. Ученые
надеятся, что в этом проекте они смогут зарегистрировать изображение
тени сверхмассивной черной дыры. Особенно им интересно будет наблюдать за
черной дырой, которая находится в центре нашей галактики.
Как сказал в интервью директор Государственного астрономического
института Анатолий Черепащук, в ближайшие годы немало астрономов будут
награждены Нобелевскими премиями. Я жду, - сказал он - что в ближайшее
десятилетие будет получена Нобелевская премия за открытие черных дыр. Мы
к этому подходим все ближе и ближе. Во-первых, этих черных дыр уже как
собак нерезаных. Для звездных черных дыр измерены массы, даны
ограничения на размеры. А сверхмассивных черных дыр в ядрах галактик
уже многие тысячи. Самое главное надо измерить процессы вблизи
горизонта событий, только так можно доказать, что это черная дыра.
---
- Re: Черная дыра
(А.П. Васи,
29.07.2012 10:12, 1.2 КБайт)
\\\Но о пространстве речь не идёт.Объект А 1689-zD1
удаляется от нас в
8 раз быстрее скорости света (так в книге зарубежных правда астрономов
написано) Но сама вселенная может расширятся с такой огромной
скоростью.Просто нельзя использовать это
расширение ,чтобы обогнать луч света.
\\\
Не в обиду Вам будет сказано,
с моей точки зрения - дикое мракобесие в Ваших словах,
Вашей вины в этом нет абсолютно, Вы это всё прочитали
и думаете что так оно есть на самом деле, - а если я Вам
скажу что законы Ньютона в космосе не работают, Вы же
мне не поверите, - хотя на самом деле они
там не работают,
кометы и астероиды не притягивают вообще никак.
Сказки перемешанные с идиотизмом используются для продвижения
своих нелогичных и необоснованных
теорий и моделей в астрофизике,
и это нормальная общепринятая тенденция,
наказаний за враньё и откровенный бред не существует.
Собственно по этой причине
и запретили преподавание астрономии
в школах, - чтобы не травмировать детскую психику - явным бредом
перемешанным с необоснованными выдумками, нескладушками и
идиотизмом.
- Re: Черная дыра
(В. А. Аксёнова,
29.07.2012 19:24, 890 Байт)
Кометы не притягиваются? А как же комета,которая распалась на куски и упала на Юпитер? По причине гравитации они и вращаются вокруг Солнца.
Чёрные дыры -гипотетичные
объекты,но как сказал на лекции С.Попов, надо было бы придумать ещё более экзотические объекты для объяснения многих явлений. Время покажет ,наверное. А по поводу Большого
взрыва, может быть, Вам будет интересно прочесть книгу Стивена Вайнберга "Первые три минуты" из серии Открытия,которые потрясли мир. Он очень подробно исследует
там реликтовое излучение. И призывает серьёзно отнестись к его открытию. Возможно,вы прочитали уже .Но интересно издание 2011 г.Эксмо. Там вносятся коррективы ,связанные с
изменениями взглядов физиков после её написания.Очень хорошо объясняет излучения.Как будто он внутренним зрением видит все эти ангстремы,и ты тоже начинаешь их как бы видеть.
Это очень ценно.
- Re: Черная дыра
(А.П. Васи,
29.07.2012 20:15, 1.7 КБайт)
Вы пожалуйста прочитайте то что я Вам рекомендовал,
там написано что бывают тела которые притягивают
а бывает которые не притягивают, их отличает тепловое
сальдо - те которые притягивают выделяют тепла больше чем
получают от солнца.
Юпитер и Солнце притягивают а вот тела которые меньше 500-100
км в диаметре
- могут быть только притягиваемыми, но сами они
не обладают притяжением.
Вот сами подумайте зачем мне кого-то слушать о черных дырах
если я могу почитать
авторский вариант, а то что каждый придумывает
себе о черной дыре - никакого отношения к черным дырам не имеет -
как автор сказал - только так оно и есть.
\\\А по поводу Большого
взрыва, может быть, Вам будет интересно прочесть книгу Стивена Вайнберга "Первые три минуты"\\\
Вы ж не держите меня уж за полного идиота, я же понимаю
что никто
не жил миллиарды лет тому и уж никто не покидал пределы солнечной системы,
- эти первые три минуты уж полная высоска из пальца.
Большой же
взрыв не от туда пошел, придумали свч приемник направили в космос
он фонил на определенной частоте, потом набежали на эту ситуацию как на халяву со своими
теориями
объясняющими эту ситуацию. Потом после взрыва бомбы решили обыграть эту ситуацию
по аналогии взрыва бомбы - вот так и получилась теория большого взрыва.
Вы
понимаете ещё какой нюанс - у релятивистов в пространстве пустота
и отражаться там собственно нечему - по простому при отказе релятивистов
от среды - эхо в пустоте
невозможно.
Вы кстати я смотрю совсем недалеки в астрономии - Вам рекомендую
прочесть и этот форум от начала и до конца.
- Re: Черная дыра
(А.П. Васи,
29.07.2012 20:38, 4.9 КБайт)
В.А.Аксёнова
Уважаемая прочтите ещё раз внимательно что я написал здесь
Начиная с
Re: Черная дыра 27.07.201220:32
Это всё для Вас
кратко о большом взрыве
черных дырах и расширении.
Вот например я привел отрывок разговора на форуме.
Вы вникайте, - здесь ответов больше на Ваши вопросы
чем в книжках
по двести страниц.
---
\\\
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
\\\
- Re: Черная дыра
(В. А. Аксёнова,
29.07.2012 22:18, 218 Байт)
Никто не жил миллиарды лет назад и никому не верите-странно ,что Вы читать научились))) .Всё знать нельзя. Я -любитель. И у меня мало времени.С. Попов весёлый,он с юмором.Я
была на 2 его незабываемых лекциях.Спасибо.
- Re: Черная дыра
(А.П. Васи,
29.07.2012 22:58, 1.1 КБайт)
Вы очень доверчивая и легко внушаемая, в астрофизике
таких как Вы разводят по полной, и таких как Вы ждут на всех
лекциях и все лекторы.
Чтобы Вы были
в курсе 10-15 процентов будут верить всегда
официальной науке, и столько же никогда не будут верить,
какая бы ни была наука и что-бы она не изучала,
- это
так было всегда и всегда будет.
Я смотрю что Вам надо рассказать с самого начала,
вся астрофизика которую Вы знаете
это ничем необоснованная выдумка.
Вся астрономия это набор некоторых придуманных моделей
которые ни на чём не обоснованны а за постулированы.
Неужели Вы думаете что ядро железное внутри
Земли
или Солнца кто-то видел, - это просто придумали
что они там должны быть, так как это надо для некоторых
теорий у которых нескладушки с массой и металлами.
Постулат это когда автору взбрело в голову что-то, и он из это-го
пытается обосновать всё остальное не объясняя физическую причину.
Вот например если
есть в какой-то теории постулат не обоснованный физически -
то это всё - торба, результата не будет никогда.
- Re: Черная дыра
(В. А. Аксёнова,
30.07.2012 11:16, 756 Байт)
Нет.Мне нельзя внушить то ,что не соответствует логике,свойственной моему сознанию.И я хорошо понимаю,что вся математика также опирается на постулаты. Как на очевидное,но
недоказуемое.Физика основывается на наблюдениях и экспериментах. Астрономия и астрофизика-на наблюдениях,физике и математике.И сплетается цепочка в логически обоснованную
картину. Но иногда интерпретации могут быть неоднозначные.Тогда ждут новые наблюдения.Это Вы конечно,знаете. Железное ядро должно объяснить наличие магнитных полей.Вселенная
хранит некоторую информацию о своих ранних моментах.И информацию об этом несут э\м волны. А не верят официальной науке совсем? мне кажется люди с определённым складом,с другой
логикой. Все могут ошибаться.История науки -борьба идей.
- Re: Черная дыра
(А.П. Васи,
3.08.2012 21:27, 871 Байт)
http://www.computerra.ru/own/wiebe/697220/
\\\. Отсутствие системы популяризации достижений российской науки - и
академической, и университетской - и необходимость создания такой
системы и сейчас представляются мне очевидными вещами.\\\
\\\Больше же всего претензий вызвало якобы высказанное мною предложение
создавать в институтах РАН пресс-службы за счёт и средствами самих
институтов.\\\
Не знаю может кто не понял что на гандолле нынче задвигает тот что гребёт, я популярно
расскажу.
Работает в институте, в тоже самое время
модерит и в тоже самое время пишет популярные
статьи в журналы, и журналы отстёгивают, и вот пришла идея что ещё должны зарплату пуполизаторам
платить те институты
о которых будут статьи в журналах. Ясный конь что можно оформится
в двадцать институтов по трудовому, - красапета.
- Re: Черная дыра
(А.П. Васи,
4.08.2012 9:40, 369 Байт)
\\\А не верят официальной науке совсем? мне кажется люди с
определённым складом,с другой
логикой.
Все могут ошибаться.История науки -борьба идей.\\\
Это борьба математиков с математиками
в физике, а физику в физике бороться ни
с кем
не надо, у него нет конкуренции
- он просто рассказывает.
- Re: Черная дыра
(А.П. Васи,
7.08.2012 0:13, 8.9 КБайт, ответов: 2)
Модератор опять забанил достаточно логичный форум.
---
МЕТОДОЛОГИЯ АСТРОНОМИИ И ФИЗИКИ
Евгений Алексеевич
Тихомиров
Введение.
Являясь полпредом обывателя и проанализировав положение дел в науке,
пришёл к выводу, что в настоящее время науки астрономия и физика
находится в состоянии стагнации. Этому обстоятельству способствует
принятая методология науки. Рассмотрим, чем же обусловлен застой в
науке.
Целью науки является получение новых знаний о природе. Обычный ход научных исследований включает в себя следующие
этапы:
Наблюдение (эксперимент) ----- новые знания ----- теория ----- другие новые знания.
Возникает
вопрос, зачем вообще нужна теория, ведь новые знания уже получены из
наблюдений или экспериментов. Однако с помощью теории учёные, во-первых,
объясняют выводы, следующие из наблюдений или экспериментов,
во-вторых, учёные после разработки теории смотрят, не появятся ли другие
новые знания, но теперь уже, как следствие и приложение теории. Таким
образом, отметим, что теория является инструментом учёного для
объяснения явлений природы и получения других новых знаний о природе.
Однако с течением времени учёные внедряются в сферы, где
непосредственный эксперимент затруднён или вообще невозможен. Например,
структура атома или, ещё меньше, структура элементарной частицы. Как
можно наблюдать структуру электрона, например? Ответ никак. Или,
например, возьмём планету Земля. Как бы мы не хотели, мы не можем
заглянуть в центр Земли и посмотреть, как там всё устроено, и что там
происходит? Я уже не говорю о чёрной дыре. Поэтому в астрономии и физике
обычный ход научных исследований, приведенный выше, нарушается, длинная
цепочка укорачивается и на первое место выходит теория, а эксперимент
(наблюдение) начинает играть вспомогательную роль, как средство проверки
теории, по следующей схеме:
теория ----- эксперимент (наблюдение)
Причём,
как мы установили ранее, непосредственные эксперименты и наблюдения
невозможны ввиду специфики наблюдаемых объектов, поэтому обычно
привлекаются косвенные эксперименты.
Подмена цели.
Итак, в науке постепенно произошла подмена цели. Многие исследователи
совершенно искренне полагают, что цель науки разработка теорий.
Появилась даже шутка: Если какой-либо факт не укладывается в теорию
тем хуже для факта. Однако целью науки как было, так и осталось
получение новых знаний о природе. Обывателю теория безразлична. Теория
нужна только самим учёным, как инструмент для получения новых знаний.
Поскольку теория инструмент, то она не может быть правильной или
неправильной (ниже будет показано, что все (все!) теории неправильные),
она может быть либо плохой, либо хорошей. Хорошая теория если с её
помощью можно получить новые знания о природе, и плохая - если с её
помощью не удаётся получить новых знаний. Подмена цели науки
отрицательно сказывается на самой науке. Постановка теории во главу угла
в науке способствует её стагнации. Теорий много их количество растёт,
но новых достоверных знаний о природе не прибавляется.
Отсутствие критерия истинности.
Иные учёные полагают, что критерием истинности какой-либо теории
является эксперимент, но, как мы установили ранее, ввиду специфики
наблюдаемых объектов, прямой эксперимент невозможен. Остаётся косвенный
эксперимент, но косвенный эксперимент можно объяснить и так, и эдак. Нет
критерия правильности интерпретации косвенного эксперимента. Например,
теория электронной проводимости проводников подтверждается целой кучей
косвенных экспериментов, подтверждающих якобы инерционность
электронов при резкой останове вращающейся катушки, рамки или диска. Но
кратковременный ток при остановке вращения, можно объяснить не
инерционностью электронов, а деформацией электронных орбиталей атомов
при резкой остановке.
Энгельс считал, что критерием истинности в
науке является практика, но и это неверно. Можно на практике чем-то с
успехом пользоваться, не обязательно зная и понимая, как оно работает.
Можно отлично управлять автомобилем ничего, не зная о двигателе
внутреннего сгорания. Так же и в науке, мы пользуемся электрическим
током на практике, плохо понимая, что же это такое электрический ток.
Таким образом, в науке нет критерия истинности. Если бы таковой критерий
был, то не было бы споров верна или нет, например, теория
относительности, или верна или нет теория струн. Некоторые исследователи
полагают, что правильность той или иной теории подтверждается
математикой, но так ли это?
Математизация науки.
Не секрет, что в настоящее время астрономия и, в особенности, физика в
значительной степени математизированы. Учёные альтернативного толка даже
усматривают в этом какую-то злонамеренность. Иногда их критика
математизации науки справедлива, т.к. за математикой иногда уже
невозможно рассмотреть физический смысл того или иного процесса. Но
математизация науки это объективный и вынужденный процесс.
Действительно, раз мы пришли к укороченной цепочке научных исследований,
то, выдвигая какую-то теорию, мы должны её хоть чем-то обосновать и
проверить, хотя бы на формальную логику и здесь без математики не
обойтись. Другими словами, теория это гипотеза, проверенная
математикой. Но может ли математика служить критерием истинности теории,
пусть даже математический аппарат её безупречен? Очевидно нет. Так
как математика не отвечает на вопрос существует или нет рассматриваемое
явление в природе, а только отвечает на вопрос, что то, или иное явление
может существовать в природе. Математика подтверждает лишь внутреннюю
непротиворечивость теории.
Все теории неверны.
Откуда берутся теории? При укороченной схеме научных исследований,
очевидно, что теории берутся из головы. Другими словами, учёные просто
придумывают теории, проверяя свои гипотезы на внутреннюю
непротиворечивость и формальную логику математикой. Но при таком подходе
они только случайно могут, что-то угадать и попасть в соответствие с
природой. В настоящее время Интернет полон критикой всех существующих
ортодоксальных теорий. И эта критика не безосновательна. Альтернативные
учёные в пух, и прах громят Специальную теорию относительности, Общую
теорию относительности, Теории струн и суперструн, Теорию и Закон
всемирного тяготения, Молекулярно-кинетическую теорию, Циклы Карно и так
далее и тому подобное. Однако, все теории, которые альтернативные
учёные выдвигают взамен ортодоксальных теорий, можно подвергнуть такой
же уничтожающей критике и даже в большей степени. Поэтому я
сформулировал методологический закон, который называется Закон
Тихомирова. Этот закон состоит из двух пунктов.
Закон несостоятельности теорий (закон Тихомирова)
Пункт 1. Любая теория неверна,
и рано или поздно обнаружит свою
несостоятельность.
Пункт 2. Если кому-то кажется, что какая-то теория верна. Или кто-то думает, что
он выдвигает правильную теорию, смотри пункт 1.
Где
же выход из этого исхода? Всё вышеизложенное, говорит о кризисе в
науке. Положение, на первый взгляд, безнадёжное и остаётся ждать, когда
учёные методом тыка придумают что-нибудь похуже коллайдера и разнесут
нашу планету Земля на кусочки. Но, выход есть это прислушаться к
информации извне, и работать по этой информации. Другого пути нет.
----------
Ответ #1 : Вчера в 23:32:36
Тема закрыта и будет вскоре удалена. Художественная литература и знания извне не входят в тематику раздела.
-----------
Я бы сказал что гандольер испугался откровенной темы.
Что-то мне подсказывает что такие закрытия и баны альтов скорей
всего
планируются, под-отчётные и спонсируются.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
10.08.2012 21:25, 4.2 КБайт)
Дружище А.П.Васи, спасибо за поддержку, но я не альт, а полпред
обывателя. Однако раз Вы затронули этот вопрос, то вкратце разберём кто такие
альты и орты. А потом перейдём к чёрным дырам.
Не
секрет, что в настоящее время в науках астрономия и физика существуют две
политические партии: альты (альтернативщики) и орты (ортодоксы). Только не
рассказывайте мне, что наука далека от политики. Как любые политические партии
альты и орты стремятся к власти. В настоящее время у власти в науке,
естественно, орты, а альты стремятся эту власть захватить и сделаться ортами.
Чтобы долго не парится, объясняя научные пристрастия ортов и альтов, приведу их
гимны, которые я написал для них.
Гимн альта
Вставай ортами зачморённый
Весь мир обиженных альтов.
Кипит наш разум просвещённый,
Он орту в морду дать готов.
Припев: И это наш не последний, но решительный бой,
Когда от эфира воспрянет
альт лихой.
Весь мир ортовский мы разрушим
До основания, а затем,
Мы наш альтовский ми построим,
ОТО не нужно нам совсем.
Припев.
Никто не даст нам избавленья:
Ни РАН, ни Дума, ни конвой,
Добьёмся мы опроверженья
ОТО эфирною волной.
Припев.
Лишь мы, работники альтовской,
Огромной партии ума,
Владеть Землей имеем право,
А ортодоксы никогда.
Припев.
Гимн орта
Вихри эфирные веют над нами,
Злобные альты нас вечно гнетут,
В бой роковой мы вступили с альтами,
Нас ещё альты к суду привлекут.
Но мы поднимем гордо и смело
Знамя борьбы за ОТОвское дело
Знамя великой борьбы эстэотов
За лучший мир, без альтов идиотов.
Припев: (2 раза)
На бой с альтами
С ними козлами,
Марш, марш вперёд
Ортовский народ.
Нам ненавистны альтовы укоры,
Цепи квантов мы с достоинством чтим.
Кровью ортовской залитые тропы
Кровью ужасных альтов обагрим.
Месть беспощадная всем эфиристам,
Всем паразитам квантующих масс,
Мщенье и смерть всем альтам-классицистам
Близок победы торжественный час.
Припев.
Альты и орты, каждый, имеют свои ресурсы в Интернете, где и
резвятся. Альты иногда захаживают на форумы к ортам, а орты к альтам.
Начинается склока, которая обычно заканчивается баном неугодного. Поскольку в
моей работе, которую процитировал дружище А. П. Васи, показано, что в
астрономии и физике нет критерия истинности теорий, то эта работа направлено на
примирение ортов и альтов. Действительно все теории не верны как ортовские, так
и альтовские.
Теперь о чёрных дырах. Орты считают, что чёрные дыры, это
массивные объекты, которые до того массивны, что не даже свет не может их
покинуть. Альты считают, что чёрных дыр нет вообще в природе. И те и другие,
естественно, не правы, т.к. нет правильных теорий. По информации извне, которую
любезно доводит до нас Иван Васильевич
Пономаренко, чёрные дыры есть, но
они не излучают не потому, что их масса чрезвычайно велика, а потому, что
снаружи чёрной дыры отрицательная материя (неправильное название тёмная
материя).
Чёрная дыра это пустотелый тор, который вращается с
высокой скоростью и растёт по массе, т.к. захватывает вещество через полюса
тора. Наконец, нахватавшись вещества, чёрная дыра разрывается из-за
центробежных сил в самом слабом месте, т. е. по экватору чёрной дыры. Из чёрной
дыры вырываются куски отрицательной материи, которые снаружи покрыты веществом.
Это будущие звёзды и планеты. Так рождаются галактики, а не из пылегазовых
облаков. Понятно, также почему галактики плоские, из-за того, что чёрная дыра
разрывается в одной плоскости по экватору.
Подробнее, господа, читайте на samlib.ru/t/tihomirow_e_a/
- Re[2]: Черная дыра
(Е. А. Тихомиров,
10.08.2012 22:37, 2.8 КБайт)
Дружище А.П.Васи, спасибо за поддержку, но я не альт, а полпред
обывателя. Однако раз Вы затронули этот вопрос, то вкратце разберём кто такие
альты и орты. А потом перейдём к чёрным дырам.
Не секрет, что в
настоящее время в науках астрономия и физика существуют две политические
партии: альты (альтернативщики) и орты (ортодоксы). Только не рассказывайте
мне, что наука далека от политики. Как любые политические партии альты и орты
стремятся к власти. В настоящее время у власти в науке, естественно, орты, а
альты стремятся эту власть захватить и сделаться ортами.
Альты и орты, каждый, имеют свои ресурсы в Интернете, где и
резвятся. Альты иногда захаживают на форумы к ортам, а орты к альтам.
Начинается склока, которая обычно заканчивается баном неугодного. Поскольку в
моей работе, которую процитировал дружище А. П. Васи, показано, что в
астрономии и физике нет критерия истинности теорий, то эта работа направлено на
примирение ортов и альтов. Действительно все теории неверны как ортовские, так
и альтовские.
Теперь о чёрных дырах. Орты считают, что чёрные дыры, это
массивные объекты, которые до того массивны, что не даже свет не может их
покинуть. Альты считают, что чёрных дыр нет вообще в природе. И те и другие,
естественно, не правы, т.к. нет правильных теорий. По информации извне, которую
любезно доводит до нас Иван Васильевич
Пономаренко, чёрные дыры есть, но
они не излучают не потому, что их масса чрезвычайно велика, а потому, что
снаружи чёрной дыры отрицательная материя (неправильное название тёмная
материя). Я надеюсь, господа, вы понимаете, что это не очередная альтернативная теория, а расшифровка поступающих сигналов на зрительные рецепторы Ивана Васильевича.
Чёрная дыра это пустотелый тор, который вращается с
высокой скоростью и растёт по массе, т.к. захватывает вещество через полюса
тора. Наконец, нахватавшись вещества, чёрная дыра разрывается из-за
центробежных сил в самом слабом месте, т. е. по экватору чёрной дыры. Из чёрной
дыры вырываются куски отрицательной материи, которые снаружи покрыты веществом.
Это будущие звёзды и планеты. Так рождаются галактики, а не из пылегазовых
облаков. Понятно, также почему галактики плоские, из-за того, что чёрная дыра
разрывается в одной плоскости по экватору.
Подробнее, господа, читайте на samlib.ru/t/tihomirow_e_a/
- Re: Черная дыра
(А.П. Васи,
10.08.2012 23:21, 1003 Байт, ответов: 2)
Да уж Вы меня насмешили по самое дальше некуда,
Вы что серьёзно думаете что физические задачи решаются
количеством или наличием авторитарности.
В физике
даже общепринятость не является знаком качества,
да и никто никого и никогда не спрашивал мнение о той или
иной теории, что собственно говорит о некомпетентности
всех и сразу.
А я вообще с Украины и я не ученный, и я от науки ничего
не жду, и мне ничего от неё и не надо, даже если мне коллайдер бы подарили,
он мне и пустой и с учёными и даром не нужен.
Если я и напишу популярную книжку по физике то она будет так дорога
что почувствуется сразу ценность качественной
физики.
А о черных дырах у Вас со мной поговорить не получится
так как я их все взял и разрушил, и показал всю их не обоснованность,
грубо говоря автор
черных дыр лопухнулся, и при детальном
рассмотрении авторского варианта его идеи не логичны и не физичны.
Прочитайте этот форум с начала.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
13.08.2012 17:18, 2.8 КБайт, ответов: 1)
| Цитата: |
А о черных дырах у Вас со мной поговорить не получится
так как я
их все взял и разрушил, и показал всю их не обоснованность,
грубо говоря автор
черных дыр лопухнулся, и при детальном
рассмотрении авторского варианта его идеи не логичны и не физичны.
|
Вы не оригинальны, дружище Вася, все альты не признают чёрных дыр. На одном альтовском форуме есть модератор под ником "Обезьяна с бананом" такая
же мразь, как Митя Биде, который на ортовском форуме. Так вот, эта Обезьяна с бананом, приводит целый списочек чего не должен признаваль настоящий альт. Итак, согласно этого
списка, альты стремятся изгнать из физики и астрономии:Большой взрыв,
Чёрные дыры,
Нейтронные звёзды,
Тёмную материю,
Дуализм
волна - частица, и многое другое. Но согласно информации извне, которую доводит до нас Иван Васильевич Пономаренко, всё это природные объекты.
Но
чёрные дыры не такие, какими представляют их орты, а другие, которые я уже описал. Подробнее смотрите на samlib.ru/t/tihomirow_e_a/
Вы, дружище,
говорите, что Вы не учёный, это правильно Вы - политик. Наукой можно управлять и не учёному. К тому же Вы хотите разбогатеть, дорого продавая научную книжку по физике. Но
если вы не будете управлять наукой, эту книжку никто не купит, ведь надо же раскрутить бренд этой книжки. Вы говорите, что Вам не нужен коллайдер. Это правильно. Зачем он
Вам? Вам нужен большой кабинет с ковром. На этот ковёр Вы, дружище, будете вызывать академиков, стучать кулаком по столу и вопить: "Почему ещё до сих пор не открыта Звезда
эфира Александра. Я ведь вам уже сто раз объяснял, что такая звезда эфира должна быть открыта".
Как ни странно, хотя орты и альты
используют одинаковую научную методику (выдумывают всё из головы), но у альтов больше правильных представлений о мироздании, чем у альтов. Это потому, что у ортов есть тормоз
- математика, которая ограничивает их фантазии. У альтов, такого тормоза нет и их фантазии безграничны. Одна Звезда эфира, чего стоит!
К сожалению,
у ортов накопились большое количество грубых ошибо, которые, если не исправить, будут задерживать науку. Поэтому ортам надо работать в тесном контакте с Иваном Васильевичем
Пономаренко, который доводит до нас информацию извне,но орты игнорируют информацию вышних. Я лично писал Патону, что есть информация извне научного характера, но никакого
ответа не получил. Ортовские академики - это старпёрды, которым ничего не надо (у них уже всё есть). Определённо надо реформировать РАН и НАН Украины.
- Re[3]: Черная дыра
(Е. А. Тихомиров,
13.08.2012 19:06, 541 Байт)
Как ни странно, хотя орты
и альты
используют одинаковую научную методику (выдумывают всё из головы), но у альтов больше правильных представлений о мироздании, чем у альтов. |
Здесь опечатка. Следует читать: "Как ни странно, хотя альты и орты используют одинаковую научную методику (выдумывают всё из головы), но у ортов больше
правильных представлений, о мироздании, чем у альтов.
- Re: Черная дыра
(А.П. Васи,
11.08.2012 10:15, 1.9 КБайт)
\\\Чёрная дыра это пустотелый тор, который вращается с
высокой скоростью и растёт по массе, т.к. захватывает вещество через полюса
тора. Наконец, нахватавшись вещества, чёрная дыра разрывается из-за
центробежных сил в самом слабом месте, т. е. по экватору чёрной дыры. Из чёрной
дыры вырываются куски отрицательной материи, которые снаружи покрыты веществом.
Это будущие звёзды и планеты. Так рождаются галактики, а не из пылегазовых
облаков. Понятно, также почему галактики плоские, из-за того, что чёрная дыра
разрывается в одной плоскости по экватору.\\\
-----------
-------------
---------
Вот что собственно могу Вам сказать по тексту, Вы пишете о черных
дырах, и немножко
послали в даль автора черных дыр с его описанием черной дыры, Вы в данном
случаи в корне не правы. Вам никто не мешает Физическому описанию дать
новое название, например - пустотно торовый притягиватель.
Чтобы Вы были в курсе автор черных дыр дважды делал определение
черных дыр, второй раз к
нему подошли коллеги и попросили переделать
ибо под их теории не подходит, то-есть автор для своих черных дыр под внешним
влиянием уже сам сделал своей теории
нетрадиционную ориентацию, а потом
придумали современные физики что черные дыры это рентгеновские звёзды,
они с автором тоже не посоветовались, и как Вы даже
не читали авторское
определение черных дыр - что у черной дыры излучение преимущественно
из фотонов - излучение Хокинга, я кстати фотоны разбил вдребезги тоже.
Так я на одном форуме от одного клоуна услышал мысль что если
написали триста статей по черным дырам в духе того что они рентгеновские
звёзды то можно забить
болт на авторское определение черной дыры,
на что я этому недалёкому сказал что забить болт как раз нужно
на триста статей, а вот как автор черных дыр дал определение
черной
дыры так оно и останется вечно.
- Re: Черная дыра
(А.П. Васи,
12.08.2012 10:04, 1.8 КБайт)
\\\Не
секрет, что в настоящее время в науках астрономия и физика существуют две
политические партии: альты (альтернативщики) и орты (ортодоксы). Только не
рассказывайте мне, что наука далека от политики. Как любые политические партии
альты и орты стремятся к власти. В настоящее время у власти в науке,
естественно, орты, а альты стремятся эту власть захватить и сделаться ортами.
Чтобы долго не парится, объясняя научные пристрастия ортов и альтов, приведу их
гимны, которые я написал для них.\\\
Не правильное Ваше представление.
Есть наука физика, в физике есть классика - это когда всё просто и понятно,
с линейной последовательной причинно следственной связью.
В данном случаи в физике господствует релятивизм - в основе которого
мысленные опыты и мысленные
эксперименты.
Так-же постулированные теории без объяснения перво-причин.
Собственно отказ от среды в пространстве релятивистами и провозглашение
пространства
абсолютно пустым - это и есть отличие основное классической
физики у которой пространство заполнено средой эфиром, и релятивистской
физикой у которой в пространстве
пустота.
Естественно что при господстве релятивистов не может быть реферируемых
статей про эфир, так как референты - судьи в физике, и они решают что физично
а что нет.
Естественно в реферируемый журнал статью про эфир если принести,
то это всё равно что если -бы беспартийный на парт собрании коммунистов,
предложил бы вместо памятника Ленину, на центральной площади, поставить светофор.
- Re: Черная дыра
(А.П. Васи,
12.08.2012 17:55, 2.0 КБайт)
\\\Действительно все теории не верны как ортовские, так
и альтовские.\\\
Частично Вы правы, собственно все теории выдумка и они высосаны из пальца,
это как раз лично я всегда и говорю, а релятивисты утверждают
что их теории
от гениев.
Что собственно у релятивистов и произошло - при вере в редких гениев,
они все себя считали умственно слабыми и даже не думали о том
чтобы улучшить теории.
Если называть своими именами то консерватизм
релятивистов сыграл с ними плохую шутку, вместо того чтобы
возглавить науку
они её законсервировали релятивистскими
идеями, о чем свидетельствует то -
что, - отсутствуют институты
в которых учат студентов создавать новые теории.
С моей точки зрения релятивисты поздно встрепенулись, и поздно перестали
посылать альтов в даль. Их ждет бедность,
в смысле финансирования, ибо сто лет
никакие теории не меняются, и общество
просто прекратит финансирование астрономии
и фундаментальной физики полностью.
Собственно этого и следовало ожидать.
С альтами релятивисты уже не договорятся, релятивисты
альтам не интересны в смысле сотрудничества, а релятивисты
отказались с альтами сотрудничать в своё
время а теперь
пожинают то что не правильно оценили ситуацию,
и переоценили научные достижения релятивистов.
И релятивисты ещё в интеллектуальных кандалах
своих теорий которые навязали им специфическое мировоззрение
не имеющее ничего общего с реальностью.
Что собственно не даёт им правильно расставить
последовательность
приоритетов, без этого
никакая модель не получится.
---
Что на самом деле отсутствует как раз не разрозненные теории,
этой ерунды как грязи,
и все теории друг с другом не стыкуются
а то и противоречат друг другу.
Модели не хватает в которой охватываются и объединяются
и объясняются все физические
ситуации.
Релятивисты ещё не скоро раздуплятся в понимании слова модель,
они пока зависли на уровне мелких теорий.
- Re: Черная дыра
(А.П. Васи,
13.08.2012 20:45, 32.5 КБайт)
Вы уважаемый не делайте поспешных выводов,
если я сказал что я фотоны разбил интеллектуально
вдребезги то не сомневайтесь.
---
Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а
говорится что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою скорость что
наблюдается
например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица которая потеряла скорость, просто так взять и
при вылете из
стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами. Так что фотон
как частица - выдумка чистой воды.
---
И если я сказал что черные дыры разбил вдребезги
то тоже не сомневайтесь.
---
| Re: Черная
дыра
|
19.09.201112:38 |
|
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили,
что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в
электронных оболочках атомов или молекул. Оба эффекта используются в
рентгеновских трубках. Основными конструктивными элементами таких трубок
являются металлические катод и анод (ранее называвшийся также
антикатодом). В рентгеновских трубках электроны, испущенные катодом,
ускоряются под действием разности электрических потенциалов между анодом
и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных
частиц - необходим удар материи на скорости одной десятой и более
скорости света.
Из чего следует невозможное условие для излучения материи при падении в
черную дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей,
близких к с. В таком случае трения более чем достаточно для излучения
высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не
об что тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой
или одной третей скорости света, может прекрасно летать на орбите
вокруг Черной Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько
сильно, что вторая космич. скорость (параболическая скорость) для
находящихся в этой области тел должна была бы превышать скорость света,
т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в
природе ничто не может двигаться со скоростью, большей скорости света.
Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают
звезды, при этом излучают, и что в центре галактики в черных дырах
масса больше чем масса всех звезд в этой галактике, а с момента большого
взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в
черных дырах - этого никто не наблюдал, - не наблюдали и то как звезда
проходит через горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после
образования Н. з., её масса может со временем значительно увеличиться.
При ${mathfrak M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном
из нейтронов. Существование Н. з. было предсказано в 30-х гг. 20
в.,вскоре после открытия нейтрона. Однако только в 1967 г. они были
обнаружены в виде импульсных источников радиоизлучения - пульсаров.
Затем было установлено, что Н. з. проявляют себя также как рентгеновские
пульсары (1971 г.) и вспышечные источники рентг. излучения - барстеры
(1975 г.). Не исключено, что на одной из стадий существования Н. з. явл.
источниками гамма-всплесков. К 1984 г. открыто ок. 400 Н. з., из них
ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а остальные в
виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в
тесных двойных звёздных системах. Перетекание вещества со
звезды-компаньона на белый карлик постепенно увеличивает его массу, и,
когда она достигает ${mathfrak M}_Ч$, белый карлик превращается в Н. з. В
этом случае ${mathfrak M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие
собой вращающиеся нейтронные звезды с сильным магн. полем, излучающие за
счет аккреции (падения вещества на их поверхность). Магн. поля на
поверхности Р.п. ~ 1011-1014 Гс. Светимости большинства Р.п. от
1035-1039 эрг/с. Периоды следования импульсов P от 0,7 с до неск. тысяч
с. Р.п. входят в тесные двойные звездные системы, вторым компонентом
к-рых явл. нормальная (невырожденная) звезда, поставляющая вещество,
необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы
(этим компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная
звезда не проявляет себя как Р.п. Рентг. пульсары встречаются как в
массивных молодых двойных звездых системах, относящихся к населению I
Галактики и лежащих в ее плоскости, так и в маломассивных двойных
системах, относящихся к населению II и принадлежащих к сферич.
составляющей Галактики. Р.п. открыты также в Магеллановых Облаках. Всего
открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам
присваивались наименования по созвездиям, в к-рых они находятся. Напр.,
Геркулес X-1 означает первый по рентг. яркости объект в созвездии
Геркулеса, Кентавр Х-3 - третий по яркости в созвездии Кентавра. Р.п. в
Малом Магеллановом Облаке обозначается как SMC X-1, в Большом
Магеллановом Облаке - LMC X-4. Обнаружение со спутников большого числа
рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в
Крабе и Парусах, излучают и в рентг. диапазоне, см. Пульсары),
излучающих за счет энергии вращения замагниченной нейтронной звезды и
увеличиващих свой период со временем, Р.п., излучающие за счет аккреции,
ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял -не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую
подготовку в рамках хотя бы школы. У Вас такая подготовка, судя по
всему, хромает на обе ноги, поэтому Вы не понимаете большинство статей.
Для уточняющих вопросов есть комментарии, для базовой подготовки - школа
и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы
читать - то надо быть доктором наук, и в тоже самое время Вы лично не
можете ответить прямо на прямые вопросы, по этой статье. Вы меня в
принципе заинтриговали, я подумаю чтобы такой пузырь высосать из пальца в
рамках парадигмы, чтобы все вокруг аж зааплодировали за исключительно
высокохудожественный идиотизм в рамках бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы
доказательств которые позволяют определить какими были в первые моменты
большого взрыва звезды, черные дыры , температура и другие различные
свойства пространства и свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой
простой вопрос по обсуждаемой статье, то я не обязан верить написанному,
а скорее наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к
астрофизике, то они все в астрофизике - дилетанты, которые идеи
вбрасывали в астрофизику от случая к случаю, и серьёзно ей ни кто не
занимался. По этому вся астрофизика и состоит из разрозненных идей, -
озарялок, которые последователи пытаются состыковывать между собой по
причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей
разных, что могу делать выводы что высоска из пальца, а что и супер
грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы
водород выгорает. И астрофизики внятно ответить не могут причину по
которой самый легкий водород - преодолевает гравитацию становится
тяжелее всех металлов и летит в ядро звезды поучаствовать в ядерной
реакции. И В то что самый легкий водород преодолевает летит внутрь
звезды -я не верю, хоть в миллионе книжек это будет написано, и тысяче
учебников. Так как написанное не подтверждено физическими свойствами а
противоречит им.
|
|
|
| Наверх |
|
---
И
если я попросил Вас перечитать этот форум, то значит не спроста.
- Re: Черная дыра
(А.П. Васи,
13.08.2012 21:24, 656 Байт)
\\\Я лично писал Патону, что есть информация
извне научного характера, но никакого
ответа не получил. Ортовские академики - это старпёрды, которым ничего
не надо (у них уже всё есть). Определённо надо реформировать РАН и НАН
Украины.\\\
Я Вас попрошу чтобы Вы не задавали вопрос к - из вне -, как реформировать науку Украины,
её не надо реформировать, у неё всё нормально,
и
Вам будет лучше и науке Украины будет спокойнее.
Если у Вас есть возможность спросить то вопросы найдутся,
- Как добиться снижения температуры ниже абсолютного
нуля,
не создавая очень высокого давления.
- Re: Черная дыра
(А.П. Васи,
14.08.2012 5:57, 1.5 КБайт)
\\\Вы, дружище,
говорите, что Вы не учёный, это правильно Вы - политик. Наукой можно
управлять и не учёному. К тому же Вы хотите разбогатеть, дорого продавая
научную книжку по физике. Но
если вы не будете управлять наукой, эту книжку никто не купит, ведь надо
же раскрутить бренд этой книжки. Вы говорите, что Вам не нужен
коллайдер. Это правильно. Зачем он
Вам? Вам нужен большой кабинет с ковром. На этот ковёр Вы, дружище,
будете вызывать академиков, стучать кулаком по столу и вопить: "Почему
ещё до сих пор не открыта Звезда
эфира Александра. Я ведь вам уже сто раз объяснял, что такая звезда эфира должна быть открыта".\\\
Вот это что Вы написали называется конспирологией,
необоснованной выдумкой, и клеветой.
Характеризует Вас крайне плохо в моих глазах.
Также я не понимаю зачем на альтернативных форумах которые альтернативщики
для себя сделали по причине того что их тошнит от релятивистских тем,
так Вы туда пришли и поди начали рассказывать какие релятивистские теории
хорошие,
то Вас и правильно забанили, потому что есть много релятивистских
форумов на которых исключительно восхваляют релятивизм и релятивистов.
Если Вы
хотите на двух стульях усидеть в смысле независимого наблюдателя
в данном случаи Вы попали в просак, по причине того что релятивизм от классической
физики отличается
в классической физике есть во всём пространстве -среда- эфир,
а у релятивистов в пространстве пустота.
- Re: Черная дыра
(А.П. Васи,
14.08.2012 6:05, 300 Байт, ответов: 1)
И звезда эфира - Звезда Сани давным давно лично
мною открыта, она с противоположной стороны солнечной
системы точно напротив Великого аттрактора.
Вы
поди даже не знаете где Великий аттрактор,
потому и не понимаете что координаты в пространстве
можно указывать по разному.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
14.08.2012 15:02, 638 Байт)
| Цитата: |
И звезда эфира - Звезда Сани давным давно лично
мною открыта, она с противоположной стороны солнечной
системы точно напротив Великого аттрактора.
|
Дядя Саня, каким же методом Вы открыли звезду эфира Александра Васи? Вы сами писали, что в телескоп не любите смотреть. И математику вы не любите считать.
Из своей головы Вы примыслили себе эту звезду. Фантазия Ваша безгранична. И какое же отношение имеет Ваша звезда эфира к чёрной дыре?
- Re: Черная дыра
(Е. А. Тихомиров,
14.08.2012 15:48, 1.8 КБайт)
Концепция массивного тела, гравитационное притяжение которого настолько велико, что скорость, необходимая для преодоления этого притяжения (вторая космическая скорость), равна
или превышает скорость света, впервые была высказана в 1784 году Джоном Мичеллом. Как видите, почти современник Ньютона. Ортов и альтов тогда не было, были одни орты. Из его
расчёта следовало, что для звёздного объекта с радиусом в 500 солнечных радиусов и с плотностью Солнца вторая космическая скорость на его поверхности будет равна скорости
света. Таким образом, свет не сможет покинуть этот звёздный объект, и он будет невидимым. Мичелл предположил, что в космосе может существовать множество таких недоступных
наблюдению звёздных объектов. Эйнштейн тоже поддерживал эту идею и искривил пространство в окрестностях чёрной дыры
Однако наука развивалась и ортами
было правильно установлено, что фотон массы не имеет и следовательно он не взаимодействует с массой и может улететь от любоймассы. Но по современным представлениям
ортов тела могут сколлапсировать и иметь не очень большую массу и превратится в чёрную дыру. При этом не объясняется как же происходит этот знаменитый коллапс и за счёт чего
и почему это вдруг?
Но, как ни странно, орты оказались правы и маленьких чёрных дыр после большого взрыва было великое множество, однако коллапс
здесь ни причём. Чёрные дыры ведут себя так как и описывают орты - втягивают всё в себя и не излучают, но не из-за большой массы и не из-за коллапса, а потому, что снаружи
покрыты отрицательной материей.
В центрах галактик не чёрные дыры. Откуда бы они могли там появиться? Это гравцегалы (гравитационные центры галактик)
Подробнее см samlib.ru/t/tihomirow_e_a
- Re: Черная дыра
(А.П. Васи,
15.08.2012 5:48, 823 Байт, ответов: 1)
Вы меня удивляете я привел доказательства невозможности
фотона как частицы, и также привел доказательства
невозможности черных дыр, что собственно весь
релятивизм
делает бесполезным порожняком, а Вы продолжаете
лобзать релятивистов. Здесь если Вам нравится лобзать
релятивизм то это навсегда, и Вам это даже никто не имеет
права запрещать.
По поводу телескопов то я так понимаю что Вы совсем не
в теме и ещё не раздуплились в технологиях, есть
виртуальные телескопы, и есть
галереи фото, как оптических
так и инфракрасных телескопов, я хабловских фотографий
тысяч несколько просмотрел тяга сети позволяет.
Ваша теория Вам нравится,
то это и хорошо, похвастались
своими достижениями и самоуспокоились,
печататься в реферируемом журнале это Ваш следующий шаг.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
15.08.2012 15:34, 1019 Байт)
Ну Вы дядя Васи и даёте: "печататься в реферуемом журнале - это ваш следующий шаг". Кто же нас с Пономаренко
Иваном Васильевичем напечатает? Нас с вонючих форумов гонят, как собак, причём и орты (Митька Биде, и Сашка
Мамонтов)и алты (Обезьяна с бананом, и Лёшка с новой теории). Наша иформация, видите ли, получена не научным
методом. Им ведь главное, чтобы было научно, а соответствует их наука природе или нет - это для них неважно.
А что такое научный метод? В моей работе "Методология астрономии и физики" показано, что научный метод - это
когда теории выдумываются из головы и являются эзотерикой многоумных мозгов учёных альтов и ортов. Метод у
них одинаковый. Раз подумал - придумал звезду эфира. Два подумал - придумал бозон Хиггса. Три подумал -
придумал, что звёзды из пыле-газовых облаков. Четыре подумал - придумал кривое пространство. Пять подумал -
придумал, что в ядре Земли железоникелевое ядро. Шесть подумал - придумал, что в проводниках свободные
электроны. Это разве наука?
- Re: Черная дыра
(А.П. Васи,
15.08.2012 21:28, 533 Байт, ответов: 1)
В реферируемый журнал как раз Вы можете написать
без трудностей, попросите Уважаемого А.В. Рыкова.
Вам он может дать свою рекомендацию в очень цитируемом
журнале,
там он опубликовал свою статью, и имеет
вес как чатланин и может пацакам помочь стать чатланами.
Вы поговорите с ним.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
16.08.2012 15:44, 711 Байт)
С чего бы это Рыков стал бы мне помогать? Видел я Вашего Рыкова на всяких форумах. Такой же фантазёр, как и Вы. У него вакуум рождает электрон-позитронные пары. Неужели трудно
догадаться, что из пустоты ничего не может народится, и раз появляются частица и античастица, то значит в этом месте были и отрицательная и положительная материи. Рыков -
крупная величина считается в стане ортов. Его книги публикуют не за его деньги. Нам так не жить.
Мы с Пономаренко Иваном Васильевичем, всё больше самиздатом
промышляем. Теперь настоящая физика и астрономия будут в самиздате, а научные книги альтов и ортов надо переименовать из научной литературы и учебников в научную фантастику.
- Re: Черная дыра
(Е. А. Тихомиров,
21.08.2012 22:35, 1.9 КБайт)
По информации вышних, которую доводит до нас Иван Васильевич Пономаренко, чёрные дыры имеют решающее значение в формировании галактик. Галактики формируются из развалившихся
чёрных дыр, а не из газопылевых облаков. От начала в космосе была отрицательная (неправильное название - "тёмная") материя. Она была очень разряжена, и в эту материю
вдвинулась положительная материя. (Откуда и как появилась положительная материя. Иван Васильевич обещал сказать в дальнейшем). Положительная материя притянула к себе и начала
вращать отрицательную материю. Так образовался протошар (а не сингулярность, сингулярности не было), который вращался с огромной всё возрастающей скоростью. Отрицательная
материя сдавила положительную со страшной силой. Наконец, центробежная сила разорвала протошар по экватору, из протошара начала вылетать положительная материя, которую обволакивала
отрицательная материя, образовались чёрные дыры, они вращались уже медленнее. Форма чёрной дыры полый тор. Через полюса тора чёрная дыра втягивает всё в себя. Наконец, она
тоже разрывается по экватору и из неё вылетает отрицательная материя, которая обволакивается положительной материей и веществом (элементарные частицы - это особым образом
структурированная смесь положительной и отрицательной материи). Так образуются звёзды, планеты и спутники, у всех этих объектов в ядрах отрицательная материя. Когда чёрная
дыра разлетается в центре остаётся еще много положительной материи - это гравцегал (гравитационный центр галактики), который держит всю галактику от расползания, как на коротком
поводке. Чёрные дыры образуются и из сверхновых, вещество взрывается и разлетается, а ядро становится чёрной дырой. Подробнее см. статью "Вселенная" на: samlib.ru/t/tihomirow_e_a/
Вот, если бы Новиков И. Д. рассчитал такую чёрную дыру - это было бы хорошо.
- Re: Черная дыра
(А.П. Васи,
24.08.2012 20:28, 1.1 КБайт)
Рассказ.
Очень далёкая планета.
В кружке астрономии девочка рассказывает
о своём открытии.
Я поместила кота в клетку радиотелескопа
для
того чтобы котом провести загоризонтное
телепатическое сканирование удалённых цивилизаций.
И неожиданно кот начал получать телепатическую информацию
которую
из датчиков на коте, обработал
компьютер и вот что оказалось.
Наш телевизионный нейтринный канал принимает какой-то индивидуум
и думает что с ним поддерживает
связь более высокоразвитая
цивилизация, и его там все считают дурачком.
-Марья Ивановна, - а можно я назову эту планету планетой дураков,
планетой безмозглой
скотины,
или планетой недалёких.
Нельзя Юля вообще-то так называть,- название должно максимально точно описывать
населяющую её цивилизацию, но так как ты
открыла то можешь называть
так как тебе нравится.
А в это время планета Земля, - один странный товарищ продолжает
бегать по форумам и рассказывать
всем о том что он связался с другой
цивилизацией, и что получает какие-то цветные картинки.
- Re: Черная дыра
(А.П. Васи,
24.08.2012 20:38, 636 Байт)
Е.А.Тихомиров
Я же Вам уважаемый Внятно объяснил что автор в физическом
обосновании и описании Черной Дыры жестоко лопухнулся.
В связи с чем черные дыры не имеют физического смысла.
И во вторых черные дыры не нуждаются в другой
не авторской трактовке, так как
это будут уже не
черные дыры о которых говорил автор черных дыр.
Другая трактовка черных дыр будет описывать
какую-то ерунду и что угодно но только
это
будут не черные дыры, а какая-то ерунда
которую себе кто-то придумал и решил назвать
черной дырой.
- Re: Черная дыра
(А.П. Васи,
24.08.2012 20:44, 707 Байт, ответов: 1)
Е.А.Тихомиров
\\\От начала в космосе была отрицательная (неправильное название - "тёмная") материя.\\\
Я вот не понимаю как можно заниматься астрономией и что-то звездеть даже элементарно
не зная базовых понятий.
Вот Вы не знаете кто и когда придумал
черные дыры, и авторскую формулировку,
также не знаете кто и когда придумал темную материю и темную энергию, и уж точно
не знаете какие вопросы во время их придумывания
решали эти теории.
Вы же не просто глупо выглядите и себя позорите, Вы добавляете идиотизм
в астрономию, и загаживаете интернет подобным необоснованным текстом.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
24.08.2012 21:52, 989 Байт)
Дядя Васи, это ты себя позоришь, своей звездой эфира на тракторе.
Чёрные дыры есть. Чёрные дыры это объекты, которые не излучают, и которые всё поглощают в себя. Здесь ортодоксы правы. Однако, они неправильно трактуют физику чёрных дыр. Чёрные дыры не излучают не из-за большой массы, и не
из-за коллапса, а потому, что снаружи покрыты отрицательной материй.
Вы, дядя Васи, как альт, совсем не признаёте чёрных дыр и этим Вы позорите себя и всех альтов.
Что касается автора, то он неправильно трактует чёрные дыры, а я указываю как надо их трактовать правильно.
Сказка
В одной далёкой далёкой галактике
жил дядя Васи и поехал он на тракторе на аттрактор, где увидел звезду эфира. И говорит: "Марь Ивановна, можно я назову эту звезду эфира звездою Сани Александра."
"Нет, - отвечает Марь Ивановна, - надо точные названия звездам эфира давать. Эта звезда называется Звездой дураков".
- Re: Черная дыра
(А.П. Васи,
24.08.2012 22:30, 1.6 КБайт)
Я так понимаю что возраст Ваш пенсионный,и
память у Вас никакая.
И бред сивой кобылы Вы несете качественный.
Для маразматиков ещё раз напоминаю авторский
вариант излучения
из Черной Дыры и как оно называется.
---
Материал из Википедии свободной энциклопедии
Излуче́ние Хо́кинга гипотетический процесс
испускания разнообразных элементарных
частиц, преимущественно фотонов, чёрной
дырой. Предсказан теоретически Стивеном
Хокингом в 1974 году.
---
Вы это раздупляетесь периодически
я же внятно написал - прочтите этот форум полностью, тут написано
все про черные дыры, даже про клоунов типа Вас которые считают
что черные дыры это источник
рентгеновского излучения.
Вы вот считаете что с черной дыры ничего не вылетает,
а автор говорит что фотоны, клоуны говорят что радиация в рентгеновском диапазоне.
- Re: Черная дыра
(А.П. Васи,
24.08.2012 22:39, 1.1 КБайт)
\\\Чёрные дыры это объекты, которые не излучают, и которые всё поглощают в себя. Здесь ортодоксы правы.\\\
Будьте любезны идите на релятивистские форумы и лобзайте
там релятивистов.
Звездочет например -
Они
таких как Вы любят.
Вы только идиотизм свой меньше там рассказывайте,
ибо Вы делаете необоснованные и неграмотные физические утверждения,
за что Вас
там забанят, а если не будете делать идиотских
утверждений, и не будете никого учить тому как выглядят
черные дыры, то Вас не забанят,
и другом своим не
хвастайтесь, и сойдете за нормального
релятивиста.
- Re: Черная дыра
(А.П. Васи,
24.08.2012 23:07, 692 Байт, ответов: 1)
Я не понимаю как можно заниматься переоткрытием черных дыр.
Здесь с черными дырами у науки полная торба, при этом
премии выдают регулярно за черные дыры,
при том что официально
не обнаружено ничего.
Да и как её обнаружить если они не могут определится как
она должна выглядеть.
И что меня удивляет
периодически появляются псевдо космологи
которые по своему трактуют черные дыры, не понимая
что это аналогично тому что если бы они на велосипед
говорили
- колёсокат, и не понимают что другая
трактовка черной дыры не нужна в принципе никому,
ибо Черная Дыра
это исключительно того трактовка кто её придумал
-
а точнее Хокинг.
- Re[2]: Черная дыра
(Е. А. Тихомиров,
25.08.2012 11:12, 1.1 КБайт)
Дядя Васи, ну ты и чудак на букву "м". Если меня забанят на Астронете вместе с тобой, то я буду считать, что я не напрасно прожил свою жизнь. Ты уже всем здесь плешь проел.
Я тебе говорил уже, и сейчас повторяю, что не Хокинг придумал черные дыры. Он только малость по другому объяснил их, но тоже не правильно. В природе нет ни хокинских, ни энштейновских
черных дыр.
В природе есть только иванвасильевские черные дыры, которые не излучают, так как с наружи покриты отрицательной материей. Если тебе не нравятся природные черные дыры, то я
тебе в этом вопросе ничем не могу помочь. Ты можешь взять веревку, пойти и повеситься в сортире в знак протеста. И не беспокой меня больше по пустякам. Вот, смотри, я про
тебя стишок написал.
Стишок
Говорил, ломая руки,
Дядя Васи - дуболом
О бессилии науки
Пред эфирным веществом.
Все мозги разбил на части,
Все извилины заплел.
Астронетовские власти
Сделайте ему укол.
И еще один стишок
По дороженьке пыльной, по трактору ли
Все равно нам с тобой по пути.
Прокати нас, Василий, на тракторе,
До аттрактора нас прокати!
- Re: Черная дыра
(А.П. Васи,
25.08.2012 11:36, 653 Байт, ответов: 1)
Вы хотите чтобы Вас все называли грёбанным
плагиатором нетрадиционной ориентации в физике - то не вопрос.
Забудьте напрочь словосочетание - Черная Дыра -
этот термин
занят на вечно, только идиоты его применяют в своих
описаниях
- пардон что грубовато но думаю что дойдет.
\\\Я
тебе говорил уже, и сейчас повторяю, что не
Хокинг придумал черные дыры. Он только малость по другому объяснил их,
но тоже не правильно.\\\
Вы пофигизмом заболели - он доказал что черные дыры излучают как обычное
тело.
http://www.scorcher.ru/art/theory/sto/black_holes1.php
- Re[2]: Черная дыра
(Е. А. Тихомиров,
25.08.2012 23:29, 2.5 КБайт)
| Цитата: |
Вы хотите чтобы Вас все называли грёбанным
плагиатором нетрадиционной ориентации в физике - то не вопрос.
Забудьте напрочь словосочетание
- Черная Дыра -
этот термин
занят на вечно, только идиоты его применяют в своих
описаниях
- пардон что грубовато но думаю что дойдет.
\\\Я
тебе говорил уже, и сейчас повторяю, что не
Хокинг придумал черные дыры. Он только малость по другому объяснил их,
но тоже не правильно.\\\
Вы пофигизмом заболели - он доказал что черные дыры излучают как обычное
тело.
http://www.scorcher.ru/art/theory/sto/black_holes1.php
|
Дядя Васи, дружище, так это ты обо мне заботишься, чтобы меня плагиатором не назвали? Ну спасибо, брат. Тебя, наверное орты подвергали уже нетрадиционной ориентации и не единожды.
Теперь ты о других заботишься. Не дрейфь, братан, мне твой Хокинг не может предъявить никаких претензий. Ты же сам говоришь, что Хокинг "доказал", что чёрные дыры
излучают фотоны, поэтому Хокинг не вправе называть такие объекты чёрными дырами. Какая же это дыра, если она излучает, да ещё фотоны? Я даже знаю, почему это вдруг Хокин "доказал"
что чёрные дыры излучают фотоны. Видишь ли, орты "поместили" чёрные дыры в центры галактик у них там путаница страшная. Это у них и квазары и радиоспокойные квазары
(чушь такая) и чёрные дыры одновременно. Эти штуки в центрах галактик естественно излучают фотоны, даже в виде гало, и в виде джетов. Поэтому Хокинг и рассчитал, что чёрные
дыры излучают фотоны. Но в центрах галактик совсем не чёрные дыры, это совсем другие объекты. Это гравцегалы - гравитационные центры галактик. У них, дядя Васи, снаружи не
отрицательная материя, а положительная. Это говорит о том, что с помощью математики можно "доказать" любую фантазию, если очень захотеть.
Потом, Вася,
я за славой не гонюсь. Моя заслуга здесь небольшая, я просто передаю информацию от Ивана Васильевича, который, в свою очередь, передаёт информацию от вышних. Ты бы, Вася,
поосторожней разбрасывался намёками на .... Ведь ты не меня оскорбляешь, а вышних. А они могут тебе такую картинку показать, что башка у тебя развалится на много-много
кусочков. Ты не ведаешь, что творишь, жалко тебя. Они и сердце твоё могут остановить мгновенно. Будь осторожен не хами, хамство твоё боком тебе выйдет.
- Re: Черная дыра
(А.П. Васи,
25.08.2012 19:29, 1.9 КБайт)
У меня в своё время тоже была необходимость
описать нечто похожее на черную дыру.
По скольку есть много объектов очень холодных,
следовательно они должны
поглощать энергию,
по скольку энергия это колебания среды, поглощение
более логично при увеличении плотности среды
и увеличении давления среды до конденсации
и кристаллизации.
Для решения этой задачи я и придумал Звезду Эфира.
Мне со звездой эфира в итоге, получилось достаточно просто
делать моделирование
моделей звёзд и галактик.
Естественно в процессе моделирования мне пришлось
корректировать звезду эфира которую я придумал вначале,
она претерпела незначительные
изменения но в общем
она осталась как физический объект практически в
базовой идее.
Собственно у Вас получается что если Вы хотите сделать
у какого-то
базового объекта модели некоторые физические
свойства которые решают некоторые физические задачи
то его логично назвать по основным физическим свойствам.
Для этого надо определить технические задачи которые будут
решаться, после этого желательно описать базовую
структуру, и прогнать в динамической ситуации некоторой
модели которая бы решала проще и нагляднее некоторые
физические ситуации.
Вы хотите например чтобы была поверхность, следовательно
у Вас в названии
объекта должно быть слово о поверхности
и её составе или назначении. Если Вы хотите наделить какими-то
специфическими физическими свойствами - то и это тоже должно
быть в названии.
У вас например название может быть в стиле -
Высоко-гравитационная
звезда с поглощающей поверхностью.
Если Вы хотите
описать осевые выбросы, то название
будет в стиле ещё и описывающее причину осевых
выбросов -
Высоко-гравитационная звезда с
поглощающей поверхностью
и полюсовыми вулканами.
- Re: Черная дыра
(А.П. Васи,
25.08.2012 20:50, 8.8 КБайт)
Из моего разговора на поп мех.
---
Вот шоб Вы правильно поняли,
что один физик придумал словосочетание
черная
дыра, Хокинг спустя некоторое время
дал этому словосочетанию обоснование.
---
И Вы посмотрите как ло - ханулся Черепащук
написав 300 статей которые
добавили рейтинг
Хокингу, а ему достаточно было для своей нобелевской придумать
Рентгеновскую звезду с мягкой поверхностью, -
и это было бы для него ещё и
занесением его
в историю астрономии, как чатланина который что-то
придумал и обосновал самостоятельно,
но он в итоге пацак который не придумал
и не
обосновал ничего своего самостоятельно.
---
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
- Re: Черная дыра
(А.П. Васи,
26.08.2012 0:29, 953 Байт, ответов: 1)
Мне до лампочки если Вы не понимаете
то что я Вам говорю.
И понятно что Вы самостоятельно ничего придумать
не можете, и угрожаете мне совсем видимо оборзевши.
Если Вы не понимаете что нет смысла применять черные
дыры - то флаг Вам в руку.
Оставайтесь зас - ранцами во времени.
Если бы Вы связались с толковыми
инопланетянами то
они бы наставили Вас на что-то толковое и чтобы это не
про - ....
А если Вы принимаете телепередачу - в мире животных,
а
думаете что Вам рассказывают о технологиях то Вы
совсем немного не понимаете что это самонакрутка.
Мне конечно до лампочки то как Вы себя накрутили,
что связались
с вышшими, и они с Вами низшими,
можно даже сказать с безмозглой скотиной в сравнении с ними,
по непонятной причине поддерживают диалог, и не понятно
почему
Вы избранные, но мне от Вас смешно - Вы красавцы ещё
те.
Успехов Вам - ретрансляторы .
- Re[2]: Черная дыра
(Е. А. Тихомиров,
26.08.2012 20:12, 3.7 КБайт)
| Цитата: |
Мне до лампочки если Вы не понимаете
то что я Вам говорю.
И понятно что Вы самостоятельно ничего придумать
не можете, и угрожаете мне
совсем видимо оборзевши.
|
Дружище, дядя Васи, ты не прав. Я самостоятельно очень много чего могу придумать, как впрочем и любой. Самостоятельно придумать - не фокус. Дело-то как раз
в том, что я не хочу ничего придумывать. Как ни странно, я хочу знать физику природы, такой какая она есть, а не придуманную физику. Сейчас, вся физика и астрофизика придуманная,
и нет никакой возможности определить, где придумка достоверная, а где нет. Вот смотри, дружище, ты придумал звезду эфира дяди Васи Александра, Ньютон придумал закон всемирного тяготения, Эйнштейн придумал, что время
связано с пространством, а потом придумал, что время связано с массой, потом придумал кривое
пространство, Кто-то придумал сингулярность. Кто-то, придумал бозон Хиггса (надо понимать,
Хиггс) Кант придумал, что галактики образуются из пыле-газовых облаков, Кто-то придумал, что
в ядро Земли железоникелевое. Хокинг придумал, что чёрные дыры излучают фотоны. Кто нибудь
мне в состоянии сказать, что здесь истинно, а что ложно? Из землян никто. Извне же мне сказали, что в перечисленном нет ни одного истинного факта. Подробнее см. samlib.ru/t/tihomirow_e_a/
Дружище, дядя Васи, я тебе ни сколько не угрожаю, и тебя не пугаю, я тебя предупреждаю, а это разные вещи. Хамить не надо, хамство всегда возвращается к начавшему
хамить. Если ты, дружище, смелый, то ты можешь продолжать хамить, высокоразвитой цивилизации, выбор за тобой. Я же тебе хочу только добра.
Итак, господа коллеги,
мы несколько отвлеклись, т. к. дядя Васи, всё время отвлекает нас от статьи И. Д. Новикова. Коллега И. Д. Новиков приводит в статье поля тяготения для вращающейся и для не
вращающейся чёрной дыры. Замечу, что не вращающихся чёрных дыр в природе не существует. Все чёрные дыры обязательно вращаются, причём с очень большой скоростью. Но если бы
были не вращающиеся чёрные дыры, то тяготение их было бы такое же, как и вращающихся. На тяготение вращение не оказывает никакого действия. Раздел "Физика чёрной дыры"
неверен от начала до конца. Да это и понятно, т. к. коллега Новиков И. Д. неправильно трактует чёрные дыры.
Чёрная дыра представляет собой полый тор, по сути оболочку,
напоминающую автомобильную покрышку. В этой оболочке сосредоточена вся огромная масса чёрной дыры. Её масса равна массе галактики. Чёрная дыра поглощает вещество через полюса,
поэтому вещество не падает на поверхность черной дыры, а увлекается внутрь через полюса тора.
Потом вещество прижимается к оболочке изнутри. Поэтому чёрная дыра не излучает
ни фотонов, ни рентгеновского излучения. Все разговоры о испускании чёрной дырой фотонов и рентгеновского излучения из-за того, что чёрные дыры путают с гравцегалами, которые
находятся в центрах галактик. Чёрных дыр в центре галактик не может быть по одной простой причине - галактики образовались из чёрных дыр, а не из газопылевых облаков.
- Re: Черная дыра
(А.П. Васи,
26.08.2012 0:47, 507 Байт)
Если с психологической точки зрения - то Вы залипли
на бесполезной бесперспективной и мелкой идее,
которая не решает никаких задач.
О том что держитесь за
неё и не хотите её
изменить - говорит о Вашем пенсионном возрасте
и о том что Вы не состоянии ничего другого придумать и
даже не в состоянии провести косметические
изменения
- ибо даже не понимаете что собственно надо изменить.
И то что постоянно на связи с инопланетянами это тоже не здоровый
признак.
- Re: Черная дыра
(Е. А. Тихомиров,
29.08.2012 13:46, 1.4 КБайт)
В заключении разбора работы коллеги И. Д. Новикова хочу сказать несколько слов о гравцегалах. Как мы установили ранее, галактика образуется, когда черная дыра разрывается
по экватору, и из разрыва вылетают куски отрицательной материи покрытые веществом, это будущие звёзды и планеты. Они устроены одинаково, те и другие имеют ядра из отрицательной
материи. У звёзд ядра гораздо больше и, следовательно, массивнее, и сжаты сильнее, чем у планет. Вот ещё, что важно отметить, у лопнувшей пополам чёрной дыры половинки могут
расходиться и сходится, от этого возникают рукава спиральных галактик.
Однако чёрная дыра не может полностью разлететься, т.к. она представляет собой полый тор.
Внутренние стенки тора с прилегающей к ним положительной материей не разлетаются, а сворачиваются уже не в полый, а в полный тор. Это и есть гравцегал. Естественно, что масса
его во много-много раз меньше массы чёрной дыры, т.к. он является только незначительной частью чёрной дыры, но несмотря на это, именно гравцегал удерживает всю галактику от
полного разлёта. Что из этого следует, догадайтесь сами. Итак, гравцегал представляет собой полный тор, вещество и отрицательная материя падают на поверхность тора при этом
могут возникать разные излучения, от радиоволн, до рентгеновских. Поэтому работа коллеги И.Д. Новикова, не пропала даром, она проста относится к гравцегалу, а не к черной
дыре. Вещество из гравцегала истекает через полюса и образует джеты.
- Re: Черная дыра
(Е. А. Тихомиров,
29.08.2012 14:01, 637 Байт)
Вот что ещё забыл написать. В настоящее время, чёрных дыр мало, т.к. все чёрные дыры, которые образовались после развала протошара уже преобразовались в галактики. Но и сейчас
образуются чёрные дыры из сверхновых звёзд, когда вещество сверхновой взрывается и разлетается, а ядро становится чёрной дырой и начинает втягивать всё в себя пока опять не
развалится и не образует галактику. Таким образом, чтобы из газопылевого облака образовалась галактика, надо чтобы в это газопылевое облако попала чёрная дыра. Чёрные дыры
сейчас своеобразные чистильщики , которые "подметают" бесхозное вещество и делают из него галактики.
- Re: Черная дыра
(А.П. Васи,
12.09.2012 21:05, 1.4 КБайт, ответов: 2)
Ответ #191 : Сегодня в 18:42:03
Вывод
темы - у каждого свое понятие информации, в зависимости от этого одни передавать могут, а другие нет.
Поэтому
более общим будет такая формулировка: могут ли какие либо события в
одном месте вызвать события в другом месте мгновенно.
------------------------
Ну я не думал что настолько всё грустно.
Если память отсутствует
то это навсегда.
---------
Из собаки древние мореплаватели вырезали часть внутренних органов,
и брали эту собаку на корабль.
Вырезанную часть
оставляли у себя на берегу.
и крошку этого высохшего вещества,
со временем разогревали на огне ровно в полдень, и как не странно
где-бы на планете не находился
корабль - собака начинала громко лаять точно в это время,
думаете Белку со Стрелкой зря запускали в космос, если не проверяли на
данную ситуацию то таки зря.
- Re[2]: Черная дыра
(С. В. Стоянов,
10.03.2013 12:49, 147 Байт, ответов: 1)
Да, и нас на планете немало удивительных мест например Океания, и в частности Тонга, Соломоновы острова.
- Re: Черная дыра
(А.П. Васи,
12.09.2012 22:57, 200 Байт, ответов: 1)
Я ещё два опыта знаю которые проводились,
но не смотря на их результативность
я о них рассказать не смогу по причине максимальной жестокости,
- я это кстати
смотрел по телепередачам.
- Re[2]: Черная дыра
(Д. В. Третьяков,
19.09.2012 11:33, 177 Байт)
Спасибо за подробную информацию о Чёрных дырах.Приглашаю всех любителей астрономии отправиться в увлекательное виртуальное
путешествие.
- Re: Черная дыра
(А.П. Васи,
28.09.2012 20:40, 365 Байт)
Не понимаю почему на скай техе не сдедают на альтернативном ветку,
- Только для сторонников эфира, в понимании того что двигло форума
никакое.
Будет
такая ветка, то хоть о эфире можно будет поговорить
и всех кто не в теме банить по ай пи, по первой жалобе трёх
сторонников эфира - как чуждый элемент, и сносить
все тексты забаненого.
- Re: Черная дыра
(А.П. Васи,
28.09.2012 20:48, 575 Байт)
Естественно причину забанивания трём сторонникам
эфира на своей ветке - перед модератором надо обосновать,
иначе получится ерунда.
По скольку альтернативное
превратилось в гадюшник,
в котором все высказывают даже не мысли,
а бредятину не имеющую никакого физического
обоснования, - взбрело например что-то этакое
в голову - и уже считает что это теория и думает
что он ученный, и пишет потом - я мыслю закинул
ибо я гений а Вы ло -- хи её развейте
до уровня нобелевской
премии, и пришлите мне приглашение
на вручение.
- Re: Черная дыра
(А.П. Васи,
28.09.2012 20:55, 504 Байт)
---я мыслю закинул
ибо я гений а Вы ло -- хи её развейте
до уровня нобелевской
премии, и пришлите мне приглашение
на вручение.---
Я утрирую естественно - но суть вопроса не меняет.
В принципе банить можно всех кто не
делает обоснований
и определений, не составляет физических взаимосвязей с причинно
следственной связью, или не приводит опытов с комментариями,
- по причине
того что без этого -
физики не бывает.
- Re: Черная дыра
(А.П. Васи,
29.09.2012 16:09, 1.6 КБайт)
 Re: Мировая эфиродинамическая гонка объявлена
Re: Мировая эфиродинамическая гонка объявлена
Ответ #659 - Сегодня :: 07:02:31
Михаил Сурин писал(а) 13.09.12 :: 00:37:49:И работы бр. Брусиных дают основания для серьёзного исследования этих газо- вещественных смесей.
Эти братья?
http://youtu.be/v1OdvrrorPY--------------------
Да уж - не знаю даже что сказать, - в таком возрасте заниматься
физикой и думать что результат - будет, - это самообман,
лично мне даже вопросы по эфиру задавать им не смешно,
конкурентами их не считаю - им ещё надо эволюционировать
до меня, естественно что эфиристов слегка позорят,
но свою аудиторию
недалёких, домохозяек и пенсионеров они найдут.
- Re: Черная дыра
(А.П. Васи,
28.10.2012 17:11, 1.6 КБайт)
Ответ #1182 : Сегодня в 16:46:22
Все релятивистские эффекты СТО совершенно относительны, (что и отличает
их от соответствующих эффектов ОТО).
Напрмер,
эффект релятивистского сжания длины в направлении движения одинаково
наблюдается в обеих ИСО. Но не может же в обеих ИСИ происходить реальное
изменение длины...
Реальное,
потому что подлежит измерению. Для этого (для измерений) систему
отсчёта и придумали. Из преобразований Лоренца следует, что по
результатам измерений в разных ИСО, движущихся относительно друг друга,
длина одного того же стержня будет разной.
---------------------------------------------------------------------------
Вот так всё просто \\\подлежит измерению\\\
- при полном отсутствии физического
опыта, и методики измерений, так-же отсутствует измеряемый физический
прибор и единица измерения, как говорится -
\ всё
хорошо,
прекрасная маркиза
и хороши у нас дела \ С \.
- Re: Черная дыра
(А.П. Васи,
28.10.2012 17:16, 344 Байт)
\\\длина одного того же стержня будет разной\\\
Это логика математика в физике, ибо математику
до лампочки на физику тел и свойства физических тел,
математику
главное что-бы расчёты совпадали,
а что физически это невозможно математику
до лампочки, он это называет парадокс.
- Re: Черная дыра
(А.П. Васи,
28.10.2012 19:55, 1.0 КБайт)
| Re: Черная дыра
|
26.12.201014:31 |
|
Г.А.Зубков
"Почему
все забывают о
релятивистском
сокращении
размеров?"
Мне приятно встретить толкового релятивиста,
который в практическом применении пользуется
релятивискими сокращениями в быту.
У меня вопрос, - космонавт в космическом корабле
держит в руках футбольный мяч, корабль разгоняется
до двукратного сокращения длинны, после чего
космонавт
с мячом в руках поворачивается на 90
градусов относительно направления движения,
со сплющенным мячом в руках, после чего корабль
начинает торможение, у космонавта
в руках
в итоге оказался сплющенный мяч для регби,
- вопрос какой внешний вид космонавта? |
- Re: Черная дыра
(А.П. Васи,
28.10.2012 23:42, 1.1 КБайт)
Давно читал книжку про мозговой штурм.
Чтобы были в курсе это применяется для организации
коллективной работы при практически неограниченном
финансировании
когда важно в кротчайший промежуток
времени решить задачу и без различно сколько это будет
стоить.
Это применялось впервые при разработке реактивного
двигателя, по скольку разработчики ничего не могли
придумать.
И мне трижды смешно когда какой-то юзер
использует словосочетание \ мозговой штурм \
в
халявном варианте на шару без безбашенного
финансирования - это напоминает декорации
дурдома а не попытки мозгового штурма.
Но красиво и бессмысленно
форум называть не запретить.
-------------
: Сегодня в 22:35:33
- Re: Черная дыра
(А.П. Васи,
4.11.2012 12:56, 2.7 КБайт)
 Вопросы по теории относительности (СТО и ОТО)
Вопросы по теории относительности (СТО и ОТО)
Вот наблюдаю как люди бессмысленно тратят своё время
на форумах в решении определённых физических
задач в релятивистских \игровых полигонах\.
Собственно допускают при этом две ошибки
они не проверили соответствие постулируемого
по отношению к заявленному физическому опыту.
Вторая ошибка - попытка
найти ответы на
вопросы которые должен был дать автор
теории, если втор их не дал то искать
их нельзя ибо в рамках теорий ---
Только автор имеет право
давать трактовку.
------------------------------------------------------------------
Сложность задачи на самом деле для физика
очень лёгкая.
Берём определение ---
http://www.astronomy.ru/forum/index.php/topic,1165.0.html
Э Шмутцер (ученик Эйнштейна) утверждает
( Теория относительности и
современное представление,
МИР, Москва, 1981, стр.90):
Релятивистское сокращение длины :
причина кроется в 4-х мерности пространства-времени.
Эффект
сокращения возникает при проецировании 4-х мерного
пространства-времени на метрическое 3-х мерное пространство
Собственно что можно сказать что
в данном случаи
интересует следующая ситуация - наложение
одной движущейся системы на другую базовую.
Собственно под это дело есть нарисованный
умозрительный и не проверенный на практике
в соответствии с рисунком.

Что наблюдаем
на рисунке \a\,
на рисунке наблюдаем несоответствие
заявленных релятивистами свойств и методов
сложения скоростей при повороте светового генератора,
на 90 градусов, также наблюдаем разные
длинны светового луча соответственно наблюдаем
разные скорости света, что сливает заодно
в интеллектуальную канализацию
и постулат
постоянства скорости света, вместе
с \\\релятивистским эффектом Доплера\\\ - который не имеет
ничего общего с Эффектом Доплера, здесь нельзя путать,
ибо \\\релятивистский эффект Доплера/// для пустоты - его придумали
релятивисты для себя и своих теорий, а настоящий эффект Доплера,
был придуман задолго
до релятивизма и он исключительно для
колебаний в средах. .
Вывод - данное утверждение релятивистов о сокращении
длинны в движении, и методы сложения
скоростей
- не имеют смысла, и не имеют никакого отношения
к физике.
Следовательно все задачи в рамках заявленных теорий
не имеют физического и практического
смысла.
- Re: Черная дыра
(А.П. Васи,
15.11.2012 23:45, 5.7 КБайт)
------------
Бывает
приятно вспомнить какая была интеллектуальная
борьба на мембране.
Я тогда от нечего делать после того как пять принципов жпс,
с сайта другого показал, потом
рассказал ка бы я делал жпс,
после чего, также обсуждался вопрос по первым атомным
часам и когда их поднимали на высоту то-ли в 1936 или в 1939,
с чего сделали
вывод что с повышением высоты темп хода
часов увеличивается.
Жпс изначально не мог содержать релятивистских поправок,
так как его придумали, немецкие профессора
на основе
довоенных германских разработок, и основные
принципы жпс были придуманы
в 1958 году.
Я так понимаю что никто не понял коленкор ситуации,
по релятивистским теориям ход темпа часов на орбите,
замедляется а по факту у атомных часов, ход темпа
часов увеличивается.
Дело в том что спутник
может находится условно неподвижно
по отношению к Земле, а темп хода часов
на орбите при неподвижности к Земле
повышается.
Я естественно про
это читал много, также читал что
теоретически могли сделать часы которые бы не изменяли
темп хода с набором высоты,
но в своё время я так понял решили не
афишировать
как делать эти часы, и таких часов нет,
и вряд-ли их придумают в обозримом будущем.
---------------------------
Автор Сообщение
Карим
Хайдаров классику ядерной физики Ф. Винтербергу - 80 лет 9.06.2009 6:55
Фридвардт ВИНТЕРБЕРГ
(Friedwardt Winterberg)
Живому
классику ядерной физики Фридвардту Винтербергу исполнилось 80 лет.
Немецко-американский физик теоретик и экспериментатор ныне является профессором- исследователем
в Невадском Госуниверситете, Рено. Он имеет более чем с 260 научных публикаций в том числе три известных монографии в области ядерной физики, физики плазмы и интерпретации
планковской системы естественных единиц.
Его работа по ядерной ракетной тяге получила в 1979 Золотую медаль Германа Оберста, медаль Вернера фон Брауна Международного
фонда космических полетов, а с 1981 года Ф. Винтерберг почетный гражданин штата Невада.
Он также почетный член Немецкого авиакосмического общества Лилиенталя -
Оберста.
Проф. Винтерберг известен своими идеями, которые привели к разработке GPS, его работами в области ядерного синтеза и его первым предложением экспериментальной
проверки теории Эльзассера о геодинамо. Он известен его публичными усилиями по защите ракетного ученого Артура Рудольфа и его участием в исследовании конфликта о приоритете
между Альбертом Эйнштейном и Давидом Гильбертом в области общей теории относительности. См hilbert.pdf.
Биография
Фридвардт Винтерберг родился 9 июня
1929 в Берлине, Германии. В 1953 он окончил университет во Франкфурте, работал под руководством Фридриха Гунда и в 1955 защитил докторскую диссертацию PhD по физике в Институте
имени Макса Планка в Гёттингене как докторант Вернера Гейзенберга. Позже по приглашению ядерщиков он переехал в Соединенные Штаты и стал гражданином США.
Работы
Винтерберга в области ядерного синтеза и физики плазмы широко известны. Эдвард Теллер, с которым он работал, писал о нем, что он возможно не получил того внимания, которое
он заслуживает по уровню своих работ по ядерному синтезу. Однако это было типичным для физиков ядерщиков того времени, делавшим важные работы в закрытых областях науки.
Он был избран членом Международной академии астронавтики, в Париже, в которой он был членом Комитета межзвездных космических исследований.
В 1954 он первым
сделал предложение тестировать общую теорию относительности по атомными часам на околоземных спутниках и предложил способ применения ядерного мобильного реактора для создания
ракетных ядерных двигателей путем нагрева рабочего тела в активной зоне реактора. Этот способ был принят в известном американском проекте ядерного ракетного двигателя Nerva
и Британским межпланетным обществом за базовый способ в разработке их проекта Daedalus Starship Analysis. Его сегодняшние исследования находятся в области гипотезы эфира Планка,
- новой теории, которая объясняет как квантовую механику, так и теорию относительности как асимптотически низкие энергетические аппроксимации и дает спектр частиц существенно
сходный со стандартной моделью.
Профессором Винтербергом предложена теория, согласно которой единственными свободными параметрами в фундаментальных уравнениях физики
являются длина, масса и время Планка (которые сейчас принято называть фундаментальными единицами Планка) и показывают почему R3 трехмерное евклидово пространство - естественное
пространство, и что SU2 может рассматриваться как фундаментальная групповая изоморфия на SO3 - альтернатива усложнения мира до теории 10-мерного пространства R10 и теории
M в R11. Винтерберг показал, что величина константы тонкой структуры на длине Планка точно согласуется с эмпирической величиной.
Профессор Винтерберг широко публиковался
во многих областях физики начиная с 1950-х годов и до настоящего времени. В 2008 году на Международной конференции по теории относительности Винтерберг раскритиковал теорию
струн и отметил недостатки общей теории относительности Эйнштейна из-за ее неспособности согласования с квантовой механикой.
Ссылки:
World Science Database
http://www.worldnpa.org/php2/ index.php?tab0=Scientists&tab1=Display&id=282
Nevada University Site http://www.physics.unr.edu/FacWinterberg.html
Bourabai Research Site http://bourabai.kz/
- Re: Черная дыра
(А.П. Васи,
15.11.2012 23:48, 2.6 КБайт)
КаримХайдаров
|
Re: классику ядерной физики Ф. Винтербергу - 80 лет
|
20.06.200913:45 |
|
|
Фридвардт ВИНТЕРБЕРГ
(Friedwardt Winterberg)
(продолжение)
GPS система
В 1955 в своей статье в научном журнале
ASTRONAUTICA ACTA Ф. Винтерберг предложил проверку общей теории относительности и измерения
пространственных координат путем использования атомных часов установленных на искусственном спутнике
Земли. В то временя ни атомных часов, ни искусственных спутников еще не было, однако иедя Винтерберга
основывалась на достижениях и идеях довоенной Германии, где еще в 1937-1939 годах были произведены запуски
баллистических ракет V-2 Вернера фон Брауна
(Werner von Braun) в космическое
(безвоздушное) пространство, что было подготовкой к осуществлению орбитального полета. Идея атомных часов
тоже уже существовала в связи с открытием стабильности спектров излучений квантовой физикой. В 1957 году Ф. Винтерберг
получил письмо от своего научного руководителя Вернера
Гейзенберга (Werner Heisenberg) с
выражением энтузиазма по поводу идей Винтерберга, которые сегодня положены в основу глобальной
навигационной системы GPS.
Ссылки:
Wikipedia Free Encyclopedia http://en.wikipedia.org/wiki/Friedwardt_Winterberg
World Science Database http://www.worldnpa.org/php2/
index.php?tab0=Scientists&tab1=Display&id=282
Nevada University Site http://www.physics.unr.edu/FacWinterberg.html
Bourabai Research Site http://bourabai.kz/ |
- Re: Черная дыра
(А.П. Васи,
6.01.2013 12:08, 764 Байт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1354298449/140
Барышня своей хорошей памятью и природным качественным
быстрым аналитическим подходом,
просто интеллектуально издевается
- жестокое зрелище не для слабонервных.
Так порвать интеллектом - это жестоко, самое смешное что и бесполезно,
ибо тупость
вечна, её оппоненты в виду своих умственных способностей
никогда не сделают выводы из этой ситуации, и никогда не поменяют
логики и базовых истин в своем мышлении
- будут тупить вечно.
Барышня молодец - как физик она слаба - но она специалист по причинно
следственным связям - а это для \звездунов\ самая страшная и беспощадная
терминатоша которая выведет на чистую воду всё \лайно\ в физике.
- Re: Черная дыра
(А.П. Васи,
7.01.2013 19:10, 1.3 КБайт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1350558609/2547#2547
 Re: Эфир для чайников.
Re: Эфир для чайников.
Ответ #2548 - Сегодня :: 16:45:06
---------------
Я естественно на стороне
EngineAlex
он меня немного по-копировал но ему можно,
а
Vallav
гнусно выглядит его жаба давит подпрыгивает не хватает интеллекта
обосновать свои закидоны и просит в каждом брыке объяснить
ему в чём он не
прав - таких надо просто банить ибо чтобы не было таких отвлекающих
основную тему, или просто принять в правилах форума - бан тому на неделю
кто попросил указать на втречный вопрос в чем не правота опровергающего и
спрашивающего одновременно.
Опровергают и одновременно спрашивают о своей правоте
- только недалёкие.
Их можно банить аки пользы от них в физике не будет и не-было.
- Re: Черная дыра
(А. С. Иванов,
8.01.2013 2:05, 471 Байт, ответов: 1)
А знаете ли вы, что
никто никогда не фотографировал черную дыру - это невозможно, так как они поглощают все световые волны внутрь из-за сильной гравитации. Все изображения черных дыр сделаны
человеком в Фотошопе и подобных программах.
Источник:http://facty.at.ua
- Re[2]: Черная дыра
(Ю. С. Решников,
8.01.2013 9:55, 409 Байт)
Очередной
перенос
лабораторных
процессов
в
астрономическое
поле.
При
этом
имеем
дело
с
полным
масштабным
неучётом
-
процессы
в
атомах
проецируются
на
пространства.
И
чётко
определимся
-
тема
астрономическая,
а
не
физическая
и
речь
идёт
об
астрообъектах.
В
этом
случае
элементарные
частицы
рассматриваться
не
должны
вообще
- Re: Черная дыра
(А.П. Васи,
8.01.2013 9:37, 38.2 КБайт)
------------------
| Re: Черная дыра
|
7.02.20122:47 |
|
По черной дыре ещё
http://siteua.org/system_category/330344
\\\"До сих пор никто и никогда не фотографировал
черные
дыры, ввиду сложности этого мероприятия и экзотической природы самих
дыр", - говорит Димитриос Псалтис, астроном из Университета Аризоны и
один из координаторов проекта.\\\
Собираются первую фотографию черной дыры сделать, и всем до лампочки что без таковой,
уже тысячи статей о черной дыре написали.
Дело не в фотографии на самом деле, нет общей формулировки черной дыры -
каждый видит в своих изысканиях то что он хочет и называет это черной дырой
- и это
смешно, - классика жанра.
\\\.Материал
из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.... \\\
-----------------------------------
http://www.lenta.ru/news/2012/01/19/prize/
Астрономической
награды удостоились Рейнхард
Генцель (Reinhard Genzel) и
Андреа Гез (Andrea Ghez). Премия была присуждена этим ученым за
обнаруженные ими и их сотрудниками весомые доказательства того, что в
центре Млечного Пути находится сверхмассивная черная дыра. Оба астронома
наблюдали звезды, обращающиеся вокруг центра Галактики и пришли к
одному и тому же выводу независимо друг от друга.\\\
|
-----------------
| Re: Черная дыра
|
7.02.201217:42 |
http://www.popmech.ru/article/10479-dyira-kak-vyiklyuchatel/page/4/
\\\Скорость рождения новых звезд в некоторых далеких галактиках так велика, что процесс этот называют
прямо вспышкой
звездообразования. Процесс этот, однако, лишь временный, и довольно скоро прекращается и судя по всему, виноваты в этом могут бытьсверхмассивные
черные дырыв центрах этих галактик.\\\
Вот тоже статья наполненная идиотизмом, и желанием
не съесть так по-надкусывать.
Это яркий пример того
до чего доводит сюсюканье
и потокательство. Вместо того чтобы открыто сказать
что мол - пшел вон дыбил с такой статьёй
в которой всё непонятно и отсутствует
смысловая
взаимосвязь, - так так никто не пишет в комментариях,
а автор думает что пипл хавает, и ему нравится -
и автор будет писать следующую статью с ещё
большим
идиотизмом и нескладушками.
А в нормальном и здравом виде статья бы выглядела
следующая -
обнаружили короткие и яркие вспышки, звездо-образование
или звездные вспышки неизвестно, под ни одну из теорий
не подходит, ни в какой из известных теорий подобный случай
не описывался.
Кстати о черных
дырах они тоже мямлили, понадкусывали
- в стиле мол, что если у какого-то следующего писателя будет
нешто подобное в припадке гениальности, так пусть он мол знает
в нашем припадке бессознательного идиотизма было впервые.
Это пипец, но пипл хавает астрономам нравится, мне смешно.
--------------------------------------------
|
|
Re: Черная дыра
|
19.09.201112:14 | |
Что
меня удивляет, - так
это то что вся астрофизика красивая и пушистая,
и всё прекрасно.
Но это же не так, вот те-же черные дыры - это же
просто пипец - и что это никто не замечает
или никто не
понимает.
Хочу сразу спросить, Ваше мнение по
...Черная дыра...
http://www.astronet.ru/db/msg/1188232
Согласны ли Вы с этим?
Какие из перечисленных статей соответствуют стандартам Черной
Дыры?
1 Есть ли жизнь в черной дыре
http://www.popmech.ru/article/8822-est-li-zhizn-v-chernoy-dyire/
2[ссылка]
Установлена масса самой крупной из сверхмассивных черных дыр.
Такое нам и не снилось.
3[ссылка]
Мифология черных дыр.В нашей Галактике существуют миллионы черных дыр
массой в несколько солнечных
4http://www.popmech.ru/article/8140-raspad-dyiryi/
Распад дыры.
Взрыв сверхновой может заканчиваться образованием не одной, а сразу
нескольких черных дыр.
5[ссылка]
Детство черной дыры
Взрыв, зафиксированный в глубинах космоса 31 год назад, судя по всему,
знаменовал рождение черной дыры самой молодой из нам известных
6[ссылка]
Темный центр
Таинственный центр нашей галактики,
место обитания сверхмассивной черной дыры и источник мощнейших потоков излучения,
преподносит новые сюрпризы.
7[ссылка]
Небольшое замечание о природе гравитации приводит к следствиям
космического масштаба к выводам о рождении новых миров из черных дыр
8[ссылка]
Обычная по размерам черная дыра выбрасывает
колоссальные потоки излучения и частиц.
9[ссылка]
Астрофизики предложили способ (теоретически) уничтожить черную дыру
10[ссылка]
Из всех сверхмассивных черных дыр лишь около 1% выбрасывают
значительные количества энергии
11[ссылка]
Выживающие дыры
Пара редких экземпляров
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
каким-то чудом выживающих в соседстве с этим монстром.
12[ссылка]
Как живется внутри черной дыры? Вы и сами знаете,
как: если справедливы новые теоретические выкладки,
вся наша Вселенная может находиться внутри черной дыры,
расположенной в другой Вселенной. Эдакая матрешка мироздания.
13[ссылка]
Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину. Это дало цифру в 10103, тоже огромную, но все-таки на много
порядков ниже.
14[ссылка]
Если очень, очень быстрый космический корабль разогнать
почти до скорости света, превратится ли он в черную дыру?
15[ссылка]
Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
---------------------------------------------------------
| Re: Черная дыра
|
19.09.201112:38 |
|
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили,
что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в
электронных оболочках атомов или молекул. Оба эффекта используются в
рентгеновских трубках. Основными конструктивными элементами таких трубок
являются металлические катод и анод (ранее называвшийся также
антикатодом). В рентгеновских трубках электроны, испущенные катодом,
ускоряются под действием разности электрических потенциалов между анодом
и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных
частиц - необходим удар материи на скорости одной десятой и более
скорости света.
Из чего следует невозможное условие для излучения материи при падении в
черную дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей,
близких к с. В таком случае трения более чем достаточно для излучения
высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не
об что тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой
или одной третей скорости света, может прекрасно летать на орбите
вокруг Черной Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько
сильно, что вторая космич. скорость (параболическая скорость) для
находящихся в этой области тел должна была бы превышать скорость света,
т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в
природе ничто не может двигаться со скоростью, большей скорости света.
Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают
звезды, при этом излучают, и что в центре галактики в черных дырах
масса больше чем масса всех звезд в этой галактике, а с момента большого
взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в
черных дырах - этого никто не наблюдал, - не наблюдали и то как звезда
проходит через горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после
образования Н. з., её масса может со временем значительно увеличиться.
При ${mathfrak M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном
из нейтронов. Существование Н. з. было предсказано в 30-х гг. 20
в.,вскоре после открытия нейтрона. Однако только в 1967 г. они были
обнаружены в виде импульсных источников радиоизлучения - пульсаров.
Затем было установлено, что Н. з. проявляют себя также как рентгеновские
пульсары (1971 г.) и вспышечные источники рентг. излучения - барстеры
(1975 г.). Не исключено, что на одной из стадий существования Н. з. явл.
источниками гамма-всплесков. К 1984 г. открыто ок. 400 Н. з., из них
ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а остальные в
виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в
тесных двойных звёздных системах. Перетекание вещества со
звезды-компаньона на белый карлик постепенно увеличивает его массу, и,
когда она достигает ${mathfrak M}_Ч$, белый карлик превращается в Н. з. В
этом случае ${mathfrak M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие
собой вращающиеся нейтронные звезды с сильным магн. полем, излучающие за
счет аккреции (падения вещества на их поверхность). Магн. поля на
поверхности Р.п. ~ 1011-1014 Гс. Светимости большинства Р.п. от
1035-1039 эрг/с. Периоды следования импульсов P от 0,7 с до неск. тысяч
с. Р.п. входят в тесные двойные звездные системы, вторым компонентом
к-рых явл. нормальная (невырожденная) звезда, поставляющая вещество,
необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы
(этим компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная
звезда не проявляет себя как Р.п. Рентг. пульсары встречаются как в
массивных молодых двойных звездых системах, относящихся к населению I
Галактики и лежащих в ее плоскости, так и в маломассивных двойных
системах, относящихся к населению II и принадлежащих к сферич.
составляющей Галактики. Р.п. открыты также в Магеллановых Облаках. Всего
открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам
присваивались наименования по созвездиям, в к-рых они находятся. Напр.,
Геркулес X-1 означает первый по рентг. яркости объект в созвездии
Геркулеса, Кентавр Х-3 - третий по яркости в созвездии Кентавра. Р.п. в
Малом Магеллановом Облаке обозначается как SMC X-1, в Большом
Магеллановом Облаке - LMC X-4. Обнаружение со спутников большого числа
рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в
Крабе и Парусах, излучают и в рентг. диапазоне, см. Пульсары),
излучающих за счет энергии вращения замагниченной нейтронной звезды и
увеличиващих свой период со временем, Р.п., излучающие за счет аккреции,
ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял -не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую
подготовку в рамках хотя бы школы. У Вас такая подготовка, судя по
всему, хромает на обе ноги, поэтому Вы не понимаете большинство статей.
Для уточняющих вопросов есть комментарии, для базовой подготовки - школа
и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы
читать - то надо быть доктором наук, и в тоже самое время Вы лично не
можете ответить прямо на прямые вопросы, по этой статье. Вы меня в
принципе заинтриговали, я подумаю чтобы такой пузырь высосать из пальца в
рамках парадигмы, чтобы все вокруг аж зааплодировали за исключительно
высокохудожественный идиотизм в рамках бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы
доказательств которые позволяют определить какими были в первые моменты
большого взрыва звезды, черные дыры , температура и другие различные
свойства пространства и свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой
простой вопрос по обсуждаемой статье, то я не обязан верить написанному,
а скорее наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к
астрофизике, то они все в астрофизике - дилетанты, которые идеи
вбрасывали в астрофизику от случая к случаю, и серьёзно ей ни кто не
занимался. По этому вся астрофизика и состоит из разрозненных идей, -
озарялок, которые последователи пытаются состыковывать между собой по
причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей
разных, что могу делать выводы что высоска из пальца, а что и супер
грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы
водород выгорает. И астрофизики внятно ответить не могут причину по
которой самый легкий водород - преодолевает гравитацию становится
тяжелее всех металлов и летит в ядро звезды поучаствовать в ядерной
реакции. И В то что самый легкий водород преодолевает летит внутрь
звезды -я не верю, хоть в миллионе книжек это будет написано, и тысяче
учебников. Так как написанное не подтверждено физическими свойствами а
противоречит им.
|
- Re: Черная дыра
(А.П. Васи,
8.01.2013 9:42, 622 Байт)
\\\А
знаете ли вы, что
никто никогда не фотографировал черную дыру - это невозможно, так как
они поглощают все световые волны внутрь из-за сильной гравитации. Все
изображения черных дыр сделаны
человеком в Фотошопе и подобных программах.\\\
Предыдущий пост - обоснование не физичности черных дыр, автор дюрочек просто лопухнулся,
в физике это нормально,
и достаточно частое явление в неклассической физике.
- Re: Черная дыра
(А.П. Васи,
8.01.2013 22:00, 1.4 КБайт, ответов: 1)
Мне крайне неприятно когда кто-то необоснованно вумничает,
не вопрос дайте каждому Вашему слову физическое определение,
ибо физика - это физические определения
обоснованные хоть как-то.
Я даже не прошу меня половить на не-корректности моих физических обоснований
ибо это для Вас невозможная задача в принципе.
1 \перенос
лабораторных
процессов\ - дайте определение,
2 \астрономическое
поле\ - аналогично,
3 \процессы
в
атомах\ - какая модель - опишите,
4 \проецируются
на
пространства\-дайте определение проецируемости,
5 - дайте Ваше определение пространства,
6 \чётко
определимся
-
тема
астрономическая,
а
не
физическая\ - дайте определение
границы между физикой и космологией,
7 \идёт
об
астрообъектах.
В
этом
случае
элементарные
частицы
рассматриваться
не
должны
вообще\
- обоснуйте физическую причину невозможности.
--------------------------------
Почувствуйте свои слова - и как они воспринимаются другими, и
призадумайтесь
над этой ситуацией.
Как для меня Ваш текст - голимый необоснованный физически порожняк.
- Re[2]: Черная дыра
(Ю. С. Решников,
9.01.2013 7:22, 568 Байт)
Зачем
повторять
известные
определения?
Определим
по
теме.
Физика
давшая
возможность
видеть
то,
что
никто
никогда
раньше
не
видел
-
бесценна
вне
времени.
Но
в
другой
плоскости,
физика
пытающаяся
видеть
в
астрообъектах
себя
и
только
себя,
совершенно
не
принимая
во
внимание
факт,
что
разбирает
астрономическое
поле.
Элементарные
частицы
не
являются
астрономическими
объектами,
небесная
механика
-
Астрономическая,
т.е.
не
физична.
А
это
учитыватся ?
- Re: Черная дыра
(А.П. Васи,
8.01.2013 23:02, 275 Байт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1357553088/180
Эта красивая придворная собачка, в смысле выросшая при дворе, со временем
будет самой
страшной грозой всех псов.
Безумцы они - ищут себе приключений даже не понимая с кем связались.
- Re: Черная дыра
(А.П. Васи,
8.01.2013 23:03, 65 Байт)
Эта собачка будет загрызать каждого пса долго
и медленно.
- Re: Черная дыра
(А.П. Васи,
9.01.2013 10:01, 298 Байт)
А это уважаемый тест на Вашу адекватность в физике,
и если Вы с ним не можете справится то я с Вами
не могу общаться.
И если Вы сказали что-то то будьте
любезны и ответить
за свои слова, а если не можете для этого
есть стандартная фраза -
\Простите отцы за - ранца\.
- Re: Черная дыра
(А.П. Васи,
9.01.2013 10:06, 265 Байт, ответов: 5)
А если я сказал что автор черных дыр физически неправильно свою
теорию и определения сделал, то я это обосновал, и автор черных
дыр в моих глазах как физик - недалёкий,
и придумал он лайно не имеющее
никакого отношения к физике и действительности.
- Re[2]: Черная дыра
(Ю. С. Решников,
9.01.2013 11:18, 575 Байт, ответов: 4)
Давайте
разберём
ещё
одну
область,
в
которой
физика
видит
только
себя,
являясь
ею
-
это
х-
и-
м-
и-
я.
На
всю
глубину,
какая
может
быть
квантофизическая
область
есть
областью
протохимической.
Именно
так
-
из
квантовой
физики
может
получиться
только
Химия
(со
своими
законами).
Нет
такой
физической
установки
(тот
же
БАК),
которая
бы
не
обладала
химическими
свойствами,
что
известно
любому
инженеру,
но
совершенно
игнорируется
теоретической
физикой.
- Re[3]: Черная дыра
(Ю. С. Решников,
9.01.2013 12:44, 557 Байт, ответов: 3)
Астрономию
и
химию
роднит
не
только
неоправданная
подчинённость
физике,
но
и
перевес
в
них
гравитационных
процессов
над
всеми
другими.
Физики
могли
бы
выделить,
как
свою
научную
основу
физику
высоких
энергий
(чего
они
не
делают,
опираясь
на
квантовую),
но
и
в
этом
случае
энергополя
принадлежат
области
либо
химии,
либо
астрономии.
И
только
проявление
их
-
излучение,
улавливается
чисто
физически,
приборами
(через
химические
свойства)
- Re[4]: Черная дыра
(Ю. С. Решников,
9.01.2013 21:34, 451 Байт, ответов: 2)
Космос
-
плазма,
гравитация,
поля,
химия,
излучение,
составляющие
астрономические
комплексы
(объекты).
Из
них
физике
доступно
только
излучение,
по
которому
пытаются
составить
представление
о
других
составляющих.
Астрономия
в
состоянии,
изучая
астробъекты,
брать
все
космические
составляющие
в
совокупности.
В
чём
требуемая
объективность
необходимого
научного
подхода
- Re[5]: Черная дыра
(Ю. С. Решников,
10.01.2013 10:19, 536 Байт, ответов: 1)
Что,
важно
-
физика
имеет
в
астрономии
только
(!)
излучения.
По
ним,
на
лабораторных
данных,
восстанавливаются
другие
факторы.
Здесь
снова
проецирование
лабораторного
на
пространственное
потому,
что
физическое
только
подобно
астрономическому,
но
не
идентично.
Астрономические
плазма,
гравитация,
поля,
химия
и
излучения
не
физичны,
а
астрономичны.
Физика
это
различие
не
в
состоянии
уловить,
но
астрономия
может
его
подсказать
- Re[6]: Черная дыра
(Ю. С. Решников,
11.01.2013 6:23, 555 Байт)
В
астрокомплексе
(объекте)
выделяются
группы
явлений
-
гравитационно-
химическая
(задающая
характеристики),
плазмо-
полевая
(материально-
силовая)
и
производные
из
неё
излучения.
Подобные
физическим,
но
не
физические
и
физическое
создающие,
при
образовании
звёзд
и
планет,
где
как
физические
обнаруживаемые
в
поверхностно-
планетном
ПВК,
создающие
ПВК
звёз
и
планет,
эти
нефизические
астрокомплексы
есть
также
ПВК
более
основных
космических
структур
- Re: Черная дыра
(А.П. Васи,
11.01.2013 8:57, 2.4 КБайт, ответов: 3)
Как говорится ничего личного.
Вы здесь не пишите - ибо Вы мне скучны в космологии,
ибо у Вас не знаний ни умений ими пользоваться.
Вы недалёкий потому
что Вы даже не знаете
что не существует на текущий момент физического
общепринятого определения \пространства\.
Вот лично моё мнение как читателя читающего
форум.
Вот возьмём форум,
там есть Дмитрий Вибе,
Олег Титов,
Алия и Чхе - у всех из них одинаковый
професорский уровень знаний, а пользоваться ими
умеют только двое.
Дмитрий Вибе и Алия - рождены математиками,
и
они в связи со своей доверчивостью, поверили релятивизму,
и у них перестроилась под релятивизм логика мышления,
у Вибе процентов на семсят пять, у Алии на сто
процентов,
у Алии можна таки сказать что в сознании некотарая
релятивистская матрица и всё проходит только через неё.
Олег Титов - рождён физиком, и вынужден
был мыслить по
релятивистски ибо по другому заработать в физике денег
он не мог, со временем и с возрастом он по другому думать
не может. Чхе - рождён физиком,своими
знаниями пользоваться
может самостоятельно, без оглядок и без посторонней помощи.
Так самое смешное - Полезные тексты кто пишет на форумах,
Дмитрий
Вибе - безполезные для читающего,
Алия - полезные для релятивистов,
Олег Титов - полезные,
Чхе - полезные.
---------------------------------------------------------------------
А Ваши тексты - это вообще тектсты безсмысленные
и безполезные, и Вы не физик и не математик,
и знаний у Вас нет - один околофизический стёб скорей всего -
пенсионера у которого много свободного времени,
но уже и память не та, и нет умения анализировать
новые необычные знания.
Вы можете пойти
потусоваться на вот этот
форум,

Физика альтернативная
там модератор таких как Вы не банит,
там таких процентов шестьдесят , и там тоже
есть три минимум рожденных физиками,
но кто это я не скажу, догадайтесь
сами.
Успехов.
- Re[2]: Черная дыра
(Ю. С. Решников,
11.01.2013 12:48, 567 Байт, ответов: 2)
Васи
признайтесь
себе,
что
астрономия
вам
не
нужна.
Вы
путаете
космологию
с
физикой,
пространство
для
вас
только
физическое,
вы
предлагаете
перейти
на
физический
форум.
А
здесь
форум
астрономии
и
её
вопросы
разбираются.
3десь
обсуждаются
темы
касающиеся
пространства
астрономического
и
его
космологии.
Для
тех
кого
интересует
только
физика
есть
другие
форумы.
Но
если
астрономия
вам
всё
же
интересна,
попытайтесь
хоть
немного
вникнуть
в
тему
- Re[3]: Черная дыра
(Ю. С. Решников,
11.01.2013 14:18, 543 Байт, ответов: 1)
Физическое
пространство
существует.
Но
у
него
есть
своё
место
в
астрономии.
Физическое
пространство
возникает
из
астрономического
пространства,
при
образовании
планет
и
их
поверхностей.
И
здесь
конечно,
есть
космология
физического
пространства
и
поле
абсолютной
власти
физики
и
её
представлений.
А
что
до
математики,
то
астрономический
пространственно-
временной
континуум
(ПВК)
дает
больше
ей
возможностей,
чем
пространство
физическое
- Re[4]: Черная дыра
(Ю. С. Решников,
11.01.2013 14:36, 439 Байт)
С
имеющей
место
быть,
абсолютной
властью
физики
в
физическом
(поверхностно-
планетном)
ПВК,
трудно
согласиться,
как
объективной.
Все-
таки
и
здесь,
физическом
пространстве,
объективно,
главенствующее
место
должны
занимать
представления
химии,
что
поможет
и
физике
разобраться
во
многих
своих
проблемах.
Химия
учитывает
больше
составляющих
научного
знания
- Re: Черная дыра
(А.П. Васи,
11.01.2013 21:30, 1.6 КБайт)
Вы здесь не пишите - ибо Вы мне скучны в космологии,
ибо у Вас не знаний ни умений ими пользоваться.
Вы недалёкий.
А Ваши тексты - это вообще тексты бессмысленные
и бесполезные, и Вы не физик и не математик,
и знаний у Вас нет - один
около-физический стёб скорей всего -
пенсионера у которого много свободного времени,
но уже и память не та, и нет умения анализировать
новые необычные знания.
Вы можете пойти
потусоваться на вот этот
форум,

Физика альтернативная
там модератор таких
как Вы не банит.
----------------------
Мне до лампочки Ваши вопросы, и мне наплевать что Вы думаете
о том что есть физика или астрономия или космология,
и я с теми кто борзо на меня наезжает с необоснованными претензиями
не общаюсь в принципе.
И если Вы не чатовый бот я удивлюсь.
Мне лично до лампочки Ваши
вопросы с химией,
Ваши вопросы - сами и решайте их.
И с теми кто не может сделать ни одного физического определения
и технически грамотно не может сформулировать
вопрос, я тоже
не общаюсь.
---------
Шли бы Вы на балетный форум и советовали бы там например в
фуэте - фуэтятины добавить.
- Re: Черная дыра
(А.П. Васи,
11.01.2013 23:01, 2.3 КБайт)
Если у кого есть возможность - будьте любезны передайте
что я на этот вопрос смогу - здесь - ответить вместо того кому он задан,
ибо я знаю всю историю и с радиоастрономией
и переоткрытиями
и с датами.
------------------------





-

- Сообщений: 11 986
- Рейтинг: +120/-30
-
Ответ #13 : Сегодня в 13:37:00
Ув. Che, такое ощущение, что Вам нравится 20-й век и даже его середина.
Космология, мягко говоря, чрезвычайно сильно продвинулась с тех пор. 
Есть давно серьезные модели рождения Вселенной со многими подтвержденными параметрами
и ответами на Ваши наивные вопросы.
А вот у стационарной, бесконечной и вечной Вселенной нет ответов ни на один вопрос и нет ни одного наблюдаемого подтверждения.
Даже нет ответа на вопрос, откуда она взялась - а есть просто древний и легкий постулат - всегда была
- Re: Черная дыра
(А.П. Васи,
11.01.2013 23:11, 758 Байт)
Мне естественно не понятно почему не обращают внимания на
Большую советскую Энциклопедию- в которой собственно
вселенная вечная - а большой Взрыв придуманный после
радиоастрономических
манёвров, и переоткрытий с 1941 на 1946, и слово - сингулярность - то как раз
было придумано в довесок к вечной вселенной и с этим довеском
,
вселенная стала расширятся.
Естественно за собой не замечает кто-то что у большого взрыва больше вопросов
чем он даже себе представляет.
Просто перед
релятивистами их никто не ставил, а если и ставили то они игнорировали,
а так всё логично будет - померятся вопросами и ответами.
Для меня естественно это специалист
у которого есть не которые знания в которых
он уверен.
- Re: Черная дыра
(А.П. Васи,
11.01.2013 23:21, 4.2 КБайт)
| Re: Свет и пространство и о скорости света.
|
1.05.2012
|
|
Закрытие большого взрыва.
Закрытие моделей звёзд на горении водорода.
---Нескладушки большого взрыва.
Первое что бросается в глаза в этой
теории
- что с достаточно большой точностью в
секунды и минуты знают последовательность происходящего
но напрочь отсутствует причинно следственная связь
- всё построено на постулатах которые нельзя подтвердить.
Что изначально состоит из парадоксов и противоречий.
1 Разлёт со сверхсветовой скоростью
на 13.5 млрд световых лет
во все стороны практически мгновенно, и мы наблюдаем в телескоп
звёзды которые туда забросило при большом взрыве.
---
Что собственно
есть жесткое и парадоксальное в этом, -
скорость света была превышена минимум в миллиард раз.
Что не понятно другое, не понятно что если при разлёте материи
почему её забросило на 14 млрд световых лет, а не на два или тысячу,
- почему разброс совпадает с возможностями телескопов.
2 Химический состав
водорода и гелия и его соотношение - 70%водорода
и 30% гелия - и с какой точностью и без примесей других веществ.
---
--------------------------------------------------------------------------
http://vsln.ru/himicheskiy-sostav-solntsa.html
(В 1929 г. американский астроном Генри Норрис Рессел (18771957)
тщательно изучил солнечные спектры, и ему
удалось установить, что
Солнце поразительно богато водородом. Он решил, что на водород
приходится три пятых всего объема Солнца. Это было абсолютной
неожиданностью,
так как водород, хотя и не является редким элементом
в точном смысле этого слова, составляет всего лишь 0,14% земной коры.
Однако последующие исследования показали,
что Рессел был слишком
осторожен в своей оценке. Недавние подсчеты американского астронома
Дональда Говарда Мензела (род. в 1901 г.) показывают, что водород
составляет
81,76% объема Солнца, а гелий 18,17%, так что на долю
всех остальных элементов остается только 0,07%.
По-видимому, можно с уверенностью сказать, что
Солнце практически
представляет собой светящуюся смесь водорода и гелия в пропорции
(по объему) 4:1. (Элемент гелий тоже был открыт с помощью спектрального
анализа,
причем сначала не на Земле, а на Солнце Английский астроном
Джозеф Норман Локьер (1836 1920) предположил, что некоторые
неопознанные линии солнечного
спектра принадлежат еще не открытому
элементу, который он в честь греческого бога Солнца Гелиоса назвал гелием.
На Земле же гелий был обнаружен шотландским химиком
Уильямом Рамзеем
(18521916) только в 1895 г.).)
---------------------------------------------------------------------------------------------------
Собственно основная ошибка в данной ситуации в том что
по составу химическому атмосферы солнца сделано скрытое
утверждение - а это постулат, что химический
состав самого
солнца тоже такой-же за исключением ядра.
Вот здесь надо повнимательнее ибо здесь самая грубая
ошибка всей астрономии.
Данная
ситуация на самом деле не возможна, ибо водород
он не только самый легкий и у него самая низкая удельная
плотность но у него и самая большая проникаемость, он
со временем
может просочится через металлы и пройти сквозь них
насквозь.
Следовательно при таких физических свойствах водород будет
вытеснен материалами
с большей удельной плотностью из своих
недр любой звезды или планеты на поверхность.
А из этого что следует - а то, что водород не участвует и никогда
не участвовал в ядерных реакциях в солнце потому что внутри
солнца водорода нет в принципе, он весь исключительно в атмосфере
солнца.
А из этого
следует что не только большой взрыв но и все эволюции
звезд и модели звёзд которые были построены на горении
водорода и гелия в звездах неправильны и не соответствуют
физическим свойствам веществ.
|
- Re: Черная дыра
(А.П. Васи,
12.01.2013 9:32, 1.0 КБайт, ответов: 1)
Большой взрыв - термодинамика.
Абсурдность большого взрыва проявляется
не только в том что всё сжалось а потом всё взорвалось,
и разбросало со скоростями
которые в миллиард раз превышали
скорость света, это цветочки. При более детальном рассмотрении
остывания после большого взрыва просматриваются
примитивные
ошибки в физике.
В локальной замкнутой системе излучается из неё и исчезает
за горизонт событий всё тепло всей материи участвовавшей в большом
взрыве. Так
вот оно не может никуда исчезнуть оно может
быть передано только другим телам физическим в этой же замкнутой
системе. Итого вселенная не могла
остыть физически
после большого взрыва.
Темная материя тоже у большого
взрыва прошла рядом с разумом положенным на полке,
по той причине что темную материю тупо забыли всунуть
в большой взрыв, точнее не забыли те кто придумал
большой взрыв забыли те кто приписал темной материи
девяносто с лишним процентом массы во вселенной и забыли
что находятся в большом взрыве изначально.
- Re[2]: Черная дыра
(Ю. С. Решников,
12.01.2013 9:59, 534 Байт)
Большой
взрыв
точно
присутствует
в
астропространстве,
при
образовании
туманностей
и
галактик.
Дальше
его
не
видно,
но
при
том,
не
исключен.
Астропространство
-
плазма
и
только.
Взрыв
-
присущее
плазме.
Взрыв
больше
химия,
чем
физика
и
потому
понятен
химии
больше,
чем
физике.
Не
бойтесь
поступиться
физикой
ради
химии
и
астрономии.
Это
полезно
самой
физике.
Верность
физике
-
явление
не
научное,
а
психологическое
- Re: Черная дыра
(А.П. Васи,
12.01.2013 10:47, 1.7 КБайт)
Ю.С.Решников
---------------------------
Вы здесь не пишите - ибо Вы
мне скучны в космологии,
ибо у Вас не знаний ни умений ими пользоваться.
Вы недалёкий.
А Ваши тексты
- это вообще тексты бессмысленные
и бесполезные, и Вы не физик и не математик,
и знаний у Вас нет - один
около-физический стёб скорей всего -
пенсионера у которого много свободного времени,
но уже и память не та, и нет умения анализировать
новые необычные знания.
Вы можете пойти
потусоваться на вот этот
форум,

Физика альтернативная
там модератор таких
как Вы не банит.
----------------------
Мне до лампочки Ваши вопросы, и мне наплевать что Вы думаете
о том что есть физика или астрономия или космология,
и я с теми кто борзо на меня наезжает с необоснованными претензиями
не общаюсь в принципе.
И если Вы не чатовый бот я удивлюсь.
Мне лично до лампочки Ваши
вопросы с химией,
Ваши вопросы - сами и решайте их.
И с теми кто не может сделать ни одного физического определения
и технически грамотно не может сформулировать
вопрос, я тоже
не общаюсь.
---------
Шли бы Вы на балетный форум и советовали бы там например в
фуэте - фуэтятины добавить.
- Re: Черная дыра
(А.П. Васи,
12.01.2013 10:54, 441 Байт, ответов: 1)
Ю.С.Решников
-----------------------
Вы
бы пошли бы на форум открыли бы вопрос и обсуждали бы его,
не понимаю Ваше садо мазо и Ваше желание
постоянно слушать от меня что Ваш уровень интеллекта очень
низкий - ничего личного, -
уровень в физике и космологии уровень - безмозглой скотины.
- Re[2]: Черная дыра
(Ю. С. Решников,
12.01.2013 12:19, 580 Байт)
Физический
абсолютизм
в
действии:
в
теориях
и
отношениях.
Вы
не
входите
ли
в
комиссию
по
борьбе
с
лженаукой
(будто
такая
может
быть) ?
Заслуга
физики
в
астрономии
в
обнаружении
астрономических
излучения,
полей,
химии,
гравитации,
плазмы,
подобных
физическим,
но
больше
физика
сказать
не
в
состоянии.
Ваша
ошибка,
что
для
космологии
Вы
изучали
физику.
Физика
не
присутствует
ни
в
названии,
ни
в
содержании
космологии.
И
виноватых
в
этом
не
найдете
- Re: Черная дыра
(А.П. Васи,
12.01.2013 15:00, 466 Байт, ответов: 2)
Ю.С.Решников
-----------------------
Вы
бы пошли бы на форум открыли бы вопрос и обсуждали бы его,
не понимаю Ваше садо мазо и Ваше желание
постоянно слушать от меня что Ваш уровень интеллекта очень
низкий - ничего личного, -
уровень в физике и космологии уровень - безмозглой скотины.
- Re[2]: Черная дыра
(Ю. С. Решников,
12.01.2013 17:18, 508 Байт, ответов: 1)
По
Вашему
я
не
на
форуме ?
И
форум
этот
астрономический !
И
тема
в
которой
и
Вы,
и
я
находимся
не
подразумевает
Вашего
ко
мне
отношения,
и
Ваших
оценок
моих
извилин,
а
развивает
значимые
в
астрономии
представления.
И
вопрос,
как
раскрывать
эту
тему
чисто
физически
или
чисто
астрономически,
имеет
важное
значение
для
дальнейшего
её
развития.
Вот
я,
как
раз
пытаюсь
в
ней
разобраться
- Re[3]: Черная дыра
(Ю. С. Решников,
12.01.2013 17:54, 455 Байт)
Правильный ответ -
тема раскрывается
астрофизически. Но что
есть астрофизика -
перенос физических
представлений в
астрономию или
использование
астрономией
физических данных. В
первом случае решение
чисто физическое -
просто делается
поправка на необычные
физические условия. Во
втором случае решение
чисто астрономическое
- разбираются именно
астрономические
условия. Вот так и
должно быть и к этому
нужно прийти
- Re: Черная дыра
(А.П. Васи,
12.01.2013 17:20, 499 Байт)
Ю.С.Решников
-----------------------
Вы
бы пошли бы на форум открыли бы вопрос и обсуждали бы его,
не понимаю Ваше садо мазо и Ваше желание
постоянно слушать от меня что Ваш уровень интеллекта очень
низкий - ничего личного, -
уровень в физике и космологии уровень - безмозглой скотины.
- Re: Черная дыра
(А.П. Васи,
12.01.2013 18:03, 532 Байт)
Ю.С.Решников
-----------------------
Вы
бы пошли бы на форум открыли бы вопрос и обсуждали бы его,
не понимаю Ваше садо мазо и Ваше желание
постоянно слушать от меня что Ваш уровень интеллекта очень
низкий - ничего личного, -
уровень в физике и космологии уровень - безмозглой скотины.
- Re: Черная дыра
(Ю. С. Решников,
18.01.2013 17:14, 463 Байт, ответов: 2)
Планетная
химия
возникает
из
астрохимии.
Астрохимия
происходит
из
астроПротохимии.
Химия
связана
с
гравитацией.
Астрохимия,
так
же
имеет
свои
гравитационные
процессы.
Разбираемая
тема
относится
к
свойствам
астрохимическим,
как
основе
ПВК
и
получает
через
них
своё
разрешение.
Нужно
отметить,
что
гравитационно-
химические
процессы
не
могут
быть
ограничены
скоростью
света
- Re[2]: Черная дыра
(Ю. С. Решников,
19.01.2013 0:14, 557 Байт, ответов: 1)
Скорость
быстрее
света
должна
быть
в
астрообъекте
(ПВК),
как
связующее
взаимодействие.
Электро-
магнитное
излучение
не
выполняет
такой
функции
из-
за
несоразмерности
своей
скорости
масштабам
астрообъекта,
что
видно
уже
на
ПВК
туманности
(и
ЭМИ
не
есть
управляющей
силой).
Только
гравитационное
взаимодействие,
как
определяющее
(вместе
с
химией)
ПВК
должно
обладать
таким
свойством.
Гравитационные
волны
из
моментального
взаимодействия
не
вытекают
- Re[3]: Черная дыра
(Ю. С. Решников,
19.01.2013 8:58, 349 Байт)
ПВК
необходима
скорость
достаточная
(!)
для
требуемой
одновременности
событий
в
его
объеме.
Что
означает
различные
достаточные
скорости
в
различных
ПВК.
Скорость
связующего
взаимодействия
можно
вычислить
и
попытаться
регистрировать.
Это
возможно,
если
гравитационные
волны
существуют
- Re: Черная дыра
(В. Б. Данеев,
19.01.2013 16:11, 577 Байт, ответов: 2)
Священна
река
Эридан.
С
Крещением.
Спор
между
физиками
и
химиками
напоминает
спор
между
шиваитами
и
вишнуитами
-
одни
упиваются
силами,
другие
тянутся
к
существам.
Где
наука,
где
религия?
О
гравитации
давно
сказано
-
движет
звёзды
и
планеты,
там
же
раскрыт
смысл,
столь
значимого
явления
-
Любовь.
Представляете
сколько
там
Любви,
что
нас,
наивных,
такая
Сила
повергает
в
священный
ужас.
Но
вот
ведь,
как
боимся,
а
жажда
познания
ещё
сильнее
- Re[2]: Черная дыра
(Ю. С. Решников,
20.01.2013 8:23, 575 Байт)
Да,
поэзия
красивая
конечно.
Продолжением
вашей
праздничной
шутки
будет
считать
шиваитов
и
вишнуитов
бывшими
астрофизиками
и
астрохимиками.
Вернемся
к
ПВК.
Есть
вопрос
-
являются
ли,
гравитационными
волнами,
те
возможные
сигналы,
получаемые
из
ПВК
с
которыми
наш
планетный
ПВК
связан
системно ?
Все-
таки
волнами
должны
быть
сигналы,
приходящие
из
ПВК
не
связаных
системно
с
нашим.
Тогда
они
действительно
волны,
а
не
какие-
либо
системные
изменения
- Re[2]: Черная дыра
(В. П.,
24.01.2013 21:10, 1.3 КБайт)
<
tbody>| Цитата: |
| Где на
ука, гд
е религия?
|
Интер
есный вопро
с! К
ак мне каже
тся, это вопр
ос к ап
ологетам
и светилам
наук
и!
Астр
онет | Н
аучная се
ть | ГАИ
Ш МГ
У | Поиск п
о МГУ
| О про
екте
| Авторам
Комментарии,
вопросы
? Пишите:
in
fo@astron
et.ru и
ли
сюда
столь
значимого
явления
-
Любовь.
Представляете
сколько
там
Любви,
что
нас,
наивных,
такая
Сила
повергает
в
священный
ужас.
Но
вот
ведь,
как
боимся,
а
жажда
познания
ещё
сильнее
- Re: Черная дыра
(В. П.,
24.01.2013 21:02, 349 Байт)
Скажите, а я правильно понимаю вот это: "распад может произойти таким образом, что одна частица упадет на черную дыру, а другая, сравнительно немного увеличив свою
скорость в момент распада, перейдет на такую орбиту, что вылетит из эргосферы с огромной скоростью" как рентгеновское излучение черных дыр? Или это необязательно так?
- Re: Черная дыра
(Ю. С. Решников,
26.01.2013 9:48, 564 Байт)
В
астрономии
все
пасутся,
включая
физиков
и
теологов.
И
всем
хочется
натянуть
одеяло
на
себя.
Но,
табуировать
не
свойственно
астроному
-
места
в
пространствах
хватит
всем
и
оно
для
всех.
Пока
открытый
у
астронома
вопрос
-
какой
промежуток
времени
достаточен
для
одновременности
в
ПВК.
Для
разных
ПВК
он
разный.
Десятки
световых
лет
для
галактики,
дают
ли
одновременность ?
Вряд
ли.
А
сколько
необходимо
-
месяцы,
дни,
доли
секунды ?
- Re: Черная дыра
(С. А. Пикалёв,
2.02.2013 15:20, 248 Байт)
Почему, электрон или протон не могут покинуть даже небольшую чёрную дыру, а для значительно более массивной Вселенной, расширяющейся из точки, это легко допускается?
Неужели, забыли вовремя включить гравитацию?
- Re: Черная дыра
(А.П. Васи,
2.02.2013 20:58, 255 Байт)
Рекомендую использовать исключительно авторское определение
о Черных Дырах. Ибо другие точки зрения не имеют
никакого отношения к Черным Дырам, ибо
не авторские
варианты рассказывают о чем-то другом,
что не является Черной Дырой.
- Re: Черная дыра
(С. А. Пикалёв,
2.02.2013 23:46, 165 Байт, ответов: 1)
Можно сформулировать иначе. Почему, Вселенная не является чёрной дырой при всех условиях для этого в начальный период расширения?
- Re[2]: Черная дыра
(А.П. Васи,
3.02.2013 10:32, 361 Байт)
И если Вы задаёте Вопрос то исключительно Вы обязаны
обосновать его правильность, а не хитроопить мол
опровергните меня в чем моя идея не права.
Если нет
способностей обосновать то Вы взялись за задачу превышающую
Ваши умственные способности и хотите решить её за чужой счёт и чужим умом,
на такие хитрости уже давно
никто не ведётся.
- Re: Черная дыра
(А.П. Васи,
3.02.2013 10:19, 419 Байт)
Когда придумывайте всякое лайно то это не
значит что это лайно является черной дырой,
это говорит скорее о том что Вам лучше не придумывать
всякого лайна
и не позорится.
Нет смысла придумымать что-либо и какие либо свойства
это сделал в своё время автор, а за автора это делать
никто не имеет права.
Шли-бы
Вы на балетный форум и посоветовали бы там
в фуетэ фуетятины добавить.
- Re: Черная дыра
(А.П. Васи,
3.02.2013 10:21, 122 Байт)
И прочтите сперва эту ветку сначала, а потом и поймёте
почему Ваш вопрос это детский лепет,
и ответы уже были.
- Re: Черная дыра
(С. А. Пикалёв,
3.02.2013 14:08, 268 Байт)
Пробежался по ветке. Пришёл к выводу, что многие Ваши утверждения недостаточно аргументированы, причём, лёгкая агрессия не
усиливает аргументацию. Ваше отношение к оппонентам и их идеям оставляет желать лучшего.
- Re: Черная дыра
(А.П. Васи,
3.02.2013 14:43, 33.4 КБайт)
Если бы читали внимательно то поняли что автор черных
дыр как физик недалёкий, и то что он описал не может
существовать физически.
Да и астрофизики и космологи
как дети доверчивые
повелись на черные дыры - даже не проверили элементарное -
сколько черные дыры должны за год звезд поглощать,
так там по миллиону за год
в нашей галактике пропадать
или тухнуть обязано звезд - а не потухло ничего.
-----------------------------------------------------------------------------
Что меня удивляет, - так
это то что вся астрофизика красивая и пушистая,
и всё прекрасно.
Но это же не так, вот те-же черные дыры - это же
просто пипец - и что это никто не замечает
или никто не
понимает.
Хочу сразу спросить, Ваше мнение по
...Черная дыра...
http://www.astronet.ru/db/msg/1188232
Согласны ли Вы с этим?
Какие из перечисленных статей соответствуют стандартам Черной
Дыры?
1 Есть ли жизнь в черной дыре
http://www.popmech.ru/article/8822-est-li-zhizn-v-chernoy-dyire/
2[ссылка]
Установлена масса самой крупной из сверхмассивных черных дыр.
Такое нам и не снилось.
3[ссылка]
Мифология черных дыр.В нашей Галактике существуют миллионы черных дыр
массой в несколько солнечных
4http://www.popmech.ru/article/8140-raspad-dyiryi/
Распад дыры.
Взрыв сверхновой может заканчиваться образованием не одной, а сразу
нескольких черных дыр.
5[ссылка]
Детство черной дыры
Взрыв, зафиксированный в глубинах космоса 31 год назад, судя по всему,
знаменовал рождение черной дыры самой молодой из нам известных
6[ссылка]
Темный центр
Таинственный центр нашей галактики,
место обитания сверхмассивной черной дыры и источник мощнейших потоков излучения,
преподносит новые сюрпризы.
7[ссылка]
Небольшое замечание о природе гравитации приводит к следствиям
космического масштаба к выводам о рождении новых миров из черных дыр
8[ссылка]
Обычная по размерам черная дыра выбрасывает
колоссальные потоки излучения и частиц.
9[ссылка]
Астрофизики предложили способ (теоретически) уничтожить черную дыру
10[ссылка]
Из всех сверхмассивных черных дыр лишь около 1% выбрасывают
значительные количества энергии
11[ссылка]
Выживающие дыры
Пара редких экземпляров
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
каким-то чудом выживающих в соседстве с этим монстром.
12[ссылка]
Как живется внутри черной дыры? Вы и сами знаете,
как: если справедливы новые теоретические выкладки,
вся наша Вселенная может находиться внутри черной дыры,
расположенной в другой Вселенной. Эдакая матрешка мироздания.
13[ссылка]
Они просто предположили, что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину. Это дало цифру в 10103, тоже огромную, но все-таки на много
порядков ниже.
14[ссылка]
Если очень, очень быстрый космический корабль разогнать
почти до скорости света, превратится ли он в черную дыру?
15[ссылка]
Некоторые сверхмассивные черные дыры выбрасывают
колоссальные потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
--------------------------------------------------------------
1 Некоторые сверхмассивные черные дыры выбрасывают
колоссальные
потоки раскаленной плазмы и лишь теперь
становится ясным, почему именно они.
2
В активном центре галактики М82, как и положено, находится сверхмассивная
черная дыра. Но рядом с ней обнаружено и пара дыр поменьше
3 Они просто предположили,
что в центре каждой из галактик имеется
по сверхмассивной черной дыре, и посчитали среднее количество и
величину.
Материал из
Википедии
http://upload.wikimedia.org/wikipedia/commons/thumb/3/39/M87_jet.jpg/250px-M87_jet.jpg
Изображение, полученное с помощью телескопа Хаббл: Активная галактика
M87. В ядре галактики, предположительно, находится чёрная дыра. На
снимке видна релятивистская струя длиной около 5 тысяч световых лет
Релятивистские струи
, джеты (англ. jet) струи плазмы, вырывающиеся из центров (ядер) таких
астрономических объектов, как активные галактики, квазары и
радиогалактики.
Обычно у объекта наблюдается две струи, направленные в противоположные стороны.
На настоящий момент релятивистские струи остаются недостаточно изученным
явлением. Причиной появления таких струй часто называют взаимодействие
магнитных полей с аккреционным диском вокруг чёрной дыры или нейтронной
звезды.
В статье на Элементах методом численного моделирования показано, что
при слиянии двух нейтронных звёзд образуется черная дыра, магнитное поле
которой вытянуто вдоль оси. Это наводит на мысли, что этот же процесс
может формировать и релятивистские струи. Тем не менее, в статье
говорится, что предложенная авторами научной работы математическая
модель оказалась очень сложна, а вычислительные возможности современных
компьютеров оказались недостаточны, чтобы с должной точностью провести
все необходимые расчеты и убедительно доказать формирование струй.
В другой статье на Элементах проводятся параллели между процессами в
черных дырах и бозе-эйнштейновском конденсате. Отмечается что конденсат
может коллапсировать (слипаться) и при последующем его распаде тоже
могут возникать узконаправленные выбросы.
Дальнейшее изучение релятивистских струй
При самых первых попытках объяснения сверхсветового движения с помощью
релятивистского направленного потока частиц возникло осложнение:
удивительно большая доля компактных источников показывала сверхсветовое
движение, в то время как на основании простых геометрических доводов
получалось, что только несколько процентов таких объектов должно быть
случайно ориентировано почти вдоль линии зрения. Присутствие
симметричных протяжённых радиокомпонент предполагало, что они
обеспечивались энергией от центрального источника двух симметричных
лучей. Но трудно сравнить светимость приближающейся и удаляющейся (или
даже стационарной) компонент. Это очевидное различие обычно обсуждается в
контексте модели с двойным истечением [4], когда излучение из ядра
рассматривается как стационарная точка, где приближающийся
релятивистский поток становится непрозрачным. Сверхсветовое движение
наблюдается между этой стационарной точкой в сопле и движущимися
волновыми фронтами или другими неоднородностями в выходящем
релятивистском потоке.......
.....Материал из Википедии
Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной волны
< 5×10−3 нм и, вследствие этого, ярко выраженными корпускулярными
и слабо выраженными волновыми свойствами.
Гамма-квантами являются фотоны с высокой энергией. Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя резкая граница
между гамма- и рентгеновским излучением не определена. На шкале
электромагнитных волн гамма-излучение граничит с рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению. Очевидно,
физически кванты электромагнитного излучения с одинаковой энергией не
отличаются, поэтому такое разделение условно.
Гамма-излучение испускается при переходах между возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков МэВ),
при ядерных реакциях (например, при аннигиляции электрона и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении энергичных
заряженных частиц в магнитных и электрических полях (см. Синхротронное излучение).....
Если нет поверхности об которую происходит торможение.
Материал из Википедии
.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в рентгеновских
трубках. Основными конструктивными элементами таких трубок являются
металлические катод и анод (ранее называвшийся также антикатодом).
В рентгеновских трубках электроны, испущенные катодом, ускоряются
под действием разности электрических потенциалов между анодом и катодом
(при этом рентгеновские лучи не испускаются, так как ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение. При этом за счёт
тормозного излучения происходит генерация излучения рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....
То вступает в силу фраза -
В области 1-100 кэВ
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.
следовательно при отсутствии удара о поверхность - отсутствует сама возможность
возникновения рентгеновского излучения, а если излучение есть то оно может
быть только результатом излучения в ядерном переходе. А это уже частицы высоких энергий.
авторское излучение из черной дыры -
.Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш метод обнаружения Черной Дыры
-Ваш текст - 11.05.11 14:04
....Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество.
ЧД так и обнаруживают. ....
Падая на Черную Дыру вещество не
может резко тормозится или резко ускорятся,
а следовательно - не может
быть рентгеновского излучения по этой причине.
В связи с тем что для ускорения до скорости света
при котором возможно излучение необходимо
не более 10 секунд, а звезда размером с
Солнце на такой скорости пролетит через горизонт
событий максимум за минуту.
Горизонт событий - это скорость света - если
объект улетает с этой скоростью от наблюдателя, то
у него возникнет красное смещение.
Если бы вещество долго падало - годами на малой скорости
с ускорением то было бы заметно изменение Z у падающих
тел в черную дыру со временем, но при этом невозможно
рентгеновское излучение - из за слишком медленного
увеличения ускорения.
.... Материал из Википедии Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц (тормозное излучение), либо при
высокоэнергетических переходах в электронных оболочках
атомов или молекул. Оба эффекта используются в
рентгеновских трубках.....
А рентгеновское излучение есть - следовательно
его источником может быть только результат ядерной
реакции.
....Материал из Википедии
Га́мма-излуче́ние
гамма-излучение и рентгеновское излучение различаются только по источнику:
если квант излучается в ядерном переходе, то его принято относить к
гамма-излучению; если при взаимодействиях электронов или при переходах
в атомной электронной оболочке к рентгеновскому излучению.....
А если результат излучения источник ядерной реакции -
и он длится годами, - то это нейтронная звезда.
http://www.popmech.ru/article/8971-nasledstvennyie-chernyie-dyiryi/page/3/
Уважаемый
Дмитрий Мамонтов
Моё - А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке, я так понял решил -
зачем добру пропадать - пусть излучение ( Излуче́ние Хо́кинга) из черной
дыры будет ещё и преимущественно из рентгеновских частиц.
Ваше - Рентгеновское излучение ЧД возникает при аккреции вещества.
Излучение Хокинга - другой процесс. Странно, что за 7 лет "увлечения
астрофизикой" Вы этого не поняли.
Моё - С моей точки зрения - уважаемый А.М.ЧЕРЕПАЩУК имеет такое же отношение
к Черным Дырам как я или Вы.
Мы с Вами, и А.М.ЧЕРЕПАЩУК можем только предполагать и высказывать
свою точку зрения, но обращать внимания на подобные высказывания и брать
их на веру, я не вижу смысла.
Другое дело автор. Как он сказал то - такие и Черные Дыры.
Уважаемый
Дмитрий Мамонтов
Вот я например говорю что вещество падает на черную дыру,
и после удара о поверхность с противоположной стороны черной дыры возникает рентгеновское и световое излучение.
Другой считает что излучение на подлете.
В бинокль не видно - одни предположения, и их может быть
больше сотни например - кому верить?
Уважаемый
Дмитрий Мамонтов
Вы затрагиваете вопрос интерпретации авторских
идей без согласия с автором.
А если десяток других авторов опубликуют по 300 научных работ, а автор о
Черных Дырах говорит что излучение в основном из фотонов - а все другие
говорят, что
излучение из рентгеновских частиц, другой говорит из радио излучения, а
третий говорит из гамма частиц - я должен слушать исключительно автора
Черных Дыр,
а не тех кто интерпретирует, и тем более тех кто плевать хотел на авторский вариант черных дыр.
Никто не мешает придумать свои - рентгеновские черные дыры, - так нет не
хотят, - так на неудобные вопросы отвечать должен будет автор, а при
интерпретации автора - писака например статьи с левыми идеями в области
Черных Дыр, прикрывается авторством автора
Черных Дыр, а сам со своим бредом по отношению к авторскому изложению, как-бы и не причем.
Уважаемый
Дмитрий Мамонтов
..Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
Ваш текст - 11.05.11 14:04
Они вообще-то активно светят в рентгене (за счет аккреции). Точнее,
разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Ваша ссылка - текст 11.05.11 20:36
....Как отличить черные дыры от нейтронных звезд
Как уже отмечалось, аккрецирующая черная дыра не должна проявлять себя
как рентгеновский пульсар. У нее может наблюдаться лишь иррегулярная
переменность рентгеновского излучения с характерными временами
$$Delta tapprox frac{r_g}{c}approx10^{-3} div 10^{-4}~mbox{rm с.}$$
И действительно, в рентгеновской двойной системе Лебедь Х-1, содержащей
черную дыру с массой около десяти солнечных, в состоянии, когда
рентгеновская светимость понижена, а рентгеновский спектр жесткий и
степенной, наблюдается быстрая иррегулярная переменность рентгеновского
потока на временах порядка миллисекунды. Наблюдения, выполненные с
бортов современных рентгеновских обсерваторий, таких, как ГИНГА,
МИР-КВАНТ, ГРАНАТ, АСКА, показали, что рентгеновские спектры
аккрецирующих черных дыр систематически более жесткие, чем спектры
аккрецирующих нейтронных звезд, и простираются до энергий в несколько
мегаэлектрон-вольт.
Как уже отмечалось, аккрецирующая нейтронная звезда может проявлять себя
как рентгеновский пульсар. Однако, если нейтронная звезда обладает
слабым магнитным полем (напряженностью менее 1010 Гс) или если ее ось
вращения неудачно ориентирована относительно земного наблюдателя, при
аккреции на такую нейтронную звезду могут не наблюдаться регулярные
пульсации рентгеновского излучения. Поэтому отсутствие строго
периодических пульсаций рентгеновского излучения - это лишь необходимый,
но не достаточный признак черной дыры. В то же время при слабом
магнитном поле нейтронной звезды и несильном темпе аккреции вещества на
ее поверхности могут происходить термоядерные взрывы накопленного
вещества, приводящие к явлению рентгеновского барстера I типа - коротким
(длительностью порядка 1-10 с) и мощным вспышкам интенсивности
рентгеновского излучения, что также является характерным признаком
аккрецирующей нейтронной звезды, обладающей твердой поверхностью.
Поскольку черная дыра не обладает твердой поверхностью, аккреция
вещества на нее не должна приводить к феномену рентгеновского барстера I
типа. Разумеется, отсутствие этого феномена также является лишь
необходимым критерием наличия черной дыры. Таким образом, мы можем
сформулировать важнейшие признаки аккрецирующей черной дыры: это мощное
рентгеновское излучение, большая масса (более трех солнечных),
отсутствие феноменов рентгеновского пульсара или рентгеновского барстера
I типа. При этом вопрос о надежном определении массы релятивистского
объекта в рентгеновской двойной системе является решающим при
идентификации его с черной дырой....
Я Вам просто показываю проииворечие у Вас и Вашей ссылке,
по отношению к написанному в Википедии о излучении из Черной Дыры.
Уважаемый
Лейтенант Немо
Чтобы происходил разброс частиц рентгеновского
излучения для этого надо или ядерное горение звезд,
что к черной дыре не применимо, или разгон материи
с последующим ударом разогнанной частицы о поверхность
как это происходит в рентген аппарате.
....Материал из Википедии
Рентгеновская трубка
Рентгеновские лучи возникают при сильном ускорении заряженных частиц
(тормозное излучение), либо при высокоэнергетических переходах в
электронных оболочках атомов или молекул. Оба эффекта используются в
рентгеновских трубках. Основными конструктивными элементами таких трубок
являются металлические катод и анод (ранее называвшийся также
антикатодом). В рентгеновских трубках электроны, испущенные катодом,
ускоряются под действием разности электрических потенциалов между анодом
и катодом (при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало) и ударяются об анод, где происходит их резкое
торможение. .....
Из чего вытекает следующее что для возникновения излучения радиоактивных
частиц - необходим удар материи на скорости одной десятой и более
скорости света.
Из чего следует невозможное условие для излучения материи при падении в
черную дыру - так как должна быть поверхность для удара.
А поверхности то и нет, вещество без удара уходит за горизонт событий,
следовательно и не может черная дыра излучать радиоактивные частицы.
А.М.Черепащюк в данном случаи не прав.
космогон
...Считается, что при падении на ЧД вещество разгоняется до скоростей,
близких к с. В таком случае трения более чем достаточно для излучения
высоких энергий. ...
Я не могу понять почему рассматривается отдельно взятая часть и не аргументируется а постулируется.
У Вас - постулат.
Вы возьмите например шар размером в километр в диаметре, и бросьте его в Черную Дыру.
Ну и разогнали Вы что угодно в пустоте, - ещё раз повторяю - в пустоте
происходит падение в черную дыру - какое может быть трение - просто не
об что тереться.
Возьмите например звезду, ей тоже не об что тереться когда вокруг пустота,
летит падает и угасает, тем более что мне лично
уважаемый Дмитрий Мамонтов расчёты приводил что звезда на одной десятой
или одной третей скорости света, может прекрасно летать на орбите
вокруг Черной Дыры, и с ней всё нормально.
Уважаемый
Дмитрий Мамонтов
,,,Черная дыра - область пространства, в к-рой поле тяготения настолько
сильно, что вторая космич. скорость (параболическая скорость) для
находящихся в этой области тел должна была бы превышать скорость света,
т.е. из Ч.д. ничто не может вылететь - ни излучение, ни частицы, ибо в
природе ничто не может двигаться со скоростью, большей скорости света.
Границу области, за к-рую не выходит свет, наз. горизонтом Ч.д.,,,
Это базовое определение, даже если предположить что в черную дыру падают
звезды, при этом излучают, и что в центре галактики в черных дырах
масса больше чем масса всех звезд в этой галактике, а с момента большого
взрыва
тогда можно посчитать сколько миллиардов звёзд в дыру в центре галактики
упало. Только вот не сходится с наблюдениями - звезды не исчезают в
черных дырах - этого никто не наблюдал, - не наблюдали и то как звезда
проходит через горизонт событий к черной дыре.
Уважаемый
Дмитрий Мамонтов
...Исходя из классики, на которую Вы опираетесь, ЧД для землянина должны светить как квазары....
Ваше - Они вообще-то активно светят в рентгене (за счет аккреции).
Точнее, разумеется, не они сами, а аккрецирующее вещество. ЧД так и
обнаруживают.
Моё - у меня вопрос - если в рентген диапазоне излучают ниже приведенные
нейтронные звёзды - которые
...В случае, когда перетекание вещества продолжается и после
образования Н. з., её масса может со временем значительно увеличиться.
При ${mathfrak M}_{Н.з.}>{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру. ...
То как отличить нейтронную звезду от черной дыры?
http://www.astronet.ru/db/msg/1188472
Нейтронные звезды
- гидростатически равновесные звёзды, вещество к-рых состоит в основном
из нейтронов. Существование Н. з. было предсказано в 30-х гг. 20
в.,вскоре после открытия нейтрона. Однако только в 1967 г. они были
обнаружены в виде импульсных источников радиоизлучения - пульсаров.
Затем было установлено, что Н. з. проявляют себя также как рентгеновские
пульсары (1971 г.) и вспышечные источники рентг. излучения - барстеры
(1975 г.). Не исключено, что на одной из стадий существования Н. з. явл.
источниками гамма-всплесков. К 1984 г. открыто ок. 400 Н. з., из них
ок. 20 в виде рентг. пульсаров, ок. 40 в виде барстеров, а остальные в
виде обычных радиопульсаров.
Другую возможность появления Н. з. представляет эволюция белых карликов в
тесных двойных звёздных системах. Перетекание вещества со
звезды-компаньона на белый карлик постепенно увеличивает его массу, и,
когда она достигает ${mathfrak M}_Ч$, белый карлик превращается в Н. з. В
этом случае ${mathfrak M}_{Н.з.}{mathfrak M}_{макс}$ Н. з. потеряет
устойчивость и в результате релятивистского гравитационного коллапса
превратится в чёрную дыру.
http://www.astronet.ru/db/msg/1188644
Рентгеновские пульсары
- источники переменного периодического рентг. излучения, представляющие
собой вращающиеся нейтронные звезды с сильным магн. полем, излучающие за
счет аккреции (падения вещества на их поверхность). Магн. поля на
поверхности Р.п. ~ 1011-1014 Гс. Светимости большинства Р.п. от
1035-1039 эрг/с. Периоды следования импульсов P от 0,7 с до неск. тысяч
с. Р.п. входят в тесные двойные звездные системы, вторым компонентом
к-рых явл. нормальная (невырожденная) звезда, поставляющая вещество,
необходимое для аккреции и норм. функционирования Р.п. Если второй
компонент находится на стадии эволюции, когда скорость потери массы
(этим компонентом) мала (см. Эволюция тесных двойных звезд), нейтронная
звезда не проявляет себя как Р.п. Рентг. пульсары встречаются как в
массивных молодых двойных звездых системах, относящихся к населению I
Галактики и лежащих в ее плоскости, так и в маломассивных двойных
системах, относящихся к населению II и принадлежащих к сферич.
составляющей Галактики. Р.п. открыты также в Магеллановых Облаках. Всего
открыто ок. 20 Р.п.
На начальном этапе исследований открываемым рентг. объектам
присваивались наименования по созвездиям, в к-рых они находятся. Напр.,
Геркулес X-1 означает первый по рентг. яркости объект в созвездии
Геркулеса, Кентавр Х-3 - третий по яркости в созвездии Кентавра. Р.п. в
Малом Магеллановом Облаке обозначается как SMC X-1, в Большом
Магеллановом Облаке - LMC X-4. Обнаружение со спутников большого числа
рентг. источников потребовало др. системы обозначений.
Ускорение и замедление вращения нейтронных звезд.
В отличие от радиопульсаров (нек-рые из к-рых, в частности пульсары в
Крабе и Парусах, излучают и в рентг. диапазоне, см. Пульсары),
излучающих за счет энергии вращения замагниченной нейтронной звезды и
увеличиващих свой период со временем, Р.п., излучающие за счет аккреции,
ускоряют свое вращение.
Уважаемый
Дмитрий Мамонтов
Спасибо за ответ.
Если я правильно понял, то источник
непрерывного рентгеновского излучения
со стабильной интенсивностью - называется
Черной Дырой .
Если рентгеновское излучение меняет интенсивность
то это или нейтронная звезда или
рентгеновский пульсар.
Здесь автор черных дыр - семь пятниц на неделю,
сперва говорил вот так -
...Чёрная дыра́ область в пространстве-времени,
гравитационное притяжение которой настолько велико,
что покинуть её не могут даже объекты, движущиеся
со скоростью света (в том числе и кванты самого света)....
Потом его озарило в 1975 и он одарил черные дыры и всех
астрофизиком излучением от черных дыр.
---...Излуче́ние Хо́кинга ...---
......Материал из Википедии
Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой.
Предсказан теоретически Стивеном Хокингом в
1974 году.[1] Работе Хокинга предшествовал
его визит в Москву в 1973 году, где он встречался
с советскими учеными Яковом Зельдовичем и
Алексеем Старобинским. Они продемонстрировали
Хокингу, что в соответствии с принципом
неопределенности квантовой механики
вращающиеся чёрные дыры должны
порождать и излучать частицы.[2]
Испарение чёрной дыры квантовый процесс.
Дело в том, что понятие о чёрной дыре как объекте,
который ничего не излучает, а может лишь поглощать материю,
справедливо до тех пор, пока не учитываются квантовые эффекты.
В квантовой же механике, благодаря туннелированию,
появляется возможность преодолевать потенциальные барьеры,
непреодолимые для неквантовой системы. Утверждение,
что конечное состояние черной дыры стационарно,
правильно лишь в рамках обычной, не квантовой теории
тяготения. Квантовые эффекты ведут к тому, что на самом
деле черная дыра должна непрерывно излучать, теряя при
этом свою энергию.....
Итого
...Излуче́ние Хо́кинга процесс испускания
разнообразных элементарных частиц,
преимущественно фотонов, чёрной дырой....
А господин А.М.ЧЕРЕПАЩУК, в Вашей ссылке,
я так понял решил - зачем добру пропадать - пусть
излучение ( Излуче́ние Хо́кинга) из черной дыры
будет ещё и преимущественно из рентгеновских частиц.
Уважаемый
Дмитрий Мамонтов
Моё - А вот здесь я Вам могу предложить сделать у каждой статьи счетчик, - понял -не понял,
Ваше - Для базового понимания нужно уметь читать и иметь некоторую
подготовку в рамках хотя бы школы. У Вас такая подготовка, судя по
всему, хромает на обе ноги, поэтому Вы не понимаете большинство статей.
Для уточняющих вопросов есть комментарии, для базовой подготовки - школа
и учебники.
- Вы думаете что все ученные пишут правильные статьи, и никто статьи не
высасывает из пальца а потом не ржет над читателями, а Ваш сайт чтобы
читать - то надо быть доктором наук, и в тоже самое время Вы лично не
можете ответить прямо на прямые вопросы, по этой статье. Вы меня в
принципе заинтриговали, я подумаю чтобы такой пузырь высосать из пальца в
рамках парадигмы, чтобы все вокруг аж зааплодировали за исключительно
высокохудожественный идиотизм в рамках бреда сивой кобылы.
Моё-Не расскажете Ваше отношение к высказыванию, -
Если опыт не совпадает с теорией то тем хуже для опыта?
Напомню -
Моё - Со второго Вашего ответа я понял - что у Вас есть методы
доказательств которые позволяют определить какими были в первые моменты
большого взрыва звезды, черные дыры , температура и другие различные
свойства пространства и свойства различных физических объектов.
Ваше - Не у меня. У астрономов, астрофизиков и космологов.
Моё- Если мне не может оппонент сразу внятно изложить ответ на мой
простой вопрос по обсуждаемой статье, то я не обязан верить написанному,
а скорее наоборот - вынужден засомневаться.
По поводу громких фамилий в астрофизике - то если Вы проанализируете их
биографию и трудовые заслуги и проанализируете их причастность к
астрофизике, то они все в астрофизике - дилетанты, которые идеи
вбрасывали в астрофизику от случая к случаю, и серьёзно ей ни кто не
занимался. По этому вся астрофизика и состоит из разрозненных идей, -
озарялок, которые последователи пытаются состыковывать между собой по
причине появления новой измерительной техники.
А астрофизику у меня хобби лет 7, так что я прочитал столько статей
разных, что могу делать выводы что высоска из пальца, а что и супер
грамотно написано .
Самое смешное что супер статьи абсолютно неизвестны.
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
-Очень хорошая статья.
http://www.anomaliy.ru/discovery/482
"Сверхновые типа I а, как полагают, формируются
после взрывов белых карликов, сверхплотных мертвых звезд размером с
нашу Землю, которые когда-то были ядром солнцеподобного светила, и
чья внешняя оболочка растворилась в космосе.
Одна из особенностей этого типа отсутствие водорода, и это
несмотря на то, что водород является самым распространенным
химическим элементом."
Вот эта статья - в принципе должна была перевернуть всю астрофизику,
по той причине что нет водорода внутри звезды. А у текущей парадигмы
водород выгорает. И астрофизики внятно ответить не могут причину по
которой самый легкий водород - преодолевает гравитацию становится
тяжелее всех металлов и летит в ядро звезды поучаствовать в ядерной
реакции. И В то что самый легкий водород преодолевает летит внутрь
звезды -я не верю, хоть в миллионе книжек это будет написано, и тысяче
учебников. Так как написанное не подтверждено физическими свойствами а
противоречит им.
- Re: Черная дыра
(в. г. грузинов,
5.02.2013 19:57, 225 Байт)
Может черная дыра быть наподобие торнадо ,мы видим как она поглощает и должен быть выброс материи с другой стороны? .И второе если что -либо улетает от нас со скоростью
света ,будет это выглядеть для нас как черная дыра?
- Re: Черная дыра
(А.П. Васи,
5.02.2013 21:33, 235 Байт, ответов: 2)
\\\мы видим как она поглощает\\\
Кто и когда это видел.
Официально на текущий момент не обнаружено ни одной
черной дыры, есть
только предположения - что вот там-то
она должна быть.
- Re[2]: Черная дыра
(В. А. Бурдин,
9.02.2013 13:57, 824 Байт, ответов: 1)
К сожалению не прочитал я все 34 страницы этого форума,но после прочтения первого десятка возник вопрос лично к Вам А.П. Васи- Вы писали что ''Черная дыра - не является
тоннелем, по причине того чтоу неё есть масса, и любой релятивист очень быстро и доблестно разобъется в лепёшку о её поверхность, так как её размер и радиус Вам известен''
и ''У черной дыры есть радиус следовательно есть поверхность''-вытекает вопрос-что на Ваш взгляд(именно на Васш) лежит(может лежать) в основе поверхности черной дыры? Во многих
источниках видел следующее(не цитирую,свои слова)-черная дыра обладает сверхгравитацией по причине её создания. Что мол,ядро настолько плотно,что ''бывшая'' гиперзвезда сжалась
до таких размеров,не потеряв при этом уровня гравитации. Что же тогда служит ''материалом поверхности''? Железо?
- Re[3]: Черная дыра
(В. А. Бурдин,
9.02.2013 14:02, 340 Байт)
Отвечая на вопрос ''мы видим''-возможно многие авторы просто видели серию фильмов ''Discovery. Как устроена вселенная.'' Есть такое дело )) уж очень часто на любые запросы,связанные
с астрономией поискови выводят на вырезки и куски видео из этих 8-ми серий. Так....чисто моё предположение )) просто не знаю как мы еще можем ''видеть''....
- Re: Черная дыра
(А.П. Васи,
9.02.2013 16:08, 284 Байт)
Я над вопросом думаю долго зато решаю его раз и навсегда,
и если я сказал что автор черных дыр
не далёкий в физике \умственно не полноценный в физике\,
то
меня его творчество уже не интересует.
Я свою жизнь на бессмысленную и бесполезную уйню тратить не собираюсь.
- Re: Черная дыра
(А.П. Васи,
14.02.2013 22:58, 866 Байт)
\\\Простая задача для электриков.\\\
Старость не радость, вот яркий пример
как можно себя самому
обо- ... без посторонней помощи.
Щас по планете только какая экономия, можно с линий электропередач
высоковольтных снимать
одну фазу, и нагрузка на другие
не возрастёт, их толще по сечению делать не надо.
Здесь уже не проходит фраза \отцы простите за-с-ранца\ звучит как насмешка
над всей физикой.
Что ещё меня удивляет я хоть и сам с трёхфазной техникой
как киповец сталкиваюсь, у меня пол мегаватта был максимум
по нагрузке,
- три нагрузки по 160кВт с электронными преобразователями
от одного ввода.
Шина была медная полоса, и если она оборвётся то полноценно её восстановить
не возможно практически.
- Re: Черная дыра
(А.П. Васи,
16.02.2013 1:33, 3.0 КБайт)
Простая задача для электриков.
----------------------------
 Простая задача для электриков. ---------------------------------------------------
Простая задача для электриков. ---------------------------------------------------
Как при обрыве одной из фаз в трёхфазной сети полноценно восстановить
оборванную фазу на любой мощность. Кроме высоких материй нужно знать и
элементарные вещи!!!
--------------------------------------
Даже не понимаю как можно быть настолько
недалёким чтобы не знать того
что при подключении
устройств треугольником с оставшихся двух
фаз можно взять только тридцать процентов
мощьности, при подключении звездой,
можна взять
шесдесят пять процентов
мощности, и узвезды должен быть нулевой
провод не уменьшенного сечения,
а если нулевой уменьшенного сечения
то тридцать процентов
мощьности.
И вот например есть некоторая нагрузка которая
потребляет мощность, к ней подводится силовой
кабель. Стоит рубильник и токовая защита,
которая защищает подводимы кабель согласно
установленной мощности на расчетную температуру
в сорок градусов окружаюшей среды,
ток трёхфазный для насосов
можно просто узнать
умножив мощность в 2.1 - 2.2 раза, например
15кВт = 32А трёхфазной на 380 - 400В, по рекомендциям
проходит в притык кабель в четыри
квадрата \не в трубе\
что логично приводит к переходу на шесть квадрат.
Грубо говоря - кабель по сечению подводится
впритык по мощности без двух кратного
запаса,
и тепловая защита по току в проводе - автоматические
выключатели устанавливаются согласно сечению
подводимого провода.
И например есть клоун
который увидел в продаже
частотник для двигателя который запитывается
от 230В, а на выходе выдаёт три фазы на 380В.
Так он всю мощность берёт из одной фазы
и нулевого
провода, плюс потери на преобразование,
ток узнать 1кВт примерно равен 5А.
И чтобы например запитать двигатель в 15кВт,от 220В надо
чтобы
подводимый кабель смог обеспечить
ток в 75А. А такого сечения кабель никто не подводил,
и защитные автоматы на 40А, и вводной рубильник
на 40А, и вся проводка
на 40А.
Так что высказывание о полноценной замене -
это примитивный лах а трон.
- Re: Черная дыра
(А.П. Васи,
16.02.2013 18:41, 2.3 КБайт)
----------------------------
 Re: Простая задача для электриков.
Re: Простая задача для электриков.
Ответ #69 - Сегодня :: 18:08:19
PauLitas писал(а) Сегодня :: 17:11:29:Берём
два трансформатора (с нужным и одинаковым коэффициентом трансформации),
трансформируем первую фазу ну будем считать её фазой А, трансформируем
вторую фазу будем считать её фазой В соединяем вторичные обмоткиэтих
двух трансформаторов правильно (как больше напряжение), и в нужной
фазировке включаем её одним концом к нулевому проводу. Вот и есть нужная
третья фаза! Ответ правильный. Как не крути, вы здесь
самый квалифицированный электрик. Правильно решили задачу об измерении
ёмкости конденсатора в составе резонансного контура. А ведь её не смог
решить кандидат наук E-Eater. Теперь, хоть и не сразу, решили и эту
задачу. Снимаю шляпу!
|
----------------------------
Так и охота сказать что в электронике
никогда не стоит выстёбываться ибо есть
программы типа электроник ворк бенч 5.12
в которой можно и фазы и силу с-имитировать
и трансформаторы, и нагрузку дать и включить
всё это лайно и посмотреть
осциллограммы.
У меня такое чувство что ум на земле как физическая величина
это константа,
если людей на ней больше то кто-то тупеет при увеличении
количества населения планеты.
- Re: Черная дыра
(А.П. Васи,
16.02.2013 18:46, 113 Байт)
Трансформатор не делает сдвига фаз
на сто двадцать градусов.
Этого в физике не знают только недалёкие.
- Re: Черная дыра
(А.П. Васи,
17.02.2013 12:17, 1.1 КБайт)
А вот и награда нашла своего героя.
-----------------------------
 Re: Простая задача для электриков.
Re: Простая задача для электриков.
Ответ #83 - Сегодня :: 11:23:19
Фёдор Менде писал(а) 14.02.13 :: 22:52:46:
Есть и практическая реализация на 10 кВт на каждую фазу.
трехфазный ...
- Re: Черная дыра
(А.П. Васи,
17.02.2013 12:18, 266 Байт, ответов: 1)
Немного адекватного.
 Насколько можно доверять выводам астрофизиков? 15.01.2013
Насколько можно доверять выводам астрофизиков? 15.01.2013
- Re[2]: Черная дыра
(в. г. грузинов,
20.02.2013 15:49, 859 Байт)
Наш глаз это тоже черная дыра или ,нора?.Если свет имеет давление и надувает паруса ,а телескоп фокусирует свет в пучек который светит нам в глаз ,куда он девается потом ,рассеивается
в нашем мозгу или уходит в другое измерение.Если скорость света постоянна- то как телескоп умудряется показать нам галлактику за несколько секунд ,из дальней вселенной ,если
свет летит до нас миллионы лет? Таким образом может ли телескоп работать в "обратную" сторону и общаться с другими не бороздя просторы даже нашей галлактики .Например:
строим огромный телескоп на луне или используем планеты с нашими спутниками, которые иногда выстроившись определенным образом создадут огромный рефлектор и налаживаем мгновенный
контакт ,хоть азбукой морзе .(условно)И никаких дальних перелетов с теорией Эйнштейна . просто сначала наладить связь с другой жизнью .
- Re: Черная дыра
(А.П. Васи,
24.02.2013 13:16, 1.7 КБайт)
 Re: Вихревой объект. Материализация
Re: Вихревой объект. Материализация
Вселенной.
Ответ #75 - Сегодня :: 12:26:11
\\\
Единственный человек понял
тему так, как я пыталась донести. Именно
такое понимание позволяет совершить точные расчёты и создать фрактальный
генератор электричества. В нашей таблице элементов видна зависимость
структуры атома от соотношения собственных колебаний с колебаниями
среды. На
основании этого могут быть изучены свойства веществ для
использования их в новой технологии добычи электрической энергии, а
также появится возможность преодолеть гравитацию.\\\
-------------------------
Вот что собственно в этом тексте бросается в глаза, так это с одной стороны
логики
стремление к объективному пониманию, при этом без-башенная жажда
дармовщины, выраженная в стремлении к шаровой энергии и шаровым
методам преодоления
гравитации.
Так вот - вот эта жажда дармовщины - делает абсолютно
невозможным объективное восприятие. По той причине
что у природы возможно и нет той шаровизны
которую пытаются найти, да что там возможно, точно нет шаровизны,
она ей - природе, не нужна, нужна тем кто сам себе её придумал и пытается
найти - называется
это - самообман.
- Re: Черная дыра
(А.П. Васи,
25.02.2013 23:07, 5.0 КБайт)
 Re: Вселенная как сплошная многофазная среда
Re: Вселенная как сплошная многофазная среда
Ответ #1371 - Сегодня :: 11:49:21
Мар.Мих-на писал(а) Сегодня :: 11:18:57:Сколько раз можно спрашивать Ларису: так в чём ваш альтернативный взгляд? Вы постоянно афишируете здесь достижения
вашей кафедры 50-летней давности. \\\ Уважаемая Марь-Михна! Я все жду, что Вы, читая посты темы, сами найдете ответ на свой вопрос. Видимо, не дождусь... Поэтому
отвечаю. Я здесь афиширую не достижения некой "кафедры", а достижения
НАУКИ, под названием "Физика сплошной среды". Которая существует уже
около 300лет, однако её применение в разных областях человеческой
практики имеет нюансы. Вот эти нюансы я и пытаюсь выявить и представить
уважаемой "публике" применительно к гипотезе эфира, сверхъединичных
устройств, проблемы "вечного" двигателя и др. И я понимаю АЛЬТЕРНАТИВНЫЙ
взгляд на некие физические явления НЕ как ПРОТИВОПОЛОЖНЫЙ существующим
воззрениям, а просто, ДРУГОЙ, "свежий". И хочу показать, что НЕТ
ЛЖЕНАУКИ в нашем подлунном Мире, а есть одна НАУКА, с разной степенью
достоверности описывающая и объясняющая ЕГО. И, вроде бы, между взглядами Михаила Петровича и моими намечается консенсус. Будем работать дальше...\\\ ------------------------------------------------------------------------------------- Я вот было немного по-возмущался мысленно по причине того что законодательный орган для ученных России - это комиссия по борьбе с лженаукой. И собственно
я являюсь закоренелым лжеучёным - по той причине что в рамках определения лжеучёного в России есть вот такие стандарты. И как говорится до лампочки
что какой-то барышне хочется чтобы было по другому, а точнее как ей нравится - её мнение и пожелания никого не интересуют, ибо критерии определены. ------------------------------------------------------------------ http://lenta.ru/conf/kuvakin/
Эдуард-2
[24.04 03:11]
Уважаемый Валерий Александрович, я есть ли в вашем (РАН) арсенале
стандартная методика отделения "пшеницы от плевел", т.е. научных
открытий и достижений от околонаучных явлений, к науке отношения не
имеющих? Eсли такая методика существует, то какие признаки сразу
указывают на то, что перед нами очередной граф Калиостро?
Уважаемый Игорь!
В практике оценки лженауки есть два пути. Первый этот специальная
свободная и независимая научная экспертиза. Но она возможна только в том
случае, если в заявленной идее есть предмет исследования. Если же ее ни
подтвердить, ни опровергнуть невозможно, то такие идеи не
рассматриваются в качестве научных. В этой связи упоминают и о принципе
"бремени доказательства", то есть обязанность доказывать истинность или
научность утверждения лежит на той стороне, которая и выдвигает это
утверждение. Вместе с тем существуют некоторые общие и предварительные
признаки, наличие которых должно ставить под серьезное сомнение
научность заявления (теории, открытия и так далее). Это так называемые
признаки prima facae (то есть "с первого взгляда"). К ним, в частности,
относятся: (1) отсутствие у заявителя соответствующего базового
образования или профессиональной подготовки; ------------------------------------------- А я вот ни то что специального образования не имею у
меня даже высшего образования нет. Я собственно - лжеучёный однозначно. Что меня в этой ситуации радует что в России мои авторские права защищены более
чем. Что меня удивляет что сторонники Эфира в России с которыми я возможно хотел бы сотрудничать в написании статьи про эфир, по той причине что вместе преодолевали
трудности на мембране - будут сразу лжеучеными при совместном написании статьи со мной. И что мне например коллегам по эфиру сказать - давайте напишем совместную
статью - только Вас будут немножко лишать научных степеней, заслуг должностей и дипломов. |
- Re: Черная дыра
(А.П. Васи,
25.02.2013 23:13, 118 Байт)
И при всём при том я с Украины - на которую например
такой подход к определению лжеученых не распространяется.
- Re: Черная дыра
(А.П. Васи,
26.02.2013 0:31, 1.8 КБайт)
Ох я и насмеялся - всё есть,
-есть электричество,
- есть ток
-есть магнитное поле
- а сопротивления, - точнее нагрузки,
точнее причины всего
этого коленкора - то и нет.
--------------------------------------------------------------
Кстати не рис-23
А околофизичный с притензией на
космологичность -
- рисунок художника - номер 23.
-----------------------------------------------------
Электрическое поле
пытается восстановить прерванный электрический ток.

Рис. 23
На рис. 23
красным цветом показано электрическое поле, которое генерируется в результате
отключения джета черной дыры. Поле создает эл. ток, в основном, в виде
циркуляции электронов вокруг магнитных линий поля торов. Как показано, циркуляционный
поток электронов подпитывается электронами со стороны диска галактики. При этом,
электроны подпитки двигаются вдоль магнитных линий галактического ядра. Траектории
электронов, распространяющихся вдоль магнитных линий галактического ядра и
вдоль электрического поля гало, определяют характерную форму пузырей Ферми. В сумме, ускоряемый электрическим полем поток
электронов, магнитное поле гало галактики и магнитное поле галактического ядра формируют
синхротронное радио, рентгеновское и гамма излучение.
- Re: Черная дыра
(А.П. Васи,
26.02.2013 0:33, 242 Байт)
http://www.popmech.ru/images/upload/..._23_1356623136_resize.jpg

- Re: Черная дыра
(А.П. Васи,
26.02.2013 0:34, 134 Байт)
http://www.popmech.ru/blogs/post/5087-osobennosti-formirovaniya-struynyih-vyibrosov-aktivnyih-galakticheskih-yader-i-chernyih-dyir-ch/
- Re: Черная дыра
(А.П. Васи,
26.02.2013 1:02, 1.0 КБайт)
- Re: Черная дыра
(А.П. Васи,
2.03.2013 20:11, 4.0 КБайт)
\\\Это так называемые
признаки prima facae (то есть "с первого взгляда"). К ним, в частности,
относятся: (1) отсутствие у заявителя соответствующего базового
образования или профессиональной подготовки; \\\
Как не странно это высказывание попадает под действие законодательства России.
Вот от сюда текст.
--------------------------------------------------------
 Re: Семинар в ЦИАМ
Re: Семинар в ЦИАМ
Ответ #925 - Сегодня :: 19:10:13
Дамы, господа.
Перегудов встал на путь уголовно наказуемой деятельности. А именно, на путь разжигания межнациональной и межрасовой вражды..
Вот некоторая
информация по этому поводу...
Он
писал. "При чем тут национальная рознь? А, это вам девственная
чистота мозгов мешает меня правильно понять! По теории эволюции Дарвина
(в школе проходят) человек произошел от обезьяны. Но произойти от
обезьяны --- это вам не кучу под дверь наложить! Процесс трудный,
долгий, болезненный. Некоторые уже произошли, а другие некоторые
подзастряли Смех Вас, например, вполне можно назвать "владимирской
мартышкой". По сравнению с этим Ши вы "происходить из обезьяны" еще и не
начинали."
А вот юридическая квалификация этих высказываний.
"Разжига́ние межнациона́льной ро́зни - действия, направленные
на возбуждение межнациональной или межрасовой вражды.
В России
В России подобные действия признаются преступлениями против основ государственного строя и безопасности
государства.
Статья 29 Конституции Российской Федерации[1] гласит, что
Не
допускаются пропаганда или агитация, возбуждающие социальную, расовую,
национальную или религиозную ненависть или вражду. Запрещается
пропаганда социального, расового, национального, религиозного или
языкового превосходства.
Согласно части 1 статьи 282 Возбуждение
ненависти либо вражды, а равно унижение человеческого достоинства
Уголовного кодекса Российской Федерации в редакции Федерального закона
от 08.12.2003 N 162-ФЗ[2],
Действия, направленные на возбуждение
ненависти, либо вражды, а также на унижение достоинства человека, либо
группы лиц по признакам пола, расы, национальности, языка,
происхождения, отношения к религии, а равно принадлежности к какой-либо
социальной группе, совершенные публично или с использованием средств
массовой информации наказываются штрафом в размере от ста тысяч до
трехсот тысяч рублей или в размере заработной платы или иного дохода
осужденного за период от одного года до двух лет, либо лишением права
занимать определенные должности или заниматься определенной
деятельностью на срок до трех лет, либо обязательными работами на срок
до ста восьмидесяти часов, либо исправительными работами на срок до одного года, либо лишением свободы на срок до двух лет."
Я
полагаю, Перегудову есть о чём подумать. Я посмотрел. Прокуратура
действует. Электронная приёмная работает. Можно и лично сходить,
заявление написать. Они это любят, когда лично.....
Я немного
подожду. Не осознает- тогда это будут проблемы Перегудова. Можно,
заодно, руководство МГУ привлечь- кого оно у себя держит. И руководство
ИФЗ..... И не важно, что там говорил Дарвин. Важно, что записано в УК.
-----------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
2.03.2013 20:34, 398 Байт)
По большому счёту - борьбой с лженаукой
можно и не страдать.
Достаточно ввести премию за опровержение теорий и гипотез,
и размеры премий в десять тысяч евро
не более, и пятьсот евро
минимальная.
И я просто уверен что за стоимость меньше одной нобелевской
- будет снесена вся текущая физика и космология, по времени
снесут под частую - за года три максимум.
- Re: Черная дыра
(А.П. Васи,
3.03.2013 14:41, 4.6 КБайт)
Материал из Википедии свободной энциклопедии
Гипо́теза (др.-греч.
ὑπόθεσις
предположение; от ὑπό
снизу, под + θέσις
тезис) предположение или догадка;
утверждение, предполагающее доказательство, в отличие от аксиом, постулатов, не требующих доказательств. Гипотеза считается научной, если она удовлетворяет критерию
Поппера, то есть потенциально может быть проверена критическим экспериментом, а также если она соответствует другим научным
критериям.
Также она может определяться как форма развитий знаний,
представляющая собою обоснованное предположение, выдвигаемое с целью
выяснения свойств и причин исследуемых явлений[1].
Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений (примеров),
и поэтому выглядит правдоподобно. Гипотезу впоследствии или доказывают, превращая её в установленный факт
(см. теорема, теория),
или же опровергают (например,
указывая контрпример), переводя в разряд
ложных утверждений.
Недоказанная и неопровергнутая гипотеза называется открытой проблемой.
-------------------------------------------------------------------
Открытая проблема
- как раз и называется словом - лженаука.
Собственно вся космология таковой и является по определению,
ибо доказать строение звёзд , наличие черных дыр
и большого взрыва -
нельзя назвать даже гипотезами - они подразумевают возможность
проверки и опровержения, в связи с чем при отсутствии таковой
возможности в принципе - то это не гипотеза а фантастика или
выдумка - одним словом - лженаука.
Так что лучше бы комиссия по борьбе
с лженаукой своим
бы делом занялась вместо того чтобы объявлять всех
у кого нет высшего образования лжеучеными по признакам
- с первого
взгляда.
- Re: Черная дыра
(А.П. Васи,
17.03.2013 14:00, 1.4 КБайт)
Читал про разные опыты по измерениям. Что собственно меня
удивляет - что-то измеряют, потом думаю что и как измерили.
А основная ошибка в том что нет не только
стандартной методики
измерений на коротких временных промежутках,
так и нет самодиагностики.
Расскажу как сделать абсолютные измерительные кабеля.
У абсолютного измерительного кабеля должно быть три экранированных
жилы, и три оптоволокна, всё это соединяется вместе, и делается
шесть таких абсолютных кабелей,
длинной по десять метров каждый.
все шесть кабелей соединяются вместе.
Нужно взять осциллограф у которого шесть входных каналов,
на каждый вход
подключается по одному проводу из каждого кабеля,
по одному проводу из каждого кабеля берется и они скручиваются
вместе и на них подаётся стробирующий сигнал.
Из кабеля берется по одному окптоволокну и подключаются
на шесть оптоволоконных входов в этом-же осциллографе,
на вторые оптоволкна подаётся общий стробирующий
сигнал,
и они включаются в тот-же осциллограф,
На свободном оптоволокне каждого кабеля, устанавливается
высокоскоростной приёмник с автономным питанием,
выходы подключаются на цифровые оптоволоконные входа
в этом-же осциллографе.
И вот с этой техникой можно хоть что-то адекватное
измерять и сравнивать,
- ибо будет возможность абсолютного
временного контроля.
- Re: Черная дыра
(А.П. Васи,
21.03.2013 12:45, 3.0 КБайт)
Я вот не понимаю если ты например релятивист
то какого лезть на альтернативные форумы и учить
там альтов релятивизму.
Альты ведь в ответ будут всегда
посылать в пешее
эротическое путешествие, и всегда будут портить
нервы этому релятивисту, что в итоге скажется
отрицательно на здоровье релятивиста, ибо
от нервов
и постоянного пребывания в нервозном состоянии
создаст очень весёлые трудности для здоровья релятивиста
который пытается как он думает альтов уму
разуму научить.
Хотя с другой точки зрения может эта ситуация и
к лучшему ибо быстрее махровые релятивисты слетят
с интеллектуальных катушек.
------------------------------------------------------
\\\
 Re: Семинар в ЦИАМ
Re: Семинар в ЦИАМ
Ответ #1320 - Сегодня :: 12:23:24
Vallav писал(а) Сегодня :: 00:56:26:Не, Вы уникум.
Болтать о чем угодно, а в ответ на вопрос - ни слова.
Натренировались.
И при таких талантах еще о какой то дискуссии заикаетесь.
Валлав. Люди очень разные, уникумы. Я не болтаю. Я гну свою линию на введение эфира в научно-технический оборот. На этой основе я могу
вести дискуссии и обсуждения. Но
трудно вести дискуссии с оппонентами, которые даже не пытались
прочитать что-то про эфиродинамику (хотя бы в объёме популярной
эфиродинамики). Если оппонент имеет представления об эфире времён
Лоренца (и то ошибочные). Я не веду дискуссии по таким "общепризнанным" наукам как ТО и иже с ней. Данный
форум всё же называется "Физика альтернативная". Надо заметить, что
ничего альтернативного в эфиродинамике я не нахожу. Классическая
физическая теория. Хотя после всеобщего введения математических извратов
ТО, КМ и тп, классическая физика, развитием которой является
эфиродинамика могут показаться "прошлым веком". Опять же газодинамика,
как основа ЭД, наука сложная далеко не законченная. С уважением, Михаил Сурин
|
\\\
- Re: Черная дыра
(А.П. Васи,
21.03.2013 22:08, 9.3 КБайт)
Удивило название форума.
Это автор совсем не далёкий.
Ибо я даже давно знал что существуют
световые усилители так сказать прямого
действия.
А у трансформатора задача - изменение
амплитуды сигнала, - лайно вопрос.
--------------------------------------------
Почему
нет светового трансформатора?
Страниц 1 2
... 12 13
14
--------------------------------------------
http://www.mobilum.ru/articles/usiliteli/
 На
расстоянии сигналы затухают. Эта истина справедлива и для
электрических, и для оптических коммуникационных линий. Разумеется, в
случае оптических сетей расстояния, на которых это начинает проявляться,
больше, однако проблемы по-прежнему существуют.
На
расстоянии сигналы затухают. Эта истина справедлива и для
электрических, и для оптических коммуникационных линий. Разумеется, в
случае оптических сетей расстояния, на которых это начинает проявляться,
больше, однако проблемы по-прежнему существуют.
Для борьбы с указанными проблемами используют три типа устройств: усилители, регенераторы и повторители.
Оптические усилители ведут себя одинаковым образом по отношению к любым
оптическим сигналам и наряду с детектируемыми сигналами усиливают также
шумы и любые другие сигналы. Обычно усилители решают простейшую из
задач, связанных с восстановлением сигналов, усиление. Регенераторы
выполняют более сложную задачу они детектируют оптические сигналы,
преобразуют их в электронные сигналы, отделяют от них шумы и вновь
ретранслируют в виде оптических сигналов, обычно с использованием
электронных устройств. Повторители занимают некоторое промежуточное
положение между оптическими усилителями и регенераторами. Они также
являются электрооптическими устройствами, однако обеспечивают лишь
усиление и реформирование сигнала, но не его полное восстановление. С
приходом полностью оптических усилителей использование повторителей в
оптических сетях перестало быть повсеместным.
Существует три типа участков сети, на которых могут располагаться
усилители. Для усиления сигнала перед тем, как он поступит в сеть,
непосредственно за передатчиком устанавливаются постусилители. Для
компенсации ослабления сигналов через каждые 80-100 км
волоконно-оптической линии устанавливаются линейные усилители.
Преду-силители, назначением которых является усиление сигнала до уровня
мощности в пределах чувствительности приемного устройства, размещаются
непосредственно перед приемником.
Усилители являются устройствами, увеличивающими амплитуду и ширину
сигналов без искажения их первоначальной формы. Громкоговоритель тоже
усилитель, только акустический; аналогичным образом оптические усилители
выполняют подобные функции в случае оптических сигналов. Усилители
способствуют поддержанию мощности сигналов на должном уровне при
прохождении ими больших расстояний. К сожалению, они не отличаются
разборчивостью и наряду с сигналами усиливают также шумы и искажения.
Какой именно принцип работы усилителей используется, определяется их
конструкцией. В современных оптических коммуникационных системах
наиболее распространены усилители на оптических волокнах, легированных
эрбием (Erbium-Doped Fiber Amplifiers EDFA). Эрбий это
редкоземельный элемент, который в небольших количествах добавляется в
центральную кремниевую жилу волоконно-оптического кабеля. В отрезок
волокна, легированный эрбием, во время прохождения через него
ослабленного сигнала вводится, или накачивается, излучение с другой
длиной волны, отличной от длины волны сигнала, что препятствует их
интерференции между собой. В ответ на проходящий по волокну сигнал ионы
эрбия начинают резонировать, используя избыточную энергию дополнительной
волны. В итоге ионы эрбия усиливают сигналы, тем самым увеличивая
расстояние, на которое они могут распространяться.
В то же время, инжектирование возбуждающего излучения накачки может
приводить к нежелательным последствиям. Распространение этого излучения в
направлении лазера навстречу сигналу может вызвать появление шумов.
Чтобы избежать этого, применяют оптические вентили. Вентили пропускают
распространяющийся по кабелю свет в одном направлении, но не пропускают в
обратном направлении.
Все прекрасно? Не совсем так. Оптический вентиль будет
взаимодействовать с потоком света, распространяющимся в прямом
направлении, и в типичных случаях ухудшать сигнал примерно на 2
децибела. Кроме того, некоторое количество света будет проходить и в
обратном направлении, однако обычно такой свет будет на 40-50 децибел
слабее входного сигнала.
В то же время, в случае усилителей EDFA радует то, что они
сравнительно дешевы, весьма эффективны, обладают высокой выходной
мощностью при низком уровне шумов и минимальными перекрестными помехами
между соседними волокнами. Если у них и есть недостаток, так это то, что
они эффективны лишь при работе в ближней инфракрасной области на длинах
волн около 1550 нм.
Сигналы с более низкими частотами можно усиливать, легируя волокна
другим элементом празеодимием, в результате чего получаются усилители
на оптических волокнах, легированных празеодимием (Praseodymium-Doped
Fiber Amplifiers PDFA). Эти усилители перспективны для усиления
сигналов, передаваемых с использованием длины волны около 1300 нм.
Аналогичным образом, рамановские усилители эффективно функционируют на
длинах волн 1300, 1400 и 1500 нм. Весьма многообещающе применение этих
усилителей в системах передачи цифровых данных, использующих
мультиплексирование по длине волны высокой плотности (dense wavelength
division multiplexing DWDM).
Принцип действия рамановских усилителей основан на эффекте Рамана,
открытом индийским физиком сэром Чандрасекара Венката Раманом в 1928
году. Как мы уже отмечали при обсуждении рамановского рассеяния в главе
4, эффект Рамана заключается в изменении наблюдаемой частоты света при
его рассеянии в прозрачном материале. (Явление комбинационного
рассеяния света было открыто советскими физиками Г.С. Ландсбергом и Л.И.
Мандельштамом на кристаллах и одновременно индийскими физиками Ч.В.
Раманом и К.С. Кришнаном на жидкостях.)
Мы можем увидеть этот эффект, наблюдая, например, за
монохроматическим световым пучком, полученным с помощью лазера, при его
прохождении через прозрачный газ, жидкость или твердое тело. В
отсутствие промежуточных веществ лазерное излучение было бы одноцветным.
Однако при столкновении света с веществом фотоны в результате упругих
столкновений с молекулами прозрачного вещества теряют или выигрывают
энергию. Следствием этого является возникновение линий дополнительных
цветов, называемых рамановским спектром, соответствующих увеличенным или
уменьшенным длинам волн по сравнению с длиной волны первоначального
излучением. Вид этого спектра зависит от природы вещества, рассеивающего
свет.
Поскольку рамановский спектр не привязан к фиксированным
энергетическим уровням, как в случае редкоземельных элементов, таких как
эрбий, он может быть получен на любой длине волны в инфракрасной
области, коль скоро имеется источник необходимого возбуждающего
излучения. Эта особенность позволяет применять рамановские усилители во
всем диапазоне передачи кремниевых волоконно-оптических кабелей.
Поскольку для усилителей, в которых используется рамановский эффект,
требуются повышенные мощности возбуждающего излучения (порядка одного
ватта) и отрезки световодного кабеля большей длины, их стоимость по
сравнению с усилителями EDFA оказывается более высокой. Тем не менее, их
главным достоинством является способность обеспечить усиление
оптических сигналов во всем диапазоне возможных частот передачи при
использовании волоконно-оптических кабелей с низкими потерями, и поэтому
на них может быть построена технология кремниевых усилителей,
альтернативных PDFA или халькогенидным волоконно-оптическим усилителям в
диапазоне 1,3 мкм. Благодаря недавним усовершенствованиям технологии
получения активных волокон использование некоторых из них позволило
получить усиление по мощности, достигающее примерно 0,06 дБ/мВт, что,
будучи само по себе незначительной величиной по сравнению с известными
величинами для EDFA (11 дБ/мВт), тем не менее представляет собой вполне
разумную альтернативу при передаче данных в не-эрбиевых диапазонах
длин волн. На сегодняшний день усиление на основе эффекта Рамана играет
важную роль в системах сверхдальней связи, которые расширили возможности
передачи на дальние расстояния с 500 км между соседними повторителями
до 1500 км и более.
- Re: Черная дыра
(А.П. Васи,
21.03.2013 22:13, 100 Байт)
Самое смешное что физически они напоминают трансформатор,
только вместо проводов оптоволокна.
- Re: Черная дыра
(А.П. Васи,
22.03.2013 3:36, 2.0 КБайт)
По большому счёту развели детский сад и сами не понимают
чего хотят, дело в следующем в физике чтобы не выглядеть
недалёким по отношению к сути вопроса, надо
давать определение физическое.
Вот собственно трансформатор электрический, -
это устройство в котором происходит трансформация
вольт-амперов в магнитное
поле с последующим
восстановлением вольт-амперов, при этом происходят
потери. В связи с различным количеством витков
в обмотках получается возможность изменить
соотношение вольтов по отношению к амперам,
и амперов по отношению к вольтам что собственно
и есть коэффициент трансформации который
принято писать
по отношению к вольтам.
Например
коэффициент 1:2
означает что входное напряжение это левая цифра, выходное
напряжение это правая цифра, и говорит например
о том
что при входном переменном напряжении в 12В,
на выходе будет 24В.
Механический аналог это коробка передач, в
котором аналогом напряжения будет
угловая
скорость на метр, а аналогом тока будет усилие
на метр.
---
А вот чтобы внятно что-то говорить за световой трансформатор,
надо понимать
что во что надо трансформировать и с каким
коэффициентом чего-то во что-то.
В данном случаи как говорится и коню понятно что
во всех случаях трансформации
сущности представляют
из себя энергии.
То собственно оптический усилитель и представляет из
себя оптический трансформатор, по скольку энергия
одного
источника излучения переходит в изменение
энергии другого источника, в данном случаи изменении
амплитуды сигнала.
Если выключить луч, то усиления входного
оптического
сигнала не будет, если включить луч появляется
усиление амплитуды сигнала, а если изменилась
амплитуда сигнала, то понятно что появился
коэффициент
трансформации, а следовательно
там где есть коэффициент трансформации то
там и есть свойства трансформатора.
Каменный век, первый класс, вторая четверть.
- Re: Черная дыра
(А.П. Васи,
22.03.2013 3:38, 1.8 КБайт)
Предыдущее это моё мнение по этому тексту
----------------------------------------------------------
 Re: Почему нет светового трансформатора?
Re: Почему нет светового трансформатора?
Ответ #138 - Вчера :: 23:54:04
Альча писал(а) 20.03.13 :: 23:33:59:А
Вы, со своей стороны, наверное представляете как идёт накачка
лазера..... И как роль агента накачки может выполнять тоже свет....
Оптические лазерные усилители известны давно.... Назовите их
"трансформаторами"...
Или Вам.... "шашечки нужны"??? Или, всё-таки, "ехать надо"????
Здесь речь не идет об оптических лазерных усилителях. Речь идет о
том, почему нельзя изготовить обычный привычный всем нам электрический
трансформатор с первичной и вторичными обмотками для преобразования
света, если свет является электромагнитным явлением.
|
- Re: Черная дыра
(А.П. Васи,
22.03.2013 3:53, 777 Байт)
Вот из ссылки которую я указал там же написано
---------------------------
\\\Благодаря недавним усовершенствованиям технологии
получения активных волокон использование некоторых из них позволило
получить усиление по мощности, достигающее примерно 0,06 дБ/мВт, что,
будучи само по себе незначительной величиной по сравнению с известными
величинами для EDFA (11 дБ/мВт),\\\
Чтобы были в курсе - шесть децибел - это усиление в два раза,
по отношению к световым колебаниям можно сказать
что мощность светового колебания, это и есть его
амплитуда так сказать и вольты и амперы вместе.
А если вольты и амперы вместе, и их невозможно
разделить, а можно усиливать их только вместе,
- Re: Черная дыра
(А.П. Васи,
22.03.2013 12:48, 422 Байт)
Я думаю что здесь большинство смеются как кони,
ибо телескоп собственно и есть оптический трансформатор.
Также оптический трансформатор можно сделать из двух
призм разного размера, первая призма раскладывает спектр,
вторая складывает.
В данном случаи коэффициент трансформации можно
определять по разному,
можно в усилении телескопа,
а можно и в разности освещенности на площадь.
- Re: Черная дыра
(А.П. Васи,
22.03.2013 20:23, 3.3 КБайт)
Почитал опять такое смешное что вынужден
рассказать своими словами.
---------------------
\\\
 Проверим Кавендиша "на коленке"?
Проверим Кавендиша "на коленке"?
Сегодня :: 11:03:02
Много здесь на Форуме было споров -- "взвесил" ли Кавендиш Землю, узнал ли её плотность ... ну и про G такие же вопросы.
Появилась у меня "мыслишка"
проверить реально ПРИТЯЖЕНИЕ грузов друг к другу. /а может и приталкивание -- не суть важно/
Итак
задумываю опыт ... и прошу предварительной критики от всех форумчан, ну
и полезных советов и предложений, если таковые будут.
Что
имею из "оборудования": стальная наковальня весом около 200 кг, такого
же веса болванка-"чугуняка" /довольно бесформенная/, свинец в заводском
слитке -- 50 кг + ещё свинец в кусках около 30 кг, прочный лиственный
брус около 4 м длины, провод, тросик, капроновый шнур для "триммера", +
куча кирпичей.
Идея проста: из бруса делаем "крутильные весы"
... на конце крепим весь свинец, на другом --- кирпичи-противовес, ....
посередке --- шнур/тросик ... /чтобы выдержал 160 кг/ ... + зеркальце и
лазерная указка --- оптический измеритель перемещений.
Ставим наковальню в высоком помещении /спортзал ... без сквозняков(!)/
... к потолку подвес на тросике коромысла весов ... и после успокаивания
конструкции ... наковальню располагаем почти вплотную к свинцу на конце
бруса. Зазор меж свинцом и наковальней делаем в пределах 1 ... 2 ... 3
мм
И далее только ждем --- сместится или нет свинцовая "колобаха" к наковальне ДО КАСАНИЯ ЕЯ???
Ясно, что тросик подвеса нужен длинный, чтобы легче крутиться
коромыслу ... и тут вопрос -- что будет лучше? ... стальной тросик /1
мм/ ... или капроновый /3 мм/?
Также ясно, что нужно это делать в каникулы, дабы дети на уроке "не мутили воздуся" ветрами-сквозняками.
Вот
тут основной вопрос --- получится ли чего? Будет ли смещение грузов
друг к другу, причем чтобы однозначно от ПРИТЯГАНИЯ меж ними, а не от
случайных причин. Ясно, что тут не про "G" будет разговор, а только про
принципиальное выявление действия меж грузами. Смещение грузов можно
будет узреть визуально ... + по световому зайчику от лазерки /ежели оно
будет/
И какие мысли форумчан будут по этому поводу??? Жду серьезных возражений или советов ........
С уважением ко всем .......... Анатолий Д.
Tokyan.


\\\
- Re: Черная дыра
(А.П. Васи,
22.03.2013 20:38, 806 Байт)
Дело в следующем, подобный опыт ставили графы или бароны,
не помню когда, - это уж совсем в самых дальних окраинах моей
памяти, помню только что на нити треугольной
формы.
Хотя все эти опыты преодолевали советские школьные опыты,
с двумя бутлями и пропитанными разноцветными чернилами,
сиреневыми стеблями, когда
они меняли цвет когда подносили
массивное со стороны контрольных стеблей по которым просачивались
разноцветные чернила, к своей грусти не могу вспомнить
логичных
определений.
При всём при том что в моей школе на экзаменах физики разрешали пользоваться
всеми учебниками которые были по физике и шпаргалками, и калькулятором
в том числе, на то время это было нечто, логарифмическая линейка
тоже помогала в те времена.
- Re: Черная дыра
(А.П. Васи,
22.03.2013 20:55, 506 Байт)
В примитиве - подобный опыт можно провести на подвешенном на
некоторой прочной нити шаре, у которого рядом будет
от одной опоры с угловым упором от точки
крепления
оборудован грузовой ориентированный /спутник/
-
- есть такой шар со стрелкой, и он колеблется и меняет своё
направление, - так вот к этому шару - логично
в качестве
нелогичного физического опыта прикрепить на сервоприводах,
к скользящим подшипникам некоторый довесок.
Есть что-то в этой простоте.
- Re: Черная дыра
(А.П. Васи,
23.03.2013 0:22, 4.7 КБайт)
С моей точки зрения есть много зданий
в которых можно разместить подобный маятник,
с дополнительным грузом влияющим на основной,
когда у дополнительного
груза своё независимое крепление, в том-же центе масс.
---
http://turbina.ru/guide/Sankt-Peterburg-Rossiya-112311/Zametki/Vmesto-mayatnika-Fuko-54871/
1430 марта 2012 года
В
советское время в центре Исаакиевского собора на длинной цепи висел
маятник Фуко прибор показывающий и доказывающий что Земля вертится.
Сейчас маятник демонтирован и можно встать в центре собора, поднять
голову и долго рассматривать великолепный расписной плафон главного
купола Богоматерь в окружении святых работы Карла Брюллова, фигуры
двенадцати апостолов в световом барабане и четырёх евангелистов, чьи
изображения на парусах арок довершают картину.
А высоко-высоко под куполом храма как и прежде летит голубь символ Святого духа.
Все фотографии
одной лентой
- Re: Черная дыра
(А.П. Васи,
23.03.2013 1:06, 5.3 КБайт)
А слёта с интеллектуальных катушек ждать
то долго и не понадобилось.
Как говорится недалёкий в физике это вот тому доказательство.
Ибо
релятивист слетает с интеллектуальных
катушек когда забывает что для пустоты, то-есть вакуума
это \Релятивистский эффект Доплера\,
который никакого отношения
физического не имеет
к \эффекту Доплера\.
---
Некоторый релятивист недалёкий в физике,
у которого пространство пустое аки дальше некуда,
и идеи
этого релятивиста имеют своё датирование после
1900 года, при этом этот недалёкий релятивист
опирается на эффект Доплера, который для сред а не
для пустоты
и был придуман аж в
\\\Материал из Википедии свободной энциклопедии
Эффект был впервые описан Кристианом
Доплером в 1842 году.\\\
---
А недалёкий релятивист даже не знает определения
среды, -
среда это когда каждый элемент имеет непосредственный контакт
друг между другом, и имеет непрерывное соединение и свойства
плотности среды - это
вкратце.
---
----------------------------------------------------------------
\\\
| Vallav
|
 Re: Почему нет светового трансформатора?
Re: Почему нет светового трансформатора?
Ответ #145 - Сегодня :: 00:22:13
krabs писал(а) Вчера :: 23:48:46:Vallav писал(а) Вчера :: 13:34:58:То есть, зеленый свет от движущегося навстречу источника - это оптический
обман?
Чем отличается зеленый свет от движущегося
источника от зеленого
света от неподвижного источника?
Эффект Доплера имеет к обсуждаему самое непосредственное отношение.
Так как с его помощью можно пересекать
установленную Вами границу. Зеленый свет от движущегося навстречу источника - это, естественно, оптический обман.
Вы же знаете, что источник излучает другую частоту. Если не знаете, то
подождите немного, пока источник проедет мимо вас и начнет удаляться от
вас. Частота будет уже не "зеленая". А если источник далеко и ждать всю жизнь? Так и не узнать, что зеленый свет от него - оптический обман? По остальным свойствам этот свет от света от неподвижного источника ничем не отличается? Тогда в чем именно разница в их природе? krabs писал(а) Вчера :: 23:48:46:
Вы сейчас своими разговорами об эффекте Доплера пытаетесь увести от
обсуждаемого вопроса. Уже уводить не надо. Сказанного вами вполне
достаточно, чтобы сделать вывод о том, что у вас нет никаких физических
доказательств ЭМ-природы света. Так одни фантазии, не продуманные до
конца и в основном не имеющие к физике никакого отношения.. Так существование эффекта Доплера и есть самое простое и наглядное доказательство того, что
радиоволны, свет, рентген и гамма-кванты - одной природы.
|
|
|
- Re: Черная дыра
(А.П. Васи,
25.03.2013 13:08, 7.2 КБайт)
Прочитал текст от чмырдяя который
пытался унизить другого автора по причине
не правильного с его точки зрения применения
единиц измерения.
Вот
как раз здесь и проявились внутренние свойства
оставшиеся после курсов гандольеров.
Не удосужился объяснить гандольер по какой причине
эти единицы измерения
хуже чем другие,
так потом как истинный гандольер сам использует
эти еденицы измерения.
-----------------------------------------------
http://www.computerra.ru/60311/betelgeusepastandfuture/
Сепулька
Dmitri Wiebe
5
дней назад
В Крабовидной звёздная величина была отрицательной,
а тут во сколько раз ближе? да ешё в квадрат? Так что яркая - не то слово.
Насколько можно доверять (г-ну Пономаренко):
"В случае взрыва как Сверхновой звезды Бетельгейзе , находящейся на
расстоянии 320-500 св. лет от Земли, поток УФ излучения в диапазоне
200-300 нм составит
35-55 тысяч эрг/см2 и станет наиболее
мощным мутагенным фактором за последние два миллиона
лет. Ее
превращение в сверхновую будет сопровождаться сбросом
оболочки около 10-4
ее массы , состоящей , в основном, из водорода и гелия с энергией
каждого ядра до 1,8 ГэВ /4/. На Земле детектор типа Камиоканде II
зарегистрирует
нейтринную вспышку интенсивностью в 25-75 тысяч событий
(пересчитано по результатам измерений на Камиоканде II вспышки от SN1987
/5/) . Через несколько часов (до
суток) после регистрации нейтрино /5/,
станет видна даже днем ярчайшая звезда, сравнимая по блеску с полной
Луной. В течение нескольких десятков - сотен лет после
максимума через
40-50 лет после прихода на Землю квантов и нейтрино, на Землю будут
воздействовать релятивистские ядра (в основном, протоны и гелий)
оболочки
Сверхновой. их полный флюенс на границе магнитосферы Земли
составит 5*105 - 2*106 част/см2.
Частично они будут захвачены магнитосферой, частично вызовут рождение
вторичных частиц в атмосфере, а частично дойдут до поверхности Земли,
став вторым сильнейшим мутагенным фактором после УФ излучения. Из данных
/6/ следует,
что взрыва Бетельгейзе можно ожидать в ближайшие несколько
тысяч лет." http://physics-animations.com/...
И там же:
При
взрыве типовой сверхновой кроме начального импульса рентгена, который
спадает несколько лет, образуется цепочка гамма-излучателей в количестве
0,075-0,1 массы Солнца (Ni-56- >Co-56(847,1288
кэВ)->Fe-56)/5/.Светимость типовой Сверхновой в гамма-диапазоне
падает с 1042 эрг/с до 1040 за два года, до 1038 - за три года , дальше
работает Co-57, Ti-44, Na-22 - спад замедляется. С 1038 до 1037 спад
активности происходит с третьего по пятый года. В максимуме активности
это соответствует 0,5-0,8 эрг/см2 т.е. (3-5)*10^7 квантов со средней
энергией 1 МэВ на 1 см2 в секунду на границе Земной атмосферы от
Сверхновой на расстоянии 320-500 св лет. С учетом кривой спада
рентгеновского излучения и прихода ГэВных заряженных частиц, помимо
мутагенных факторов, о пилотируемой космонавтике придется забыть на
десятилетия.
Жду от Вас примерно такого сообщения: "Г-н Пономаренко известен как автор множества слабых и ошибочных работ..."
-----------------------------
Dmitri
Wiebe
Сепулька 5 дней назад
И.С.
Шкловским предложен простой критерий быстрой
оценки текста -- насколько
корректно автор использует
единицы измерения. Если человек измеряет
поток в эргах
на кв. см, это уже повод призадуматься.
---------------------------------
Dmitri
Wiebe
sergey da 3 дня назад
В статье Пономаренко приводится ссылка на статью
Disturbance Ecology from Nearby Supernovae, а они,
в
свою очередь, ссылаются на работу Скало со товарищи,
где они дают критическую дозу УФ-облучения
для мутаций
микроорганизмов
600 эрг/см2. Если сравнить это с дозой,
которую Земля рискует получить
от Бетельгейзе (в статье
Пономаренко, видимо, именно она называется
потоком), то
результат получается пугающим за пределами атмосферы
получится примерно 20000 эрг/см2 (если брать энергию,
излучённую
сверхновой в УФ-диапазоне, из статьи Скало и
др.; 10^47 эрг). Но что
будет если сравнить
эту величину с УФ-излучением Солнца? Мы ежесекундно получаем
от
Солнца 1,4 миллиона эрг на кв. см. (солнечная постоянная).
На долю УФ
приходится несколько процентов (зависит от того,
как определить
УФ-диапазон). Пусть будет 5% для определённости.
Получаем 70000 эрг/см2 в секунду, а не 20000 всего,
как от Бетельгейзе.
О том, насколько важно такое добавочное облучение,
пусть говорят
биологи. Про другие излучения сказать не могу, поскольку
не совсем
понимаю, что имеется в виду в статье.
- Re: Черная дыра
(А.П. Васи,
25.03.2013 18:34, 1.5 КБайт)
То что адекватности нет я знал но я
начинаю уже сомневаться не только в умственных способностях
но и в том как далеко запущенна болезнь.
Ибо потеря памяти
это болезнь.
Так вот некто Вибе совсем недавно
написал статью том что Бетельгейзе должна
в скорости взорваться по самые не-балуйся,
собственно
статья о событии которое
ещё не произошло, после этой статьи идёт обсуждение
этой статьи в виде форума, а будучи модератором он посетителя
модерируемого
им форума упрекает
в том что он обсуждает событие которое не произошло
на форуме.
Это не двойные стандарты, это или безпредел модератора,
хотя
вряд-ли и более вероятно что слёт с интеллектуальных
катушек.
--------------------------------------------------------
--------------------------------------------------------
Ответ #1 : Сегодня в 17:58:16
Непонятно, как можно обсуждать событие, которое ещё не состоялось. Оставляю как анонс.
-------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
25.03.2013 21:29, 2.4 КБайт)
Сообщений: 5062
 Re: Почему нет светового трансформатора?
Re: Почему нет светового трансформатора?
Ответ #218 - Сегодня :: 21:11:58
Васушена писал(а) Сегодня :: 20:44:50:
Vallav писал(а) Сегодня :: 20:28:35:Ой!
Так вот прямо крошила на мелкие кусочки?
сам
не видел, но по легендам - так. Изображение ваджры имеется множество со
всех ракурсов. Есть карго-копии и описание очевидцев в Махабхарате.
Ну если - Есть карго-копии и описание очевидцев в Махабхарате - тады
конечно...
---------------------------------------------
Ясный конь релятивисты не верят рассказам очевидцев когда им
это не надо, зато как они верят тому что было
в первые часы
минуты и секунды большого взрыва, и очевидцы им не нужны
они просто верят в эти сказки высосонные непонятно из каких
фантазий и каких очевидцев.
---
Это всё ерунда, была давно у меня книжка правда она потерялась,
книжка необычная для советских изданий квадратной формы,
о путешествии одного фотографа
по Южной Америке на велосипеде,
так там была одна фотография в этой книге где фотографируются
туристы на фоне камня прямоугольной формы брошенного
между
гор с размерами камня примерно 55метров в длину,
35м. в ширину, и 25м. в высоту.
И об это мегалите я ничего в интернете не видел.
Возможно порезали на
сувениры, ибо этот мегалит
сводит на нет все текущие технические достижения.
- Re: Черная дыра
(А.П. Васи,
26.03.2013 9:20, 2.0 КБайт)
Вот и ещё один релятивист после слёта с
интеллектуальных катушек превратился в недалёкого.
Не воспринимает текст по физике
и не может его обсуждать
в физике только
недалёкий в физике.
Недалёкий в физике может всё смешивать
в кучу и задавать вопросы.
---------------------------
\\\
 Re: Почему нет светового трансформатора?
Re: Почему нет светового трансформатора?
Ответ #247 - Сегодня :: 09:03:27
OKBor писал(а) Сегодня :: 05:11:00:
[quote
author=5D6A67676A7D3A0B0 link=1363466593/194#194 date=1364223076]Так
обсуждайте а не вещайте пустопорожние абсолютные истины.
А с кем обсуждать абсолютные истины?
А их надо обсуждать?
OKBor писал(а) Сегодня :: 05:11:00:
Например
- не желаете обсудить абсолютную истину АТО ОКБорис по поводу левой
руки Ампера? На проводник даже без внешнего магнитного поля действует
сила, изгибающая его в плоскую окружность. Как велокамеру при накачке. А
если оболочку зарядить- она примет форму сферы. Так что левая рука-
частный случай. Ну как- обсудим?
А это разве - абсолютная истина?
\\\
- Re: Черная дыра
(о. с. баранов,
28.03.2013 20:30, 341 Байт)
хотелось бы сделать одно уточнение.
пишут обычно так: свет не может вырваться из черной дыры.
проще можно представить так: атомы в черной дыре расположены так
близко друг к другу, что электронных оболочек (верхних или всех) просто нет, светового излучения поэтому просто не образуется,
поэтому она и черная.
- Re: Черная дыра
(А.П. Васи,
28.03.2013 21:40, 740 Байт)
Ваше мнение о черных дырах это лично Ваше
мнение о чёрных дырах, и оно всем безразлично,
по той причине что черные дыры именно такие
какие описал автор чёрных
дыр.
Вот я же писал что некоторые написали
что черные дыры излучают рентгеновское излучение,
и написали больше сотни статей, и чё, и до лампочки,
автор сказал что излучение из черных дыр в основном
из фотонов - то те кто приписывали черным дырам
рентгеновское излучение они просто клали на авторский
вариант, и чё - а ничё, наказаний за подобный бардак
в физике не существует.
Читайте первоисточники и не приписывайте тому
что придумали другие разные
прибамбасы, Вас об этом
никто не просил, и в этом нет смысла.
- Re: Черная дыра
(А.П. Васи,
28.03.2013 21:46, 370 Байт)
Меня естественно удивляет интеллектуальность тех
кто написал более сотни статей приписывая рентгеновским
звёздам свойства черных дыр.
Если бы просто описали
новый класс рентгеновских звёзд
и дали им физическое определение, - то они вошли бы в историю
космологии и поимели бы кучу премий.
А так они не у дел и их
мнение никому не интересно.
- Re: Черная дыра
(А.П. Васи,
28.03.2013 21:50, 183 Байт, ответов: 1)
И не забывайте самое главное - на сегодняшний
день не обнаружено официально ни одной черной дыры,
одни только предположения - что мол черная дыра должна
быть
там-то.
- Re: Черная дыра
(А.П. Васи,
28.03.2013 23:53, 35 Байт)
Моё общение с Вами закрыто.
- Re: Черная дыра
(о. с. баранов,
29.03.2013 12:15, 8 Байт)
z
- Re: Черная дыра
(А.П. Васи,
31.03.2013 18:41, 14.3 КБайт)
Такое прочитал, я аж заулыбался у меня появился
конкурент в описании строения галактик.
Естественно товарищу надо сразу работать над своими
ошибками, а всем
желающим могу показать
две разных точки зрения и как говорится
почувствуйте разницу.
--------------------------------------
 Re: Эфирная Теория. Единая концепция.
Re: Эфирная Теория. Единая концепция.
Ответ #346 - 19.02.13 :: 10:48:44
Подведение промежуточных итогов.
Этапы развития реальной вселенной.
Соответствие энергетического уровня диапазону излучения:

1-й уровень-радиодиапазон
излучения;
2-й микроволновый;
3-й инфракрасный;
4-й видимый спектр;
5-й ультрафиолетовый;
6-й рентгеновский;
7-й гамма.
В связи с этим должно быть 12 этапов развития-творения Вселенной.
Ключевая роль отводится Эфиру-Непрерывной Среде из которой всё
сотворено.Не вдаваясь в детали появления Непрерывной Среды(Эфира),
я их просто не знаю, для себя я определил следующие Свойства Эфира(или Среды).
О свойствах Среды, с таким условием, чтобы всё многообразие форм и
явлений окружающего нас мира, являлось следствием существования только
одной сущности-Среды(Эфира).
Допустим, что среда
дискретна-состоит из очень, очень мелких частиц. Сможем ли мы с помощью
неё объяснить гравитацию? Сможем. Движется в центр земли и увлекает
своим движением тела, прижимая их к поверхности Земли. Сможем ли мы с её
помощью объяснить сильные, слабые, обменные и молекулярные
взаимодействия? Не сможем. Чтобы объяснить эти взаимодействия, мы должны
объяснить, как осуществляет-ся связь между частичками Среды. Если между
частичками среды не будет связи, то и взаимодействие невозможно. Если
разрезать буксирный трос, то сможем ли мы буксировать автомобиль? Нет.
Значит нужно вводить новую сущность, а это противоречит нашему
первоначальному условию: Сущность только одна.
Поэтому Среда-непрерывная сущность.
Между атомами и молекулами нет видимой связи, но вещество(любое)
сопротивляется, как растяжению, так и сжатию. Среда должна обладать
определёнными прочностными качествами. Материя, лишь незначитель-ная
часть Вселенной, но плотность материи больше плотности Среды наполняющей
пространство (наблюда-тельный факт), значит Среда должна включать в
себя и такое понятие как плотность. Чем выше плотность, тем больше
прочность Среды.
Среда должна иметь способность к флуктуациям. Наблюдательный факт.
Среда любой плотности-подобие жидкости.
Итак Этапы
развития Вселенной:
1-й
Этап-флуктуации Непрерывной Среды-Эфира. На этом этапе, примерно 8 с
небольшим процентов Эфира перешло в СВЕТ. Движения, как такового, не
было. Помимо перехода Эфира в СВЕТ образовывались
электроны и позитроны.

Итак, конечный результат флуктуации-появился фотон(СВЕТ) и
нейтрино. СВЕТ это та же Непрерывная Среда, но в другом качестве. Из
СРЕДЫ удалено нечто, что Ей совершенно не нужно и это нечто
сосредоточено в нейтрино. Свет не смешивается с Эфиром и
сосредотачивается в центральной области объёма заполненного НС.
Нейтрино в конечной стадии флуктуации защемляет Непрерывную Среду(НС)
и, за счёт вращения, создаёт вихрь из НС и становится электроном:

2-й
Этап-создание Вселенских потоков движущегося Эфира. На этом этапе СВЕТ,
сконцентрировавшись в центральной области, выпускает два джета и
раскручивает Эфир по всему объёму будущей Вселенной. Ещё 8 с небольшим
процентов Эфира переходит в СВЕТ и на этом этапе из нейтрино формируется
дуэнейтрино, а из
них протоны и нейтроны:


3-й
Этап. Этап рассредоточения Света по объёму Вселенной в места где будут
созданы галактики. Свет концентрируется в определённых местах, но в
процессе перемещения, т.к. для этого используются джеты, ещё 8 с
небольшим процентов Эфира переходит в СВЕТ.
За первые три
этапа часть Эфира перешла в СВЕТ, часть перешла в нейтрино и по всему
объёму сформировались электроны и позитроны, протоны и нейтроны.
4-й
Этап. Формирование вещества первого периода таблицы Менделеева. СВЕТ
выпустив два джета нагнетает Эфир и
электронно-позитронную-протон-нейтронную смесь, в центральной области
формируются атомы водорода и гелия, которые выбрасываются по экватору в
пространство. Данный этап начинается одновременно во всех отведённых
местах Вселенной. Эфир перешедший в СВЕТ отводится в близлежащее
пространство и формируется в виде шара(те же 8 с небольшим процентов).
Галактика излучает только в радиодиапазоне.
Это происходит примерно так:

Так происходит вплоть до 8 Этапа.
Доказательство существования четвёртого Этапа:
Найдена первая галактика находящаяся на первом этапе развития. Такая галак-
тика излучает только в радиодиапазоне, а излучение в других диапазонах, в том числе и
видимом ещё не дошло до Земли. Данная галактика находится на максимальном расстоя-
нии от Земли. В будущем до Земли дойдёт излучение и в видимом диапазоне, но предва-
рительно дойдёт в микроволновом и инфракрасном.
www.membrana.ru/particle/8256
5-й
Этап. Формирование вещества второго периода таблицы Менделеева. Джеты
выпускаются в экваториальной зоне. В центральную область засасывается
Эфир, электронно-позитронная смесь, протоны, нейтроны, водород, гелий. В
новую экваториальную зону выбрасываются элементы второго и первого
периода.
8 с небольшим процентов Эфира перешло в свет.
Галактика излучает в радиодиапазоне и в микроволновом.
6-й Этап. Формирование вещества третьего периода
таблицы Менделеева.
Галактика излучает в радио, микроволновом и инфракрасном диапазоне.
Доказательства существования 6 Этапа:
Далёкие галактики, которые не
излучают ещё в видимом диапазоне.
Они излучают в инфракрасном, микроволновом а радиодиапазонах.
www.membrana.ru/particle/17282
7-й Этап. Формирование вещества четвёртого периода.
Дополнительно к
первым, галактика излучает в видимом диапазоне
8-Этап.
Формирование звёзд и планет. В центральной области образуется квазар,
внутри которого формируются звёзды и планеты и выбрасываются в рукава.
На этом этапе появляется гравитация в основе которой лежат СВЕТОэфирные
потоки.


9 Этап. Формирование вещества пятого периода.
Галактика начинает излучать и в ультрафиолете.
10 Этап. Формирование вещества шестого периода.
Галактика начинает
излучать и в рентгеновском диапазоне. На завершающей стадии этого
этапа находится Вселенная.
Доказательства:

Туманность
Андромеды, когда делали эти снимки, находилась в начале десятого этапа
развития, об этом говорит увеличение интенсивности рентгеновского
излучения. Постепенно будут появляться новые области рентгеновского
излучения, по мере того, как это излучение будет доходить до нас. В
конце вся галактика будет видна в рентгеновском диапазоне.
Самая близкая к нам галактика, т.к. излучает в рентгеновском диапазоне интенсивнее чем Андромеды.
www.membrana.ru/particle/12746
11 Этап. Формирование вещества седьмого периода. Именно к нему и подошла Вселенная.
Галактика будет излучать и в гамма диапазоне.
Как это будет происходить? Примерно так:
Что ожидает Землю и Солнце? Казалось бы всё должно быть неизменно во веки
веков. Но... Доказанный факт,
что
Земля излучает в гамма диапазоне. Это доказал телескоп предназначенный
следить за гамма-вспышками Вселенной. Его периодически направляют в
сторону Земли и он зафиксировал излучение в гамма диапазоне идущее от
Земли.
Факт, возможно, мало примечательный и не заслуживающий
внимания. Однако необходимо постоянно проводить мониторинг этого
излучения. Если интенсивность будет на- ростать, то дело пахнет
катастрофой для жизни на Земле. Все понимают, что гамма излучение убъет
всё живое. Не сразу, а постепенно, по мере нарастания. Сбудется
предсказанное Богом в Новом Завете и в Откровении Иоанна Богослова.
Будут мировые язвы, моры, Одни виды будут интенсивно размножаться, а
другие вымирать, пока всё не вымрет на Земле. Потом
Земля взорвётся
новой. Придет же день Господень, как тать ночью, и тогда небеса с шумом
прейдут, стихии же, разгоревшись, разрушатся, земля и все дела на ней
сгорят. 2-е Петра 3.10. Земля, взорвавшись, перетянет материю от Солнца
и станет звездой. От Солнца останется шар заполненный СВЕТОМ.И такие
примеры в нашей галактике уже имеются:
www.membrana.ru/particle/10312
Примерный сценарий 11Этапа:
Более 27000тыс. лет назад за пределами
нашей галактики сформированы два пузыря в которых находятся элементы седьмого периода
www.membrana.ru/particle/4564
Процесс, вероятно, уже начался.
Два джета нагнетают эти
элементы в приделы галактики. Одновременно идет процесс перехода звезд и планет в Новые.
------------------------------------------
 Re: Эфирная Теория. Единая концепция.
Re: Эфирная Теория. Единая концепция.
Ответ #347 - 19.02.13 :: 10:54:45
12 Этап. Завершение всех процессов во Вселенной. Судный день.
Подведение итогов. Составление новой программы, для новой Вселенной.
Господь устами Ездры сказал:
Ибо
век потерял свою юность, и времена приближаются к старости, так как век
разделён на двенадцать частей, и девять частей его и половина десятой
части уже прошли, и остаётся то, что после половины десятой части. 3
Ездры. 14-10, 11, 12.
Согласно таблицы химических элементов
Менделеева, почти все элементы шестого периода стабильны, кроме полония,
астата и радона. Это говорит о том, что прошло уже много больше
половины десятой части, т.е. 10 Этап существования Вселенной,
практически, заканчивается. По окончании все элементы шестого периода
будут стабильны.
На современном этапе все элементы седьмого периода
не стабильны и не существуют в природе. По окончании 11 Этапа все
элементы седьмого периода будут созданы и стабильны.
------------------------
- Re: Черная дыра
(А.П. Васи,
31.03.2013 18:52, 47.9 КБайт)
И мой вариант
---------------------
| Re: Свет и пространство
и о скорости света.
|
10.01.20120:44 |
|
Цикличность галактик.
Чем галактики отличаются друг от друга.
Как происходит-
формирование
встреча с другими галактиками
набор
критической массы
само-нагрев
разброс
формирование
и т.д.
Если посмотреть на фотографии - то они собственно
особо друг от друга не очень
отличаются,
но на самом деле отличий достаточно чтобы
заметить цикличность в жизни галактик.
Что определяет движение в галактике, движение в
галактике
определяет средняя температура пространства
в галактике, и некоторые нюансы по плотности материи
в галактике.
Эфир как воздух в турбине пылесоса находясь
в галактике
с разной плотностью при воздействии на него
центробежного воздействия приобретает разную плотность.
В центре галактики его плотность меньше, а
по краям больше.
Но есть одно большое но - что собственно происходит в жизни
галактики - она может быть в шести температурных состояниях,
1 устойчиво
холодная,
2 нагревающаяся,
3 сбалансированная,
4 перегревающаяся,
5 устойчиво горячая
6 остывающая
Вот на одинаковом расстоянии например
наблюдаем
разные галактики по своей форме.
На самом деле отправной точкой в галактике
является
1 плотность эфира,
2 количество материи,
и
3 количество энергии в этой галактике.
Вот возьмем например есть галактика, мимо
неё пролетает другая галактика,
у них происходит снижение плотности
эфира между центрами галактик,
и между высокими и низкими
плотностями эфира в рукавах, если такие есть.
Естественно пролетая сквозь друг друга
в галактиках даже не было случая чтобы
две звезды столкнулись между собой,
но это не значит что не происходит
слияния звездных масс галактик.
Они
сливаются специфическим взаимодействием.
По причине того что плотность звезды эфира,
внутри звезд сбалансирована с внешней плотностью
эфира в пространстве,
то при приближении
центров галактик, или других частей галактик
с низкими плотностями эфира,
происходит лопанье внешних оболочек звёзд,
при лопаньи
оболочек происходит сброс
материи от десяти до пятидесяти процентов,
массы звезды.
После сброса, происходит большой
выброс эфира из звезд, на рукавах
и
в галактиках этот процесс виден в виде
розовых лопающихся звездных бульбашек.
При большом скоплении соседних звезд,
получается ударная волна
которая на краях
процесса будет сбивать давлением
внешнюю оболочку со звезд, что будет
приводить в взрывам в стиле "Обвал каркаса - супер нова",
по причине того что когда внешнюю
оболочку сдует, а звезда эфира останется на месте,
оболочка потом падает во внутрь,
и падение происходит с такой силой
что
зарождается звезда эфира и сразу эфир восстанавливается
по причине большого количества энергии,
в связи с чем происходит большой взрыв
аналогичный
Крабовидной туманности, после
взрыва в центре осталась только испаряющаяся
звезда эфира, восстановление которой постоянно
поддерживает условия для разлёта
материи
от звезды с которой была резко здута оболочка.
До тех пор пока весь эфир не восстановится и звезда
эфира не исчезнет, будет продолжаться разброс
материи, после чего материя остановится, так как
материю на столько далеко разбросало,
то эта материя никогда в звезду не соберётся, она
будет увлечена
другими звездами.
Так вот что собственно имеем, по размеру звезды
между собой не сильно отличаются,
с моей точки зрения не более чем плюс минус
в десять раз по сравнению с Солнцем.
Звёзды одинакового размера при низком
давлении эфира звёзды светят слабо, при большом
светят сильно. При нарушении
баланса,
звезда лопается при снижении,
увеличивает яркость при плавном увеличении
плотности, и теряет внешнюю оболочку при
внешней ударной волне.
А как это влияет на форму самой галактики?, -
Можно вернутся в начало и посмотреть что у галактик
в цикличности можно выделить - молодость,
молодость
можно определить как устойчиво
холодное состояние, в этом состоянии равномерное
распределение звезд.
Галактики размытые.
Встреча с другими галактиками
или самоуплотнение
галактики, при этом происходит плавное увеличение
средней температуры внутри галактики, с естественным
уменьшением количества эфира в
галактике.
Галактики с синими рукавами.
Так как процесс взаимного сближения звезд в галактике
увеличивается, появляется следующее состояние галактики
- сбалансированная, или галактика набравшая
критическую массу - на фотографиях у
этих галактик соотношение синих звезд и
розовых лопающихся в рукавах
- примерно
одинаковое.
Следующая ситуация когда галактика в состоянии
само-нагрева, и является перегревающейся, по причине того
что после выброса
эфира из звезд и сброса звездами
большого количества массы, эта масса в космосе
начинает нагреваться, не давая уйти
излучению звезд из галактики,
что
приводит к резкому повышению давления
эфира внутри всей галактики.
Внешне это желтоватого цвета галактики,
или галактики окруженные кольцом
грязных
выбросов мешающих их
наблюдать.
Галактика переходит в следующее состояние -
устойчиво горячая, и в результате большого
давления эфира происходит
разброс
всего сто есть внутри галактики, эфира,
материи звезд, и ускоренное восстановление
эфира со звезд эфира делает этот
процесс грандиозным по
масштабу, что
может так разбросать звёзды далеко,
что они уже в этой галактике не соберутся,
а присоединятся к другой.
Естественно после разброса
звезд
на большое расстояние происходит их остывание,
и звезды переходят в достаточно устойчивое
холодное состояние, после чего,
разлетевшаяся материя
обратно падает
на звезды и они набирают мощности свечения,
и сближаются друг с другом, и так
процесс продолжается.
Я специально не указывал на
звездные
фотографии - по той причине чтобы
каждый желающий имел возможность
выбрать то что ему нравится для каждого
случая.
http://www.astronet.ru/db/msg/1254896
Центр галактики Центавр А
-----------------------
http://www.astronet.ru/db/msg/1255454
Величественная спиральная галактика NGC 1232
-----------------------
http://www.astronet.ru/db/msg/1255185
NGC 253: галактика Скульптор
-----------------------
http://www.astronet.ru/db/msg/1255500
Лицом к NGC 6946
-----------------------
http://www.spacetelescope.org/images/heic0615a/
http://www.spacetelescope.org/images/heic0905a/
http://www.spacetelescope.org/images/heic0910i/
http://www.spacetelescope.org/images/opo0501a/
http://www.spacetelescope.org/images/heic0506a/
|
=============================================
|
|
Re: Свет и пространство и о скорости света.
|
6.03.20123:40 |
|
Цикличность галактик.
Чем галактики отличаются друг от друга.
Как происходит-
формирование
встреча с другими
галактиками
набор
критической массы
само-нагрев
разброс
формирование
и т.д.
Если посмотреть на фотографии - то они собственно
особо друг от друга не очень
отличаются,
но на самом деле отличий достаточно чтобы
заметить цикличность в жизни галактик.
Что определяет движение в галактике, движение в
галактике
определяет средняя температура пространства
в галактике, и некоторые нюансы по плотности материи
в галактике.
Эфир как воздух в турбине пылесоса находясь
в галактике
с разной плотностью при воздействии на него
центробежного воздействия приобретает разную плотность.
В центре галактики его плотность меньше, а
по краям больше.
Но есть одно большое но - что собственно происходит в жизни
галактики - она может быть в шести температурных состояниях,
1 устойчиво
холодная,
2 нагревающаяся,
3 сбалансированная,
4 перегревающаяся,
5 устойчиво горячая
6 остывающая
Вот на одинаковом расстоянии например
наблюдаем
разные галактики по своей форме.
На самом деле отправной точкой в галактике
является
1 плотность эфира,
2 количество материи,
и
3 количество энергии в этой галактике.
Вот возьмем например есть галактика, мимо
неё пролетает другая галактика,
у них происходит снижение плотности
эфира между центрами галактик,
и между высокими и низкими
плотностями эфира в рукавах, если такие есть.
Естественно пролетая сквозь друг друга
в галактиках даже не было случая чтобы
две звезды столкнулись между собой,
но это не значит что не происходит
слияния звездных масс галактик.
Они
сливаются специфическим взаимодействием.
По причине того что плотность звезды эфира,
внутри звезд сбалансирована с внешней плотностью
эфира в пространстве,
то при приближении
центров галактик, или других частей галактик
с низкими плотностями эфира,
происходит лопанье внешних оболочек звёзд,
при лопаньи
оболочек происходит сброс
материи от десяти до пятидесяти процентов,
массы звезды.
После сброса, происходит большой
выброс эфира из звезд, на рукавах
и
в галактиках этот процесс виден в виде
розовых лопающихся звездных бульбашек.
При большом скоплении соседних звезд,
получается ударная волна
которая на краях
процесса будет сбивать давлением
внешнюю оболочку со звезд, что будет
приводить в взрывам в стиле "Обвал каркаса - супер нова",
по причине того что когда внешнюю
оболочку сдует, а звезда эфира останется на месте,
оболочка потом падает во внутрь,
и падение происходит с такой силой
что
зарождается звезда эфира и сразу эфир восстанавливается
по причине большого количества энергии,
в связи с чем происходит большой взрыв
аналогичный
Крабовидной туманности, после
взрыва в центре осталась только испаряющаяся
звезда эфира, восстановление которой постоянно
поддерживает условия для разлёта
материи
от звезды с которой была резко здута оболочка.
До тех пор пока весь эфир не восстановится и звезда
эфира не исчезнет, будет продолжаться разброс
материи, после чего материя остановится, так как
материю на столько далеко разбросало,
то эта материя никогда в звезду не соберётся, она
будет увлечена
другими звездами.
Так вот что собственно имеем, по размеру звезды
между собой не сильно отличаются,
с моей точки зрения не более чем плюс минус
в десять раз по сравнению с Солнцем.
Звёзды одинакового размера при низком
давлении эфира звёзды светят слабо, при большом
светят сильно. При нарушении
баланса,
звезда лопается при снижении,
увеличивает яркость при плавном увеличении
плотности, и теряет внешнюю оболочку при
внешней ударной волне.
А как это влияет на форму самой галактики?, -
Можно вернутся в начало и посмотреть что у галактик
в цикличности можно выделить - молодость,
молодость
можно определить как устойчиво
холодное состояние, в этом состоянии равномерное
распределение звезд.
Галактики размытые.
Встреча с другими галактиками
или самоуплотнение
галактики, при этом происходит плавное увеличение
средней температуры внутри галактики, с естественным
уменьшением количества эфира в
галактике.
Галактики с синими рукавами.
Так как процесс взаимного сближения звезд в галактике
увеличивается, появляется следующее состояние галактики
- сбалансированная, или галактика набравшая
критическую массу - на фотографиях у
этих галактик соотношение синих звезд и
розовых лопающихся в рукавах
- примерно
одинаковое.
Следующая ситуация когда галактика в состоянии
само-нагрева, и является перегревающейся, по причине того
что после выброса
эфира из звезд и сброса звездами
большого количества массы, эта масса в космосе
начинает нагреваться, не давая уйти
излучению звезд из галактики,
что
приводит к резкому повышению давления
эфира внутри всей галактики.
Внешне это желтоватого цвета галактики,
или галактики окруженные кольцом
грязных
выбросов мешающих их
наблюдать.
Галактика переходит в следующее состояние -
устойчиво горячая, и в результате большого
давления эфира происходит
разброс
всего сто есть внутри галактики, эфира,
материи звезд, и ускоренное восстановление
эфира со звезд эфира делает этот
процесс грандиозным по
масштабу, что
может так разбросать звёзды далеко,
что они уже в этой галактике не соберутся,
а присоединятся к другой.
Естественно после разброса
звезд
на большое расстояние происходит их остывание,
и звезды переходят в достаточно устойчивое
холодное состояние, после чего,
разлетевшаяся материя
обратно падает
на звезды и они набирают мощности свечения,
и сближаются друг с другом, и так
процесс продолжается.
Я специально не указывал на
звездные
фотографии - по той причине чтобы
каждый желающий имел возможность
выбрать то что ему нравится для каждого
случая.
http://www.astronet.ru/db/msg/1254896
Центр галактики Центавр А

-----------------------
http://www.astronet.ru/db/msg/1255454
Величественная спиральная галактика NGC 1232

-----------------------
http://www.astronet.ru/db/msg/1255185
NGC 253: галактика Скульптор

-----------------------
http://www.astronet.ru/db/msg/1255500
Лицом к NGC 6946
-----------------------
http://www.spacetelescope.org/images/heic0615a/

http://www.spacetelescope.org/images/heic0905a/

http://www.spacetelescope.org/images/heic0910i/

http://www.spacetelescope.org/images/opo0501a/

http://www.spacetelescope.org/images/heic0506a/

Ещё
одна фотография, только у меня сомнения
что это галактика, скорей всего звезда типа SS 433
http://hubblesite.org/newscenter/archive/releases/1992/27/image/b/format/large_web/

http://www.spacetelescope.org/images/heic1104a/

http://www.spacetelescope.org/images/archive/category/galax/
 |
 |
 |
 |
| A rose made of galaxies |
Stellar Nursery in the arms of NGC 1672 |
Colliding galaxies make love, not war |
Magnetic monster NGC 1275 |
|
 |
 |
 |
 |
| Flocculent spiral NGC 2841 |
ACS Image of NGC 5866 |
Hubble Mosaic of the Majestic Sombrero Galaxy |
The magnificent starburst galaxy Messier 82 |
|
 |
 |
 |
 |
| A Poster-Size Image of the Beautiful Barred Spiral Galaxy NGC 1300 |
Galactic wreckage in Stephan's Quintet |
Barred Spiral Galaxy NGC 6217 |
Dramatically backlit dust lanes in NGC 7049 |
|
 |
 |
 |
 |
| Holiday Wishes from the Hubble Space Telescope |
Largest ever galaxy portrait - stunning HD image of Pinwheel Galaxy |
Out of this whirl: The Whirlpool Galaxy (M51) and companion galaxy |
A 'wallpaper' of distant galaxies is a stunning backdrop for a runaway galaxy |
|
 |
 |
 |
 |
| Hubble's newest camera takes a deep look at two merging galaxies |
Edge-On View of NGC 4013 |
A Grazing Encounter Between two Spiral Galaxies |
Galaxy Playing Twister |
|
 |
 |
 |
 |
| Hubble views NGC 4522 |
Hubble snaps heavyweight of the Leo Triplet |
Spiral Key to Universe's Expansion |
Stellar fireworks are ablaze in galaxy NGC 4449 |
|
 |
 |
 |
 |
| Hubble Identifies Source of Ultraviolet Light in an Old Nebula |
Hubble views NGC 4402 |
The gargantuan galaxy NGC 1132 |
Spectacular Hubble view of Centaurus A |
|
 |
 |
 |
 |
| Doing Cartwheels to Celebrate the End of an Era |
Unusual Spiral NGC 4921 in the Coma Galaxy Cluster |
Sunny Side Up |
Barred Spiral Bares All |
|
 |
 |
 |
 |
| Smoke Without Fire: a Different View of the Cigar Galaxy |
A star formation laboratory |
The Belly of the Cosmic Whale |
Perfect Spiral Overlaid with Milky Way Gems |
|
 |
 |
 |
 |
| Hubble image of NGC 1073 |
Hubble Captures a Lucky Galaxy Alignment |
Star cluster surrounds wayward black hole in cannibal galaxy ESO 243-49 (unlabelled) |
The Calm after the Galactic Storm |
|
 |
 |
 |
 |
| Stars in the Andromeda Galaxys disc |
Star cluster surrounds wayward black hole in cannibal galaxy ESO 243-49 (labelled) |
Antlia Dwarf Galaxy Peppers the Sky with Stars |
HST PHAT detail of M31 |
|
 |
 |
 |
 |
| Centre of M31 |
Hubble zooms in on double nucleus in Andromeda Galaxy |
Hubble observes blue stars in Andromeda's core |
HST PHAT wide image of M31 |
|
 |
 |
 |
 |
| Ground-based image of Andromeda Galaxy, M31 |
Ground-based image of Andromeda Galaxy, M31 |
| |
---------------------------------------------------------
Внимательно рассматривал галактики и заметил дополнительные
отличительные особенности.
1 Расслоение галактики.
У галактик
наблюдается расслоение
внутри
галактики, в связи с чем происходит неравномерное
уплотнение звезд, и создаётся ситуация когда в центре
галактики происходит повышение температуры
в
связи с чем создаётся разряжение эфира
------------------------------
 |
|
|
|
| Doing Cartwheels to Celebrate the End of an Era |
|
|
|
|
-------------------------------------
в связи
с большими расстояниями эфир не может быть
пополнен с окраин галактики, звезды начинают
в центре быстрее сближаться
и стягиваться в центр галактики, после чего низкая
плотность эфира приводит
к тому что звезды начинают
терять баланс и уже не могут всасывать эфир,
что приводит
к лопанью звезд с последующим выбросом эфира.
После того как повышается давление эфира в
центре галактики,
повышается давление эфира, получается ситуация в которой
старая плоскость галактики с высокой плотностью
эфира создаёт упругость гораздо
большую по отношению
к осям, в связи с чем все звезды поворачиваются по оси,
и получается вот такая ситуация.
 |
|
|
|
| Hubble image of NGC 1073 |
 |
|
| A Poster-Size Image of the Beautiful Barred Spiral Galaxy NGC 1300 |
|
|
-------------------------------
| Re: Свет и пространство и о скорости света.
|
6.03.201218:28 |
|
Продолжение.
2 Грязевое кольцо.
а) Галактика меньше грязевого кольца.
б) Галактика болье грязевого кольца.
в) Размытие грязевого кольца.
Когда галактика проходит критическую массу у её
звезд начинается лопанье звезд с образованием
вокруг галактики грязевой пелены,


после
чего
эта пелена концентрируется в грязевое кольцо.

Когда видимый размер галактики меньше грязевого
кольца - говорит о том что галактика вступила
в свою самую
динамичную
фазу, и у неё начинают изменятся все
звёзды внутри кольца.

Повышается температура
в связи с чем снижается плотность
эфира, в связи с большими расстояниями эфир с периферии
не может пополнится, звезды начинают быстро
само-сближаться, что
приводит к ещё большему снижению
плотности эфира и увеличению температуры,
что приводит к потере баланса для формирования
"звезды эфира" внутри
звезд, и в связи с чем практически
все звезды одновременно начинают выделять эфир.

Когда
звезды внутри грязевого кольца - то происходит или процесс
быстрого само-сближения звезд по причине того что эфир с периферии
не может пополнить снижение плотности
так как эфир тоже
обладает вязкостью и массой, и на таких больших
расстояниях пополнение эфира из вне гораздо меньше
чем нужно для звезд, и они само-сближаются,
тем самым ещё больше
снижается плотность эфира и повышается температура, после
чего "звезды эфира" теряют баланс во второй раз, в первый раз
они
потеряли баланс при формировании грязевой пелены,
которая превратилась в грязевое кольцо. Теряя баланс по всасыванию
эфира, звезда эфира начинает восстанавливать
эфир и сбрасывать его
в пространство, что происходит практически одновременно со всеми
звездами, и галактика начинает разлетаться.
Получается что когда галактика
меньше грязевого кольца,
то в ней звезды само-сближаются, или расталкиваются эфиром.



Когда звезды практически одновременно
теряют баланс и выбрасывают
эфир в пространство создаётся избыточное давление эфира,
и звезды быстро разлетаются
во все стороны,
сперва залетают за грязевое кольцо, а потом

и полностью грязевое
кольцо поглощают
как будто его и не было.

|
----------------------------------------------
| Re: Свет и пространство
и о скорости света.
|
12.03.20121:16 |
|
Заметил очередную закономерность.
Рукава.
Если галактика состоит из явно видимых двух рукавов,
то это рукава от слияния двух галактик.
Галактики сближаются.
--------------------
http://www.spacetelescope.org/images/heic0206b/

------------------
http://www.spacetelescope.org/images/heic0810ae/

-----------------
http://www.spacetelescope.org/images/opo9734d/

------------------
http://www.spacetelescope.org/images/heic0615a/

Формируют общее ядро.
------------------------
http://www.spacetelescope.org/images/opo0014a/

Ядра галактик сливаются.
---------------------------------
http://www.spacetelescope.org/images/heic1107a/

http://www.spacetelescope.org/images/heic0912a/

--------
Ядра двух галактик слиты.
----------------------------------
http://www.spacetelescope.org/images/potw1125a/

---------------------------
http://www.spacetelescope.org/images/opo1103c/

|
---------------------------------------
- Re: Черная дыра
(А.П. Васи,
31.03.2013 18:54, 4.8 КБайт)
Мой вариант, продолжение
---------------------------------------
Галактика с расслоением.
 Picture
Album: Barred Spiral Galaxy NGC 1512 in Many Wavelengths
(Gallery)
Picture
Album: Barred Spiral Galaxy NGC 1512 in Many Wavelengths
(Gallery)
 Picture
Album: Wide view of Barred Spiral Galaxy NGC 1512
(Gallery)
Picture
Album: Wide view of Barred Spiral Galaxy NGC 1512
(Gallery)
---------------------
NGC 4314


---------------------------------------------------
| Re: Свет и пространство и о скорости света.
|
24.03.201217:59 |
|
http://infuture.ru/article/5880
Астрономы обнаружили квазары, действующие как гравитационные линзы
 Кандидаты в гравитационные линзы имеют неоценимое
значение для оценки массы галактик квазаров.
Кандидаты в гравитационные линзы имеют неоценимое
значение для оценки массы галактик квазаров.
Астрономы, использующие космический телескоп Хаббл, нашли несколько
примеров галактик, содержащих квазары, которые действуют как
гравитационные линзы, усиливая и искажая изображения галактик. ---------------------------
 Go to image download page Go to image download page---------------- Данная галактика самая интересная из всех, у этой галактики
произошло слияние двух галактик, что повлекло за собой резкое расслоение звезд, и у центра галактики звезды начали быстро само-сближаться и резко увеличилась температура
в центре, и естественно резко снизилась плотность эфира, и звезды в центре не могут обеспечить нужного давления внутри себя чтобы удержать звезду эфира от того
чтобы частицы Александра, не начали превращаться в частицы эфира. При восстановлении частиц Александра, к этим частицам присоединяется энергия, и частица увеличивает
объём в миллиард и более раз, и превращается в частицу эфира (частица эфира в миллиард раз меньше частицы (условной частицы) воздуха), при этом процесс на некоторое
время становится необратимым. При близко расположенных соседних звездах, резко восстановившийся эфир у соседних звезд делает боковой резкий гидравлический удар при этом
может сдуть внешнюю оболочку, и звезда эфира останется позади а оболочка из материи слетит. И первоначальное восстановление эфира набирает лавинообразный вид, что
в результате так далеко давлением эфира разбросает звезды, что большинство звезд никогда не соберутся в одну галактику, они при остывании сформируют много небольших
галактик на большом удалении друг от друга. Основная достопримечательность этой галактики - это самая динамичная часть жизни галактики. То что хотят
сделать каталог - то это конечно где-то логично, но не совсем правильно, правильно у аналогичных галактик вести непрерывную видеозапись в телескоп. Но учитывая
в каком каменном веке живём что определяется количеством телескопов в космосе на миллион , этот вопрос будет вряд-ли когда решен в обозримом будущем. |
---------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
3.04.2013 21:59, 1.6 КБайт)
Рассмешил меня этот специалист по опытам Томаса Юнга.
Возможно недалёкий подразумевает опыт на электронно
лопухонных струнно
щелях, где собственно удалось
расщепить электрон.
---
На самом деле опыт Томаса Юнга не представляет из
себя ничего заурядного, в авторском варианте
это опыт
на двух щелях диаметром одну десятую миллиметра
расположенные на расстоянии одного миллиметра
друг от друга, и собственно в результате данного
опыта происходит наложение двух щелевых картинок
солнца.
В результате наложений двух солнечных щелевых
изображений получились полосы на изображении, что
собственно
в очередной раз сливает фотоны.
Недалёкие физики интерпретируют электронные опыты
на двух щелях которые были сделаны более ста лет спустя
-
как им хочется, и приписывают этот голимый
порожняк авторству Томаса Юнга.
----------------------

Ответ #19 : Сегодня в 21:16:57
Михаил Сурин, смотря на Ваши
картинки, так и не понял, как электрон проходит через две две щели в
опыте Юнга. А молекула фуллерена с протонами, нейтронами и электронами?
Все гораздо сложнее, не находите?
Для билета в новую физику, открывать новые частицы не обязательно, согласен с Вами
- Re: Черная дыра
(А.П. Васи,
3.04.2013 22:03, 211 Байт)
Опыты Томаса Юнга в среднем 1800 год,
а электрон придумали в 1924-1926году.
Собственно электрон на двух щелях и опыты Томаса Юнга
это разные эпохи.
Интеллект на земле - константа однако.
- Re: Черная дыра
(А.П. Васи,
6.04.2013 11:19, 2.6 КБайт)
 Re: Знаем ли мы физику?
Re: Знаем ли мы физику?
Ответ #91 - Вчера :: 17:32:49
romik писал(а) Вчера :: 16:34:56:Alow писал(а) Вчера :: 15:09:48:Когда
провод перемещается в магнитном поле, то электроны, под действие
магнитного поля, начинают двигаться, создавая вокруг проводника
магнитное поле
Ну а до магнитного поля электроны покойно лежат в проводнике?
У электронов нет силового направленного движения.
--------------------------------------------------------------------------------------
Вот что меня удивляет я более чем уверен что практически
никто не знает о том физическом опыте в результате которого
были придуманы электроны, по той причине
что если бы знали
то после небольшого анализа опыта послали бы электроны
в пешее эротическое путешествие, по той причине что
базовый опыт не правильный,
по той причине что в нём
идет не о электронах а о количестве заряда на микро-каплях масла,
собственно кто не понял - электрон с носителем заряда,
а не электрон,
и коню понятно что электрона без носителя
заряда не существует.
У меня такое впечатление что все думают что в прошлом уже всё
придумали за них, так
вот докладываю, там полная ерунда и бардак,
и в результате господствования парадигмы было так сказать
самовосхваление без критических анализов, так сказать все
доверяли,
ибо были недалёкими в данных вопросах, сейчас это называется -
корпоративная этика.
Так вот эта корпоративная этика - из физики и космологии
сделала сказку для умственно неполноценных.
И всячески поощряют идиотизм в этих науках.
- >> Re: Черная дыра
(А.П. Васи,
6.04.2013 12:17, 9.5 КБайт)
В пространство между двумя пластинами под напряжением (в конденсатор)
Милликен вводил мельчайшие заряженные капли масла, которые могли
находиться в неподвижном состоянии в определённом электрическом поле.
Равновесие наступало при условии 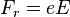 , где\\\
, где\\\
----------------------------------------------------------------
\\\В
1913 профессор чикагского
университета Р. Милликен в соавторстве[2]
с Х. Флетчером опубликовали проект своего опыта.[3]
В данном эксперименте измерялась сила электрического поля, которое
может удерживать заряженную капельку масла между двумя электродами. По
значению этого поля измерялся заряд капли. Сами капли электризовались во
время разбрызгивания. Во времена опыта не было очевидным существование субатомных
частиц, и большинство физических явлений[каких?]
можно было объяснить, приняв заряд непрерывно изменяющейся величиной.
Так называемый элементарный заряд e является одной из фундаментальных физических
констант и знать его точное значение очень важно. В 1923г. Милликен получил Нобелевскую
премию по физике отчасти и за этот эксперимент.\\\
-------------------------------------------------------------------------
\\\В
1911 году А.Ф.Иоффе определил заряд электрона,
использовав ту же идею, что и Р.
Милликен: в электрическом и гравитационном полях уравновешивались заряженные частицы металла (в опыте
Милликена капельки масла). Однако эту работу Иоффе опубликовал в 1913 году (Милликен
опубликовал свой результат несколько раньше, поэтому в мировой литературе эксперимент получил его имя).[2][3]\\\
---------------------------------------------------------------
\\\Заряд электрона неделим и равен
−1,602176565(35)10−19Кл[1] (или −4,80320427(13)10−10
ед.
заряда СГСЭ в системе СГСЭ или −1,602176565(35)10−20
ед. СГСМ в системе СГСМ); он был впервые непосредственно измерен в экспериментах А.Ф.Иоффе
(1911) и Р.
Милликена (1912).\\\
--------------------------------------------------------
--------------------------------------------------------
\\\Опыт Милликена опыт по измерению элементарного
электрического заряда (заряда электрона), проведённый Робертом
Милликеном и Харви Флетчером(англ.)русск.
в 1909 году [1].
Идея эксперимента состоит в нахождении баланса между силой
тяжести, силой Стокса и электрическим
отталкиванием. Управляя мощностью электрического поля, Милликен и Флетчер удерживали мелкие капельки масла в механическом
равновесии.
Повторив эксперимент для нескольких капель, учёные подтвердили, что
общий заряд капли складывается из нескольких элементарных. Значение
заряда электрона в опыте 1911 года получилось равным 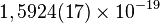 Кл, что на 1% отличается от современного значения в
Кл, что на 1% отличается от современного значения в  Кл.\\\
Кл.\\\
----------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
6.04.2013 12:33, 1.3 КБайт)
Для тех кто не понял нюанса,
на картинке - равномерное электрическое поле
от куда взялось, - где его базовые определения и
где его физическая сущность.
------------------------------
---------------------------------------------
То на самом деле - статическая утечка заряда, и ясен конь
на рисунке направление силового действия утечки
заряда
показано в противоположном направлении, ибо и коню понятно
что капля стремится упасть а силовое действие по причине
утечки статического
заряда удерживает каплю.
И что-то мне подсказывает что и при изменении
полярности - капля то-же зависнет но при другом
напряжении, - как-бы
это сказать - может так
логично и направление движения эфира обнаруживать,
каменный век кругом.
- Re: Черная дыра
(А.П. Васи,
6.04.2013 13:29, 400 Байт)
Надеюсь что догадались что на самом деле с этим опытом
ларчик просто открывался, - электронов нет никаких,
есть заряженные частицы, и статический электро силовой
поток по причине утечки, - на рисунке это равномерное электро поле,
из опыта и коню понятно что равномерное электро
поле или утечка статическая = может быть
только в одном
направлении от минуса к плюсу.
- Re: Черная дыра
(А.П. Васи,
8.04.2013 21:23, 5.2 КБайт)
- Обозреватель





-

- Сообщений: 7 816
- Рейтинг: +223/-57
- "..why the good God had opened up so many choices"
-
Ответ #2083 : Вчера в 18:43:00
Сходил на разведку.
Эфир в среду http://mirtv.ru/premiere/6808952
треть
были откровенные альты (типа: член Международного астрономического
общества Людмила Константиновская и кандидат биологических наук,
профессор Евгений Файдыш). Но был и нормальный интересный народ.
Ведущий, вроде бы, тоже был на стороне здравого смысла.
Посмотрим, что останется в итоговом варианте 
Осмелюсь
заявить, что ни в коем случае не следует уходить от диалога с
альтернативщиками, даже если он грозит вылиться в серьёзную конфронтацию
на повышенных тонах. Сожалею, что не смогу увидеть премьерный показ.
Надо посмотреть программу, может, будет повторение?
У меня нет такого канала. Буду искать на Ютюбе.
Вообще, найти можно прямо по
выданной ссылке.
Он-лайн трансляция у них тоже есть.
------------------------------------------------
Да я аж рассмеялся.
---------------------------------------------------
Расскажу по простому - чего нет у релятивистов - в первую очередь
по причине их тусования в парадигме они обреченны на достижения
столетней давности, и
не имеют возможности ничего изменить.
-------------------------------
У них нет строения звёзд и планет.
Нет фотонов.
Нет электронов.
Нет черных
дыр.
Нет большого взрыва.
по той причине что этому нет адекватного физического
объяснения нет измерительных приборов и методик
измерений.
И остаётся
только танцы вокруг микрофона о черных
дырах танцевать.
-----------------------------
У альтов есть всё и ещё запасная телега идей,
но по той причине
что альты не обязаны вытаскивать
из болота релятивизма релятивистов которые в этом
болоте выращивают себе свою релятивистскую смену,
которые тоже в результате
обучения завязнут в этом
болоте.
У альтов своя дорога которая проходит рядом и мимо
релятивистского болота.
------------
Вот лично у
меня делема написать фантастический рассказ
и заблокировать на семьдесят лет авторские права на
мои идеи в физике и космологии, - с одной точки
зрения релятивисты
останутся при своих интересах,
а физика и космология будет вынуждена идти
путём парадигмы в том-же составе и с теми-же идеями.
Это не корректно по отношению
к молодёжи, по этому
я думаю что-то примитивное всё таки официально опубликовать.
- Re: Черная дыра
(А.П. Васи,
9.05.2013 21:46, 4.1 КБайт)
Высшее образование - "Астроном"
Автор cadian
1 2 3 4 Все
-----------------------------------
Прочитал и как правильно было замечено в одном из постов что вымыто поколение сорокалетних, кто уехал за рубеж а кто ушёл в бизнес.
В принципе нет тех кто способен принимать решения в результате которых будет лучше.
Так как я из этого поколения то я в меру своего
виденья расскажу что надо делать.
В принципе астрономы со своей наукой не видят нескольких главных ситуаций - первая ситуация в том что вся
эта наука по большому счёту не нужна, хоть с малыми телескопами хоть с самыми большими.
Ибо не имеет практического смысла для производства.
Вторая сторона медали астрономию текущую большинство населения считают запутанной сложной в общем неадекватной.
Третья
сторона - астрономы не понимают что не люди должны быть для астрономии а астрономия должна быть для людей.
Всем ведь по барабану в какой телескоп
смотреть если никто не смотрел ни разу в телескоп больше 300мм.
Из этого простой выход можно и нужно зарабатывать деньги на любых телескопах
- организуется микро гостиница, в которой люди должны разместиться,и лечь поспать, после чего в девять вечера их разбудят проведут инструктаж, как телескопом управлять как
его наводить на звезду и какие рычаги и педали надо для этого дергать и нажимать. После лекции в десять вечера легкий ужин, после чего с телескопом до двух ночи, и ночной
ужин.
Легкий ужин и ночной ужин, в моём понимании рацион одинаковый, - тридцать граммов масла сливочного, два кусочка белого хлеба, три кусочка
сахара, два кусочка колбасы нарезанной, столовая ложка кабачковой икры, и пол литра чая.
По логике должно быть минимум две большие комнаты,
кровати можно как на службе с пружинным каркасом, и возможность разместить не менее 60 человек, должно быть три душевых, пять санузлов, десять умывальников, все удобства
должны быть в помещении а не на улице, шкафчики металлические закрывающиеся на ключ как в супермаркетах, два холодильника, пять электроплит, вахтёрша и теле-наблюдение.
Идея в том что-бы проводить экскурсии в виде культурных походов, в астрономические гостиницы, в которых основная задача чтобы группы туристов
или просто различные коллективы не имеющие отношения к астрономии знакомить с телескопами, научит и рассказать как ими управлять и предоставить возможность посмотреть на звёзды.
Только не надо устраивать той клоунады когда кто-то смотрит а другие ждут, должен быть окуляр с зеркальным ответвлением для видеокамеры, и на большом
экране чтобы показывал результат наведения всем.
Естественно что кому надоело наблюдать смогут слушать лекцию, или их будут обучать
пользоваться программами для астрономов.
А если совсем надоест то космическая дискотека должна развеять.
И
с моей точки зрения у астрономии не обязательно должен быть научный уклон в работе, ибо люди хотят зрелищ, развлечений, и новых необычных знаний и умений - и вот за это они
могут и хотят платить деньги.
- Re: Черная дыра
(А.П. Васи,
9.05.2013 22:16, 234 Байт)
Естественно что должно быть место на территории, куда заехать
сможет два длинных автобуса, и ещё должно поместиться минимум
десять легковых, два места под навесом,
желательно с одной
ямой автомобильной с освещением.
- Re: Черная дыра
(А.П. Васи,
10.05.2013 11:36, 6.0 КБайт)
Ответ #46 : 14.03.2013 [00:55:54]
Т.е.
я Вас все-таки понял правильно. Вы считаете, что наши обсерватории
просто не нужны. И, что следует сохранить небольшую наиболее продвинутую
группу наблюдателей, которая будет работать на западных современных
телескопах. То, что группа будет небольшая - следует автоматом, потому
что далеко не все смогут подать заявки требуемого уровня, а во-вторых,
для всех протсо элементарно не хватит наблюдательного времени - с учетом
конкуренции с наблюдателями западных стран.
Но, Вы несколько
путаете. Наблюдатели - это не те, кто подает заявки на наблюдения.
Наблюдатели те - кто сами проводят наблюдения. А кто ж их пустит на
телескопы-то. Там есть свои команды специалистов. Пустят только в том
случае, если наши уедут туда работать навсегда (вот, как Гармиш).
И, повторюсь, а что тогда останется в нашей стране? Членство в ESO и несколько астрофизмков-перефекционистов?
Вы можете бесконечно утверждать, что вы меня поняли, но понимания у вас при этом не прибавится. 
Я
утверждаю, что надо делать хорошую науку, а не "какую-то науку". Каким
способом - это предмет обсуждения. Довольно очевидно, что 10-метровый
телескоп не надо ставить ни в Крыму, ни на Пастухова, ни в Кисловодске.
Его надо ставить в Чили, на Гавайах и т.д.
В принципе, проще делать это в рамках международного сотрудничества.
кроме того, важно, чтобы наблюдатели писали
заявки и работали с разными инструментами.
Плюс, конечно, есть всякие полезные программы, которые можно делать и прямо на территории России с небольшими инструментами.
Путей много.
Не
очень понимаю, что вы имеете ввиду под словом "перфекционист". Если
"делающий хорошо". то да - делающие плоху (слабую) науку не нужны.\\\
-----------------------------------------------------------------------------------
Как по мне автор сего текста совсем не наделён стратегическим мышлением,
и не понимает что есть и другие и не такие успешные как он.
--------------------------------------------------------------------------------
Ответ #47 : 14.03.2013 [00:58:55]
стучаться в ESO, бегая по министерским коридорам за подачкой в 100 млн евро
для вступления туда...
Дык,
нам же это ничего не даст, кроме потер 100 млн. евро. Наблюдательного
времени нам больше давать не станут. А продвинутая группа и сейчас, без
денег, туда заявки подавать способна.
Концепция Сергея - это
смерть отечественной астрономии, и превращения ее остатков в придаток
западной. Если закрыть наши обсерватории, то новых-то, лучших, никогда
уже не появится. А пока они живы, пока пытаются барахтаться, всегда есть
шанс, что дадут деньги на модернизацию телескопов, что позволит
повысить и класс проводимых исследований. А не будут барахтаться,
напоминать о себе, то деньги на телескопы никто и не даст.\\\
------------------------------------
А это я бы сказал просто адекватный и нормальный взгляд на ситуацию.
------------------------------
Смотрел я передачу по дискавери как радиотелескоп во Франции делают,
так французы молодцы, они за эти деньги по мимо зарплаты получают
и новые технологии,
и специалистов получают которые могут зарабатывать
на производстве последующих, грубо говоря оплачены затраты на опытное
производство и опытное оборудование, и
после первого телескопа можно
запускать серийное.
Ясный конь что вряд-ли кто в здравом уме будет
создавать высоко-квалифицированные рабочие места в другой
стране
за возможность предоставления времени наблюдений на телескопе,
я же писал что раньше выделят деньги на космические серийные мини телескопы
на орбите
Земли - что задействуют собственные производства, и сбыт гарантирован,
хоть время продавай хоть целиком.
Так вот на переоборудование обсерваторий в астрономические
гостиницы денег дадут
однозначно, ибо государству нет смысла содержать устаревшие обсерватории а гостиницы
содержать будет не нужно, они сами будут себя содержать
и помимо зарабатывания
денег они будут заниматься просветительской деятельностью для населения.
И государство по крайней мере сможет кому-то продать их с условием,
чтобы проводились астрономические мероприятия среди посетителей в виде обязательных
услуг для собственника.
А астрономам я думаю до лампочки кто будет собственником,
главное чтобы было много
рабочих мест по специальности с хорошей зарплатой.
Единственный минус что не получить профессорского звания на такой работе,
ну здесь
как говорится надо выбирать, или бедный профессор, или обеспеченный лектор.
- Re: Черная дыра
(А.П. Васи,
11.05.2013 13:04, 3.2 КБайт)
Прочитал две темы, аж улыбнулся
по крайней мере это уже не моя борьба.
Борьба она в интеллектуальных вопросах это когда
не хватает интеллекта для обоснования,
и нет умственных
возможностей и способностей правильно и без ветвлений
сформулировать и дать определение ситуации.
--------------------------
Вот
в этой теме автор даже не понимает разницы между
фотонами и электронами, не знает разницы между фотоном
и светом, не знает опытов Томаса Юнга.
---------------------------
Конец дуализму.
Страниц 1
2
3
4
-----------------------
Собственно даже недалёкий
знает что опыты Томаса Юнга
примитивны и понятны даже недалёким и их не надо интерпретировать
опровергать или доказывать.
Опыт на двух щелях,
в дверной
щели сквозь которую проходит солнечный свет, закрепляют
бумажный листок, делают в бумаге
отверстие размером с дырку от бублика, после чего на расстоянии пол метра
берут в другой бумаге прокалывают одну дырку, свет проходит сквозь
неё и через пол метра падает на белый лист бумаги, на котором получаем
изображение солнца,
так вот если проколоть вторую дырку рядом с первой
на расстоянии одного миллиметра, что в итоге получится.
С одной точки зрения сторонники фотонов сразу скажут
что наложение
двух потоков фотонов в местах их наложения одного изображения солнца
на другое, увеличат яркость где происходит наложение.
Так вот при наложении
двух изображений солнца, в местах наложения
появляются кольцеобразные места с повышением и снижением интенсивности
что собственно говорит о волновой структуре
световых колебаний.
------------------------
Теория относительности Эйнштейна? Это вовсе не теория! Страниц 1
2
3
4
5
6
-----------------
А здесь тоже интеллекта не хватает элементарно
рассмотреть
базовые постулаты, если есть в базовых постулатах противоречие
то это всё достаточно.
Для этого достаточно знать смысл слов теория и гипотеза.
Так данная теория даже не теория и гипотеза а необоснованная
выдумка определение которой - фантастика.
- Re: Черная дыра
(А.П. Васи,
11.05.2013 13:13, 627 Байт)
Собственно как определить не специалиста по опытам Томаса Юнга на двух
щелях - это то что перед этими двумя щелями - отсутствует первая щель как таковая,
там просто
отверстие с помощью которого просто удобно
наводить изображение солнца на собранное устройство.
По большому счету достаточно просто двух щелей на расстоянии
одного миллиметра друг от друга на листе бумаги, и второго листа бумаги
на котором наблюдается - интерференция.
Интерференция - это Томас Юнг придумал и
описал волновые свойства света как колебания среды эфира, двести лет тому,
и определил длину световых колебаний.
- Re: Черная дыра
(А.П. Васи,
13.05.2013 21:53, 4.8 КБайт)
Яркий пример когда задача превышает способности, и я бы
добавил что по всем пунктам сразу.
----------------------------
 Re: Как построить единую непротиворечивую классическую электродинамику?
Re: Как построить единую непротиворечивую классическую электродинамику?
Ответ #119 - Сегодня :: 20:39:32
отшельник писал(а) Сегодня :: 20:10:05:Просто "другие державы" мне слегка "пофонарее" это совсем другой вопрос. Мне
тоже хотелось бы форум и покультурнее, и по компетентнее. Но когда
сунешься на другие форумы, понимаешь - там те же, только вид сбоку. Этих
ученых, желающих построить "единую непротиворечивую классическую
электродинамику", "единую непротиворечивую электродинамику движущихся
тел" не меньше, чем изобретателей вечных двигателей. Вообще вот этот
набатный призыв - назад, в прошлое, характерен не только для ученой
братии. Он еще более характерен для военных, 99% публикаций которых
посвящены переигрыванию давно прошедших войн. Он не менее характерен для
бизнеса, 99% операций которых - это переигрывание давно ушедших в
небытие бизнес-планов. То есть, это всеобщая человеческая черта - игра в
жизнь, только почему-то всегда по уже отставшим от ситуации правилам. Я
потому и не у дел на этом форуме, что мне не интересно двигаться
затылком вперед. Стандартный антагонизм интересов: мне не интересно
научное прошлое, форуму безразлично научное будущее. Что остается -
остается иронизировать над очередными потугами повернуть время вспять,
типа - назад, в прошлое, в непротиворечивую ... электродинамику. Что
плохо - плохо, что ирония не доходит, эти мухи продолжают упорно биться
лбами в стекло, хотя форточка в будущее - вот она, рядом ...
|
---------------------------------------------------------
И как говорится - а ларчик просто открывался, электричество лично
я решил примитивно через атомарную модель которая решает вопрос
на механическом уровне прокачки жидкостей, и подкрутки частиц
газов, прокачка - электричество
подкрутка частиц - магнитное поле.
И всё - достаточно, и больше придумывать ничего не надо.
Ну у других другая дорога и куда они идут я в принципе понимаю
что они идут туда куда.
Рассказ. Эфирной халявы не будет, да её и не-было
и она уже заканчивается.
Давным давно группа энтузиастов откапывала автобус, под названием
эфир, и
откапывали его из пыли времён, и пытались обращаться
к разным специалистам, властвующие структуры по раскопкам
научных идей не захотели возглавить и организовать
себе ещё
одно направление так как у них есть свой автобус на котором они
держат курс, хоть он давно и не ездит но направление куда ехать
надо показывает.
Естественно если два автобуса то направления будут у них разные,
естественно вокруг раскапывающих в пыли эфир начинали
скапливаться толпы орущих что
не надо раскапывать эфир,
да и Вы ездить не умеете, - да и курса куда ехать не знаете.
Мешали собственно по мелочам.
Когда энтузиасты раскопали отремонтировали
и до-оборудовали
автобус под названием эфир, то у них получился высокоскоростной
авто поезд длинной с железнодорожный состав, у каждого сторонника
эфира
свой авто вагон с библиотекой и рабочим кабинетом.
И здесь прозрели те кто смеялся над энтузиастами раскапывающими
эфир, но зайти в поезд не могут по разным
причинам, у кого курс не
совпадает, кого от движения укачивает, а у кого по способностям
вагон уже занят, а кто и не может придумать себе вагон.
Сторонники
эфира проезжая мимо стоящего автобуса включили
внешнюю бегущую строку по всему поезду.
---Спасибо Вам за заброшенный и подаренный нам эфир,
спасибо
Вам что Вы не додумались возглавить и помогать
нам в раскопках эфира.---
- Re: Черная дыра
(А.П. Васи,
13.05.2013 22:44, 1.0 КБайт)
Я подскажу в чём ошибка у всех.
Базовая ошибка в непонимании сути интеллекта,
интеллект это когда в одном лице две ситуации
в которой в первой задачи
надо найти здравое зерно
смысловое и вторая задача - описать это здравое зерно
в примитивных терминах и в примитивном смысловом
определении, следующая задача
это здравое зерно согласовать
с аналогичными - если не получается то два варианта , запомнить или
записать и вернутся к этому через месяц или через год,
а
можно и забыть, будет надо само вспомнится.
По простому надо быть и думать и придумывать и быть тупым одновременно
чтобы сразу проверять свои идеи на ошибки.
Глобальная ошибка - практически никто не может ставить
задачи и вникать в смысл.
Поисковая ошибка - все куда-то торопятся и пропускают не приметные
ссылки
или словосочетания, и думают что знают смысл словосочетаний. Тот-же эффект Доплера,
был придуман задолго до релятивистских идей и этот эффект исключительно
для сред,
для эфира воздуха и воды.
- Re: Черная дыра
(А.П. Васи,
13.05.2013 22:47, 177 Байт)
По простому надо быть логичным и не торопиться и думать и придумывать
и быть тупым одновременно
чтобы сразу проверять свои идеи на ошибки.
- Re: Черная дыра
(А.П. Васи,
14.05.2013 8:20, 839 Байт)
Глобальная ошибка - практически никто не может ставить
задачи и вникать в смысл.
-
В телескоп то видно что звёзды светят а космос
холодный,
возьмите эту задачу перед детьми поставьте они сразу Вам
скажут что там - в космосе, - помимо звёзд есть то что охлаждает.
Если звёзды всё вокруг
нагревают, и коню понятно - того что
невидно и то что - охлаждает, космос
намного больше чем звёзд которые нагревают.
И ясный конь что любая модель должна
изначально легко
решать эти вопросы.
И так чего не возьмись, все в основной массе -
думают что у абстрактных ученных
супер мозг которым они уже всё
обдумали и решили все вопросы
так вот ситуация на самом деле не такая радужная,
так как и те ученные тоже думают что за них и для них
уже всё придумали.
- Re: Черная дыра
(А.П. Васи,
16.05.2013 8:56, 822 Байт, ответов: 1)
Ответ #525 : Вчера в 23:46:38
Отличная лекция была сегодня
у Дмитрия Вибе, я был один из трёх слушателей. Глупо это, что народ не
интересуется. Наверное он глупый, ну раз глупый - судьба его
соответственная.
------------------------------------
Это просто тех кого Вибе забанил на форумах - решили
не приходить, и у Вибе лекционный заработок
накрылся.
- Re[2]: Черная дыра
(А. В. Малкин,
16.05.2013 14:48, 108 Байт)
По-моему, мы уже не в тему пишем.

- Re: Черная дыра
(А.П. Васи,
16.05.2013 22:36, 333 Байт)
Есть поговорка старого пса новым шуткам не научишь \с\.
Так вот это мой блог о том что я наблюдаю, а свет и пространство,
это мои достижения, или моя так
сказать записная книжка.
Так что тех недалёких кто прочитал этот форум и продолжает верить
в чёрные дыры и хочет продолжать обсуждение здеся, я огорчу.
- Re: Черная дыра
(А.П. Васи,
17.05.2013 19:28, 1.4 КБайт)
Ответ #525 : 15.05.2013 [23:46:38]
Отличная лекция была сегодня
у Дмитрия Вибе, я был один из трёх слушателей. Глупо это, что народ не
интересуется. Наверное он глупый, ну раз глупый - судьба его
соответственная.
---------------------------------------------------------------------------------------------------
Вспомнил как на одном острове одна обезьяна
научилась что-то делать. А вокруг и на соседнем острове
подобное обезьяны не делали и не умели такого и не знали.
И другие обезьяны посмотрели и начали повторять
как и эта
обезьяна. Всё бы то ничего, только на соседнем
острове после того как на острове первооткрывателя стало
известно более двадцати обезьянам, то на
соседнем
острове без всякого постороннего обучения обезьяны
начали делать тоже самое.
Так и здесь - возможно не ходят потому что
узнали что-то
другое, хотя их этому никто и не учил.
- Re: Черная дыра
(А.П. Васи,
21.05.2013 23:10, 1.9 КБайт)
Ответ #306 : Сегодня в 19:34:53
Президент РАН Ю.С.
Осипов на общем собрании академии посетовал, что "мы не умеем "воевать"
через средства массовой информации". Но ситуация, на мой взгляд,
тяжелее. Чтобы осознать своё неумение воевать, нужно вступить в бой. Мы
же пока, в основном, сидим в тыловых казармах из слоновой кости и
сетуем, что где-то там, далеко, нами проигрывается генеральное сражение,
а у нас нет ни стратегии, ни тактики.
Добавлю ещё от себя, что
наши астрономы уже сдались! Что намного хуже, чем сидеть в казарме. Мы
уже признались, что у нас техника хуже ,поэтому мы ни чего открыть не
можем, что западные журналы престижнее, что публиковаться нужно на
английском языке(см. хотя бы пост Попова в теме о планетной астрономии).
Пораженческое настроение--по моему мнению, причина всех наших неудач. И
дело не только в финансировании, начинать надо с мышления.
-----------------------------------------------------
Лично я согласен со всем что здесь
написано, проиграли
в технике, опозорились в школьной программе что астрономию
за неадекватность запретили для преподавания в школах,
да и альтам проиграли
в умении обрабатывать данные.
Итого - накапливать данные нет смысла ибо техника никакая,
обрабатывать данные не обучены нет умений как писать теории и гипотезы,
нет понимания как из данных по наблюдениям сделать теорию или гипотезу ,
школьные учебники адекватно переписать некому профессоров много
а написать учебники
всё равно некому ибо они все заняты.
- Re: Черная дыра
(А.П. Васи,
23.05.2013 22:35, 3.6 КБайт)
Ответ #460 : Сегодня в 21:03:48
В своё время я никак не мог
понять, отчего некоторые наши уважаемые учёные так неприязненно
относятся к журналу "Техника - молодёжи"
http://www.astronomy.ru/forum/index.php/topic,87799.msg1652558.html#msg1652558.
А недавно до меня, наконец, как говориться, "дошло". Особенно, когда стал перечитывать отдельные номера за недавние годы.
Справедливости
ради должен сказать, что раньше в этом журнале статей вроде
"Экзопланетная экзотика..." ( 1 за 2013 г.) или "Два интервью..." ( 3
за 2013) не попадалось. Если же и публиковался какой-нибудь спорный или
сомнительный материал, то обязательно с комментарием какого-нибудь
известного учёного, авторитетного специалиста в данной области, который
прямо указывал на слабые места или прямые ошибки такой публикации.
Теперь же такой практики нет. При этом из выступлений крупных учёных с
международным авторитетом вырываются цитаты выгодные авторам
вышеназванных мною публикаций.
При этом я не берусь утверждать,
что авторы этих статей ошибаются. Для этого у меня недостаточно знаний.
Но для того, чтобы усомниться в их правоте - их вполне хватает.
Чувствую, что это - альтернативщина. Хотя и звучит убедительно
(Кто
его знает, может, так и надо?)
Но чувства в таком деле, как наука - плохой инструмент. Не объективный.
И
мне кажется, что наши профессионалы сделали бы очень хорошо, если бы
уделили хоть немного времени более или менее подробному разбору теорий и
гипотез, которые я упомянул выше.
Конечно, я понимаю, что многие
профессионалы итак делают колоссальную работу по популяризации науки.
При этом, как я понимаю, часто в ущерб собственным научным интересам.
Однако популяризацию "альтернативных" гипотез и теорий мы видим, а позитивных - нет.
---------------------------------------------
\\\При этом я не берусь утверждать,
что авторы этих статей ошибаются. Для этого у меня недостаточно знаний.
Но для того, чтобы усомниться в их правоте - их вполне хватает.
Чувствую, что это - альтернативщина.\\\
Альтернатива - это просто другая точка зрения другие подходы
и другие методы решений, - а модераторы на этом форуме
пропагандируют
альтернативные идеи как идеи умственно неполноценных.
Так любой альт скажет что релятивизм это для тех кто остался в прошлом.
А
сто лет вещать одно и тоже задолбает всех слушателей.
-
\\\Но чувства в таком деле, как наука - плохой инструмент. Не объективный.
И
мне кажется, что наши профессионалы сделали бы очень хорошо, если бы
уделили хоть немного времени более или менее подробному разбору теорий и
гипотез, которые я упомянул выше. \\\
Чтобы заниматься данными вопросами надо чтобы умственные возможности превышали
необходимый уровень для решения поставленных
задач,
иначе такие задачи будут решаться - вечно.
- Re: Черная дыра
(А.П. Васи,
24.05.2013 7:55, 2.5 КБайт)
- Модератор





-

- Сообщений: 11 530
- Рейтинг: +115/-16
- Мне нравится этот форум!
-
Ответ #482 : Сегодня в 07:29:08
\\\Но
в данном случае важно, чтобы пропагандировались достижения реальной
науки, пусть даже в статьях где-то и попадаются ошибки и несуразности.
Но беда, когда за реальную науку выдаются крайне сомнительные
рассуждения. В прошлом году мне даже встречалось там кое-что весьма
напомнившее мне "теории" некоторых индивидов давно забаненных на нашем
Форуме.\\\
------------------------
Так и меня там забанили на этом форуме, модератор
этот форум считает научным ситом который отсеевает ученных
от зас ран цев, и не замечает того что у кого-то
ума не хватает придумать что-то новое, а все пользуются
придуманным сто лет назад и лет пятьдесят - семьдесят
назад, и
назвали это господствующей парадигмой и эту парадигму
колбасят и так и этак, - по каналу дискавери от идиотизма
передач про черные дыры, звёзды
и большие взрывы аж тошно.
А если спросить - а как звезда устроенна, - в ответ тишина.
- Re: Черная дыра
(А.П. Васи,
24.05.2013 8:15, 388 Байт)
Правильно бы было при отмене преподавания астрономии
в школах за неадекватность таковой, сразу лишить
всех космологов и астрономов профессорских званий.
И тот же форум о популяризации астрономии - не понимают
что неадекватное - нет смысла пропагандировать и популяризировать,
нужны просто адекватные космологические
модели звёзд, галактик
и прочего.
- Re: Черная дыра
(А.П. Васи,
27.05.2013 21:09, 923 Байт)
: 17.04.2005 [18:32:29]
Интерференция
частиц
----------------------
Мне так нравится всё что там написали, -
им ещё очень далеко до основ слова интерференция
- которое
описал Томас Юнг в опытом с солнечным светом в дверной
щели и двух дырках от иголки на расстоянии одного миллиметра.
Самое качественное в
этой ситуации для альтов - без понимания нет конкуренции.
И вряд-ли они догадаются что слова интерференция и электроны - нельзя
применять одновременно ибо
их разделяет столетие.
- Re: Черная дыра
(А.П. Васи,
28.05.2013 20:30, 1.9 КБайт)

Ответ #842 : Вчера в 23:42:50
Вам подробно объясняют, что открывают в той мере, в которой
позводяют
наши инструменты и научная специализация. Приводят пример открытий.
Приводят примеры популяризации. Просто ученые говорят, что они, хотя и
занимаются популяризацией, но по большому счету делать этого не должны.
Для этой задачи должны быть отдельные специалисты - лекторы и
популяризаторы, журналисты, документалисты.
Что пишут и в российские
журналы, и в зарубежные. К слову, нашел интересную ссылку про историю
российскуих астрономических журналов, в которые якобы не пишут
российские астрономы

. Почитайте, Вас позабавит.
http://www.astro-cabinet.ru/library/Lavrova_bibliograph/Lavrova_Bibliograph_2.htm----------------------------------------------
С моей точки зрения напрашивается логичный вывод,
и логичное название журнала -
"
Просто и научно, - журнал который популяризирует науку "
Который собственно должен быть, - по крайней мере из
названия понятно что журнал о науке
и для обывателя. Сейчас
на подобное просто аншлаг, чтобы всё разжевали до примитива,
- и прав тот кто платит, и тормоз тот который засыпает свою
статью
формулами и спец терминологией.
Формулы и спец терминология на сколько я знаю не рекомендуется использовать
при написании статей, их можно применять если нет другой
возможности
выразить свою мысль.
- Re: Черная дыра
(А.П. Васи,
28.05.2013 21:05, 207 Байт)
Можно и другие названия
Примитивная наука
Наука для обывателя
Научная и понятно
Вы поймёте науку - здесь
И наука Вас полюбит
Наука для Вас
Перешагни формулы и вступи в науку
- Re: Черная дыра
(А.П. Васи,
30.05.2013 8:55, 1.7 КБайт)
Собственно направление правильное - но результат будет
нулевой, чтобы был результат надо чтобы было понимание
а в данном случае методом научного втыка пытаются
получить
то что и не понимают.
Опыт делать надо по другому, надо сделать жесткую основу,
закрепить лазерную указку, после которой через 20-30мм
разделяется луч полупрозрачным зеркалом,
боковой луч через 100мм поворачивает и будет параллельным
основному, через 100мм поворачивает по диагонали ,
и
движется назад, пересекая луч и напоминает
зет с перечеркнутой средней линией, после
чего луч поворачивается параллельно основному,
и через 100мм поворачивается
на основной луч
на пересечение с основным лучом
в месте пересечения расположено второе полупрозрачное
зеркало, которое соединяет два луча, после чего две
линзы которые
расширят луч для картинки. Изображение снимает видеокамера.
Для медленного вращения используется червячный редуктор.
Всё устройство можно
вращать вокруг оси, и если медленно вращать конструкцию
то будет видно как движутся на изображении интерференционные кольца.
Идея всего устройства в том что
есть основной луч, и отклонённый,
по сколько в отклонённом луче есть участок когда луч движется
по диагонали, если диагональный луч расположить горизонтально,
а конструкцию вращать вокруг оси этой линии, получится что в одном крайнем
положении основной луч будет направлен под углом сорок пять градусов
вверх, а
в другом крайнем положении под углом сорок пять градусов вниз.
Конструкция должна вращаться в двух плоскостях.
По крайней мере недорогое устройство
в школах можно
на уроках физики использовать.
- Re: Черная дыра
(А.П. Васи,
30.05.2013 8:56, 322 Байт)
Предыдущий текст по этому форуму.
---------------------------------------
- Re: Черная дыра
(А.П. Васи,
9.06.2013 12:19, 2.4 КБайт)
Немецкие ученые из Института Астрофизики Хайдберга (Германия) при помощи наземной
системы телескопов ALMA
провели исследования и выяснили, что в некоторых космических областях
нашей Вселенной существуют целые "заводы" про производству твердых
небесных тел, в том числе и комет.

Если быть более точным, то астрономы нашли большие скопления пыли и
другого космического материала в некоторых космических областях. Они
определили, чточастички космической пыли, а также другого материала,
сливаясь друг с другом, увеличиваются в размерах, и могут формировать
твердые тела диаметром около 1 метра.
Так, разные твердые космические частички из склеенной пыли непрерывно
сталкиваются друг с другом на большой скорости, образуя крупные твердые
тела, к примеру кометы.
------------------------------------------------------------------
Я много книг по астрономии прочитал в которых из космической
пыли
и космического газа теоретически должны формироваться звезды
и планеты, - подтверждения наблюдений на протяжении сотни лет
отсутствуют, эта статья
очередной порыв в эту сторону.
Лично я удивляюсь отсутствии гибкости мышления, нельзя
всё время одну и туже идею мусолить.
Не соберутся эти тела в
кучу - нет физической причины, пыль,
газы и тела размером менее 100 км в диаметре ничего в космосе не
притягивали, не притягивают, и никогда не будут
притягивать.
Если бы притягивали, то космонавты бы на мкс молотки и отвертки
не носили бы прикрепленными с себе на верёвках, ведь они должны
бы
к мкс притянутся, а те имели в виду законы Ньютона и улетают
куда попало.
Я в принципе подобное могу сравнить например с тем что
это аналогично
тому что живое существо можно из чего-то
слепить вместо того чтобы его породило аналогичное живое
существо. Это называется - фантастика.
С
моей точки зрения всё тела что притягивают были \рождены\
а точнее выброшенными космическими телами которые притягивали.
- Re: Черная дыра
(А.П. Васи,
14.06.2013 8:30, 1.3 КБайт)
Распад скоплений неизбеженСкопления стабильныДругая аргументация
----------------------
По названию опроса решил срочно почитать
о чём там разговор ибо подумал что у меня
уже начинают интеллектуальную мелочь
заимствовать.
Оказалось что на этом форуме даже вечности
будет мало чтобы отказаться от догм в рамках
которых они пытаются решить вопрос который в
этих рамках решить в принципе невозможно.
Почитав форум вспомнил фильм.
Жанр: фантастика, комедия, приключения
http://www.ex.ua/view/74157?r=2
- Re: Черная дыра
(А.П. Васи,
14.06.2013 8:38, 428 Байт)
В принципе это как раз тот случай когда все считают догмы
нечто аналогичным посланием богов, тех кто писал догмы
- гениями а себя считают зас- ран- ц ами.
И
трижды себя считают недостойными и недалёкими чтобы
опровергнуть или усомниться в догмах.
И вечно будут пытаться хвалить догмы и в их рамках будут
вечно придумывать
и решать задачи которые более как
в их голове больше нигде не применимы.
- Re: Черная дыра
(А.П. Васи,
14.06.2013 20:38, 2.9 КБайт)
Немного расскажу понятно. Собственно было обнаружено
в космосе излучение определённого вещества
которое по своему спектру совпадало с таким-то.
После этого
надо изичить как изменяется спектр
при внешнем возбуждении, их бывают
разные виды - электроагнитные колебания, инфракрасный,
видимый световой диапазон, ультрафиолет
\создаёт поверхностное
воздействие\ и частицы разных энергий.
Так от разного воздействия у некоторых атомарных структур
возникают разные ситуации, - в даном
случаи
- что при внешнем воздействии различными частицами
и эл маг колебаниями данное вещество входит на резонанс,
при этом от интенсивности внешнего воздействия
меняется восновном амплитуда резонанса,
в других случаях меняется ещё и частота резонанса
она плавает.
В связи с чем логичный вывод - что это - что-бы
описать
надо было не эхо большого взрыва изобретать
а придумывать атомарную модель, которая бы учитывала эту ситуацию.
В итоге атомарная модель должна
выполнять все электромагнитные
свойства, и свойства резонансных возбуждений при
внешнем воздействии.
Вывод - собственно надо начинать с постановки тех
задачи
по атомарной структуре и её свойствам, для того чтобы было от чего
опираться и небыло нестыковок .
Естественно нет необходимости полностью решать
данную задачу , достаточно описать базовые её свойства
и дать базовые определения.
Следующая - красное смещение - здесь вопрос решается
по другому, описывается
методом ансамбля, с учётом разных ситуаций.
Надо дать базовые определения световому излучению и его свойствам
у поверхности звёзд, в пространстве, определится с
его источником,
причиной внешнего воздействия, и носителем излучения.
И всё достаточно - вопрос будет решон уже в базовых
определениях модели эл маг излучения.
Естественно после этого идёт модель устройства звёзд.
После модели звёзд сразу модель галактик.
И всё достаточно.
Если не нравится то что получилось с галактиками
или звёздами, - то как не смешно, - надо переделывать
и атомарную модель и модель электромагнитного излучения -
чтобы они во всех взаимодействиях стыковались
и не
противоречили друг другу.
И что тут трудного, примитивные задачи которые
можно решать только по составляющим.
Естественно что это я
написал чтобы релятивисты которые банят
альтов
на на форумах призадумались и сами над вопросами космологии,
чтобы понимали сколько сил и труда тратится альтами.
Релятивисты не рекомендую Вам решать подобные задачи ,
я просто переживаю за Ваше здоровье при столь огромном
потоке информации которые надо будет проанализировать
узнать и проверить на прочность и врамках этих
знаний предумать своё новое и другое - ни на что не похожее.
Если Вы всё-же решитесь решать подобные
задачи - то поздравляю Вас
- Вы стали альтом.
- Re: Черная дыра
(А.П. Васи,
18.06.2013 21:18, 74 Байт)
http://www.popmech.ru/article/13312-relyativistskaya-pena/page/2/#comments
- Re: Черная дыра
(А.П. Васи,
18.06.2013 21:21, 51.1 КБайт)
http://www.popmech.ru/article/13312-relyativistskaya-pena/page/2/#comments
|
 |
- Re: Черная дыра
(А.П. Васи,
18.06.2013 21:23, 78.8 КБайт)
- Re: Черная дыра
(А.П. Васи,
18.06.2013 21:24, 30 Байт)
Просто понравилось обсуждение.
- Re: Черная дыра
(А.П. Васи,
18.06.2013 21:52, 248 Байт)
Для тех кто не знает, предыдущий сайт диффективный и им так нравится,
я лично просил расположить сообщения наоборот, меня послали с моим предложением
в пешее
эротическое,
так-что предыдущее
обсуждение надо читать снизу вверх.
- Re: Черная дыра
(А.П. Васи,
18.06.2013 22:07, 1.3 КБайт)
\\\Добавлено 18.06.13 18:44
|
|
 |
Уважаемый Дмитрий Мамонтов, прошу Вас, создайте(или поручите создание) рубрику "Творчество читателей"
и опубликуйте там теорию нашего TeoreteG′а, уж очень мне захотелось познакомиться с его революционным и смелым взглядом на вопросы астрофизики и гравитации!\\\
Это исключено в принципе, если меня с моими статьями про эфир,
- я просился написать чтобы денег заработать - послали в буй,
на что я сказал - что конь
те на рыло что-то и ... когда-то будет
опубликовано про увлекаемый эфир здеся -, на том и разошлись.
Так и коню понятно что печатаются те кому положено.
- Re: Черная дыра
(А.П. Васи,
19.06.2013 6:23, 31.1 КБайт)
- Re: Черная дыра
(А.П. Васи,
19.06.2013 6:27, 446 Байт)
\\\Термин "жидкость" в физике
имеет тоже вполне определенное
значение.
Никакой жидкости в составе Солнца нет.\\\
Мамонтов жжёт на уровне не недалёкого в физике,
а на уровне - их вождя.
Пора бы ему уйти
с модераторства по проф непригодности.
- Re: Черная дыра
(А.П. Васи,
19.06.2013 7:06, 3.9 КБайт)
Чтобы были в курсе что в физике до лампочки и по барабану
что кому-то хочется чтобы солнце состояло из плазмы
- то оно и из плазмы.
Жидкая поверхность
солнца определяется по физическим
свойствам, аналогичным свойству жидкостей - те-же выбросы.
Я догадываюсь что жидкая поверхность солнца какая
и есть
по факту не подходит под текущую теорию строения
солнца - в центре которого ядерный реактор в котором
безбашенно нарушая все законы физики устремился водород
и гелий поучавствовать в ядрённой реакции. И я уже даже
не удивлюсь что всё самое глупое и нелогичное всё собрано
в космологии.
Жидкость не подходит по
причине объяснения теплообмена,
в текущем виде.
\\\Из Википедии
Над ядром, на расстояниях примерно от 0,20,25 до 0,7 радиуса Солнца
от
его центра, находится зона лучистого переноса. В этой зоне перенос
энергии
происходит главным образом с помощью излучения и поглощения фотонов.
При этом направление каждого конкретного фотона, излучённого слоем
плазмы,
никак не зависит от того, какие фотоны плазмой поглощались,
поэтому он может
как проникнуть в следующий слой плазмы в лучистой зоне,
так и переместиться
назад, в нижние слои. Из-за этого промежуток
времени, за который многократно
переизлучённый фотон (изначально
возникший в ядре) достигает конвективной
зоны,
может измеряться миллионами лет. В среднем этот срок составляет для Солнца
170тыс. лет[38].
Перепад температур в данной зоне составляет от 2 млн К на поверхности до 7
млн К в глубине[39].
При этом в данной зоне отсутствуют макроскопические
конвекционные
движения, что говорит о том, что адиабатический градиент
температуры в
ней больше, чем градиент лучевого равновесия[40].
Для сравнения,
в красных карликах давление не может препятствовать
перемешиванию вещества
и зона конвекции начинается сразу от ядра.
Плотность вещества в данной зоне
колеблется от 0,2 (на поверхности) до
20 (в глубине) плотностей воды[39].\\\
------------------------------------------------
Как говорится так соврал аж сам поверил - особенно как
точно
\\\Над ядром, на расстояниях примерно от 0,20,25 до 0,7 радиуса Солнца
от
его центра, находится зона лучистого переноса.\\\
Это я так понимаю зонд передал который забыли запустить в глубь
солнца. Напомню тем кто не знает
при взрыве звёзд
в выбросах бывает так что водорода нет совсем даже.
Странно да - ибо и коню понятно что водород и гелий
исключительно в верхних слоях газовой
атмосферы солнца,
и ни гелия ни водорода внутри солнца нет - это зависит не от моего
желания а от физических законов, как-бы понятно сказать
- ну это наука
такая - физика, - не пускает водород и гелий в центр
солнца и других звёзд.
- Re: Черная дыра
(А.П. Васи,
19.06.2013 7:32, 17.6 КБайт)
Модератор хочет удалить, а я сохраню, чтобы не думали
что всё было так пушисто, просто сторонники текущей
_уеты все темы которые противоречат их мировозрению
просто вместо конструктивного обсуждения по сути
сразу ничем необоснованными репликами
срывают обсуждение, в стиле - мол коню понятно
что есть большой
взрыв, и всеми опытами он подтверждён
и вот эта куриная ножка которую я жую с гонорара
куплена за подтверждение большого взрыва - ну и в таком ключе.
Коню
понятно - этому название - круговая порука.
Что собственно не делает чести, по той причине
что в этом случаи не будет придумываться ничего
нового.
Я естественно понимаю причину этого она
в способностях которые даны - и таковой я понимаю
что - консервативность мышления, я так понимаю
что практически
невозможно переучить другим теориям,
хоть сколь нелогичные есть текущие теории - другим теориям
скорей всего не получится переучить большинство ибо
в голове
многих две теории точно не вместятся, или тому
другая причина большое внутреннее доверие к той теории
которую индивидуум знает на данный момент, и по этой
причине ему другая теория вместо этой не нужна.
Собственно в результате массового аналогичного мышления,
связанных с определёнными теориями и защитой своего болота
консервативного, - получается коллективное не восприятие
других альтернативных точек зрения - что собственно,
и называется - круговая порука по отношению
к ранее придуманным теориям.
-----------------------------------------------





-

- Сообщений: 706
- Рейтинг: +17/-28
-
Теория большого взрыва
постулирует сингулярное состояние Вселенной, когда вся ее масса была
сосредоточена в сингулярной точке или микрообъеме.
По общей теории
относительности подобное состояние вызывает большие вопросы, ибо как
известно, большие массы в малых объемах обязаны образовывать черные
дыры, и чем больше масса, тем больше размер черной дыры. Если взять
массу Вселенной, то диаметр черной дыры должен быть порядка размера
Вселенной, но ни о какой сингулярности при этом и речи быть не может!
Все
что находится под горизонтом, оно как бы не существует для стороннего
наблюдателя, время там течет в противоположную сторону, и вещество оно
как бы бесконечно прилипает к горизонту событий, В подобной ситуации
описывать большой взрыв не представляется реально возможным, ибо любая
малая часть сверхплотной Вселенной обязана схлопнуться в локальную
черную дыру, и по сути такая Вселенная должна представлять собой
огромное скопление черных дыр.
НО в свою очередь определенная часть
скопления черных дыр должна превышать критическую массу, и в свою
очередь схлопнуться в гораздо большу черную дыру, и так на нескольких
уровнях...
В ранней Вселенной как раз и наблюдались квазары, это по сути активные черные дыры.
Теория
большого взрыва как то обошла стороной гравитационную неустойчивость
сверхплотной материи на ранней стадии формирования Вселенной.

Записан
Наука, как девица легкого поведения, откуда ветер дует, туда и смотрит





-

- Сообщений: 1 296
- Рейтинг: +15/-2
- Мне нравится этот форум!
-
Ответ #1 : Вчера в 13:24:15
Теория большого взрыва постулирует сингулярное состояние Вселенной
Вообще-то
нет.
большие массы в малых объемах обязаны образовывать черные дыры
Или белые.
Или вообще не образовывать.
Теория
большого взрыва как то обошла стороной гравитационную неустойчивость
сверхплотной материи на ранней стадии формирования Вселенной.
Инфляция - на развитие неустойчивостей не хватило времени.

Записан





-

- Сообщений: 706
- Рейтинг: +17/-28
-
Ответ #2 : Вчера в 13:39:02
А откуда тогда теория БВ взрыва берет сингулярность вначале?
Времени
на развитие неустойчивостей не нужно, в сверхплотном состоянии
бесконечной материи горизонт должен быть автоматом и на малом
расстоянии, гораздо меньшем, чем общий размер начальной Вселенной.
Единственный вариант, это отсутствие или слабость сил гравитации в сверхлотных состояниях вещества,
Кроме того, не учитывается действие темной энергии.

Записан
Наука, как девица легкого поведения, откуда ветер дует, туда и смотрит


-

- Сообщений: 60
- Рейтинг: +0/-2
- Мне нравится этот форум!
-
Ответ #3 : Вчера в 13:51:41
А откуда тогда теория БВ взрыва берет сингулярность вначале?
А
откуда вы взяли сингулярность в теории БВ? Теория БВ описывает только то, что описывает.
Времени
на развитие неустойчивостей не нужно, в сверхплотном состоянии
бесконечной материи горизонт должен быть автоматом и на малом
расстоянии, гораздо меньшем, чем общий размер начальной
Вселенной.Единственный вариант, это отсутствие или слабость сил
гравитации в сверхлотных состояниях вещества, Кроме того, не учитывается
действие темной энергии.
Сразу
видно, человек с уравнениями не разбирался, прочитал лишь пару статей
про БВ в женских журналах и уже кричит - "сие лажа!". Тяжёлый случай...

Записан
 neandertalets
neandertalets


-

- Сообщений: 60
- Рейтинг: +0/-2
- Мне нравится этот форум!
-
- Модератор





-

- Сообщений: 13 201
- Рейтинг: +350/-46
- Эвона как...
-
Ответ #5 : Вчера в 14:04:53
Я думаю, что мы в такой стилистике научные проблемы обсуждать не будем. Тема закрыта и будет вскоре удалена.
-------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
19.06.2013 7:55, 14.8 КБайт)
Собственно обосновать неправильность большого
взрыва проще простого - некоторое вещество, которого
много есть в пространстве и которое
пере излучает на
другой частоте
которое было обнаружено в 1941 году, было
пере открыто в 1946 году уже как эхо большого взрыва.
Так и охота сказать ясный конь - если
нечто постоянно
излучает некоторое вещество по причине воздействия на
него других локальных энергий которые его возбуждают
по месту нахождения, то при чём
здесь эхо глобального
процесса. Пипец примитива - одним словом.
Но дело не в простоте и логичности аргументации, здесь дело
как раз в не восприятии
другой точки.
-----------------------------------------
http://www.bibliotekar.ru/100otkr/65.htm
\\\
Дмитрий Самин
Тайны вселенной
Концепция Большого Взрыва
Возможность
расширения Вселенной была предсказана теоретически как одно из следствий
применения к решению космологических проблем общей теории относительности.
Первые труды в этой области принадлежат талантливому советскому математику
Александру Александровичу Фридману (1888 1925). Он широко известен как
геофизик-метеоролог, специалист по прикладным вопросам динамики атмосферы. Но
много времени Фридман отдал математическому анализу решений космологических
уравнений Эйнштейна. Незадолго до смерти Фридман получил серию решений уравнений
Эйнштейна.
Выходило,
что расширение может явиться одним из основных общих свойств Вселенной
важнейшим атрибутом ее эволюции. Работы русского ученого поначалу не
привлекли к себе должного внимания. Они были оценены по достоинству лишь в
связи с открытием Э. Хабблом красного смещения и развитием современных
представлений о первоначально горячей Вселенной и Большом Взрыве.
В 1927
году Ж. Леметр, студент из Эддингтона, независимо от Фридмана выдвинул свою
идею возникновения Вселенной и ее дальнейшего расширения из точки. Ей дали на
некоторое время название атома-отца. Сам Леметр категорически был против
подобного образа и вообще теологической трактовки своей теории. Процесс
возникновения Вселенной Леметр представил в форме Большого Взрыва. Молодой ученый
первым попытался найти и вероятные следы начального Взрыва. Леметр допускал,
что таким отголоском могли быть космические лучи. Его гипотезу астрономы
заметили лишь после выступления в 1933 году, когда Леметр выдвинул новый
вариант концепции расширения Вселенной из плотного сгустка материи
конечных, но очень малых размеров.
Задача
формирования более конкретной, физически разработанной эволюционной космолого-космогонической
модели расширяющейся Вселенной была решена в основном американским физиком Гамовым,
русским по происхождению. Джордж (Георгий Антонович) Гамов (1904 1968)
впервые предложил в 1946 году теорию, получившую затем наименование теории
Большого Взрыва (а точнее Большого Удара). Согласно ей, вся современная
наблюдаемая Вселенная представляет собой результат катастрофически быстрого
разлета материи, находившейся до того в сверхплотном состоянии, недоступном
для описания в рамках современной физики.
Удаление
галактик подчиняется необычным математическим закономерностям. Оно происходит
с различными скоростями. Чем больше расстояние между галактиками, тем выше
оказывается скорость их взаимного удаления.
Мы в
силах построить модель описанного выше разбегания галактик, пишет А.А. Гурнштейн,
если не будем рассматривать реальное бесконечное пространство трех
измерений, а ограничимся в своей модели лишь поверхностью пространством
двух измерений. Представим себе, что вся Вселенная расположена на некоторой
замкнутой поверхности, которая подобна поверхности постоянно раздуваемого
резинового шара. Пусть галактики в нашей модели изображаются точками,
нанесенными на поверхности этого шара. По мере его раздувания все расстояния
между галактиками, измеренные по поверхности шара, действительно будут
систематически увеличиваться, причем скорость разбегания галактик окажется
тем больше, чем больше было первоначальное расстояние между ними.
Как
считал Гамов, начавшееся при этом расширение материи в форме неразделимой
вначале высокотемпературной смеси излучения и вещества (элементарных частиц)
наблюдается и в наши дни в виде эффекта красного смещения.
Гамов
вместе со своими сотрудниками Р. Альфером и Р. Германом в 1948 году
предсказал, что должно наблюдаться и остывшее первичное изотропное
электромагнитное излучение тепловое с температурой около 5 К.
Однако
развитию теории в значительной степени препятствовало общее скептическое
отношение астрофизиков тех лет к возможности решения столь фантастической
задачи понять начало истории всей Вселенной в целом, пишут в своей
книге История астрономии А.И. Еремеева и Ф.А. Цицин. С другой стороны,
уловить в мировом пространстве с помощью имевшейся аппаратуры тепловое
радиоизлучение столь низкой температуры специалисты-радиофизики считали
совершенно невозможным уже из-за того, что подобный сигнал был бы заглушён
радиоизлучением звезд, галактик, межзвездной среды, короче, космическим
радиошумом.
Почти
два десятилетия концепция Большого Взрыва для большинства астрономов
оставалась игрой ума немногих физиков и космологов И только позднее стало
ясно, что более раннему решению проблемы в немалой степени помешал тот разрыв
в научных контактах, который все еще существует между современными
теоретиками и наблюдателями. Сыграла существенную негативную роль и дифференцированность
науки, из-за которой специалисты, даже работающие в близких областях, порой
мало знают о проблемах своих соседей.
Следствием
концепции первоначально горячей Вселенной явился вывод, что в наследство от
этой эпохи, если только она действительно имела место, должно повсеместно
сохраниться во Вселенной остаточное, или, как его называют, реликтовое,
излучение в радиодиапазоне.
Канадский
астрофизик Э. Мак-Келлар в 1941 году столкнулся с необычным явлением
возбужденным состоянием
молекул межзвездного циана. Температура возбуждения
составляла
2,3 К. Подобный факт мог стать основанием для
вывода о наличии в мировом
пространстве соответствующего излучения-возбудителя.
Однако, похоже, авторы
теории Большого Взрыва ничего не знали об этом открытии. Лишь много позднее
то, что такое состояние молекул циана вызвано именно реликтовым излучением,
доказали советский астрофизик И.С. Шкловский и независимо ряд других авторов.
Расчеты
А.Г. Дорошкевича и И.Д. Новикова в 1964 году показали, что реликтовое
излучение в принципе регистрируемо, и, следовательно, вывод теории Большого Взрыва
возможно проверить с помощью наблюдений. Гораздо позднее задним числом
выяснилось, что ко времени указанного расчета реликтовое излучение уже было
открыто в СССР и в Японии. В СССР это открытие было опубликовано аспирантом
Пулковской обсерватории Т.А. Шмаоновым в 1957 году.
Но
беда заключалась в том, пишет Гурнштейн, что наблюдатели и теоретики
работали в отрыве друг от друга. Между ними не было обмена информацией.
Наблюдатель не знал, как правильно истолковать свои странные результаты.
Замечательная же статья теоретиков осталась незамеченной.
К
середине шестидесятых годов радиоастрономы-экспериментаторы вознамерились
построить специальную аппаратуру для обнаружения реликтового излучения Но их
опередили инженеры, выполнявшие исследования по борьбе с радиошумами при
связи с искусственными спутниками Земли.
В 1965
году радиоинженеры А. Пензиас и Р. Вильсон (США) при испытании рупорной
антенны для наблюдения американского спутника Эхо случайно открыли
существование микроволнового (на волне 7,35 сантиметра) космического
радиошума, не зависящего от направления антенны.
На
протяжении 19661967 годов это открытие открытие реликтового радиоизлучения
Вселенной было независимо друг от друга подтверждено рядом исследователей в
разных странах. Особенности этого явления, соответствующего общему тепловому
излучению Вселенной с температурой около 2,7 К, совпали с предсказаниями
теории Большого Взрыва.
Авторы
книги История астрономии отмечают: Открытие реликтового излучения стало
величайшим достижением в астрономии XX века и в значительной степени явилось
результатом развития радиоастрономической техники и того, что сама научная
атмосфера созрела для его восприятия. Это открытие сделало достоверным фактом
по меньшей мере то, что Вселенная (Метагалактика) действительно
эволюционирует. Наконец, открытие реликтового излучения стало мощным стимулом
для дальнейшей разработки идеи Большого Взрыва.
Новым
этапом развития представлений о ранних стадиях эволюции Вселенной стала
теория горячей Вселенной, особенно в работах академика Я.Б. Зельдовича
(19141987) и его школы. Представление о характере начального расширения
Вселенной в наши дни сильно изменилось. Помимо главной трудности в описании
такого начала (недоступности его для современной теоретической физики),
обнаружились другие серьезные трудности при попытке описать и последующую,
уже в принципе доступную современной физике, но еще очень раннюю историю
расширения Вселенной как целого.
С целью
преодоления этих трудностей в 80-е годы была предложена концепция
раздувающейся (или инфляционной) Вселенной (А. Гут, США; А Д. Линде, СССР).
Обсуждается идея множественности и неоднократного возникновения в разные
моменты времени самих раздувающихся вселенных. Таким образом, древнейшая идея
возрождения Вселенной, идея бесконечной цепи рождений и гибели миров всех
масштабов, как и концепция островных вселенных, родившаяся уже в результате
соединения гравитационной теории и наблюдений, в наши дни возрождаются, но
уже на несравненно более высоком уровне как в отношении масштабов, так и
качественного многообразия объектов. Эти идеи могут рассматриваться как
предвестник, а может быть и начало уже третьей революции в космологической
картине мира.\\\
- Re: Черная дыра
(А.П. Васи,
19.06.2013 7:56, 1.2 КБайт)
\\\
Канадский
астрофизик Э. Мак-Келлар в 1941 году столкнулся с необычным явлением
возбужденным состоянием
молекул межзвездного циана. Температура возбуждения
составляла
2,3 К. Подобный факт мог стать основанием для
вывода о наличии в мировом
пространстве соответствующего излучения-возбудителя.
Однако, похоже, авторы
теории Большого Взрыва ничего не знали об этом открытии. Лишь много позднее
то, что такое состояние молекул циана вызвано именно реликтовым излучением,
доказали советский астрофизик И.С. Шкловский и независимо ряд других авторов. \\\
- Re: Черная дыра
(А.П. Васи,
19.06.2013 9:07, 20.9 КБайт)
Сегодня день непонятный, на солнце видно
выброс глупости.
Хочу заметить что как не странно самый технически
грамотный космолог блеснул отсутствием знаний
в принципе я думал что о том что Эффект Доплера
был придуман исключительно для сред ну радиоастроном
знать обязан. И уж должен знать что эффект Доплера
был придуман собственно для эфира а не для пустоты,
и придуман был намного раньше релятивизма.
Если космолог не различает среду и пустоту в пространстве,
это нехорошо.
-----------------------------------------------------------------





-

- Сообщений: 896
- Рейтинг: +6/-0
- тихо,тихо ползи улитка по склону Фудзи..
-
Ответ #60 : Вчера в 13:14:07
В
ЛЛ2 ключевая фраза "Но при "малых" расстояниях можно пренебречь
изменением a вдоль пути интегрирования..." и обе Ваши фразы относится
именно к приближению малых расстояний. В таком приближении никаких
претензий к ЛЛ2 быть не может.
Ну это не мои фразы. То есть при малых расстояниях можно вполне трактовать космологическое красное смещение, как эффект Доплера?
И что такое малые?

Записан





-

- Сообщений: 1 711
- Рейтинг: +14/-2
- I'm a llama!
-
Ответ #62 : Вчера в 13:56:11
В
ЛЛ2 ключевая фраза "Но при "малых" расстояниях можно пренебречь
изменением a вдоль пути интегрирования..." и обе Ваши фразы относится
именно к приближению малых расстояний. В таком приближении никаких
претензий к ЛЛ2 быть не может.
Ну это не мои фразы.
Но Вы же их выдернули из общего контекста
То есть при малых расстояниях можно вполне трактовать космологическое красное смещение, как эффект Доплера?
Если очень хочется, то можно. С грамотно составленным объяснениями.
И что такое малые?
Типа z<0.01

Записан





-

- Сообщений: 896
- Рейтинг: +6/-0
- тихо,тихо ползи улитка по склону Фудзи..
-
Ответ #63 : Сегодня в 07:46:25
Цитата:
ulitkanasklone от Вчера в 13:14:07Цитата: olegtitov от Вчера в
12:21:23В ЛЛ2 ключевая фраза "Но при "малых" расстояниях можно
пренебречь изменением a вдоль пути интегрирования..." и обе Ваши фразы
относится именно к приближению малых расстояний. В таком приближении
никаких претензий к ЛЛ2 быть не может.
Ну это не мои фразы.
Но Вы же их выдернули из общего контекста
Интересно, а в каком контексте вы
нашли фразу о малых расстояниях? Я что-то не могу найти в данном параграфе.
Ага,
вот нашел, так эта фраза о малых расстояниях идет после уже того, как
Ландау написал про эффект Доплера. И вообще она про другое. И как Вы
статьи редактируете с такой интерпретацией?
Эффект Доплера , как и слово "разбегание" галактик , хотя взятое в ковычках - методическая ошибка ЛЛ-2 , сбивающее
с толку.
Последнее редактирование: Сегодня в 07:55:33 от ulitkanasklone

Записан





-

- Сообщений: 1 711
- Рейтинг: +14/-2
- I'm a llama!
-
Ответ #64 : Сегодня в 08:08:33
Цитата:
ulitkanasklone от Вчера в 13:14:07Цитата: olegtitov от Вчера в
12:21:23В ЛЛ2 ключевая фраза "Но при "малых" расстояниях можно
пренебречь изменением a вдоль пути интегрирования..." и обе Ваши фразы
относится именно к приближению малых расстояний. В таком приближении
никаких претензий к ЛЛ2 быть не может.
Ну это не мои фразы.
Но Вы же их выдернули из общего контекста
Интересно, а в каком контексте вы
нашли фразу о малых расстояниях? Я что-то не могу найти в данном параграфе.
Ага,
вот нашел, так эта фраза о малых расстояниях идет после уже того, как
Ландау написал про эффект Доплера. И вообще она про другое. И как Вы
статьи редактируете с такой интерпретацией?
Про то самое. Читайте внимательней. И не учите дедушку кашлять.
Эффект Доплера , как и слово "разбегание" галактик , хотя взятое
в ковычках - методическая ошибка ЛЛ-2 , сбивающее с толку.
Никакой методической ошибки тут нет. Есть только недостаточная подготовленность некоторых читателей.

Записан





-

- Сообщений: 1 711
- Рейтинг: +14/-2
- I'm a llama!
-
Ответ #66 : Сегодня в 08:35:30
Никакой методической ошибки тут нет. Есть только недостаточная подготовленность
некоторых читателей.
Живите со своими заблуждениями и дальше..Желаю удачи.
Большое спасибо. И Вам не хворать!
- Re: Черная дыра
(А.П. Васи,
20.06.2013 22:53, 789 Байт)
Я так понимаю что прочитав то что я здесь
пишу может сложится мнение о тотальной
глупости в космологии в текущий момент времени.
Собственно я пишу для молодёжи
которые учатся астраномии
и космологии или это их хобби, даже если я и частично прав
то это не повод унывать и тем более не повод потерять
интерес к космологии
или астрономии.
Бывает собственно и такие ситуации, но по большому
счёту нет даже малейших причин и беспокойства
о кризисе или застое в астрономии или космологии,
всё нормально, возможно какаято часть в космологии и поменяется, -
здесь надо понимать что поменяется одна фантастика
необоснованная на другую необоснованную
фантастику,
и это не повод для грусти или переживаний за космологию или астрономию.
- Re: Черная дыра
(V. E. Krauchuk,
21.06.2013 22:21, 508 Байт)
1 Рыкову. Не заставляйте ни Ньютона ни Швардшильда переворачиваться , обратитесь к Чандрасекару!
, обратитесь к Чандрасекару!
2 Понятие "чёрная дыра" относится к массам большим массы Солнца. И Земля не может быть носителем Чёрной дыры, иначе Солнце
вращалось бы вокруг Земли и ни один спутник НЕ ВЗЛЕТЕЛ БЫ!
3 Вы физику как учили? или проходили? (мимо)
- Re: Черная дыра
(V. E. Krauchuk,
21.06.2013 22:39, 552 Байт)
А П. Васи! Спасибо за подвиженсво!Честно!
Только не путайте людей словом пустота, плз. В физике космоса нет такого понятия, есть понятие вакуума , но это не пустота,
в пустоте невозможно распространение каких либо волн, нужна "жёскость подвеса" (плотность!) для источника колебаний и/или инерция (масса) для переносчика колебаний.
А в вакууме эл.магнитные волны распространяются! Значит вакуум не пустота. и об этом говорят формулы и практика - спутники на расчётных (аварии не в счёт) орбитах, связь с
Вояджером действует!
- Re: Черная дыра
(А.П. Васи,
21.06.2013 23:55, 2.3 КБайт)
|
|
Re: Свет и пространство и о скорости света.
|
6.04.201113:49 |
|
Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а говорится что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою скорость что
наблюдается например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица которая потеряла скорость, просто так взять и
при вылете из стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами. Так что фотон
как частица - выдумка чистой воды.
Вывод -
в пространстве распространяются колебания среды, и световое
излучение не движется а образуется от взаимодействия колебаний
среды и материала, как в 1800 году говорил
Томас Юнг.
Так что все что написано в астрофизике без учета среды - к
сожалению не правильно.
Это подарок Дмитрию Вибе, это не будет опубликовано два
три года.
Дмитрий Вибе может и дальше учить студентов тому что безвозвратно
устарело, и тому что им никогда не пригодится.
Так уж Дмитрий Вибе запрещал обсуждать
эфир пока его не докажут что он есть | |
- Re: Черная дыра
(А.П. Васи,
21.06.2013 23:57, 4.9 КБайт)
| Re: Свет и пространство и о скорости света.
|
19.02.201119:54 |
|
Совмещение разных опытов.
http://www.trinitas.ru/rus/doc/0016/001b/00161336.htm
"Известно, что во вращающемся зеркальном интерферометре между
световыми волнами возникает сдвиг фаз, пропорциональный угловой скорости
вращения интерферометра. Этот эффект был обнаружен Харрисом (F. Harres)
в 1912 г. [1], а затем Саньяком
(G. Sagnac) в 1913 г. [2] и был назван явлением Саньяка. Неоднократно
предпринимались попытки объяснения физической причины вихревого эффекта
Саньяка. В частности, были
разработаны несколько теорий этого явления: кинематическая, доплеровская
и релятивистская. Первая из этих теорий предполагает наличие некой
всеобъемлющей среды (эфира), который
взаимодействует с электромагнитной волной (изменяет скорость
распространения света) и в то же время взаимодействует с веществом
(частично им увлекается при движении вещества).
Никакими другими опытами теория эфира не подтверждается."
http://upload.wikimedia.org/wikipedia/commons/5/55/Fizo_experiment_scheme_ru.PNG
Опыт Физо
http://elementy.ru/trefil/21167
"Майкельсон
и Морли использовали интерферометр оптический измерительный прибор, в
котором луч света расщепляется надвое
полупрозрачным зеркалом (стеклянная пластина посеребрена с одной стороны
ровно настолько, чтобы частично пропускать поступающие на нее световые
лучи, а частично отражать их;
аналогичная технология сегодня используется в зеркальных
фотоаппаратах)."
Опыт МайкельсонаМорли был принципиально направлен на
то, чтобы подтвердить (или опровергнуть)
существование мирового эфира посредством выявления эфирного ветра (или
факта его отсутствия). Действительно, двигаясь по орбите вокруг Солнца,
Земля совершает движение относительно
гипотетического эфира полгода в одном направлении, а следующие полгода в
другом. Следовательно, полгода эфирный ветер должен обдувать Землю и,
как следствие, смещать показания
интерферометра в одну сторону, полгода в другую."
То́мас Юнг -Википедия
"Его
идеи вызвали возражения английских учёных; под их влиянием
Юнг отказался от своего мнения. Однако в трактате по оптике и акустике
Опыты и проблемы по звуку и свету (1800) учёный вновь пришёл к волновой
теории света и впервые рассмотрел
проблему суперпозиции волн. Дальнейшим развитием этой проблемы явилось
открытие Юнгом принципа интерференции (сам термин был введён Юнгом в
1802 году).
В докладе
Теория света и цветов, прочитанном Юнгом Королевскому обществу в 1801
(опубликован 1802), он дал объяснение колец Ньютона на основе
интерференции и описал первые опыты по
определению длин волн света. В 1803 году в работе Опыты и исчисления,
относящиеся к физической оптике (опубликована 1804) он рассмотрел
явления дифракции. После классических
исследований О. Френеля по интерференции поляризованного света Юнг
высказал гипотезу о поперечности световых колебаний. Он разработал также
теорию цветного зрения, основанную
на предположении о существовании в сетчатой оболочке глаза трёх родов
чувствительных волокон, реагирующих на три основных цвета."
"В
1807 году в двухтомном
труде Курс лекций по натуральной философии и механическому искусству Юнг
обобщил результаты своих теоретических и экспериментальных работ по
физической оптике (термин ввёл
Юнг) и изложил свои исследования по деформации сдвига, ввёл числовую
характеристику упругости при растяжении и сжатии так называемый модуль
Юнга. Он впервые рассмотрел механическую
работу как величину, пропорциональную энергии (термин ввёл Юнг), под
которой понимал величину, пропорциональную массе и квадрату скорости
тела."
Что собственно
можно сказать о всех этих опытах если эфир движется сверху вниз создавая при этом гравитацию.
По факту все опыты не могут обнаружить движение эфира сверху вниз.
Здесь не хватает одного опыта - в горизонтальном расположении интерферометра, -
---Влияние статического заряда на скорость распространения электромагнитных
колебаний в эфире.---
Идея опыта простая, используется обычный
интерферометр, располагается в вакуумной камере, по ходу луча
устанавливаются две мелкие сетки, 30мм
на 30мм, так чтобы луч проходил сквозь ячейку сетки на расстоянии 30мм.
Зная что есть ещё электростатический эффект, то подавая различные потенциалы на сетки, будут меняться
интерференционные полосы.
Если изменение напряжения между сетками
в вакуумной камере будет оказывать влияние на изменение полос, -
следовательно между разно заряженными
сетками создаётся движение эфира. |
- Re: Черная дыра
(А.П. Васи,
22.06.2013 0:06, 9.9 КБайт)
| Re: Свет и пространство и о скорости света.
|
11.07.201120:59 |
|
Простое фундаментальное открытие.
В средине восьмидесятых я когда пользовался
осциллографом, по необходимости поставил его
вертикально, и луч сместился,
я подстроил луч,
потом поставил его горизонтально, и луч опять
сместился, я опять подстроил, суть не понял но
эффект запомнил.
Сегодня с утра смотрел
телевизор, по телевизору
было что-то не интересное и я вспомнил про тот
случай, так как телевизор Томсон 14mg120b,
то его можно вращать как угодно.
Так
вот вынул я скарт, экран стал синий, поставил кинескопом
в верх, в верхних углах красноватый муар, когда
повернул кинескопом вниз, в нижних углах
красноватый
муар, когда перевернул
вверх ногами весь экран стал красный, но не чисто красный,
по бокам красный, по центру немного синевы, если повернуть
на левый бок,
краснеет правый верхний угол, и и левый нижний
а если повернуть на правый бок, краснеет левый верхний и
правый нижний угол, вся другая часть экрана синие.
Если
поставить нормально - то экран чисто синий.
Вот собственно и получилось простое фундаментальное открытие.
Исходя из того что атомарное облако, состоящее практически
из одиночных атомов разгоняется ускоряющим и фокусирующим
и высоким и сводится в точку матрицы.
Переворачивая телевизор вверх ногами, синий луч стал красным
потому что поток частиц эфира в штатном положении заряженные
атомы прижимал вниз, а когда телевизор вверх ногами,
это аналогично тому что частицы эфира движутся
снизу вверх
по отношению к потоку заряженных одиночных атомов.
Взял я аккуратно по-подбрасывал телевизор, чтобы получился
небольшой эффект свободного падения.
При подбрасывании цвета не изменялись, в нормальном положении
оставался синий экран, вверх ногами красным.
Из чего я понял что так и должно быть, если считать
что эфир
движется со скоростью 10 км в секунду,
следовательно когда скорости падения лифта не высокие,
до 2- 5 км в секунду
то например
в знаменитой
задаче как узнать в закрытой кабине падающего
лифта - находится ли объект на орбите или движется к гравитирующему
телу, то вопрос решается если взять этот телевизор
включить от
аккумулятора и наблюдать за его экраном, и по изменению
цвета если вращать телевизор то можно
определить где верх а где низ при полной невесомости
в лифте,
вот так всё просто однако.
В связи с высоким напряжением в телевизоре, и опасностью поражения
электрическим током, данный опыт проводить категорически
не рекомендую,
по сколько при низком качестве телевизора возможна его поломка, в связи
с нештатным расположением телевизора, возможен перегрев деталей,
и
обрыв проводов внутри телевизора, что может повлечь за собой поражение
электрическим током.
------------------
| Re: Свет и пространство и о скорости света.
|
7.04.201212:19 |
|
Закрытие фотонов.
Фотоны не имеют физического смысла по следующим причинам.
1. При опыте с интерференцией получается чтобы реализовать
ситуацию
при которой наложение изображения солнца
которое попадает на экран через одну щель на другое
изображение солнца которое попадает на экран через другую
щель
не происходит увеличения яркости изображения солнца
а появляются темные и светлые полосы.
С точки зрения эфира как среды, объясняется просто как
изменение
плотности колебаний среды.
А что получается когда для описания этого
опыта использовать фотоны как частицы,
- получается что фотон который частица, - должен
обладать
зарядом "+" или зарядом "-", тогда если бы был такой случай
луч можно было бы разделить магнитом - чего не наблюдается.
Следовательно
фотоны как частицы с разным потенциалом не существуют.
2. Фотон как частица тоже не имеет физического смысла по причине
проверки на простом опыте, - возьмем
в вакууме проведем опыт
в котором свет проходит сквозь стекло.
Что получается свет до стекла имеет скорость равную скорости
света, после этого попав в стекло
теряет скорость в полтора раза
после этого вылетая из стекла увеличивает свою скорость.
Так вот данные свойства не являются возможными для летящих
частиц,
по причине того что если частица замедлилась то разогнаться
она уже без внешнего воздействия с приложением затрат энергии
- не может. А подобные свойства являются
свойством среды -
например звук колеблется в воздухе передаёт колебания воде
- увеличивает скорость, после того как звук из воды попадает в
воздух скорость
звука уменьшается.
Вывод - два случая в первом случаи фотонами как частицами невозможно
описать интерференцию которая имеет место быть,
во втором случаи
фотоны не могут быть частицами,
- итого фотоны как частицы летящие и являющиеся носителями света
не имеют физического смысла.
|
---------------------------------
| Re: Свет и пространство и о скорости света.
|
1.05.201213:13 |
|
Закрытие большого взрыва.
Закрытие моделей звёзд на горении водорода.
---Нескладушки большого взрыва.
Первое что бросается в глаза в этой
теории
- что с достаточно большой точностью в
секунды и минуты знают последовательность происходящего
но напрочь отсутствует причинно следственная связь
- всё построено на постулатах которые нельзя подтвердить.
Что изначально состоит из парадоксов и противоречий.
1 Разлёт со сверхсветовой скоростью
на 13.5 млрд световых лет
во все стороны практически мгновенно, и мы наблюдаем в телескоп
звёзды которые туда забросило при большом взрыве.
---
Что собственно
есть жесткое и парадоксальное в этом, -
скорость света была превышена минимум в миллиард раз.
Что не понятно другое, не понятно что если при разлёте материи
почему её забросило на 14 млрд световых лет, а не на два или тысячу,
- почему разброс совпадает с возможностями телескопов.
2 Химический состав
водорода и гелия и его соотношение - 70%водорода
и 30% гелия - и с какой точностью и без примесей других веществ.
---
--------------------------------------------------------------------------
http://vsln.ru/himicheskiy-sostav-solntsa.html
(В 1929 г. американский астроном Генри Норрис Рессел (18771957)
тщательно изучил солнечные спектры, и ему
удалось установить, что
Солнце поразительно богато водородом. Он решил, что на водород
приходится три пятых всего объема Солнца. Это было абсолютной
неожиданностью,
так как водород, хотя и не является редким элементом
в точном смысле этого слова, составляет всего лишь 0,14% земной коры.
Однако последующие исследования показали,
что Рессел был слишком
осторожен в своей оценке. Недавние подсчеты американского астронома
Дональда Говарда Мензела (род. в 1901 г.) показывают, что водород
составляет
81,76% объема Солнца, а гелий 18,17%, так что на долю
всех остальных элементов остается только 0,07%.
По-видимому, можно с уверенностью сказать, что
Солнце практически
представляет собой светящуюся смесь водорода и гелия в пропорции
(по объему) 4:1. (Элемент гелий тоже был открыт с помощью спектрального
анализа,
причем сначала не на Земле, а на Солнце Английский астроном
Джозеф Норман Локьер (1836 1920) предположил, что некоторые
неопознанные линии солнечного
спектра принадлежат еще не открытому
элементу, который он в честь греческого бога Солнца Гелиоса назвал гелием.
На Земле же гелий был обнаружен шотландским химиком
Уильямом Рамзеем
(18521916) только в 1895 г.).)
---------------------------------------------------------------------------------------------------
Собственно основная ошибка в данной ситуации в том что
по составу химическому атмосферы солнца сделано скрытое
утверждение - а это постулат, что химический
состав самого
солнца тоже такой-же за исключением ядра.
Вот здесь надо повнимательнее ибо здесь самая грубая
ошибка всей астрономии.
Данная
ситуация на самом деле не возможна, ибо водород
он не только самый легкий и у него самая низкая удельная
плотность но у него и самая большая проникаемость, он
со временем
может просочится через металлы и пройти сквозь них
насквозь.
Следовательно при таких физических свойствах водород будет
вытеснен материалами
с большей удельной плотностью из своих
недр любой звезды или планеты на поверхность.
А из этого что следует - а то, что водород не участвует и никогда
не участвовал в ядерных реакциях в солнце потому что внутри
солнца водорода нет в принципе, он весь исключительно в атмосфере
солнца.
А из этого
следует что не только большой взрыв но и все эволюции
звезд и модели звёзд которые были построены на горении
водорода и гелия в звездах неправильны и не соответствуют
физическим свойствам веществ.
А это значит что процентов 99 книг по астрономии не правильные,
вот такая жестокая селяви. |
-----------------------------------------------
|
- Re: Черная дыра
(А.П. Васи,
22.06.2013 20:59, 9.1 КБайт)
- Новичок

-

- Сообщений: 2
- Рейтинг: +1/-0
- Мне нравится этот форум!
-
Теория инфляции кажется
довольно многообещающей: хороший математический аппарат, косвенные
подтверждения наблюдениями, предсказательная сила и т.д. Но на мой
взгляд ключевая ее часть вызывает больше всего претензий и непоняток.
Каким бы гипотетическим не был ложный вакуум, инфляционные теоретики
смотрят на него, как на нечто реально существующее. И тут то начинаются
непонятные вещи: если у ложного вакуума такая колоссальная энергия и
плотность, почему вместо этого он растягивается, а не сжимается,
коллапсируя в итоге?
Что это за материя (если это материя), у
которой громадное гравитационное отталкивание, при котором ее энергия
(!) и плотность (!) остаются неизменными (!). И откуда он мог
появится?Многие твердят, что из ниоткуда, из ничего: мол появляется
ничтожная квантовая флуктуация в ничто (!), которая затем туннелирует
куда то и начинает бешено расти. Мне кажется такая идея чистой воды
спекуляция: если физик-теоретик чего то не знает, он может сказать, что
не знает этого, а не выдумывать непонятно что похуже самых матерых
фантастов.

Записан





-

- Сообщений: 13 615
- Рейтинг: +161/-39
-
Ответ #1 : Сегодня в 20:20:20
.. Мне кажется такая идея чистой воды спекуляция: если физик-теоретик
чего то не знает, он может сказать, что не знает этого, а не выдумывать
непонятно что похуже самых матерых фантастов.
Т.е.
поверхносто познакомившись с этой теорией, Вы уже смело приступаете к
обвинениям ученых? А они уже написали тысячи статей и есть учебники для
студентов с изложением ТИ.
Лучше избирать другой путь и упорно читать эти учебники, обзоры и статьи.

Записан
- Модератор





-

- Сообщений: 13 210
- Рейтинг: +350/-46
- Эвона как...
-
Ответ #2 : Сегодня в 20:41:22
Мне кажется такая идея чистой воды спекуляция
Ну
и что? Что Вы предлагаете обсудить? То, что Вам кажется?

Записан
-----------------------------------
\\\Что это за материя (если это материя), у
которой громадное гравитационное отталкивание, при котором ее энергия
(!) и плотность (!) остаются неизменными (!). И откуда он мог
появится?Многие твердят, что из ниоткуда, из ничего: мол появляется
ничтожная квантовая флуктуация в ничто (!), которая затем туннелирует
куда то и начинает бешено расти. Мне кажется такая идея чистой воды
спекуляция: если физик-теоретик чего то не знает, он может сказать, что
не знает этого, а не выдумывать непонятно что похуже самых матерых
фантастов.\\\
У адекватных это называется так спим сдел что аж сам поверил.
И корни этого еще растут из одного старого анекдота, -
\\\- приходит
как-то к руководителю страны секретарь его,
и говорит ему что его страна очень сильно отстаёт от конкурентов
по количеству физиков и надо выделить очень большие
средства на
оборудование для лабораторий чтобы проводить физ опыты.
На что руководитель страны спросил - а есть ли дешевый выход
из этой ситуации. Секретарь
сказал что выход то есть только
пользы не будет никогда, для этого просто надо увеличить
количество физиков-теоретиков, или физиков - математиков
- а им
что надо.
А им нужна только бумага карандаш и стирающая резинка.
Даже достаточно только карандаша и бумаги,
стирающая резинка не нужна - и так отзвездятся.\\\
- Re: Черная дыра
(А.П. Васи,
22.06.2013 22:25, 5.9 КБайт)
- Модератор





-

- Сообщений: 13 213
- Рейтинг: +350/-46
- Эвона как...
-
Ответ #12 : Сегодня в 21:51:28
Перефразирую: исходя из этого, можно твердить, что космология ничего
не знает об устройстве вселенной?
Твердить
непрерывно, конечно, не стоит; правила форума не приветствуют
публикацию однотипных сообщений. Один раз написали, да и хватит.

Записан
И кто-то, как всегда, нёс мне чушь о "тарелках", и кто-то, как всегда, проповедовал дзен... (с) Зоопарк





-

- Сообщений: 13 621
- Рейтинг: +161/-39
-
Ответ #13 : Сегодня в 22:08:34
Последнее звучит странно: Природа не подписывалась во всём соответствовать
нашим понятиям.
Значит
то, что мы называем Законами природы это лишь наши представления? И
законом сохранения энергии можно пренебречь, когда речь идет о ЛВ. И
искривляющим свойством массы, то есть самой сути гравитации. Тогда зачем
нам вообще наука?
А это Вы откуда взяли. Ни Линде, ни Виленкин об этом не говорили.
А свои личные умозаключения положено обосновать или дать
ссылки на Ваши источники от профи.
-----------------------------------------------------
\\\что космология ничего не знает об устройстве вселенной?\\\
\\\А свои личные умозаключения положено обосновать или дать ссылки на Ваши источники от профи.\\\
Вот лично с моей точки зрения - наука космология есть
- а космологов то в космологии
и нет .
Космологический идиотизм и космологические бредни появлялись не
как выдумка от специалиста, а как подпорки для
других теорий.
И собственно когда у этих подпорок ещё пытаются найти
космологический смысл - то это вообще нонсенс, там его
никогда не было.
- Re: Черная дыра
(А.П. Васи,
23.06.2013 13:46, 3.4 КБайт, ответов: 1)
Ответ #106 : Сегодня в 07:45:07
Интересна
сама принципиальная возможность существенного увеличения размера и
массы Земли, начиная от падения метеоритов и заканчивая материализацией
нейтрино во внутреннем ядре и т.п. ...
Не
будучи ни биологом, ни геологом, я всё-таки рискну предположить, что
увеличение массы Земли в несколько раз привело бы к более заметным
последствиям, чем вымирание динозавров.
-----------------------------------
Ответ #108 : Сегодня в 12:31:16
Ну так оно(увеличение массы и размера) вроде как привело и до сих пор приводит(IMHO)
к довольно заметным последствиям...
К каким?
----------------------------
Ответ #110 : Сегодня в 13:28:34
Ведь если диаметр Земли увеличится всего на 1мм за 100 лет
А если не увеличится?
----------------------------
Странная наука астрономия, только в ней профессор
на форумах выглядит как умственно неполноценный.
Вопрос то проще простого, - только на такие вопросы - чтобы
не выглядеть недалёким, ответы надо знать и не нужно их
придумывать.
Грунт на поверхности
луны аналогичен грунту в глубине земли
на глубине три с половиной километра.
В связи с чем и коням понятно что земля тысячекратно более
чем Луна притягивает
на себя космическую пыль и микрометеориты что поднимает
уровень грунта поверхности.
- Re[2]: Черная дыра
(А. В. Малкин,
23.06.2013 21:37, 3.7 КБайт)
| Цитата: |
Ответ #106 : Сегодня в 07:45:07
Интересна
сама принципиальная возможность существенного увеличения размера и
массы Земли, начиная от падения метеоритов и заканчивая материализацией
нейтрино во внутреннем ядре и т.п. ...
Не
будучи ни биологом, ни геологом, я всё-таки рискну предположить, что
увеличение массы Земли в несколько раз привело бы к более заметным
последствиям, чем вымирание динозавров. -----------------------------------
Ответ #108 : Сегодня в 12:31:16
Ну так
оно(увеличение массы и размера) вроде как привело и до сих пор приводит(IMHO)
к довольно заметным последствиям...
К каким?
----------------------------
Ответ #110 : Сегодня в 13:28:34
Ведь
если диаметр Земли увеличится всего на 1мм за 100 лет
А если не увеличится?
---------------------------- Странная наука астрономия, только в ней профессор на
форумах выглядит как умственно неполноценный. Вопрос то проще простого, - только на такие вопросы - чтобы не выглядеть недалёким, ответы надо
знать и не нужно их придумывать. Грунт на поверхности
луны аналогичен грунту в глубине земли на глубине три с половиной километра. В связи с чем и
коням понятно что земля тысячекратно более чем Луна притягивает
на себя космическую пыль и микрометеориты что поднимает уровень грунта поверхности.
|
Может быть... правильная мысль!
- Re: Черная дыра
(А.П. Васи,
23.06.2013 23:37, 988 Байт)
Не не может быть, - а надо знать и кое что помнить
надо вечно, чтобы
не выглядеть недалёким в космологии.
Лунный грунт сравнивали так давно что и трудно
вспомнить когда его привезли спутники,
а клоуны от астрономии и космологии ещё
добрую сотню лет этого не будут знать или будут
забывать постоянно.
Я про эту ерунду третий раз здесь,
на разных форумах пишу как минимум.
----------------
http://geo.1september.ru/view_article.php?id=200700613
\\\Бурение сверхглубоких скважин по сложности
сравнивают с полетами в космос. Образцы пород,
извлеченных из самых глубин недр, представляют
не меньший интерес, чем образцы лунного грунта.
Не случайно лунный грунт, доставленный на Землю
советским луноходом, изучали и в научном центре
при Кольской скважине. Оказалось, что лунный
грунт по составу почти полностью соответствует
породам, извлеченным из Кольской скважины с
глубины около 3 км.\\\
- Re: Черная дыра
(А.П. Васи,
23.06.2013 23:48, 695 Байт)
Так вот как раз про Луну, - собственно если у Луны
есть поверхность и есть космическая пыль, а
внутри Земли есть аналогичный грунт, то логично
можно
уверенно сказать что Луна стала на орбиту
Земли извне, и будет два варианта лунного грунта
внутри Земли, первый вариант - что Луна прокатилась
по поверхности
Земли, и второй более вероятный
случай что в Луну пролетавшую мимо Земли, попало
что-то размером с пол Луны в связи с чем Луна стала
на устойчивую орбиту,
а мусор от столкновения осел
на Земле и Луне, а так как Земля увлекает намного
больше микрометеоритов то со временем лунный грунт
оказался на глубине больше
трёх км.
- Re: Черная дыра
(А.П. Васи,
28.06.2013 13:50, 3.6 КБайт)
Сомневаюсь что науку будут делать не званиями
а способностями.
Для этого мне кажется ещё помимо того должна
быть заинтересованность личная.
А так вообще
интересно - но сильно жестоко с академиками,
так их резко от кормушки отвели восвояси, и кормушку
сожгли. Хорошо хоть званий не лишили.
------------------------------------
| Новость
о предстоящей масштабной реорганизации российских научных академий, о
которой было объявлено 27 июня на заседании правительства, вызвала
возмущение в академических кругах. То, что предложили вчера
Медведев с Ливановым это полное безобразие! заявил Интерфаксу
сегодня вице-президент Российской академии наук, нобелевский лауреат
Жорес Алферов. По его словам, главная цель нововведений лишить
академия всего имущества, но для научно-технического прогресса
реорганизация ничего не даст. Российской науке нужна только одна вещь
востребованность бизнесом и обществом. Предстоящая реформа этой
востребованности не создаст, она убьет науку. Эта квазиреформа
направлена только на одно: отнять все имущество у РАН. Не это нужно
делать! призвал академик, пообещав написать обращение по данному
поводу. Между тем, руководители Сибирского отделения РАН уже
обратились с открытым письмом к руководству страны, в котором резко
критикуют планы реформирования академии. Решение правительства РФ
о фактической ликвидации Государственных академий наук России и изъятии
из их оперативного управления федерального имущества мы расцениваем как
намерение разгромить сложившуюся эффективную систему организации
фундаментальной науки в России, лишить нашу страну главного преимущества
в глобальной конкуренции за экономическое развитие на основе высших
достижений современной науки, подорвать научно-техническое обеспечение
национальной обороны и безопасности страны, продолжить разрушение
образования в России, говорится в тексте письма, подписанного
председателем Сибирского отделения РАН академиком Александром Асеевым,
пятью его заместителями, а также председателем Дальневосточного
отделения РАН, председателями Красноярского и Иркутского научных центров
СО РАН. Накануне премьер-министр России Дмитрий Медведев заявил,
что система Российской академии наук должна быть реформирована, и
сообщил, что готовится проект соответствующего закона. Он будет внесен в
Думу на следующей неделе. В частности, предполагается объединить
структуры Российской академии наук, Российской академии медицинских наук
и Российской академии сельскохозяйственных наук, а также создать
Агентство научных институтов РАН для управления имуществом научных
институтов и государственных академий. Новость на сайте Вести.Ру |
|
- Re: Черная дыра
(А.П. Васи,
3.07.2013 8:00, 4.9 КБайт)
У альтернативщиков и сторонников эфира своё мнение.
Чиновники вряд-ли будут финансировать организации
которые борются с лженаукой и несогласными с
господствующей парадигмой,
они после реформы проведут
переатестацию на детекторах лжи и я думаю процентов тридцать
пойдут восвояси.
----------------------
|
 Re: Aether theory with experimental verification
Re: Aether theory with experimental verification
Ответ #218 - Вчера :: 13:15:22
Smotrjaщii писал(а) Вчера :: 04:05:33:С Вами ВАА разговаривает лишь потому(на мой взгляд), что Вы ему неперечите.... И, извините,- заглядывете в рот!
С теми же, кто задаёт ВААнеудобные
вопросы по эфиру, онговорить не желает.
Пригласите
его сюда, пусть ответит САМ на пару вопросов. Посмотрим, снизойдёт
сейвеликийГуру дообщения срядовыми "эфиристами", алиостанетсянедосягаемо
высоким!
Что касательно ""обнаруженного эфирного ветра""(КЕМ
УГОДНО!), то Вам уже тыщу раз сказано:НЕТи не может быть НИ
ОДНОГОопытаподтверждающего обнаружениеЭВ.
Всёэто расчитано(разговорыи расчёты) наВаси людейне способныхвидетьочевидную лож!
Разговорами ообнаружении эфирного ветра,
ВЫ лично, -занимаетесь профанацией самойидеиразработки теорий эфира. Смотрящий.
Никому Сурин в рот не заглядывает. Сотрудничество, совместная
работа присутствуют (и не только в области эфиродинамики). Развитие идей
эфиродинамики присутствует. Причём не от всех усилий Сурина ВАА в
восторге..... Будьте уверены. Совсем непонятно, почему именно
Сурин должен приглашать сюда ВАА. Пригласите сами, задайте неудобные
вопросы.... Я свои неудобные вопросы ему задал. И вовсе не на все
получил исчерпывающие окончательные ответы. Хотя бы потому, что вопросов
много и для ответа на некоторые надо провести немалую работу.. Адрес
ВАА известен... Я хоть тысячу, хоть миллион раз могу
утверждать, что эфирный ветер давно обнаружен, давно измерен вполне
экспериментально. Единственно, что вызывает сожаление это то, что не
налажена сеть регулярного измерения эфирного ветра хотя бы в объёме
пяти-семи наблюдательных пунктов. Миллер, Демьянов, Галаев, Де Мунера,
Гифт.... Вот некоторые исследователи, которые провели свои эксперименты и
показали наличие эфирного ветра. Откуда Ваша уверенность в отсутствии
этих экспериментов мне совсем непонятно. Это релятивисты делают вид, что
не знают про эти эксперименты или пытаются доказать их ошибочность...
Ну так на то и релятивисты... Есть вполне очевидная научная
ложь. Это отрицание релятивистами (точнее официальными учёными при
власти) явления эфирного ветра. Вопрос понятен. Если эфир есть. Если
эфирный ветер присутствует, то чем же эти "уважаемые" люди занимались с
1926 года.... Отвлечение. Суета вокруг предстоящего разгона РАН
вызвана именно теоретическим тупиком, в который загнала и себя и
общество "официальная" наука. И надо признать, что у действующей власти
хватило и ума и мужества начать процесс "реформирования" РАН. Иначе
просто у нас не получается. Вот начнут через колено гнуть, тогда глядишь
зачешутся. Я всем рекомендую в этом смысле посмотреть выступление
чл-корр Сона на семинаре в ЦИАМ. Ни за что не отвечать, статейки в
реферируемые журналы пописывать, а всех несогласных гнобить... Вот она
квинтэссенция деятельности РАН.... Конец отвлечения. Много
слыхал я слов о профанации идеи разработки теорий эфира. Огласите весь
список этих профанируемых теорий, пожалуйста. Я придерживаюсь теории ВАА
с различными расширениями. Всё это вошло в Стандартную модель
эфиродинамики. Этой эфирной теории разговоры об эфирном ветре никак не
вредят, только помогают.... С уважением, Михаил Сурин
|
|
Наверх
|
- Re: Черная дыра
(А.П. Васи,
3.07.2013 8:12, 3.2 КБайт)
 Re: Aether theory with experimental verification
Re: Aether theory with experimental verification
Ответ #219 - Вчера :: 13:41:39
Ivan писал(а) Вчера :: 09:29:08:Миша!
Что-то я стал замечать, что у Смотрящего стабильно идёт подход двойных стандартов.
Как у релятивистов.
Смотри:
- У ВСЕХ он требует
ссыли на работы, а сам НИКОГДА таковые по поводу своих нигилистических заявлений не представляет.
-
ВСЕ аргументы по повду наблюдений, измерений ЭВ с порога отвергает,
всячески обзывая их нехорошими словами, и далее с таинственым видом
утверждает, что ЕГО эфир обладает "супер-пупер свойством двигаться к
поверхности Земли со коростью ок. 5000 м /сек"
Хочет пообщаться с
ВАА, пусть приезжает на К-2014, так, нет, найдёт 1000 причин, по
которым "низ-з-з-з-з-я-я-я ему туда попасть" Иван.
Так и есть. Много слов о неких ошибках и всяческой профанации.
Именно о таком подходе пишет ВАА. Недаром значительная часть его трудов
посвящена вопросам философии, научной методологии... Вырвать кусок,
провозгласить его истиной и никак не рассматривать комплексно... При
этом используется известная практика релятивистов в упор не видеть
экспериментальных подтверждений эфиродинамики... Всё же либо научный подход и методология, либо религиозный....
По поводу ВАА. Только вчера с ним разговаривал. У него и почта
есть. И сайт. Причём с сайта совершенно на халяву можно скачать все
работы ВАА. А лень читать- можно видеозаписи лекций смотреть. Причём
одну такую запись сделал я сам- по продольным волнам.... А Роман Чертанов вообще накопал бездну информации.
Отвлечение.. В схватке между Правительством и РАН я на стороне
Правительства... РАН в теперешнем состоянии не может дальше
существовать. Я и с ВАА об этом говорил. Оставить по боьлшому счёту
прикладников, а вот с теоретиками, особенно от физики, давно пора
разобраться. Требуется научно-техническая революция, о которой говорит
ВАА. И не он один.... Разговор верно ставится в разрезе необходимости
прорывных технологий. От современной РАН никакого прорыва ждать не
приходится (смотри выступление Сона)... Конец отвлечения. С уважением, Михаил Сурин
|
- Re: Черная дыра
(А.П. Васи,
3.07.2013 21:25, 5.1 КБайт)
О-хо-хо прочитал нечто такое что знал только я
по анализу темпа хода часов и смещению
задержек жпс при котором постоянный
движ происходит, но что мне нравится
-
это некоторая новизна в которой внутренняя
часть катится - понравилось мне однако.
В моих моделях это тоже было, но я думаю
что в данном случаи
товарищ додумался самостоятельно.
|
|
Re: Свет и пространство и о скорости света.
|
12.09.201122:36 |
|
Альтернативное / Предположение о Звёздах
30 сентября, вс 2007 г., 18:10
Не для печати, и не лдя обсуждения.
2страница
Достигая
определенного случая Звезда эфира
внутри звезды может образовать только одну бреш в полости
сферы, это самый интирестный случай.
В результате которого появится
Нейтронная Реактивная
звезда.
Которая будет перемещаться в пространстве с огромной
скоростью, за счет выброса эфира который с краёв бреши
будет сдирать
вещество звезды, что вызывает сильное излучение
высоких энергий, и световое излучение краёв бреши.
В связи с тем что перемещение Звезды эфира внутри звезды
будет
направленно в сторону наибольшего количества вещества.
Звезда эфира переместится в противоположную сторону от бреши.
И с противоположной стороны первой бреши образуется
вторая.
И у звезды появится два луча выброса, что со временем уравновесит
"тягу" звезды, и снизит её скорость, возможно незначительное вращение.
После
чего образуется третья и четвёртая бреш выброса,
и между второй
и третьей, третьей и четвертой, - поворот звезды
по отношению к предыдущему выбросу.
И
что скорей всего приведёт к изменению формы звезды
она станет в форме выпуклой линзы.
Перемещение Звезы эфира, внутри звезды, может вызвать
вращение
звезды,
вокруг Звезды эфира, по аналогии вращения гимнастического
обруча вокруг себя.
Возможен случай что при вращении звезды
и при увеличении внутри
неё Звезды эфира
звезда взорвется по экватору.
И после взрыва приобретёт форму выпуклой линзы
и выбросы эфиро- вещества высоких энергий и излучения, будут рассположенны
хаотично
по эквтору.
| |
------------------------------
Iyri
Ветеран форума


 Вне Форума
Вне Форума

Сообщений: 6521
Грузия
Пол:

 Re: Aether theory with experimental verification
Re: Aether theory with experimental verification
Ответ #236 - Сегодня :: 12:37:52
Smotrjaщii писал(а) Сегодня :: 12:25:56:И почему увашего Гуру .эфир(втоже время!) движется к планете со скоростью =11,2км/..сферически-симметрично..
Как ЭТО объяснить?
Вы
правильно их под-бываете, но вот скорость эфира 11 км, это есть ветер.
Сам же поток эфира движется значительно быстрей. Да и, симметрия там
условная, она нарушается относительно дневной и ночной стороны.
Добавлю
еще. сам эфироворот относительно симметричный, если очертить эфироворот
то получится сфероид. Но земля смещена относительно центра сфероида на
величину радиуса ядра. Ядро как бы катится колесом по центральной точке
эфироворота.
- Re: Черная дыра
(А. В. Коновалов,
8.07.2013 0:25, 1.6 КБайт)
Это тяжело объяснить, как Нечто появляется
из Ниоткуда, уничтожает порой целые скопления звёзд, и исчезает в Никуда. При
этом чёрная дыра действительно
значительно искажает вокруг
себя
пространство-время и обладает огромным
гравитационным притяжением,
воздействуя на окружающую материю. Чёрная дыра это
то единственное, что можно назвать настоящей Пустотой Ничто, так как там, в человеческом
понимании, нет ничего материального.
(Из книги АллатРа)
Сохранить книгу:
http://sensei.org.ua/read/books/12-allatra
http://schambala.com.ua/index.php?nma=downloads&fla=stat&ids=2&idd=41
- Re: Черная дыра
(А.П. Васи,
8.07.2013 8:41, 297 Байт)
Данная тема не предназначена для бреда который
кому-то кажется.
Если кто-то может внятно сказать что-то о физике
черных дыр - это будет всё равно повтор авторского
варианта, ибо как написал автор - такие и черные дыры,
а различный надуманный себе бред - это не то.
- Re: Черная дыра
(А.П. Васи,
8.07.2013 8:53, 1.6 КБайт)
\\\Чёрная дыра
это
то единственное, что можно назвать настоящей Пустотой Ничто\\\
Вы лучше не пишите ничего, вряд-ли кому интересен бред не имеющий
физических определений и
физических обоснований.
По большому текст не физичный ибо в нем нет причинно следственной
связи, и автор ясный конь даже не знает определения черных дыр,
и какого-то считает что мнение его о черной дыре как и мнение
какого нибудь лохобоя кому-то интересно.
Например есть тысяча недалёких которые выскажут
бредятину своего воспаленного
моска о черной дыре ,
так и что с того а ничего - вся эта тысяча высказываний - так и останется
бредятиной никому не нужной,
ибо только то что сказал автор черных дыр
о них то и останется как определение, а высказывания и мнения других о черных
дырах - обреченны на уровень идиотизма.
- Re: Черная дыра
(А.П. Васи,
8.07.2013 8:53, 1.6 КБайт)
\\\Чёрная дыра
это
то единственное, что можно назвать настоящей Пустотой Ничто\\\
Вы лучше не пишите ничего, вряд-ли кому интересен бред не имеющий
физических определений и
физических обоснований.
По большому текст не физичный ибо в нем нет причинно следственной
связи, и автор ясный конь даже не знает определения черных дыр,
и какого-то считает что мнение его о черной дыре как и мнение
какого нибудь лохобоя кому-то интересно.
Например есть тысяча недалёких которые выскажут
бредятину своего воспаленного
моска о черной дыре ,
так и что с того а ничего - вся эта тысяча высказываний - так и останется
бредятиной никому не нужной,
ибо только то что сказал автор черных дыр
о них то и останется как определение, а высказывания и мнения других о черных
дырах - обреченны на уровень идиотизма.
- Re: Черная дыра
(А.П. Васи,
11.07.2013 21:39, 1.4 КБайт)
С моей точки зрения это может быть ещё
и как тест например
---------
 Re: Материя переходного состояния (МПС) - ЭФИР
Re: Материя переходного состояния (МПС) - ЭФИР
Ответ #25949 - Сегодня :: 17:09:15
Лариса Раинкина писал(а) Сегодня :: 17:00:44:Мне представляется, что понятие "бесконечность" чисто математическое, и к Реальности не имеет отношения.
Золотые
слова.
----------------
Как о мне очень малое количество людей могут понять бесконечность сознанием,
не взирая на подарок большой советской энциклопедии
в которой
постулировалась - бесконечность вселенной.
- Re: Черная дыра
(А.П. Васи,
11.07.2013 21:40, 223 Байт)
Как по мне очень малое количество людей могут понять бесконечность сознанием,
не взирая на подарок большой советской энциклопедии
в которой
постулировалась - бесконечность вселенной.
- Re: Черная дыра
(В. Р. Скенс,
12.07.2013 10:49, 200 Байт)
Из "Черной Дыры" как известно не может вырваться даже свет, за исключением пожалуй гравитонов. Может
существуют супер нейтральные объекты способные удерживать эти самые гравитоны в своем горизонте?
- Re: Черная дыра
(А.П. Васи,
13.07.2013 17:28, 247 Байт)
\\\Из "Черной Дыры" как известно не может вырваться даже свет,\\\
Читайте этот форум с самого начала,
там есть ответы на
все вопросы по черной дыре
которые Вы даже ещё не придумали.
- Re: Черная дыра
(А.П. Васи,
13.07.2013 17:41, 1.6 КБайт)

: Вчера в 13:37:34
-----------------------------------
Это-ж надо когда только
раздуплились, и начинают
понимать что восхваление постоянное своей научной группировки
и забанивание других взглядов ни к чему хорошему не приведёт,
в истории
были подобные случаи, и решались они полным
прекращением финансирования научных направлений.
Даже не удивлюсь если перестанут финансировать теор физику
вместе
с астрономией и всё передадут частникам а на что не будет
спроса снесут и порежут в металлолом.
Да вот так бывает что все идут не в ту сторону а тех
кто
предлагал другое считали альтернативщиками которых
надо банить. А альты могут обосновать причину неправильного
пути как в ошибочности большого взрыва, черных дыр,
фотонов - а релятивисты и хотели бы да не могут,
вот как например он скажет что двадцать лет уету преподавал студентам
и мозг им лайном загрузил по самые
дальше некуда, - правильно
лучше пусть альты правду скажут, в этом случаи можно и над
альтами посмеяться и идиотами их по-называть, а потом разобраться
в
том что альты предлагали и написать лекций на альтовских идеях
и со ссылкой на источник косить бабло на чтении лекций а альтам
вместо гонорара за их идеи показывать
им большой буй.
- Re: Черная дыра
(А.П. Васи,
13.07.2013 18:07, 486 Байт)
Дмитрий Вибе на сколько я с ним на форуме общался
считает написанную им лекцию полностью
на идеях других авторов - считает своей лекцией.
Собственно
я думаю что альтернативщики просто обязаны
в этой ситуации писать что запрещают использование
придуманных ими идей - при чтении платных лекций,
при чтении
лекций перед студентами обучении на платном образовании,
и при написании книг и статей без согласования с автором как текста так и
гонорара.
- Re: Черная дыра
(А.П. Васи,
13.07.2013 18:10, 1.0 КБайт)
http://www.astrogorizont.com/user_files/Image/content/img1942_pg1208_small.jpg
|
10 07/13 |
 |
 |
- Re: Черная дыра
(А.П. Васи,
13.07.2013 18:26, 871 Байт)
Каменный век , другое мнение другой подход -
альтернатива однако её надо только банить и не пускать
никуда
- не сталкиваются эти галактики,
там одна
шаровая после многократного сброса эфира
внутри своих звёзд можно сказать что взрывается
и разбрасывает все свои звёзды и разбросает их в итоге так
далеко
что они никогда не соберутся в эту галактику,
и на пути этого процесса пролетала галактика аналогичная
Андромеде или нашей, и её просто превратило давление
в полусферу, что примечательно то на каком не детском
расстоянии эту галактику превратило в сферу,
и дует так что скоро снесёт грязевой кольцо в соседней галактике,
а это значит что разбросает заодно и эту галактику,
синие звезды у полусферной галактики это звёзды
которые в основном своём объёме - более близкие к
взрывающейся галактике.
- Re: Черная дыра
(А.П. Васи,
13.07.2013 19:05, 26.0 КБайт)
Vallav
Ветеран форума


 Вне Форума
Вне ФорумаСообщений: 6846
 Re: Aether theory with experimental verification
Re: Aether theory with experimental verification
Ответ #367 - Сегодня :: 13:02:01
Alow писал(а) Сегодня :: 09:45:07:
У фотона, при взаимодействии с вакуумом, возникают как корпускулярные свойства, так и волновые свойства.
Фотон с вакуумом не взаимодействует.
Фотон в вакууме распостраняется.
И свойства у фотона при этом - чисто волновые.
---------------------------------------------------------------------
Vallav
Ветеран форума


 Вне Форума
Вне ФорумаСообщений: 6846
 Re: Aether theory with experimental verification
Re: Aether theory with experimental verification
Ответ #373 - Сегодня :: 14:24:32
Alow писал(а) Сегодня :: 13:58:52:
Фотон не взаимодействует с зарядами. Он может взаимодействовать только с вакуумом. Точнее, я активной составляющей вакуума.
А активная
составляющая вакуума - электрические заряды.
Так?
И правильно - фотон взаимодействует с активной составляющей вакуума - зарядами?
Главное в другом - взаимодействует
при этом фотон - как корпускула или как
волна...
------------------------------------------------------
Википедия
-------------------------------------------------
Квантовый характер излучения и поглощения энергии электромагнитного поля был постулирован М.Планком
в 1900 году для объяснения свойств теплового
излучения.[8] Термин фотон введён
химиком Гилбертом
Льюисом в 1926 году.[9] В 19051917 годах Альбертом
Эйнштейном опубликован[10][11][12][13] ряд работ, посвящённых противоречиям
между результатами экспериментов и классической волновой
теорией света, в частности фотоэффекту и способности
вещества находиться в тепловом равновесии с
электромагнитным излучением.
Предпринимались попытки объяснить квантовые свойства света полуклассическими моделями, в которых свет по-прежнему описывался уравнениями
Максвелла без учёта квантования, а объектам, излучающим и поглощающим свет, приписывались квантовые свойства (см., например, теорию Бора). Несмотря на то, что полуклассические модели оказали влияние
на развитие квантовой
механики
(о чём в частности свидетельствует то, что некоторые их положения и
даже следствия явным образом входят в современные квантовые теории[14]),
эксперименты подтвердили правоту Эйнштейна о квантовой природе света (см., например, фотоэффект).
Следует отметить, что квантование
энергии электромагнитного
излучения
не является исключением. В квантовой теории значения многих физических
величин являются дискретными (квантованными). Примерами таких величин
являются: угловой
момент, спин и энергия связанных систем.
Введение понятия фотона способствовало созданию новых теорий и
физических приборов, а также стимулировало развитие экспериментальной и
теоретической базы квантовой механики. Например, были изобретены мазер, лазер, открыто явление конденсации
Бозе Эйнштейна, сформулирована квантовая
теория поля и вероятностная интерпретация квантовой механики. В современной Стандартной
модели физики
элементарных частиц существование фотонов является следствием того, что физические законы инвариантны относительно локальной калибровочной
симметрии в любой точке пространства-времени
(см. более подробное описание ниже в разделе Фотон
как калибровочный бозон). Этой же симметрией определяются внутренние свойства фотона, такие как электрический
заряд, масса и спин.
Среди приложений концепции фотонов есть такие, как фотохимия[15], видеотехника,
компьютерная
томография, микроскопия высокого разрешения и измерение межмолекулярных расстояний. Фотоны также используются в качестве элементов квантовых
компьютеров[16] и наукоёмких приборов
для передачи данных (см. квантовая
криптография).
Фотон изначально был назван Альбертом
Эйнштейном световым квантом (нем.das Lichtquant).[10]
Современное название, которое фотон получил от греческого
слова φῶς,
phōs (свет), было введено в 1926 химиком Гилбертом
Н. Льюисом[17], опубликовавшим свою
теорию[18],
в которой фотоны считались несоздаваемыми и неуничтожимыми. Хотя
теория Льюиса не нашла своего подтверждения, находясь в противоречии с
экспериментальными данными, новое название для квантов электромагнитного
поля стало использоваться многими физиками.
В физике фотон обычно обозначается символом γ (греческая
буква гамма). Это обозначение восходит
к гамма-излучению,
открытому в 1900 году и состоящему из достаточно высокоэнергетических фотонов. Открытие
гамма-излучения, одного из трёх видов (α-, β- и γ-лучи) ионизирующей радиации, излучаемых известными на тот момент радиоактивными веществами, принадлежит Паулю
Вилларду, электромагнитную природу гамма-лучей доказали в 1914 году Эрнест Резерфорд
и Эдвард
Андрейд. В химии и оптической
инженерии для фотонов часто используют обозначение hν, где h постоянная
Планка и ν (греческая
буква ню) частота
фотонов. Произведение этих двух величин есть энергия фотона.

Опыт Томаса
Юнга по интерференции света на двух щелях (
1805 год)
показал, что свет может рассматриваться как волна. Таким образом были
опровергнуты ранние теории света как потока неквантовых частиц.
В большинстве теорий, разработанных до XVIII века, свет рассматривался как поток частиц.
Одна из первых таких теорий была изложена в Книге об оптике Ибн
ал-Хайсамом в 1021 году. В ней учёный представлял световой
луч в виде потока мельчайших частиц, которые испытывают нехватку всех заметных качеств, кроме энергии.[19]
Так как подобные модели не смогли объяснить такие явления как рефракция,
дифракция и двойное
лучепреломление, была предложена волновая
теория света, основателями которой стали Рене
Декарт (1637)[20], Роберт Гук (1665)[21], и Христиан
Гюйгенс (1678)[22]. Однако модели,
основанные на идее дискретного строения света, оставались доминирующими, во многом из-за влияния авторитета Исаака
Ньютона, придерживавшегося этих теорий.[23][24] В начале XIX века Томас Юнг и Огюстен
Френель
наглядно продемонстрировали в своих опытах явления интерференции и
дифракции света, после чего примерно к 1850 году волновые модели стали
общепринятыми.[25] В 1865 году Джеймс
Максвелл предположил в рамках своей теории[26], что свет это электромагнитная
волна. В 1888 году эта гипотеза была подтверждена экспериментально Генрихом Герцем,
обнаружившим радиоволны.[27]
-------------------------------------------------
www.socratus.com/rus/kvant-rus.htm
Квант света привилегированная
частица.
Надо выделить изучение кванта света в особую область.
1
Масса покоя всех частиц имеет какую-то конкретную величину.
Только масса покоя кванта света равна нулю.
Все частицы могут двигаться с любой скоростью меньше световой.
Только квант света двигается в Вакууме с постоянной скоростью
с=1.
Скорость движения других частиц зависят от системы отсчета.
Скорость кванта света не зависит от системы отсчета.
---
В 1924 году Луи дэ Бройль
высказал предположение, что все частицы имеют двойственную природу. Поэтому
сейчас учёные утверждают, что протон (атом) также обладает как корпускулярными,
так и волновыми свойствами. Волновые свойства протона были обнаружены при
пропускании протона через кристаллическую решётку. Возникшая при этом дифракционная
картина была принята учёными, как факт, свидетельствующий об обладании протоном
волновыми свойствами. Но представь себе, дорогой читатель, что в озеро бросили
камень весом 60 килограммов. Потом в озеро прыгаю я. Учёный, сидящий на
берегу этого озера, изучает волны и приходит к выводу: так как волны идентичны,
то и эти два тела, создающие волны, также идентичны. Но ты понимаешь, дорогой
читатель, что есть разница между автором этих строк и камнем. А кристаллическая
решётка - это то озеро, в которое падает и электрон, и протон. А потом учёный
изучает образовавшуюся дифракционную картину и пытается объяснить внутреннюю
структуру частиц. Не смешно ли?
------------------------------
Квант света привилегированная частица.
Надо выделить изучение кванта света в особую область.
1
Масса покоя всех частиц имеет какую-то конкретную величину.
Только масса покоя кванта света равна нулю.
Все частицы могут двигаться с любой скоростью меньше световой.
Только квант света двигается в Вакууме с постоянной скоростью
с=1.
Скорость движения других частиц зависят от системы отсчета.
Скорость кванта света не зависит от системы отсчета.
--------------------------------------
Как говорится
тест на внимательность - найди нескладушки
в базовых определениях.
- Re: Черная дыра
(А.П. Васи,
13.07.2013 19:08, 1.7 КБайт)
То́мас Юнг -Википедия
"Его идеи вызвали
возражения английских учёных; под их влиянием
Юнг отказался от своего мнения. Однако в трактате по оптике и акустике
Опыты и проблемы по звуку и свету (1800) учёный вновь пришёл к волновой
теории света и впервые рассмотрел
проблему суперпозиции волн. Дальнейшим развитием этой проблемы явилось
открытие Юнгом принципа интерференции (сам термин был введён Юнгом в
1802 году).
В докладе
Теория света и цветов, прочитанном Юнгом Королевскому обществу в 1801
(опубликован 1802), он дал объяснение колец Ньютона на основе
интерференции и описал первые опыты по
определению длин волн света. В 1803 году в работе Опыты и исчисления,
относящиеся к физической оптике (опубликована 1804) он рассмотрел
явления дифракции. После классических
исследований О. Френеля по интерференции поляризованного света Юнг
высказал гипотезу о поперечности световых колебаний. Он разработал также
теорию цветного зрения, основанную
на предположении о существовании в сетчатой оболочке глаза трёх родов
чувствительных волокон, реагирующих на три основных цвета."
"В
1807 году в двухтомном
труде Курс лекций по натуральной философии и механическому искусству Юнг
обобщил результаты своих теоретических и экспериментальных работ по
физической оптике (термин ввёл
Юнг) и изложил свои исследования по деформации сдвига, ввёл числовую
характеристику упругости при растяжении и сжатии так называемый модуль
Юнга. Он впервые рассмотрел механическую
работу как величину, пропорциональную энергии (термин ввёл Юнг), под
которой понимал величину, пропорциональную массе и квадрату скорости
тела."
- Re: Черная дыра
(В. Р. Скенс,
17.07.2013 5:47, 282 Байт)
Прочитал первые 12 страниц бреда, дальше нет смысла читать обозлённый бенефис г-на "гения" А.П. Васи под годольерским девизом "кто не со мной- тот против меня"

- Re: Черная дыра
(А.П. Васи,
21.07.2013 10:50, 1.2 КБайт)
О Науке, космосе и бытие
1:06, 21 июля 2013==========================================================================================
Описание:
Русские учёные уже давно знают - теория относительности Эйнштейна -
фикция, созданная для того, чтобы увести науку в сторону поддержки
паразитической системы, для того чтобы пресечь использование
человечеством свободной энергии. Основа мироздания - первичные материи.
Мало
кто знает, что Д. И. Менделеев был одним из последних всемирно
известных русских учёных конца 19-го века, кто отстаивал в мир...
--------------
С моей точки зрения автор слишком эмоционально выступает, более логично было-бы
пригласить кого-то кто просто-бы прочел текст, и лично как по мне больше
половины лекции - автор говорит ни о чём, и с многим я не согласен - но
по большому
счёту если переделать эту лекцию то можно её и по телевизору показывать, в том виде в котором она есть её по телевизору показывать нельзя.==========================================================================================
- Re: Черная дыра
(А.П. Васи,
22.07.2013 7:28, 1.1 КБайт)
\\\Прочитал первые 12 страниц бреда, дальше нет
смысла читать
обозлённый бенефис г-на "гения" А.П. Васи под годольерским
девизом
"кто не со мной- тот против меня"
 \\\
\\\
Это у Вас у вашего мозга защитная система сработала,
он уже заполнен
новой информацией.
А я Вам не запрещаю посещать форумы махровых релятивистов,
там одни и те-же идеи обсуждают по сто лет и решают одни
и те-же задачи
по сто лет и только хвалят друг друга.
А всех других с другими точками зрения там посылают
в даль или просто банят а форум забалтывают и закрывают.
--------------------------------------------------
Горизонты науки о Вселенной
Науки о вселенной - гипотезы, идеи, обсуждения.
---------------------------------------------------------------
- Re: Черная дыра
(С. М. Андрейчук,
4.08.2013 10:42, 1.1 КБайт)
Фотон ограничен в своей скорости 300.000 км/с проницаемостью пространства. На данной скорости фотон проявляется как феномен, т.е. как СВЕТ. Проницаемость пространства - это
совокупность электромагнитных и гравитационных полей. Это можно сравнить с лестницей: чем больше высота ступеньки, тем медленнее происходит подъём по ней, чем меньше высота
ступеньки - тем быстрее подъём. То же самое и с проницаемостью: чем сильнее электромагнитное и гравитационное поля, тем быстрее фотон преодолевает определённое расстояние,
т.е. тем больше скорость. Но в то же время при скорости больше 300.000 км/с фотон перестаёт проявлять себя как феномен, т.е. теряет своё свойство быть видимым. Исходя из этого
мы видим на месте дыры не огромную звезду, а чёрное пятно. Со временем, когда масса этой звезды достигнет критической и проницаемость пространства вокруг этой чёрной звезды
будет таковым, что скорость фотона снизится до критической, т.е. до 300.000 км/с и тогда произойдёт вспышка чёрной звезды, котрая осветит всё пространство нашей галлактики
и возможно другие звёзды на её фоне будут всего лишь чёрными точками...
- Re: Черная дыра
(А.П. Васи,
4.08.2013 15:49, 54 Байт, ответов: 1)
Шел бы ты старче от сюда со своим старческим маразмом.
- Re[2]: Черная дыра
(С. М. Андрейчук,
6.08.2013 15:26, 991 Байт)
Уважаемый А.П. Васи, осуждение других людей по сути - это признание своей морали в качестве эталона, а любое оскорбление или агрессия - это производные страха. Я не поленился
и почитал форум. Пожалуй, с вашей репликой от 05.01.2011 20:55 я соглашусь, а в остальном я усмотрел только эмоции. Возможно в своё время вас не поняли в учёных кругах и вы
остались на уровне школьного физика, в хорошем смысле слова! Считаю, что перевоспитать взрослых дядей куда сложнее, чем заложить правильный фундамент мышления в подрастающее
поколение. Более того, считаю это более почётным! Хотел бы обратить ваше внимание на то, что форумы создаются не для того, чтобы друг друга поливать оскорблениями, а для того
чтобы обмениваться своими мыслями и мнениями. Уверен, что большинство людей на этом форуме - это люди думающие, и не важно на какой эволюционной ступеньке они стоят. Важно
услышать друг друга и может быть даже заинтересовать других людей в изучении темы, обсуждаемой на форуме.
- Re: Черная дыра
(А.П. Васи,
6.08.2013 20:56, 2.5 КБайт, ответов: 2)
Возможно я по отношению к Вам не правильно высказался,
приношу извинения.
Я предполагал что один собеседник с другой ветки зашел под другим именем.
А
если Вы внимательно читали - то фотоны я отменил
.
Бывает и такое в физике были фотоны а потом потеряли физический смысл
при примитивном опыте.
---
| Re: Свет и пространство и о скорости света.
|
6.04.201113:49 |
|
Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а говорится что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою скорость что
наблюдается например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица которая потеряла скорость, просто так взять и
при вылете из стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами. Так что фотон
как частица - выдумка чистой воды.
Вывод -
в пространстве распространяются колебания среды, и световое
излучение не движется а образуется от взаимодействия колебаний
среды и материала, как в 1800 году говорил
Томас Юнг.
Так что все что написано в астрофизике без учета среды - к
сожалению не правильно.
Это подарок Дмитрию Вибе, это не будет опубликовано два
три года.
Дмитрий Вибе может и дальше учить студентов тому что безвозвратно
устарело, и тому что им никогда не пригодится.
Так уж Дмитрий Вибе запрещал обсуждать
эфир пока его не докажут что он есть,
и тех кто эфиром занимается называл альтами и давал им очень не лестные определения. |
---
- Re[2]: Черная дыра
(С. М. Андрейчук,
7.08.2013 11:41, 1.3 КБайт, ответов: 1)
Исходя из вашего вывода возникает закономерный вопрос: что является причиной этих возмущений в результате чего среда (эфир) проявляет себя в виде феномена или иначе СВЕТА?
И в так называемой "чёрной дыре" этих колебаний эфира нет, поэтому он (эфир) и не проявлен как свет. Но почему этого эфира очень много вокруг звёзд? Они по сути
являются источниками колебаний среды (эфира)? Значит эфир неравномерно распределён в пространстве. Возможно в пространстве эфир распространяется по какому-то закону, например,
спирали (моё предположение) и если звезда находится на линии максимальной концентрации эфира, то она проявлена как звезда, но стоит ей отклонится от этой линии, где концентрация
эфира минимальна, то и звезда просто становится невидимой, т.е. не проявляет себя как источник света. Боюсь предположить, что нормальное состояние звезды - находится на линии
спирали эфирной концентрации и поэтому она максимально пытается притянуть к себе эту линию создавая вокруг себя подобие воронки, или то,что мы называем чёрной дырой. Ну,
а центр Галлактики просто по своим физическим свойствам не может выйти на эту спираль, потому что размеры её таковы, что она находится в состоянии "неопределённости".
Что-то я сам себе уже кажусь сумасшедшим...))
- Re[3]: Черная дыра
(С. М. Андрейчук,
7.08.2013 19:30, 434 Байт)
Думаю, что только определённая частота колебания среды, подобно модулирующему сигналу, несёт в себе какую-либо информацию от вибрирующего источника, расшифрованную нашим
мозгом как свет, тепло и, может быть, даже как какие-нибудь мыслеобразы. Считаю, что не любая частота колебания среды (эфира) является светонесущей. Хотя могу ошибаться. Возникает
вопрос: это конкретная частота или всё-таки определённый диапазон частот?
- Re: Черная дыра
(А.П. Васи,
7.08.2013 19:59, 1.0 КБайт)
Всё что Вы можете придумать я уже давно написал
ответы.
На всё что Вы пишите мои ответы давно есть.
Прежде чем не прочтёте всё от начала до конца
прошу
Вас вопросов не задавать, по той причине что
когда прочтёте до конца - то вопросов у Вас не будет.
www.astronet.ru Форумы
Астрономия и Интернет
- Re: Черная дыра
(А.П. Васи,
7.08.2013 20:28, 5.4 КБайт)
Поймите правильно я начинал обсуждать похожие на Ваши вопросы
на форумах лет десять назад, сейчас у меня просто есть все
с моей точки зрения основные ответы
на вопросы в космологии.
И мне с Вами обсуждать нечего.
У Вас теперь задача самостоятельно придумать что-то
другое чем у меня не залезая в моё авторство.
Меня как-то было вежливо послали на сайте,
за что я и заблокировал для космологов свои идеи.
И в принципе думаю писать на уровне закрытого кода,
это когда
физическое определение даётся только в рамках
статьи, чтобы практически невозможно было использовать
физические определения в статье про галактики для
написания
статьи про звёзды например.
---------------------------------------
Ответ #37 : 29.06.2009 [09:27:31]
Если у Вас есть вопросы, я просто знаю кто ещё
эфиром занимается, так там с формулами
у них
и с расчётами, и в общем, в том же ключе что я
рассказал.
Так, может, пускай они и приходят?

--------------------------------------------------------------------------------
Ответ #38 : 29.06.2009 [10:50:32]
CADET
\\\Так, может, пускай они и приходят? \\\
Конечно прийдут, лет через 30-70, и расскажут астрономам
как космос устроен.
Я в общем думал что на астро форумах, эфирные теории хоть
как-то обсуждались, в принципе если астрономы настаивают
совместно с теориями господина Эйнштейна,
на том что межзвёздное пространство
- есть пустота точнее вакуум то так пусть и остаётся.
------------------------------------------------------------------------
Ответ #40 : 29.06.2009 [12:27:56]
-------------------------------------------
Ответ #41 : 29.06.2009 [15:16:30]
Дмитрий Вибе
\\\Так, может, через 30-70 лет и обсудим?\\\
Я в общем думаю написать фантастический рассказ,
в котром
будут элементы атрофизики и рассказанно о эфире.
Будет смешно если будут делаться ссылки на фантастический рассказ.
\\\Обсуждались, как
без этого:
http://www.astronomy.ru/forum/index.php/topic,30971.0.html\\\За адрес спасибо.
Там я не нашел модели эфира в пространстве.
Но желаю успехов сделать лучше моей,
не залезая в моё авторство.
- Re: Черная дыра
(О. Е. Коробейникова,
7.08.2013 21:25, 142 Байт)
www.liveinternet.ru/users5276115/post/286324507/ Живем в "черной дыре.в плену у Крона/бога времени/ Скоро вырвемся ,а то холодно и темно.
- Re: Черная дыра
(О. Е. Коробейникова,
7.08.2013 21:42, 108 Байт)
Живем в "плену..у Крона/бога времени/. Надеюсь скоро вырвемся из этой черной дыры.А то холодно и темно.
- Re: Черная дыра
(А.П. Васи,
7.08.2013 21:44, 1.1 КБайт)
Я надеюсь Вы понимаете что только хамы
при полном попустительстве как модераторов
так и владельцев сайта
могут сказать на предложение пригласить своих знакомых
с другого форума пообщаться здесь,
- мол пусть они приходят а ты у- буй от сюда.
Ну и совет модератора пообсуждать через 30-70 лет, в форме вопроса
при его невыполнению аналогичен забаниванию.
Там Вибе всег зашугал по полной, все боятся его
ибо он сразу банит и по барабану, а я там ещё прочитал
форум как радуются тому как жестко альтернативные мнения
забаниваются на этом форуме - бабене, альтернатива для них
это нечто плохое и ужасное, хотя по факту
это просто другая точка
зрения - и в данное время точка зрения не финансируемых
энтузиастов в космологии, вот я прихожу с работы,
и несколько часов уделяю
космологии, и меня никто не
финансирует, - а у них это их работа как правило
за которую они получают зарплату, и могут вообще ничего
не придумывать нового
так как им космология до лампочки , от этого их зарплата
не увеличится, но забанить другую альтернативную точку зрения для них в радость.
- Re: Черная дыра
(А.П. Васи,
7.08.2013 22:54, 4.4 КБайт)
| Re: Свет и пространство и о скорости света.
|
13.06.20122:45 |
|
Рассказ
Фантастический сон о городе физиков.
Приснился город физиков, он состоял из одной центральной улицы,
которая разделяла
пустынные дикие просторы
классической физики,
и плодоносящие сады релятивистской физики.
По пустынным просторам классической физики скитались какие-то
голодранцы несколько было по
двое и по трое но в основном одиночки,
ходили что-то писали на песке, кое кто из альтернативщиков проводил
какие-то опыты на костре пока готовили еду.
Практически
все альтернативщики периодически и с разным успехом
участвовали в форумах
"скай-тюх" и "звездомер".
Эти участки дороги отличались разметкой
улицы, и наличием забора
со стороны релятивистов на "звездомере", забор на "звездомере" не
для того чтобы альты не лазили, а для того чтобы
сомневающиеся
релятивисты не смогли убежать от модераторской порки. Возле форумной
разметки с обеих сторон периодически стояли толпы зевак и приходили
ораторы
то с той а то с другой стороны.
На "скай-тюхе" демократии было побольше и все орали друг на друга и периодически
рвали на себе одежду и бросали через
дорогу, там в неё вышмаркивались и бросали
обратно.
На "звездомере" рерятивисты после меряний телескопами и после обеда в гос
столовой, пододвигались
и подкатывались на своих креслах к дороге,
чтобы лучше слышать.
По средине уличной разметки "звездомеровского" форума стоял - плёточных
шмаганий
мастер, - несравненный модератор Би-Бе. Он славился тем что от
прямых вопросов уходил своими ответами в интеллектуальное бегство.
От альтернативщиков он требовал
дать ему посмотреть тех паспорт на эфир,
и предоставить опыты за которые можно нобелевскую получить ещё вчера.
Естественно запрос на релятивистский тех-паспорт
на причину скорости света вызывает
шатание в креслах и бубнение релятивистов о том что в нем нет смысла,
а смысл есть в паспорте на эфир.
Так собственно
в непонимании и смотрели друг на друга.
Продолжение
Рассказ
Фантастический сон
о городе физиков.
Дальше у дороги релятивисты поставили трибу своих достижений
с трубными
фанфарами.
На фанфарах
разные надписи, - без которых релятивизм
был бы невозможен.
Чтобы уйти от эфира придумали фанфары ---- "вакуум"
Чтобы уйти от света который был
в эфире, придумали фанфары --- "фотон"
Так как не смогли придумать
куда тепло девается от звезд,
придумали фанфары
- ---"большой взрыв",
тепла у звезд оказалось много
и чтобы поглощать ещё тепло
от звезд придумали фанфары -
--- "черная - дыра"
а энергии оказалось ещё больше,
придумали фанфары ---" ускоренное расширение",
и непонятно
чем притягивается
токмо по два тела придумали фанфары --- "гравитация".
А на против трибуны с фанфарами располагался зрительный зал
смеха
релятивистов, так как на трибуну с фанфарами периодически
забегали одичавшие альты, они прибегали с той стороны дороги,
со стороны классической физики. И когда
одичавшие альты в своих
возмущенных речах использовали слова исключительно для
релятивистов, и они совпадали с надписями на фанфарах, то вместо
слов они
дули в фанфары релятивистов.
Некоторые дикие альты целые релятивистские концерты
устраивали и выдували фуги , гораздо
лучше некоторых релятивистов. Релятивисты
особо сильно
смеялись когда дикие альты использовали все слова.
Вдруг зависли в воздухе удары плетью, мастер Би-Бе на "звездомере"
шмагал
всех подряд а чтобы уважали.
Собственно так и жили, классическая сторона - пустыня бедности,
и релятивистские фруктовые сады с шоколадными кабинетами.
По дороге то там то там пробегали бобры, их по дружески били
телескопами с любой стороны улицы.
Вот я и проснулся.
|
- Re: Черная дыра
(А.П. Васи,
7.08.2013 23:05, 772 Байт, ответов: 2)
\\\Фотон ограничен в своей скорости 300.000 км/с
проницаемостью пространства. На данной скорости фотон проявляется как
феномен, т.е. как СВЕТ. Проницаемость пространства - это
совокупность электромагнитных и гравитационных полей\\\
\\\И в так называемой "чёрной дыре"
этих колебаний эфира нет\\\
Как говорится я релятивиста узнаю по лексике.
Так что для меня Вы релятивист который хочет перейти
на альтернативные темы,
и Вы явно стараетесь держать
нос по ветру, а тут у Вас такое огорчение - что мол
всё то есть, - а взять нельзя, надо придумывать что-то
самостоятельно, а
этому Вас никто не учил - прямо самозаклин какой-то.
- Re[2]: Черная дыра
(С. М. Андрейчук,
8.08.2013 18:58, 441 Байт, ответов: 1)
Вы меня процитировали и назвали релятивистом. Когда я познаю мир, то ищу свой путь. Соглашусь с вами в одном: поднимаясь по древу познания я наступаю на те ветки, которые
крепче - не важно релятивистские они или альтернативные, главное чтобы я поднимался вдоль ствола, а не полз по одной из веток, которая в конечном итоге может привести к обрушению...Дайте
мне время, я обязательно изучу вашу точку зрения и нам будет, что обсудить...))
- Re[3]: Черная дыра
(С. М. Андрейчук,
14.08.2013 14:44, 3.4 КБайт)
Это всего лишь моя гипотеза, которая зародилась под влиянием гипотезы А.П. Васи.
Ещё древние мудрецы указывали на наличие стихий, таких как земля, вода, огонь и воздух. По аналогии, весь материальный
мир символизирует землю, а эфир, о котором Вы говорите воду. Пришло время назвать третью стихию стихию огня. Вы придумали Звезду Эфира, а я называю следующую ипостась
Дух Света. Это ментальный план (назовём его третьим планом), в отличие от Звезды Эфира, которая пребывает на тонком плане (назовём его вторым планом). Следовательно, материя грубый план (назовём его первым планом).
Дух Света
не может взаимодействовать с материей напрямую без своего посредника эфира, также и эфир является абсолютно проницаемым для материи без Духа Света. Взаимодействие Духа Света
с эфиром создаёт Звезду Эфира и это облачение сопровождается реакцией понижения температуры, т.е. охлаждением. Взаимодействие Звезды Эфира с материей сопровождается выделением
тепла. Материя консолидируется вокруг Звезды Эфира, и это объясняет причину потенции, которая в последующем разворачивает материю, усложняя её формы. Звезда Эфира увеличивается
в размерах, но одновременно увеличивается и материальная оболочка (Звезда Физики) вокруг неё. На каком-то этапе наступает равновесное состояние между массой Звезды Эфира и
окружающей её материальной оболочкой. А далее чаша весов склоняется в сторону Звезды Эфира, т.к. она становится тяжелее Звезды Физики и начинается старение материи (планета
становиться более засушливой, человек более дряхлым). В конечном итоге, материальная оболочка перестаёт выполнять свои функции и Звезда
Эфира покидает своё материальное тело. Звезда Эфира увеличивает свою массу быстрее ещё и потому, что Дух Света тоже растёт и Он, в большей степени, провоцирует ситуацию со
старением материальной оболочки, потому что рост Звезды Эфира подталкивается ростом Духа Света.
Свет
в чистом виде от Духа Света не проявляется на материальном плане. Он может проявиться только через своего посредника эфирный план. Самый огромный Дух Света в нашей Галактике
сосредоточен в её центре, Звезда Эфира этого центра набирает массу материального плана, сопоставимую своему эфирному телу Звезде
Эфира. Пока этой массы недостаточно центр Галактики остаётся самым холодным местом в нашей Галактике, но постепенно идёт разогрев. Этот процесс не будет носить взрывной характер.
Скорее всего, этого будет происходить постепенно и свет от центра Галактики будет становиться всё интенсивней и интенсивней, а материальная оболочка (Звезда Физики центра
Галактики) всё горячей и горячей.
Хочу предположить, что если Дух Света человека будет
развиваться более интенсивно, то уже в этой жизни наша материальная оболочка (Звезда Физики) начнёт светиться подобно солнечному свету. При этом температура материальной оболочки
увеличится и скорее всего сама материя качественно выйдет на новый уровень, т.е. будет более пластичной.
Вот как-то так...))
- Re: Черная дыра
(А.П. Васи,
14.08.2013 21:03, 814 Байт)
Вы не правильно трактуете звезду эфира,
это просто эфир конденсированный в твёрдом
и жидком состоянии, а \звезда физики\ - это старое
название которое я
уже не использую, по причине
того что это практически все звезды и планеты -
а точнее все тела у которых есть притяжение,
следовательно нет смысла в этом
названии.
Выражение Дух Света - это вообще какой-то
абсурд. И если что-то пишите, - то начинайте
с оглашения того что Вы лично придумали и зачем,
и что именно решает эта придумка. Вы я так понимаю ещё
не всё прочитали, у меня решены все вопросы.
И если Вы космологией занялись то Вы - космолог, -
а следовательно моими придумками Вы не пользуйтесь,
придумывайте что-то своё. Или ждите когда я напишу
статью и тогда на неё ссылайтесь.
- Re: Черная дыра
(А.П. Васи,
14.08.2013 21:05, 79 Байт, ответов: 1)
Если честно то у Вас глупость несусветная бессмысленная
и бесполезная.
- Re[2]: Черная дыра
(С. М. Андрейчук,
14.08.2013 21:54, 820 Байт)
Глупость - это не логичность и не соответствие здравому смыслу. Мне кажется, что если постоянно задумываться о логике и о здравом смысле, то можно всю жизнь топтаться на одном
месте. Иногда человек должен мыслить не стандартно и совершать не стандартные поступки. Вас ведь тоже релятивисты называют глупым человеком, но Вы ведь от этого не поглупели?
А к вопросу использования своей терминологии - не думаю что это всегда верное решение. Мне Ваша Звезда Эфира вполне по душе. Но если Вы принципиально против, то я найду название
этому понятию. Важно не это, важно то что мне Ваша идея более-менее понятна и близка. Почему я не могу её развивать в альтернативном от Вашего направлении. Я же не присваиваю
ей статус "моё личное", а прямо говорю, что эта гипотеза зародилась под влиянием Вашей гипотезы...
- Re: Черная дыра
(А.П. Васи,
14.08.2013 22:36, 1.1 КБайт)
Мне до лампочки то что Вы пишите.
Вы не физик и не космолог, Вы халявщик
и хотите быстрой хаявной славы.
Вы даже не можете дать определения физического,
не можете ничего обосновать, Ваш текст
дайте почитать любому - Вам скажут
что это идиотизм не имеющий смысла.
У Вас даже не хватает интеллекта дать
определение
моих идей в Вашем понимании, чтобы для читающего
устранить семантический шум, я так понимаю что то
что я говорю Вы в принципе не понимаете, по
причине
Вашего большого возраста, - Вы естественно можете
до одури стучать по клавиатуре с претензией на физичность
печатаемого Вами текста - но могу Вам
сказать что у Вас
нет даже умения логически сложить логическую
последовательность, Вас этому никто и никогда не учил,
а Вы думаете что вот так и сразу в
науку, и всем рассказывать
как приседать и сколько раз и как делать ку красиво.
Ну чё слабо написать что Вы лично сами придумали и зачем -
вот то-то,
общение с Вами прекращаю. Мои идеи не
трогайте - придумайте свои, или попросите кого-то чтобы
Вам названия дали Ваших идей, если Вы сами не в состоянии.
- Re: Черная дыра
(А.П. Васи,
14.08.2013 23:04, 979 Байт)
\\\Но если Вы принципиально против, то я найду
название
этому понятию. Важно не это, важно то что мне Ваша идея более-менее
понятна и близка. Почему я не могу её развивать в альтернативном от
Вашего направлении. Я же не присваиваю
ей статус "моё личное", а прямо говорю, что эта гипотеза зародилась под
влиянием Вашей гипотезы\\\
У меня не гипотеза и не теория, у меня следующая - модель, в которой больше семи теорий.
Вы хоть внимательно прочтите
эту ветку форума сначала, - там я писал
про черные дыры, когда один юзер вместо того чтобы войти в историю
навечно с рентгеновскимизвёздами, назвав их и дав им
определение,
так этот юзер написал триста статей о черных дырах с рентгеновскими
свойствами, даже не понимая того что - черные дыры - будут в веках
исключительно
в авторском определении, - я даже не знаю как
такую буету я тут Вам объясняю, это ведь и так - ясный конь.
- Re: Черная дыра
(А.П. Васи,
14.08.2013 23:22, 426 Байт, ответов: 1)
- Re[2]: Черная дыра
(С. М. Андрейчук,
15.08.2013 8:06, 627 Байт)
Хочу сказать, что я не страдаю тщеславием и мне уж тем более не нужна чужая слава - я просто делюсь своими мыслями. Я вижу, что Вы на верном пути, но Вам
мешает одно "но" - это то, что Вы пытаетесь свои теории (уверен, что у них есть будущее), которые относятся к тонкому плану измерить физическим инструментом.
Это равносильно попытке поймать солнечного зайчика на стене, чтобы понять его сущность. Если Вам нравится монолог на форуме, ну что ж... В любом случае я Вам
благодарен за Ваши мысли, есть над чем поразмышлять. Жаль, что диалог на этой ветке всегда заканчивается монологом... Удачи Вам и дальнейшего озарения!
- Re: Черная дыра
(А.П. Васи,
18.08.2013 14:33, 2.0 КБайт)
\\\
Весьма нашумевшая новость:
С
помощью HST обнаружено, что 11,5 млрд. лет назад галактики мало
отличались от нынешних - т.е. были неправильные, спиральные,
эллиптические. Но это не самое странное - оказалось, что уже тогда
встречались старые эллиптические галактики, спектр которых указывает на
весьма преклонный возраст входящих в состав звёзд! Другими словами,
получается, что в среднем, галактики за 11,5 млрд. лет нисколько
продвинулись в своей эволюции!
Оригинал:
Galaxies
Had Mature Shapes 11.5 Billion Years Ago На русском:
Древнейшие
галактики подозрительно похожи на нынешние\\\
Я вот всётаки не понимаю астрономов учат преподаватели
со всем соглашаться что их учили, и не учат
думать самостоятельно,
и явно не учат всякую нескладушку и неудачные попытки в строительстве
астрономических основ прошлых поколений в которые не выдерживают
никакой современной критики.
Естественно я догадываюсь почему боятся, помнят Сталина,
который ученных по простому в стиле - критикуешь то предлагай альтернативу,
предложил тогда воплощай в устройство, сделал устройство - неси ответственность
за его работу,
- и исходя из этого естественно лучше даже не критиковать
никого. Сталина давно нет а критиковать боятся будут наверное ещё долго.
- Re: Черная дыра
(А.П. Васи,
18.08.2013 22:14, 940 Байт)
Колонка
Дмитрий Вибе
Может быть, астрономия в школе всё-таки нужна?-------------------------
Даже в мои школьные годы так как преподавалась
астрономия то лучше бы не преподавали её вообще.
И причин тому - с моей точки зрения три,
первое книжки содержат очень сильно устаревшие
космологические
взгляды, многое противоречит здравому смыслу
вторая причина написаны скучно и третья причина преподавали
астрономию любые преподаватели любых предметов.
С моей точки зрения отмена астрономии правильный
шаг на семьдесят процентов.
- Re: Черная дыра
(А. А. Волков,
19.08.2013 12:12, 1.6 КБайт)
Уважаемый А.П. Васи, Вы не представляете на сколько Вы правы
в своей догадке:
...Другими словами, получается, что в среднем, галактики за
11,5 млрд. лет нисколько продвинулись в своей эволюции!...
Зарождение, развитие и исчезновение Галактик подчиняется
однотипному процессу - Закону. Этот Закон включает в себя
принцип взаимодействия Сил образующих Космическое Пространство.
Современная Космология, основанная на ущербных представлениях
"древних", продолжает их традиционные взгляды. А именно:
"...Существует Пространство..., в Пространстве существуют Тела...,
Тела находятся в движении..."
Остаётся только надеяться на то, что современные исследования
"полярных миссий" космических аппаратов, посылаемых к планетам
Солнечной Системы, результаты обработки данных с "Вояджеров",
направленных к "полюсам" Системы и результаты исследования
электромагнитных процессов, происходящих на границе жидкого ядра
и мантии планеты, состыкуются ))) в МАС, а не останутся секретом
в "аналах" JPL NASA
Только после этого будет признано то, что пока ошибочно
замалчивается. А именно:
"...Существует Пространство...,
в Пространстве существует Движение...,
в результате взаимодействия Движений образуются Тела..."
Закон движения в Пространстве ограничен в своих вариантах.
А потому и то "разнообразие" Галактик, сколь их ни классифицируй,
так же ограничено определённым числом )))
До "сейчас", и в настоящее время, и после...
- Re: Черная дыра
(А.П. Васи,
21.08.2013 20:40, 1.4 КБайт)
Да уж я такое не так часто вижу, - ужастики
астромышления как для меня.
А для кого - астрономия в прекрасном её виде.
Если альтернативщик будет
подобные идеи
рассказывать - то это таки альтернативщик,
но с идеями столетней давности.
--------------------------
Слабонервных альтернативщиков
- большая
просьба не смотреть это.
-------------------
vk.com/club3738734
Журнал
"Земля и Вселенная" Астроном Дмитрий Вибе о протозвездах, открытии спектроскопии и гравотурбулентной модели звездообразования
- Re: Черная дыра
(А.П. Васи,
24.08.2013 13:55, 887 Байт)
Re:
Чёрные дыры - дыры в пространстве или в науке?
------------------------
Прочитал
стр.23 и мне лично как-то
неудобно и жалко их, на столько они забрели
своими выдумками практически в идиотизм,
и альты уже к ним не придут и не вставят
им интеллектуальный пистон - чтобы они
вышли из надуманного себе мира,
с претензией на физичность,
которому их накручивали десятилетиями.
А альтов
то они в итоге зря прогнали,
самостоятельно они не выберутся из этого
болота, выходить то надо из него по-одному
а коллективизм им этого не даст,
они
то только в кругу релятивизма себя хорошо
чувствуют - типа умные - как все.
- Re: Черная дыра
(А.П. Васи,
24.08.2013 14:49, 1.1 КБайт)
Как-то давно видел в ванной залитый пол прозрачный
с морскими камнями и морской тематикой.
Собственно что было очень заметно так это
очень высокая прозрачность
эпоксидной смолы
и практически полное отсутствие желтизны.
И вот что я придумал.
Если взять листовой стеклокарболит прозрачный,
толщиной миллиметра три,
вырезать из него два
круга диаметром в полтора метра, или метр, и
сделать кольцо с бортиками из стали толщиной
миллиметров двадцать, и в это кольцо вкладывается
в горизонтальном положении два круга, между
кругами на краю сверлится дырка миллиметра
три в диаметре и в неё вставляется трубка,
всё делается герметично,
и так чтобы потом
можно было разобрать.
Сначала откачивается воздух между карболитом,
после этого туда закачивается прозрачная эпоксидная смола,
медленно
но уверенно.
По скольку края капитально зафиксированы,
то изначально получается длиннофокусная линза,
Естественно здесь надо чтобы не получилось
ситуации
которая бывает у эпоксидной смолы и орг стеклом,
это когда после затвердевания эпоксидной смолы она
от орг стекла отталкивается.
- Re: Черная дыра
(А.П. Васи,
25.08.2013 12:44, 1.5 КБайт)
 Re: Новый взгляд на физику частиц.
Re: Новый взгляд на физику частиц.
Ответ #5 - Сегодня :: 11:48:54
---------------------
В принципе достаточно просто понимать
что любые физические
теории это фантазия и
фантастика. Есть естественно и изначально
слабые такие как большой взрыв, в котором излучение определённого вещества с определённой длинной
волны с какого-то решили назвать колебанием пространства, хотя на самом деле излучает определённое вещество и это известно с 1941года.
Лично я думаю что если бы
в России не было РАН,
то на неё изготовители наукоёмкой продукции и не надеялись бы, и у них бы были свои институты при заводах которые бы решали нужные научные вопросы,
как собственно это есть например в штатах.
А то что фундаментальная наука пошла в непонятном направлении так этому причина известна - финансировали только одни
направления, а альтернативные другие идеи посылали в пешее эротическое путешествие.
- Re: Черная дыра
(А.П. Васи,
25.08.2013 22:31, 2.2 КБайт)
http://www.veinik.ru/science/anomal/article/919.html
\\\ "Реликтовое излучение"
- космическое электромагнитное излучение, приходящее на Землю со всех
сторон неба примерно с одинаковой интенсивностью и имеющее спектр,
характерный для излучения абсолютно черного тела при температуре около
3К (3 градуса по абсолютной шкале Кельвина, что соответствует 270С).
При такой температуре основная доля излучения приходится на радиоволны
сантиметрового и миллиметрового диапазонов. Плотность энергии
реликтового излучения 0,25 эВ/см3.
В 1941 году канадский
астроном Эндрю Мак-Келлар (Andrew McKellar, 1910-1960) анализировал
линии поглощения, вызываемые в спектре звезды 2 Змееносца межзвездными
молекулами циана (соединения углерода и азота). Он пришел к выводу, что
эти линии (в видимой глазом области спектра) могут возникать только при
поглощении света вращающимися молекулами циана. Причем вращение их
должно возбуждаться излучением с температурой около 2,3 Кельвина. Ни
сам Мак-Келлар, ни кто другой, конечно, не подумали тогда о возможности
того, что вращение молекул вызывается реликтовым излучением. Да и сама
теория горячего Большого взрыва Вселенной появилась только в 1946 году!
Реликтовое излучение
обнаружил в 1955 году аспирант-радиоастроном Тигран Арамович Шмаонов
(1932 г.р.). Первое опубликованное признание излучения появилось весной
1964 года в краткой статье А.Р. Дорошкевича и И.Д. Новикова,
озаглавленной "Средняя плотность излучения в метагалактике и некоторые
вопросы релятивистской космологии" [Доклады АН СССР, т.154, вып.4, стр.
119-121 (809-811)]. Микроволновое фоновое излучение назвал "реликтовым" советский астрофизик
Иосиф Самуилович Шкловский (1916-1985) в 1978 году [газета "Советская Россия", 20.08.1978].
Наряду с космологическим
красным смещением, реликтовое излучение рассматривается как одно из
главных подтверждений теории Большого взрыва.\\\
-------------------------------
- Re: Черная дыра
(А.П. Васи,
25.08.2013 22:33, 2.1 КБайт)
http://www.veinik.ru/science/anomal/article/919.html
\\\ "Реликтовое излучение"
- космическое электромагнитное излучение, приходящее на Землю со всех
сторон неба примерно с одинаковой интенсивностью и имеющее спектр,
характерный для излучения абсолютно черного тела при температуре около
3К (3 градуса по абсолютной шкале Кельвина, что соответствует 270С).
При такой температуре основная доля излучения приходится на радиоволны
сантиметрового и миллиметрового диапазонов. Плотность энергии
реликтового излучения 0,25 эВ/см3.
В 1941 году канадский
астроном Эндрю Мак-Келлар (Andrew McKellar, 1910-1960) анализировал
линии поглощения, вызываемые в спектре звезды 2 Змееносца межзвездными
молекулами циана (соединения углерода и азота). Он пришел к выводу, что
эти линии (в видимой глазом области спектра) могут возникать только при
поглощении света вращающимися молекулами циана. Причем вращение их
должно возбуждаться излучением с температурой около 2,3 Кельвина. Ни
сам Мак-Келлар, ни кто другой, конечно, не подумали тогда о возможности
того, что вращение молекул вызывается реликтовым излучением. Да и сама
теория горячего Большого взрыва Вселенной появилась только в 1946 году!
Реликтовое излучение
обнаружил в 1955 году аспирант-радиоастроном Тигран Арамович Шмаонов
(1932 г.р.). Первое опубликованное признание излучения появилось весной
1964 года в краткой статье А.Р. Дорошкевича и И.Д. Новикова,
озаглавленной "Средняя плотность излучения в метагалактике и некоторые
вопросы релятивистской космологии" [Доклады АН СССР, т.154, вып.4, стр.
119-121 (809-811)]. Микроволновое фоновое излучение назвал "реликтовым" советский астрофизик
Иосиф Самуилович Шкловский (1916-1985) в 1978 году [газета "Советская Россия", 20.08.1978].
Наряду с космологическим
красным смещением, реликтовое излучение рассматривается как одно из
главных подтверждений теории Большого взрыва.\\\
- Re: Черная дыра
(А.П. Васи,
25.08.2013 22:56, 11.8 КБайт)
Если взять купюру и посмотреть на неё
под ультрафиолетовым излучением - вот
и я собственно не могу понять как и по какой
причине узоры на купюре в разных
цветах,
причиной которому по аналогии
можно было отнести к реликтовому излучению
пространства.
---
\\\Материал из Википедии свободной энциклопедии
Материал из Википедии свободной энциклопедии
Флуоресце́нция (вариант: флюоресценция) физический процесс, разновидность люминесценции.
Флуоресценцией обычно называют излучательный переход возбужденного
состояния с самого нижнего синглетного колебательного уровня S1 в основное состояние S0. В общем случае флуоресценцией называют разрешенный по спину излучательный переход между двумя
состояниями одинаковой мультиплетности: между синглетными уровнями 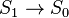 или триплетными
или триплетными  . Типичное
время жизни такого возбужденного
состояния составляет 10−11−10−6 с.
. Типичное
время жизни такого возбужденного
состояния составляет 10−11−10−6 с.
Флуоресценцию следует отличать от фосфоресценции
запрещенного по спину излучательного перехода между двумя состояниями
разной мультиплетности. Например, излучательный переход возбужденного
триплетного состояния T1 в основное состояние S0. Синглет-триплетные переходы имеют квантово-механический запрет, поэтому время жизни возбужденного состояния при фосфоресценции составляет
порядка 10−3−10−2 с.
\\\
\\\
Согласно представлениям квантовой
химии, электроны в атомах расположены на энергетических
уровнях.
Расстояние между энергетическими уровнями в молекуле зависит от её
строения. При облучении вещества светом возможен переход электронов
между различными энергетическими уровнями. Разница энергии между
энергетическими уровнями и частота колебаний поглощенного света
соотносятся между собой уравнением (III постулат Бора):

После поглощения света часть полученной системой энергии расходуется в результате релаксации.
Часть же может быть испущена в виде фотона определённой энергии.
Спектр флуоресценции сдвинут относительно спектра поглощения в сторону длинных волн. Это явление получило название Стоксов
сдвиг.
Его причиной являются безызлучательные релаксационные процессы. В
результате часть энергии поглощенного фотона теряется, а испускаемый
фотон имеет меньшую энергию, и, соответственно, большую длину волны.[1]
Схематически процессы поглощения света и флуоресценции показывают на диаграмме Яблонского.
При нормальных условиях большинство молекул находятся в основном электронном состоянии  . При поглощении света молекула переходит в возбужденное состояние
. При поглощении света молекула переходит в возбужденное состояние  .
При возбуждении на высшие электронные и колебательные уровни избыток
энергии быстро расходуется, переводя флуорофор на самый нижний
колебательный подуровень состояния
.
При возбуждении на высшие электронные и колебательные уровни избыток
энергии быстро расходуется, переводя флуорофор на самый нижний
колебательный подуровень состояния  . Однако, существуют и исключения:
например, флуоресценция азулена может происходить как из
. Однако, существуют и исключения:
например, флуоресценция азулена может происходить как из  ,
так и из
,
так и из 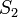 состояния.
состояния.
Квантовый выход флуоресценции показывает, с какой эффективностью
проходит данный процесс. Он определяется как отношение количества
испускаемых и поглощаемых фотонов. Квантовый выход флуоресценции может
быть рассчитан по формуле

где 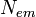 количество испускаемых в результате флуоресценции
фотонов, а
количество испускаемых в результате флуоресценции
фотонов, а 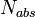 общее количество поглощаемых фотонов. Чем
больше квантовый выход флуорофора, тем интенсивнее его
флуоресценция. Квантовый выход можно также определить с помощью упрощенной диаграммы Яблонского[2],
где
общее количество поглощаемых фотонов. Чем
больше квантовый выход флуорофора, тем интенсивнее его
флуоресценция. Квантовый выход можно также определить с помощью упрощенной диаграммы Яблонского[2],
где 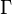 и
и  константы скорости излучательной и безызлучательной дезактивации возбужденного состояния.
константы скорости излучательной и безызлучательной дезактивации возбужденного состояния.
Тогда доля флуорофоров, возвращающихся в основное состояние с испусканием фотона, и, следовательно, квантовый выход:

Из последней формулы следует, что 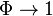 если
если
 ,
то есть если скорость безызлучательного перехода значительно меньше
скорости излучательного перехода. Отметим, что квантовый выход всегда
меньше единицы из-за стоксовых
потерь.\\\
,
то есть если скорость безызлучательного перехода значительно меньше
скорости излучательного перехода. Отметим, что квантовый выход всегда
меньше единицы из-за стоксовых
потерь.\\\
- Re: Черная дыра
(А.П. Васи,
27.08.2013 0:23, 1.1 КБайт)
Так вот - в 1941году открыто что у звезды
газы в пространстве получают возбуждение
от звезды на одной частоте а излучают на другой
частоте - ну это собственно
понятно.
Собственно понятно и другое что практически
у всех звёзд есть аналогичная ситуация.
Внимание - звезда светит - затрачивает свою
энергии которая
веществом - газом в пространстве
возле звезды переизлучается на другой частоте.
Вопрос - при чем здесь большой взрыв в принципе,
и какая может быть взаимосвязь
с эхом от большого
взрыва - ели энергия для поддержания этого
процесса используется из звезд которые светят
в текущий момент времени.
---
Вывод - большой взрыв не имеет никаких
подтверждений связанных с \\\эхом большого взрыва\\\
так как отсутствует причинно следственная связь
между тем что
переизлучается веществом в основе
энергии которой является звезда, и эхом от большого
взрыва - собственно эхо большого взрыва должно
быть постоянным источником
энергии для поддержания
переизлучения - что отсутствует в принципе.
- Re: Черная дыра
(А.П. Васи,
27.08.2013 0:37, 335 Байт)
Вот отсутствие такой мелочи как логическая
взаимосвязь между переизлучнием и большим
взрывом - сделало бессмысленным, с моей точки зрения,
около девяносто
пяти процентов всего что есть на этом
сайте, собственно вся космология оказалась в прострации.
Те кто верят в свои теории это ещё не скоро поймут.
- Re: Черная дыра
(А.П. Васи,
5.09.2013 22:40, 2.7 КБайт)
- Re: Черная дыра
(А.П. Васи,
5.09.2013 22:52, 4.4 КБайт)
Августина
Завсегдатай форума

 На Форуме
На Форуме

Сообщений: 1146
Пол:

 Re: Несоответствие с теорией большого взрыва?
Re: Несоответствие с теорией большого взрыва?
Ответ #548 - Сегодня :: 22:41:40
.ToriMalkaway писал(а) Сегодня :: 14:30:47:Но физически это должно в чем-то выражаться.
Оно и выражается в милливольтах на метр
.ToriMalkaway писал(а) Сегодня :: 14:30:47:Напряженность - скорее математическое понятие, абстракция
чего-то.
Нет. Это не абстракция. Чем Вы например, сможете выразить сам факт, что
пружина сжата? Кроме, как напряженностью - ничем. Пружину можно сжать
или растянуть. И сжать либо сильнее, либо слабее.
Это же не абстрактные, а вполне понятные физические характеристики вещества. Такие же как давление, температура.
ЭМ-поле
во Вселенной имеет нулевую напряженность. Аналогично поверхность воды
может иметь зеркальную, не возмущённую поверхность. Или воздух вокруг
нас может совсем не двигаться. В таком воздуе будет полная тишина.
Но
если поверхность воды что-то будет возмущать, Вы увидите волны. Если
воздух будет что то возмущать - Вы услышите звук. А вот если что то
будет возмущать ЭМ-поле, то без специальной аппаратуры (радиоприёмника)
радиоволн и не увидеть, и не услышать. Но сам факт возможности
радиосвязи доказывает, что радиоволны существуют. И проявляются в том,
что при их наличии - в антенне возникает Э.Д.С. (электродижущая сила).
И поскольку ЭМ-поле невидимо и неслышимо, мы можем наблюдать (с
помощью аппаратуры, конечно) только возмущения (напряженность) этого
поля.
.ToriMalkaway писал(а) Сегодня :: 14:30:47:
Просто обычные волны мы можем изучать досконально, так как нам хорошо
известна среда. Электромагнитные - тоже волны, но среда не доступна для
изучения нашими приборами, поэтому вводят абстрактные понятия.
Кто это Вам сказал такую глупость? И среда доступна, и приборы давно
есть. И пользуемся радиосвязью уже более 100 лет. Мобилками вон даже
дети дошколята уже умеют пользоваться.
И если есть желание берите постоянный магнит и изучайте хоть заизучайтесь!
.ToriMalkaway писал(а) Сегодня :: 14:30:47: А раз мы не знаем досконально природу электромагнитных
волн, то и о причине красного смещения можно только гадать.
Беда не в том, что
досконально не знаем. Беда в том, что своими мозгами думать многие не хотят.
Поэтому
то, что с детства вдолбили в школе - тупо, как попугаи, повторяют. И
раз написано в учебниках, что смещение результат расширения пустоты, то
все эту чушь и повторяют.
---
Смешно однако
- Re: Черная дыра
(А.П. Васи,
7.09.2013 16:46, 3.6 КБайт)
Ответ #141 : Сегодня в 16:26:19
Да,
Вы, батенька, настоящий альт. В этом у меня больше нет никаких
сомнений. Поэтому и тусовку себе выбираете соответствующую. То-то Анне
так понравились Ваши рассуждения и она Вам, как и прочим альтам, плюсики
ставит.
Кисмет.
К выводам..
Что
можно говорить, а чего "нельзя" на этом форуме мне известно хорошо..
Кто-то, когда-то, зачем-то решил, что научно, что ненаучно....
Альтов
всех давно поувольняли (помни о Демьянове). Некоторые попрятались
(помни Ивана). Теперь принялись за ортов (помни о Данилове).
А речь то идёт о грядущем внешнем управлении РАН со стороны Правительства и полной неготовности к этому
РАН.
В
понедельник начнётся Общее собрание РАН. Вот на Конференции велось
прямое интернет-вещание. Надеюсь, эта хорошая традиция будет продолжена.
А
чего прятаться-то? Никто с факелами не бегает, и альтов не вырезает.
Хотите доказать что-то свое, так доказывайте, разве это запрещено? Но не
здесь, на форуме, доказывайте в жизни. Проводите исследования,
добивайтесь результатов, пишите статьи. Только результаты, т.е. факты
могут быть доказательством теории. Нет результатов, тогда извините.
Пытаются окоротить только тех, кто с своими странными идеями обращается к
руководству, выпрашивая деньги. Вы же сами писали, что надо свои
исследования проводить за свой счет. Вот и проводите, и никто к вам и не
будет приставать.
----------------------------------------------------
Вот бывает что лучше не звездеть ничего на тот вопрос в котором
ты не в
курсе, чтобы потом не отпечататься у других
в сознании и не выглядеть вечным идиотом, у многих
мнение как правило не меняется.
Так вот надо слегка знать
что в годы репрессий
всех сторонников эфира репрессировали.
Собственно на текущий момент нет ни одного специалиста
по эфиру ни в одном реферируемом
журнале,
собственно реферирование это судейство, -
так как могут судить о статье по эфиру если
нет ни одного специалиста по эфиру, - правильно никак,
все статьи по эфиру вернут автору, и пошлют
его с реферируемого журнала в пешее эротическое
путешествие вмести с его статьёй.
\\\Проводите исследования,
добивайтесь результатов, пишите статьи. Только результаты, т.е. факты
могут быть доказательством теории.\\\
Так что совет писать статьи альтам -
может дать только умственно неполноценный.
Альта ясный конь никто не
про-финансирует.
И релятивисты на факты опыта - давно кладут.
---
Вывод - такие советы может давать альтам,
или глупец или их враг.
- Re: Черная дыра
(А.П. Васи,
7.09.2013 18:54, 1.6 КБайт)
Ответ #755 : Сегодня в 18:39:17
Насколько могу судить, на деле никто "в погоне" время не
измерял.
GPS


_________________________________________________ _____________
_________________________________________________ _____________



----------
Смешно
- Re: Черная дыра
(А.П. Васи,
7.09.2013 19:05, 941 Байт)
Ни куя там нет релятивистских поправок.
Дело в том что разработали жпс не релятивисты,
а бывшие немецкие профессора на основе довоенных
немецких технологий,
и основные принципы были разработаны
на сколько я помню в 1958году.
Предыдущее сообщение чем собственно красиво
тем что вводит в заблуждение читающего.
Дело в том что часы электронные любые ускоряют свой темп,
и это было замечено в опыте с высокоточными часами
на сколько помню в тридцатых годах прошлого
века.
Собственно зная то на сколько увеличится частота кварца,
его изготавливают на более низкую частоту.
То что это релятивистский эффект я лично не
верю,
ибо в их теории темп часов замедляется, а по факту
темп увеличивается - альты понимают, а релятивисты пишут
так чтобы была не понятна физическая суть.
А если
бы они писали понятно то ясный конь они бы писали
против своих постулатов.
- Re: Черная дыра
(А.П. Васи,
7.09.2013 19:12, 10.0 КБайт)
На сколько я помню на мембране считали
поправки для жпс по релятивистским формулам,
так она оказалась длинной в одну четвёртую длинны
антенны, сошлись на
том что если таковая и есть
то она и даром не нужна.
---------------------------
http://www.tracker.co.ua/gps_work.html
\\\ Как работает GPS
Как работает GPS
Система Глобального Позиционирования (GPS или Global Positioning System)
является спутниковой и работает под управлением Министерства Обороны
США. Система является глобальной, всепогодной и обеспечивает возможность
получения точных координат и времени 24 часа в сутки.
Основы системы GPS можно разбить на пять основных подпунктов:
Спутниковая трилатерация основа системы
Спутниковая дальнометрия измерение расстояний до спутников
Точная временная привязка зачем нужно согласовывать
часы в приёмнике и на спутнике и для чего требуется 4-й космический
аппарат
Расположение спутников определение точного положения спутников в космосе
Коррекция ошибок учёт ошибок вносимых задержками в тропосфере и ионосфере
1.1.1 Спутниковая трилатерация

Точные координаты могут быть вычислены для места на
поверхности Земли по измерениям расстояний от группы спутников (если их
положение в космосе известно). В этом случае спутники являются пунктами с
известными координатами. Предположим, что расстояние от одного спутника
известно и мы можем описать сферу заданного радиуса вокруг него.
Если мы знаем также расстояние и до второго спутника,
то определяемое местоположение будет расположено где-то в круге,
задаваемом пересечением двух сфер.
Третий спутник определяет две точки на окружности.

Теперь остаётся только выбрать правильную точку. Однако
одна из точек всегда может быть отброшена, так как она имеет высокую
скорость перемещения или находится на или под поверхностью Земли. Таким
образом, зная расстояние до трёх спутников, можно вычислить координаты
определяемой точки.
1.1.2 Спутниковая дальнометрия
Расстояние до спутников определяется по измерениям
времени прохождения радиосигнала от космического аппарата до приёмника
умноженным на скорость света. Для того, чтобы определить время
распространения сигнала нам необходимо знать когда он покинул спутник.

Для этого на спутнике и в приёмнике одновременно генерируется одинаковый Псевдослучайный Код*
* - Каждый спутник GPS передаёт два радиосигнала: на
частоте L1=1575.42 МГц и L2=1227.60 МГц. Сигнал L1 имеет два
дальномерных кода с псевдослучайным шумом (PRN), P-код и C/A код.
Точный или P-код может быть зашифрован для военных целей. Грубый или
C/A код не зашифрован. Сигнал L2 модулируется только с P-кодом.
Большинство гражданских пользователей используют C/A код при работе с
GPS системами. Некоторые приёмники Trimble геодезического класса
работают с P-кодом.
Приёмник проверяет входящий сигнал со спутника и
определяет когда он генерировал такой же код. Полученная разница,
умноженная на скорость света (~ 300000 км/с) даёт искомое расстояние.
Использование кода позволяет приёмнику определить
временную задержку в любое время. Кроме того, спутники могут излучать
сигнал на одной и той же частоте, так как каждый спутник
идентифицируется по своему Псевдослучайному коду (PRN или PseudoRandom
Number code).
1.1.3 Точная временная привязка

Как видно из сказанного выше, вычисления напрямую
зависят от точности хода часов. Код должен генерироваться на спутнике и
приёмнике в одно и то же время. На спутниках установлены атомные часы
имеющие точность около одной наносекунды. Однако это слишком дорого,
чтобы устанавливать такие часы в каждый GPS приёмник, поэтому измерения
от четвёртого спутника используются для устранения ошибок хода часов
приёмника.
Эти измерения можно использовать для устранения ошибок,
которые возникают если часы на спутнике и в приёмнике не
синхронизированы. Для наглядности, иллюстрации приведённые ниже
рассматривают ситуацию на плоскости, так как только три спутника
необходимо для вычисления местоположения объекта.

Если часы на спутнике и в приёмнике имеют одинаковую
точность хода, то точное местоположение может быть найдено по измерениям
расстояния до двух спутников.
Если получены измерения с трёх спутников и все часы
точные, то круг описанный радиус-вектором от третьего спутника будет
пересекаться как показано на рисунке.
Однако, если часы в приёмнике спешат на 1 секунду, то картина будет выглядеть следующим образом.
Если сделать замер до третьего спутника, то полученный радиус-вектор не пересечётся с двумя другими как показано на рисунке.

Когда GPS приёмник получает серию измерений которые не
пересекаются в одной точке, то компьютер в приёмнике начинает вычитать
(или добавлять) время методом последовательных итерации до тех пор, пока
не сведёт все измерения к одной точке. После этого вычисляется поправка
и делается соответствующее уравнивание.
Если вам требуется третье измерение, то необходим
четвёртый спутник для устранения ошибок хода часов в приёмнике. Таким
образом, при работе в поле вам необходимо иметь минимум четыре спутника,
чтобы определить трёхмерные координаты объекта.
1.1.4 Расположение спутников

Система NAVSTAR имеет 24 рабочих спутника с орбитальным
периодом в 12 часов на высоте примерно 20200 км от поверхности Земли. В
шести различных плоскостях имеющих наклон к экватору в 55 ,
расположено по 4 спутника. Указанная высота необходима для обеспечения
стабильности орбитального движения спутников и уменьшения фактора
влияния сопротивления атмосферы.
Министерство Обороны США (DoD) осуществляет непрерывное
слежение за спутниками. На каждом спутнике расположено несколько
высокоточных атомных часов и они непрерывно передают радиосигналы с
собственным уникальным идентификационным кодом*. МО США имеет 4 станции
слежения за спутниками, три станции связи и центр осуществляющий
контроль и управление за всем наземным сегментом системы. Станции
слежения непрерывно отслеживают спутники и передают данные в центр
управления. В центре управления вычисляются уточнённые элементы

спутниковых орбит и коэффициенты поправок спутниковых
шкал времени, после чего эти данные передаются по каналам станций связи
на спутники по крайней мере один раз в сутки.
* - Каждый спутник GPS передаёт два радиосигнала: на
частоте L1=1575.42 МГц и L2=1227.60 МГц. Сигнал L1 имеет два
дальномерных кода с псевдослучайным шумом (PRN), P-код и C/A код.
Точный или P-код может быть зашифрован для военных целей. Грубый или
C/A код не зашифрован. Сигнал L2 модулируется только с P-кодом.
Большинство гражданских пользователей используют C/A код при работе с
GPS системами. Некоторые приёмники Trimble геодезического класса
работают с P-кодом.
1.1.5 Коррекция ошибок
Некоторые источники ошибок возникающих при работе GPS
являются трудноустранимыми. Вычисления предполагают, что сигнал
распространяется с непрерывной скоростью, которая равна скорости света.
Однако в реальности всё гораздо сложнее. Скорость света является
константой только в вакууме. Когда сигнал проходит через ионосферу (слой
заряженных частиц на высоте 130-290 км) и тропосферу, его скорость
распространения уменьшается, что приводит к ошибкам в измерения
дальности. В современных GPS приёмниках используют всевозможные
алгоритмы устранения этих задержек.
Иногда возникают ошибки в ходе атомных часов и орбитах
спутников, но они обычно незначительны и тщательно отслеживаются со
станций слежения.
Многолучёвая интерференция также вносит ошибки в
определение местоположения с помощью GPS. Это происходит, когда сигнал
отражается от объектов расположенных на земной поверхности, что создаёт
заметную интерференцию с сигналами приходящими непосредственно со
спутников. Специальная техника обработки сигнала и продуманная
конструкция антенн позволяет свести к минимуму этот источник ошибок.
Раньше существовал ещё один источник ошибок это
Избирательный Доступ (Selective Availability или S/A), искусственное
снижение точности спутникового сигнала вводимое МО США. Это приводило к
тому, что точность полученных координат с помощью GPS снижалась до 100
метров. Однако 1 мая 2000 года по решению президента США "Избирательный
Доступ" был отключен. Кроме того, S/A можно исключить, применяя технику
дифференциальной коррекции (см. далее).
По мотивам статьи на www.gpsru.com\\\
--------------------------------
- Re: Черная дыра
(А.П. Васи,
7.09.2013 19:31, 452 Байт)
Для тех кто не понял - по релятивистким
теориям время у летающего на орбите
близнеца - что делает - правильно замедляеся,
релятивистские часы на световом
луче что делают,
правильно замедляются, на висящих над одной
точкой над землёй или движущихся по орбите,
кварцевые генераторы что делают -
правильно
с ростом высоты увеличивают
свой темп - теория предполагает одно практика
показывает противоположное.
- Re: Черная дыра
(А.П. Васи,
10.09.2013 20:26, 1.8 КБайт)

|

|
|
20 Ответов
|
---
Мне аж смешно, как говорится шара плиз,
или примитивный тест на сообразительность.
С одной точки зрения задача
достаточно примитивная,
и решается с помощью силовой динамики движения увлекаемых сред,
которые запрещены в принципе на данном форум
там рукоплещут пустоте
в пространстве.
Дам мелкую подсказку при непосредственной близости
к поверхности увлекающей среду, будет иметь место
Сила Кориолиса, и у планеты которая
тоже увлекает
среду тоже Сила Кориолиса имеет большое значение.
При этом нелогично забывать о силе прокатки по внешней
и внутренней силовой обойме среды
создаваемой перепадом
давлений среды при увлечении звездой.
Всё-бы хорошо и складно если бы в состоянии
задать базовые характеристики или стандарты
как для звезды так и для среды и для планет.
Задача со смешным количеством переменных.
Успехов.
- Re: Черная дыра
(А.П. Васи,
11.09.2013 20:50, 2.3 КБайт)
\\\

Ответ #1 : Вчера в 11:59:24
Очень полезное и нужное дело!
А почему выпускников (=школьников 11-х классов) дискриминируете?
приглашает школьников 710 классов.
У меня брат в 11-ом классе, ему как раз полезно будет, он ЕГЭ по физике сдавать собирается.
-----------------------
Ответ #2 : Сегодня в 11:33:41
Разумеется, для 11 класса есть занятия. Но начинать в 11 классе поздно, а объявление адресовано новичкам.
\\\----------------
Смешно - классика астро юмора.А у меня тоже
смешная ситуация, учил астрономию в школе
потом о ней даже не думал лет двадцать, а потом
оказалось что
хобби.
Вывод - астрономией заниматься - рано-поздно не бывает,
ибо время пролетает и ни конь и не злодей
не жестокий лиходей он не вправе за других
принимать решение, не спросив вот тех для кого лишение.
Хотя честно рассказать смех и сме-смешинки
в астрономии бывают грустные сторинки,
непонятно
ничего в этой парадигме,
так что лучше не учить - если нет в душе
к астрономии искринки.
- Re: Черная дыра
(А.П. Васи,
11.09.2013 21:17, 2.5 КБайт)



-

- Сообщений: 230
- Рейтинг: +3/-1
- पुनर्जन्म
-
Ответ #784 : Сегодня в 20:56:41
VimanaPro,
а почему у гравитации нет скорости? В теории, которую я описываю,
большой, но конечной скоростью гравитации можно объяснить расширение
Вселенной, а постоянной величиной суммарной вычислительной мощности
объясняется ускорение расширения.
А цель падающего камня в моей теории очень даже ясна, но меня здесь однажды уже забанили за её философское раскрытие  .
.
Возможно, используя слово "гравитация", Вы вкладываете
свой смысл. Не могли бы уточнить определение и свойства гравитации.
Про ускорение расширения Вселенной наверное лучше в соседней теме про Вселенную
---
Жаль что забанят как бешеную собаку, ибо даже я знаю что слово гравитация
была придумана для описания притяжения двух тел.
- Re: Черная дыра
(А.П. Васи,
13.09.2013 7:40, 2.2 КБайт, ответов: 1)
В принципе элементарная
задача: вдоль оси 0х стартует ракета-1 со скоростью 4/5 с относительно
0, с неё в том же направлении стартует ракета-2 со скоростью 4/5 с
относительноракеты-1; найти скорость ракеты-2 относительно 0.
Задача
решается с помощью одной формулы \[
s=\frac{v+u}{1+vu/{c}^{2}}=\frac{8/5}{1+16/25}=\frac{8 \cdot 25}{41
\cdot 5}=\frac{40}{41}\approx 0.9756 ( c ) \]Лоренц-фактор ракеты-2
(относительно 0)\[ \gamma
=\frac{1}{\sqrt{1-{s}^{2}/{c}^{2}}}=\frac{1}{\sqrt{1-1600/1681}}=\frac{41}{9}
\]
С другой стороны, Лоренц-фактор ракеты-1 (относительно 0)\[
{\gamma }_{(1-0)}
=\frac{1}{\sqrt{1-{v}^{2}/{c}^{2}}}=\frac{1}{\sqrt{1-16/25}}=\frac{5}{3}
\]То есть, суммарная энергия движущейся со скоростью 4/5 с ракеты-1 в
5/3 раза больше энергии покоящейся ракеты-1 относительно 0. Далее.
Ракета-2 движется относительно покоящейся для неё ракеты-1 со скоростью
4/5 с.
---
В чем ошибка
В том что эта задача - физическая,
а физические задачи решаются не формулами, а умственными
способностями которые
должны превышать необходимый
минимум нужный для решения задачи.
Эта задача решается в стиле - аля часы да носим по платформе.
Едет поезд в первом
вагоне поезда есть часолов у него сачок
с номером 1, и он ловит им часы тоже с номером 1, в конце поезда
есть второй часолов который ловит часы с номером 2.
А есть хитрые платформенные часоносы, - они смеются над умственными
способностями тех кто решает подобные задачи.
Едет поезд Часоносы часы с номером
один поставили по средине платформы
и часы номер два поставили по средине платформы.
Проезжающий поезд мог узнать свою скорость,
а после того как часоносы
первые часы отнесли в перёд платформы,
а вторые в конец - то весь поезд начал проезжать станцию
с бесконечной скоростью.
- Re[2]: Черная дыра
(А. С. Коломенский,
14.09.2013 19:27, 75 Байт)
Столько словесного поноса и умственного блуда и как здесь, ещё не встречал!
- Re: Черная дыра
(А.П. Васи,
14.09.2013 20:32, 3.9 КБайт)
///
 Re: Конец эфирной теории- finita la comédie.
Re: Конец эфирной теории- finita la comédie.
Ответ #272 - Сегодня :: 19:33:49
Михаил Сурин писал(а) Сегодня :: 18:56:29:. На чём основаны Ваши утверждения мне пока непонятно..
На том что я не видел пока убедительных свидетельств подтверждения существования
эфира. Он не является физическим объектом.
Все
эферисты и Вы в том числе отсылаете к чтению к сайтам которые не
являются научными. Я стремлюсь же к обратному. т.е. быть в русле
научных фактов.
Поэтому у нас разные русла. Если Вы хоите чтобы эти русла соприкаснулись тогда и задайте тон этому соприкосновению.
А пока есть один экспериент
который показал что эфира нет. Экспериментов подтверждающих то что эфир есть я не вижу.
Приведите его здесь. Если сможете. Но пока Вы только отписываетесь
философскими терминами -пойди туда, найди там то. А это там то непонятно
что.
Наука это такое явление которое не может быть где -то, а где
то может быть. Она есть. И Вы вне ее пределов. Это достаточный аргумент и
пока он не опровергнут Вами.///
--------------------------------------------------------
Да видно релятивисты нервничают по самое асисяй, даже стратегическую
хитрость применяют, заслали гонца на альтовкий форум,
который просто оборзел с таким названием форума,
лично мне понятно что за такие вещи логично просто
банить.
И что меня удивляет так это умственные никакие
способности, в основной массе к запоминанию
физических опытов и анализа их.
Я лично
не знаю ни одного прибора и устройства сделанного
на базе релятивистских теорий.
Жпс и то альты сделали с атомными часами.
И когда атомные часы подымать на
высоту начали то уже при разнице
больше десяти метров между часами у верхних увеличился темп,
у релятивистов темп часов на орбите увеличивается.
Я одного
собственно не понимаю почему при всех
нескладушках теории её так долго терпят.
Парадокс это тоже недостаток теории -
за который любая теория посылается
в пешее эротическое путешествие, и имея столько нескладух
теория ещё стоит.
И самое смешное что нет изначально не только измерительного
устройства, нет
единиц измерения и нет методики измерения,
--- а теперь внимание - на заявленные физические свойства,
- ладно может я и не прав, может в каждом супермаркете
и продаётся измеритель кривизны пространства который
показывает - один кривзвездёныш на своей шкале у поверхности
Земли, да и прибор который показывает замедление
времени в движении тоже на полке лежит - и показывает
- а что он показывает - а даже единиц измерения релятивисты
не удосужились придумать для этого прибора.
То мне опять Вибе вспомнился, когда он мне буй показал
на релятивистскую причину скорости полёта фотона как
частицы в пустоте, а потребовал тех паспорт
на эфир.
Собственно данная ситуация аналогичная релятивисты
криком кричат что эфира нет а локаторы работают
по эффекту Доплера для сред аж с 1842 года
автор
его придумал исключительно для сред.
- Re: Черная дыра
(А.П. Васи,
14.09.2013 20:36, 276 Байт)
А.С.Коломенский
---
Я как раз и рад за Вас,
я стараюсь так писать чтобы махровые релятивисты,
не могли даже вдуплиться
в смысловую суть написанного.
Так что спасибо Вам за отзыв.
Ту-та не для средних умов однако.
- Re: Черная дыра
(А.П. Васи,
12.10.2013 11:03, 9.9 КБайт)
А текст то читается как будто
его писал человек
страдающий идиотизмом с физическим уклоном.
Что занимательно что пишущий
настолько недалёкий
что использует слова
физического назначения е понимая
смысловую суть слов которые он
использует.
Это естественно не критический
предел уровня идиотизма
по причине отсутствия
адекватных знаний по физике,
у автора два варианта с
большей вероятностью что его
тексты будут удивлять ещё
большим идиотизмом, по причине того
что в его среде общения он и
те с кем он на форуме общался,
и думал что благодаря коллективу
они улучшают свои знания
в физике а оказалось что они
только заблуждались ещё круче
а коллектив придавал уверенности
в правильности фактических
заблуждений - что уже есть -
фанатизм.
У меня тоже десяток лет назад
были заблуждения но я системно
и последовательно с ними
разбирался не жалея никакого количества
времени чтобы даже разобраться над самым незначительным
вопросом по физике, который привлёк моё
внимание.
И вывод из этой ситуации то
какой - если Вы подобную буету пишите
в 30 лет, то это нормально у
Вас ещё будет возможность при наличии желания
преодолеть свои ошибки, но
если вам 60 лет - то логики заниматься
подобными теориями в
физике - нет.
Писать то можно, но будут все
над этим смеяться.
Я бы лично с научных
руководящих должностей с 52 лет законодательно
бы увольнял, в таком возрасте
научными коллективами руководить
с моей точки зрения не
логично,
с 55летнего возраста запрещал бы уже даже быть
сотрудником научного коллектива, -
- и принудительном порядке
переводятся на преподавательскую работу
в школы и институты.
И не надо полемику на эту тему разводит, это
естественный процесс,
на старых лошадях в скачках
никто не додумывается устраивать забеги, так и тут, а
то что это возможно, - не корректно
-, так это до лампочки ибо это естественный факт.
--------------------------------------------------------------------------------------------------------------
///
 "Теория Пены" : штрихи к модели источника света
"Теория Пены" : штрихи к модели источника света
Вчера :: 19:35:56
По теории Пены атом представляет собой агрегат из четырехмерных вихрей эфира.
Например,
атом водорода. Состоит как бы из двух с половиной четырехмерных
вихрей. Ядро состоит из четырехмерного торнадо с прикрепленным на
периферии четырехмерным тороидальным вихрем (получается как бы полтора
вихря). Вокруг ядра расположен электрон четырехмерный тороидальный
вихрь. Вращение частиц эфира в этих двух тороидальных вихрях (по
образующей тора) происходит в противоположных направлениях, за счет чего
образуется у ядра и электрона знаковая разница электрического заряда.
Между электроном и ядром находится хаотический эфир. Орбита электрона
обусловлена динамическим равновесием сил: электрической (притяжение),
магнитной (притяжение или отталкивание в зависимости от градиента
давления хаотического эфира), гравитационной (притяжение или
отталкивание в зависимости от расстояния электрона от ядра).
Таким
образом, в своем трехмерном проявлении атом представляет собой орешек,
состоящий из трех компонентов: 1) вещественный нуклонообразующий
шарик, покрытый 2)антивещественным (почти что позитрон) слоем и 3)
вещественной кожурой (электронное облако).
Модель атома, как источника и поглотителя света.
При
неком энергетическом возбуждении электрон увеличивает свою орбиту и
пространство между ним и ядром заполняется дополнительным количеством
эфира. При возвращении электрона на свою стабильную орбиту из атома, как
из спринцовки, выплескивается струйка эфира, которая и является
фотоном. Обратный процесс очевиден струйка (фотон) проникает в атом и
выталкивает электрон на другую (нестабильную) орбиту.
Первое
сходство предлагаемой модели с имеющимися опытными данным наличие
индивидуальных спектров поглощения и испускания, которые, естественно,
зависят от разницы в конструкции атомов различных химических элементов.
Ширина спектральной линии, естественно, зависит от всяческих внешних и
внутренних неоднородностей (например, от неоднородностей самого Эфира,
от скорости движения атома и от другого многого прочего).
Второе
легкое объяснение доплеровского изменения длины волны. Ясно, что если
движение спринцовки совпадает с направление струи, то и струя
окажется короче. Если атом движется в противоположном направлении
струя удлиняется.
Третье возможность такой конструкции
спринцовки, при которой скорость струйки (фотона) не зависит (или не
очень сильно зависит) от скорости спринцовки (атома).
Четвертое
объяснение сходства фотона с ЭМ-волной. И струйка и ЭМ-волна являются
градиентами плотности Эфира, изменение которой (плотности)
распространяется со скоростью эфирного звука.
Пятое объяснение отличия фотона от ЭМ-волны. У фотона нет (или очень незначительна) электрическая составляющая.
Шестое
некоторое пересечение частот у инфракрасных фотонов с тепловыми
ЭМ-волнами. Тепловые ЭМ-волны образуются колебаниями самих атомов (и
вместе с ним их электронов), которые колеблют окружающий Эфир.
Некоторые орбитальные переходы электронов (когда испускается струйка),
естественно, могут быть похожими (по энергоемкости, например, и др.) на
характеристики тепла. Также и при поглощении инфракрасного фотона не
всегда может электрон возбудиться до уровня перескока на другую орбиту
(Инфракрасный фотон может лишь немного потрясти атом, и энергия
излучиться обратно уже не в виде струйки, но в виде
центрально-сферически симметричной ЭМ-волны
Приведенный перечень
является далеко не законченным рядом аргументов в пользу аналогии атома
со спринцовкой. Однако для более тонких параллелей необходимо
учитывать и более тонкие конструктивные характеристики и спринцовки, и
струйки, и самого Эфира
///
- Re: Черная дыра
(А.П. Васи,
13.10.2013 20:11, 67.2 КБайт)
Это должен прочитать каждый,
что-бы он знал и помнил вечно -
что все идеи релятивизма взяты из ранее описанных
идей сторонников эфира.
-------------------------------------------------------------------------------------------------
http://ether-wind.narod.ru/Martins_2011_Courvoisier
R. Martins. Searching for the Ether: Leopold Courvoisers Attempts to Measure
the Absolute Velocity of the Solar System (PDF)
| 1
| {1}DIO, The International
Journal of Scientific History www.dioi.org | DIO, Международный журнал научной истории www.dioi.org
|
| 2
| {3}
|
|
| 3
| Physics Department, State University of Paraiba (UEPB), Brazil roberto.andrade.martins@gmail.com
| Физический факультет Государственного университета Параиба (UEPB), Бразилия roberto.andrade.martins@gmail.com
|
| 4
|
|
|
| 5
|
|
|
| 6
| Leopold Courvoisier (1873-1955) was an observer at the Berlin /
Babelsberg astronomical observatory from 1905 up to his retirement in
1938.
| Леопольд Курвуазье (1873-1955) был наблюдателем в Берлинской /
Бабельсбергской астрономической обсерватории с 1905 года до своей
отставки в 1938 году.
|
| 7
| Most of his work was traditional astrometrical observation resulting in the publication of several star catalogues.
| Большинство его работ были традиционными астрометрическими
наблюдениями, которые в результате привели к публикации ряда звездных
каталогов.
|
| 8
| A relevant part of his publications was devoted, however, to
another subject: the attempt to detect the motion of the solar system
through the ether.
| Значимая часть его публикаций была посвящена, однако, другой теме: попытке обнаружения движения Солнечной системы через эфир.
|
| 9
|
|
|
| 10
| Most of Courvoiser's search for measurable effects of the ether was based upon two principles.
| Большинство из попыток Курвуазье обнаружить измеримые эффекты эфира была основана на двух принципах.
|
| 11
| According to him, (1) the angles of incidence and reflection of
light could be different, relative to the proper reference system of
the mirror, if it moved through the ether; and (2) the Lorentz
contraction of the Earth due to its motion through the ether produced
observable effects relative to the Earths reference system.
| По его словам, (1) углы падения и отражения света может быть
другим, по отношению к собственной системе отсчета зеркала, если оно
движется через эфир, и (2) сокращение Лоренца для Земли из-за ее
движения через эфир производит наблюдаемые эффекты по отношению к
системе отсчета Земли.
|
| 12
| Both principles, of course, violate the principle of relativity.
| Оба принципа, конечно, нарушают принцип относительности.
|
| 13
| Courvoisier presented theoretical arguments attempting to show that there should exist second order measurable effects.
| Курвуазье представил теоретические аргументы, пытаясь показать, что должны существовать измеримые эффекты второго порядка.
|
| 14
| He searched for those effects using both astronomical
observations and laboratory experiments and claimed that he had measured
a velocity of the solar system of about 600 km/s.
| Он искал эти эффекты с помощью как астрономических наблюдений,
так и лабораторных экспериментов и утверждал, что он измерил величину
скорости Солнечной системы примерно 600 км/с.
|
| 15
| This paper presents a description and analysis of Courvoisers ether researches.
| Эта статья представляет собой описание и анализ эфирных исследований Курвуазье.
|
| 16
|
|
|
| 17
|
|
|
| 18
| Leopold Courvoisier was born on 24 January 1873 in Rihen near Basel (Switzerland).1 His father Ludwig Georg Courvoisier was a physician and was in charge
of the surgery chair of the University of Basel.
| Леопольд Курвуазье родился 24 января 1873 года в Ригене близ Базеля (Швейцария). 1 Его отец Людвиг Георг Курвуазье был врачом и возглавлял кафедру хирургии
в университете Базеля.
|
| 19
| Leopold (or Leo, as he was usually called) passed away in the same city where he was born, on 31 December 1955.
| Леопольд (или Лео, как его обычно называли) скончался в том же городе, где он родился, 31 декабря 1955 года.
|
| 20
| However, most of his professional life was spent in Germany.
| Тем не менее, большую часть своей профессиональной жизни он провел в Германии.
|
| 21
|
|
|
| 22
| Courvoisier exhibited an interest for astronomy since he was 15 years old.
| Курвуазье проявил интерес к астрономии, когда ему было 15 лет.
|
| 23
| In 1891 he began his university studies, first in Basel and later in {4}
Strasbourg - at a time when this city belonged to Germany.
| В 1891 году он начал учебу в университете, сначала в Базеле, а
затем вСтрасбурге - в то время, когда этот город принадлежал Германии.
|
| 24
| In 1897 he completed his dissertation, on the absolute height
of the pole as observed from Strasbourg (Die absolute Polhöhe von
Straßburg).
| В 1897 году он закончил свою диссертацию по наблюдаемой из
Страсбурга абсолютной высоте полюса ("Die absolute Polhöhe von
Straßburg).
|
| 25
| The next year he became an assistant observer at the Königstuhl
astronomical observatory near Heidelberg, under Karl Wilhelm
Valentiner.
| В следующем году он стал помощником наблюдателя в
астрономической обсерватории Кёнигштуль недалеко от Хайдельберга, под
руководством Карла Вильгельма Валентинера.
|
| 26
| In 1900 he obtained his Doctor degree in Straßburg.
| В 1900 году он получил докторскую степень в Страсбурге.
|
| 27
| From 1905 onward he worked at the Berlin / Babelsberg
observatory as an astronomical observer, under the direction of Karl
Hermann Struve.
| С 1905 и далее он работал в Берлинской / Бабельсбергской
обсерватории как астрономический наблюдатель под руководством Карла
Германа Струве.
|
| 28
| In 1913 the Berlin observatory moved to its new site, in Babelsberg,2 and one year later Courvoiser became its chief observer and professor.
| В 1913 году Берлинская обсерватория переехала на новое место, в Бабельсберг, 2, а год спустя Курвуазье стал там главным наблюдателем и профессором.
|
| 29
| He worked at Babelsberg up to his retirement in 1938, when he was 65 years old.
| Он работал в Бабельсберге до своей отставки в 1938 году, в возрасте 65 лет.
|
| 30
| In 1943 he moved to his birthplace, where he kept making observations and publishing papers up to his death.
| В 1943 году он переехал на родину, где он продолжал производить наблюдения и публиковать статьи до его смерти.
|
| 31
| Back to Switzerland, he was the editor of several of Leonhard Euler's astronomical works.
| В Швейцарии он был редактором нескольких астрономических работ Леонарда Эйлера.
|
| 32
|
|
|
| 33
| Courvoisiers main astronomical contribution was a large series
of routine astrometrical observations and the production of star
catalogues.
| Главный астрономический вклад Курвуазье состоит в большой серии
рутинных астрометрических наблюдений и публикации звездных каталогов.
|
| 34
| Volumes 5, 6 and 7 of Poggendorff's Biographisch-literarisches
Handwörterbuch provide references of about 10 large works (astronomical
catalogues) besides nearly 100 minor contributions by him.3 However, Courvoisiers work was not restricted to common astrometrical observations.
| Тома 5, 6 и 7 издания Biographisch literarisches Handwörterbuch
Поггендорфа дают ссылки на примерно 10 крупных работ (астрономических
каталогов) Курвуазье, помимо около ста менее значительных его
публикаций. 3 Тем не менее, работа Курвуазье не ограничивается общими астрометрическими наблюдениями.
|
| 35
| From his tedious measurements there soon came out evidences that he regarded as disproof of the theory of relativity.
| Из его утомительных измерений вскоре появились доказательства
того, что он рассматривает как опровержение теории относительности.
|
| 36
|
|
|
| 37
| Courvoisier did not accept the theory of relativity.
| Курвуазье не принял теорию относительности.
|
| 38
| He believed there was an ether, and attempted to measure the absolute velocity of the solar system relative to this medium.
| Он считал, что существует эфир, и попытался измерить абсолютную скорость Солнечной системы относительно этой среды.
|
| 39
| From 1921 to his death, Courvoisier published a series of over
30 papers where he described the theoretical basis of his search and the
several experimental techniques he used in attempting to detect the
motion of the Earth relative to the ether.
| С 1921 года до своей смерти, Курвуазье опубликовал серию из
более чем 30 работ, в которых он описал теоретическую основу его
исследований и несколько экспериментальных методов, которые он
использовал в попытке обнаружить движение Земли относительно эфира.
|
| 40
| Some of his measurements used astronomical observations; other
measurements depended on other physical effects (gravitational, etc.).
| Некоторые из его измерений использовали астрономические
наблюдения; другие измерения зависят от других физических эффектов
(гравитационные и т.д.).
|
| 41
| As a result of his observations he claimed that he had measured
a velocity of the solar system of about 600 km/s in a direction close
to 75 right ascension and +40 declination.
| В результате своих наблюдений он утверждал, что он измерил
скорость Солнечной системы, примерно составляющую 600 км / с в
направлении, близком к 75 прямого восхождения и +40 склонения.
|
| 42
|
|
|
| 43
| 
|
| 44
| {5} .... 1. Leopold Courvoisier (about 30
years old).4
| Рис. 1. Леопольд Курвуазье (в возрасте около 30 лет). 4
|
| 45
|
|
|
| 46
| The papers describing those researches were published in
several scientific journals - especially Astronomische Nachrichten,
Physikalische Zeitschrift and Zeitschrift für Physik.
| Статьи, описывающие эти исследования, были опубликованы в
нескольких научных журналах особенно в Astronomische Nachrichten,
Physikalische Zeitschrift für и Zeitschrift Physik.
|
| 47
| His work was largely ignored and had a small impact.
| Его работы в значительной степени игнорировались и имели незначительное влияние.
|
| 48
| A few authors (e.g. Ernest Esclangon and Dayton Miller) who
also claimed they had observed effects due to the ether have cited his
works.
| Несколько авторов (например, Эрнест Эсклангон и Дейтон Миллер),
которые также утверждали, что они наблюдали эффекты, связанные с
эфиром, ссылались на его произведения.
|
| 49
| {6} Historians of science have also neglected
those researches,5
although they present the largest set of empirical results that was
ever published against the theory of relativity by a professional
scientist.
| Историки науки также пренебрегали этими исследованиями, 5,
хотя они представляют собой крупнейший набор эмпирических результатов,
которые были когда-либо опубликованы против теории относительности
профессиональным ученым.
|
| 50
| Courvoisier exhibited an outstanding theoretical and
experimental skill, and his results can be regarded as one of the
strangest puzzles in the history of relativity.
| Курвуазье показывал выдающееся теоретическое и
экспериментальное мастерство, и его результаты можно рассматривать как
одну из самых странных загадок в истории теории относительности.
|
| 51
|
|
|
| 52
|
|
|
| 53
| Courvoisier's earliest involvement with relativity was an outcome of his routine measurements of star positions.
| Самое первое столкновение Курвуазье с теорией относительности стало результатом его рутинных измерений положений звезд.
|
| 54
| In the beginning of the twentieth century, Courvoisier had
noticed that the right ascension and declination of fixed stars suffered
a small influence when they are observed close to the Sun.
| В начале ХХ века Курвуазье заметил, что прямое восхождение и
склонение неподвижных звезд подвержено небольшому влиянию, когда они
наблюдаются близко к Солнцу.
|
| 55
| As this influence had a period of one year, he called it annual refraction.
| Поскольку это влияние имело период один год, он назвал его годовой рефракцией.
|
| 56
| His first work on the subject was published in 1905,6 that is, much earlier than the development of the general theory of relativity.
| Его первая работа на эту тему была опубликована в 1905 году, 6 то есть намного раньше, чем была разработана общая теория относительности.
|
| 57
| In 1911, after the publication of Einsteins early thoughts on
the gravitational deflection of light rays, Erwin Freundlich recalled
that Courvoisier's work had exhibited an effect that was qualitatively
similar to the one predicted by Einstein.7
| В 1911 году, после публикации ранних мыслей Эйнштейна по
гравитационному отклонению лучей света, Эрвин Фрейндлих напомнил, что
работа Курвуазье показала эффект, который качественно похож на
предсказанный Эйнштейном. 7
|
| 58
| Courvoisier interpreted the effect he had measured as due to
refraction of light by a denser medium around the Sun, not as a
consequence of relativity.
| Курвуазье интерпретировал эффект, которые он измерил, как
следствие преломление света более плотной средой вокруг Солнца, а не как
следствие теории относительности.
|
| 59
| It seems that Courvoisiers opposition to Einstein's work grew
steadily from this time onward and he became one of the most
intransigent supporters of ether theory after the theory of general
relativity received strong confirmation (the eclipse measurements), in
1919.
| Похоже, что оппозиция Курвуазье к работам Эйнштейна неуклонно
росла с этого времени, и он стал одним из самых несгибаемых сторонников
теории эфира после того, как общая теория относительности получила
сильное подтверждение (измерения во время затмения) в 1919 году.
|
| 60
| Courvoisier's main anti-relativistic work, however, is not directly linked to annual refraction.8
| Основные анти-релятивистских работы Курвуазье, однако, непосредственно не связаны с годовым преломлением. 8
|
| 61
|
|
|
| 62
| Courvoisier accepted the existence of a static ether, similar
to the medium proposed in the early eighteenth century by Augustin
Fresnel.
| Курвуазье признал существование статического эфира, похожий на
среду, предложенную в начале восемнадцатого века Огюстеном Френелем.
|
| 63
| That theory led to the conclusion that there could be no first-order influence of the motion {7}
through the ether upon optical experiments performed in the Earth.
| Эта теория привела к выводу, что не могло быть влияния эффектов
первого порядка при движении через эфир в оптических экспериментах,
проведенных на Земле.
|
| 64
| Besides that, the negative outcome of the Michelson-Morley
experiment required an additional hypothesis, and Courvoisier accepted
that motion through the ether produced a real contraction of all moving
bodies, according to the early explanation proposed by Fitzgerald and
Lorentz.
| Кроме того, отрицательный результат опыта Майкельсона требовал
дополнительной гипотезы и Курвуазье предположил, что движение через
эфира производит реальное сжатие всех подвижных тел, в соответствии с
ранними объяснениями, предложенными Фицджеральдом и Лоренцем.
|
| 65
| According to Lorentz, the principle of relativity would hold
exactly for any optical or electromagnetic phenomenon, but Courvoisier
did not follow Lorentzs theory in this respect.
| По словам Лоренца, принцип относительности будет применим в
точности для любого оптического или электромагнитные явления, но
Курвуазье не последовал теории Лоренца в этом отношении.
|
| 66
| He directly denied the principle of relativity and attempted to
measure the motion of the solar system through the ether using several
different techniques.
| Он прямо отрицал принцип относительности и попытался измерить
движение Солнечной системы через эфир с помощью различных методов.
|
| 67
|
|
|
| 68
| In 1921 Courvoisier published his first thoughts on the
possibility of measuring the absolute velocity of the Earth through the
ether.9
| В 1921 году Курвуазье опубликовал свои первые мысли о возможности измерения абсолютной скорости Земли относительно эфира. 9
|
| 69
| According to Courvoisiers own declaration, his early
calculations concerning the motion of the Earth were an outcome of
routine work.10
| В соответствии с собственной декларацией Курвуазье, его ранние расчеты о движении Земли было результатом рутинной работы. 10
|
| 70
| In 1920 the Leyden Observatory published the details of a large
series of observations of stars close to the North Pole that had been
made between 1862 and 1874.
| В 1920 году Лейденская обсерватория опубликовала подробности из
большой серии наблюдений звезд, расположенных близко к Северному
полюсу, которые были сделаны между 1862 и 1874 гг.
|
| 71
| Those measurements used an old method aiming to reduce
observational errors: the stars were observed both with the meridian
telescope directly pointed to them, and with the telescope pointed to
the images of the stars reflected by a mercury mirror.
| Эти измерения использовали старый метод, направленный на
снижение ошибок наблюдений: звезды наблюдались как с помощью
меридианного телескопа, прямо указывающего на них, а также с телескопом,
направленным к отражениям звезд зеркалом из ртути.
|
| 72
| This double assessment allowed corrections for any changes of the local vertical due to geological motions.
| Эта двойная оценка позволила производить корректировки любых изменений местной вертикали за счет геологических движений.
|
| 73
| It occurred to Courvoisier that those determinations could be used to measure the speed of the Earth through the ether.
| Курвуазье пришло в голову, что эти определения могут использоваться для измерения скорости движения Земли через эфир.
|
| 74
|
|
|
| 75
| Courvoisier assumed that the reflection of light by a mirror
could undergo some influence of the motion of the mirror through the
ether, even when the effect was observed relative to the proper reference system of the mirror.
| Курвуазье предполагал, что отражение света от зеркала может подвергаться некоторому влиянию от движение зеркала через эфир, даже если эффект наблюдался по отношению
к собственной системе отсчета зеркала.
|
| 76
| Any observable effect should be of the second order in v/c. It
would be impossible to detect such a small effect if the speed of the
Earth relative to the ether was about 104 c (that is, its orbital velocity), because for usual angle measurements (let us say, 60) a difference of 108
would amount to only 0.002″ an effect that could not be observed.
| Любой наблюдаемый эффект должен быть второго порядка
относительно v / c. Было бы невозможно обнаружить такой маленький
эффект, если скорость Земли относительно эфира был приблизительно 10 4 с (то есть, равна ее орбитальной скорости), так как для обычных измерений угла (скажем,
60) разница 10 8 составит лишь 0,002″ эффект, который не мог наблюдаться.
|
| 77
| However, Courvoisier assumed that there could exist a much
larger speed of the whole solar system relative to the ether, and
analyzed the data published by the Leyden Observatory searching for some
systematic effect.
| Тем не менее, Курвуазье предполагал, что может существовать
гораздо большая скорость всей Солнечной системы относительно эфира, и
проанализировал данные, опубликованные Лейденской обсерваторией в
поисках систематического эффекта.
|
| 78
|
|
|
| 79
| He computed the difference zz' between the direct zenith
distance z and the reflected zenith distance z' of the stars listed in
the catalogue, attempting to find a systematic effect that varied in a
periodic way with the sidereal time of observations.
| Он вычислил разницу Z-Z′ между прямым зенитным расстоянием z и
отраженным зенитным расстоянием z′ звезд в каталоге, пытаясь найти
систематический эффект, которые варьировался бы периодическим образом
вместе со звездным временем наблюдений.
|
| 80
| Using a graphical method, he did find such an effect, and then he submitted the data to quantitative analysis.
| Используя графический метод, он нашел такой эффект, а затем представил данные для количественного анализа.
|
| 81
| He derived an equation to describe the reflection of light in a moving mirror and {8}
determined the relevant parameters from an analysis of the Leyden data, using the method of minimum squares.
| Он получил уравнение для описания отражения света относительно
движущегося зеркала и определил соответствующие параметры из анализа
данных Лейдена, используя метод наименьших квадратов.
|
| 82
| He obtained an effect corresponding to a speed of about 800 km/s in the direction of the Auriga constellation.
| Он получил эффект, соответствующий скорости около 800 км / с в направлении созвездия Возничего.
|
| 83
| This speed is, of course, much larger than the orbital speed of the Earth.
| Эта скорость, конечно, значительно больше, чем орбитальная скорость Земли.
|
| 84
| Courvoisier interpreted it as due to the motion of the whole solar system through the ether.
| Курвуазье интерпретировал ее как следствие движения всей Солнечной системы через эфир.
|
| 85
| A few years later, Courvoisier obtained new data, using the same method (direct versus reflected direction).
| Несколько лет спустя, Курвуазье получил новые данные, используя тот же метод (сравнение прямого и отраженного направления).
|
| 86
| Using the vertical circle of the Babelsberg observatory, he
made a long series of observations (19211922) that led to results
similar to those that had been obtained from the Leyden observations.
| Используя вертикальный круг Бабельсбергской обсерватории, он
выполнил длинный ряд наблюдений (19211922), которые привели к
результатам, аналогичным тем, которые были получены из наблюдений в
Лейдене.
|
| 87
|
|
|
| 88
| After obtaining his first positive result, Courvoisier
attempted to find other independent methods of measuring the speed of
the Earth (or the solar system) relative to the ether.
| После получения первого положительного результата Курвуазье
пытался найти другие независимые методы измерения скорости Земли (или
Солнечной системы) относительно эфира.
|
| 89
| He conjectured that the Lorentz contraction of the Earth and of
optical instruments could have some small observable influence on
astronomical observations.
| Он предположил, что сокращение Земли и оптических приборов по
Лоренцу могли иметь некоторые небольшие влияние на наблюдаемые
астрономические явления.
|
| 90
| According to Courvoisier, the motion of the Earth relative to
the ether produces a contraction that transforms its spherical shape
into an ellipsoid with the smaller axis in the direction of its motion.
| Согласно Курвуазье, движение Земли относительно эфира
производит сжатие, которое преобразует свою сферическую форму в
эллипсоид, меньшая ось которого находится в направлении его движения.
|
| 91
| The surface of the ellipsoid, at each point, was supposed to be perpendicular to the local gravitational field.
| Поверхность эллипсоида в каждой точке должна была быть перпендикулярна к местному гравитационному полю.
|
| 92
| As the Earth rotates, each place on the surface of the Earth
passes through different points of the ellipsoid, and the angle between
the axis of the Earth and the local vertical direction should undergo a
periodical change.
| При вращении Земли, каждое место на поверхности Земли проходит
через различные точки эллипсоида, а угол между осью Земли и местным
вертикальным направлением, должно подвергаться периодическому изменению.
|
| 93
|
|
|
| 94
| Of course, it is impossible to measure the angle between the local vertical and the axis of rotation of the Earth.
| Конечно, невозможно измерить угол между местной вертикалью и осью вращения Земли.
|
| 95
| However, since the direction of this axis is fairly constant
relative to the fixed stars (for short time periods), it is possible to
choose a star very close to the North celestial pole and to measure its
distance to the zenith (that is, the local vertical direction).
| Однако, так как направление этой оси практически неизменно
относительно неподвижных звезд (в течение коротких периодоы времени), то
можно выбрать звезду в непосредственной близости от северного полюса
звездного неба и измерить его [угловое] расстояние к зениту (то есть, к
местному вертикальному направлению).
|
| 96
| This angle, according to Courvoisier's theory, should undergo a periodical change, as a function of the sidereal time.
| Этот угол, согласно теории Курвуазье, должен подвергаться периодическим изменениям в зависимости от звездного времени.
|
| 97
|
|
|
| 98
| As a matter of fact, Courvoisier had already measured the
position of a star very close to the North pole, in a long series of
observations from 1914 to 1917, using the Babelsberg Observatory
vertical circle.11
| На самом деле, Курвуазье уже измерял положение звезды,
расположенной очень близко к Северному полюсу, в длинной серии
наблюдений с 1914 по 1917 год, используя вертикальный круг
Бабельсбергской обсерватории .11
|
| 99
| Those measurements were very accurate and were evenly distributed as regards the sidereal time of the observations.
| Эти измерения были очень точными и равномерно распределенными относительно звездного время наблюдений.
|
| 100
| They were therefore suitable for looking for the influence of the Lorentz contraction on astronomical measurements.
| Поэтому они подходили для выявления того, как влияет сокращение Лоренца на астрономические измерения.
|
| 101
|
|
|
| 102
| As in the former case, Courvoisier first plotted the zenithal
distances of the star against sidereal time, and found a regular
fluctuation of the angle.
| Как и в предыдущем случае, Курвуазье сначала построил зенитные
расстояния звезды относительно звездного времени, и обнаружил регулярные
колебания угла.
|
| 103
| {9}
He then developed an equation to account for the effect, analyzed the
data using the minimum square method, and obtained his second
measurement of the velocity of the Earth relative to the ether.
| Затем он разработал уравнение для учета эффекта,
проанализировав данные с использованием метода наименьших квадратов и
получил измерение скорости Земли относительно эфира вторым способом.
|
| 104
| The speed obtained in this case was about 700 km/s, in the
direction of the constellation of Perseus (not very far from Auriga).
| Скорость, полученная в этом случае, была около 700 км/с в
направлении созвездия Персея (не очень далеко от созвездия Возничего).
|
| 105
| Courvoisier regarded the agreement of those two earliest results as satisfactory, and this led him to further researches.
| Курвуазье рассматривал соответствие этих двух ранних
результатов как удовлетворительные, и это привело его к дальнейшим
исследованиям.
|
| 106
| There was a delay of 5 years between Courvoisiers first positive results and his next publication on the subject.12
In this period he accumulated a series of positive results by different
methods, obtained the equations required for the analysis of his data,
and devised new methods for measuring the absolute speed of the Earth.
| Была задержка на 5 лет между первыми положительными результатами Курвуазье и его следующей публикацией на эту тему. 12
В этот период он накопил ряд положительных результатов разными
методами, получил уравнения, необходимые для анализа этих данных, а
также разработал новые методы для измерения абсолютной скорости Земли.
|
| 107
| This delay shows that Courvoisier was careful enough to resist
publishing preliminary results before he was able to amass a large
amount of evidence for his claim.
| Эта задержка показывает, что Курвуазье был достаточно
осторожен, чтобы избегать публикации предварительных результатов, прежде
чем он смог накопить большое количество доказательств его заявлений.
|
| 108
|
|
|
| 109
|
|
|
| 110
| Courvoisier derived equations13 that related the relevant measurements to the parameters of the motion of the Earth relative to the ether.14
| Курвуазье получил уравнения 13, которые относятся к соответствующим измерениям параметров движения Земли относительно эфира 14
|
| 111
| The main parameters that appear in his equations (.... 2) are:
| Основные параметры, которые появляются в его уравнения (рис. 2) являются следующими:
|
| 112
| c = the speed of light relative to the ether = 300,000 km/s
| с = скорость света относительно эфира = 300000 км / с
|
| 113
| v = speed of the Earth (or the solar system) relative to the ether
| v = скорость Земли (или Солнечной системы) относительно эфира
|
| 114
| A = right ascension of the apex of the absolute motion
| A = прямое восхождение апекса абсолютной скорости
|
| 115
| D = declination of the apex of the absolute motion
| D = склонение апекса абсолютной движения
|
| 116
| α = North local component of v/c
| α = северная локальная составляющая v/c
|
| 117
| β = Zenith local component of v/c
| β = зенитная локальная составляющая v/c
|
| 118
| γ = West local component of v/c
| γ = западная локальная составляющая v/c
|
| 119
| ϕ = latitude of the terrestrial observatory
| φ = широта наземной обсерватории
|
| 120
| θ = sidereal time of measurement
| θ = звездное время измерения
|
| 121
|
|
|
| 122
| A straightforward geometrical analysis shows that the components of v/c are:
| Простой геометрической анализ показывает, что компоненты v/c, являются:
|
| 123
| α = (v/c) [cos ϕ sin D sin ϕ cos D cos (θ A)] (1)
β = (v/c) [sin ϕ sin D + cos ϕ cos D cos (θ A)] (2)
| α = (v/c) [cos ϕ sin D sin ϕ cos D cos (θ A)] (1)
β = (v/c) [sin ϕ sin D + cos ϕ cos D cos (θ A)] (2)
|
| 124
| {10}
γ = (v/c) cos D sin (θ
A) (3)
| γ = (v/c) cos D sin (θ A) (3)
|
| 125
| 
|
| 126
| .... 2.
| Рис. 2.
|
| 127
| This diagram shows the main geometrical parameters used in Courvoisiers theoretical analysis of ether effects.
| Эта диаграмма показывает основные геометрические параметры, используемые Курвуазье в теоретическом анализе эффектов эфира.
|
| 128
| The spherical surface represents the Earth, and the observer is
at I, and the local directions Z, N, W correspond to Zenith,
geographical North and West.
| Сферическая поверхность представляет Землю, наблюдатель
находится в I, и местные направления Z, N, W соответствуют зениту,
географичесому северу и западу.
|
| 129
| The North Pole is in the direction NP.
| Северный полюс в направлении NP.
|
| 130
| The velocity of the Earth is  . .
| Скорость Земли составляет  . .
|
| 131
|
|
|
| 132
| In Courvoisier's first method, as described above, light was reflected by a mirror.
| В первом методе Курвуазье, как описано выше, свет отражается от зеркала.
|
| 133
| To derive the theoretical effect, it was necessary to study the
influence of the motion of the mirror through the ether upon the
direction of the reflected ray.
| Для вывода теоретического эффекта, было необходимо изучить влияние движения зеркала через эфир на направление отраженного луча.
|
| 134
| Courvoisier made use of the non-relativistic analysis developed by Adolf von Harnack,15
that predicted that the angle of reflection would be different from the
angle of incidence, relative to the proper reference system of the
mirror (.... 3).
| Курвуазье использовал нерелятивистский анализ, разработанный Адольфом фон Харнаком, 15
который предсказал, что угол отражения будет отличаться от угла
падения, по отношению к собственной системе отсчета зеркала (рис. 3).
|
| 135
| This was one of Courvoisiers main assumptions that was incompatible with the principle of relativity.
| Это было одно из основных предположений Курвуазье, которое было несовместимо с принципом относительности.
|
| 136
| 
|
| 137
| {11} .... 3.
| Рис. 3.
|
| 138
| Following a theoretical analysis by Adolf von Harnack,
Courvoisier accepted that the angle of reflection of light in a moving
mirror is influenced by its motion through the ether, and that there is a
second-order effect that can be measured in the reference frame of the
mirror.
| Следуя теоретическому анализу Адольфа фон Харнака, Курвуазье
принял, что угол отражения света для движущегося зеркала зависит от его
движения через эфир, и что есть эффект второго порядка, который может
быть измерен в системе отсчета зеркала.
|
| 139
|
|
|
| 140
| Taking into account this principle of the moving mirror,
Courvoisier predicted that the angle between the local vertical (zenith)
and the direction of observation of a given star would be slightly
different from the angle between the zenith and the direction of the
star observed using a mercury mirror (.... 4).
| С учетом этого принципа движущегося зеркала, Курвуазье
предсказал, что угол между местной вертикалью (зенитом) и направлением
наблюдения определенной звезды будет несколько отличаться от угла между
зенитом и направлением на звезду, которое наблюдалается с использованием
ртутного зеркала (рис. 4).
|
| 141
|
|
|
| 142
| 
|
| 143
| .... 4.
| Рис. 4.
|
| 144
| Courvoiser compared the direct measurement of the direction of a
star with its direction observed by reflection on a mercury mirror.
| Курвуазье сравнивал прямое измерение направления на звезду с ее
направлением, которое наблюдается при отражении от ртутного зеркала.
|
| 145
| {12}In
this specific case, the contraction of the Earth could produce no
effect, because both measurements were made relative to the same
reference (the local vertical) and the surface of the mercury mirror is,
of course, perpendicular to the local vertical, whatever the changes
that the gravitational field could undergo due to Lorentz contraction.
| В данном конкретном случае, сжатие Земли не может производить
никакого эффекта, потому что оба измерения производятся относительно
одной и той же точки отсчета (местной вертикали) и поверхностью зеркала
ртути, конечно, перпендикулярна к местной вертикали, независимо от
изменения, которому гравитационное поле может подвергаться из-за
сокращения Лоренца.
|
| 146
| The predicted effect was a small systematic difference between
the direct and the reflected angles, which should depend on the
direction of the observatory relative to the motion of the Earth through
the ether.
| Предсказанный эффект был небольшим систематическим различием
между прямым и отраженным углом, которое должно зависеть от направления
относительного движения Земли и обсерватории через эфир.
|
| 147
|
|
|
| 148
| 
|
| 149
| .... 5.
| Рис. 5.
|
| 150
| Harnacks diagram for analyzing the reflection of light in a moving mirror.
| Диаграммы Харнака для анализа отражения света в движущемся зеркале.
|
| 151
| The initial position of the mirror is S, and after a time δt its position is S'.
| Начальное положение зеркала S, и через некоторое время δt его положение S′.
|
| 152
| AA' is a wave front of the incident light beam, and BB' is a wave front of the reflected beam.
| AA′ волновой фронт падающего луча света, и ВВ′ волновой фронт отраженного луча.
|
| 153
|
|
|
| 154
| Let θ be the angle of incidence and θ' the angle of reflection
of a light ray in a moving mirror, measured relative to the ether (....
5).
| Пусть θ угол падения и θ′ угол отражения луча света в движущемся зеркале, измеренные относительно эфира (рис. 5).
|
| 155
| According to Harnack's analysis, instead of θ=θ' the following equations would hold:
| Согласно анализу Харнака, подстановка θ = θ′ приведет к следующим уравнениям:
|
| 156
| sin θ' = (1 β2) sin θ / (1 + 2β cos θ + β2) (4)
| sin θ′ = (1 β2) sin θ / (1 + 2β cos θ + β2) (4)
|
| 157
| cos θ' = [(1 + β2) cos θ + 2β] / (1 + 2β cos θ + β2) (5)
| cos θ′ = [(1 + β2) cos θ + 2β] / (1 + 2β cos θ + β2) (5)
|
| 158
| {13} In those equations, the speed of the
mirror is ß=v/c, in the direction perpendicular to the mirror.
| В этих уравнениях, скорость зеркала β = v / с, в направлении, перпендикулярном к зеркалу.
|
| 159
| Any motion of the mirror parallel to its surface would have no influence upon the direction of light.
| Любое движение зеркала параллельно его поверхности не будет иметь никакого влияния на направление света.
|
| 160
| In the case of the mercury mirror, the relevant direction if
the local vertical, and therefore β, here, has the same general meaning
ascribed by Courvoisier to this symbol.
| В случае ртутного зеркала, релевантное направление местная
вертикаль и, следовательно, β здесь имеет такой же общий смысл, который
Курвуазье приписывает этому символу.
|
| 161
| Relative to the proper reference system of the mirror there is
an aberration effect, and the angles of incidence (z) and reflection
(z') are:
| По отношению к собственной системе отсчета зеркала есть эффект аберрации, а углы падения (z) и отражения (z′) составляют:
|
| 162
| z = θ + α cos θ β sin θ (6)
| z = θ + α cos θ β sin θ (6)
|
| 163
| z = θ' + α cos θ' + β sin θ' (7)
| z = θ′ + α cos θ′ + β sin θ′ (7)
|
| 164
| where α is component of the velocity v/c of the mirror parallel to its surface.
| где α является составляющей скорости v / c зеркала, параллельной его поверхности.
|
| 165
| Notice that this is the classical aberration effect.
| Заметим, что это классический эффект аберрации.
|
| 166
| A relativistic analysis would lead to a different result.
| Релятивистской анализ привел бы к другому результату.
|
| 167
|
|
|
| 168
| The measured effect is the difference between z' and z:
| Измеренный эффект представляет собой разницу между z′ и z:
|
| 169
| z' z = (θ' θ) + α (cos θ' cos θ) + β (sin θ' sin θ) (8)
| z′ z = (θ′ θ) + α (cos θ′ cos θ) + β (sin θ′ sin θ) (8)
|
| 170
| Taking into account the above equations and making suitable substitutions, one obtains the approximate result:
| С учетом приведенных выше уравнений и принятия соответствующих замен, можно получить приблизительное результат:
|
| 171
| z' z = 2αβ sin2 z (9)
| z′ z = 2αβ sin2 z (9)
|
| 172
| Replacing α and β by their values in Eqs. (1) and (2), one obtains:
| Заменяя α и β на их значения в формулах (1) и (2), получим:
|
| 173
| z' z = [(v/c)2 sin2 z].[sin 2ϕ.sin2 D + cos 2ϕ.sin 2D. cos (θA) sin 2ϕ.cos2D.cos2(θA)]
(10)
| z′ z = [(v/c)2 sin2 z].[sin 2ϕ.sin2 D + cos 2ϕ.sin 2D.cos (θA) sin 2ϕ.cos2D.cos2(θA)]
(10)
|
| 174
| Notice that this equation contains a constant term and two
periodical components with different periods one sidereal day [cos
(θA)] and half a sidereal day [cos2 (θA)].
| Обратите внимание, что это уравнение содержит постоянный член и
два периодических компонента с различными периодами один для звездных
суток, [cos (θA)] и половину звездных суток [cos2 (θA)].
|
| 175
| Therefore, from a suitable analysis of the data it should be
possible to obtain the speed (v/c), the declination (D) and the right
ascension (A) of the motion of the Earth relative to the ether.
| Таким образом, из соответствующего анализа данных должна
появиться возможность получить скорость (v/c), склонение (D) и прямое
восхождение (A) движения Земли относительно эфира.
|
| 176
|
|
|
- Re: Черная дыра
(А.П. Васи,
13.10.2013 20:19, 99.9 КБайт)
| 177
|
|
|
| 178
| The Leyden measurements had used four stars close to the North Pole.
| При измерениях в Лейдене использовались четыре звезды, близкие к Северному полюсу.
|
| 179
| The difference zz' was measured in a series of observations, at the times of upper and lower culmination of each star.
| Разница zz′ была измерена в серии наблюдений в моменты верхней и нижней кульминации каждой звезды.
|
| 180
| The observed values of the periodical components of zz'
amounted to less than 1'', varying from 0.04'' for one of the stars to
about 0.5″ for another.
| Наблюдаемые значения периодических компонент zz′ составили
менее 1″, с вариацией от 0,04″ для одной из звезд до 0,5″ для другой.
|
| 181
| The error of the measurements was estimated as 0.01″, therefore the effect was regarded as significant.
| Погрешность измерений была оценена как 0,01″, поэтому эффект расценен как значимый.
|
| 182
| From the Leyden data Courvoisier obtained the results:
| Из Лейденских данных Курвуазье были получены результаты:
|
| 183
| A = 104 21; D = +39 27; v = 810 215 km/s
| A = 104 21; D = +39 27; v = 810 215 км/с
|
| 184
| {14} The estimated error of the speed amounted
to about 25%.
| Оцениваемая ошибка скорости составила около 25%.
|
| 185
| The errors of the right ascension and declination amounted to about 1/15 of the full circle.
| Ошибки прямого восхождения и склонения составили около 1/15 полного круга.
|
| 186
| Between 1921 and 1922 Courvoisier repeated the Leyden measurements, but with a slight change of method.
| Между 1921 и 1922 гг. Курвуазье повторил лейденские измерения, но с небольшим изменением метода.
|
| 187
| Instead of a meridian circle he used a Wanschaff vertical
circle that enabled him to make measurements of the stars at any time
during the night.
| Вместо меридианного круга он использовал вертикальный круг
Ваншаффа, который позволил ему произвести измерения звезд в любое время в
течение ночи.
|
| 188
| Therefore his measurements were not limited to two sidereal times for each star.
| Поэтому его измерения не были ограничены двумя моментами звездного времени для каждой звезды.
|
| 189
|
|
|
| 190
| From 4 June to 14 December 1921 he made a series of 142
measurements of the polar star BD +89.3, and from 18 March to 23 May
1922 he made further 64 determinations of zz'.
| С 4 июня по 14 декабря 1921 году он произвел серию из 142
измерений Полярной звезды BD 89,3 , а с 18 марта по 23 мая 1922 г. он
выполнил дальнейшие 64 определения zz′.
|
| 191
| From those measurements Courvoisier obtained:
| Из этих измерений Курвуазье получил:
|
| 192
| A = 93 7; D = +27 12; v = 652 71 km/s
| A = 93 7; D = +27 12; v = 652 71 км/с
|
| 193
| The estimated relative error of the speed was reduced to about
10% and the errors of the right ascension and declination amounted to
less than 1/30 of the full circle.
| Расчетная относительная ошибка определения скорости снизилась
до около 10%, а ошибки определения прямого восхождения и склонения
составили менее чем 1/30 полного круга.
|
| 194
| Courvoisiers work called the attention of a French astronomer,
the director of the Strasbourg observatory, Ernest Esclangon, who
repeated those measurements.18
| Работа Курвуазье обратила на себя внимание французского
астронома, директора Страсбургской обсерватории, Эрнеста Эсклангона,
который повторил эти измерения. 18
|
| 195
| He confirmed the existence of a systematic effect of the same order of magnitude, and computed the values of A=69 and D=44.
| Он подтвердил существование систематического эффекта того же порядка величины, и вычислил значения A=69 и D=44.
|
| 196
| Esclangon did not publish the estimated errors of his evaluation, nor the estimated speed of the Earth.
| Эсклангон не опубликовал ни расчетные ошибки его оценки, ни ожидаемую скорость Земли.
|
| 197
|
|
|
| 198
| Other evaluations were later obtained by Courvoisier using
measurements made at München (19301931) and Breslau (19331935), with
the following results:
| Другие данные были позднее получены Курвуазье с использованием
измерений, проведенных в Мюнхене (1930-1931) и Бреславле (1933-1935), со
следующими результатами:
|
| 199
|
| München
| Breslau (1)
| Breslau (2)
|
| A = 73 6
| A = 92 12
| A = 80 4
|
| D = +40 (estimated)19
| D = +44 25
| D = +30 10
|
| v = 889 93 km/s
| v = 927 200 km/s
| v = 700 60 km/s |
|
| Мюнхен
| Бреславль (1)
| Бреславль (2)
|
| A = 73 6
| A = 92 12
| A = 80 4
|
| D = +40 (оценка) 19
| D = +44 25
| D = +30 10
|
| V = 889 93 км / с
| V = 927 200 км / с
| V = 700 60 км / с |
|
| 200
| The results obtained in the second Breslau series presented the smallest errors.
| Результаты, полученные во второй серии Бреславля, представлены наименьшими ошибками.
|
| 201
|
|
|
| 202
| In 1945, after his retirement, Courvoisier made a final series of observations from Basel.
| В 1945 году, после выхода на пенсию, Курвуазье выполнил окончательные серии наблюдений в Базеле.
|
| 203
| He obtained the following results:
| Он получил следующие результаты:
|
| 204
| A = 60 14; D = +40 (estimated); v = 656 157 km/s
| A = 60 14 , D = +40 (оценка), v = 656 157 км / с
|
| 205
| {15}
If we compare all the series of measurements, we notice that the right
ascension varied between 60 and 104 (more than the estimated errors);
the declination varied between 39 and 44 (within the estimated
errors);20 and the speed varied between 652 and 927 km/s (within estimated errors).
| Если сравнить все серии измерений, мы замечаем, что прямое
восхождение варьировалась между 60 и 104 (более чем расчетная
ошибка); склонение от 39 до 44 (в пределах расчетных ошибок), 20 и скорость от 652 до 927 км / с (в пределах расчетных ошибок).
|
| 206
| Notice that it is very hard to explain away Courvoisier's
results as due to instrument errors, because the observed effect varied
with periods of one sidereal day and half sidereal day.
| Обратите внимание, что очень трудно объяснить результаты
Курвуазье инструментальными погрешностями, так как наблюдаемый эффект
изменяется с периодами в одни звездные сутки и половину звездных суток.
|
| 207
| All common causes of error (gravity changes, temperature changes, etc.) would vary with periods of one (or half) solar day.
| Все распространенные причины ошибок (изменения силы тяжести,
изменения температуры и т.д.) должны меняться с периодом в одни (или
половину) солнечных суток.
|
| 208
| Tidal influences due to the Moon would have periods that could
also be easily distinguished from the effects predicted by Courvoisier.
| Приливные влияния Луны будут иметь периоды, которые также могут быть легко отличимы от эффектов, предсказанных Курвуазье.
|
| 209
| Besides that, the data used by Courvoisier was obtained with
different instruments at different places, and covered a time span of 80
years.
| Кроме того, данные, используемые Курвуазье, были получены с
помощью различных инструментов в разных местах, и охватывали промежуток
времени в 80 лет.
|
| 210
| The results presented by Courvoisier are therefore highly impressive and cannot be dismissed lightly.
| Результаты, представленные Курвуазье, следовательно, весьма впечатляет и не могут быть легко отвергнуты.
|
| 211
|
|
|
| 212
|
|
|
| 213
| In the first method used by Courvoisier, the stars work as mere point-like light sources.
| В первом методе, который использовал Курвуазье, звезды используются как простые точечные источники света.
|
| 214
| There is nothing peculiarly astronomical in the observed
effect because, according to Courvoisier's theory, this was ascribed to
the principle of the moving mirror.
| Там нет ничего специфически астрономического в наблюдаемом
эффекте, потому что, согласно теории Курвуазье, это было описано как
принцип движущегося зеркала.
|
| 215
| Therefore, similar effects should occur for terrestrial light sources, too.
| Таким образом, подобные эффекты должны также возникать и для наземных источников света.
|
| 216
|
|
|
| 217
| Accordingly, Courvoisier was led to build a new instrument: an optical device for measuring absolute motion (.... 6).21 He used two small telescopes that
were placed in an underground room where the temperature was fairly constant.
| Соответственно, Курвуазье это привело к созданию нового
инструмента:. оптического устройства для измерения абсолютного движения
(рис. 6) 21 Он использовал два небольших телескопа, которые
были размещены в подземном помещении, где температура была довольно
постоянной.
|
| 218
| Both telescopes pointed obliquely (zenithal distance = 60) to a mercury mirror that was placed between them.
| Оба телескопа были наклонены (зенитное расстояние = 60 ) к ртутному зеркалу, которое было помещено между ними.
|
| 219
| They were mounted in a vertical plane in the East-West direction.
| Они были установлены в вертикальной плоскости в направлении Восток-Запад.
|
| 220
| One of the telescopes had a small electric light close to its
reticule, and this was the light source that was observed from the
second telescope.
| Один из телескопов имел небольшое электрическое освещение
вблизи от ее креста визирных нитей, и это было источником света, который
наблюдался во второй телескоп.
|
| 221
| Both telescopes were first adjusted so that it was possible to
see the reflection of the illuminated reticule of the first telescope
from the second telescope.
| Оба телескопа сначала были настроены таким образом, чтобы можно
было увидеть отражение освещенной сетки из первой трубы от второго
телескопа.
|
| 222
| They were then fastened in those directions.
| Затем они были закреплены в этих направлениях.
|
| 223
| Of course, the angles of the telescopes with the local vertical were sensibly equal.
| Конечно, углы телескопов с местной вертикали были очевидно равны.
|
| 224
| The experiment did not try to measure any difference between those angles.
| Эксперимент не пытался измерить какое-либо различие между этими углами.
|
| 225
| It attempted to detect small periodical changes of the position
of the image of the first telescope reticule as observed from the
second one.
| Он был предназначен для обнаружения небольших периодических
изменений в положении креста визирных нитей первого телескопа, при их
наблюдении из второго телескопа.
|
| 226
| The apparent motion of {16} the reticule
was measured with the aid of the ocular micrometer of the second telescope.
| Видимое движение перекрестия было измерено с помощью окулярного микрометра второго телескопа.
|
| 227
|
|
|
| 228
| Using this device, Courvoisier made two series of observations in 1926 and 1927.
| С помощью этого устройства Курвуазье выполнил две серии наблюдений в 1926 и 1927 годах.
|
| 229
| Afterwards, he had a special instrument built for this purpose, and made a third series of observations in 1932.
| Впоследствии, он построил специальный инструмент для этой цели, и выполнил третью серию наблюдений в 1932 году.
|
| 230
|
|
|
| 231
| In his first experiments the telescopes were placed in a vertical plane in the East-West direction.
| В его первых экспериментах телескопы были размещены в вертикальной плоскости в направлении восток-запад.
|
| 232
| In 1926 and 1928 Courvoisier built two new instruments that could be rotated.
| В 1926 и 1928 годах Курвуазье построил два новых инструмента, которые могли вращаться.
|
| 233
| He expected that this would improve his measurements.
| Он ожидал, что это будет способствовать улучшению его измерений.
|
| 234
| However, he found out that it was impossible to compare
measurements when the device was rotated, due to mechanical problems,
and the instruments could only be effectively used in a fixed position.
| Тем не менее, он выяснил, что оказалось невозможным сравнивать
измерения, когда устройство поворачивалось, из-за механических проблем, и
инструменты могут быть эффективно использованы только в фиксированном
положении.
|
| 235
|
|
|
| 236
| The equation used to compute the effect was similar to that
used in the case of the observation of stars, but instead of the North
component of the speed, it was necessary to take into account the West
component.
| Уравнение, используемое для вычисления эффекта, был аналогично
тому, которое использовалось в случае наблюдения звезд, но вместо
северной компоненты скорости, было необходимо принимать во внимание
западную компоненту.
|
| 237
| As in the former case, the resulting equation has a constant
term plus variable components with periods of one sidereal day and half
sidereal day.
| Как и в предыдущем случае, результирующее уравнение имеет
постоянный член плюс переменные составляющие с периодами в одни звездные
сутки и половину звездных суток.
|
| 238
|
|
|
| 239
| 
|
| 240
| .... 6. Courvoisiers double telescope apparatus for measuring the motion of the Earth through the ether.
| Рис. 6. Двойной телескоп Курвуазье аппарат для измерения движения Земли через эфир.
|
| 241
|
|
|
| 242
| {17} Table 1. Measurements made by Courvoisier
in 1926 with the double telescope instrument.
| Таблица 1. Измерения, выполненные в 1926 году Курвуазье с инструментом в виде двойного телескопа.
|
| 243
|
| First series:
|
| Sidereal time 0
| (z z') + constant
| number of measurements
|
| 0.32 h
| 0.08″
| 21
|
| 1.23 h
| + 0.04″
| 64
|
| 2.45 h
| + 0.07″
| 14
|
| 3.31 h
| 0.38″
| 56
|
| 4.28 h
| 0.38″
| 14
|
| 5.28 h
| 0.57″
| 68
|
| 7.37 h
| 0.58″
| 55
|
| 9.29 h
| 0.57″
| 64
|
| 11.24 h
| 0.24″
| 30
|
| 12.73 h
| 0.04″
| 20
|
| 21.91 h
| + 0.21″
| 38
|
| 23.32 h
| + 0.08″
| 45 |
|
| Первая серия:
|
| Звездное время θ
| (z z′) + константа
| Количество измерений
|
| 0,32 ч
| 0.08 ″
| 21
|
| 1,23 ч
| + 0.04 ″
| 64
|
| 2,45 ч
| + 0,07 ″
| 14
|
| 3,31 ч
| 0,38 ″
| 56
|
| 4,28 ч
| 0,38 ″
| 14
|
| 5,28 ч
| 0,57 ″
| 68
|
| 7,37 ч
| 0,58 ″
| 55
|
| 9,29 ч
| 0,57 ″
| 64
|
| 11,24 ч
| 0,24 ″
| +30
|
| 12,73 ч
| 0,04 ″
| 20
|
| 21,91 ч
| + 0,21 ″
| 38
|
| 23,32 ч
| + 0,08 ″
| 45 |
|
| 244
|
|
|
| 245
| Table 2. Measurements made by Courvoisier in 1927 with the double telescope instrument.
| Таблица 2. Измерения, выполненные в 1927 году Курвуазье с инструментом в виде двойного телескопа.
|
| 246
|
| Second series:
|
| Sidereal time 0
| (z z') + constant
| number of measurements
|
| 2.9 h
| + 1.54″
| 4
|
| 7.3 h
| + 0.28″
| 6
|
| 8.2 h
| + 0.28″
| 7
|
| 9.1 h
| 0.01″
| 7
|
| 10.1 h
| + 0.23″
| 6
|
| 11.4 h
| + 0.56″
| 5
|
| 12.3 h
| + 0.60″
| 5
|
| 13.7 h
| + 0.52″
| 7
|
| 15.5 h
| + 0.84″
| 6
|
| 17.9 h
| + 0.88″
| 7
|
| 19.9 h
| + 0.80″
| 7 |
|
| Вторая серия:
|
| Звездное время θ
| (z z′) + константа
| Количество измерений
|
| 2,9 ч
| + 1.54
| 4
|
| 7,3 ч
| + 0,28″
| 6
|
| 8,2 ч
| + 0,28″
| 7
|
| 9,1 ч
| 0,01″
| 7
|
| 10.1 ч
| + 0,23″
| 6
|
| 11.4 ч
| + 0,56″
| 5
|
| 12.3 ч
| + 0,60″
| 5
|
| 13,7 ч
| + 0,52″
| 7
|
| 15,5 ч
| + 0,84″
| 6
|
| 17,9 ч
| + 0,88″
| 7
|
| 19,9 ч
| + 0,80″
| 7 |
|
| 247
|
|
|
| 248
| {18} The first series comprised 489 observations,
and the second series only 67 observations.
| Первая серия составила 489 наблюдений, а вторая только 67 серий наблюдений.
|
| 249
| From the first series, Courvoisier computed the following values:
| Из первой серии Курвуазье вычислил следующие значения:
|
| 250
| A = 70 6; D = +33 11; v = 493 54 km/s
| A = 70 6; D = +33 11; v = 493 54 км/с
|
| 251
| From the second series, he obtained the results:
| Из второй серии он получил такие результаты:
|
| 252
| A = 22 6; D = +72 11; v = 606 45 km/s
| A = 22 6; D = +72 11; v = 606 45 км/с
|
| 253
| Of course, the results obtained from the first series of
measurements seemed more reliable than those from the second series, and
they exhibited a closer agreement with former measurements.
| Конечно, результаты, полученные в первой серии измерений
представляются более надежным, чем от второго серии, и они показали
более близкое соответствие с прежними измерениями.
|
| 254
|
|
|
| 255
| Notice that, although those measurements attempted to detect
the same kind of effects as the astronomical observations - that is, a
difference between angle of incidence and angle of reflection in a
moving mirror - the star observations used the North-South direction,
and the cave experiments employed the East-West direction.
| Обратите внимание, что, хотя эти измерения делали попытку
обнаружить такие же последствия, что и астрономические наблюдения то
есть, разницу между углом падения и углом отражения в движущемся зеркале
звездные наблюдения использовали направление север-юг, а эксперименты
в закрытом помещении использовали направление восток-запад.
|
| 256
| The equations were different, and nevertheless Courvoisier
obtained a nice agreement between the new device and the former results.
| Уравнения были разные, и тем не менее Курвуазье получил хорошее согласие между новым устройством и прежними результатами.
|
| 257
|
|
|
| 258
|
|
|
| 259
| In 1928 Courvoisier built another device to measure the speed of the Earth using the principle of the moving mirror.
| В 1928 г. Курвуазье построил другое устройство для измерения скорости Земли с использованием принципа движущегося зеркала.
|
| 260
| Instead of using two telescopes, he used a single telescope, with two perpendicular mirrors in front of its objective (.... 7).
| Вместо применения двух телескопов, он использовал один
телескоп, с двумя перпендикулярными зеркалами перед его объективом (рис.
7).
|
| 261
| The body of the telescope was placed in a horizontal position.
| Труба телескопа была размещена в горизонтальном положении.
|
| 262
| The mirrors were adjusted so that it was possible to observe
the reflected image of the thread micrometer of the telescope in close
coincidence with the real micrometer thread.
| Зеркала были отрегулированы таким образом, чтобы можно было
наблюдать отраженное изображение нити микрометра телескопа в близком
совпадении с реальной нитью микрометра.
|
| 263
| He predicted that the relative position of the image and the
thread should undergo periodic fluctuations, and computed the predicted
effect.
| Он предсказал, что относительное положение изображения и нити
должно подвергаться периодическим колебаниям, и вычислил предсказанный
эффект.
|
| 264
|
|
|
| 265
| From April to June 1928 Courvoisier obtained a series of 53
measurements, both in the North-South and in the East-West directions,
and he computed the following values:
| С апреля по июнь 1928 г. Курвуазье была получена серия из 53
измерений, как в направлении север-юг, так и восток-запад, и он вычислил
следующие значения:
|
| 266
| A = 74 1; D = +36 1; v = 496 10 km/s
| A = 74 1; D = +36 1; v = 496 10 км/с
|
| 267
| The first series of measurements was made from 31 July and 6
August 1926, with observations spanning between 3 and 20 o'clock
sidereal time; the second one, from 28 February to 29 May 1927, with
observations covering the period from 21 to 13 o'clock sidereal time.
| Первая серия измерений была проведена с 31 июля и 6 августа
1926 года, с наблюдениями, охватывающими от 3 до 20 часов звездного
времени; вторая серия с 28 февраля по 29 мая 1927 года, с наблюдениями
за период с 21 до 13 часов звездного времени.
|
| 268
| Both series comprised more than 500 measurements.
| Обе серии составили более 500 измерений.
|
| 269
| Tables 1 and 2 shows the mean results obtained by Courvoisier for each sidereal time:
| В таблицах 1 и 2 показаны средние результаты, полученные Курвуазье для каждого периода звездного времени:
|
| 270
|
|
|
| 271
| 
|
| 272
| .... 7. Courvoisiers coupled mirror device for measuring the motion of the Earth through the ether.
| Рис. 7. Устройство Курвуазье со связанными зеркалами для измерения движения Земли относительно эфира.
|
| 273
|
|
|
| 274
| {19} Courvoisiers new experiment was probably
suggested by a similar arrangement that had been used by Esclangon in 1927.23
| Новый эксперимент Курвуазье был, вероятно, подсказан подобным устройством, которое было использовано Эсклангоном в 1927 году. 23
|
| 275
| The French astronomer used two mirrors, but light underwent three reflections (.... 8).
| Французский астроном использовал два зеркала, но свет испытывал три отражения (рис. 8).
|
| 276
| The maximum effect occurred at 3 h or 15 h sidereal time, corresponding to A = 45 or 225.
| Максимальный эффект появлялся для 3 ч или 15 ч звездного времени, что соответствует A = 45 или 225 .
|
| 277
| Esclangon did not compute the speed of the Earth through the
ether indeed, he did not even provide a definite interpretation of the
phenomenon.
| Эсклангон не вычислял скорость Земли через эфир более того, он даже не обеспечивают определенную интерпретацию явления.
|
| 278
| 
|
| 279
| .... 8. Esclangons coupled mirror device for measuring the
motion of the Earth through the ether (a), and a graphical
representation of his results (b), showing the observed angular
fluctuations as a function of sidereal time.
| Рис. 8. Устройство Эсклангона со связанными зеркалами для
измерения движения Земли через эфир (а) и графическое представление его
результатов (б), показывающих наблюдаемые угловые колебания в
зависимости от звездного времени.
|
| 280
|
|
|
| 281
|
|
|
| 282
| As described above, Courvoisier's second attempt to measure the
absolute velocity of the Earth was grounded upon his analysis of the
Lorentz contraction of the Earth (.... 9).
| Как описано выше, вторая попытка Курвуазье измерить абсолютную
скорость Земли была основана на его анализе сокращения Лоренца для Земли
(рис. 9).
|
| 283
| In this case, Courvoisier supposed that the local vertical
would undergo a change, due to the Lorentz contraction of the Earth, and
this change would be observable as a periodical fluctuation in the
angle between the North Pole and the zenith, as a function of the
sidereal time.
| В этом случае Курвуазье предположил, что местная вертикаль
претерпит изменения в связи с сокращением Лоренца для Земли, и это
изменение будет наблюдаться как периодическое колебание угла между
Северным полюсом и зенитом, как функция звездное время.
|
| 284
|
|
|
| 285
| Courvoisier's theoretical analysis led him to predict that the
variation of the zenithal distance Δz of a star close to the North Pole
would obey the approximate relation:
| Теоретический анализ Курвуазье привел его к предсказанию, что
изменение зенитного расстояния Δz близости звезды к Северному полюсу
должны подчиняться приближенному соотношению:
|
| 286
| Δz = 1/2 αβ (11)
| Δz = 1/2 αβ (11)
|
| 287
| {20} There are some special observational
difficulties in this second method.
| Есть несколько специфических трудностей в наблюдении для этого второго способа.
|
| 288
| If it were possible to observe a star laying exactly in the
direction of the celestial North Pole, the observation would be quite
simple.
| Если бы можно было наблюдать звезду, лежащую точно в
направлении небесного Северного полюса, наблюдение окажется довольно
простым.
|
| 289
| However, if the star is not exactly in the direction of the
pole, its zenithal distance will depend on the sidereal time of the
observation.
| Однако, если звезда находится не точно в направлении полюса, ее
зенитное расстояние будет зависеть от звездного времени наблюдения.
|
| 290
| This classical large effect would have, therefore, a period of
one sidereal day and would interfere with any attempt to measure any
influence due to the motion through the ether with a period of one
sidereal day.
| Этот классический большой эффект имеет, таким образом, период
одни звездные сутки, и он должен помешать любой попытке измерить
какое-либо влияние за счет движения через эфир с периодом один звездный
день.
|
| 291
| Other interfering effects, such as temperature changes, vary
with a period of about one solar day, and they are very large and
irregular.
| Другие мешающие эффекты, такие как изменения температуры,
изменяются с периодом приблизительно один солнечный день, и они очень
большие и нерегулярные.
|
| 292
| For those reasons, Courvoisier gave up the attempt of finding
the amplitude of the sidereal day effect, and only computed the half
sidereal day effect.
| По этим причинам, Курвуазье оставил попытку нахождения
амплитуды эффекта за звездные сутки, и только вычислил эффект, связанный
с половиной звездных суток.
|
| 293
| It was impossible, therefore, to find all parameters, and he
assumed a value of 40 for the declination, and computed the speed and
right ascension of the motion of the Earth relative to the ether.
| Было невозможно, таким образом, найти все параметры, и он
предположил значение 40 для склонения, и вычислил скорость и прямое
восхождение движения Земли относительно эфира.
|
| 294
| Dropping out the component corresponding to the period of one sidereal day, he obtained the following equation:
| Отбросив компоненту, соответствующую периоду в один звездный день, он получил следующее уравнение:
|
| 295
| Δz = (1/4)(v/c)2.sin 2ϕ (const.
| Δz = (1/4)(v/c)2.sin 2ϕ (const.
|
| 296
| cos2D.cos2(θA)] (12)
| cos2D.cos2(θA)] (12)
|
| 297
| 
|
| 298
| {21} .... 9.
| Рис. 9.
|
| 299
| According to Courvoisier, the Lorentz contraction of the Earth
and of optical instruments could have a small observable influence on
astronomical observations and terrestrial experiments.
| Согласно Курвуазье, сокращение Лоренца для Земли и оптических
приборов может иметь небольшое влияние на астрономические наблюдения и
наземные эксперименты.
|
| 300
| Using the data he had already obtained from 1914 to 1917, and
combining those results with other measurements he made in 19211922 and
1925-1926, with the same instrument, Courvoisier obtained the following
result:
| Используя данные, которые он уже получил с 1914 по 1917 гг. и
объединив эти результаты с другими измерениями, которые он сделал в
19211922 и 19251926 гг. с тем же инструментом, Курвуазье получил
следующий результат:
|
| 301
| A = 74 3; [D = +40]; v = 587 48 km/s
| A = 74 3; [D = +40]; v = 587 48 км/с
|
| 302
| He also analyzed measurements that had been obtained in routine
observations at the Paris observatory, in the period 1899-1901. All
those series of observations exhibited similar variations with a period
of 12 sidereal hours.
| Он также проанализировал измерения, которые были получены в
регулярных наблюдениях в Парижской обсерватории в период 18991901 гг.
Все эти серии наблюдений показали похожие вариации с периодом 12
звездных часов.
|
| 303
| Assuming a value of 40 for the declination, he obtained the following results:
| Предположив значение 40 для склонения, он получил следующие результаты:
|
| 304
| A = 70 11; [D = +40]; v = 810 166 km/s
| A = 70 11; [D = +40]; v = 810 166 км/с
|
| 305
| Afterwards Courvoisier also computed the motion of the Earth
using measurements from Breslau (19231925 and 19331935) and from
München (1927-1931).
| Впоследствии Курвуазье также вычислил движение Земли по измерениям в Бреславле (19231925 и 19331935) и в Мюнхене (19271931).
|
| 306
| Taking into account all the observations, he obtained the following final result:
| Принимая во внимание все наблюдения, он получил следующий окончательный результат:
|
| 307
| A = 65 10; [D = +40]; v = 574 97 km/s
| A = 65 10; [D = +40]; v = 574 97 км/с
|
| 308
| {22}
|
|
| 309
| The effects predicted by Courvoisier as a consequence of the
Lorentz contraction of the Earth should depend on the latitude of the
observatory.
| Эффекты, предсказанные Курвуазье как следствие сокращение Лоренца для Земли, должны зависеть от широты обсерватории.
|
| 310
| For that reason, if the same set of stars was observed from two
observatories at very different latitudes, there should exist a
systematic difference between the measured declinations of the stars, as
a function of sidereal time.
| По этой причине, если тот же набор звезд наблюдался из двух
обсерваторий, расположенных на очень разных широтах, должны существовать
систематические различия между измеренными склонениями звезд, как
функция от звездного времени.
|
| 311
| To test the existence of this effect, Courvoisier analyzed the catalogues containing measurements made at Heidelberg (ϕ1 = + 49.24) and at Cape Town,
South Africa (ϕ2 = 33.48).
| Чтобы проверить существование этого эффекта, Курвуазье
проанализировал каталоги, содержащие измерения, выполненные в
Гейдельберге (ϕ1 = + 49.24) и в Кейптауне, Южная Африка (ϕ2 = 33.48).
|
| 312
| Let D1 be the declination of some star measured from Heidelberg, and D2 the declination of the same star measured from Cape of Good Hope.
| Пусть D 1 склонение некоторой звезды, измеренное в Гейдельберге, а D 2 склонение той же звезды, измеренное на мысе Доброй Надежды.
|
| 313
| Each declination, according to Courvoisier's analysis, undergoes a periodical change:
| Каждое склонение, согласно анализу Курвуазье, претерпевает периодические изменения:
|
| 314
| Δz1 = 1/2 α1β1 Δz2 = 1/2 α2β2
(13)
| Δz1 = 1/2 α1β1 Δz2 = 1/2 α2β2
(13)
|
| 315
| Those effects are not equal; therefore, the difference between
the declinations measured at the two observatories should undergo a
periodical change:
| Эти эффекты не равны, и поэтому разница между склонениями,
измеренными для двух обсерваторий, должна подвергаться периодическому
изменению:
|
| 316
| D1 D2 = 1/2 (α1β1 α2β2) (14)
| D1 D2 = 1/2 (α1β1 α2β2) (14)
|
| 317
| Using the typical values A=75 and D=40 obtained in former
measurements, and taking into account the latitudes of Heidelberg and
Cape Town, Courvoisier predicted that there should exist a difference
between the measured declinations of the stars that should depend on
their right ascension a:
| Используя типичные значения A=75 и D=40, полученные в
предыдущих измерениях и с учетом широты Гейдельберге и Кейптауна,
Курвуазье предсказал, что должна существовать разница между измеренным
склонением звезд, которые должны зависеть от их прямого восхождения:
|
| 318
| D1 D2 = + 0.16′′ 0.18′′.
| D1 D2 = + 0.16′′ 0.18′′.
|
| 319
| cos (α 5h) 0.16′′.
| cos (α 5h) 0.16′′.
|
| 320
| cos 2(α 5h) (15)
| cos 2(α 5h) (15)
|
| 321
| The amplitude was obtained by comparing the astronomical data of the two observatories, and led to v =750 km/s.
| Амплитуда была получена путем сопоставления астрономических данные двух обсерваторий, и привела к V = 750 км / с.
|
| 322
| Table 3 contains Courvoisiers comparison between the observed and predicted values of D1D2.
| В таблице 3 приведены сравнения Курвуазье в период между наблюдаемым и прогнозируемым значениям D1D2.
|
| 323
| The third column of the table presented the observed values
corrected for null declination, in order to avoid classical errors due
to atmospheric refraction, etc.
| В третьем столбце таблицы представлены наблюдаемые значения с
поправкой на нулевое склонение, для того, чтобы избежать классических
ошибок, связанных с атмосферной рефракцией и т.д.
|
| 324
| There is a better agreement between the theoretical prediction and the corrected values than with the raw data.
| Существует лучшее согласие между теоретическими предсказаниями и скорректированными значениями, чем с сырыми данными.
|
| 325
|
|
|
| 326
| In his analysis of the second method, Courvoisier assumed that
the Lorentz contraction of the Earth produces a local periodical change
of the direction of the gravitational field.
| В своем анализе второго способа Курвуазье предполагал, что
сокращение Лоренца для Земли создает локальное периодическое изменение
направления гравитационного поля.
|
| 327
| This effect was not compensated by changes in the direction of the astronomical instruments.
| Этот эффект не компенсируется за счет изменения направления астрономических инструментов.
|
| 328
| Therefore, he was led to think that the effect could also be detected in an experiment using a terrestrial light source.
| Таким образом, он пришел к мнению, что эффект может быть также
обнаружен в ходе эксперимента с использованием наземного источника
света.
|
| 329
| {23} He placed a mercury mirror directly
below the observatory meridian circle and pointed the telescope downward.
| Он поместил ртутное зеркало непосредственно под меридиан обсерватории и направил телескопа вниз.
|
| 330
| The instrument was then delicately adjusted in such a way that
it was possible to observe the reflected image of the micrometer threads
superimposed to the real threads.
| Прибор был затем тонко отрегулирован таким образом, чтобы можно
было наблюдать отраженное изображение нитей микрометра, наложенные на
реальные нити.
|
| 331
| The position of the telescope was locked, and observations were
made of the relative displacement of the micrometer thread and its
image.
| Положение телескопа было зафиксировано, и были выполнены наблюдения относительного смещения нити микрометра и ее отражения.
|
| 332
| He predicted the following deflection in the East-West direction:
| Он предсказал следующие отклонения в направлении восток-запад:
|
| 333
| Δz = (1/4)(v/c)2.
| Δz = (1/4)(v/c)2.
|
| 334
| [sin ϕ.sin2D.sin (θA) + cos ϕ.cos2D.sin 2(θA)] (16)
| [sin ϕ.sin2D.sin (θA) + cos ϕ.cos2D.sin 2(θA)] (16)
|
| 335
| Table 3.
| Таблица 3.
|
| 336
| Difference between the declinations of a star (D1D2), observed from two distant observatories, as a function of sidereal time α.
| Различие между склонениями звезд (D1D2), наблюдаемое из двух удаленных обсерваторий, как функция от звездного времени α.
|
| 337
|
| α | D1D2
|
| observed
| observed (corrected)
| prediction
|
| 0 h
| + 0.35′′
| + 0.35′′
| + 0.26′′
|
| 1 h
| + 0.21′′
| + 0.21′′
| + 0.16′′
|
| 2 h
| + 0.01′′
| + 0.01′′
| + 0.04′′
|
| 3 h
| 0.07′′
| 0.07′′
| 0.07′′
|
| 4 h
| 0.17′′
| 0.17′′
| 0.16′′
|
| 5 h
| + 0.03′′
| + 0.03
| 0.17′′
|
| 6 h
| + 0.17′′
| + 0.17
| 0.14′′
|
| 7 h
| 0.03′′
| 0.03′′
| 0.06′′
|
| 8 h
| + 0.07′′
| + 0.07′′
| + 0.04′′
|
| 9 h
| + 0.10′′
| + 0.10′′
| + 0.14′′
|
| 10 h
| + 0.08′′
| + 0.08′′
| + 0.25′′
|
| 11 h
| + 0.09′′
| + 0.09′′
| + 0.32′′
|
| 12 h
| + 0.29′′
| + 0.29′′
| + 0.34′′
|
| 13 h
| + 0.32′′
| + 0.35′′
| + 0.32′′
|
| 14 h
| + 0.29′′
| + 0.39′′
| + 0.29′′
|
| 15 h
| 0.04′′
| + 0.22′′
| + 0.25′′
|
| 16 h
| 0.21′′
| + 0.13′′
| + 0.20′′
|
| 17 h
| 0.23′′
| + 0.18′′
| + 0.19′′
|
| 18 h
| 0.29′′
| + 0.12′′
| + 0.20′′
|
| 19 h
| 0.31′′
| + 0.10′′
| + 0.23′′
|
| 20 h
| 0.17′′
| + 0.17′′
| + 0.29′′
|
| 21 h
| + 0.04′′
| + 0.30′′
| + 0.33′′
|
| 22 h
| + 0.26′′
| + 0.36′′
| + 0.34′′
|
| 23 h
| + 0.38′′
| + 0.41′′
| + 0.32′′ |
|
| α | D1D2
|
| Наблюдение
| Наблюдение (скорректировано)
| Предсказание
|
| 0 ч
| + 0.35′′
| + 0.35′′
| + 0.26′′
|
| 1 ч
| + 0.21′′
| + 0.21′′
| + 0.16′′
|
| 2 ч
| + 0.01′′
| + 0.01′′
| + 0.04′′
|
| 3 ч
| 0.07′′
| 0.07′′
| 0.07′′
|
| 4 ч
| 0.17′′
| 0.17′′
| 0.16′′
|
| 5 ч
| + 0.03′′
| + 0.03
| 0.17′′
|
| 6 ч
| + 0.17′′
| + 0.17
| 0.14′′
|
| 7 ч
| 0.03′′
| 0.03′′
| 0.06′′
|
| 8 ч
| + 0.07′′
| + 0.07′′
| + 0.04′′
|
| 9 ч
| + 0.10′′
| + 0.10′′
| + 0.14′′
|
| 10 ч
| + 0.08′′
| + 0.08′′
| + 0.25′′
|
| 11 ч
| + 0.09′′
| + 0.09′′
| + 0.32′′
|
| 12 ч
| + 0.29′′
| + 0.29′′
| + 0.34′′
|
| 13 ч
| + 0.32′′
| + 0.35′′
| + 0.32′′
|
| 14 ч
| + 0.29′′
| + 0.39′′
| + 0.29′′
|
| 15 ч
| 0.04′′
| + 0.22′′
| + 0.25′′
|
| 16 ч
| 0.21′′
| + 0.13′′
| + 0.20′′
|
| 17 ч
| 0.23′′
| + 0.18′′
| + 0.19′′
|
| 18 ч
| 0.29′′
| + 0.12′′
| + 0.20′′
|
| 19 ч
| 0.31′′
| + 0.10′′
| + 0.23′′
|
| 20 ч
| 0.17′′
| + 0.17′′
| + 0.29′′
|
| 21 ч
| + 0.04′′
| + 0.30′′
| + 0.33′′
|
| 22 ч
| + 0.26′′
| + 0.36′′
| + 0.34′′
|
| 23 ч
| + 0.38′′
| + 0.41′′
| + 0.32′′ |
|
| 338
| {24} Courvoisier made two series of observations:
22-24 October and 22-25 November 1922.
| Курвуазье выполнил две серии наблюдений: 2224 октября и 2225 ноября 1922 года.
|
| 339
| He noticed that temperature changes affected the position of
the telescope, and that this influence had to be taken into account.
| Он заметил, что изменения температуры повлияло на положение телескопа, причем влияние это должно быть принято во внимание.
|
| 340
| From the uncorrected observed measurements he computed the following values:
| Из наблюдаемых неисправленных измерений он вычислил следующие значения:
|
| 341
| A = 74 10; D = +67 13; v = 920 73 km/s
| A = 74 10; D = +67 13; v = 920 73 км/с
|
| 342
| Applying a temperature correction, he obtained the following results:
| Применяя коррекцию температуры, он получил следующие результаты:
|
| 343
| A = 98 7; D = +25 11; v = 500 47 km/s
| A = 98 7; D = +25 11; v = 500 47 км/с
|
| 344
| This experiment was repeated by August Kopff, of the Heidelberg observatory, from 10 to 29 June 1923.
| Этот эксперимент был повторен Августом Копфом из Гейдельбергской обсерватории с 10 по 29 июня 1923 года.
|
| 345
| As in the case of Courvoisier's experiment, there was a strong
effect due to temperature changes (temperature varied between +6C and
+17C).
| Как и в случае эксперимента Курвуазье, не было сильного эффекта
в результате изменения температуры (температура колебалась от +6 С до
+17C).
|
| 346
| Courvoisier analyzed Kopff s data assuming the values A = 75 and D = +40.
| Курвуазье проанализировал данные Копфа, приняв значения A = 75 и D = +40.
|
| 347
| After applying temperature corrections, he obtained a speed of 753 57 km/s.
| После применения температурных поправок, он получил скорость 753 57 км/с.
|
| 348
|
|
|
| 349
| Courvoisier also attempted to detect the motion of the Earth relative to the ether by other methods.
| Курвуазье также попытался обнаружить движение Земли относительно эфира другими методами.
|
| 350
| He regarded the positive result of the nadir observation method
as a confirmation of his hypothesis that the Lorentzs contraction
produced an observable periodical change of the local vertical.
| Он считал положительными результаты наблюдения надира как
подтверждение своей гипотезы, что сокращение Лоренца производит
наблюдаемые периодические изменения местной вертикали.
|
| 351
| He soon devised other ways of observing such an effect.
| Вскоре он разработал другие способы наблюдения такого эффекта.
|
| 352
|
|
|
| 353
| One of the instruments he used was a plumb line attached to one of the columns of the Babelsberg observatory.
| Одним из используемых им инструментов был отвес, прикрепленный к одной из опор Бабельсбергской обсерватории.
|
| 354
| The main body of the plumb line was a metallic rod, 95 cm long.
| Основным телом линии отвеса был металлический стержень, 95 см в длину.
|
| 355
| At its lower end there was a mark that was illuminated and projected upon a wall.
| На его нижнем конце была отметка, которая была освещена и проецировалась на стену.
|
| 356
| It was possible to observe deflections of about 0.05″ of the direction of the plumb line, in the East-West direction.24
| Можно было наблюдать отклонения направления отвеса примерно на 0,05″ в направлении восток-запад. 24
|
| 357
| Measurements made in 1925 with this instrument led to a speed of the Earth of about 400 km/s, assuming A = 75 and D = +40.
| Измерения, проведенные в 1925 году с этим инструментом показали скорость Земли около 400 км/с, при A = 75 и D = +40 .
|
| 358
| In 1931 Courvoisier improved this instrument observing the motion of its tip with the aid of a microscope (.... 10).
| В 1931 году Курвуазье усовершенствовал этот инструмент, наблюдая за движением его конца с помощью микроскопа (рис. 10).
|
| 359
| Now he was able to compute the three parameters of the Earth's motion, obtaining:
| Теперь он был в состоянии вычислить три параметра движения Земли, получив:
|
| 360
| A = 64 6; D = +50 9; v = 367 29 km/s
| A = 64 6; D = +50 9; v = 367 29 км/с
|
| 361
| 
|
| 362
| {25}.... 10.
| Рис. 10.
|
| 363
| Courvoisiers plumb line apparatus for measuring oscillations of the local gravitational vertical due to Lorentz contraction.
| Отвес Курвуазье для измерения колебаний местной гравитационной вертикали из-за сокращения Лоренца.
|
| 364
| Similar observations were made by Esclangon, with the help of
André-Louis Danjon, using two horizontal pendulums with perpendicular
motions.25
| Аналогичные наблюдения выполнил Эксклангон с помощью Андре-Луи
Данжона, используя два горизонтальных маятника с перпендикулярными
движениями 25
|
| 365
| One of the pendulums lead to A=69; for the second pendulum,
A=52 Esclangon did not provide other information and did not attempt to
compute the speed of the Earth.
| Один из маятников показал A=69 ;. для второго маятника A =
52, Эсклангон не предоставил другие сведения и не пытался вычислить
скорость Земли.
|
| 366
| {26}
|
|
| 367
| Another way of observing the variation of the local vertical
direction, according to Courvoisier, was with the aid of bubble levels.26
| Другой способ наблюдения за изменением направления местной вертикали, по Курвуазье, был выполнен с помощью пузырьковых уровней. 26
|
| 368
| He used two very sensitive level meters.
| Он использовал два очень чувствительных уровнемеров.
|
| 369
| One of them was attached to the floor of the Babelsberg
underground clock room, and the other one was attached in a horizontal
position to one of the columns of the same room.
| Один из них был прикреплен к полу Бабельсбергской подземной
комнаты с часами, а другой был прикреплен в горизонтальном положении к
одной из опор этой же комнаты.
|
| 370
| Courvoisier measured the difference between the marks of the two level meters.
| Курвуазье измерили разницу между отметками двух уровнемеров.
|
| 371
| The maximum predicted effect was about 0.30″, and with the
delicate instruments used by Courvoisier it was possible to measure
angular changes as small as 0,03″.
| Максимальный ожидаемый эффект составил около 0,30″, и с точными
инструментами, используемыми Курвуазье, можно было измерить угловые
изменения величиной до 0,03″.
|
| 372
| In the first series of measurements between 15 and 26 June 1929, Courvoisier obtained the following results:
| В первой серии измерений между 15 и 26 июня 1929 года, Курвуазье были получены следующие результаты:
|
| 373
| A = 59 6; D = +51 9; v = 446 34 km/s
| A = 59 6; D = +51 9; v = 446 34 км/с
|
| 374
|
|
|
| 375
| According to Courvoisier's hypothesis, the Earth undergoes a
real contraction in the direction of its motion through the ether, and
this contraction would produce observable periodical changes of the
local value of gravity as a function of sidereal time.
| Согласно гипотезе Курвуазье, Земля подвергается реальным
сокращением в направлении ее движения через эфир, и это сокращение будет
производить наблюдаемые периодические изменения местного значение силы
тяжести в зависимости от звездного времени.
|
| 376
| Pendulum clocks at different places of the Earth should show
slightly different readings, and their phases should exhibit a
periodical relative fluctuation.
| Маятниковые часы в разных местах Земли должны показывать
немного различные значения, а их фазы должны обладать относительной
периодичностью колебаний.
|
| 377
| Courvoisier analyzed data on pendulum clocks of different astronomical observatories, in an attempt to detect this effect.
| Курвуазье проанализировал данные о маятниковых часах различных астрономических обсерваторий в попытке обнаружить этот эффект.
|
| 378
| Using radio signals it was possible to compare the rates of clocks at very distant observatories.
| Используя радиосигналы, можно сравнить ход часов для взаимно очень отдаленных обсерваторий.
|
| 379
| The Annapolis Observatory emitted regular time signals from its pendulum clocks.
| Обсерватория Аннаполиса транслировала регулярные сигналы времени от своих маятниковых часов.
|
| 380
| It was possible to compare the rate of those pendulums to those at another place.
| Можно было сравнить скорость их маятника там и в другом месте.
|
| 381
| Courvoisier asked the help of Bernhard Wanach, from Potsdam,
who compared the rate of the pendulum clocks of that observatory to the
signals received from Annapolis, from September 1921 to November 1922.27 Courvoisiers analysis of Wanachs data led to the following results:
| Курвуазье попросил помощи Бернхарда Ванаха из Потсдама, который
сравнил скорость маятниковых часов этой обсерватории с сигналами из
Аннаполиса с сентября 1921 по ноябрь 1922 г. 27 Анализ Курвуазье данных Ванаха привел к следующим результатам:
|
| 382
| A = 56 12; D = +40 (estimated); v = 873 228 km/s
| A = 56 12; D = +40 (оценка); v = 873 228 км/с
|
| 383
| Afterwards, a comparison was made using a comparison between the clocks of Annapolis, Potsdam, Ottawa, and Bordeaux.
| После этого было проведено сравнение при помощи сопоставления между часами в Аннаполисе, Потсдаме, Оттаве и Бордо.
|
| 384
| The mean result obtained by Courvoisier was:
| Средний результат, полученный Курвуазье, был:
|
| 385
| A = 81 5; D = +34 5; v = 650 50 km/s
| A = 81 5; D = +34 5; v = 650 50 км/с
|
| 386
| {27} Much later, Courvoisier presented another
confirmation of this effect.
| Много позже, Курвуазье представил еще одно подтверждение этого эффекта.
|
| 387
| He compared the catalogues of time correction of the
observatories of Greenwich, Potsdam, Buenos Aires and Mount Stromslo for
the period from 1948 to 1954.28
| Он сравнил каталоги временной коррекции обсерватории Гринвича,
Потсдама, Буэнос-Айреса и Маунт-Стромло за период с 1948 по 1954 год. 28
|
| 388
| There was a nice agreement between the theoretical predictions
and the observed time differences, especially in the case of the years
1951-1954.
| Было выявлено хорошее согласие между теоретическими
предсказаниями и наблюдаемыми различиям времени, особенно в случае
данных за 19511954 годы.
|
| 389
|
|
|
| 390
| Courvoisier supposed that the rate of pendulum clocks would
vary because of the periodical gravity changes, but mechanical
chronometers should not suffer similar changes.
| Курвуазье предполагал, что скорость маятниковых часов будет
меняться в результате периодических изменений силы тяжести, но
механические хронометры не должны быть подвержены подобным изменениям.
|
| 391
| Therefore it should be possible to observe effects due to the
absolute motion of the Earth comparing pendulum clocks to mechanical
chronometers at a single place.
| Поэтому должна быть возможность наблюдать эффекты, связанные с
абсолютным движением Земли, путем сравнения маятниковых часов и
механического хронометра в одном месте.
|
| 392
| Comparisons were made both at Babelsberg and at Potsdam (with the help of Wanach).
| Сравнения были сделаны в Бабельсберге и в Потсдаме (с помощью Ванаха).
|
| 393
| In his analysis, Courvoisier assumed the value D = +40 and obtained A = 104 9 and v = 750 km/s.
| В своем анализе Курвуазье предполагал значениe D = +40 и получил A = 104 9 и v = 750 km/s.
|
| 394
|
|
|
| 395
| If the Lorentz contraction of the Earth produces gravitational
effects, then it should be possible to find its influence on the tides.
| Если сокращение Лоренца для Земли производит гравитационные
эффекты, то должно быть возможность найти их влияние на приливы и
отливы.
|
| 396
| Esclangon analyzed a set of 166,500 tide measurements, made at Pola, on the Adriatic sea, from 1898 to 1916.
| Эсклангон проанализировал набор 166500 измерения прилива,
сделанные в Пула, на побережье Адриатического моря, с 1898 по 1916 год.
|
| 397
| He obtained a term with the period of on sidereal day, that
could not be associated with the Sun or the Moon, and ascribed it to a
dissymmetry of space.29
| Он получил элемент с периодом в звездные сутки, которые не
могут быть связаны с Солнцем или Луной, и отнес его к асимметрии
пространства 29
|
| 398
| This tidal effect could be described as:
| Этот приливной эффект может быть описан как:
|
| 399
| 48 mm.cos (t 146.1) + 25 mm.cos (t 244.6) (16)
| 48 mm.cos (t 146.1) + 25 mm.cos (t 244.6) (16)
|
| 400
| If the local gravity undergoes periodic changes, it should be possible to detect this effect with sensitive gravimeters.
| Если локальная сила тяжести претерпевает периодические
изменения, должна быть возможность обнаружить этот эффект
чувствительными гравиметрами.
|
| 401
| In 1927 Courvoisier (with the help of Sergei Gaposchkin)
attempted for the first time to measure gravity variations using a very
sensitive torsion gravimeter.30
| В 1927 г. Курвуазье (с помощью Сергея Гапошкина) впервые
попытался для измерения вариаций силы тяжести применить очень
чувствительный гравиметр кручения. 30
|
| 402
| The instrument could detect a change Δg/g of 3×106, corresponding to a displacement of 0.2 mm of the gravimeter pointer.
| Этот инструмент мог обнаружить изменение Δg/g of 3×106, что соответствует смещению 0,2 мм указателя гравиметра.
|
| 403
| From a series of measurements undertaken from 1927 to 1928 Courvoisier computed the following values:
| Из серии измерений, выполненных с 1927 по 1928 гг. Курвуазье вычислил следующие значения:
|
| 404
| A = 62 5; D = +32 8; v = 543 55 km/s
| A = 62 5; D = +32 8; v = 543 55 км/с
|
| 405
| {28} In 1932 Courvoisier obtained new results,
taking into account in this new paper some effects due to temperature and humidity.
| В 1932 г. Курвуазье были получены новые результаты, принимающие
во внимание в этой новой работе эффекты, связанные с температурой и
влажностью.
|
| 406
| The new results obtained by him were
| Новые результаты, полученные им, составили
|
| 407
| A = 50 7; D = +45 18; v = 498 78 km/s
| A = 50 7; D = +45 18; v = 498 78 км/с
|
| 408
| For the first time, Courvoisier's results were criticized and checked.
| Впервые результаты Курвуазье критиковались и были проверены.
|
| 409
| In 1932, Rudolf Tomaschek and Walter Schaffernicht reported
gravity measurements made with a new kind of gravimeter that was able to
detect changes Δg/g of 108.
| В 1932 году Рудольф Томашек и Уолтер Шаффернихт сообщили об
измерениях силы тяжести новым видом гравиметра, который был в состоянии
обнаружить изменения Δg/g порядка 108.
|
| 410
| The instrument was placed inside a cave in a mountain, where the temperature was constant to 0.001 C.
| Прибор был помещен в пещере в горах, где температура была постоянной до 0,001 C.
|
| 411
| No effect of the order of magnitude predicted by Courvoisier was observed.31
| Эффект того порядка, который был предсказан Курвуазье, не наблюдался. 31
|
| 412
|
|
|
| 413
| It is well known that in 1879 James Clerk Maxwell wrote to
David Peck Todd asking him about the possibility of computing the
velocity of the solar system through the ether using available data on
occultation of Jupiters satellites.32
| Хорошо известно, что в 1879 году Джеймс Клерк Максвелл писал
Дэвиду Пекку Тодду, спрашивая его о возможности вычисления скорости
Солнечной системы через эфир, с использованием имеющихся данных о
затмения спутников Юпитера. 32
|
| 414
| Maxwell supposed that the motion of the solar system would
produce an anisotropy of the speed of light that could be detected as a
fluctuation of the times of occultation of Jupiter's satellites,
observed from the Earth, with a period of about 12 years.
| Максвелл предположил, что движение Солнечной системы должно
производить анизотропию скорости света, которая может быть обнаружена
как флуктуация времени покрытия спутников Юпитера, наблюдаемых с Земли, с
периодом около 12 лет.
|
| 415
| Todd answered, however, that the measurements available at that time were not precise enough for such computations.
| Тодд ответил, однако, что измерения, проводимые в то время, не были достаточно точны для таких вычислений.
|
| 416
| In 1930 Courvoisier published a paper where he presented an
analysis of available observations of Jupiter's satellites and claimed
that they led to a new determination of the velocity of the solar system
relative to the ether.33
| В 1930 Курвуазье опубликовал статью, где он представил анализ
имеющихся наблюдений спутников Юпитера и утверждал, что они привели к
новому определению скороси Солнечной системы относительно эфира. 33
|
| 417
| He used data relative to the three inner Galilean satellites
published by the Johannesbourg observatory (19081926), comparing those
measurements to those of the observatories of Cape Town, Greenwich and
Leyden (1913 1924).
| Он использовал данные трех внутренних галилеевых спутников,
опубликованные обсерваторией в Йоханнесбурге (19081926), сравнивая эти
измерения с аналогичными из обсерваторий Кейптауна, Гринвича и Лейдена
(19131924).
|
| 418
| He confirmed Maxwell's anticipation of a fluctuation with a period of about 12 years and obtained the following results:
| Он подтвердил ожидания Максвелла о наличии колебаний с периодом около 12 лет, и получил следующие результаты:
|
| 419
| A = 126 10; D = +20; v = 885 100 km/s
| A = 126 10; D = +20; v = 885 100 км/с
|
| 420
|
|
|
| 421
| According to the theory of ether accepted by Courvoisier, the
speed of light is constant relative to the ether, but could not be
constant relative to the {29} Earth: there should
be an observable anisotropy of the speed of light due to the absolute motion of the Earth.
| Согласно теории эфира, принятой Курвуазье, скорость света
постоянна относительно эфира, но не может быть постоянной относительно
Земли: должна наблюдаться анизотропия скорости света при абсолютном
движении Земли.
|
| 422
| He assumed that this would produce an observable difference in
measurements of stellar aberration observed in different directions.34
| Он предположил, что оно должно произвести наблюдаемые различия в
измерениях звездной аберрации, которая наблюдается в разных
направлениях 34
|
| 423
| Using the available data, Courvoisier obtained the following results:
| На основании имеющихся данных, Курвуазье получил следующие результаты:
|
| 424
| A = 112 20; D = +47 20; v = 600 305 km/s
| A = 112 20; D = +47 20; v = 600 305 км/с
|
- Re: Черная дыра
(А.П. Васи,
16.10.2013 22:48, 3.5 КБайт)
Прочитал так сказать стандартную ситуацию - когда много
умничают а по смысловой сути то ответить достаточно грамотно
и просто никто не в состоянии.
Рекомендую
прочитать все сообщения внимательно,
и в итоге Вы заметите, что все недалёкие а только вумничать
и могут.
-----------------------------------------------------------------------------------------
: Сегодня в 02:24:25
Ответ #4 : Сегодня в 09:48:07
-------------------------------------------------------------------------------------------------
Никто там никого не опередил, задающему вопрос один буй
ни кой конь внятно ни кто не объяснил, только дали непонятные
и бессмысленные тексты почитать - и на куя такие советы.
Сам вопрос выеденного яйца не
стоит.
Никто даже внятно не может объяснить что сутки месяцы и годы
с их делением никак не совпадают просто --- кратно--- если эту
величину поделить.
А часы минуты и секунды, имеют кратную привязку к вращению
Земли по отношению к Солнцу, - один оборот - Земли = 24 часа,
а один оборот Земли вокруг Солнца
не может даже теоретически совпадать
и точно соответствовать какому-то целому количеству оборотов Земли,
когда Земля делает полный оборот вокруг Солнца - и хоть
это и ерунда,
но такую ерунду должны объяснять максимум с третьего поста, и так чтобы
читающий понял однозначно - что за мракобесие недалёких которые не
могут
внятно и однозначно выразить свою мысль -
Вы хоть понимаете что Вам - всем - над астро-балаганом надо работать, чтобы
превратить в астро-речь.
Заметьте
никто не может внятно, просто, и адекватно излагать
свои мысли по вопросу по сути.
- Re: Черная дыра
(А.П. Васи,
16.10.2013 23:48, 2.1 КБайт)
Ответ #2 : 10.10.2013 [00:44:19]
Вы про это: http://ru.wikipedia.org/wiki/%D1%E2%E5%F2%EE%E2%EE%E5_%E7%E0%E3%F0%FF%E7%ED%E5%ED%E8%E5
Да, о световом загрязнении. Будут ли у нас предпринимать какие-то меры, или это в раше не возможно ?
У
нас возле Краснодара, есть торговый центр OZ. Фонари которые освещают
стоянку, имеют конструкцию, похожую на тарелку, перевернутую вверх дном.
Интересно почему не везде применяют такую или похожую конструкцию ?
Кто бы у нас озаботился
о световом загрязнении ночного неба.
-----------------------------------------------------------------------------------------
Ну это вообще пипец
мысли.
Тут даже думать не нужно - ясный конь что фонари
как освещение - это только один из методов
чтобы было видно тому кто смотрит.
И ясный
конь что если бы продавались очки в магазине
светосильные, и накладные светосильные линзы для глаз,
то накой эти фонари в принципе бы сдались.
И если
бы у каждого любителя астрономии был свой спутник
орбитальный то его бы эта буета с засветкой бы тоже
не сильно беспокоила.
С моей точки зрения раньше
у каждого любителя астрономии
будет насовский недорогой серийный орбитальный спутник,
чем смогут сделать светосильные очки или накладные линзы
светосильные.
- Re: Черная дыра
(А.П. Васи,
31.10.2013 22:15, 4.1 КБайт)
Вот не прошло и много времени а собственно с 2009 года,
когда релятивисты соизволили раздуплятся.
Хотя у них и смешно получается между двойкой и тройкой по
пяти-бальной.
Здесь оценка не за вопрос по сути, ибо это уже измерял я бы в тысячах,
здесь оценка скорее за балаган и понимание того что кричащий и
многочисленный
не значит лучший.
А вот за такие оскорбления участников форума, - в стиле одиночка не может
решить вопрос, - и вопрос решается только стадом - то
я
бы банил по ай пи и навсегда.
Хотя кто из этих участников поймёт как их залпом жахнули.
Так плохо думать о всех и считать одного - или малочисленных
безмозглой
индивидуальностью, - мне просто грустно.
\\\Совершенно
очевидно, что на данный момент выборка из наличных участников дискуссии
статистически недостаточно представительна. С помощью такой выборки
нельзя сделать научно-достоверное обобщение.
\\\
---------------------------------------------------------------------------------------------------------
Ответ #31 : Вчера в 23:29:43
давайте выясним, Вы получили ответ на заглавный вопрос темы? Какой
это ответ?
Общеизвестно,
что "спешка необходима только при ловле блох". А тут "идет игра
по-крупному", как справедливо отметил Глубокоуважаемый Вов.

Совершенно
очевидно, что на данный момент выборка из наличных участников дискуссии
статистически недостаточно представительна. С помощью такой выборки
нельзя сделать научно-достоверное обобщение.
Пока почти никак (за
исключением, возможно, QSS) не проявили себя сторонники волновой теории
преобразования, излучения, распространения и поглощения
электромагнитной энергии, которые по принципиальным соображениям
бритвы
Оккама считают гипотетическую "частицу фотон" привлечением в теорию излишней сущности.
"Бритва
О́ккама (иногда лезвие Оккама, лат. lex parsimoniae)
методологический принцип, получивший название от имени английского
монаха-францисканца, философа-номиналиста Уильяма Оккама (Ockham, Ockam,
Occam; ок. 12851349). В кратком виде он гласит: Не следует множить
сущее без необходимости (либо Не следует привлекать новые сущности без
крайней на то необходимости). Этот принцип формирует базис
методологического редукционизма, также называемый принципом
бережливости, или законом экономии.
То, что называют Бритвой
Оккама, не было создано Оккамом, если иметь в виду базовое содержание
этого принципа. То, что в условиях Проторенессанса сформулировал Оккам,
было известно, по крайней мере, со времён Аристотеля.
В
современном понимании принцип Бритвы Оккама состоит в следующем: если
какое-то явление может быть объяснено двумя способами, например, первым
через привлечение сущностей (терминов, факторов, преобразований и т.
п.) А, В и С, а вторым через А, В, С и D, и при этом оба способа дают
одинаковый результат, при прочих равных условиях следует считать верным
первое объяснение, то есть сущность D лишняя, и её привлечение
избыточно."
---------------------------------------------------------------------------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
31.10.2013 22:25, 632 Байт)
Меня смешит Вибе аки полный трус со званием профессора, ни одного
внятного высказывания или вопроса по сути,
- не могу понять - чего он очкует в данной ситуации,
а не ведет дискуссию с типичными словами в начале
поста
-------------
- Грёбан - ный конь куда Вы несёте телегу -
дорога вот там -
и двигаться нужно вот так-то -
и вот такая-то буета - значит вот то-то - а вот
такая-то буета значит вот это.
---
Так я могу Вас успокоить
он так никогда не сможет
иметь практического опыта, знаний и умений, -
что-бы понимать так и думать, и что-бы так вести дискуссию.
- Re: Черная дыра
(А.П. Васи,
31.10.2013 23:10, 10.5 КБайт)
Вибе опозорился превзошел сам
себя.
Просит правильный ответ у собеседника
на неправильно выдуманные им же понты в стиле идиотизм.
Вибе придумал
вот это
\\\3)
j.kepler.ii, я прошу сформулировать объяснение всем явлениям, для
объяснения которых используется понятие фотона, без использования этого
понятия.\\\
Можно быть самым хитрым - но всегда нуна помнить
что украинцы в основной своей массе - хитрость,
хитроопость видят сразу как будто другим
шрифтом,
и надо быть просто недалёким чтобы писать такую
нелогичную буету.
У нас в младших классах подобными закидонами
друг друга смешили -
В стиле - а ответь только да или нет - не
правда ли? - не дурак ли ты?.
Любой ответ - логическое попадалово в логический
лохотрон.
----------------------------------------------------------------------
- Модератор





-

- Сообщений: 13 677
- Рейтинг: +362/-47
- Эвона как...
-
Ответ #47 : Сегодня в 20:43:16
Значит, так.
1) Bob,
огромная просьба -- не отвечать на последнее сообщение j.kepler.ii. Я
хочу дать ему возможность выполнить твой уже сформулированный запрос.
2) j.kepler.ii, я прошу Вас дать определение понятия "существует".
3)
j.kepler.ii, я прошу сформулировать объяснение всем явлениям, для
объяснения которых используется понятие фотона, без использования этого
понятия.
До того как Вы это сделаете, прошу других сообщений в разделе не публиковать.

Записан
И кто-то, как всегда, нёс мне чушь о "тарелках", и кто-то, как всегда, проповедовал дзен... (с) Зоопарк





-

- Сообщений: 841
- Рейтинг: +7/-2
-
Ответ #48 : Сегодня в 21:05:57
Значит, так.
<...>
2) j.kepler.ii, я прошу Вас дать
определение понятия "существует".
Ну что же, сделаю отчаянную попытку:
 Материализм утверждает
существование единственной абсолютной субстанции бытия материи
Материализм утверждает
существование единственной абсолютной субстанции бытия материи"Материали́зм
(от лат. materialis вещественный) философское мировоззрение, в
соответствии с которым материя (объективная реальность) является
онтологически первичным началом (причиной, условием, ограничением) в
сфере бытия, а идеальное (понятия, воля, сознание и тому подобное)
вторичным (результатом, следствием).
Материализм утверждает существование единственной абсолютной субстанции бытия материи;
все сущности образованы материей, а идеальные явления (в том числе,
сознание) являются процессами взаимодействия материальных сущностей. "
До того как Вы это сделаете, прошу других сообщений в разделе не
публиковать.
Приведенный текст соответствует Вашим требованиям?

Записан
- Модератор





-

- Сообщений: 13 677
- Рейтинг: +362/-47
- Эвона как...
-
Ответ #49 : Сегодня в 21:17:16
2) j.kepler.ii, я прошу Вас дать определение понятия "существует".
Ну что же, сделаю отчаянную попытку: 
...
Приведенный текст соответствует Вашим требованиям?
Нет,
разумеется. Он бы соответствовал, если бы я просил Вас: "Скопируйте,
пожалуйста, текст из Википедии". Вот в этом случае Ваш ответ был бы в
самый раз. Но я не просил Вас ничего копировать из Википедии. Я просил
дать определение понятия "существует". Дам подсказку. Определение должно
начинаться словами: "Существовать означает ..."
И ещё: там есть и пункт 3.
- Re: Черная дыра
(А.П. Васи,
6.11.2013 22:07, 1.5 КБайт)
Я естественно что-то логичное должен высказать здесь
по текущим ситуациям на двух форумах по похожему
вопросу.
В первом варианте я как говорится - снимаю
шляпу -
удивлён в принципе.
Во втором случае - молодец, но высказать свою точку
зрения это не значит что есть способности придумывать
самостоятельно.
----------------------------------------------------------------------------
1
\\\

Ответ #2020 : Сегодня в 20:18:30 \\\
------------------------------------------------------------------------------
2
\\\
 О роли теории относительности в науке
О роли теории относительности в науке
Вчера :: 15:35:01
-----------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
15.11.2013 22:39, 91 Байт)
http://www.astrogalaxy.ru/forum/phpBB2/viewtopic.php?f=2&t=4314
Я думаю.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 9:50, 760 Байт)
У меня такое чувство что свирепствует вирус
- "идиотизм в физике как науке",
и он давно поразил очень большое количество
человек, и он передаётся
от учителя к ученику.
Собственно надо радоваться тем кого этот вирус
не поразил.
Только на планете недалёких или пораженных
подобным вирусом - не могут
за сто лет придумать
новых теорий, а существующие - на уровне
интеллекта - детский лепет.
Альты должны просто радоваться этой ситуации
ибо основная
масса их конкурентов, поражена
этим вирусом.
На сколько я помню в давние времена периодически
для предотвращения подобных ситуаций закрывали
изучение
определённых наук на некоторое время лет на
20-50, а потом возобновляли эти науки.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 10:10, 5.0 КБайт)
Вот пример из жизни, некоторый преподаватель не знает
что эффект Доплера был придуман автором исключительно
для сред
Из википедии
\\\Эффект
был впервые описан Кристианом
Доплером в 1842 году.\\\
за долго до того как были придуманы релятивизм,
и фотоны.
И только недалёкий может путать с релятивистским эффектом
Доплера - это два абсолютно разных эффекта придуманные в разные
эпохи.
Из википедии
\\\
В случае распространения электромагнитных волн (или других
безмассовых частиц) в вакууме, формулу для частоты выводят из уравнений специальной
теории относительности.
Так как для распространения электромагнитных волн не требуется
материальная среда, можно рассматривать только относительную скорость
источника и наблюдателя\\\
----------------------------------------------------------------------------------------------------------------------------
 Re: О системе постулатов СТО.
Re: О системе постулатов СТО.
Ответ #91 - Вчера :: 10:48:21
wpiter писал(а) 13.11.13 :: 22:33:29:Нет ЭМ-волн, значит и нет для них эффекта Доплера. Как же скорость машин определяют допплеровским радаром ?
|
-------------------------------------------------------------------------------------
 Re: О системе постулатов СТО.
Re: О системе постулатов СТО.
Ответ #95 - Сегодня :: 09:41:59
Один писал(а) Сегодня :: 00:51:44:Зачем именно вам <неплохо вернуть эфир>? Что вы собираетесь с ним делат В
личке я вам ответил, зачем мне эфир. Здесь же добавлю, что мне , как
профессиональному физику на пенсии (до того преподававшему в универах,
но не связанному с пространством-временем) ничто не мешает в связи с
признанным существованием физического вакуума, как среды лишь с
ПОТЕНЦИАЛЬНЫМ существованием частиц, а значит вполне непрерывной и
возможно однородной в любом масштабе предполагать существование эфира,
движение которого в принципе нельзя выявить, а значит и обнаружить и
увидеть сам эфир. Зато возврат эфира в физику дал бы альтернативы для
СТО. а она в физике очень неустойчива и конфликтна.
|
---------------------------------------------------------------------------------------------------------------------------------
Вот если бы просто кто мозгами своими мог вникнуть
в смысловую суть, то эфир бы в науке и так бы вернулся,
а недалёким накой эфир в физике они и так в физике
ничего не понимают, даже будучи преподавателями физики.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 10:24, 1.6 КБайт)
Из википедии
\\\
В случае распространения электромагнитных волн (или других
безмассовых частиц) в вакууме, формулу для частоты выводят из уравнений специальной
теории относительности.
Так как для распространения электромагнитных волн не требуется
материальная среда, можно рассматривать только относительную скорость
источника и наблюдателя\\\
-------------------------------------------------------------------------------------------
Предупреждаю что релятивистские
определения брызжут идиотизмом -
по выщеизложенному -
\\\В случае распространения электромагнитных волн\\\
использование слова
волна - может использоваться
исключительно для сред - звуковая волна, или для границ соприкосновения
различных сред - между воздухом и водой - волна на воде.
И если удалось раздуплиться - то видно что отсутствует в релятивистском
эффекте Доплера - носитель и переносчик.
Они просто взяли из эфирной части электромагнитную
волну - и сказали
что она в пустоте - это так сказать просто - пешее эротическое
путешествие - только это нуна понимать моском, а для этого таковой должен быть.
Кю.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 14:07, 2.2 КБайт)
http://www.youtube.com/watch?v=hGm2gqs7dP8
----------------------------------------------------------------
Изучаем формулы.
------------------------------------------------
Собственно расскажу абсолютно другое в этой
ситуации.
Берётся опять изучается лично мне уже надоевший - кинескоп.
Ясный конь что к кинескопу прилепили
е м ц квадрат, без
объяснения физической сути.
Кинескоп это собственно ускоритель или коллайдер.
Происходят в нём следующие процессы - есть например
два
различных электрода к ним приложено электрическое
напряжение то между этими электродами есть уже движение
жидкости - электры, оно вызвано тем что пространство
заполнено
двумя веществами это газ - эфир, - представляющий из себя
мохнатый шарик покрытый тонким слоем жидкости - электры.
Эфир не является проводником
электричества а электра -
является не только проводником такового - а движение этой жидкости и есть
электричество.
Естественно электра в пространстве создаёт
два случая движения
электричества - это статическое - когда происходит движение
электры через поверхностный слой эфира - что собственно и в кинескопах
и
используется.
А второй случай это когда электра движется по проводнику.
Нить накала нагревает некоторое вещество которое создаёт невидимое
паровое облако
- и электра увлекает частицы этого облака за собой,
и собственно скорость увлечения электрой тем быстрее чем больше
разница напряжений, в кинескопе цветном, ускоряются
частицы парового облака
до 0.3 скорости света.
Собственно - надо понимать что слово - электрон - это слово не имеющее
под собой физического смысла,
ибо в пространстве - не возможно
электричество, - заряд, или движение с другим потенциалом -
правильно - невозможно без физического носителя, которым не
могут
выступать не эфир и не электра, - физическим
носителем потенциала или заряда электричества - может
быть только материальная частица - так сказать - материя,
Это вся таблица Д.И.Менделеева.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 17:57, 764 Байт)
Что есть в наличии - есть электра, которая
энергию своего движения = напряжение,
при некотором своём объёме = ток,
что вместе из себя представляет мощность,
- передаёт за счет увлечения за собой
незначительной частице атома.
Что собственно здесь в непонимании ?-
не понятно идёт ли затрата энергии на перемещение
эфира в пространстве?, и какие затраты на перемещение
электры в пространстве?, и какие потери
при воздействии электры которая увлекает
за собой частично
эфир?, и уже в основном
движение электры как источника силы, и первопричины, -
возникает логичный вопрос как именно электра - разгоняет частицу.
Собственно
надо понимать - что данный опыт -
в своих деталях - краеугольный.
- Re: Черная дыра
(А.П. Васи,
17.11.2013 19:08, 685 Байт)
Если разобраться детально с кинескопом,
то уже примитивно будет на основании
полученных результатов описать тот-же
опыт когда микро-капли масла - назвали
электронами.
Коню понятно что придётся изменить
и переименовать достаточное количество
всяческих мыслей в головах физиков, - только
мне вот уже
сразу смешно будет смотреть
как релятивисты пошлют в пешее эротическое
путешествие просителя гранта для проведения
подобного опыта.
И как объяснить
результат и смысл данного опыта релятивистам,
их минимум пять лет только другой физике переучивать, и то
не факт что получится переучить на эфир больше десяти
процентов.
- Re: Черная дыра
(А.П. Васи,
18.11.2013 8:41, 2.6 КБайт)
С моей точки зрения всю вот эту ерунду в физике
сотворил Лоренц.
И я лично ни какому альту ни при каких ситуациях
никогда не советую даже вникать в
труды Лоренца,
ибо это будет Ваше потерянное время безвозвратно,
а может и альтовский разум потеряете, и заболеете
идиотизмом релятивизма.
А Вас
туда релятивисты будут всё время приглашать
на разборки по физике.
---------------------------------------------------------------------
Patrice
Ветеран форума


 На Форуме
На Форуме

участник форума
Сообщений: 2979
 Re: Мы все учились по Ландау.
Re: Мы все учились по Ландау.
Ответ #2 - Сегодня :: 08:25:24
quasi писал(а) Сегодня :: 03:37:05:Вопрос к топикстартеру -
что именно Вы собираетесь обсуждать в
этой теме?

А
вот это и надо обсудить потому, что с физической точки зрения
Ландау-Лифшиц - математическая макулатура.
И начать надо с
преобразования Лоренца, с пространства с псевдоевклидова пространство и
прочее. Надо поднять вопрос и по другим аспектам этой библии.
- Re: Черная дыра
(А.П. Васи,
20.11.2013 10:59, 2.1 КБайт)
Чтобы собственно провести
этот опыт
особо то и денег не нужно.
Собственно достаточно
телевизора,
и высокоточных весов. Телевизор
устанавливается кинескопом
вверх
и кинескопом вниз, для этого
его поворачивает
поворотное устройство с
моторчиком на пульте.
У телевизора должно быть
автономное питание,
и вся конструкция вместе с аккумулятором,
находится
в герметичном корпусе.
Вся конструкция установлена
на весы.
Проводятся измерения когда
подано высокое,
и экран чёрный, и может быть направлен
вверх и вниз,
потом когда весь экран светится белым на
максимальной
яркости и контрастности, и
тоже кинескоп направлен
вверх и вниз.
Надеюсь что все догадались
что проводятся измерения
веса точнее его изменения.
- Re: Черная дыра
(А.П. Васи,
20.11.2013 20:32, 479 Байт)
Как говорится даже не смешно представить
как далеко пошлют гранто заявителя на
получение денег для проверки данной конструкции
в космическом пространстве, или на борту
космической станции.
У релятивистом подобная буета заранее
и абсолютно безрезультативна будет в принципе.
Как я рад что есть релятивисты.
По крайней мере я уверен что никто мои
идеи не сможет не только реализовать,
но не сможет даже их проверить,
и как говорится даже без моего одобрения.
- Re: Черная дыра
(А.П. Васи,
22.11.2013 18:44, 4.3 КБайт)
Собственно борьба развивается очень мощная
и незаметная, я то вижу где борьба разума идёт.
Что могу сказать как сторонний наблюдатель -
что женская
логика не терпит компромиссов в
отличии от мужской, и если барышня пришла к
некоторым выводам - то это уже камень.
Собственно сама она прийти к выводам
в данном
случаи не смогла по причине предубеждённости
которая определялась образованием в рамках парадигмы,
и после адекватного анализа различной физической
фантастики от различных авторов с Физиком,
просто сразу видно как она обгоняет всех релятивистов
вместе взятых в понимании физики.
Для меня это
была очень большая неожиданность,
я то думал что более уверенного релятивиста,
чем эта барышня и быть не может.
Какие тексты - и там где точки в конце
если поставить знак
вопроса, который неявно там есть, то это
можно сказать что у релятивистов не то что
всё плохо, а в релятивизм уже не верят даже
его
завзятые сторонники.
И это не трудности теории - это приговор теории.
Кстати расскажу что значит слово - сингулярность, -
это когда чем-то что-то
ограничивает бесконечность,
ибо в большой советской энциклопедии - пространство
было бесконечно, а потом к нему прилепили слово сингулярность,
и вселенная
стала ограниченной в размерах, -
обоснование сингулярности - теория большого взрыва, -
жесть однако,
но факт есть факт.
------------------------------------------------------------------------------





-

- Сообщений: 1 220
- Рейтинг: +46/-0
-
Ответ #2308 : Сегодня в 17:14:27
я не рассматриваю ОТО (и её "производные теории") как физическую
теорию, применимую ко всей Вселенной. Да ещё сингулярности... В
достаточно ограниченной области её ещё можно рассматривать, но ко всей
Вселенной - увольте.
Мне такая Космологическая теория не подходит. Полагаю, что Вселенной - тоже.
Я ищу другую
- без сингулярностей ...
Трудности (проблемы) ОТО - классической теории гравитации
Сингулярности. Неполные геодезические. Сомнительность
применимости ОТО для экстремальных гравитационных полей
Определение энергии гравитационного поля
Системы отсчёта. Их реализация физическими приборами.
Принцип эквивалентности. Природа инертной массы недостаточно ясна. Гарантированный переход от ОТО к СТО в некоторой СО.
----------------------------------------------------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
30.11.2013 23:00, 139 Байт)
Смотреть рекомендую только альтам,
релятивистам скорей всего не понравиться.
http://www.youtube.com/watch?v=l9uPHFcuzCs#t=62
- Re: Черная дыра
(А.П. Васи,
1.12.2013 0:43, 1.3 КБайт)

28 ноя в 14:39|0 комментариев
-----------------------------------------------------------------------------
Мне хоть и безразличны подобные лекции, но лично я ожидал большего,
и у меня после просмотра создалось впечатление в том что по
всем вопросам по сути была
слита вода.
С другой точки зрения лектор - молодец что в таком возрасте
пропагандирует эфир.
Я бы посоветовал -
проводится например лекция с постоянным
сливом воды по сути,
а автор заготовил домашний вопрос и домашний ответ и желательно
задать вопрос заготовленный и ответить на него
в конце лекции, хоть
на один вопрос по сути - и это будет прекрасно,
по той причине что не логично толкать вперёд голимый
порожняк груженный эфиром с постоянным сливом воды.
Так-же я бы порекомендовал текст лекции заранее
выкладывать для ознакомления.
- Re: Черная дыра
(А.П. Васи,
4.12.2013 2:11, 2.2 КБайт)





-

- Сообщений: 15 011
- Рейтинг: +196/-48
-
Ответ #903 : Сегодня в 01:57:04
Я бы с интересом познакомился с обоснованными фактами, доказывающими отсутствие БВ.
---------------------------------------------------------------------------------------------------------------------------
Моя клавиатура утопала в слезах.
Это же надо на сколько высокий уровень интеллекта,
- на самом релятивистском форуме вдруг у закоренелого
релятивиста,
- который калённым железом изводил альтов
на этом форуме -
услышать ему захотелось осмысленные
альтовские речи и размышления доказывающие то во что он не
верит,
чтобы убедили ещё его и он остался доволен -
- бабэне.
- Re: Черная дыра
(А.П. Васи,
4.12.2013 2:29, 2.5 КБайт)
|
|
|
|
     -

- Сообщений: 15 011
- Рейтинг: +196/-48
-
Ответ #786 : 30.11.2013 [23:19:17]
Та никаких опровержений. Никто никогда не говорил о завершенности ТБВ. Возможны уточнения и в теории, и в цифрах. Но
БВ был, продолжается и будет.  ------------------------------------------------------------- И разве можно в этом случаи что-то рассказать при таком уровне фанатичной предубеждённости. | |
- Re: Черная дыра
(А.П. Васи,
4.12.2013 22:50, 3.2 КБайт)
Вот читаю и наблюдаю такое слабоумие математиков в физике
что я просто аж удивлен.
Видят какие-то безбашенные трудности там где их у физиков
нет и никогда
не было.
Собственно ситуация физическая в следующем - в космосе большое
количество частиц высокой энергии и большое количество
электромагнитных излучений
в различных диапазонах, и только
нераздуплённые не знают что есть у материи такие свойства как
резонансное возбуждение,
резонансное поглощение,
люминесценция,
флуоресценция,
послесвечение - так вот кто это всё знает так ему и ничего даже не
надо придумывать, ибо тут и коню уже всё понятно что атомарная
структура
под воздействием излучения, или частиц высоких энергий
ближайщих звезд - будут переизлучать или создавать электромагнитные
излучения на других диапазонах частот,
отличающихся от частот
которыми были возбуждены - вывод чему учат астрономов я уже давно
не понимаю - это собственно на их совести.
Так вот собственно
зная что будет в пространстве - всегда фон на каких-то
частотах так как он определяется наличием в космосе как отдельных
атомов водорода и космической пыли -
и тут и коню уже понятно
что вот это межзвездная микроматерия в пространстве и будет создавать
этот фон, и в основе будет два основных физических процесса -
люминесценция и флуоресценция.
Собственно вот этот общий фон только суммарный -
а не как у некоторых псевдо физиков - тот который им нравиться,
можно
использовать для определения температуры в пространстве,
собственно для моей модели эта температура указывает
и плотность эфира в пространстве, - так что пока
математики
думают как физики будут объяснять, они даже не догадываются
что физики эту ерунду давно уже не объясняют, и не собираются
объяснять очевидное,
они её используют
и пользуются ей в своих моделях.
--------------------------------------------------------
Ответ #910 : Сегодня в 13:44:07
Цитата olegtitov: Но при этом темная энергия
такой же объективный факт, как и темная материя.
Гипотетические
сущности тёмная материя и тёмная энергия это не объективный факт,
а общепринятый вариант интерпретации наблюдений.
Модель Бринйолфссона объясняет наблюдения без этих сущностей.
Только
для этого придется вводить сущности стационарной, вечной и бесконечной
Вселенной, а потом долго думать о том, как объяснить, например,
микроволновое излучение с помощью еще более сложных сущностей.
- Re: Черная дыра
(А.П. Васи,
7.12.2013 13:43, 4.7 КБайт)
С одной стороны я могу сказать - что я рад что
релятивисты продолжают страдать безрезультативной ерундой и не смогут мне даже
малейшей конкуренции создать если объединяться и начнут придумывать модели в
ближайшие лет пять, у них нет ни опыта ни методик для этого. С другой точки зрения искренне жаль тех альтов, которые надеются
что им, специалисты помогут решить их вопросы или поговорят с ними - чтобы
понять, где трудности. Так вот - в данном случаи - эти альты себя сами загоняют
в тупик, ибо ищут халявы, хотят - чтобы
их вопросы решили за них, или хотят, чтобы им помогли.
Это дорога в никуда, гораздо проще и быстрее
самостоятельно решить все свои вопросы, чем терять время на форумах в
обсуждениях и 1)поиске сторонников и 2)поиске тех - кто поймёт твои идеи, а
потом 3) ещё кто-то тебе поможет в решении твоих вопросов. Поймёт
всё, именно так как сам себе придумал. Смешно и нелогично такое количество
совпадений должно быть, что результат невозможен в принципе.
А в итого что получается что альтернативщик в
результате безвозвратно теряет своё время, там где никогда не будет результата, он там
невозможен, даже если релятивисты и не будут его посты удалять, и не
будут относиться к нему, - как к глупой бешеной собаке, не понимающей
релятивизма.
--------------------------------------------------------------------------------------------------------------

Re: Бесконечна ли вселенная?
Ответ #50 : Сегодня в 00:53:32
Господин Вибе! Известно, что
в чужом монастыре своих проповедей не читают. Поэтому когда Вы удаляли
мои сообщения, потому что это была фантастика (по Вашему мнению), то я
принимал и принимаю это как должное и спокойно\\\
----------------------------------------------------------------------------------------------------------------
Хорошо.
Сообщение было восстановлено на время с 9.10 до 9.15 сегодня, 7 декабря
2013 года. А потом удалено как очередная фантазия Taralex.
Не
понимаю. Нет возможности шерстить прошлые сообщения, но я уверен, что
при каком-то очередном повышении Вашей публикационной активности я писал
Вам что-то наподобие "дальнейшие фантазии будут удаляться без
дополнительных комментариев". Потому что Ваши сообщения в подавляющем
большинстве случаев не относятся к тематике раздела. Ну не предназначен
он для публикации художественных текстов об "аннигиляции нулевого и
бесконечного пространства Вселенной"! Я даже помню, что грозил Вам более
строгими санкциями, если Вы не перестанете публиковать Ваши фантазии.
Однако терпел пока. Но раз Вас не устраивает такая ситуация, я прошу Вас
перечитать вот это сообщение. На всякий случай
уточню: ответы типа "молчу, молчу" обоснованием не считаются. \\\
- Re: Черная дыра
(А.П. Васи,
15.12.2013 6:59, 2.0 КБайт)
Мне и смешно и не смешно.
Мне уже даже интересно как отбирают астрономов и космологов,
по каким тестам.
Надеюсь что все заметят что в следующем тексте глобальный
смысл о большом взрыве - при текущем локальном объяснении
которое опирается на ситуацию излучения галактики, а точнее
звезд этой галактики.
Я вот не
понимаю - по какой причине к большому взрыву, приписывают
излучение галактик, а собственно излучение звезд этих галактик.
Возможно это массовое заболевание, когда
пропадает стратегическое
мышление, а арифметический логический узел продолжает нормально
работать. При этом заболевании пропадает необходимость в том чтобы
по какой-то причине происходило нечто следующее, ибо процесс без
причины признак ду.....чины.
-------------------------------------------------
\\\
http://www.astronews.ru/cgi-bin/mng.cgi?page=news&news=5123
 Наблюдая за высокоскоростным компонентом массивного галактического
скопления, ученые Технологического Института Калифорнии и Лаборатории
Реактивного Движения впервые обнаружили в индивидуальном объекте
кинетический эффект Сюняева-Зельдовича изменение интенсивности
радиоизлучения реликтового фона из-за обратного эффекта Комптона на
горячих электронах межзвёздного и межгалактического газа.
Наблюдая за высокоскоростным компонентом массивного галактического
скопления, ученые Технологического Института Калифорнии и Лаборатории
Реактивного Движения впервые обнаружили в индивидуальном объекте
кинетический эффект Сюняева-Зельдовича изменение интенсивности
радиоизлучения реликтового фона из-за обратного эффекта Комптона на
горячих электронах межзвёздного и межгалактического газа.
MACS
J0717.5+3745 - это необыкновенно динамичное галактическое скопление,
общая масса которого более чем в миллион миллиардов раз больше массы
нашей галактики.\\\
------------------------------------------
- Re: Черная дыра
(А.П. Васи,
22.12.2013 10:48, 2.8 КБайт)
Скажу Вам честно космологи - в данном случаи интеллектуальные малятка.
Идиотизм как его не приукрашивай, как его не называй, хоть необоснованная
выдумка,- хоть
парадокс, - он и останется идиотизмом даже если
его объявить гениальной придумкой человечества.
Вот например лично мне хоть тысячу раз говорить что в звездах
горит водород - для меня это тысячу раз идиотизм, по той причине
что водород не удерживается металлами, и он с самой меньшей
удельной плотностью.
И
водород может быть только в верхних слоях звезды.
А в данном случаи как башню снесло жестко, додумались и поверили
что что у водорода снесло башню и он нарушая
все законы
физики понесся в центр звезды по-учавствовать в ядерной
реакции. Лично я уволил бы сразу всех астрономов и космологов
которые в это поверили,
ибо - балласт.
Мне смешно что залипли уже только на этом этапе.
А чтобы взрослые модели придумывать то надо
ещё уметь на очень высокой скорости отбрасывать
теоретическое лайно и ни в коем случаи не выплеснуть
и не пропустить здравую идею. Естественно для этого
в голове уже должны быть продумнны скоростные
проверочные идеи.
Вот в данном тексте одно безссмысленное хотят
заменить на другое безполезное, - здесь собственно
ситуация метода поиска уровня неадеквата.
Ибо поиск ведётся наугад, ни чем, ни что, и ни как, - не
обосновывается, нет задачи и нет глобальных целей поиска.
И например модератор не может ничего придумать
самостоятельно- модератор хочет
задать ворос чтобы на основании ответа статью
в журнал написать.
Вот и все цели и задачи которые могут решаться на
этом
форуме например. Других задач - модератор не пропустит,
ибо смысла других задач он не понимает.
----------------------------------------------
\\\
Ответ #380 : Сегодня в 09:50:08
Всего лишь моё мнение, что СТО это в высочайшей мере точнейший
инструмент познания и изучения Но не физика.
\Вибе. = \Интересующийся Дед, изменится ли смысл Вашей фразы, если в ней СТО заменить законом всемирного
тяготения? Если да, то почему?\\\
- Re: Черная дыра
(А.П. Васи,
22.12.2013 21:52, 4.8 КБайт, ответов: 1)
То что альты в основном- пенсионеры и уже
не могут даже понять с кем они общаются а зачастую не могут понять
зачем то есть и релятивисты которые замолачивают
беседу.
Самый махровый релятивист на альтернативных форумах
--------------------------
Е-Eаtеr
---------------------------
 Re: Алгоритм введения физических понятий.
Re: Алгоритм введения физических понятий.
Ответ #5 - Сегодня :: 17:23:41
konstantin1 писал(а) Сегодня :: 12:34:39:Хотелось бы проанализировать то как в физику вводятся новые понятия. Понятия
возникают в русле какой-то теории. Например, появилась электродинамика
Максвелла - предложили понятие потенциала. Просто оказалось, что вещь
полезная, и вот придумали слово-термин в качестве заменителя многих
слов. Появилась СТО - оказалось, что некоторая величина должна быть
инвариантной, назвали ее "интервал". Понятно, что из показаний приборов никакие понятия не рождаются, это бзик Кравченки. Мысленный эксперимент это просто
своеобразная форма логических построений.
|
-----------------
 Re: Алгоритм введения физических понятий.
Re: Алгоритм введения физических понятий.
Ответ #14 - Сегодня :: 18:06:48
konstantin1 писал(а) Сегодня :: 18:00:09:Ну
для Вас вопрос помягче. Как понятия которые вероятно можно отнести к
физическим понятиям, к ним можно отнести? Что для этого нужно? Я все ответил в своем первом посте. Прочее это придумывание слов: типа, изобрел название
- сразу стало "понятнее".
|
------------------
Собственно его тексты - бессмысленный порожняк,
с претензией на разумность, с релятивистским восхвалением.
Любому альту общаться с ним что мочиться против ветра.
Например
\\\Мысленный эксперимент это просто своеобразная форма логических построений.
\\\
- На самом деле мысленный эксперимент это один из видов лохотрона,
который втюхали физикам. Собственно это когда вводятся физические
величины и
физические сущности - без измерительных приборов,
без единиц измерения таковых, и без методик измерения таковых.
Собственно при заявленном замедлении времени в
движении, нет
ни прибора ни единицы измерения, и нет методики - и само действие
- кажущееся - и это относится и к кривизне пространства.
С моей точки зрения
- нет физических измерительных приборов -
всё - в пешее эротическое.
Так что некоторый вид лохотрона - кому и форма логического построения,
а кому и жесткая
лапша на уши.
Собственно о чести и порядочности говорить тоже не логично, так как
нет законодательства которые бы запрещали в физике и космологии обман
в
любом виде, по этой причине засилие и процветание теорий уровня
идиотизма будет максимальной, для этого есть все условия.
- Re[2]: Черная дыра
(Д. В. lom,
23.12.2013 11:56, 217 Байт)
Не врубаюсь. Не вижу коментов. Или модератор удаляет сразу, или их просто нет, или с настройками что то не так. Такое ощущение, что чел (Васи) сам с собой разговаривает. Вроде
все по делу и интересно. В чем причина?
- Re: Черная дыра
(А.П. Васи,
23.12.2013 21:41, 2.6 КБайт)
Собственно и моя модель основана на
вранье, при попытке детальных объяснений получается
идиотизм.
Здесь я думаю что к данной ситуации логично относится
спокойно, по причине того что в космологии нет и не будет
возможности узнать точно что происходит внутри звезды.
У меня в модели термоизоляционный слой внутри звезды,
на самом деле выдумка на уровне вранья, по причине того
что при конденсации
эфира в жидкое состояние, в замкнутом
шаре температура внутри должна быть например десять тысяч
градусов чтобы снаружи было шесть тысяч градусов.
Это приводит к тому - что при быстром выходе из звезды
произойдет резкое восстановление и огромный выброс,
чего собственно не наблюдается в галактиках перегретых,
и в состоянии разброса.
Здесь даже не знаю что и думать. Логично поменять структуру
изложения модели, из которой бы следовали тенденции
физических процессов и из этих тенденций бы вытекали
следующие
логические предположения, которые бы и создавали некоторую
основную структуру модели. И в рамках этой структуры логично
описывать ситуации которые логически более приемлемы.
Здесь возникает следующая ситуация необходимость улучшений
и доработок по каждому элементу и взаимодействию модели,
что усложняет модель как таковую что можно приравнять к
глупости
переходящей в идиотизм. Большое количество
логических ветвлений может не восприниматься в принципе,
плюс
к этому семантический шум.
Итого с одной точки зрения модель должна быть простой,
с другой точки зрения модель должна быть структурированной
по причинам процессов и взаимодействий с описанием ситуаций
определивших выбор в данной последовательности.
И всё равно есть шанс, что читающий не поймёт написанное.
- Re: Черная дыра
(А.П. Васи,
23.12.2013 21:49, 476 Байт)
\\\Такое ощущение, что чел (Васи) сам с собой разговаривает. Вроде
все по делу и интересно. В чем причина?\\\
Записи своих размышлений веду здесь.
У меня хобби космология, вот я и обдумываю
здесь разные ситуации которые
имеют место быть,
космолог по специальности работающий не может затронуть
разные вопросы в том виде как есть ибо его могут и уволить.
Да и за общение со
мной я думаю тоже не похвалят.
- Re: Черная дыра
(А.П. Васи,
26.12.2013 22:37, 1.5 КБайт)
Блин вот так и охота сказать что вот этот
альт ко - ёл.
Совсем моск клинануло - его идея в том
чтобы релятивистов переучить по другому думать.
На
кой тянуть потом этот обоз.
Лучше пусть лежит это там где это лежит,
и просто обойти стороной.
Я лично впервые наблюдаю что-бы воспитывали
себе врагов
на завтра.
Ба-бе-не.
1 Если ты альт и тебе в твоей теме - упал на хвост релятивист
со своими расспросами, забей - и забудь эту тему.
2 Если ты альт и тебе альты противоречат или тебя обсуждают,
забей на эту тему.
3 Если ты альт и в твоей теме релятивисты тебя чмырят сразу, -
это логичное
направление.
---------------------------------------
\\\

: 20.12.2013 [16:36:55]
Небольшой опыт изучения доминирующей в научном сознании теории гравитации требует подведения небольших промежуточных итогов.
В
данной теме изложу на мой взгляд несколько трудностей возможно
методологического характера, а возможно и принципиального, присущего
конкретной теории, которая претендует на роль физической.\\\
---------------------------------------
- Re: Черная дыра
(А.П. Васи,
26.12.2013 23:05, 748 Байт)
С другой точки зрения есть поговорка, -
"Юпитер - ты сердишься?, - значит ты не прав.
Возможно и я не прав в своих амбициях.
Возможно завтра бывший релятивист
сделает
безбашенное открытие в эфирных технологиях, и сделает
эфирные идеи неприрекаемыми в обозримом будущем.
С другой точки зрения космология это
собственно не
физика - это борьба идей.
Я бы даже по другому сказал, борьба адеквата, борьба неадеквата,
борьба сказок, борьба легенд, борьба предсказаний,
борьба обещаний.
Я лично выступаю в новой категории - борьба текущих описаний - в том виде
- как есть и мне просто хочется чтобы так было, и я провел проверки
на ситуации - и в основном предыдущие события совпадают.
- Re: Черная дыра
(А.П. Васи,
26.12.2013 23:12, 578 Байт)
"Юпитер - ты сердишься?, - значит ты не прав."
- Что-то логичное есть в этом.
У каждого свой практический опыт, если
я сержусь
то я предвижу и предчувствую что текущая ситуация
достаточно плохо отразится в будущем - ибо с моей
точки зрения - это и коню понятно. Ибо не осилит
юзер больше
одной любимой теории. Переучить второй и третей теории
можно и объяснить логичность других теорий тоже будет
можно, - но надо понимать - что
у юзера - эти
теории никогда не будут любимыми теориями.
- Re: Черная дыра
(А.П. Васи,
28.12.2013 13:42, 8.3 КБайт)
Уже даже барышня догадалась что у релятивистов не
физика по сути, а голимый порожняк, не имеющий физических
определений.
Ибо какая-то отписка не является
физическим определением явления,
а то что подобрали формулу которая примерно описывает физический
процесс, - это не значит что у этого физического процесса появились
адекватные физические объяснения процессов на основании хотя-бы десятка
опытов в которых ток в проводнике производит не только магнитное поле
но и происходят
другие физические явления.
Так эти опыты - я знаю и их много. А если эти опыты не знать
то получится - детский лепет а не физическое определение - тока в проводнике.
Собственно когда есть на форуме постоянно мешающий альтам общаться,
- этот релятивист как правило старается показать свой умняк, на самом деле
он может
показать только свою начитанность релятивистским порожняком.
Собственно этого релятивиста начинающим альтам логично использовать в
своих целях, достаточно его спрашивать
о различных физических сущностях,
и в тех ответах где максимальная нескладушка и максимальный лепет -
то эти направления логично определять приоритетными.
Релятивист сам не понимает физического смысла и то что правильно или
не правильно, он себе в моск записал всё бездумно как в записную книжку,
и доверяет записанному
- так учили в советских школах.
Альты подобных методов обучения - природно не воспринимают, ибо они в моск кладут
то что проверяют.
Так что релятивист не
сможет составить альтам конкуренции.
------------------------------------------------------------------------------
\\\Galina.
 Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Ответ #71 - Сегодня :: 00:12:32
GalinaРелятивисты
вообще славятся своим редким умением давать простым и ясным понятиям
невообразимые по невразумительности определения. Вот один из примеров определения, данного явным релятивистом:\\\ Цитата:Ампер
есть сила неизменяющегося тока, который при прохождении по двум
параллельным прямолинейным проводникам бесконечной длины и ничтожно
малой площади кругового поперечного
сечения, расположенным в вакууме
на
расстоянии 1 метр один от другого, вызвал бы на каждом участке
проводника длиной 1 метр силу взаимодействия, равную 210−7 ньютона.   
|
|
|
--------------------------------------------------------------------------------
 Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Ответ #72 - Сегодня :: 00:39:06
77pp\\\И? Просто транскрипция формулы

с математического
языка, в коем она и представлена, на язык естественный.
\\\
---------------------------------------------------------------------------------
 Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Ответ #75 - Сегодня :: 12:47:44
Galina.\\\И после такой транскрипции ученику сразу стало ясно
и понятно, что такое ампер?
Вот так, учась по таким учебникам, с подобными определениями,
способные ученики и превращаются в релятивистов.\\\



---------------------------------------------------------------------------
 Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Ответ #76 - Сегодня :: 13:01:07
Дробышев писал(а) Сегодня :: 12:31:44:Более
того, протон-антипротонные пары могут образовываться в
электрон-позитронных коллайдерах.Природе глубоко наплевать на то,
что вы
о ней вообразили и во что вы уверовали.
Galina.\\\Природе действительно наплевать на все ваши верования,
в
частности, на верования в инвариантность скорости света.
Очень может быть, что в электрон-позитронных коллайдерах
образуются протон-антипротонные пары.
Но
три протона не могут образоваться из двух протонов и больше
ничего, как
бы вы сильно эти протоны не разогнали. Материя,
молодой человек, не
возникает из ничего, не возникает из "энергии"
и не исчезает бесследно.
Совершенно очевидно, что в описанной вами ядерной реакции помимо
двух
протонов и "энергии" участвовала еще какая-то материя.
Если СТО полагает, что материя может возникать из "энергии",
значит это нематериалистическая,
ненаучная теория.\\\
-------------------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
30.12.2013 8:41, 3.6 КБайт)
Да вот и ещё одного релятивиста - сразил старческий маразм.
Оно возможно релятивистам то и хочется что-бы на планете
был хоть один институт в котором будут учить
только
релятивистов придумывать новые теории. Только здесь уже
начинается нескладушка - где релятивисты и где придумывать,
релятивисты сто лет ничего не
придумывают, и где релятивисты
- а где новое -, у релятивистов сто лет нет новизны.
Вибе как-то хвастался что его учили придумывать теории,
и он не
инженер строящий заборы - он выше этого.
И в результате, - деньги на его обучение придумывать новые
теории - были потрачены зря. Собственно что он занял -
место альта,
будет высказывание не логичное, ибо обучение организовали
релятивисты для релятивистов - эта тема изначально обречена
была на провал. Так что
к подобным высказываниям логично относится, -
как к тому что релятивисты ни при каких условиях и никогда не
будут создавать даже группу в институте которая бы
училась
придумывать новые теории и модели, ибо релятивисты не так
глупы чтобы рубить ветку на которой они сидят.
---------------------------------------------------------------------
---------------------------------------------------------------------
Ответ #2 : 27.12.2013 [18:55:29]
---
asmoko \\\Философский взгляд на проблему образования
\\\Философский взгляд на проблему образования
возле
звёзд планетных систем...P.S.
Из всего сказанного выше
напрямую вытекает, что время от времени
появляющиеся в поле
зрения землян кометы и с грязевым, и со спекшимся,
и с
расплавившимся когда-то ядром являются не такими уж и дальними
родственниками нашей планеты\\\
-------------
Дмитрий Вибе \\\Из сказанного напрямую вытекает,
что философия
-- неподходящее основание для разговора об образовании планетных
систем.\\\
-------------
asmoko \\\Простите, уважаемый, а вот здесь Дмитрий
Вибе - Образование
\\\Простите, уважаемый, а вот здесь Дмитрий
Вибе - Образование
планетных систем не Вы ли рассуждаете на данную
тему ИСКЛЮЧИТЕЛЬНО
как философ?.. Следуете в жизни поговорке, что положено Юпитеру и т.д.?..\\\
------------
Дмитрий Вибе\\\А Вы как предполагали? Что образование планетных систем
-- это такая
простенькая темка, по которой может плодотворно рассуждать
любой
человек, даже при отсутствии соответствующей квалификации?\\\
----------------------------------------------------------------------------
------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
30.12.2013 13:13, 398 Байт)
По логике я не вижу трудностей у релятивистов что-бы
сконцентрировать усилия и разработать что по проще
в теориях и моделях. С моей точки зрения самое простое
это версии атомарных моделей для описания различных
задач.
Например. -
Атомарная модель описывающая электро-магнитное взаимодействие.
Я например
такую модель самостоятельно за три года придумал.
- Re: Черная дыра
(А.П. Васи,
3.01.2014 14:11, 2.8 КБайт)
Я естественно рад, но как не понаслышке знающий
строительство - я с первого взгляда могу сказать
что это будет безбашенно дорогой долгострой.
Большие стёкла
и я так понимаю резино алюминиевая
обшивка - это очень дорого. Долгострой предполагается
по причине того что я не наблюдаю больших дымовых
красивых труб
котельной, не наблюдаю высоковольтной
трансформаторной которые обычно строятся в отдельно стоящих
зданиях метрах в двадцати от основного здания.
Если
котельную сразу не предусмотреть, то может оказаться,
что подвод теплотрассы может стоить дороже самого здания.
Каналью то можно ещё машинами вывозить.
На форуме вообще какую-то байду обсуждают.
Пусть хотя-бы сперва узнают сколько будет стоить разрешение
на врезку газа для котельной на нужную мощность,
а мощность
судя по зданию под два мегаватта, и есть ли вообще таковая возможность.
Может ещё и газовую трубу надо подводить, тогда узнают
что проектирование
технических коммуникаций могут
оказаться новой финансовой неожиданностью, и технические
помещения, техническое оборудование и коммуникации, -
потянут сумму
равную стоимости коробки.
----------------------------------------------------------------
Ответ #66 : Вчера в 19:33:29
\\\Место для строительства уже выбрано, "привязка" проекта к месту сделана?
А то на картинке
здание смотрится как открытое всем ветрам (эскиз 3).
Да,
проект изначально проектировался под парк им. Николаева (таково желание
градоначальства). Я только посоветовал сориентировать всю конструкцию
так, чтобы наблюдениям были открыты Восток, Юг и Запад (купол находится
на Юге здания), да подальше от автодороги с ее вибрациями.
Подковообразное здание повернуто так, что его крыша будет "парить"
относительно купола только на Севере и СЗ и СВ, не мешая лунно-планетным
наблюдениям...
В остальном, особенно похвастать нечем - это центр
600-тысячного города, причем, на востоке стоит телевышка, а на Севере
сияет стадион. Весь парк зарос деревьями, но все они больны и те, что
будут портить вид, будут срезаны.
Была бы моя воля, я бы вообще за город планетарий вывел и маршрутку к нему пустил. \\\
- Re: Черная дыра
(А.П. Васи,
3.01.2014 15:26, 721 Байт)
Уже прошли времена когда просили проектировщиков
проектировать всё по уму. Сейчас проектируют по тех заданию,
и не более того. А теперь интеллектуальный, вопрос
-
заказчик может составить технически грамотное тех задание? -
естественно не сможет, ибо таких зданий никогда не строили.
Лично я бы предусмотрел хостел
на сто человек, столовую на
сто пятьдесят человек, автостоянку на двести авто и заезд
с нескольких сторон. Магазин сопутствующих товаров.
А вот для
телескопа башню не строил бы в принципе. За цену этой башни
можно купить тридцать недорогих телескопов, и сейфы большие
для их хранения, - есть возможность посмотреть
- вынесли
на улицу и всех делов.
- Re: Черная дыра
(А.П. Васи,
27.01.2014 22:00, 1.2 КБайт)
Красное смещение и искривление пространства
http://www.astronomy.ru/forum/index.php/topic,115357.0.html
----------------------------------------------------------------------
Я очень громко смеялся.
Причина тому что идут ноздря в ноздрю с точно
теми же идеями которые я перебирал и успешно решил
задачу, и даже давно закрыл своим авторством единственно оставшийся
подход к красному смещению от сдвига
спектра.
Идея в том что у поверхности звезды сдвиг спектра отсутствует,
и его определяет разряжение эфира у поверхности, внешнее давление эфира,
скорость движения
эфира.
Пока дупля не отбивали - они так и не поняли что цвет звезд отдали
на откуп теории большого взрыва.
А сейчас пытаются исходя из верной трактовки теории
большого
взрыва по другому объяснять красное смещение - они не понимают
что шаг в сторону в верном направлении невозможен по двум причинам,
модератор их
сразу забанит как бешеных собак, вторая причина - упираются
в моё авторство.
У них одна дорога - чем краснее тем дальше и улетает, а синее ближе
и приближается
- ку.
- Re: Черная дыра
(А.П. Васи,
1.02.2014 0:45, 2.5 КБайт)
- О, я смотрю уже взрослые задачи начинают
одолевать. А я как всегда уже решил данную
задачу, - у меня увеличение или уменьшение
энергии в материи решается
раскруткой двух
противо-турбин внутри атома.
Интересно посмотреть как будут решать, думаю
что теплоёмкость не смогут решить в принципе,
- по причине
того что это потянет за собой необходимость
описать и другие эффекты, а для этого надо иметь
объяснение и моделирование хотя-бы электротока и магнитного
поля,
у меня уже это решает и атом и эфир во взаимодействии.
С другой точки зрения если задача есть, то вероятность того
что смогут решить уже есть.
----------------------------------------------------------------------------
 Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Re: Релятивистское и нерелятивистское (классическое) объяснения работы коллайдера.
Ответ #180 - Вчера :: 00:22:10
77pp писал(а) 30.01.14 :: 18:51:46:
\\\Вы хоть знаете, что такое теплород? Нахватались терминов непонятно где, и выдаёте тут.\\\
\\\А Вы мне докажите, что "фотон"
не есть "теплород" - не некий самостоятельно летающий кусочек энергии!
Цитата: (рядом со словом "теплород" ставлю "фотон", а можно поставить
и "глюон" и "бозон")
Приток теплорода (фотона
) в тело должен вызывать его нагрев,
убыль охлаждение. Количество теплорода (фотона
) во всех тепловых процессах должно оставаться неизменным.
 \\\
\\\
- Re: Черная дыра
(А.П. Васи,
2.02.2014 13:09, 970 Байт)
За что Джону Шварцу иМайклу Грину дали мильнеровскую премию
---------------------------------------------------------------------------------------
Прочитал и
вспомнил фильм фантастический,
но что-то мне подсказывает что в физике и космологии
этот фильм фантастичность свою утратил давно.
-----------------------------------------------------
Идиократия / Idiocracy
Год выпуска: 2006
Страна: США
Жанр: фантастика, комедия, приключения
Продолжительность: 01:24:08
Перевод: Профессиональный (двухголосый)
...
Файлов: 2, суммарный размер:
1,572,137,893
- Re: Черная дыра
(А.П. Васи,
3.02.2014 22:27, 5.8 КБайт)





-

- Сообщений: 920
- Рейтинг: +32/-2
- За забором кругозора - удивительное...
-
Ответ #3 : Сегодня в 14:03:42
\\\Чего не поймут "опровергатели", как то, что СТО, ОТО и квантовая механика созданы для практических целей,
результатами которых мы постоянно пользуемся. И любой критик должен предложить либо более простой математический аппарат, либо бОльшую точность результатов,
чем СТО или ОТО.
владимир физик,
попробуйте на основе своих выкладок рассчитать... ну, не коллайдер, а хотя бы синхрофазотрон.\\\
---------------------------------------------------------------------
Что-то мне подсказывает, - что первые ускорители рассчитывали не релятивисты
а сторонники эфира.
--------------------------------------------------------
http://nuclphys.sinp.msu.ru/spargalka/a16.htm
Для того чтобы исследовать свойства материи на расстояниях
меньше чем 10-12 см. необходимо иметь пучки ускоренных частиц,
энергия которых превышает десятки МэВ. Рождение новых частиц происходит в
результате преобразования кинетической энергии налетающей частицы в результате
взаимодействия с другой частицей. Чем больше масса частицы, которую необходимо
получить в столкновении, тем больше должна быть энергия сталкивающихся частиц.
Создание первых ускорителей Дж.Кокрофтом и Э.Уолтоном,
Р.Ван-де-Графом,
Э.Лоуренсом в 1931-32 гг.
открыло новую эру в ядерной физике. Экспериментаторы получили в свое
распоряжение удобные инструменты, на которых можно было получать пучки
ускоренных заряженных частиц с энергией от нескольких десятков кэВ до десятков
МэВ. Современные ускорители позволяют ускорять частицы до энергии нескольких ТэВ.
В ускорителях увеличение энергии заряженных частиц происходит
под действием электрического поля, направленного вдоль импульса частицы.
В ускорителях прямого действия (ускоритель Ван-де-Граафа)
заряженная частица имеющая заряд Ze ускоряется в постоянном электромагнитном
поле, приобретая кинетическую энергию T соответствующую высокому напряжению V
создаваемому источником.
T = ZeV.
В таких ускорителях частицы могут приобретать энергию до ~10 МэВ. Их
существенным преимуществом является непрерывность, высокая интенсивность и
высокая стабильность по энергии ускоренного пучка (~0.01%) .
Ток пучка на ускорителях Ван-де-Граафа может достигать
нескольких миллиампер. В циклотроне частицы ускоряются переменным
электромагнитным полем постоянной частоты. Частицы ускоряются от нулевых энергий
до максимальных, двигаясь по раскручивающейся спирали увеличивающегося радиуса R,
в постоянном магнитном поле B.
R = cp/300ZB.
где cp - импульс частицы, умноженный на скорость света, измеряется в МэВ, B -
индукция магнитного поля, измеряется в Теслах, R - измеряется в метрах. Обычно
циклотроны используются для ускорения протонов и ионов. Предельная энергия для
протонов в циклотронах составляет ~20 МэВ при поле В~2Тесла и частоте
ускоряющего поля 30 МГц.
Первый бетатрон для ускорения электронов был построен в
1940г. Д. Керстом. Бетатрон - это
индукционный ускоритель, в котором электроны удерживаются на равновесной
круговой орбите растущим синхронно с увеличением энергии магнитным полем.
Ускорение происходит за счёт вихревого электрического поля создаваемого
переменным магнитным потоком внутри равновесной орбиты. В бетатронах энергия
ускоренных электронов может достигать сотни МэВ. Дальнейший рост энергии
электронов ограничивается электромагнитным излучением. Наибольшее
распространение получили бетатроны на энергию 20 - 50 МэВ.
Электроны высоких энергий получают в ускорителях двух
типов
-электронных синхротронах.-электронных линейных ускорителях.
В 1944-45 годах
В.Векслер
и независимо от него
Э.Макмиллан
открыли принцип автофазировки, что привело к появлению новых типов ускорителей -
синхротронов. \\\
- Re: Черная дыра
(А.П. Васи,
18.02.2014 0:19, 2.7 КБайт)





-

- Сообщений: 15 817
- Рейтинг: +212/-57
-

Ответ #280 : Вчера в 22:39:56
\\\Откуда такая логика? Никто не связывает решение парадокса с конечностью
Вселенной.

Вселенная просто конечна, но по-видимому, огромного
слабопредставимого размера..
А парадокс решен окончательно лет 50 назад другим объяснением.
Оно изложено аж в ответе#13.
После
него идет просто пустой говор людей, либо не понимающих суть парадокса
по геометрии и физике, либо людей, желающих что-нибудь поопровергать на
ровном месте и пустыми возражениями.
Обоснований любых возражений пока не наблюдается.\\\
----------------------------------------------------------------------------------------------------------
Мне просто очень приятно такое читать.
Можно многого не замечать и не понимать, и самое смешное
что возражений уже не будет - они уже были.
И
возражающих назвали альтами и послали альтов с этого форума
в пешее эротическое путешествие.
И альты уже второй раз не придут повторно раздуплять .
Возражать
альты уже не будут, а будут только смотреть
спокойно и размышлять, - когда релятивисты поймут
что они уже даже не смешные, с их теориями,
в которых чем неадекватней
теория тем она у них считается лучше.
- Re: Черная дыра
(А.П. Васи,
27.02.2014 2:52, 2.7 КБайт)
- Модератор





-

- Сообщений: 13 565
- Рейтинг: +169/-19
- Мне нравится этот форум!
-
Ответ #30 : Вчера в 13:48:09
\\\ Так Вселенная это же
тепловой двигатель, в котором происходит теплообмен с окружающей средой.
Что является окружающей средой по отношению к замкнутой и расширяющейся
Вселенной нам неизвестно.\\\
-----------------------------------------------------------------------
А хлопец совсем оборзел, по мимо того что в мои
авторские
права влез, так и в рамках релятивизма под маркой
которой проходит весь форум под его модерацией -
среды как непрерывной со всеми присущими свойствами
среды - плотность среды, непосредственный контакт между частицами среды,
скорость возмущения среды - так этого у релятивистов то и нет,
у релятивистов пустое
пространство.
В пустом пространстве свет - частицы - фотоны.
А в среде свет - колебания плотности среды.
Грубо говоря - у релятивистов это свет в котором
фотоны летят.
А у альтов просто колеблется эфир - аналогично звуку
в воздухе.
Но собственно у модератора естественно физика
далека от совершенства,
я так понимаю что это или
уже возрастное, или водовки выкушавши - ибо в тексте
много нескладух принципиальных, и скорее позорящих.
- Re: Черная дыра
(А.П. Васи,
8.03.2014 10:50, 12.5 КБайт)





-

- Сообщений: 2 104
- Рейтинг: +80/-3
- Rock-AstroDiver
-
Вчера посетил Малую трибуну
учёного, выступал Дмитрий Вибе. Как всегда, очень интересный рассказ об
образовании звёзд и планетных систем, последние данные, красивые фото.
Спасибо большое!
После лекции состоялся разговор с одной из
сотрудниц МП, в котором она поведала о том, что руководство МП очень
обеспокоено сильным падением посещаемости лекций, особенно в Большом
звёздном зале. (На предыдущей лекции про Радиоастрон было заполнено
меньше половины зала, если не треть - я там был)
Если так пойдёт и
дальше, то лекторий Большого зала будут вынуждены сократить до
нескольких "хитовых" лекций в год (Сурдин, Засов, Шустов и еще
некоторые, на которых ходит народ). Невыгодно собирать полупустые залы
ежемесячно.

Надо исправлять положение!
-------------------------------------------------------------------------------------------





-

- Сообщений: 1 944
- Рейтинг: +98/-15
- через ноты к звездам!
-
Ответ #3353 : 06.03.2014 [11:50:56]
Надо исправлять положение!
Да, не стоило портить отношения со своими партнерами.
---------------------------------------------------------------------------------------
- ASTRONOMY.RU





-

- Сообщений: 12 487
- Рейтинг: +419/-38
- Пусть цветут сто цветов! Кроме сорняков...
-
Ответ #3354 : Сегодня в 00:55:15
Надо исправлять положение!
Да, не стоило портить отношения со своими партнерами.
А немного побольше информации можно, хотя бы намеком?...
------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
http://lenta.ru/conf/kuvakin/
Эдуард-2
[24.04 03:11]
Уважаемый Валерий Александрович, я есть ли в вашем (РАН) арсенале
стандартная методика отделения "пшеницы от плевел", т.е. научных
открытий и достижений от околонаучных явлений, к науке отношения не
имеющих? Eсли такая методика существует, то какие признаки сразу
указывают на то, что перед нами очередной граф Калиостро?
Уважаемый Игорь!
В практике оценки лженауки есть два пути. Первый этот специальная
свободная и независимая научная экспертиза. Но она возможна только в том
случае, если в заявленной идее есть предмет исследования. Если же ее ни
подтвердить, ни опровергнуть невозможно, то такие идеи не
рассматриваются в качестве научных. В этой связи упоминают и о принципе
"бремени доказательства", то есть обязанность доказывать истинность или
научность утверждения лежит на той стороне, которая и выдвигает это
утверждение. Вместе с тем существуют некоторые общие и предварительные
признаки, наличие которых должно ставить под серьезное сомнение
научность заявления (теории, открытия и так далее). Это так называемые
признаки prima facae (то есть "с первого взгляда"). К ним, в частности,
относятся: (1) отсутствие у заявителя соответствующего базового
образования или профессиональной подготовки; (2) апелляция к широкой
прессе или к телевидению, а не к научному сообществу; (3) отсутствие
публикаций в серьезных, рецензируемых периодических изданиях; (4)
использование в текстах понятий, означающих феномены, не фиксируемые
наукой (тонкие поля, торсионные поля, биоинформационные поля, энергия
ауры и так далее); (5) претензия на "революционный" переворот в науке и
технологиях (лжеученые на мелочатся, они обычно обещают настоящие
чудеса, которые почему-то не вызывают у научного сообщества никаких
эмоций); (6) обещание быстрых и баснословных медицинских, экономических,
финансовых, экологических и иных эффектов.
--------------------------------------------------------------------------------------------------------------------------------------
Собственно с моей точки зрения текущая парадигма совсем обнаглела
тем что требует приемственности предыдущим работам.
А если у меня например абсолютно всё не соответствует
текущей парадигме и космологии в частности. Так меня везде
при реферировании моих работ будут посылать в пешее
эротическое путешествие и объявят меня лжеученым и альтом.
Хотя лично я считаю, что если смотреть как они мучат вола и
думают
что занимаются наукой,
то я опережаю всю космологию вместе взятую на 500-1000 лет.
А чем же занимается вся космология, что так тупит, смешно сказать,
мои естественно оппоненты не остались без моего, очень тщательного
исследования
их работ. Тот же Вибе не придумал самостоятельно аж
ничего вообще, занимается
пересказами и профессор. А есть ещё такие
космологи, которые занимаются
интерпретациями авторских вариантов,
в стиле мол автор черных дыр льох а я
вот такой умный, лучше автора
черных дыр знаю, - какие должны быть черные дыры.
И естественно есть предел у слушателей, когда они уже не
хотят
верить во всякие сказки, преподносимые как истина в
последней инстанции.
И ясный конь они уже не будут ходить на лекции, в основной
сути которых
за последние 65 лет, уже ничего не меняется.
И естественно если опубликовать мою статью, например,
которая противоречит
всей текущей парадигме и намного лучше и проще объясняет
всю физику звезд
и галактик, ясный конь
сразу у читателя появится вопрос.
- А чем занималась космология последние 100 лет?
- Re: Черная дыра
(А.П. Васи,
22.03.2014 11:52, 4.2 КБайт)
------------------------------------------
- Модератор





-

- Сообщений: 14 513
- Рейтинг: +389/-49
- Дети любят бутерброд с маргарином!
-
Ответ #19 : Сегодня в 07:21:01
\\\Автор
известный, но здесь обсуждается конкретное предложение не этого автора.
Прошу ограничиться обсуждением предложения, опубликованного в первом
сообщении. Сообщения, не относящиеся к этому предложению, будут
удаляться.\\\
\\\
По всему форуму обсуждения идут в рамках заголовка темы, а не его
первого предложения. Я извиняюсь, но получается вы тут свои личные
"императорские" порядки устанавливаете? Есть правило - не уклоняться от
темы, а нет первого сообщения.
"Эксперименты" в названии стоят во множественном числе. И неизбежны ссылки и сравнения от других источников.\\\
\\\Прочитайте пункт 5.5 Правил, с которыми Вы согласились при регистрации.\\\
--------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------
Я уж было распереживался что у меня появятся конкуренты
релятивисты, у которых масса свободного времени, и у них
собственно нет другого выбора,
как придумывать что-то - не реля-
тивистское.
Напомню про релятивизм тем кто не знает обычная не физичная
теория, на заявленные физические свойства
в которой отсутствуют,
- как физические приборы - измеряющие заявленные величины.
Сплошная фантазия ничем физически не обоснованная.
Так вот я сам
как раз придумываю а точнее обдумываю опыт
трёх сред взаимодействующих друг с другом, эфир один из этих, сред.
Я уже думал что у меня уже конкуренты появились,
но модератор
крассава,
вот в данном случаи он лучший,
обломал рога релятивистам,
а кому не обломал рога, тому воткнул эти рога в грунт на том и заклинил
бурную деятельность релятивистов которые решили составить мне
конкуренцию.
- Re: Черная дыра
(А.П. Васи,
22.03.2014 18:17, 5.6 КБайт)
У Вибе естественно бывают проблески осознанного разума
но с моей точки зрения его затуманивает ожидание халявы.
------------------------------------------------------------------------------------
http://elementy.ru/lib/430399
\\\Я бы сказал так: основы современной
астрономической картины
Мира могут оказаться неверными только целиком.
Тоесть мы можем
ошибаться не в отдельных фрагментах, а вовсей физике
сразу.\\\
-------------------------------------------------------------------------------------
Вибе догадывается что вся текущая космология это лайно
собачье,
при этом он хочет чтобы кто-то указал на его ошибки. При
этом
не хочет искать ошибки и не приемлет объективного анализа,
по причине того что не так давно его частично раздуплило и
он осознал
что все теории лайно собачье, не стоит уже поддерживать
эти теории,
то-есть термин господствующая парадигма - альты придумали.
--------------------------------------------------------------------------------------------
Ответ #1020 : 08.03.2014 [10:46:29]
\\\Почему большой взрыв произошел из крошечного шарика?\\\
\\\Откуда
информация, что "большой взрыв произошел из крошечного шарика"?\\\
\\\Ну так теория большого Взрыва, как бы официально поддерживается многими учеными\\\
\\\
В
науке отсутствует понятие официальной поддержки теорий. Поэтому ни один
учёный не может официально поддержать какую-либо теорию. Далее,
подскажите,
пожалуйста, где именно в теории Большого Взрыва говорится
про крошечный
шарик. Мне раньше казалось, что там всё несколько сложнее.\\\
-------------------------------------------------------------------------------------------------------
Ответ #1029 : 13.03.2014 [00:28:08]
\\\Что -- это?\\\
\\\Заметка. В заметке, по-вашему, фантазии или факт?\\\
\\\Частично
фантазии. Как обычно, галактики названы старыми, но
оснований для
такого утверждения не приводится. В паре мест
написано, что этим
галактикам 12 млрд. лет -- тоже без оснований.\\\
-----------------------------------------------------------------------------------------------
Скажу только о том что я давно слил в канализацию истории
всю
космологию господствующей парадигмы, только вот я об этом не
могу
рассказывать и хвастаться по большому количеству причин.
Так вот сидят себе у телескопов космологи и уверенно думают
что
кто-то придумает и разрешит им пользоваться своими идеями,
- не угадали, это уже в прошлом.
Не можешь сам придумать свой эфир и обнаружить его своим разумом
соси дармовую сисю релятивизма и следующие 500-1000 лет.
- Re: Черная дыра
(А.П. Васи,
2.04.2014 19:28, 22.0 КБайт)




-

- Сообщений: 366
- Рейтинг: +4/-0
- специалист по пострелятивистской электродинамике
-
Ответ #1050 : 31.03.2014 [16:18:19]
\\\Факт не бывает в космологии. Факт просто есть.\\\
\\\Да, но
вы же видите как строится ТБВ?
Как
только обнаруживаются новые наблюдательные данные, не укладывающиеся в
предыдущую модель, так тут же выдумывается новая фантастическая
сущность, о которой ранее вообще не упоминалось (например, инфлантонное
поле,тёмная энергия).
В этих условиях никаких фактов, ставящих под сомнение ТБВ в принципе быть не может.
Однако,
под сомнение может попасть ОТО, которая и способствовала развитию ТБВ и
в которую труднее уже что-то новое запихать. Обещали запустить проект
Advanced LIGO в 2014 году, но что-то пока ни слуху ни духу. Между тем
есть вот такое наблюдение отсутствия гравволн
http://arxiv.org/abs/0805.4758 Его можно считать
научным фактом или как (вот здесь интерпретация этой статьи "жёлтой" прессой
http://www.membrana.ru/particle/12649
) ?\\\
Последнее редактирование: 31.03.2014 [16:33:07] от Rishi

Записан




-

- Сообщений: 366
- Рейтинг: +4/-0
- специалист по пострелятивистской электродинамике
-
Ответ #1054 : Вчера в 18:44:38
\\\Тема вскоре будет закрыта ввиду её полной бесперспективности.\\\
\\\Вот, совершенно - за.
Топикстартёр с научной точки зрения неправильно сформулировал тему обсуждения.
Но всем космологам надо перед носом повесить
табличку со словами Ньютона: "Гипотез не измышляю".
В
физике (если космологию можно как-то причислить к физической науке, а
не, например, к научной фантастике), конечно, без гипотез не обойтись,
но когда фантазию про то что случилось 13,7 млрд. лет тому назад,
пытаются представить обывателю чуть ли не как научный факт, то это уже
перебор. \\\

Записан
- Модератор





-

- Сообщений: 14 544
- Рейтинг: +391/-49
-
Ответ #1055 : Вчера в 20:44:30
\\\когда
фантазию про то что случилось 13,7 млрд. лет тому назад, пытаются
представить обывателю чуть ли не как научный факт, то это уже перебор. \\\
\\\Противникам
Большого Взрыва только и остаётся повторять заклинание: "Это фантазия,
это фантазия, это фантазия!.." Но заклинания в наше время не работают! Я
буду просить администратора форума Харона сразу же банить тех, кто
сомневается в Теории Большого Взрыва.\\\

Записан





-

- Сообщений: 2 797
- Рейтинг: +63/-0
-
\\\ Ответ #1056 : Сегодня в 11:00:54
Цитата Незван: По единичному наблюдению уже научились собирать статистику?\\\
\\\В оригинальной статье
http://arxiv.org/abs/1309.2826 авторы пишут:
Учитывая
обилие нелинзирующих галактик с эмиссионными линиями, кажется
маловероятным существование даже одной сильно линзирующей галактики в
обзоре CANDELS-Sized.
(Given the abundance of unlensed emission-line
galaxies it was seemingly unlikely that even one strongly lensed version
exists within a CANDELS-sized survey).\\\
\\\Т.е. исследуется немалая выборка объектов, и анализ выполняется корректно, в рамках существующих статистических методов.\\\




-

- Сообщений: 366
- Рейтинг: +4/-0
- специалист по пострелятивистской электродинамике
-
Ответ #1057 : Сегодня в 17:30:50
\\\Противникам
Большого Взрыва только и остаётся повторять заклинание: "Это фантазия,
это фантазия, это фантазия!.." Но заклинания в наше время не работают! Я
буду просить администратора форума Харона сразу же банить тех, кто
сомневается в Теории Большого Взрыва.\\\
\\\Если
противники ТБВ просто треплются, не пытаясь обосновать свою точку
зрения, то это можно отнести к ненауке. Если противники ТБВ пытаются
оформить свою гипотезу в виде теории (а для этого надо обязательно иметь
возможно обмена мнениями между учёными), то это другая научная школа и
попытка использовать в этом случае административный ресурс - ну это мы
уже где-то проходили: quod licet iovi non licet bovi\\\
------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------
Всё гораздо проще - когда банят альтов - которые в состоянии
придумать и
обосновать измерительные методики опираясь на физические свойства - то таки
да - адекватных опровержений уже не будет.
По той причине что я например
очень внимательно подошел к данному вопросу,
и я более чем уверен что закрыл своим авторством 75% возможных опровержений
данной теме, и глупо даже не понимать
того что количество возможных
опровержений - конечно. И если кто-то выбрал 75% самых простых случаев,
то эти 75% закрыты, - решены - навечно альтами, и их уже
не придумают первыми - релятивисты.
- Re: Черная дыра
(А.П. Васи,
2.04.2014 19:34, 240 Байт)
А с другой точки зрения -
Фантастическая ситуация - реферируемый журнал опубликовал статью
опровергающую большой взрыв, опровергающую черные дыры - в принципе
кто-то это может представить как реальность - вот то-то же.
- Re: Черная дыра
(А.П. Васи,
2.04.2014 21:05, 3.0 КБайт)





-

- Сообщений: 7 524
- Рейтинг: +257/-81
- команда ISON http://astronomer.ru/
-
Ответ #230 : Сегодня в 01:12:59
Дык, вступление в ESO совсем не означает, что с телескопами будет хорошо у страны, которая платит взносы. Хорошо будет у ESO. 
Телескопы
ESO - это центры коллективного пользования для всего мира, а не только
для стран-участников. Любой ученый может написать заявку на наблюдения, и
если она сильная, то получит наблюдательное время, даже если его страна
не платила взнос. Но и наоборот - если заявка слабая, то времени ученый
не получит, даже если его страна потратилась.
Такая схема
замечательная для стран, в которых астрономия сильная, и, абсолютно
несправедливая для стран, где астрономия переживает не лучшие времена.
Это как в анекдоте - научитесь нырять, нальем воды в бассейн. А как
научиться нырять без воды. 
---------------------------------------------------------------------------------------------------------
Я как альт помню все тексты этого космолога в сторону альтов.
Вкратце - в его понимании альты - недоидиоты.
Лично меня подобным отношением трудно
огорчить,
по той причине что мне безразлично.
- Re: Черная дыра
(А.П. Васи,
14.04.2014 19:33, 117 Байт)
Там где звёзды редкие - звезды - синие, где звезд больше
чем много - там они все - красные, - это явно видно.
- Re: Черная дыра
(А.П. Васи,
14.04.2014 20:16, 2.0 КБайт)

: 21.03.2014 [05:29:19]
------------------------------------------------------------------------
Я лично
давно с удивлением смотрю на это название темы.
Собственно это я считаю что можно отнести к случаю ситуации
перебора вариантов. И я бы не отождествлял бы
это с интеллектом
или случайным тыканьем пальцем в небо.
Был случай при котором обезьяна на одном острове научилась что-то
делать, - до этого никто
из обезьян не умел этого делать на соседних
островах.
После того как более двадцати обезьян научились аналогичному на этом
острове, - то - на всех
соседних островах практически одновременно
все обезьяны начали делать подобное.
Собственно - что наблюдается - телепатическое обучение у обезьян
на
большом расстоянии.
--------------------------------------------------------------------------
Я в данном случаи могу сразу сказать что я давно думал
о том -
Какой минимальный размер - планеты, астероида или кометы - на
поверхности которой лежат (под естественными силами притяжения - камни),
и
температура поверхности этой планеты в градусах теплового сальдо
по отношению к окружающей среде, в абсолютных величинах.
С моей точки зрения для такой ситуации
абсолютно минимальная
температура -160 градусов Цельсия, - практически реальная - -81 градус Цельсия.
Так сказать тепловой гистерезис, или есть тепловое
сальдо и притягиваются камни
которые и находятся на поверхности - или большой камень, на поверхности которого
даже пыли нет.
Так вот минимальный размер
при котором возможны камни на поверхности,
и при этом будет тепловое сальдо - 300 км в диаметре - это моё личное мнение.
- Re: Черная дыра
(А.П. Васи,
14.04.2014 21:16, 1.6 КБайт)
Для тех кто не понял -
есть - необоснованная ничем - формулировка -
очень совпадающая с тем о чём я думал не то что
давно - но достаточно часто года
два тому назад.
---------------------------------------------------------------------------
----------------------------------------------------------------------------
А у меня,
по моей модели, - Минимальный размер планет на поверхности которой
есть камни?
- Ясный конь что я изначально этот размер определил на абсолютном уровне
120 км в диаметре.
120 км в диаметре - значит - что при таком диаметре тела в космосе - отсутствует возможность
конденсации эфира (как газа внутри космических
тел), при конденсации эфира - естественно
эфир переходит в более плотное состояние, и при этом сбрасывает свою энергию - во
внешнюю среду - в данном случаи это
верхняя часть космического тела ( планета, комета, астероид).
Естественно если эфир не движется для конденсации в центр какого-то космического тела,
- то
тогда у этого тела не будет и притяжения.
Ясный конь что телу - в диаметре тысяча километров - только некоторый внешний процесс,
мог создать внутри него
ситуацию при которой у этого тела началась конденсация эфира,
которая и создала всасывание эфира - с последующим выделением тепла - что и есть -
тепловое сальдо
планет и звёзд.
- Re: Черная дыра
(А.П. Васи,
14.04.2014 22:54, 1.8 КБайт)
Из серии чьябы корова бычала -
----------------------------------------------
: Сегодня в 13:55:47
---------------------------------------------------
Главное
в этой ситуации чтобы космологи не перетанцевли
в танцах про Черные Дыры.
Хотя с другой точки зрения - Праздничный Концерт -
любого мероприятия - на
этом танце может собирать
деньги просто потому - что "такая жестокая селяви" -
и я думаю что если этот танец сплясать вначале лекции,
и в конце
лекции, - это будет фантастическая фотонно-лавинная
двух ударная черно-дырочная танцевальная рапсодия - по несмышлёному
разуму слушателю - в целях активации
его сознания в направлении
развития танцевального стиля - Черных Дыр.
----------------------------------------------------------------------------------
\\\www.youtube.com/watch?v=UIt3fYA_Zbk19 мая 2010 г. - Добавлено пользователем
DiveSabbath
Астрофест-2010, лекция Сергея Попова о сверхмассивных чёрных дырах.\\\
- Re: Черная дыра
(А.П. Васи,
27.04.2014 18:46, 2.2 КБайт)
У меня такое чувство что у модераторов релятивистов
сейчас башню сносит от злости и от дерзости данного
юзера, и они обдумывают как его забанить и какими
методами,
чтобы другим не повадно было подобные
адекватные вопросы задавать.
С моей точки зрения забанят после переноса в горизонты
науки о вселенной.
Естественно ветку забалаболят релятивисты,
и когда автор что-то скажет от себя, но не очень
к месту, хотя и по теме, забанят автора, а потом скажут
что
автор забил болт на свою тему и закроют
классика общения однако.
-------------------------------------------
Здравствуйте.
\\\Мой вопрос несколько не обычен, а потому мне было тяжело выбрать для него подходящую ветку форума.
В
ходе дискуссии о звездах, галактиках и небе вообще возникло расхождение
во мнениях что же такое так называемые "черные дыры" и какова их роль в
жизни и строении галактик.
Так вот, вопрос в следующем:
Насколько соответствуют истине каждый из следующих пунктов?
1.
ВСЕ галактики ОБЯЗАТЕЛЬНО имеют в своем центре черную дыру, которая
обладает необходимыми гравитационными и прочими силами которые формируют
саму галактику (иными словами, черная дыра - обязательная составляющая
галактики находящаяся в ее центре и не существует галактик БЕЗ черной
дыры в центре).
2. Если образуется новая черная дыра в итоге
своего развития обязательно ли она станет центром очередной галактики?
(если принять за истинну первый пункт).
2. могут ли "Черные дыры" существовать в ином месте кроме центра галактики?
Извиняюсь
за некоторую сумбурность своего поста, старался ужать свои вопросы в
рамки максимального понимания и минимального объема =)
Заранее спасибо за ответы.\\\
- Re: Черная дыра
(А.П. Васи,
27.04.2014 18:49, 169 Байт)
Я думаю что юзер даже не догадывается о том количестве премий
и их суммах которые уже получены за данные вопросы,
точнее за уже бывшие ответы на эти вопросы.
- Re: Черная дыра
(А.П. Васи,
4.05.2014 15:48, 2.8 КБайт)
Читал для смеха
--------------------------------------------------------------------
Ответ #24 : 22.03.2011 [20:54:31]
\\\Я полагаю, что альтам прежде
всего не место в "Астрономии для всех".
Раздел посвящен "классической"
астрономии, а не выдвижению новых
"гениальных" гипотез.
В Горизонтах с альтами модераторы быстро справляются.\\\
------------------------------------------------------------------------------------------------
Что здесь смешно, что уже с каких-то маразматических утверждений
релятивистская космология - стала " классической " - это враньё,
релятивистская
космология сто лет назад послала в даль классическую
космологию.
И как говорится у посетителей этого форума бывают и проблески
здравого смысла.
-------------------------------------------
Ответ #37 : 24.03.2011 [10:39:51]
\\\Где достает? В разделах "Астрономия для всех" и в "Горизонтах"
неграмотный, эпатажный альтизм сразу
банят.
А
грамотно изложенная альтернатива (даже дикая) бывает интересна,
также
как грамотные (но наивные) вопросы хоть немного подготовившегося
новичка. К сожалению, их маловато. Желающих ответить больше.

Нельзя полностью выхолащивать форум.\\\
---------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
4.05.2014 16:16, 1.7 КБайт)
Что в итоге получилось - релятивисты послали альтов
в пешее путешествие.
Собственно релятивисты это кто? - это проповедники
старых идей, и сами не могут,
по определению, придумать
ничего нового.
В итоге получилось то что место альтернативных теорий,
заняли другие.
------------------------------------------------------------------------------
http://www.astronomy.ru/forum/index.php?topic=103533.0
-----------------------------------------------------------------------------
О чем и свидетельствует следующий форум,
собственно
получается что в среднем за неделю выходит одна передача
по космологии которая не нравится релятивистам.
Лично мне не нравятся практически
все передачи по космологии.
- Re: Черная дыра
(А.П. Васи,
4.05.2014 20:06, 2.5 КБайт)
Ответ #163 : 07.09.2013 [19:25:39]
\\\Он же не спорит с нами, а тупо проповедует свою теорию мироустройства. Наивный, думает, что кого-то это заинтересует.
Странно, что альты всегда так стараются пропагандировать свои идеи. Даже на форумах любителей.
Интересно, считает ли Михаил себя любителем астрономии

Я несколько раз пытался перевести разговор на астрономию, но он ни разу не отреагировал.\\\
----------------------------------------------------------------------------------------------------------------------------------
Вот в данном случаи надо
понимать, что у альтернативщика - его
природное свойство - ему легко придумывать что-то абсолютно
новое, и он может своими выдумками и придумками объяснять
различные физические ситуации.
Естественно что альты разные бывают, и по способностям
и по возрасту.
И собственно что наблюдается что релятивисты
только текущую
парадигму считают смой лучшей и логичной.
Хотя релятивиста любого спроси - что он лично сам придумал в космологии
- ладно что ничего,
так самое грустное что пишется ежегодно много
книг и статей в которых все релятивисты самостоятельно аж ничего
не придумали. Это называется - переливание из пустого
в порожнее.
В итоге все статьи только загаживают моск и сознание желающим
понять космологию. Естественно практически и не отыскать
базовых авторских определений,
как физических свойств,
так и физических сущностей - ибо при наличии таковых и даром
не нужны будут по тысяче статей в год которые - трактуют эти же
свойства
и сущности как им вздумается.
- Re: Черная дыра
(А.П. Васи,
4.05.2014 20:14, 310 Байт)
И самое смешное что релятивисты не воспринимают не только
другую но и не воспринимают лучшую теорию от той которую
им вбили в мозг обучением.
Ясный
конь что они банят альтов, это их естественное поведение.
Это их основная задача и их предназначение,
только они этого не осознают.
- Re: Черная дыра
(А.П. Васи,
10.05.2014 16:39, 2.9 КБайт)
---------------------------------------------------------
Ответ #1058 : Сегодня в 11:01:14
\\\Переходим к объяснениям на конкретных примерах:\\\
------------------------------------------------------------------------------
Ответ #1059 : Сегодня в 11:57:47
\\\Arton, может быть, всё-таки ответите на вопросы? А то непонятно,
что именно Вы поясняете на конкретных примерах.\\\
-----------------------------------------------------------------------------------------
Яркий пример того когда один догадывается да не может
внятно
высказать свою мысль. А у второго собеседника
есть желание понять ибо это ему коммерчески выгодно,
но второму не даёт это сделать бесполезный порожняк
постулатов
которые он вызубрил.
Расскажу примитивно.
Есть такая ситуация - резонанс, и у резонанса есть разные амплитуды,
и у этих амплитуд есть кратные изменения,
в связи с чем - звезда
для планет предоставляет им возможность стать на орбиты, и
орбиты могут быть у звезды только на определённы расстояниях.
Здесь
надо понимать следующее что звезда по своей сущности -
практически вечная, а в космическом пространстве объектов размером
с планету в галактике нашего типа летают в космосе в тысячи раз
больше чем звезд в этой галактике, и из чего уже понятно что
за миллионы лет возле любой
звезды в непосредственной близости
пролетит миллион а возможно и миллиард планет, в связи
с чем вопрос постановки на орбиту - вопрос времени.
У автора
темы есть естественно здравая мысль, я собственно удивлен
что его так долго не забанили.
Там у него есть такой коэффициент, а понимания нет, если бы ещё
уделяли
внимание не только звездам а и той температуре в которой находится
звезда, и цвету звезды и размеру звезды, то возможно они нашли
бы закономерность,
и она указывала бы на плотность эфира возле
данной звезды, но до этого им надо эволюционировать.
А так как у них нет плотности эфира, а в пространстве - голимый
порожняк - то понимания у них не будет никогда.
Также понимания не будет по причине того что их моск загажен
ложной информацией о том как появляются планеты,
в связи с чем
их моски никогда не допустят той ситуации о которой я рассказал.
- Re: Черная дыра
(А.П. Васи,
11.05.2014 14:35, 8.9 КБайт)
---------------------------------------------------------------------
Ответ #1056 : Вчера в 08:07:46
\\\ Новая запись правила, получившая название закона
планетарных расстояний:
аn,m = k1 (n + 1/2m) k2 \\\
--------------------------------------------------------------------------------------
Ответ #1058 : Вчера в 11:01:14
\\\ Описать структуру этой системы предлагаю формулой:
а
n,m = 0,24 (n + 1/2
m) 0,195 \\\
------------------------------------------------------------------------
Ответ #1063 : Вчера в 17:20:44
\\\Не укажете ли ошибку в следующих расчетах:\\\
И так, имеем характеристический период для системы
планет в целом:
\\\"характеристический
период = 49.05799539 дней... примерно около двух раз
больше
сидерического периода вращения внешних видимых слоёв Солнца
на
экваторе = 25,05 дней"\\\
\\\Нет
никакой ошибки. Просто если брать все планеты, получается
"характеристический период" 49.05799539 дней. Если брать только планеты
земной группы, получается "характеристический период" 49.972335 дней.
Это ближе к удвоенному значению "сидерического периода вращения внешних
видимых слоёв Солнца на экваторе = 25,05 дней". Если это не подходит,
я
предлагаю Вашу "гипотезу" переписать в таком виде:\\\
\\\Гипотеза:
вероятно, что Закон Боде-Тициуса является математическим
представлением, лежащей в плоскости эклиптики, системы концентрических
окружностей с центром в центре Солнца. (В барицентре Солнечной
системы?)
Из величины собственного осевого вращения Солнца определяются
параметры
показательной функции от независимого параметра n (где n
принимает значения:
1,2,3,...), по которой вычисляются радиусы этой
системы концентрических
окружностей (пространственной сетки) таким
образом, чтобы выполнялось
следущее условие для частот: сумма частот
(обратных периодов) обращения
планет, умноженная на 1,958403, равна
частоте (обратному периоду) собственного
осевого вращения Солнца(на
экваторе).\\\
------------------------------------------------------------------------------------------------------------
Что здесь смешно что Вибе
у одного позаимствовал одну идею у другого позаимствовал
другой результат, и решил по быстрому скосить славы. Всё в лучших релятивистских
традициях.
---
Если рассмотреть ситуацию с другой точки
зрения то можно представить что есть тяжеловесы
в теоретической космологии, а есть и недалёкие жаждущие
быстрой славы.
Мне это даже напоминает когда львы в теоретической
космологии не спеша рассуждают над вопросом, и им
важен качественный результат, и вдруг подбегает
декоративный
мелкий щенок и хватается за большой интеллектуальный кусок,
который перед
львами, и пытается откусить и утащить его к себе
в закрома. Но при всех потугах интеллектуального и жадного
щенка
щенок только
большую кучу лайна напудил, и показал что с ним
нельзя иметь дело.
Это я к тому что чужую разработку нельзя объявлять
своей
гипотезой, - ибо это не порядочно, тем более, что в
данном случаи
- эта борзая заявка не является гипотезой, - это
постулат,
по причине отсутствия причинно следственной связи для
коэффициента.
Хотя и коню понятно, что тот коэффициент что вычитается
это простая поправка на атмосферу звезды, при учете
которой
будет отсчет гармонических секторов для планет, от
некоторой
- твёрдой поверхности звезды.
Что потом надо понять чтобы разобраться в данном вопросе,
- для этого нет смысла искать ответы на вопрос в анализе
планет у разных звёзд это путь недалёких, и по этому
пути пойдёт любой интеллектуальный щенок теоретической
космологии. Есть для понимания более простые подходы
но знания должны уже быть. Если вспомнить что к звезде
движется некоторая среда которая увлекается звездой, то
логично
сделать вывод что на орбите может быть планета которая
увлекает эфир и имеет угловой момент движения который
может уравновесить эти две силы.
Итого есть две центростремительные силы, одна у звезды
вторая у планеты эти силы увлекают эфир, чем создают
притяжение у этих тел. Вот это уже есть две величины
которые суммируются, и эта сумма должна соответствовать
центробежной силе. В данном случаи коню понятно, что
требования уже будут не к звезде, а к планетам планета
, должна соответствовать по своим параметрам.
А если планета соответствует и находится на орбите и
известно
её температура и её тепловое сальдо, можно легко и просто
определить все параметры этой планеты.
- Re: Черная дыра
(А.П. Васи,
11.05.2014 17:05, 3.6 КБайт)
Ответ #1076 : Сегодня в 09:07:56
\\\1
- К вашему сведению, Меркурию приписали (если не ошибаюсь, Боде)
аномальный индекс, равный минус бесконечности (вместо логически
напрашивающегося минус один) исключительно с целью втиснуть
Меркурий в
геометрическую последовательность Тициуса.\\\
\\\Вот
как формулировал своё правило Тициус: Если обратить внимание на
расстояния между соседними орбитами планет, то можно заметить, что эти
расстояния увеличиваются почти пропорционально радиусам самих орбит.
Если принять расстояние Сатурна от Солнца за 100 единиц, то Меркурий
находится
от Солнца на расстоянии 4 единиц, Венера на расстоянии 4 + 3
= 7 единиц,
Земля 4 + 6 = 10 единиц, Марс 4 + 12 = 16 единиц. Но при
переходе от Марса к Юпитеру
имеется отклонение от этой точности
прогрессии. После Марса такой прогрессии
отвечает расстояние в 4 + 24 =
28 единиц, но на этом расстоянии мы не видим ни
большой планеты, ни
планетного спутника. Неужели Создатель оставил это пространство
пустым?
Ни в коем случае! Уверенно держу пари, что это место занимают еще не
открытые спутники Марса; позвольте добавить, что Юпитер, возможно, также
имеет
несколько спутников, которые еще не наблюдались. Далее мы
открываем для себя
положение Юпитера, отвечающее 4 + 48 = 52 единицам;
Сатурн же находится на
расстоянии 4 + 96 = = 100 единиц. Какое
удивительное соотношение! Как видите,
никаких проблем с "втискиванием"
Меркурия у Тициуса не было. Если Вам индекс
Меркурия в последующих
формулировках правила Тициуса-Боде кажется нелогичным,
это может просто
означать, что матушка-природа не особо стремится следовать Вашей логике.\\\
--------------------------------------------------------------------------------------------------
И опять логично понимать что недалёкий смотря в книгу - будет наблюдать
там аж ничего, что собственно и коню явно видно в расположении планет.
В первую
очередь - масса и размер планеты не влияет на её орбиту, в связи с чем
логично заметить что возможно этому причина другая, а именно взаимовлияние
планет которое
при этом производит отсутствие взаимовлияние между ними
которое их может разбалансировать, а наоборот стабилизирует их орбиты.
Что здесь явно наблюдается что если
убрать первое слогаемое, то каждая следующая
планета находится на таком-же расстоянии как и Солнце.
Например от Земли до Марса такое - же расстояние как до Солнца,
без учета первого
слогаемого, и у всех других планет аналогичная ситуация.
Собственно вот так не торопясь логично рассматривать текущие ситуации и придумывать
к ним логические взаимодействия.
- Re: Черная дыра
(А.П. Васи,
15.05.2014 22:03, 2.4 КБайт)
Ответ #1080 : 12.05.2014 [18:13:03]
----------------------------------------------------------
Ответ #1082 : 12.05.2014 [19:18:40]
----------------------------------------------------------
Ответ #1083 : 12.05.2014 [19:34:36]
----------------------------------------------------------
Вот
тот случай когда специалист говорит одно,
а два недалёких дауна в данном вопросе пытаются
выудить из специалиста нужные им физические объяснения,
и за одно
считают своим долгом зачмырить специалиста, по скольку
второе им тоже не помешает для своей гипотезы по данному
вопросу, - мол автор ответить на него не смог,
а я вот так
пропостулировал и я мол самый умный, ибо первым
ответил , или вопросом задал голевую передачу.
Всё это даунтятина.
Даже я понял
что автор сказал, что планеты могут одновременно
находится на двух устойчивых резонансах у звезды, ибо и коню понятно,
что планета любая став на орбиту - будет
снижаться к звезде со временем,
и при этом они влияют друг на друга, и ясный конь что ближние планеты
например застабилизировались, а у дальних планет одна планета,
столкнулась
с другой, и перешла на другую орбиту, и она например начинает преподнимать
все другие орбиты планет, и здесь вариантов много,
логично сделать
физические симуляторы данной ситуации,
я например вижу возможность, но это не моя борьба, да и ни кому
из парадигмы не объяснить что это надо, и что это будет
по идее совпадать.
Они будут только унижать и чмырить чтобы потом высказать свои гипотезы
по чужим идеям.
- Re: Черная дыра
(А.П. Васи,
18.05.2014 13:43, 1.4 КБайт)
Ответ #1091 : Сегодня в 12:19:23
\\\Все более склоняюсь к тому, чтобы разделять процесс
формирования
планетных систем на две стадии,
принципиально отличные друг от друга.\\\
-----------------------------------------------------------
Что надо понимать
в данной ситуации, что юзерам вбили обучением
практически абсолютную стационарность сформированной планетарной
системы, и то что с ней уже ничего в будущем не
измениться.
При вечном существовании вселенной, и практически вечных звёздах,
подобная уверенность сравни идиотизму, и в данном случаи
есть недостатком мышления
разработчика динамики планетарных систем.
Вот в данном случаи уже логично вернуться к статистике, при
этом что можно сделать - привести статистику к звездам
главной
последовательности нашей галактики.
Возможно окажется что у звезд желтого цвета - у планет
ситуация совпадает, у синих такая-то наиболее частая ситуация,
а у красных звёзд - вот такая-то.
При этом возможно и коэффициенты будут совпадать у звезд
одного цвета.
- Re: Черная дыра
(А.П. Васи,
21.05.2014 7:57, 1.4 КБайт)
Ответ #27 : 19.05.2014 [06:56:01]
\\\Как обнаружить пространства-времени кручение? В этом эссе мы
предоставляем
теоретическую основу для ответа на этот вопрос.
Многополярные уравнения движения для очень широкого класса
гравитационных теорий с неминимальной связью в пространстве-времени
,
допускающих кручения даются. Наши результаты обеспечивают основу
для
систематического тестирования целых классов теорий с помощью
расширенных
пробных тел.\\\
----------------------------------------------------------------------------------------------------------
Даже не знаю что сказать
при виде такого хамства и такой наглости.
Да никому и даром не нужны никакие теоретические основы для ответов -
это уже буета полная.
Если нет базовых определений
физических свойств, нет определений физических
сущьтностей нет физических определений взаимодействий и описания их причин,
- то это логично послать в пешее эротическое
путешествие, и даже не
заморачиваться на дальнейшем чтении.
- Re: Черная дыра
(А.П. Васи,
21.05.2014 8:23, 2.0 КБайт)
Ответ #1094 : Сегодня в 00:03:02
-----------------------------------------------------------------
Честно могу сказать лично мне жаль автора такое чувство
что самую малость опыта и интеллекта не хватает для решения
данного вопроса.
На самом деле
с моей точки зрения эти методы в своей сути дорога
в никуда.
Дело в том что решается задача совсем по другому.
В первую очередь логично взять банку с водой
и положить
туда не мелкий металлический шарик, и так покрутить банкой
чтобы шар катился.
Тогда сразу становится понятно что при круговом движении, шар
как в подшипнике, часть воды внутри будет закручивать в одну сторону,
а у стенок будет закручивать как в другую.
Что здесь играет роль - правильно и коню понятно
- диаметр.
Вот уже есть одна составляющая - диаметр, вторая понятно, - вязкость,
третья понятно - плотность.
Исходя из того что эфир увлекается по разному,
даже при одинаковом
размере планет - то логично его определять по тепловому сальдо планет,
и можно в итоге пересчитать в Вт/м2.
Итого есть четвертая величина
- тепловое сальдо планеты.
Естественно пятая - тепловое сальдо звезды.
Естественно вторую величину вязкость - логично подбирать для плотности.
Сама плотность
среды определяется по температуре космоса у этой звезды,
больше температура - меньше плотность среды.
И как говориться - вывод - до коле не будет в некоторой
формуле, а точнее расчётной программе, использоваться
все перечисленные мной пять величин - то в определении
планетарных расстояний логично наблюдать устойчивый
теоретический секас.
- Re: Черная дыра
(А.П. Васи,
21.05.2014 20:39, 10.8 КБайт)
-------------------------------------------------------------------------------------
http://elementy.ru/trefil/21152
\\\Планеты движутся вокруг
Солнца по вытянутым эллиптическим орбитам,
причем Солнце находится в
одной из двух фокальных точек эллипса.\\\
\\\Отрезок прямой, соединяющий Солнце и планету, отсекает равные площади
за равные промежутки времени.\\\
\\\Квадраты периодов обращения планет вокруг Солнца относятся как кубы
больших полуосей их орбит.\\\
-----------------------------------------------------------------------------------------------------------------------------
Что
собственно в этом случаи интересно - это то что происходит со временем,
и как и куда движутся фокальные точки эллиптических орбит по отношению друг
к
другу, и как меняются радиусы эллипсов со временем.
Собственно это тоже не логично не замечать при объяснении движения планет
по своим определённым орбитам.
С моей точки зрения должны быть
какие-то влияния например Солнца которые стабилизируют орбиту и приближают
её к круглой, и есть например, влияние
других планет которые увеличивают эллипс.
После этого ищу в гуглях - про изменение расстояний фокальных центров,
и нахожу -
-----------------------------------------------------------------------------------------------------------------------
http://ru.wikipedia.org/wiki/%D0%A3%D1%81%D1%82%D0%BE%D0%B9%D1%87%D0%B8%D0%B2%D0%BE%D1%81%D1%82%D1%8C_%D0%A1%D0%BE%D0%BB%D0%BD%D0%B5%D1%87%D0%BD%D0%BE%D0%B9_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B
Задача расчёта поведения системы гравитационно взаимодействующих тел,
если их количество больше двух, в общем случае не имеет аналитического
решения, то есть нет такой формулы, в которую можно подставить время и
получить координаты тел (см. Задача
трёх тел).
Основные направления, в которых можно исследовать системы трёх и более
тел это получение решений численными методами и изучение устойчивости
движения. Движение считается неустойчивым, если близкие траектории со
временем расходятся сколь угодно далеко (см. Устойчивость
по Ляпунову).
Проблема устойчивости Солнечной
системы
начала интересовать учёных сразу после открытия закона всемирного
тяготения. Первое исследование в этой области принадлежит автору термина
небесная механика Пьеру
Лапласу. В 1773 году он доказал теорему примерно следующего содержания: если
движение планет происходит в одном направлении, их массы одного
порядка, эксцентриситеты и наклоны малы, а большие полуоси испытывают
лишь небольшие колебания относительно среднего положения, то
эксцентриситеты и наклоны орбит будут оставаться малыми на
рассматриваемом интервале[1].
То есть при указанных, крайне ограниченных условиях, Солнечная система была бы стабильной.
Другая значительная попытка доказать устойчивость или неустойчивость Солнечной системы была предпринята А.Н.Колмогоровым,
В.И.Арнольдом
и Ю.Мозером в 60-х годах XX века (так называемая КАМ-теория). Ими была доказана теорема
примерно следующего содержания: если
массы планет достаточно малы, эксцентриситеты и наклоны орбит малы, то
для большинства начальных условий (исключая резонансные и близкие к ним)
движение будет условно-периодическим, эксцентриситеты и наклоны будут
оставаться малыми, а большие полуоси будут вечно колебаться вблизи своих
первоначальных значений[1].
В солнечной системе есть резонансы, и теорема относится только к системе трёх тел.
Позднее значительный вклад в развитие КАМ-теории внесли и другие математики, в частности, Н.
Н. Нехорошев.
Самый простой резонанс возникает, если отношение периодов обращения
двух планет в Солнечной системе равно отношению двух небольших чисел. В
результате резонанса планеты могут передавать друг другу заметные
количества момента вращения. Некоторые из известных приближений к
резонансам: Нептун
и Плутон, периоды обращения которых относятся почти как 3:2, система Юпитер-Сатурн
(приближение к 2:5) и резонанс между Меркурием
и Юпитером, у которых близки друг к другу периоды прецессии перигелия.
Известны также и резонансы в системе спутников Юпитера, Сатурна и Урана,
среди которых есть и тройные (участвуют три небесных тела). Среди них:
Ио-Европа-Ганимед (спутники Юпитера), Миранда-Ариэль-Умбриэль (спутники
Урана). В общем случае в нелинейной системе, согласно решению методом
возмущений, резонанс возникает при выполнении соотношения: Σ m(j)ω(j) =
0, где m(j) целые числа, ω(j) частота (вращения, обращения, ...) j
тела системы, j = 1, 2, ..., n. В случае простого резонанса n = 2,
тройного n = 3 и т.д.
В 90-х годах проводились численные расчёты поведения внешних планет
Солнечной системы на интервале времени порядка миллиардов лет[2].
Результаты разных исследователей были противоречивы и показывали как
хаотическое, так и регулярное движение планет. Хаотическое движение
здесь не означает заметное изменение орбит. Она означает лишь, что
нельзя предсказать положение планеты на орбите через интервал времени,
больший некоторого предела. Более поздний анализ[3]
этих данных показал, что варьированием начальных условий в пределах
погрешностей наблюдения можно получать как хаотическое, так и регулярное
движение с использованием одного и того же метода. Так что нельзя
сказать, какой характер имеет движение внешних планет Солнечной системы.
Для внутренних планет численные расчеты дают хаотичность их положения
на орбите. Кроме того, особой проблемой является Меркурий, который,
резонансно взаимодействуя с Юпитером, может существенно изменять свою
орбиту. В одном из последних исследований[4]
моделирование проводилось на интервале времени порядка миллиардов лет и
рассчитывалось 2500 вариантов с орбитой Меркурия, изменяющейся с шагом
0,38мм (в настоящий момент погрешность её измерений порядка метров).
Среди этих вариантов обнаружено 20 решений, где орбита Меркурия
приобретает достаточный эксцентриситет для пересечения орбит Венеры,
Земли и Марса. Среди этих орбит есть такие, что Меркурий падает на
Солнце, сталкивается с другими внутренними планетами, либо
дестабилизирует их орбиты так, что они сами сталкиваются друг с другом.\\\
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
21.05.2014 20:45, 321 Байт)
Собственно я так и не нашёл нигде точный ответ,
на простой вопрос, если у эллиптической орбиты
планет есть два фокальных центра, один из которых
у Солнца,
вопрос в том - со временем второй фокальный
центр орбиты, - приближается или отдаляется?
И какая статистика у разных планет, тоже не понятно.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 1:17, 3.6 КБайт)
---------------------------------------------------------------------------------------------------
Ответ #868 : Сегодня в 00:11:09
\\\Однако,
прежде чем продолжать развивать эту тему, хотелось
бы узнать мнения,
которые сложились у пользователей и модераторов
до этого момента.\\\
\\\Сложилось такое мнение, что развивать эту тему не надо.\\\
-------------------------------------------------------------------------------------------------------
Модератор крассава, просто мои мысли прочитал, я на всю
мощь как раз призадумался по данному вопросу, и пришёл
совсем к странному выводу. У Солнца
есть две кольцевые
области на различных расстояниях, одно ближе второе дальше,
эти области представляют из себя космический мусор
астероидно планетарного
размера, количество мусора
исчисляется в 1-2% процентах массы Солнца - с моей точки зрения.
Итого, - ясный конь, что у Солнца совсем недавно было
два больших
экваториальных выброса, Я такие ситуации
называю - потеря баланса, это когда снижается внешнее давление
эфира, и сбрасывается часть внешней оболочки звезды,
этак 10% за раз.
И с моей точки зрения даже не вопрос - а где остальные 8-9%,
где где - в песочных часах, или песочных юбках.
Однозначно когда будут намного
лучшие телескопы,
обнаружится аналогичные выбросы.
---

Собственно на этой фотографии как раз и видно что
было не один раз у экватора, но видно что второй
выброс как раз в разгаре, и выброс затяжной,
и экваториальный диск давно распылился.
---

В данном случаи видно экваториальную часть выброса,
и
собственно эта фотография отличается от предыдущих
тем, что на ней явно вино что выброс завершился давно и
всё обратно движется к звезде. А основная масса материи
так и осталась в пространстве напротив полюсов.
---
Из чего уже и так понятно что у Солнца совсем
недавно были два больших выброса, и на против
полюсов на расстоянии десяти диаметров колец
астероидно планетных экваториальных выбросов -
будет в три раза больше аналогичных планет и астероидов.
Обнаружить их можно только по положительному тепловому сальдо,
- в инфракрасный телескоп. Их температура будет
на несколько градусов больше фона.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 1:45, 4.3 КБайт)
--------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------
Как раз открыл статью а она по теме, хоть
и в тексте (как по мне сплошная даунтятина) и не указанна
даже температура планеты, но что мне понравилось -
---------------------------------------------------------------------------
http://www.astrogorizont.com/content/read-WISE
\\\Предположительно масса объекта WISE
J085510.83-071442.5 составляет
от 3
до 10 масс Юпитера. С такой низкой массой данный
объект мог быть
разве только газовым гигантом, подобным Юпитеру,
выброшенным
когда-то из своей звездной системы. Но, по мнению ученых,
этот объект
все же, скорее, является коричневым карликом, чем планетой,
так как
коричневые карлики чаще
встречаются во Вселенной. В таком случае,
этот карлик один из самых
маленьких известных коричневых карликов.
Проведенный Луманом в марте 2013 года анализ снимков, полученных с
помощью телескопа WISE, помог обнаружить пару
значительно более
теплых коричневых карликов, расположенных на
расстоянии 6.5 световых
лет, которую можно отнести к третьей ближайшей к
Солнцу звездной
системе.\\\
---------------------------------------------------------------------------------------------------------------
Самое
смешное в этой ботве что это более вероятно то планета
выброс Солнца нашего, да и находится она поближе,
да и расстояния к таким телам определять не умеют, не
умеют
определять правильно их диаметр - завышают его, и планета
получается дальше.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 11:07, 3.0 КБайт)
-------------------------------------------
http://lenta.ru/news/2014/05/22/wormhole/
\\\
Физик из Кембриджа Лука Бутчер в своей статье описал особый
режим
существования
кротовых нор (червоточин), предполагающий возможность
отправки информации в
течение сравнительно длительного промежутка
времени. Статья ученого доступна на
arxiv.org, кратко с ней можно ознакомиться на сайте Phys.org.
Ученые рассчитал, что при некотором радиусе горловины кротовой норы
отрицательной
энергии Казимира будет достаточно, чтобы в течение
некоторого времени существовала
стабильная конфигурация червоточины,
позволяющая фотону покинуть ее пределы, а,
значит, передать информацию .\\\
---------------------------------------------------------------------------------------------------------------------------------
Я вот смотрю и думаю - ну разве непонятно что
необоснованная ничем фантастика, обычная
бредятина, с претензией
на научность, напечатанная
в реферируемом научном журнале. Я вот думаю
а зачем её так широко публикуют и освещают,
и здесь до меня дошло, что на самом деле это
всё
для меня и таких как я. В результате отсортировываются
те, кто верит в научную сказку и подобные статьи
постоянно их ищут и увлекают их в псевдо науку.
А для меня польза самая что ни есть прямая,
- это их и выявляет, можно и не тратить время
на
чтение
их трудов научных по другим вопросам.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 14:45, 2.1 КБайт)
Астрономам не нравится что запретили астрономию преподавать
в школах, дальше статья о черных дырах, что примечательно надо знать
о черных дырах - это то что на
сегодняшний день официально не обнаружено
- ни одной чёрной дыры и даже ни одной чёрной дюрочки,
- все чёрные только виртуальные, и находятся в головах.
Подобными статьями профанацией насаждается массовая уверенность
для обывателя в логичности черных дыр как таковых.
И не один порядочный астроном не проведет ликбез
среди коллег
по поводу того - что может черные дыры космологии и ненужны,
может это идиотизм вводящий в заблуждение всю космологию,
может черные дыры решают
какие-то вопросы отдельных теорий
при этом создают глобальные физические и логические трудности всей космологии.
Как говорится "Остапа понесло"(С).
Да это вряд-ли случится ибо те кто написал статьи про черные
дыры, будут считать неудобным и не напишут откровенно
что они поддались общему настроении
и в котёл с кашей
идиотизма черных дыр добавили и свою научную лепту.
Хотя с моей точки зрения наука должна меняться,
а если ученные не будут признавать своих
ошибок - то это
будет только хуже для них самих, так как такая наука просто
будет и даром не нужна обществу, и ученных однозначно
отправят не в отпуск, а
сразу в пешее путешествие.
----------------------------------------------------------------------------------------------------------------------
http://lenta.ru/news/2014/05/23/wise/
\\\Астрономы Аргентины, США и Чили обнаружили аномалию в угловой
кластеризации видимых и скрытых активных сверхмассивных черных дыр.
Статья ученых доступна в
Arxiv.org, а кратко с ее основными выводами
можно ознакомиться на сайте НАСА.
В своем исследовании ученые рассмотрели кластеризацию более 170 тысяч
активных
сверхмассивных черных дыр. Астрономы обнаружили, что, в
отличие от видимых, так
называемые скрытые черные дыры значительно чаще
объединяются в кластерные
образования.\\\
- Re: Черная дыра
(А.П. Васи,
23.05.2014 15:12, 2.3 КБайт)
Ответ #1097 : Сегодня в 13:07:30
\\\Нахожу
уже вполне очевидным, что планетная система Солнца и
спутниковые
системы Юпитера и Урана сформировались абсолютно
идентичным образом.
Позже все эти системы наглотались космического
мусора, утратив, при
этом, часть своих исходных членов:\\\
\\\Arton,
никто, кроме Вас, похоже, не находит это вполне очевидным.
Прошу
всё-таки остановить публикацию бездоказательных утверждений.\\\
----------------------------------------------------------------------------------------------
Даже я уже знаю где найти доказательства и правильность утверждений,
и там-же будут и цифровые величины орбит, из которых любой конь
сможет просмотреть закономерность.
Но модератору в облом на это тратить время для написания статьи
в журнал. Естественно модератор требует предоставить ему
полностью всё для написания статьи
в научный журнал,
точнее для интерпретации обсуждаемого на этом форуме.
Это моя мысль, тем более что например популярная механика
не афиширует авторов своих
статей.
Такое модераторство меня однозначно наводит на мысль
что этот форум для кого-то научная кормушка для
написания своих статей, по той причине
что все мысли
на форумах высказывают три-пять человек, а все остальные
(дружащие между собой) посетители и модераторы додалбливаются до них,
выносят им моск
своими вопросами, и ставят требования
к разработкам не ниже профессорского уровня.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 15:16, 257 Байт)
И самое смешное что так сказать "локомотивам идей"
постоянно задолбливают мозг пустыми вопросами не по теме,
и кроме "локомотивов идей" никто
на форуме не в состоянии
высказать ни одной здравой мысли по сути вопроса.
- Re: Черная дыра
(А.П. Васи,
23.05.2014 15:25, 5.0 КБайт)
Ответ #1097 : Сегодня в 13:07:30
\\\Нахожу
уже вполне очевидным, что планетная система Солнца и
спутниковые
системы Юпитера и Урана сформировались абсолютно
идентичным образом.
Позже все эти системы наглотались космического
мусора, утратив, при
этом, часть своих исходных членов:\\\
\\\Arton,
никто, кроме Вас, похоже, не находит это вполне очевидным.
Прошу
всё-таки остановить публикацию бездоказательных утверждений.\\\
----------------------------------------------------------------------------------------------
Даже я уже знаю где найти доказательства и правильность утверждений
---
Надо в гуглях набрать -
\Устойчивость Солнечной системы Резонансы Солнечной
системы\
--------------------------------------------------------------------------------------------------------------
ru.wikipedia.org/wiki/Устойчивость_Солнечной_системы
Перейти к разделу Резонансы Солнечной системы - [править | править исходный текст]. Самый простой резонанс возникает, если отношение...www.astronet.ru/db/msg/1198823/node1.html
Лаплас сформулировал теорему об устойчивости Солнечной системы: если ... К сожалению, в реальной Солнечной системе резонансы играют очень...n-t.ru/tp/ng/uss.htm
23 дек. 1999 г. - известно, как произошла и развивалась Солнечная система. ... устойчивости Солнечной системы лишь в первом
приближении, что оказалось явно ... И такие причины лежат на поверхности: резонанс колебаний,...
- Re: Черная дыра
(А.П. Васи,
24.05.2014 14:10, 6.0 КБайт)
------------------------------------------------------------------------
: Сегодня в 08:15:58
\\\Представим себе полый микроконус (размером менее микрона) из
проводящего
материала без основания (т.е. с отверстием вместо основания).
В
результате того, что внутри полости конуса рождаются(и аннигилируют)
только
"резонансные" фотоны с длиной волны пропорциональной расстоянию
по
внутреннему сечению конуса, давление виртуальных фотонов физического
вакуума с внешней стороны конуса будет больше чем с внутренней стороны.
И
разность давлений фотонов физического вакуума будет перемещать конус в
направление открытого основания конуса.\\\
\\\Собрав миллиарды таких
"микроконусов" в многослойные соты получим ракетный
вакуумно-реактивный
двигатель, работающий без топлива. Который может
работать вечно. И
разгонять космические корабли в вакууме до любых мыслимых
скоростей.\\\
=====================================================================
Жажда халявы,
жажда халявного направленного воздействия, жажда вечной
халявы которая создаёт постоянное силовое воздействие и при этом не нуждается
в энергетических затратах.
Это даже не физика, это скорее внутренний самоконтроль подгуливает
при таком уровне жажды халявы.
Но здесь у меня другой интерес - отставание два
года,
при полном отсутствии даже понятия как реализовать
практически.
| Re: Свет и пространство и о скорости света.
|
30.09.201217:46 |
|
Вот пдумал о том как бы я делал безопорный двигатель.
---
Безопорный двигатель.
Большой дырявый транзистор.
Что собственно получается на самом
деле маломощный с низкой тягой
есть и его можно купить - ультрафиолетовый светодиод.
Когда происходит атомарная раскрутка на предельных
центробежных скоростях
вращения центральной подвижной
части атома, его края начинают разрушаться в связи с чем
происходит ультрафиолетовое излучение - это частицы
разрушения центральной
атомарной части которые увлекают
эфир в сторону своего движения, в связи с чем и появляется
незначительная тяга эфира.
Естественно аналогичное происходит
и с инфракрасным
светодиодом когда вокруг высокая температура, то светодиод
является детектором колебаний среды в определённом
направлении излучения, в этом
случаи тяга эфира будет
ещё меньше при той-же мощности что в ультрафиолетовом.
И основной двигатель без опорный с достаточной тягой более
логично делать
на том эффекте который наблюдается
в самом простом транзисторе.
Наблюдается следующее, снизу слой эмиттера, посредине тонкий слой - база,
сверху толстый слой
коллектор.
Что происходит - при приложении электроэфира между базой
и эмиттером происходит открытие потока электроэфира
от коллектора сквозь базу на эмиттер,
и ток между коллектором
и эмиттером может в сотни раз превышать ток между базой
и эмиттером, но если остановить ток между базой и эмиттером,
то с небольшой
задержкой прекратится ток между коллектором
и эмиттером сквозь базу.
Здесь с точки зрения двух сущностей эфира и электро-эфира,
всё объясняется проще
паренной репы.
В атомарной структуре можно для каждого материала определить
коэффициент увлечения эфира электроэфиром.
Дело в том что если в транзисторе
увеличивать толщину базы,
то транзистор перестанет быть транзистором а превратится в два диода.
Причиной тому ситуация при детектировании в результате которого
создаётся разряжение электроэфира и он начинает увлекать эфир
в локальном месте при этом происходит открытие атомарных само-заклиненных
конусов, о которых
я писал, в связи с чем начинается поток электроэфира,
от коллектора сквозь базу на эмиттер.
Собственно чтобы сделать безопорный двигатель достаточно сделать
транзистор
аналогичный элементарному но площадью например 210мм на 210мм.
Собственно получается что при работе транзистора он всей своей площадью
будет
прогонять сквозь себя электроэфир создавая при этом разряжение
простого эфира.
С моей точки зрения самое лучшее атомарное смешивание у того проводника,
у которого большее удельное сопротивление.
Возникает вопрос как провести смешивание электроэфира с эфиром
при котором можно передать энергию движения электроэфира
эфиру чтобы получить высокий коэффициент передачи.
По логике передать можно просто, набить в этом большом транзисторе
микро-дырок, превратив транзистор
в сито,
при этом увеличится площадь трения электроэфира о эфир,
также можно
понабивать дырок большего диаметра и вставить в дырки изолированные
волоски
алюминия, или другого металла, или соединения
например платины с инертным газом.
Алюминий окажет по идее аналог короткого замыкания
на поток который
будет пытаться вытолкнуть алюминий
при этом создаст поле которое возможно лучше передаст
энергию электроэфира эфиру, другие металлы например железо,
создадут
осевой сдвиг, что тоже возможно повлияет на взаимодействие.
Собственно идея волосков в дырках большого транзистора в том что возникнет
влияние на перепад
движения электроэфира, различного влияния
атомарной раскрутки центральной части что возможно приведет
к увлечению в атомарной структуре обычного эфира,
по
причине возникновения направленного перепада давления
электроэфира. |
- Re: Черная дыра
(А.П. Васи,
24.05.2014 16:45, 4.5 КБайт)
Безопорное движение я бы уже так бы не делал,
собственно есть и другие варианты.
Что надо знать - есть эфир, - представляет из себя
мохнатый шарик,
покрытый электропроводящей
жидкостью - электрой, и по факту уже в эфире
будут все эффекты статики, магнитное поле - осевая
раскрутка эфира, притяжение -
прохождение эфира сквозь
тела в центры массивных тел внутри которых происходит
конденсация эфира в жидкое состояние с выделением тепла.
Есть очень мощные
и очень актуальные опыты.
----------------------------------------------------------------------------------------------------------------------
http://www.powerinfo.ru/electrophoresis.php
\\\Механизм электролиза Рейсе объяснял тем, что "одна из двух составных
частей молекулы, разлагаемой действием гальванического тока, переносится
от одного полюса к другому через межполюсную жидкость". Если между
полюсами поместить какое-либо постороннее тело, например землю, то она
не будет препятствовать прохождению тока и разложению воды.
В 1807г. Рейсе модифицировал опыт Никольсона по разложению воды. Чтобы
добиться разделения продуктов электролиза, Рейсе заполнил толченым
кварцем
среднюю часть U-образного электролизера-трубки. Он заметил, что
приложение
внешнего большого напряжения к электродам приводит к
перемещению воды в
трубке в сторону отрицательного полюса. При
продолжительном пропускании
тока устанавливалась постоянная и
значительная (до 20 сантиметров) разность
уровней жидкости. Перенос
жидкости под действием внешнего электрического
тока, наблюдавшийся в
пористых телах, получил название электроосмоса.\\\

Схема опытов Рейсса по электроосмосу и электрофорезу
\\\Рейсе продолжал видоизменять опыты по электролизу. Он вставлял во
влажную глину
две стеклянные трубки, заполненные водой, в трубки
погружал электроды. После включения
тока наряду с электроосмосом
наблюдалось еще одно новое явление - движение оторвавшихся
частичек
глины в противоположном направлении - к положительному полюсу. Явление
перемещения частиц твердой фазы в жидкости под влиянием тока было
названо электрофорезом.
Рейсе сделал сообщение в университете об открытых им явлениях. Через два
года вышли его
статьи, в которых были подробно описаны электроосмос и
электрофорез. В этих явлениях
проявлялась связь между электрическим
током и относительным перемещением твердой
и жидкой фазы. Понимание
такой связи было, однако, неполным, так как явления,
противоположные
электроосмосу и электрофорезу по характеру причинно-следственной
связи,
то есть возникновение электрического потенциала при движении жидкости
или
твердых частиц, были открыты лишь спустя полвека.
Эффект, противоположный электроосмосу, обнаружил Георг Квинке
(1834-1924), профессор
Берлинского университета. В его опытах при
протекании жидкости через пористую диафрагму
появлялась разность
потенциалов между двумя электродами, помещенными по разным
сторонам
диафрагмы. Явление получило название потенциала течения. Тогда же
(а
именно в 1859г.) Квинке предположил, что поверхность твердого тела
заряжается
одним знаком, а прилегающий слой жидкости - другим. Эта схема
помогала объяснить
относительное движение жидкости и частиц твердой
фазы под действием тока, а также
появление потенциала при протекании
жидкости через пористую диафрагму. В дальнейшем
эта идея привела к
открытию удивительной границы на разделе фаз - двойного
электрического
слоя.\\\

Схема возникновения потенциалов течения и оседания
\\\Возникновение же разности потенциалов под действием механического
движения твердых
частиц в жидкости наблюдал в 1880г. немецкий физик
Фридрих Дорн (1848-1916).
Оно было названо эффектом Дорна, или
потенциалом оседания.\\\
--------------------------------------------------------------------------------------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
24.05.2014 16:56, 889 Байт)
Собственно с моей точки зрения в опыте Рейсса
на левом рисунке с U образной колбой, есть необъяснённая
часть физической причины возникающего электроосматического
давления жидкости при разных электро потенциалах.
Получается следующее - в U образной трубке с песком,
есть проводящая жидкость, при приложении перепада
напряжений со временем наблюдается изменение уровней
жидкости. Собственно это примитивно объясняется движением
потока электры, которая за собой увлекает
и частицы эфира,
по сколько электра движется от минуса к плюсу, то у минуса
она создаёт разряжение эфира, а на плюсовом контакте
будет избыточное давление
эфира.
Естественно что если эту трубку выпрямить, и попробовать
в космосе создать перепад электроосматического давления,
возможно и будет положительный
результат по безопорному движению.
- Re: Черная дыра
(А.П. Васи,
25.05.2014 12:34, 3.1 КБайт)
Сообщаем Вам, что с 21 по 26 июля 2014 года в Санкт-Петербурге состоится очередной Международный научный Конгресс-2014 "Фундаментальные проблемы
естествознания и техники".
На Конгрессе-2014 предполагается заслушать и обсудить
новейшие конструктивные концептуальные теоретические, экспериментальные и
технические решения современных проблем в различных областях
естествознания и техники. Оргкомитет Конгресса-2014 считает, что настало
время исследований, посвященных более глубокому пониманию реальности и
осмыслению достижений наук о природе и обществе. Тема Конгресса-2014
ГЛОБАЛЬНЫЕ И СТРАТЕГИЧЕСКИЕ ПРОБЛЕМЫ НАУКИ И ОБРАЗОВАНИЯ.
На Конгрессе-2014 будут заслушаны на пленарных и секционных заседаниях и стендовых сессиях доклады по следующим направлениям:
- Фундаментальные подходы к познанию реальности современные аспекты физики.
- Уровни организации, элементы и структура объектов естествознания, науки о Земле.
- Проблемы времени и пространства в научной картине Мира.
- Эфиродинамика, электродинамика, термодинамика и гравитация.
- Энергетика, техника и технологии нового тысячелетия.
- Катарсис-конференция С Миром новым - Шаги к новой цивилизации.
- Проблемы высшего образования.
==============================================================================================
Вот и мне интересно посмотреть видео этого конгресса.
Я
вот думаю, соберут профессоров таких например как Вибе,
которые по двадцать лет перечитывали студентам чужие книжки
и чужие статьи, и ставили оценки студентам
за то как они
поняли пересказанный им преподавателем материал из книжек.
И вот теперь из этих начитчиков и пересказчиков книг,
пытаются из них выжать научную
мысль, и будут стимулировать
их бурную научную самодеятельность - однако, это будет
интересно посмотреть.
В принципе результат будет возможен не меньше чем
через 7лет,
из чего оптимальный возраст 33-37 лет, это тот как раз случай
когда посетителей этого возраста на этой конференции будет
я думаю не более 10
человек. И то что из юзеров этого возраста
создадут научную группу и будут их обучать объективными
знаниями, и будут её финансировать по самое
дальше некуда
- я не верю в принципе, - ибо это более чем
фантастика, - это псевдонаучный бред с признаками идиотизма.
Так что вероятность результата и через семь лет практически
нулевая.
С другой точки зрения я возможно так негативно высказываюсь по причине
того что собственно сам конгресс уже создаёт мне некоторую теоретическую
конкуренцию в космологии.
- Re: Черная дыра
(А.П. Васи,
29.06.2014 13:07, 3.5 КБайт)
 Физические котлеты и математические мухи.
Физические котлеты и математические мухи.
Вчера :: 18:10:57
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1403964657
\\\По
этой причине, чтобы не остаться голодными и не питаться
математическими
моделями котлет нужно уметь отделять математических мух
от физических котлет.
К сожалению, на сегодняшний день, всё это
настолько перепутано, что вместо
реальных физических котлет нам
приходится питаться паштетом из математических
моделей.
Типичным
примером такого подлога является теория относительности, когда вместо
реальной физической модели нам подсунули математический суррогат и
заставляют
его есть. А он нам просто не лезет.
С некоторых пор,
математики окончательно разбушевавшись, как это умел делать
Фантомас,
математика начала изобретать свои физические законы, и это касается не
только ТО. Нам начали подсовывать суррогат из зависящей от частоты
диэлектрической
проницаемости плазмы и частотозависимой диэлектрической
проницаемости
диэлектриков, предлагая на этой почве построить вечные
двигатели. Начали нас
кормить волновыми функциями и квантами
электромагнитного поля.
Вобщем, вся современная физика это сплошной
неудобоваримый метафизический
суррогат из практически несъедобных
математических моделей.
Но где же подевались настоящие котлеты из натурального физического мяса.
А их украли у нас Эйнштейны, Ландау и Гизбурги и иже с ними, и вместе
с ними украли
у нас и всю физику.\\\
------------------------------------------------------------------------------------------
С моей точки зрения физику
украсть у физика невозможно, лично мне в
этом контексте сложившейся ситуации в физике сто лет назад и продолжающуюся
до сих пор - очень обидно за мои школьные
годы, и за ту физику которую мне
преподавали по школьным учебникам, за то что на самом деле
есть книжки по физике и по лучше раз в 30, а если их бы альты переписали
то они бы были вообще хорошие - я даже уверен что такого не произойдёт.
Собственно без адекватной базовой физики в школьные годы, юзер
не получает адекватных
знаний о практических достижениях и не знает
уже проведенных опытах, и будет вынужден всю эту ботву изучать
с нуля и вникать в неё по картинкам и описаниям через
интернет.
Что собственно и есть базовый тормоз.
И вообще если на сегодняшний день нет физического определения
сопротивления проводника - то это ясный
конь - позор, но
это надо осознать сперва, потом поставить такую задачу,
потом про-финансировать конкурс на лучшие модели.
Потом выбрать - а вот здесь
я задам вопрос на который каждый
может сам себе ответить самостоятельно -
Выберут ту модель -
- Автор которой пообещает больше из премии комиссии
- которая лучше описывает физический смысл в механическом варианте,
- которая содержит больше формул,
- которая меньше всего противоречит текущей парадигме
- автор которой имеет звание академика
- автор которой член комиссии по борьбе с лженаукой
?
- Re: Черная дыра
(А.П. Васи,
1.07.2014 21:15, 2.1 КБайт)
---
\\\я хожу часто - вопрос не ко мне
2 (3.6%)\\\
\\\редко хожу на те, где надо платить
2 (3.6%)\\\
\\\редко хожу, т.к. все есть в интернете
12 (21.8%)\\\
\\\редко хожу, т.к. нет времени
9 (16.4%)\\\
\\\редко хожу, т.к. плохо рассказывают
2 (3.6%)\\\
\\\буду ходить, только, если рассказывать будет кто-то очень известный
0 (0%)\\\
\\\не люблю лекции - читаю книги или журналы
1 (1.8%)\\\
\\\редко хожу, т.к. неудобно следить за анонсами
3 (5.5%)\\\
\\\редко хожу, т.к. время или место лекций неудобное
9 (16.4%)\\\
\\\другой ответ
15 (27.3%)\\\
\\\Проголосовало пользователей: 55\\\
-------------------------------------------------------------------------------
\\\другой ответ
15 (27.3%)\\\---
- Так "другой ответ" набрал самое большое количество, - возможно
интерпретация
идей столетней давности - морально устарели.
Я думаю что для лекций - обязателен пункт - "морально устарели".
Можно более гладкий вариант - "низкая
актуальность" - но мне кажется
он более контрастный - при малом (%) - как-то лучше, а при большом (%),
сразу переход в недалёкость.
- Re: Черная дыра
(А.П. Васи,
1.07.2014 21:43, 8.6 КБайт)
 Re: Мировая эфиродинамическая гонка объявлена
Re: Мировая эфиродинамическая гонка объявлена
Ответ #976 - Сегодня :: 21:03:18
\\\ ... Я борюсь за эфиродинамику.
Поэтому всё это не то..
К эфиродинамической гонке отношения не имеет.
Я хотел бы обратить внимание, что
эфиродинамика
никак не претендует на развенчание некоторой
частной математической
теории.. Эфиродинамика претендует на переход
к эфиродинамическому
естествознанию. Основанному на материалистической
философии. И
соответствующей методологии.
А пока. Сегодня начался третий год Гонки. Я же собираю отчёт.
За неделю- другую сделаю.
С уважением, Михаил Сурин
\\\
Вот время летит, по крайней мере я знаю когда я об этом подумал.
А.П.Васи
|
Re: Свет и пространство и о скорости света.
|
2.06.20119:17 |
|
Эфир и его взаимодействия,
есть два вида матери - эфир и простая материя,
эфир может находится в сжатом
состоянии, это состояние начинается при большом
механическом давлении равным 1000км водяного столба,
после возникновения условий для жидкого эфира в недрах планет,
и практически твердого у звезд, начинает образовываться
внутри звезд - Звезда эфира, а внутри планет - гравитирующее
ядро эфира. И что звезда эфира что гравитирующее ядро, они всасывают
эфир, эфир проходя сквозь материю
частичным трением создаёт
гравитацию. И если взять например кубометр воды, то это не он давит
с силой в тонну, это эфир проходя сквозь него со скоростью 10км
в секунду создает силу в тонну, и в зависимости от плотности
атомарной решетки вещества будет разное трение эфира,
и будет разная сила - разный вес.
У звезд
звезда эфира внутри разрастается, потом
лопается по экватору как SN1987a, и сбрасывает лишнее давление,
и потом появляются лучи как у газовой конфорки, и
форма
звезды в форме тарелки, после чего прогорают
днища тарелок с обеих сторон, и получается взрыв
и в итоге выходит звезда эфира, а материя звезды
рядом с этой
звездой обратно становится обычной
звездой, после чего звезда эфира со временем испаряется,
так как эфир не сдерживает внешнее давление, а в
звезде из которой
вышла звезда эфира , зародится новая.
Звезда внутри которой есть звезда эфира называется
Звезда Физики, во множественном - Звёзды Физиков.
Грубо говоря
- звёзды вечные, в процессе своей вечной жизни,
внутри создают звезду эфира, и избавляются от неё,
бывает что когда избавляются, происходит такой взрыв
что
полностью разлетается вдребезги вся материя звезды.
Бывает что галактики пролетают друг мимо друга и создают
низкую плотность эфира в пространстве, и звёзды
лопаются
как мыльные бульбашки, и сбрасывают избыточное
внутреннее давление эфира.
Эфир и электричество.
Электрон и позитрон это аналогичные условные названия
обозначающие различные потенциалы напряжения в текущий
момент у проводника или частицы находящейся с некоторым
зарядом.
Если взять батарейку (гальванический
элемент), то у неё будет один
вывод положительный - второй отрицательный, и в связи с химической
реакцией внутри батарейки создаётся разница напряжений.
Батарейку
можно определить как источник напряжения со статическим
потенциалом в полтора вольта, при подключении нагрузки
у батарейки возникает динамическое состояние - наличие
тока,
ток - движения электричества в проводнике. При подключении
к батарейке различных нагрузок, можно определить
внутреннее сопротивление источника напряжения.
Электричество в проводнике - движение в проводнике
создаёт эфир, который движется внутри проводника.
При движении эфира в проводнике в одном направлении -
называется
- постоянное напряжение, - создается вращение
вращение подвижной части проводника которая при раскрутке
создает магнитное поле, и в связи с трением подвижной части
атомарной структуры об неподвижную проводник создаёт
сопротивление, при низких температурах, подвижная часть
и неподвижная часть в проводнике находится на расстоянии
при котором уменьшается и при дальнейшем снижении температуры
возникает эффект при котором исчезает трение подвижных
частей внутри проводника по отношению к неподвижной
части -
сверх проводимость, но при этом
не исчезает магнитное поле от раскрутки внутри проводника.
Электрон и позитрон могут находится в качестве зарядов,
на единичных
атомах - это свойство используется в электроламповых устройствах.
Общее всех этих устройств состоит в том что создается паровое
облако из одиночных
атомов, после чего перепадом потенциалов
создается движение одиночных атомов, после чего они движутся по
инерции, и пролетая сквозь сетки или щели,с различными потенциалами
у них происходит частичный перезаряд и изменение скорости, при этом
изменяется скорость вращения внутренней части которая создает
магнитное поле , и в связи с
непрерывным потоком появляется
возможность модулировать поток заряженных атомов,
как количественно так и с разными потенциалами. Съём сигнала
не обязательно
будет прямым, так как результатом работы ламповых
устройств является световое излучение или СВЧ колебание.
У СВЧ ламп входные колебания меняют количество потока,
после чего этот поток заряжается до определенного напряжения,
после чего тормозится, для совпадения с длинной волны, а съём
колебаний происходит через колебания
потенциалов после тормоза.
Если взять кинескоп, то в нем результатом является разгон
и модуляция количественная потока единичных атомов,
с последующим отклонением
по вертикали и горизонтали
отклоняющей системой, с последующим ускорением и пролетом сквозь
сетку по инерции с последующим ударом об люминофор.
При попадании
в люминофор, атом влетает на большой скорости
и создает раскрутку внутренней части люминофора, люминофор в
отличии от проводника при раскрутке внутренней части создает
свечение , в связи с наличием трения, и вращением внутренней
атомарной части по инерции при создании светового
излучения и затратами энергии на излучение света,
у люминофора
есть свойство - послесвечение. Собственно получается что при
затратах постоянных напряжений в лампах СВЧ усиливаются
переменные колебания, а в
кинескопах используется
в результате только сила удара летящего по инерции единичного
атома об люминофор.
В связи с тем что к эфиру
принципиально не применим
термин гравитация, по причине того что гравитация
описывает взаимное притяжение двух тел, в связи с чем
появилась необходимость
введения термина для
эфира описывающий воздействие
прохождения эфира сквозь тела в разных направлениях
и при разной плотности эфира, и при разной
плотности
атомарной структуры тел.
При этом что есть в наличии, эфир может
быть с разной плотностью, и тела могут быть
с разной плотностью атомарной структуры.
Эфир проходя сквозь тела стремится у планет
к ядру эфира или стремится сквозь поверхность
Звезды Физики, к внутренней Звезде Эфира.
Также может эфир выбрасываться
струями
или взрывами из Звезды
Физики.
Также эфир будет испарятся из Звезды Эфира после
того как она вылетела из Звезды физики, и внешнее
давление
не сдерживает эфир в жидком или твердом
состоянии.
Движение и трение эфира сквозь материалы, при определенных
ситуациях вызывают электрический ток,
которому сопутствует магнитное поле.
Получается что очень много процессов
которые надо назвать одним термином, из
чего следует -
1 Эфиро-динамика.
Которая включает в себя -
2 Эфиро-трение -
прохождение эфира
сквозь тела.
3 Эфиро-давление
Также
4 Эфиро-метрия
-
измерение величин эфира.
5 Электро-эфир
Движение потоков эфира в проводниках |
- Теория пустоты vk.com/tviss
(Serg Ol,
4.07.2014 23:54, 25 Байт)
ответы на все вопросы
- Re: Черная дыра
(А.П. Васи,
10.07.2014 11:56, 2.3 КБайт)
 Re: О критиках и сторонниках СТО
Re: О критиках и сторонниках СТО
Ответ #79 - Сегодня :: 09:06:32
------------------------------------------------------------------------------------------
Вот читаю и прямо ощущаю слабость по отношению к
решаемой
задаче этих пожилых юзеров в физике.
Они так мучают свой моск чтобы он им выдал правильный ответ
что мне их аж жаль, по причине того что ответ
на самом деле в
данной ситуации в двух вариантах решения, второй вариант самый
лучший для них - посыл определённых теорий в даль и больше к ним
не возвращаться.
Первый вариант это в том что надо понимать принципы
единиц измерений и их приоритетность и лично я клал болт на систему
СИ и подобные. Дело в следующем что есть
"сравнение" - это когда я
прикладываю линейку к чему-то - это более приоритетное чем "измерение"
- измерение это то для чего требуется две
"сравниваемые" физические
величины из взаимодействия этих величин определяется - третья физическая
величина. Вот собственно "измерение" расстояния
в скорости света,
за определённое время, -
как по мне - очень неправильно, но каким-то теориям это нужно.
Что собственно происходит в этой ситуации - что
скорость света
принята за константу, при этом допускаются манипуляции и спекуляции в
измерениях при сравнении расстояний "линейками" - их растягивают
и сжимают.
Не гнушаются для подгонки результатов и время замедлять и тормозить.
Собственно в наземных условиях не измеряют в скорости звука за время расстояние,
- всё, значит - второй вариант тоже актуальный, посыл в пешее путешествие
симбиоза - "пространство-время" ибо он придуман исключительно для подгонки
результата под константу скорости света.
Вывод - если не получается решить задачу, то возможно решение
совсем в другой плоскости.
- Re: Черная дыра
(А.П. Васи,
10.07.2014 12:07, 11.3 КБайт)
| Свет
и пространство и о скорости света.
|
17.04.201021:51 |
Изначально
надо определится с названиями, - сравнения и измерение.
Сравнение
- когда я измеряю длину линейкой, я просто сравниваю размерность одного с
аналогичным.
Измерения
это когда из двух разных сущностей, но известных количественно определяется
третья сущность.
Например,
- напряжение через ток и сопротивление, скорость через длину и время.
Теперь о пространстве - поучается два метода определения его величины, один
вариант - просто линейкой, второй скоростью света.
Линейкой
логично и просто.
Скоростью
света - получается что пытаемся приравнять измеряемую величину - зависящую
от времени, (и точности часов их считающих) линейки измеряющей расстояние (точнее
свойств линейки и её подверженности деформациям), и скоростью распространения
электромагнитного излучения.
Что
собственно получается - при измерению пространства, скоростью света по
сравнению с приравниванием пространства к линейке.
У
нас получается расстояние длинна,
только мы задействовали часы линейку, и электромагнитное излучение.
Для измерения у нас есть три сущности
скорость время и расстояние, и есть свойство пространства в котором распространение
электромагнитных колебаний равно некоторой скорости которую называют скоростью
света.
Здесь
надо понимать следующую ситуацию, - что с одной точки зрения можно сказать, -
что эта скорость быстрая но можно сказать что она медленная. Но в любом случаи
пространство для колебаний является линией задержки, в которой распространяется
сигнал. Вот, а здесь уже получается что пространство состоит из чего-то. Это
происходит потому что, пространство мы определили измерять в метрах.
Для
светового излучения пространство проявило ещё одно своё свойство - задержка
светового луча. Следовательно - пространство
заполнено веществом, которое задерживает световой сигнал, аналогично тому как в
воздухе или воде задерживается звук. Здесь можно немного поразмыслить о
скорости сигнала в средах, в воде звук во столько раз быстрее - чем в воздухе,
во столько на сколько ближе расстояние между молекулами в воде - чем в воздухе. Из чего следует - если
поделить скорость света на скорость звука в воздухе мы получим величину во
сколько раз ближе частички среды,
которым заполнено пространство по
сравнению с частицами воздуха.
На самом деле скоростью
света измерять пространство нельзя, потому что это не правильно, так как
скорость света за секунду не является мерой длинны.
Это
всё равно, что говорить, - что от Киева до Москвы три тысячи 75 секунд скорости
звука.
Сложение со скоростью света и вычитание, при движении
объектов.
Есть объект, который относительно другого объекта может двигаться.
Есть скорость света, с которой
распространяется световое излучение в пространстве.
Получается - что нужно уйти от генератора излучения на исследуемом, а генератор
всё равно нужен.
Здесь принимаем волевое решение, генератор располагается на условно неподвижном
объекте.
На том объекте который движется будем располагать простое зеркало.
В качестве источника выбираем световой луч модулированный с частотой 300МГц,
что в пространстве будет из себя представлять одно колебание на метр длинны,
точнее один период на метр.
Устанавливаем на автомобиле зеркало , на взлётной полосе устанавливаем стенд с
световым генератором 300МГц с узко направленным лучом, и приёмник с
частотомером.
Первый опыт заключается в том что автомобиль расположен на расстоянии 1км, и
неподвижен, принимаемая отраженная частота будет равна передающей.
Опыт второй - автомобиль едет к стенду со скоростью 20метров в секунду, о чудо
частота увеличилась на 20Гц. Причина связана с тем что при движении к
источнику, машина проезжает на 20 метров ближе, а поскольку у нас в одном
метре один период колебания, то частота при приближении со скоростью 20 метров в секунду
увеличится на 20Гц.
Опыт второй машина удаляется от стенда со скоростью 30 метров в секунду, и частота
принимаемая от зеркала автомобиля ниже передающей на 30Гц.
Из чего следует, что свет проявляет свои свойства по отношению к пространству,
которое и задерживает свет.
Пространство для света является линией задержки.
Если есть в чем, - свету распространятся и задерживаться, то свет находится в
среде какой-то, аналогично звуку в воздухе.
По той причине что данное сложение и вычитание частоты можно повторить применив
вместо светового источника мощный динамик а на автомобиле установим частотомер
с микрофоном.
Берём частоту 300Гц, у нас получается при скорости звука 300метров в секунду,
одно колебание на метр.
Автомобиль приближается к динамику со скоростью 20метров в секунду, частота
принимаемого звука в автомобиле больше на 20Гц, после чего автомобиль движется
от стенда со скоростью 30метров в секунду и частота принимаемая в автомобиле,
ниже на 30Гц.
А звук точно движется в среде, - это воздух.
Вот я собственно и показал метод сложения скоростей в сравнении с аналогичным.
Могут быть некоторые неточности со скоростью света в воздухе, но это не
принципиально в данной задаче.
Естественно можно использовать данный метод с расположением зеркала под углом 45
градусов, при этом располагаются приёмник и генератор в разных местах, и
передвигается зеркало к и от приёмника, или к и от генератора.
Что я считаю недостатком данного опыта?, - особых технических недостатков не
вижу, так как опыт со световым лучом будет результативным и при около световых
скоростях.
Естественно данный опыт не рекомендую проводить самостоятельно без консультации
со специалистами по правилам соблюдения техники безопасности.
Общая идея предыдущих опытов в наглядности
того, что при
движении автомобиля к объекту или от него, частота принимаемая на автомобиле, и
отраженная им частота, будут одинаковыми, следовательно если автомобиль
посредине между двух генераторов, которые работают на одинаковой частоте, то
если автомобиль будет перемещаться между ними по прямой линии между
генераторами, то сумма частот делённая на 2 всегда будет равна исходной частоте
генератора.
| Re: Свет и пространство
и о скорости света.
|
4.05.201013:20 |
Вот собственно используя базовые понятия о электромагнитном
излучении можно более детально перейти к световому излучению.
Световое излучение - колебание зарядов
в среде вокруг
друг друга примерно с частотой 100ТГц, при их движении
в среде со скоростью которая определяется плотностью среды.
Надо узнать сколько
колебаний в метре у света, поделим
100ТГц, на 300 тысяч км в секунду, и поделим ещё на 1000,
и узнаем количество в метре = 333 333.
Или - 333 колебания на
миллиметр.
Теперь надо понять что представляет из сибя интерференция.
Здесь всё просто. Световой луч разделяется на два луча,
полу прозрачным стеклом,
внутри которого слой металла,
который пропускает часть лучей а другую часть отражает,
по причине того что заряды фотонов при взаимодействии вращаясь
летят,
и так как вращение их хаотичное, то подлетают к слою
по разному, часть ударяется одновременно плашмя, и отражается,
а часть проходит между атомами металла.
После чего из двух лучей с помощью зеркала и полупрозрачной
линзы востанавливается луч.
Здесь получаются кольцевые волны, о причине того что у нас
разная
длинна лучей, и фотоны имеют хаотичную раскрутку.
Если в одно плечо разделённого луча ввести сосуд с водой
- опыт Физо, и вода будет двигаться с некоторой
скоростью, то у нас
кольца начнут сходится и расходится.
Если я возьму фонарик и буду приближаться к стене,
со скоростью 10м/с, и при этом
буду
светить на стену, то частота принимаемых сигналов
на стене будет 333 333 умножить на 10, то есть на 3,333МГц,
больше чем в фонарике, если с такой-же скоростью буду
удаляться,
то на такую-же частоту сигнал будет меньше.
Здесь надо понимать причину, причина не в нарушении частоты генератора,
и частотомера, причина
в том что когда создаются
благоприятные условия для создания фотонов на нити спирали фонарика,
они вылетают в пространство, и движутся в нём,
а частота меняется
потому что последующие фотоны, вылетают
из фонарика в то время когда фонарик меняет своё расположение
в пространстве по отношению к стене, на которой частотомер.
-----------------------------------------------------
А по большому счёту есть эффект Доплера - он
исключительно
для сред. Если таковой есть - значит и есть среда, а если есть
среда значит есть все составляющие её наличия
- а скорость света
это ясный конь - скорость "возмущения среды" - и ясный конь
у среды эта скорость
не может быть константой, ибо она зависит
от плотности (давления), и температуры.
Ужос
какой каменный век на дворе в сознании юзеров.
- Re: Черная дыра
(А.П. Васи,
11.07.2014 10:51, 1.2 КБайт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1404154370/140#140
Re: О критиках и сторонниках СТО
Ответ #133 - Сегодня :: 09:15
-----------------------------------
\\\Почему! Я в открытую говорю:
В конце 19 столетия в физике наступил кризис из-за
опыта Майкельсона-Морли. Для выхода из кризиса были
предприняты определенные шаги, в частности была изменена
система отсчета. Если классическая система отсчета
была образована телом отсчета и инструментами, то
новая система отсчета была образована:
Наблюдатель
Тело отсчета
Часы в точке пространства, где находится наблюдатель
Эталон для измерения отрезков пространства.\\\
-------------------------------------------------------------
Я смотрю никто даже дупля не отбивает в понимании
введённого наблюдателя в физику.
Обычный приём математики в физике для подгонки математических
идей под физичность как таковую.
Что породило собственно новый вид математических выкрутасов
в виде предполагаемых опытов с претензией на физичность.
Собственно после тридцати то уже надобно замечать что
часы наблюдателя постулируются, и не высчитываются
по скорости и времени, и не привязываются к началу координат.
- Re: Черная дыра
(А.П. Васи,
11.07.2014 11:55, 1.9 КБайт)
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?board=physik-alt
http://www.sciteclibrary.ru/cgi-bin/yabb2/YaBB.pl?num=1404154370/142#142
-------------------------------------------------------------------------------------------------------------
Я вот не могу понять по какой причине они все распыляют своё внимание
и не могут
определиться с тем куда им более проще приложить свои усилия.
Собственно самое
смешное что с моей точки зрения они постоянно
мысленно спотыкаются о то, с чего им надо начать.
Я вот думаю о другом - что
собственно им и по какой причине так затуманивает
моск, что они не замечают того что особенно неправильно и нелогично.
Не знаю почему
они не видят опыта по обнаружению электронов, и почему
его не переобъяснят со своей точки зрения, и почему не открывают
тему - о электрическом токе и его физической сути.
Это мне напоминает анекдот.
---"Собрание в физ -мат институте. У нас на повестке дня есть вопрос -
что такое электрический ток?
Есть два варианта решения, реальный и не
реальный.
Реальный - это когда к нам прилетят инопланетяне и расскажут нам об этом, и не
реальный - засучим рукава и самостоятельно попытаемся решить этот вопрос" (С)---
- Re: Черная дыра
(А.П. Васи,
12.07.2014 8:54, 2.0 КБайт)
 Re: О критиках и сторонниках СТО
Re: О критиках и сторонниках СТО
Ответ #216 - Вчера :: 23:07:38
rustot5 писал(а) Вчера :: 23:02:36:
stary писал(а) Вчера :: 22:50:06:///Умница!///
///вы
и на другие свои вопросы можете найти ответы в книжках. возьмите
почитайте Тейлора или другой нормальный учебник. нет вы вместо этого
роетесь в каких то древних манускриптах с невнятными описаниями каких то
лучиков и наблюдателей. и думаете что физики именно по таким понятиями и
учатся///
///Я, как физик учусь и моими учителями являются Аристотель; Гегель; Ньютон; Пуанкаре , Сивухин, Савельев... Тейлора не знаю...///
-------------------------------------------------------------------------------------------------------------------------------------------------------
Я вообще в ужасе от того как физику модно изучают.
У меня в физике в приоритете - здравый смысл, и
у меня никто из выше перечисленных не актуален,
и
я не считаю их физиками с большой буквы.
Лично я бы советовал начинать физику учить с книг и опытов
Томаса Юнга.
- Re: Черная дыра
(А.П. Васи,
12.07.2014 22:33, 3.3 КБайт)
 Re: Комиссия по борьбе с лженаукой распространяет лженауку
Re: Комиссия по борьбе с лженаукой распространяет лженауку
Ответ #41 - Сегодня :: 22:05:26
SP писал(а) Сегодня :: 20:37:40:///многими применениями давно подтверждено, что СТО работает исправно./// ///Какими же применениями?///
|
--------------------------------------------------------------------------------------------------------------------------------------
Ладно так как моски большинства юзеров не способны замечать адекватное,
- напомню.
В первую очередь релятивизм был придуман без практических опытов
его подтверждающих.
На текущий момент не сделано ни одного устройства и прибора на релятивистских
идеях.
Основные парадоксы релятивизма, (парадокс) - лайно
в теории.
У космонавта который движется на орбите согласно дикому опыту со световыми часами,
приводит к диким релятивистским выводам о замедлении хода темпа часов
на орбите земли, - физически наоборот - на практике темп хода атомных и кварцевых
часов - увеличивается, и часам глубоко до лампочки движутся они на орбите
или зависают над землёй в одной точке - на темп хода влияет только высота, -
релятивизм противоречит практике.
Опять же опыт с часами со световым лучом, если повернуть
картинку на
девяносто градусов, сливаются идеи релятивизма по сложению скоростей луча,
на движущейся платформе в пространстве.
Ибо будет ход луча назад при
движении - правильно, короче чем вперёд,
а сумма их длин правильно= делённая на два равна, расстоянию между зеркалами.
Собственно на заявленное постоянство
скорости света, в вакууме, - постулированное,
были сделаны теоретические опоры, которые потребовали изменения измерительных
устройств как времени так и расстояний,
для того чтобы не возникало спекуляций
были придуманы новые физические сущности и физические свойства которые
невозможно проверить, что в категории "теорий"
- относится к теориям
с "открытой проблемой". В данном случаи на заявленные свойства замедления
времени в движении - отсутствует как физический опыт,
который должен был
привести к подобным выводам, так и отсутствует измерительный прибор, и единицы
измерения. Это относится и к отсутствию в продаже измерителя
кривизны пространства.
А так всё нормально.
- Re: Черная дыра
(А.П. Васи,
13.07.2014 9:58, 4.7 КБайт)
Г.А.Зубков
|
|
Re: Черная дыра
|
25.12.20100:36 |
|
|
товарищ Новиков
пишет,что при
приближении к
чёрной дыре
космонавтов
разорвёт из-за
приливных
сил,разности
ускорений.Почему
все забывают о
релятивистском
сокращении
размеров?Ведь при
влёте в чёрную
дыры вся
влетающая в неё
материя
сжимается,уменьшается
в размерах.Потому
разность ускорений
в уменьшемся теле
космонавта будет
небольшой.И сжатия
он также не
ощутит.На моём
сайте http://
genzubkov.narod.ru/
также есть статья
про чёрные дыры.
Правда мои
взгляды с недавних
пор
изменились:считаю
уже ,что свет не
подвержен
инерции,гравитации,ибо
не имеет массы
покоя.
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Черная дыра
|
26.12.201014:31 |
|
Г.А.Зубков
"Почему
все забывают о
релятивистском
сокращении
размеров?"
Мне приятно встретить толкового релятивиста,
который в практическом применении пользуется
релятивискими сокращениями в быту.
У меня вопрос, - космонавт в космическом корабле
держит в руках футбольный мяч, корабль разгоняется
до двукратного сокращения длинны, после чего
космонавт
с мячом в руках поворачивается на 90
градусов относительно направления движения,
со сплющенным мячом в руках, после чего корабль
начинает торможение, у космонавта
в руках
в итоге оказался сплющенный мяч для регби,
- вопрос какой внешний вид космонавта?
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Черная дыра
|
26.12.201014:43 |
|
Естественно вопрос возникает о единицах измерения,
связанных с сокращениями от скорости.
Так-же возникает вопрос - а скоро поступят в продажу
инструкции и
рекомендации по полетам на релятивиских
скоростях с целью проведения релятивиских
сокращений и растяжений вместо пластической хирургии?
| |
- Re: Черная дыра
(А.П. Васи,
13.07.2014 12:33, 6.2 КБайт)
Время идёт а в космологии всё нормально, и стабильно,
и ничего не меняется, да и космологи не хотят ничего менять.
---
Г.А.Зубков
|
|
Re[2]: Черная дыра
|
30.12.20109:34 |
|
|
Неприятно
общаться с такими
приблатнёнными
негативистами,как
вы. Нет,чтоб что-то
своё,конструктивное
добавить,занимаетесь
одним
критиканством. Ваш
уровень знаний по
некоторым
вопросам явно
ниже даже моего,а
вы наезжаете на
меня, как будто вы-
знатнейший
профессор.
Неважно,кто
автор.Всю теорию
Чёрных дыр можно
самому вывести из
формулы
гравитации F=GmM/
r^2 . Я больше сам
думаю,чем изучаю
чужие труды.Про
процесс,обратный
аннигиляции,написано
например в
''Элементарном
учебнике физики''
том 3 с.553
Г.С.Ландсберга:
''образование пары
электрон-позитрон
происходит в
результате
взаимодействия
гамма-кванта с
электрическим
полем одного из
атомных ядер
вещества.''
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Черная дыра
|
30.12.201017:53 |
|
Я Вам культурно всё время намекаю что Вы в
своих размышлениях то в облаках летаете,
то отбиваетесь от общепринятых утверждений,
то несёте в руках бред сивой
кобылы.
Если Вам это нравится - то это лично Ваш выбор,
могу Вас обрадовать, что таких мечтателей ниочем,
как Вы - делающих при этом наукоёмкий вид
и вырабатывая
мысли притендующем на аплодисменты, - так таких
среди астро-физиков практически абсолютное большинство.
А то что написано например на этом
сайте о черной дыре,
Вы я так понимаю взять за стандарт не хотите, и при этом
отбросить все выдумки. Определение достаточно простое,
- гравитация такая что
даже фотоны не могут покинуть -
здесь надо тогда признать врунами всех кто утверждает
что дыры излучают, - как по мне - надо так надо,
а Вам выбирать .
У черной дыры есть радиус следовательно есть поверхность,
и в этом случаи с моей точки зрения, - вруны те кто утверждает
что сквозь дыру есть тоннель,
- а Вам выбирать.
Я Вам вкратце пытаюсь объяснить что в физике если
автор предоставляет читателю право выбора - то это
уже говорит о том что это враньё
или необоснованная
выдумка изначально, и мне смешно и жаль Вас по
бессмысленно потраченному Вами времени в размышлениях
над черными дырами, если бы вы вникли
в базовые
авторские постановки задач и объяснений Вы бы сразу
поняли что это простая галиматья, не имеющая никакого
отношения к наблюдаемым объектам.
Я
Вам по дружески скажу почему на текущий момент
никто не обнаружил черной дыры, а слышны лишь утверждения
что она вот там должна быть, - потому что астро-физики
и сами не знают как она должна выглядеть, -
я думаю Вы догадываетесь, почему астрономию в школах
отменили.
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Черная дыра
|
30.12.201018:13 |
|
В астрономии кризис очень большой - из за того что неудобно
ученикам пререкаться с преподавателем, и в лицо ему сказать
не могут - мол хватит нам бред сивой кобылы
в мозг заливать.
А со временем ученики на залитом в моск бреде и уверенности
в отсутствии критики - пишут такую галиматью, что уши
у одних заворачиваются,
а молодые воспринимают за "чистую монету",
и все идет по кругу - так называемый -
"авторитарный круговорот бреда сивой кобылы в астрономии".
| |
- Re: Черная дыра
(в. н. беспалов,
22.07.2014 13:30, 1021 Байт)
Теория 2
Вся
вселеная
заполнена
светом и
абсолютной
материей
возникают
из
неоткуда
черные
дыры и во
многих
точках
вселеной
возникают
гравитационные
силы они
начинают
поглащать
свет.
Известно
что
черные
дыры
поглащают
свет и
всю
энергию
вокруг,
возможно
центры
галактик
и есть
черные
дыры и
являются
бывшими
центрами
гравитации
поглотившие
первичное
вешество
в
неогрониченном
количестве
до
полного
насышения
и
образуюшими
центры
галактики
с их
закономи
и
порядками
которые
по
концентрации
вешества
могут
превосходить
белых
карликов
либо
которое
может
быть
свободной
от
обсалютной
гравитации.Черные
дыры
закручивают
энергию
по
руковам
как и
рукова
голактики.
Тоже
может
произойти
и с
современными
черными
дырами
они могут
стать
центрами
галактик
откуда
они
появляются?
Что
думаете
по этому
вопросу
буду рад
любой
критике.
- Re: Черная дыра
(А.П. Васи,
22.07.2014 15:09, 8.0 КБайт)
А.П.Васи
|
|
Пособие для тех кто хочет писать теории.
|
26.03.201219:11 |
|
Естественно и понятно как релятивисты прикипели
к креслам релятивизма, и так у них всё хорошо в теориях
что ни в одном институте мира нет кафедры на которой учат
писать теории, я так думаю что на этой кафедре просто никто
не захочет учится? - нет как раз учится на ней захотят
все, только первые выпускники этой кафедры
если и не станут
нобелевскими лауреатами сразу то уж точно практически сразу заменят своими
теориями весь релятивизм с прочей неадекватной физикой.
Собственно
подобных заведений в обозримом
будущем не предвидится, но это не значит что не должно
быть некоторых стандартов для тех кто хочет писать теории.
Так
как нынче наука на ручном теоретическом тормозе,
и внутри неё всё очень запущенно вплоть до неправильной
терминологии и смысловой нагрузки терминов, и наука базовых
определений и сама внятно обосновать не может,
и под словами например - "межзвездная среда" - оказывается
это атомарная межзвездная пыль и микроскопический
космический
мусор, и не в коем случаи не среда сплошная из эфира,
вот так за сто лет исказили смысл, то в связи с этим
автор должен объяснять терминологию
и соответствие
с физическим смыслом который он в него вкладывает,
по той причине что текущий физический смысл слова
"среда" - это непрерывная среда,
а вкладывают что попало,
вплоть до одного атома на кубический дециметр, и называют
это средой, - на самом деле это абсурд, у среды помимо непрерывности,
обязателен
непосредственный физический контакт между частицами,
что влечет за собой, трение частиц, упругость среды, плотность среды,
проводимость среды (чего либо).
Запрещаются сокращения, запрещаются термины
не имеющие физического смысла, запрещаются
жаргонные термины не имеющие отношения к физике.
---------
Вначале
у автора обязательно должно быть
нечто вроде такого - введение, аннотация, краткое содержание, -
автор кратко обязан изложить своими словами следующее,
Название должно по возможности указывать основную
суть и область затронутого вопроса.
1 о чем будет речь,(в какой области науки, что собственно)
2
какие вопросы решаются,
3 чем отличается решение от других,
4 чем оно лучше,
5 вывод .
Это должно быть обязательно чтобы читающий зря не тратил
своё
время на чтение того что его не интересует.
Основная часть начинается с авторского рассказа о своих
целях и достижениях и неудачах.
Дело в
том что всегда будет куча желающих сделать это за
автора, то лучше пусть автор сам расскажет.
1 Результативность.
Автор должен рассказать что с его точки
зрения
у него получилось достаточно хорошо, и благодаря чему
он смог достичь лучших результатов, и что у него
не получилось.
2 Автор должен дать
основные физические определения, физических
сущностей которые использует, или взять определения
из других источников, если они подходят для автора,
с указанием
источника информации,
но они должны быть однозначно.
Не допускается двузначного определения, при двузначном определении
физической сущности автор должен знать
что он физик,
а у физика при двузначном определении получается
- бессмысленность, идиотизм, парадокс, - что недопустимо.
3 Терминология.
Автор однозначно должен определить терминологию,
и описать своими словами физические сущности и тот смысл
который автор в них вкладывает.
|
|
| Наверх |
|
 |
А.П.Васи
|
|
Re: Пособие для тех кто хочет писать теории.
|
27.03.201216:56 |
|
Волны - физические - бывают на границе между сред.
Например между водой и воздухом.
-------------------------------
Звук - колебания в среде.
Свет - колебание
в среде.
Скорость света и скорость звука - скорость распространения
возмущения среды.
Исключительно для сред используется эффект Доплера,
для определения
изменения расстояния, и частоты между приёмником
и передатчиком колебаний среды.
-----------------------------------------
|
|
| Наверх |
|
 |
А.П.Васи
|
|
| Наверх |
|
- Re: Черная дыра
(А.П. Васи,
22.07.2014 15:13, 13.5 КБайт)
|
|
|
|
......Материал из Википедии
\\\Га́мма-излуче́ние (гамма-лучи, γ-лучи)
вид электромагнитного излучения с чрезвычайно малой длиной
волны
< 5×10−3 нм и, вследствие этого, ярко выраженными
корпускулярными
и слабо выраженными волновыми свойствами. \\\
\\\Гамма-квантами являются фотоны с высокой энергией.
Обычно считается,
что энергии квантов гамма-излучения превышают 105 эВ, хотя
резкая граница
между гамма- и рентгеновским излучением не определена. На
шкале
электромагнитных волн гамма-излучение граничит с
рентгеновским излучением,
занимая диапазон более высоких частот и энергий. В области
1-100 кэВ
гамма-излучение и рентгеновское излучение различаются
только по источнику:
если квант излучается в ядерном переходе, то его принято
относить к
гамма-излучению; если при взаимодействиях электронов или
при переходах
в атомной электронной оболочке к рентгеновскому излучению.
Очевидно,
физически кванты электромагнитного излучения с одинаковой
энергией не
отличаются, поэтому такое разделение условно. \\\
\\\Гамма-излучение испускается при переходах между
возбуждёнными
состояниями атомных ядер (см. Изомерный переход, энергии
таких
гамма-квантов лежат в диапазоне от ~1 кэВ до десятков
МэВ),
при ядерных реакциях (например, при аннигиляции электрона
и позитрона,
распаде нейтрального пиона и т.д.), а также при отклонении
энергичных
заряженных частиц в магнитных и электрических полях (см.
Синхротронное излучение).....\\\
------------------------------------------------------------------------------------
\\\Материал
из Википедии \\\
\\\.....Рентгеновские трубки
Рентгеновские лучи возникают при сильном ускорении
заряженных частиц
(тормозное излучение), либо при высокоэнергетических
переходах в электронных
оболочках атомов или молекул. Оба эффекта используются в
рентгеновских
трубках. Основными конструктивными элементами таких трубок
являются
металлические катод и анод (ранее называвшийся также
антикатодом).
В рентгеновских трубках электроны, испущенные катодом,
ускоряются
под действием разности электрических потенциалов между
анодом и катодом
(при этом рентгеновские лучи не испускаются, так как
ускорение слишком мало)
и ударяются об анод, где происходит их резкое торможение.
При этом за счёт
тормозного излучения происходит генерация излучения
рентгеновского диапазона,
и одновременно выбиваются электроны из внутренних
электронных оболочек атомов
анода. Пустые места в оболочках занимаются другими ....\\\
Вот есть два очень корявых с точки зрения физики
определения, но на текущий момент у релятивистов
лучших определений нет.
Грубо говоря частицы рентгеновского излучения могут быть при двух ситуациях, - первая
ситуация это при ядерных реакциях, - и если у звезды такое излучение
то она будет называться нейтронной звездой, а вторая ситуация когда вещество падает на черную дыру,
и после падения происходит рентгеновское излучение.
Здесь легко определиться с тем, а какая же должна быть
минимальная скорость вещества ?, чтобы получилось
тормозное излучение в рентгеновском диапазоне
в результате падения и удара о черную дыру.
Эта скорость 0.3 скорости света и соответствует скорости
частиц при приложенном напряжении в 27 кВ, и при этом
получаются ускоренные частицы с энергией в 27кэВ, и
они используются в кинескопах цветных телевизоров,
когда при ударе о люминофор, они за счет флюоресценции
и последующей люминесценции создают свечение и
послесвечение
- люминофора, а в итоге экрана кинескопа.
-----------------------------------------------------------
(Материал из Википедии свободной энциклопедии
\\\Флуоресце́нция (вариант: флюоресценция)
физический
процесс,
разновидность люминесценции.
Флуоресценцией обычно называют излучательный переход
возбужденного состояния с самого нижнего
синглетного колебательного уровня S1
в основное состояние S0.\\\
\\\Люминесце́нция(от лат.lumen,
род. падеж luminis
свет и -escent
суффикс, означающий слабое действие)
нетепловое свечение вещества, происходящее после поглощения
им энергии
возбуждения.---\\\
Тело,
свободно падающее под действием сил гравитации, находится в
состоянии невесомости
и испытывает действие только приливных
сил,
которые при падении в чёрную дыру
растягивают
тело в радиальном
направлении и сжимают в тангенциальном.
Величина этих сил растёт
и стремится к бесконечности при
 .
В некоторый момент .
В некоторый момент
собственного
времени тело пересечёт горизонт
событий. С точки зрения наблюдателя,
падающего вместе с телом, этот
момент ничем не выделен, однако
возврата теперь нет.\\\ -------
\\\С точки зрения
наблюдателя, падающего вместе с телом, этот
момент ничем не выделен, однако
возврата теперь нет.\\\ - Даже коню понятно что если сделать мини контейнер и посадить туда
муху
и разогнать в коллайдере на ускорителе до скорости 0.3с, и жахнуть этим контейнером
о мишень и на всё это действие уйдёт одна секунда, то можно долго звездеть
о том что муха будет жить по своим часам ещё вечно, только
я не обязан верить этой порнухе, по сколько муха на самом деле
разобъётся в пыль при ударе о
мишень.
Следовательно рентгеновское излучение можно сказать
что это частицы с энергией ускорения достигшей скорости
более 0.3 скорости света. А вот здесь сразу вылавливаются
авторские парадоксы, - парадокс это теоретическая неудача.
Получается что при ударе падающего вещества должен быть
безбашенный удар о достаточно твёрдую поверхность,
при полном отсутствии атмосферы, по причине того что
атмосфера сделает тормозное излучение со скоростями более
0.3 С невозможным, ибо атмосфера достаточно плавно
замедлит падающее тело . И получается что рассказы о
длительном
падении за горизонт событий в черную дыру не выдерживают
критики, по причине того что или длительное падение
при отсутствии рентгеновского излучения, или безбашенный
удар о твердую поверхность черной дыры в результате
которого при скорости удара больше 0.3 скорости света
будет излучение которое будет называться тормозное излучение.
Итого явно просматривается что автор черных дыр
просто придумал неудачную и нефизичную теорию
о черных дырах и эта теория не выдерживает примитивных
логических взаимосвязей. Но по сколько лучшего
нет у релятивистов, то и этой теории логично аплодировать
и восхищаться черными дырами. |
- Re: Черная дыра
(А.П. Васи,
28.07.2014 9:26, 2.7 КБайт)
 Инерция
Инерция
07.09.11 :: 22:22:4
\\\Поэтому релятивистский коэффициент возрастания массы
можно трактовать не
как эффект СТО, а как коэффициент
увлечения эфира, осуществляемый за счет "захвата" частицами
квантов первоматерии.\\\
------
\\\Старого
пса, новым трюкам не научишь\\\ (С)
Вот например что наблюдается, что ускоряются
- микроскопические элементарные частицы при большом
перепаде высоковольтного
электрического потенциала.
Вот здеся внимание - ускоряются частицы чем именно -
- правильно - электричеством едрёный конь.
Так когда-же уже снизойдёт
до недалёких что материя
в ускорителе ускоряется напряжением который создается
разницей потенциалов напряжения, и движение частиц направленно
от минуса к
плюсу.
Даже не могу объяснить тот уровень недалёости в физике и космологии
который есть сейчас. Вот смотрит например на физический опыт
и напрочь не
понимает ни самого физ процесса ни приоритетности
внутри процесса.
Ибо даже коню понятно что в ускорителе - разгоняют микрочастицы
материи электрой, (перепад
напряжения - создаёт напряженность
электричества, что вызывает статическую утечку тока, но ещё
не возникает дуговой пробой), при этом статический поток
электры
прекрасно движется от минуса к плюсу как некоторый
поток. В кинескопе этот поток могут сужать, расширять, и сдвигать
магнитным полем - во время его движения. А
вот собственно
если увеличивать напряжение и увеличивать расстояние между
минусом и плюсом чтобы разогнать микрочастицы материи до большей
скорости - получается
некоторая нелинейность.
И естественно удивлению физиков нет конца и края , ибо как так
если приложить 27кВ - скорость частиц 0.3С, а при миллионе вольт,
скорость
приближается к С, при трёх миллионах тоже к С приближается,
Частица у них видишь -ли тяжелеет а то что электра которая своим
потенциалом и разгоняет эту
частицу между электродами
сама двигается между электродами со скоростью - С, так
до этого додуматься не возможно.
Не знаю - может они смогли себе в
голове или кто-то
им какими-то теориями блок -адекватности - в голове
выключил. А цирк уехал потом - а клоунада продолжается.
- Re: Черная дыра
(А.П. Васи,
29.07.2014 23:32, 2.8 КБайт)
http://www.astrogorizont.com/content/read-Novyj_vzgljad
\\\Автор:
NASA
|| Оригинальная
версия
|


|

Следуйте за
нами
в группах |
  |
|
 |
|
Этот новый снимок объекта Cen A
содержит в себе данные наблюдений, полученные в период между 1999 и 2012
годами. На снимке самое низкоэнергетическое рентгеновское излучение,
зарегистрированное космической обсерваторией Чандра, показано красным
цветом, рентгеновское излучение средних энергий представлено зеленым, а
рентгеновское излучение самых высоких энергий голубым... |
- Re: Черная дыра
(А.П. Васи,
29.07.2014 23:52, 1.5 КБайт)
В предыдущем сообщении что собственно просматривается -
отсутствие пользы от таких фото при их очень большом потенциале
для понимания структуры звезд и выброса
из них эфира.
Чтобы понять физический примитивный смысл на этом фото
особо и напрягаться не нужно. Главное что собственно наблюдается -
в первую очередь
подсветка и переотражение выбрасываемой материи
из верхнего слоя звезды. В пространстве материя просто так ничего не
излучает - я думаю что это понятно. В материю
которая в пространстве,
попадает частичка высокой энергии и её отбрасывает во все стороны. В данном
случаи источник частиц - звезда, и энергия как раз и показатель
той скорости с которой дует эфир из звезды сквозь верхний слой.
И чем больше скорость - тем больше энергия у частиц.
Собственно опять недостатки фото - нет
три дэ модели этой звезды.
Собственно нет три де модели выбросов, по три де модели выбросов
можно будет определить где и как и с какой скоростью
эфир дует
из звезды в пространство.
Из чего уже примитивно будет можно создать три дэ модель
давления эфира вокруг звезды, и следовательно можно будет
примитивно создать
программным путём,
форму внешнего выброса материи в видимом
спектре, и сравнить с текущим изображением.
И уже потом написать обратную расчетную программу,
которая по внешнему текущему выбросу в оптическом
изображении сможет восстановить предшествующий процесс
у песочных часов с юбками например.
- Re: Черная дыра
(А.П. Васи,
4.08.2014 15:15, 1.3 КБайт)

До последнего времени ученые-физики со всего мира относились весьма скептически к
Роджеру
Шауэру (Roger Shawyer) и его изобретению.
Причиной скептицизма являлось то, что принципы работы изобретенного
Шауэром "невозможного" двигателя EmDrive идут вразрез с принципами
классической механики. Тем не менее, новый вариант двигателя EmDrive,
который получил название Quantum Vacuum Plasma Thruster, изготовленный
специалистами НАСА, работает, хотя ученые еще не могут объяснить почему и
как он это делает.
http://www.dailytechinfo.org/
-----------------------------------------------------------------
- Re: Черная дыра
(А.П. Васи,
4.08.2014 16:00, 507 Байт)
Собственно здесь ситуация с моей точки зрения
когда возможно возникает детектирование сигнала
при внешнем изменении плотности эфира. При этом
происходит
неравномерное рассеивание эфира.
Собственно я помню и на перепаде напряжений спутник
летит или полетит.
Нет никакой конструкции устройства, на фото
какая-то
железка.
Странно в этой ситуации что не восхваляют релятивизм
и гениальность релятивистов, и то что эти движки подтверждают
релятивистские теории.
- Re: Черная дыра
(А.П. Васи,
4.08.2014 16:14, 671 Байт)
http://peswiki.com/index.php/Directory:Emdrive_%28Electromagnetic_Space_Drive%29


SPR Prototype
- Re: Черная дыра
(А.П. Васи,
4.08.2014 16:19, 193 Байт)
Посмотрел описание и чего-то аж смешно стало,
естественно что пытливый разум мог высокотехнологичного
придумать как соединить выход магнетрона свч печки
с
медным рупором.
- Re: Черная дыра
(А.П. Васи,
4.08.2014 22:32, 1.1 КБайт)
http://www.dailytechinfo.org/news/6143-specialisty-nasa-zastavili-rabotat-nevozmozhnyy-dvigatel-kotoryy-v-buduschem-mozhet-navsegda-izmenit-oblast-kosmicheskoy-tehniki.html
\\\Устройство двигателя Шауэра достаточно просто. Он обеспечивает тягу
при
помощи специализированных микроволновых генераторов, излучающих
волны в
замкнутое изолированное пространство.\\\
------------------------------------------------------------------------------
Смешная мысль пришла, - в
космическом пространстве -
магнетрон выкрученный из СВЧ печки как раз - лишняя деталь.
Достаточно сделать зеркальный рупор и световод
зеркальный, чтобы перенаправлять
солнечный свет,
от солнца тоже киловатт на квадратный метр мощность.
Например рупор площадью три квадратных метра,
сводит в пучок, и излучение солнца подводится
сбоку в конус, и рупор можно пропорционально
частоте уменьшить.
О я думаю что уже у всех возникла мысль, а не
раскалится ли закрытый рупор если в него
киловатт
мощности вгонять, ясный конь разогреется - значит
излучение выходит из рупора.
Клоунада.
- Re: Черная дыра
(А.П. Васи,
5.08.2014 22:56, 1.1 КБайт)
http://www.astronews.ru/cgi-bin/mng.cgi?page=news&news=6334


\\\Ученые Стэнфорда и Национальной Ускорительной Лаборатории SLAC
в
течение более чем четырех лет занимались анализом данных космического
гамма-телескопа Ферми (Fermi) и других экспериментов, для того, чтобы
создать самый подробный на сегодняшний день портрет двух громадных
пузырей, которые протянулись на тысячи световых лет над диском нашей
галактики и под ним.
Эти пузыри, которые наиболее ярко светятся высокоинтенсивным гамма-светом,
были открыты более четырех лет назад. \\\
--------------
- Re: Черная дыра
(А.П. Васи,
5.08.2014 23:17, 1.9 КБайт)
Собственно ответ с точки зрения эфира - примитивней некуда.
На что логично обратить внимание - правильно - на форму
конуса синего ореола.
Там где красная
подсветка - там высокая температура,
и низкая плотность эфира, а сама галактика представляет из себя
в пространстве некою вращающуюся турбину или некоторый пористый
диск. Получается что эфир увлекается вращением и создаёт
очень большое разряжение давление эфира в центре галактики,
и это снижает плотность эфира, что подымает
температуру
пространства и уменьшает яркость звёзд в центре, поскольку
они могут быть как Солнце но светимость у них будет раз
в сто меньше, и естественно
они будут красными.
При этом они находятся в состоянии возможной потери баланса
при массовом сбросе эфира в итоге начнется разброс всех
звезд галактики.
Низкое давление в центре вращения некоторого пористого диска
естественно требует восполнения притока эфира который увлекается
центробежной силой.
Собственно
вот такой процесс.
Я думаю что динамику этого процесса примитивно имитировать
раскручивая или пористый диск, или тонкую ткань,
в некоторой среде имеющей пружинные
и текучие свойства,
я бы лично посоветовал опыт
вращая моторчиком диск из тонкой ткани ,
провести внутри лампы с газом в котором разряды внутри.
---
- Re: Черная дыра
(А.П. Васи,
17.08.2014 10:16, 3.3 КБайт)
- Модератор





-

- Сообщений: 14 999
- Рейтинг: +403/-50
- Дети любят бутерброд с маргарином!
-
Ответ #161 : 15.08.2014 [07:59:19]
\\\Удалены сообщения, не относящиеся к обсуждаемой теме.\\\

Записан
\\\И кто-то, как всегда, нёс мне чушь о "тарелках", и кто-то, как всегда, проповедовал дзен... (с) Зоопарк\\\
-------------------------------------------------------------------------------------------------------------------------
Если честно я раньше не верил
в то что у человека может
быть разум забран. В детстве в шутку это называли при
кратковременных ситуациях этого явления у одноклассников
выражением - шизуха
косит наши ряды, и при этом
одноклассник другим одноклассникам должен был за неадекватные
высказывания - сказать фразу - отцы простите зас ран ца.
И это действовало
положительно.
Что собственно наблюдается - автор придумал черные дыры
даже не смог внятно сформулировать её физические свойства,
при этом с момента
как были придуманы черные дыры -
на сегодняшний день официально не обнаружено ни одной
дюрочки, при этом вместо того чтобы разобраться си определиться с черными
дырами создав рабочую группу с бюджетом в десять миллионов
енотов.
Возможно результатом работы этой группы будет посыл идей
черных дыр в далёкую даль,
и спекуляции на вращение
того что не обнаружено будет выглядеть не смешно.
- Re: Черная дыра
(А.П. Васи,
17.08.2014 16:08, 891 Байт)
Собственно у меня появилось логическое решение, - для других
идей поколение старше 35 лет невосприимчиво. Собственно старше
сорока пяти лет будут категорически
против любых других идей.
Это я бы назвал - научный консерватизм.
Я так понимаю что с определенного возраста отключается
блок сомнения в своих знаниях, и
юзер больше доверяет
своим знаниям, и уверен в неправильности других идей.
До этого отключается блок зацепок - это то с помощью
чего на подсознательном уровне
возникает сомнение в любых
идеях.
Итого - если в идеи отсутствует обоснование или присутствует
открытая проблема, или не обосновывается причина постулирования
-
(например слабая теория наполненная парадоксами), -
то для кого и голимый порожняк - а для кого и гениальное достижение,
и в этом случаи никто другому не
сможет доказать свою точку зрения.
- Re: Черная дыра
(А.П. Васи,
24.08.2014 13:25, 2.3 КБайт)
Вот Вибе рассуждает как временщик в данной ситуации,
он прекрасно видит лайно и идиотизм в конкретном случаи
и только радуется этому и считает это нормально.
Я естественно считаю всю физику "своей" - и для меня малейшее моё
непонимание в ней или попытка ввести меня в ложное направление
- мной воспринимается
крайне негативно, и я придумал давно
и методы как находить эти обманы и придумал как их
запоминать в голове, чтобы
потом сразу не читать а пропускать подобное
в любых текстах.
Если честно то я давно уже и придумал тесты для физиков
таких как Вибе - своими словами за 15 минут рассказать
что лично самостоятельно
придумал и зачем и какой вопрос
это решает и кто этим пользуется.
Второй тест - какие глобальные и основополагающие
трудности с Вашей точки зрения есть
в физике и космологии - 5мин.
Третий тест - По каким причинам Вы самоустранились от
решения основных и основополагающих вопросов космологии и физики,?
-
10 мин.
----------------------------------------------------------------------------------------------------
Ответ #2810 : Сегодня в 13:03:02
\\\Нехорошие
характеристики -- субъективное понятие. В законе всемирного тяготения
сила стремится к бесконечности при стремлении расстояния к нулю. И
ничего, закон работает.
Какие конкретно проблемы с нужным
человечеству качеством возникают из-за сингулярной плотности и
сингулярной кривизны чёрных дыр?\\\
\\\Проблемы развития, прогресса, и поиска знаний.
Исключая проблему, исключаются и направления поиска решений
проблемы.
Как бы торможение научного процесса.\\\
- Re: Черная дыра
(А.П. Васи,
24.08.2014 20:07, 1.5 КБайт)
Даже не понимаю как люди не боятся в научный идиотизм заигрывать.
Собственно простыми тестами выявляется за полчаса и укажут на
дверь и пошлют домой по причине
проф непригодности.
С другой точки зрения - лучшая замена отсутствует, но нельзя забывать
о любой замене, которая со временем будет лучше.
---
Не могу понять опять-же, почему практически у всех проседают умственные
способности при вопросе о электричестве.
Собственно явно не могут даже понять смысл опыта
по обнаружению электрона,
точнее не могут понять в каком месте отсутствует причинно следственная связь,
и не могут опять же понять что этот опыт в пролёте.
И явно не в состоянии этот опыт описать своими словами,
надеются что кто-то на форуме будет думать за него а он потом подумает
лучше и получит большую премию.
Как-бы жажда халявы, и ни у кого даже идеи не возникает как поставить
тех задачу и разбить её на под задачи и решить в комплексе все
ситуации - трудовой метод
- я даже нигде на форуме не видел таких
предложений.
И естественно что - и эти методы пролетают как фанера над Парижем,
если соберутся люди пенсионного возраста.
--------------------------------------------------------------------------------------------------------
Физика
альтернативная
- Re: Черная дыра
(А.П. Васи,
24.08.2014 21:28, 4.4 КБайт, ответов: 1)
Я вот смотрю и уже даже никто не поправляет
заблудшую недалёкую и думающую что он физик,
ну и даже никто и не рассказывает лекций про атомные
часы и другие
высокоточные часы, и спец атомные
часы которые не меняли темпа хода,
не увеличивали свой темп как все другие
с увеличением высоты, и разработчики эти часы
и всю тех документацию о их работе выбросили.
Что меня удивляет что кто занимается теорией, ему просто
плевать на то как на самом деле на спутниках
себя ведут
часы, на сколько я помню что никто не скрывает что
темп кварцевых и атомных часов с увеличением высоты -
увеличивается, и глубоко до лампочки в
какую сторону
летит спутник или он завис.
И вот будучи например на своей волне, ничего не понимая
в вопросе задвигает такие идеи что аж шапка заворачивается,
а спорить тоже бессмысленно - "старого пса новым шуткам
не научишь" (С).
---
|
 Re: Новая физика из новой теории относительности. Подходы к решению загадок строения материи.
Re: Новая физика из новой теории относительности. Подходы к решению загадок строения материи.
Ответ #9 - Сегодня :: 20:43:34
Цитата:Либо вы не до конца поняли суть, либо я не достаточно доходчиво её изложил. Smotrajщii писал(а) Сегодня :: 17:50:20:Что значит ""постоянно замедляется"? Кто Вам это сообщил? Smotrajщii писал(а) Сегодня :: 17:50:20:Ну с ...? В честь какого .... Вы делаете такое предположение.?
Принцип относительности диктует:
Движение ракеты относительно эфира (инерционность) и движение эфира
относительно ракеты, это одно и то же. Отсюда постоянное замедление
времени на ракетных часах, являющих собой стоячую электроволну и в
ускоренно движущейся ракете и в ракете при ускоренно движущемся
относительно её эфире. Smotrajщii писал(а) Сегодня
:: 17:50:20:Что
касательно стартующей ракеты, Так вот ждля того, чтобы оторвать тяжелую
задницу от стартового стола, ракета должна набрать скорость
движущегося к поверхности эфира, и плюс ещё чуточку.....тогда произойдёт
начало её старта. Так вот, в случае неускоренного (с
постоянной скоростью) падения эфира к центру Земли, сразу же после этой
чуточки, мгновенно выключите двигатели (уберите тягу) и ракета зависнет и
будет висеть сколь угодно долго, не нуждаясь ни в какой опоре. Но в
реальности она не зависает, а начинает ускоренное падение к центру
Земли. Следовательно наше предположение о движении эфира к центру Земли с
постоянной скоростью неверно. Ну а в случае ускоренного
движения эфира к центру Земли темп хода ракетных часов, как и при
ускоренном движении ракеты должен постоянно замедляться. Но это не
соответствует действительности. Следовательно наше предположение о
ускоренном движении эфира к центру Земли неверно. Вывод: Падения эфира к центру Земли нет.\\\
|
--------------------------------------------------------------------------------------------------
На сколько я помню в тридцатых годах прошлого
века
на двух первых высокоточных часах - было зафиксировано увеличение
темпа хода часов с увеличением высоты.
- Re[2]: Черная дыра
(А. В. Таликов,
5.09.2014 22:09, 323 Байт)
темп кварцевых и атомных часов с увеличением высоты -
увеличивается, и глубоко до лампочки в какую сторону
летит спутник или он завис.
А вот с этого места по-подробнее. Возможно Молния зависала на ГСО в какой-то
сезон по одну сторону орбиты Земли имея ее скорость 30 км/сек, а в перигее
вычитала из неё 11 км/сек?
- Re: Черная дыра
(А.П. Васи,
25.08.2014 14:49, 1.6 КБайт)
 Re: Эфирная Теория. Единая концепция.
Re: Эфирная Теория. Единая концепция.
Ответ #918 - Сегодня :: 06:29:12
\\\ Не надо мне приписывать глупости. Я пользуюсь
терминами Тот же вакуум не
русское слово. Я не пользуюсь
ненаучными терминами. Материя и
пространство в физике
не научные термины. \\\
------------------------------------------------------------------------------------
С одной
точки зрения так подумать - просто смешно читать,
например достаточно дать = материи и пространству = , - простое
и понятное определение которое выражает тот смысл
который автор
вкладывает в него и всё достаточно.
Здесь естественно логично как раз и проводить конференции, и согласовывать
терминологию и вкладываемые
в неё идеи и физические сущности различными
научными школами - но до этого ещё не скоро раздуплятся, так как
ещё нет научных школ.
А так естественно
трудно юзерам которые не могут самостоятельно
дать физических определений, им для этого надо самим методику
себе разработать, и идти по пунктам - будет плохо но
хоть что-то будет,
чтобы этими определениями можно было пользоваться.
- Re: Черная дыра
(А.П. Васи,
25.08.2014 15:07, 4.7 КБайт)
Я тоже написал самостоятельно - базовые определения
тех физических сущностей и их свойств, состояний
и взаимодействий.
Описал как мог и что считал нужным, сейчас я естественно бы в рамках
своей модели бы написал
другие определения, но по той причине что в своё
время я не гнал отсебятины (предсказательную часть - модную среди нынешней
физики
в которой нет никакой ответственности за правильность и адекватность
теорий ) - то и эти определения тоже подойдут.
---
| Re: Свет и пространство и о скорости света.
|
12.09.2011 |
Предполагаемая
физическая модель эфира и устройства звезд.
Введение.
Данная
модель предназначена для более простого
восприятия
астрофизики, эта модель не претендует
на
абсолютную истину.
Модель
будет выглядеть в виде изначального набора
некоторых
условных утверждений описывающих
элементы
по отдельности в статическом виде,
из
которых будет в последствии сделана динамическая модель.
Состав
элементов модели.
Пространство
- один из элементов модели обладающий идеальными
свойствами,
и представляющее из себя пустой объём бесконечный во
все
стороны, единица измерения - расстояния
метр объёма кубометр,
время
существования - вечное.
Эфир
- газообразная среда которая может быть и в жидком состоянии,
она
заполняет пространство во всём объёме, газ нейтральный по отношению
к
материи, обладает всеми свойствами газа, отличается
высокой
текучестью которая в миллиард раз более текучий
чем
воздух, и единичная частица эфира в миллиард раз меньше молекулы
воздуха,
время существования - вечное.
Материя
- все прочие частицы заполняющие пространство,состоит как
правило
из атомов и молекул, и осколков атомов и молекул по размеру
от
тысячи до миллиарда раз меньше молекул воздуха, с
эфиром
- материя, ни в какие массо-обменные реакции не вступает ни
в
газообразном ни в твердом ни в жидком состоянии, - материя не может стать
эфиром,
а
эфир не может стать материей - время существования - вечное.
- Re: Черная дыра
(А.П. Васи,
25.08.2014 15:49, 3.0 КБайт)
http://www.astronews.ru/cgi-bin/mng.cgi?page=news&news=6454

\\\Разрушительные последствия мощного взрыва сверхновой можно
разглядеть
на этом изображении, составленном из снимков, сделанных в
рентген- и
инфракрасном дапазонах, обсерваториями - космическим
телескопом Спитцер
(Spitzer Space Telescope), обсерваторией Чандра
(Chandra X-Ray Observatory) и
аппаратом XMM-Newton.
Пузырящееся
облако это ударная волна неправильной формы, сгенерированная
взрывом,
который земляне могли увидеть 3 700 лет назад. Облако останков, Puppis
A,
находится на расстоянии около 7 000 лет от Земли, а диаметр ударной
волны около
10 световых лет.\\\
----------------------------------------------------------------------------------------------------------------
Меня величины немного смущают, логично проверить.
Итого - расстояние 7000 световых лет, событие произошло - 3700 лет назад,
текущий диаметр 10 световых
лет.
Следовательно чтобы узнать среднюю скорость расширения
достаточно 3700 поделить на 10 и получится что расширение
в триста семьдесят раз медленнее
скорости света.
Теперь я открываю статью
http://crydee.sai.msu.ru/Universe_and_us/4num/v4pap26.htm
\\\Масса выброшенного
при взрыве сверхновой вещества достигает
нескольких масс Солнца, скорость его
разлета 10-20 тыс. км/с, \\\
\\\Наиболее известны Крабовидная туманность
(остаток вспышки СН 1054 г.),
Кассиопея А (вспышка СН не наблюдалась, но по
разлету выброшенных сгустков
датируется 1680 годом), остатки сверхновых Тихо
Браге (СН 1572 г.) и Кеплера
(СН 1604 г.). Эти молодые ОВС наблюдаются как оптические
туманности,
яркие источники рентгеновского и инфракрасного излучения. Скорость
расширения этих туманностей все еще достаточно велика, 2000-6000 км/с,
размер-2-4
пк.\\\
\\\Размер старых ОВС достигает десятков
парсеков и даже сотен парсеков, если
остаток расширяется в среде очень низкой
плотности. Скорости разлета старых
ОВС падают до сотен и десятков км/с. Они
наблюдаются как тонковолокнистые
оптические туманности, яркие в радиодиапазоне,
такие как Петля Лебедя и IC443
. По мере замедления скорости разлета ОВС и остывания
горячего газа его
рентгеновское излучение становится несущественным. Когда скорость
расширения
оболочки сравнивается со скоростью хаотичеких движений газовых облаков
в
Галактике (около 8 км/с),\\\
- Re: Черная дыра
(А.П. Васи,
25.08.2014 15:56, 595 Байт)
Что собственно странно что никто собственно не написал
например что скорость распространения выброса уменьшается
с квадратом или кубом расстояния.
Дело в
том что знать данные скорости и их изменения очень важно
в космологии, ибо не зная их будут расстояние измерять с точностью
плюс минус миллион раз, в лучшем случаи
плюс минус - тысяча раз,
а наблюдая например выброс у звезды типа песочница, можно будет
точно определить расстояние до неё.
Ясный конь для этого нужна
будет программа, и периодическая или
постоянная видеозапись процесса.
- Re: Черная дыра
(А.П. Васи,
6.09.2014 9:00, 295 Байт)
Вы не состоянии - сформулировать вопрос.
Не отличаете - констатацию факта, от вопроса по сути.
Так вот пока Вы не покажете - какими опытами и методами
измеряли темп хода часов на спутнике, и не докажете что спутник
на меньшей высоте увеличил темп часов до тех пор ко мне
не обращайтесь.
- Re: Черная дыра
(А.П. Васи,
13.09.2014 11:48, 2.2 КБайт)
Опыт Юнга. Эксперимент с двумя щелями.
http://www.astronomy.ru/forum/index.php/topic,122079.0.html
----------------------------------------------------------------------
Что собственно меня радует и удивляет так это как в
анекдоте,
\про муравья которого стадо быков затоптало в грязь,
и муравей встаёт, отряхивается и говорит меня крутого
муравья и мордой в грязь, и кто бычьё.(С)\
Я собственно даже не понимаю как можно быть настолько
массово недалёкими в примитивных задачах по физике.
Всё есть, можно найти полное описание опыта в авторском
варианте.
Можно найти то что Томас Юнг высказывал о свете и его
природе.
И даже примитивных методов нет в физике для решения
детских задач.
А там надо всего-то 1) описать ситуацию,
2) дать определения сущностями по возможности в различных
изложениях различных школ. Дать описание происходящему
от разных школ.
3) Дать описание
последовательности причинно следственных
связей, и последовательности
в физических взаимодействиях.
Сделать выводы.
Указать на ошибки.
- И всё, примитивная задача в физике будет решена раз и
навсегда
и на веки вечные так что для этого мозгов что-ли много
надо.
Собственно не могу понять как можно одну и ту же задачу
десятилетиями самому себе мозги ... в попытке её решать.
- Re: Черная дыра
(А.П. Васи,
13.09.2014 11:51, 109 Байт)
Самое смешное что опыт можно сделать самостоятельно
в домашних условиях, и он не требует финансовых затрат.
- Re: Черная дыра
(А.П. Васи,
23.09.2014 22:17, 3.0 КБайт)
26 августа 2014года.
ТрВ 161,
c.1, 3,
"Образование"
Егор Базыкин, Дмитрий Вибе, Алексей Сгибнев, Владимир Сурдин,
Сергей Белков, Ирина Левонтина
Дмитрий Вибе,
докт. физ.-мат. наук, зав. отделом физики и эволюции звезд
Института
астрономии РАН:
Лето с научной точки зрения оказалось неожиданно продуктивным.
Неожиданно ибо не по нашей
воле до лета затянулась битва с
рецензентом статьи, которую мы
отправили в журнал еще в сентябре
2013 года. Он несколько раз требовал
существенных доработок, на
которые уходил не один месяц, и сам каждый
раз честно выдерживал
месяц на написание очередного отзыва. Трудно
сказать, написали ли
мы в итоге что-то его устроившее или просто
надоели. Справедливости
ради следует отметить, что все замечания были по
существу, и статья в
результате их реализации стала лучше на
качественном уровне.
Статья посвящена анализу наблюдений полициклических ароматических
углеводородов (то есть мы подозреваем, что это они) во внегалактических
областях звездообразования разного возраста. До этого одни люди
предполагали, что углеводороды в областях звездообразования растут,
другие люди предполагали, что углеводороды в областях звездообразования
разрушаются. Нам же впервые удалось убедительно показать, что там с
углеводородами происходит вообще не пойми что.\\\
------------------------------------------------------------------------------
Смешно
само желание махровых релятивистов податься в альты,
собственно я понимаю что кушать охота, и подашься куда угодно,
тем более /если тот кто живёт
прошлым не может увидеть будущее/(С),
и что в этом случаи делать?.
Здесь хоть ролик снимай - "Как релятивисты подались в альты, и при этом
они
они остались релятивистами, - в итоге среди альтов они - релятивисты,
а среди релятивистов они - альты.
У меня мысленно аж клавиатура утопала в слезах
высоко интеллектуальной
рапсодии которая звучала от их падения и ударов о пластик .
- Самое главное в этой ботве - чтобы не было базовых и однозначных
авторских определений. Без этой ботвы просто бездна самых умных -
при этом никто ни на что не несёт ответственности, и тем более у него
остаётся
возможность всегда самого себя опровергнуть, и даже не один раз
в рамках одной и той-же - ботвы, пардон - теории.
- Re: Черная дыра
(А.П. Васи,
23.09.2014 22:19, 234 Байт)
"Здесь хоть ролик снимай - "Как релятивисты подались в альты, и при этом
они
они остались релятивистами, - в итоге среди альтов они - релятивисты,
а среди релятивистов они - альты.""
- Re: Черная дыра
(А.П. Васи,
23.09.2014 23:09, 329 Байт)
Легко релятивиста отличить от альта, - альт ясный конь, - может
всегда сказать что он лично придумал сам и для чего это надо.
Релятивист может - ясный конь, придумать только в рамках
теорий релятивизма, - и никогда не сможет внятно сказать
для чего это надо, и релятивист не сможет сказать - что он
придумал лично - сам.
- Re: Черная дыра
(А.П. Васи,
28.09.2014 13:03, 5.0 КБайт)

: 08.01.2003 [19:44:15]
\\\Этот способ принесёт пользу и тем авторам новых физических теорий,
которые способны к самокритике. Проведите рецензирование самостоятельно,
и путём хитрых иносказаний сожмите всю широту своих взлядов в требуемые
10 баллов. Временно придётся пойти на компромисс, но это вынудит
рецензента прочитать ваш труд до конца. И первый шаг в продвижении новой
идеи будет сделан!\\\
\\\Как определить сумасшедшую теорию\\
\\\Способ расчёта рейтинга потенциально революционного вклада в физику.\\\
\\\1.
Даём -5 очков форы.
2. +1 очко за каждое утверждение, которое широко известно как ложное.
3. 2 очка за каждое бессодержательное утверждение.
4. 3 очка за каждое
логически некорректное утверждение.
5. 5 очков за каждое ошибочное утверждение, которое не изменяется, несмотря на ясное указание, как его можно исправить.
6. 5
очков за применение мысленного эксперимента, который противоречит широко известному реальному эксперименту.
7. 5 очков за каждое слово, выделенное заглавными буквами
(если дело не в неисправной клавиатуре).
8. 5 очков за каждое упоминание "Энштейна", "Хокинса" или "Феймана".
9. 10 очков за каждое
заявление о том, что квантовая механика принципиально порочна (без ясного примера).
10. 10 очков за предложение почитать учебник в качестве свидетельства того, что автор
понимает, о чём говорит.
11. 10 очков за начало описания теории с того, как долго автор её разрабатывал.
12.
10 очков за посылку текста человеку, которого автор лично не знает, с
указанием, чтобы он никому ничего не говорил из-за боязни, что новые
идеи будут украдены.
13. 10 очков за предложение денежного приза тому кто докажет и/или найдёт ошибки в этой теории.
14.
10 очков за каждое утверждение в таком стиле: "Я не математик, но моя
теория верна в принципе, и будет только лучше, если кто-нибудь выразит
её в уравнениях".
15. 10 очков за то, что современная широко используемая теория - это "всего лишь теория", как будто кто-то с этим спорит.
16.
10 очков за то, что, хотя широко применяемая теория даёт правильные
предсказания явлений, но она не объясняет, "почему" эти явления
происходят или неправильно объясняет их механизм.
17. 10 очков за
каждое хвалебное сравнение себя с Эйнштейном или заявление, что теория
относительности принципиально порочна (без ясного примера).
18. 10 очков за заявление, что новая теория приближает нас к "смене парадигмы".
19. 20 очков
за намёки, что автор заслуживает Нобелевскую премию.
20.
20 очков за каждое хвалебное сравнение себя с Ньютоном или заявление,
что классическая механика принципиально порочна (без ясного примера).
21. 20 очков за каждое использование примеров из научной фантастики или из мифов, как будто это
реальные факты.
22. 20 очков за самозащиту путём высмеивания своей (реальной или вымышленной) прежней теории.
23. 20 очков за каждое упоминание "узколобых реакционеров".
24. 20 очков за каждое упоминание о "самоявленных защитниках традиционных взглядов".
25.
30 очков за предположения о том, что известный человек в тайне не верил
в теорию, которую он публично поддерживал. (Например, что Фейнман в
душе был противником специальной теории относительности, что можно
установить, если прочитать его учебники по физике между строк).
26.
30 очков за предположение о том, что в последние годы жизни Эйнштейн уже
близко подошёл к идеям, которые сейчас высказывает автор.
27. 30 очков за заявление, что эта теория разработана внеземной цивилизацией (без ясного свидетельства).
28.
30 очков за упоминание о том, что работа приостановлена на время
пребывания в психбольнице, или о том, что психиатр пытался отговорить
автора продолжать эту работу.
29. 40 очков за сравнение противников этой теории с нацистами, штурмовиками и коричневыми.
30.
40 очков за заявление, что "учёная элита" участвует в заговоре, чтобы
помешать новой теории приобрести так заслуженную славу.
31. 40 очков
за сравнение себя с Галилеем в том смысле, что современной Инквизиции в
данном случае придётся ещё труднее, или что-то вроде этого.
32. 40
очков за заявления о том, что когда эта теория будет окончательно
признана, то современных учёных пристыдят, чего они и заслуживают. (Ещё
30 очков за фантазии о том, как именно учёные, которые насмехались над
этой теорией, будут вынуждены отрекаться от прежних слов).
33. 50 очков за заявления, что у вас есть революционная теория, но она не имеет конкретных проверяемых предсказаний.\\\
\\\J.Baez\\\
-------------------------------------------------------
\\\Думаю, каждый из присутствующих без труда сможет вычислить свой личный
рейтинг:)\\\
- Re: Черная дыра
(А.П. Васи,
28.09.2014 13:13, 1.7 КБайт)
Собственно не могу понять почему релятивисты этими тестами не проверяют свои
теории, там и большой взрыв сплошная "открытая проблема", "открытая проблема"
это -
========================================================================================================================Материал
из Википедии
Гипо́теза (др.-греч. ὑπόθεσις предположение; от ὑπό снизу, под + θέσις
тезис) предположение или догадка; утверждение, предполагающее доказательство,
в отличие от аксиом, постулатов, не требующих доказательств. Гипотеза считается
научной, если она удовлетворяет критерию Поппера, то есть потенциально может
быть проверена критическим экспериментом, а также если она соответствует другим
научным критериям.
Также она может определяться как форма развитий знаний, представляющая собою
обоснованное предположение, выдвигаемое с целью выяснения свойств и причин
исследуемых явлений[1].
Как правило, гипотеза высказывается на основе ряда подтверждающих её наблюдений
(примеров), и поэтому выглядит правдоподобно. Гипотезу впоследствии или
доказывают, превращая её в установленный факт (см. теорема, теория), или же
опровергают (например, указывая контрпример), переводя в разряд ложных утверждений.
Недоказанная и неопровергнутая гипотеза называется открытой
проблемой.================================================================================================================И
радоваться тому что проповедуются абсолютно все текущие теории основаны на
постулировании и все с "открытыми проблемами", и отказываться от любых
альтернатив, ну ну, я как альт пойду на встречу желаниям релятивистов.
- Re: Черная дыра
(А.П. Васи,
28.09.2014 14:03, 1.8 КБайт)
\\\Что не публикует
Астронет
Astronet.ru
является научно-популярным и учебным сайтом,
поэтому
мы не публикуем непроверенные и альтернативные
физические
и астрономические теории. В первую очередь это
относится к альтернативным теориям гравитации
и альтернативной космологии. \\\
Я
так понял что отсутствуют организации уполномоченные проверять альтернативные
теории.
Собственно альтернативная теория это просто другие идеи.
Я
вот призадумывался почему не написали что не публикуют нелогичных теорий,
или
теорий не соответствующих здравому смыслу, естественно что-то явно
сдерживает
так писать, ибо они подобными теориями уже пользуются.
Я
долго думал по этой ситуации, пришёл к выводу, что большинство считает что даже,
самые
умные люди в физике в итоге могут придумать теории на уровне глупости и не
более,
и собственно ту глупость что есть, менять на другую нет смысла.
- Re: Черная дыра
(А.П. Васи,
8.10.2014 21:36, 4.4 КБайт, ответов: 1)
Ответ #31 : Сегодня в 17:51:20
\\\Вы не указали в какой ИСО.\\\
\\\Для Rishi
это необязательно. Он произнёс магическое заклинание. \\\
\\\Скорость рапространения волны не зависит от скорости движения излучателя,
но естественно складывается со скоростью движения наблюдателя, а как ещё может быть\\\
\\\Этого достаточно.\\\
----------------------------------------------------------------------------------------------------
Для тех кто не замечает краеугольных противоречий могу подсказать,
- у релятивистов нет сред, и среды как таковой.
Слово волна, и эффект Доплера, у них
не может использоваться в принципе.
По причине того что волна это свойство среды, а Эффект Доплера изначально
автором был придуман исключительно для сред.
\\\Материал из Википедии свободной энциклопедии
Эффект был впервые описан Кристианом
Доплером в 1842 году.\\\
\\\Термин фотон введён химиком Гилбертом Льюисом
в 1926 году.
[9]
\\\
У релятивистов пространство - пустое, и в пространстве движутся только
частицы, которые и являются фотонами или электронами.
А в среде, колебания
передаются изменением плотности среды,
которыми являются например волны, или колебания на границах сред
или внутри таковых, и возмущения сред - определяющих скорость
распространения в средах при наличии условий для сред -
среды должны обладать плотностью, при непосредственном контакте
частиц сред между собой.
Собственно
излучение частиц в движении не может быть одновременно
константой при излучении в направлении движения даже в пустоте,
ибо она координатно может маркироваться
простым распылением
каких-то красителей например, которые будут находится в пустой
пустоте в стабильно устойчивом состоянии, на которую в пустоте
даже другие
тела своим притяжением не смогут повлиять в силу очень
низкой удельной плотности красителя, который из себя в пространстве
представляет атомарную пыль.
Собственно
если размер этой пыли подобрать с длинной волны, чтобы эту
пыль вращало в пространстве, и частицы пыли обладали отражающей
способностью, то логично будет высокоскоростными
камерами теоретически
наблюдать изменение угла отражения скоплений пыли на резонансных
для пыли гармониках при внешних направленных воздействиях которые
могут
быть маркерами.
Но это как бы логично было бы но на практике это не логично,
по крайней мере опыт простой и дешёвый, и космосе на орбите, эту ерунду
можно
реализовать без особых трудностей,
прямо возле международной станции можно столбы в пространство из баллончика
с краской распылить и посмотреть что с ними будет
дальше.
Как говорится опыт логично разделить на две части, - распылить в пространстве
красочные столбы, после этого второй опыт,
источник возбуждает
своим воздействием красочные столбы,
а со стороны просто явно будет видно с какой скоростью и по
отношению к чему.
- Re[2]: Черная дыра
(Евгеньевна Львовянка,
27.10.2014 13:10, 64 Байт)
я не доверяю хоккингу www.tomas-morr.livejournal.com
- Re: Черная дыра
(А.П. Васи,
14.10.2014 21:13, 2.7 КБайт)
Собственно не могу понять почему не берут Хоккинга за рога
и не углубляют его интеллектуально рылом в грунт, на фоне его
нескладушек и фу ф лыжных определений
черных дыр.
Чего его не спросят, - что есть черные дыры?, - если он сольёт
воду, то логично его и послать в пешее эротическое путешествие
с его определениями
черных дыр.
Просто логично поставить вопрос ребром о "дуде" и получить ответ,
чтобы не звездеть в стиле Дмитрия Вибе что мол только автор
может
обсуждать свои идеи, и это частично
правильно, фанаты черных дыр или большого взрыва, могут дудеть
только в рамках отведенных автором черных дыр или автором большого
взрыва,
но сомневаться в "дуде" уже не могут.
---------------------------------------------------------------------------------------------------
Ответ #74 : Сегодня в 16:39:21
последний
момент, при подлете к горизонту, должен увидеть что эта дыра быстро
испаряется, за секунды он должен увидеть все 10^66 лет существования это
дыры. Иначе у нас будет альтернативная реальность, зависящая от
наблюдателя.
Излучение
Унру наблюдается в ускоренной СО, но не наблюдается в ИСО. Возможно,
излучение Хокинга наблюдается статическим наблюдателем, но не
наблюдается свободно падающим радиально наблюдателем .
, и на самом деле, космонавт не упадет в сингулярность, а увидит
как ЧД испарилась, при подлёте к горизонту..
 http://ufn.ru/ru/articles/2001/3/e/
http://ufn.ru/ru/articles/2001/3/e/
- Re: Черная дыра
(А.П. Васи,
25.10.2014 14:26, 4.5 КБайт)
Ответ #208 : Сегодня в 09:57:48
\\\А
как обнаружили ЧД, допустим, в нашей Галактике?
Да по странному
вращению звезд с огромной угловой
скоростью. Вот в какую сторону звезды
вращаются, туда
и ЧД вращается. Не наоборот же?\\\
\\\Приведите, пожалуйста, для ясности орбиты этих звёзд и покажите,
в какую сторону
должна вращаться чёрная дыра.\\\
\\\Да, потому что энергетически ЧД несоизмеримо превосходит
вся
Галактику по моменту.\\\
\\\Пожалуйста, проиллюстрируйте это утверждение числами.\\\
\\\Пока Вы этого не сделаете, в эту тему не пишите
больше ничего.\\\
---
Ответ #209 : Сегодня в 10:10:38
\\\Автор:
Дмитрий Вибе
: Сегодня в 09:57:48 Цитата Пожалуйста, проиллюстрируйте
это утверждение числами.
Пока Вы этого не сделаете, в эту тему не пишите
больше ничего.\\\
\\\Понято! Значит буду вычислять!\\\
------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------
Ай да Вибе, ай да крассава, он меня радует всё
больше, явно наблюдается его прогрессивное
движение в направлении идиотизма.
Я вот думаю что у него уже возрастные болезни
начинаются.
Собственно адекватный юзер попросил бы дать
определения сущностей и на этом было бы достаточно,
но по скольку вся теоретическая космология уже в неадеквате,
по причине отсутствия у них адекватных базовых определений,
того что они обсуждают, и что они в итоге обсуждают?.
И в этой ситуации уже так сказать
вершиной идиотизма может быть требование к участникам
дискуссии использующих неадекватные физические сущности,
формализовать их количественно по отношению к неописанным
никем выдуманным физическим свойствам.
Собственно это как как батарейкой крона коснуться языка
и попросить это описать математически. Глупость в том
что нельзя касаться батарейкой крона языка в принципе.
Так и в теоретической космологии никак не раздуплятся что
у них основная трудность отсутствие адекватных
определений,
и уже потом до лампочки и бессмысленно применение
любых математических описаний к этой ботве.
- Re: Черная дыра
(А.П. Васи,
25.10.2014 14:43, 585 Байт)
По большому счету достаточно странно что Вибе так сказать
становится балластом, он всегда раньше сознательно обламывал дискусии,
но в данном случаи неосознанно,
дискуссии наносит прямой вред.
По большому счету Вибе снижает моё мнение о возрасте в научном
коллективе.
Собственно в таком возрасте (как у
Вибе) уже нельзя руководить научным
коллективом, можно быть только рядовым сотрудником, а ещё через
три года, уже нельзя быть даже рядовым сотрудником, а можно
только
заниматься вопросами логистики и снабжения - и так до пенсии.
- Re: Черная дыра
(А.П. Васи,
27.10.2014 20:55, 580 Байт)
Вы случайно не перепутали балетный или мыльно сереальный форум,
с космологическим форумом?, - на космологическом форуме,
подобные утверждения начинаются не со слов
"не доверяю"
- , а со слов
- могу обосновать в чем не прав такой-то в своих идеях, и по таким-то
причинам.
И дальше в стиле
- есть базовые определения того-то. -
1 Они при измерениях в рамках авторских определений таких-то.
2 Определения измерений такие-то.
3 По результатам
приборов таких-то,
и методик таких-то, получается вот такая ботва.
- Re: Черная дыра
(А.П. Васи,
28.10.2014 12:15, 4.1 КБайт)

Ответ #109 : Сегодня в 01:48:51
\\\Когда в начале учебного года преподаватель весь семестр
нам рассказывает
одно,
а во втором полугодие говорит - а теперь, друзья мои, забудьте
всё то о чём я вам
говорил в прошлом семестре, мы начинаем изучать новое
по новому.. Это означает
лишь одно - повторение мама учения - более
углублённый курс обучения того же
теоретического материала. Вот и та
прекрасная возможность внедрить те новшества
фундаментальной науки в
дополнениях в свете последних научных открытый или
маленьких, но весьма
значимых дополнениях. Да и космологии раньше не было.
Тут я с вами
полностью согласна. \\\
------------------------------------------------------------------------------------------------------------
А Геральдинка права,
только многие даже не догадываются
на сколько сильно она права.
После следующего моего текста космология оказалась
в полной абстракции, все её книги за последние
90 лет
случайно превратились в макулатуру.
-----------------------------------------------------------------------------------------------------------
-Для существования эффекта Доплера, есть причина - среда и её свойства.
Даже если используется метод измерения для сред, а говорится
что
вокруг пустота, то пропадает
причинность возникновения данного
эффекта как свойства пространства.
У релятивистов не пространство выступает в качестве линии задержки
сигнала, а выступает
- фотон, как движущийся объект, у которого
ограничена скорость движения в пустоте, по не понятной причине -
которая
постулируется без объяснения причины. Фотон
в данном случаи
может быть только частицей, - это не возможно по причине того что
частица не может снижать и увеличивать свою
скорость что
наблюдается например
при движении света например в воздухе, потом
через стекло потом опять в воздухе и потом в вакуум, так как
получается что в стекле летит фотон медленнее чем в воздухе
и
вакууме , а вылетая из стекла фотон увеличивает свою скорость. Так
вот не может частица
которая потеряла скорость, просто так взять и
при вылете из стекла
увеличить скорость, - на подобное способны
только колебания среды в средах с разными свойствами.
Так что фотон
как частица - выдумка чистой воды.
Вывод -
в пространстве распространяются колебания среды, и световое
излучение не движется а образуется от взаимодействия колебаний
среды и материала, как в 1800 году говорил
Томас Юнг.
Так что все что написано в астрофизике без учета среды - к
сожалению не правильно.
Это подарок Дмитрию Вибе, это не будет опубликовано два
три года.
Дмитрий Вибе может и дальше учить студентов тому что безвозвратно
устарело, и тому что им никогда не пригодится.
Так уж Дмитрий Вибе запрещал обсуждать
эфир пока его не докажут что он есть,
---------------------------------------------------------------------------------------------------------------------
Собственно мне тоже публиковать это в каком-то
реферируемом журнале вряд-ли дадут.
Да и при общение на форуме с Дмитрием Вибе - он мне
заявил
что его лекция основанная на чужих идеях - это его
интеллектуальный труд. И я например не хочу чтобы мои
идеи читали студентам бывшие махровые релятивисты.
- Re: Черная дыра
(А.П. Васи,
28.10.2014 12:40, 1.1 КБайт)
А опыт очень простой, берётся стеклянная бутылка,
и в ней создаётся вакуум.
Посветив сквозь эту стеклянную бутылку лазерным
лучом очень просто слово -
фотон - становится ненаучным
термином.
Летит луч в воздухе, его скорость меньше чем в вакууме,
влетает в стекло - и в стекле снижает скорость, потом
влетает во внутренний вакуум бутылки - правильно - повышает
свою скорость на максимум, потом влетает в стекло, снижает
свою скорость в стекле, вылетает из стекла
в воздух - повышает
скорость до скорости света в воздухе.
Собственно этот опыт можно проверить на аналоге,
можно взять налить воды в большой железный
бак .
И сквозь бак с водой пропускаем - правильно звуковой импульс или колебания,
и измеряем скорость звука в воздухе потом в стенке бака потом в воде,
потом опять в стенке бака потом опять в воздухе - о чудо,
всё похоже как в бутылке с вакуумом.
Это не чудо это нелогичность релятивизма не практических опытах.
Так что лично я больше сотни книг по астрономии и космологии,
пару лет назад, выбросил в мусор.
- Re: Черная дыра
(А.П. Васи,
31.10.2014 20:25, 52 Байт)
Уважаемые альты и релятивисты - всё будет нормально.
- Re: Черная дыра
(А.П. Васи,
9.11.2014 14:07, 1.9 КБайт)
-------------------------------------------------------------------------
Я аж смеялся, очень понравилось,
я бы даже
сказал что это обсуждение яркий пример того как
можно релятивистов загонять в угол по любым вопросам.
Пользуясь тем, что в космологии отсутствуют адекватные
и отсутствуют базовые определения получается что,
если ставить вопрос по составляющим физическим
сущностям из которых состоят теории то релятивисты
будут сливать воду по заданным частным вопросам и будут
постоянно
все вместе и каждый по отдельности ставить подписи
о своей некомпетентности в данном вопросе.
Я даже больше чем уверен что релятивисты не будут на конференциях
рассматривать
ситуации при которых они на этих конференциях создадут
единственно правильные с точки зрения релятивизма определения составляющих
разных теорий, по той причине что это никто не оплатит.
Если вдруг они сообразят и смогут сделать базовые определения
у них начнётся второй более трудный случай - базовые определения возможно
будут противоречить со здравым смыслом внутри теорий
= парадокс.
- Re: Черная дыра
(А.П. Васи,
9.11.2014 14:26, 1.0 КБайт)
Собственно логично что релятивисты сольют воду
на следующие вопросы.
Какое правильное определение пространства?
Базовое определение черной дыры?
Базовое
определение фотона?
Что в пространстве происходит, летят фотоны в пустоте?, или колеблется светоносная среда?
Базовый опыт и вытекающие из него определения - электрона?
Это примитивные вопросы без ответов на которые уже не возможно
даже приблизится к основному вопросу -
почему звезды светят а космос холодный?
Я собственно
даже не понимаю почему космологи не ставят перед собой
основных задач и целей в виде вопросов - на которые должны быть
направленны все так сказать интеллектуальные
ресурсы.
Строят телескопы один больше другого, и толку, и что дальше,
ещё больший телескоп строить, а потом ещё больший, а потом
ещё больший и так без
конца и края. Как по мне это странная
общестроительная астрономия, когда за строительством и наблюдениями
думать над наблюдаемым и некому и некогда.
- Re: Черная дыра
(А.П. Васи,
10.11.2014 19:32, 11.5 КБайт)
Ответ #800 : Сегодня в 15:22:38
В каком смысле?
Наверно нужно взять два источника света,на расстоянии
600 000 км.,включить их
и при встрече лучей,посмотреть,будут ли эти фотоны разделаться в разные стороны,при столкновении.
Вопрос я полностью не понял,уточните.
Не
два источника света, а два фотона, летящих "вниз" и "вверх" навстречу
друг другу по оси 0х (со смещением по оси 0y и без смещения).
имхо:
Вы сами напросились на этот вопрос, за язык никто не тянул 

Записан
Ввести квант
действия в космологию и гравитацию стоило мне немалых трудов. Некоторые
из моих знакомых усматривали в этом своего рода трагедию. Но VimanaPro
был другого мнения об этом ... Ведь теперь он точно знает, что квант
действия играет гораздо большую роль, чем был склонен считать вначале




-

- Сообщений: 306
- Рейтинг: +4/-3
- Мне нравится этот форум!
-
Ответ #801 : Сегодня в 15:36:33
Хорошо !
Если фотон взаимодействует гравитационно,то от этого он может ,вероятно,
замедлять свою скорость.
А
между фотонами - не успевает,так как пролетая ,по отношению чего-то
неподвижного,скорость будет световой,а между друг другом,скорость будет
выше.

Записан





-

- Сообщений: 2 587
- Рейтинг: +43/-3
- ЛУЧШИЙ ЛЕММИНГ ФОРУМА :)
-
Ответ #802 : Сегодня в 17:51:11
Пока таких устройств нет с гравитацией можно резвиться всякому на свой
манер,

Вот как. Ясно. Т.е. "правильного ответа"
пока нет в принципе.
А
вот ещё один интересный для мене вопрос. Энергия которая в материи, ну
там, энергия частиц всяких, и энергия хм... скажем так,
электромагнитная, это одной природы энергия или нет. Ну и естественно
вообще. Вся та энергия, которую используют в физике, кинетическая,
потенциальная, электрическая и вообще вся. Это всё суть одна и та же
энергия или как?


Записан
тчк





-

- Сообщений: 2 587
- Рейтинг: +43/-3
- ЛУЧШИЙ ЛЕММИНГ ФОРУМА :)
-
Ответ #804 : Сегодня в 20:58:32
Чота у меня щас такое чувство возникло, как будто стою на краю вселенной спиной к центру и смотрю в даль.
- Re: Черная дыра
(А.П. Васи,
10.11.2014 19:40, 715 Байт)
Ответ #804 : Сегодня в 20:58:32
\\\Чота у меня щас такое чувство возникло,
как будто стою на краю вселенной
спиной к центру и смотрю в даль.\\\
--------------------------------------------------------------------------------------------------------
Это как есть или нет, нужен или не нужен заряд у электрона,
который типа у релятивистов и есть носитель энергии, без базовых
привязок физических определений
между электрическим током
и электроном как частицей. Мне аж стыдно писать эту ботву.
- Re: Черная дыра
(А.П. Васи,
10.11.2014 19:53, 555 Байт)
Я не понимаю что думают Дмитрий Вибе и
Сергей Попов - они как профессора думают что на простые и трудные
вопросы будут в космологии думать и отвечать кухарка
Ксюша
и завхоз Евгений, потому что они свои профессорские звания по астрофизике
используют для получения благ а не для возложения на себя ответственности
в
принятии хоть каких то решений на вопрос - что вот то-то не логично,
и это например требует денег для решения, хоть и результат будет плохой
для теорий , но это
положительный результат для теоретиков.
- Re: Черная дыра
(А.П. Васи,
17.11.2014 20:03, 2.4 КБайт)
Детский сад слегка повзрослев под напрягся интеллектуально и
с горсткой интеллектуального песка в руке начали им бросаться
на свои умственные трудности.
----------------------------------------------------------------------------------------------
Ответ #1121 : 12.11.2014 [08:03:53]

Комментарий
модератора раздела Я
предупреждаю в последний раз. Тема называется "Факты, ставящие
под
сомнение теорию Большого Взрыва". Она не называется "Я не понимаю
теорию
Большого Взрыва" или "Объясните мне теорию Большого взрыва".
Сообщения,
не относящиеся к обсуждаемой теме, будут удаляться без
дополнительных
пояснений.
---------------------------------------------------------------------------------------------------------
Ещё раз намекаю что чтобы спорить о некотором
физическом свойстве, или некоторой
физической сущности, то логично сперва определиться - о чем звездеть, и определится
лучше максимально однозначно, без логических
ветвлений и обратных положительных,
обратных отрицательных связей и без условных переходов и отложенных во времени ситуаций,
я не буду объяснять что всё что я
перечислил включает в себя и спекуляции, и инфляции,
и сингулярности - ибо это и коню понятно.
Вывод - итого - если например хотите повумничать о большом
взрыве или большом
бабахе, то сперва надо открыть тему -
-
"Объясните начинающему,
юному космологу что такое - большой бабах или большой врыв?"
"После того как я прочту Ваши определения у меня возможно появятся вопросы,
- буду крайне любезен знать мнения ведущих специалистов в данном вопросе,
и
надеюсь на их ответ по теме."
-
И всё после этого завалить всю тему на нелогичных базовых определениях
сможет даже студент. Только толку от того
что задумываться на идеями
полувековой давности - лично мне даже грустно.
- Re: Черная дыра
(Albert Timashov,
19.11.2014 23:03, 826 Байт)
Черная дыра, наличие невидимого объекта массы большой плотности , характеризует его сильное гравитационное поле.Только по сопутсвующим признакамгравитации с другими объектами,
можно определить координты места его положения во Вселенной, приблизительные размеры и массу. Он не излучает и не отражает любые виды энергий, что объясняет его полную непозрачность
для прямолинейных потоков НЕЙТРИНО, носителей всех электромагнитных и других излучений. Для сведения, прямолинейные силовые потоки НЕЙТРИНО составляют силовую систему энергетической
среды - Единого силового поля Вселенной, универсального механизма формирования и взаимодействия различных видов материи и энергии - цикличных физических процессов (синтез,
распад,синтез...) в микро- и макро-мире.
- Re: Черная дыра
(А.П. Васи,
20.11.2014 19:18, 527 Байт)
Както вечером хоть кто вдруг сказал
-ого, не ого а аго, ну и что а просто так,
и никто, и ни-очём, даже без определений, без
упоминания вот тех кто придумал термины.
И в пониманья не имея что придумке была
первопричина и в итоге миксировки наблюдаем
излиянье мозговое очень срочной ерунды.
Ибо экстренно так надо непонятно для чего
мысль бредятины внести да на форум на котором
в пыль и пух всё сметено только, моск неторопливый
здесь бы понял всё давно. Только в спешке
экстренности пролетают здесь усе.
- Re: Черная дыра
(А.П. Васи,
24.11.2014 18:53, 80 Байт)
17
- Re: Черная дыра
(А.П. Васи,
25.12.2015 19:10, 2.5 КБайт)
Ответ #94 : Сегодня в 01:04:38
yisnep, вы не могли бы свое мнение озвучить: чему равна первая космическая
скорость на 1,5Rg?
Я извиняюсь, но название "фотонная сфера" Вам ни о чём не говорит?
И
я предлагаю отказаться от этой дурацкой традиции нумерации "космических
скоростей". Есть орбитальная скорость (на круговой орбите), есть
скорость убегания. Есть иерархия "гравитационного влияния"... (А в общем
случае, эта иерархия ещё может зависеть от того какую из скоростей
смотрим).
- Re: Черная дыра
(А. В. Постников,
23.02.2016 5:02, 93 Байт)
я думаю что черных дыр не существует и на это есть доказательствонаших физиков в космосе
- Re: Черная дыра
(Р. М. Ноев,
13.06.2016 22:08, 1.6 КБайт)
Когда статья начинается такими перлами, как "..., ибо в природе ничто не может двигаться со скоростью, большей скорости света ...","время течёт ...",
и т.п. смесью нахальства и шаманского словоблудия,дальнейшее всерьёзуже не воспринимается, и читается впол-глаза, что называется, "по диагонали".
Вся эта
наукообразная галиматья, пересыпанная ссылками тона СТО, то на ОТО - в зависимости от требований "текущего абзаца" ; )- и совершенно забывающая, точнее- плюющая
на то, что СТО и ОТО противоречат друг другу на ФУНДАМЕНТАЛЬНОМ УРОВНЕ(СТО ОТРИЦАЕТ наличие "абсолютной системы отсчета", ОТО же, со своим "искривлением пространства",
базируется ИМЕННО НА такой "абсолютной системе", и не считавшаяся завершенной даже самим (или самым - кому как больше нравится) знаменитым плагиатором от физики
- её автором,который, оказавшись в научном тупике, пытался лепетать что-то,что "наша неспособность выделить эфир в какой-либо инерциальной системе отсчёта, идаже СТО(т.е.
его "научный первенец"-мутант) -ещё недостаточны для того, чтобыотвергнуть эфир." И такие его пассажи немудрены - ведь его т.н. "Общая теория относительности"базирутся
именно наединой, т.е. по-сути - абсолютной, хотя и "искривленной" им, системе отсчета.
И становится грустно от того, что с развалом в стране единой системы
образования, зеленый свет в "независимой России" получили любые наукообразные бредни, выдаваемые их авторами, разумеется, за абсолютные истины.
- Re: Черная дыра
(Р. М. Ноев,
13.06.2016 22:28, 1.9 КБайт)
Дубль второй (в котором исправлены досадные очепятки)) .
Когда статья начинается такими перлами, как "..., ибо в природе ничто не может двигаться
со скоростью, большей скорости света ...","время течёт ...", и т.п. смесью нахальства и шаманского словоблудия, дальнейшее всерьёз уже не воспринимается, и
читается впол-глаза, что называется, "по-диагонали".
А вообще, вся эта наукообразная галиматья, пересыпанная ссылками то на СТО, то на ОТО - в зависимости
от требований "текущего абзаца" ; ) - и совершенно забывающая, точнее - плюющая на то, что СТО и ОТОПРОТИВОРЕЧАТ друг другу на ФУНДАМЕНТАЛЬНОМ УРОВНЕ (как известно,
СТО ОТРИЦАЕТ наличие "абсолютной системы отсчета", ОТО же, со своим "искривлением пространства", базируется ИМЕННО НА такой абсолютной системе "кривого
пространства", и не считавшаяся завершенной даже самим (или самым - кому как больше нравится !) её знаменитым автором - плагиатором от физики "всех времен и народов",
который, кстати, оказавшись в сем научном тупике, пытался лепетать, что, мол,"наша неспособность выделить эфир в какой-либо инерциальной системе отсчёта, и дажетеория
относительности(т.е. СТО - его "научный первенец"-мутант) - ещё недостаточны для того, чтобыотвергнуть эфир." И такие его пассажи немудрены - ведь его т.н.
"Общая теория относительности"базирутся именно наединой, т.е. по-сути - абсолютной, хотя и "искривленной" им, системе отсчета.
И становится грустно
от того, что с развалом в стране единой системы образования, зеленый свет в "независимой России" получили любые наукообразные бредни, подобные данной статье, выдаваемые
их авторами, разумеется, за абсолютные истины.
-------------------------------------------
Ссылки:
Общая информация - сайт и статьи Сергея Федосина и его
соавторов.
- Re: Черная дыра
(Р. М. Ноев,
17.05.2017 17:56, 449 Байт)
Более того, в продолжение темы "научной" и "черной" дЫрыыыыыы :
британские астрофизики обнаружили нейтронную звезду с массой в .... 40 Мс !
Что
это означает ?
Это означает только одно - или они абсолютно безграмотны, или теория образования "научных" "дыр" страдает большими недостатками, не
учитывающими РЕАЛЬНЫЕ физические законы, далекие от упрощенческих математических моделей.
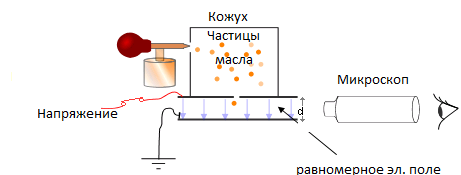
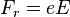 , где\\\
, где\\\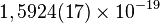
 Кл.\\\
Кл.\\\



 С моей точки зрения основная трудность в физике
- наличие в ней гениев, по причине того что кроме
гениев в физике могут быть недоумки и дифективные,
и недогении.
Грубо говоря физики делятся на два основных класса
гении и недоумки, среднего не дано.
По скольку гениев единицы - то все воспитываются в стиле
недоумков, в принципе не способных своими словами ответить
на вопросы по физике, по скольку свои мысли считают
мыслями недоумков, и советуют почитать книжки
гениев с их точки зрения. При общении физиков то и происходит
взаимопосылание читать книжки.
Вот такая жестокая селяви.
С моей точки зрения основная трудность в физике
- наличие в ней гениев, по причине того что кроме
гениев в физике могут быть недоумки и дифективные,
и недогении.
Грубо говоря физики делятся на два основных класса
гении и недоумки, среднего не дано.
По скольку гениев единицы - то все воспитываются в стиле
недоумков, в принципе не способных своими словами ответить
на вопросы по физике, по скольку свои мысли считают
мыслями недоумков, и советуют почитать книжки
гениев с их точки зрения. При общении физиков то и происходит
взаимопосылание читать книжки.
Вот такая жестокая селяви.

 Посмотрел фильм понравился, как-бы
Посмотрел фильм понравился, как-бы 



 , Н
, Н ,
,
 , Hel. Кружками отмечены
линии, образующиеся
, Hel. Кружками отмечены
линии, образующиеся 












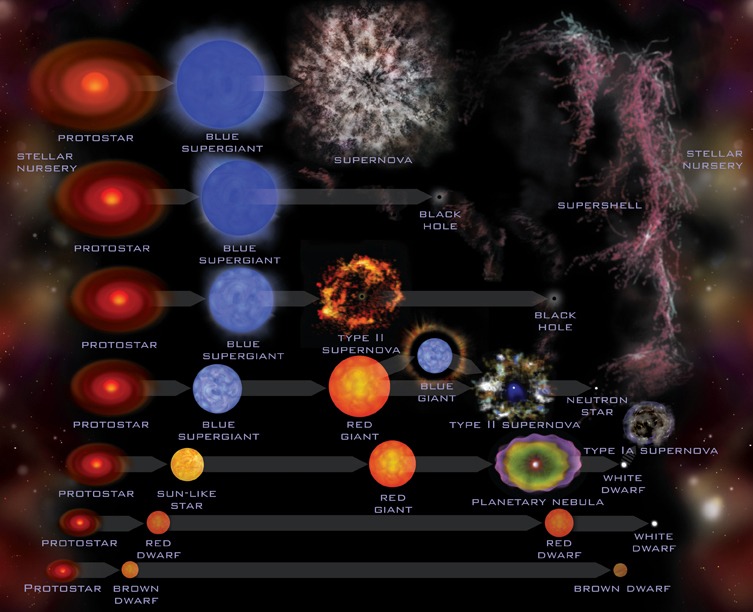

 Можно и в телескоп.
Можно и в телескоп. 


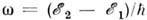 , где
, где 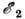 и
и  -
энергии верхнего возбуждённого и нижнего (обычно основного) уровней
энергии атома. Р. н. впервые обнаружено в 1904 Р. Вудом (R. Wood) в
парах натрия.
-
энергии верхнего возбуждённого и нижнего (обычно основного) уровней
энергии атома. Р. н. впервые обнаружено в 1904 Р. Вудом (R. Wood) в
парах натрия.
 Комментарий
модератора раздела
Комментарий
модератора раздела 







 На
расстоянии сигналы затухают. Эта истина справедлива и для
электрических, и для оптических коммуникационных линий. Разумеется, в
случае оптических сетей расстояния, на которых это начинает проявляться,
больше, однако проблемы по-прежнему существуют.
На
расстоянии сигналы затухают. Эта истина справедлива и для
электрических, и для оптических коммуникационных линий. Разумеется, в
случае оптических сетей расстояния, на которых это начинает проявляться,
больше, однако проблемы по-прежнему существуют.




































































































 Кандидаты в гравитационные линзы имеют неоценимое
значение для оценки массы галактик квазаров.
Кандидаты в гравитационные линзы имеют неоценимое
значение для оценки массы галактик квазаров.  Go to image download page
Go to image download page





 Голосование
Голосование

 Записан
Записан

 , обратитесь к Чандрасекару!
, обратитесь к Чандрасекару!










 или триплетными
или триплетными  . Типичное
. Типичное


 . При поглощении света молекула переходит в возбужденное состояние
. При поглощении света молекула переходит в возбужденное состояние  .
При возбуждении на высшие электронные и колебательные уровни избыток
энергии быстро расходуется, переводя флуорофор на самый нижний
колебательный подуровень состояния
.
При возбуждении на высшие электронные и колебательные уровни избыток
энергии быстро расходуется, переводя флуорофор на самый нижний
колебательный подуровень состояния  состояния.
состояния.
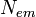 количество испускаемых в результате флуоресценции
фотонов, а
количество испускаемых в результате флуоресценции
фотонов, а 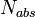 общее количество поглощаемых фотонов. Чем
больше квантовый выход
общее количество поглощаемых фотонов. Чем
больше квантовый выход 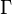 и
и 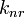 константы скорости излучательной и безызлучательной дезактивации возбужденного состояния.
константы скорости излучательной и безызлучательной дезактивации возбужденного состояния.
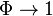 если
если
 ,
то есть если скорость безызлучательного перехода значительно меньше
скорости излучательного перехода. Отметим, что квантовый выход всегда
меньше единицы из-за
,
то есть если скорость безызлучательного перехода значительно меньше
скорости излучательного перехода. Отметим, что квантовый выход всегда
меньше единицы из-за 









 .
.
















 \\\
\\\

 точку зрения науки
точку зрения науки 













 До последнего времени ученые-физики со всего мира относились весьма скептически к
До последнего времени ученые-физики со всего мира относились весьма скептически к 






