Астронет > Форумы > Обсуждение публикаций Астронета

по текстам по форуму внутри темы

Бернулли уравнение
6.08.2001 0:00 | "Физическая Энциклопедия"/Phys.Web.Ru

Бернулли уравнение (интеграл Бернулли) в гидроаэромеханике - результат интегрирования дифференциальных уравнений установившегося движения идеальной (невязкой и нетеплопроводной) баротропной жидкости, записанных в переменных Эйлера. В баротропной жидкости плотность

[Цитировать][Ответить][Новое сообщение]

Форумы >> Обсуждение публикаций Астронета

Список / Дерево
Заголовки / Аннотации / Текст

>> Бернулли уравнение ( "Физическая Энциклопедия"/Phys.Web.Ru, 6.08.2001 0:00, 8.7 КБайт, ответов: 1)
Бернулли уравнение (интеграл Бернулли) в гидроаэромеханике - результат интегрирования дифференциальных уравнений установившегося движения идеальной (невязкой и нетеплопроводной) баротропной жидкости, записанных в переменных Эйлера. В баротропной жидкости плотность $\rho$ зависит только от давления р, то есть $p=p(\rho)$ , и уравнение Бернулли имеет вид
$$U+\int\frac{dp}{\rho}+\frac{v^2}{2}=C$,$ (1)

где U - потенциал поля объемных (массовых) сил, действующих на жидкость, v - скорость течения, C - величина, постоянная на каждой линии тока или вихревой линии, но в общем случае изменяющая свое значение при переходе от одной линии к другой.
Если потенциал U и вид функции $p(\rho)$ известны, уравнение Бернулли выражается алгебраическим соотношением. В простейшем случае несжимаемой тяжелой жидкости, когда U=gh (h - высота жидкой частицы над некоторой горизонтальной плоскостью, g - ускорение свободного падения), a $\rho=const$ , имеем
$$gh+\frac{p}{\rho}+\frac{v^2}{2}=C$,$ (2)

Для этого случая уравнение было выведено Д. Бернулли (D. Bernoulli) в 1738.
Умножив уравнение (2) на $\rho=const$ , получим, что сумма первых двух членов равна потенциальной энергии жидкости, а 3-й член $\rho v^2/2$ называется скоростным напором или динамическим давлением и равен кинетической энергии движущейся жидкости. Таким образом, уравнение Бернулли в виде (2) выражает закон сохранения энергии и устанавливает связь между давлением и скоростью движущейся жидкости: если вдоль линии тока скорость увеличивается, давление падает, и наоборот. Когда в некоторых точках потока жидкости давление вследствие роста скорости должно стать ниже некоторой малой положительной величины, близкой к давлению насыщенного пара этой жидкости, возникает кавитация.
В случае обратимых адиабатных течений совершенного газа с отношением удельных теплоемкостей $C_p/C_V=\gamma$ имеем $p/\rho^\gamma=const$ и из уравнения (1), пренебрегая влиянием силы тяжести, получим:
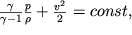
$$\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{v^2}{2}=const$,$ (3)

или, в силу термодинамического соотношения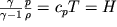 $\frac{\gamma}{\gamma-1}\frac{p}{\rho}=c_pT=H$ , где T - абсолютная температура, H-энтальпия,
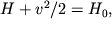
$$H+v^2/2=H_0$,$ (4)

Уравнение Бернулли для газов в форме (3) и (4) определяет параметры изоэнтропийного торможения: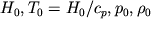 $H_0, T_0=H_0/c_p, p_0, \rho_0$ на каждой линии тока, которых газ достигает при v = 0. Они называются соответственно полной энтальпией, температурой торможения, полным давлением или давлением торможения и плотностью торможения. Уравнение Бернулли в форме (4) также выражает закон сохранения энергии для газов. Уравнение Бернулли используют при измерении скорости с помощью трубок измерительных и при других аэрогидродинамических измерениях.
В технических приложениях для осредненных по поперечному сечению параметров потока применяют так называемое обобщенное уравнение Бернулли: сохраняя форму уравнений (2)-(4), в левую часть включают работу сил трения (гидравлические потери) и механическую работу (работу компрессора или турбины) с соответствующим знаком. Обобщенным уравнением Бернулли пользуются в гидравлике при расчете течений жидкостей и газов и трубопроводах и в машиностроении при расчете компрессоров, турбин, насосов и других гидравлических и газовых машин.

Re: Бернулли уравнение (Ю. П. Карась, 4.06.2009 14:50, 2.4 КБайт) Уравнение Бернулли это и есть закон сохранения энергии для случая когда рассматриваемый объем жидкости равен единице. Три слагаемых энергий представленных в этой формуле можно получить по отдельности выполняя над рассматриваемой жидкостью последовательно три работы. Первая работа внешней силой по перемещению жидкости из неподвижного состояния в состояние движения с задаваемой скоростью. Причем эта работа при равноускоренном движении равна произведению силы F=m*a на перемещение s. Формула перемещения смотри в учебнике по физике школьном.Отсюда энергия приобретенная жидкостью равна произведению квадрату скорости на массу деленную на два. Когда жидкость будет двигаться с задаваемой скоростью, действие внешней силы прекращается, иначе при ненулевом ускорении скорость будет дальше изменяться. Аналогично вторая работа внешней силы по поднятию жидкости на высоту h будет равна произведению силы F=m*g на перемещение s=h. Аналогично и третья работа внешней силы по преобразованию жидкости с несжатого состояния в сжатое (с задаваемым к концу воздействия давлением в жидкости равным р=сила упругости в жидкости/площадь сечения потока), равна интегралу произведению внешней силы на перемещение~линейную деформацию (Интегрирование производят по перемещению). А так как жидкость обладает упругими свойствами и способностью сжиматься, то ее можно характеризовать как упруго деформируемое тело. В теории упруго деформируемого тела эта работа выполненная внешней силой (а значит и приобретаемая жидкостью энергия), равна произведению силы упругости в жидкости на линейную деформацию деленную на два. Перейдя к давлению и объемной деформации эта работа будет равна произведению давления в жидкости на объемную деформацию деленную на два. Объемная деформация это разность значений объемов жидкости до и после воздействия внешней силой. У Вас же в статье это произведение давления на сам объем жидкости, что является грубейшей ошибкой всех основ физики с точки зрения понятия работы (произведение силы на перемещение). Таким образом имеем 270 лет старую ошибку зафиксированную на сегодня во всех соответствующих изданиях планеты Земля, в интернете и которую надо исправить , чтобы не вводить подрастающее поколение в заблуждение. Надеюсь , что Вы находитесь не на том уровне знаний , что начнете разговор о несжимаемости жидкости( тогда и энергии сжатия будет ноль). Мой e-mail: karas@optima.com.ua