|
Peremennye Zvezdy (Variable Stars) 44, No. 11, 2024 Received 25 November; accepted 2 December. |
Article in PDF |
|
DOI: 10.24412/2221-0474-2024-44-131-138
|
The Apsidal Motion in the Eclipsing Binary V1437 Cas
V. S. Kozyreva1, A. I. Bogomazov1, F. B. Khamrakulov2,3
- Lomonosov Moscow State University, Sternberg Astronomical
Institute, 119234, Universitetskij prospect, 13, Moscow, Russia
- Ulugh Beg Astronomical Institute of the Academy of
Sciences of the Republic of Uzbekistan, 100052, Astronomicheskaya
str., 33, Tashkent, Uzbekistan
- Samarkand State University, 140104, University blv., 15, Samarkand, Uzbekistan
|
We estimated the apsidal motion rate in the eclipsing
binary system V1437 Cas using TESS light curves as
|
1. Introduction
The eclipsing binary V1437 Cas (TIC 314039042, NSV 14400) was
found by Nielsen (1936) on photographic plates. Its
characteristics were not specified. Later observations made it
possible to determine the variability type for this system and to
derive its orbital period
![]() (Kazarovets
2021). After that, the star was included into the General
Catalogue of Variable Stars as V1437 Cas (Kazarovets et al. 2023).
(Kazarovets
2021). After that, the star was included into the General
Catalogue of Variable Stars as V1437 Cas (Kazarovets et al. 2023).
In 2015-2018, the ZTF project (Bellm et al. 2019) obtained
observations1of V1437 Cas. These ZTF data are not well suited to find times of
minima from individual light curves, all of them being in the form
of separated pieces of light curves with gaps of ![]() day.
The photometric uncertainty is about
day.
The photometric uncertainty is about
![]() ; such data cannot
be used to determine the change of the position of the secondary
minimum, with respect to the primary minimum, with time.
; such data cannot
be used to determine the change of the position of the secondary
minimum, with respect to the primary minimum, with time.
The data obtained by the TESS satellite2 are
suitable in order to derive the apsidal motion rate of the object
under our study. The satellite
observed it3in 2019, 2020, 2022 and 2024, the precision of different sets of
observations differs significantly. The average error in 2019 and
2020 was ![]() mag, in 2022 it was
mag, in 2022 it was ![]() mag, in 2024 it was
mag, in 2024 it was
![]() mag.
mag.
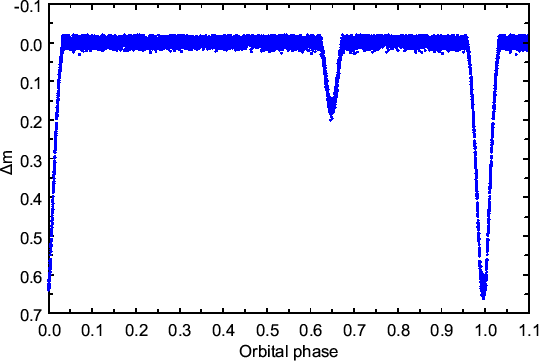
The star is a semi-detached binary with a flat plateau between
minima. This can be seen in Fig. 1 that shows a TESS light curve
of the system in 2019, minima I and II. Along the horizontal axis,
we plot phases calculated using Eq. 1; the phase of the secondary
minimum (Min II) with respect to the phase of primary minimum (Min
I) is ![]() . Along the vertical axis, we show the brightness of
the star normalized to that outside minima.
. Along the vertical axis, we show the brightness of
the star normalized to that outside minima.
To find parameters of the system, we used a program based on the model of spherical stars with a linear limb darkening (Khaliullina & Khaliullin 1984). The program calculates radii of stars, their luminosities (including a third light), eccentricity, periastron longitude and inclination of the orbit. As a parameter, the program also is able to compute the time of primary minimum and coefficients of limb darkening (Kozyreva & Zakharov 2006). A free search of limb darkening coefficients was used to calculate the coefficient for the primary star for observations in 2019 and 2020. Observations in 2022 and 2024 have, respectively, twice and three times larger uncertainties, therefore we did not calculate the coefficient in the 2022 and 2024 solutions but used a fixed value.
The secondary minimum is too small, therefore the precision of observations was not sufficient to reliably find the limb darkening coefficient of the secondary star. We used a theoretical value of limb darkening coefficient for the secondary star (van Hamme 1993) according to the assumed temperature of the star and to the spectral band of TESS observations. To find the temperature of the secondary star, we used the dependence between the temperature and surface brightness of the star.
The catalogue by Pickles (1998) contains the following parameters
for the object under study: the spectral type is A5V and the
effective temperature is
![]() K. Later
catalogues, such as the TESS input catalogue (Stassun et al.
2019), ATLAS-REFCAT2 (Tonry et al. 2018) and Gaia DR2 (Bai et al.
2019), give different values of
K. Later
catalogues, such as the TESS input catalogue (Stassun et al.
2019), ATLAS-REFCAT2 (Tonry et al. 2018) and Gaia DR2 (Bai et al.
2019), give different values of
![]() for the primary
component of V1437 Cas: respectively,
for the primary
component of V1437 Cas: respectively,
![]() K,
K,
![]() K,
K,
![]() K.
K.
| Parameter | "2019" | "2020" | "2022" | "2024" |
| 0.1251 |
0.1247 |
0.1226 |
0.1231 |
|
| 0.0855 |
0.0858 |
0.0849 |
0.0868 |
|
| 88.4 |
88.5 |
88.8 |
89.6 |
|
| 0.2932 |
0.2943 |
0.2970 |
0.2898 |
|
| 323.65 |
323.47 |
323.33 |
326.10 |
|
| 0.857 |
0.855 |
0.857 |
0.835 |
|
| 0.139 |
0.144 |
0.143 |
0.143 |
|
| 0.004 |
0.001 |
0.000 |
0.02 |
|
| 0.36 |
0.38 |
0.37 (fixed) | 0.37 (fixed) | |
| 0.47 (fixed) | 0.47(fixed) | 0.47(fixed) | 0.47(fixed) | |
| 2.88 |
2.84 |
2.87 |
2.90 |
|
| 0.005 | 0.005 | 0.011 | 0.014 |
The value of the limb darkening coefficient in our solution
(primary star, Table 1) is close to the theoretical one (van
Hamme 1993) for a star with
![]() K and with the
star's temperature in the catalogue by Pickles (1998). If this
temperature is assumed to be the temperature of the primary star,
then the temperature of the secondary star can be found using the
Stephan-Boltzmann law and the ratio of surface brightnesses of
the two stars (Table 1):
K and with the
star's temperature in the catalogue by Pickles (1998). If this
temperature is assumed to be the temperature of the primary star,
then the temperature of the secondary star can be found using the
Stephan-Boltzmann law and the ratio of surface brightnesses of
the two stars (Table 1):
| (1) |
The temperature of the secondary from Eq. 1 is 5880 K. The
theoretical limb darkening coefficient for such a temperature is
0.47 (van Hamme 1993); in our solution, we use this value for the
secondary star. Table 1 shows solutions for system's elements that
have been found in a free search for all parameters except limb
darkening coefficients. These solutions correspond to light curves
obtained in 2019, 2020, 2022, and 2024. The parameters are very
similar in all these solutions. In Table 1, ![]() is the inclination
of the orbit;
is the inclination
of the orbit; ![]() is the eccentricity of the orbit;
is the eccentricity of the orbit; ![]() is
the ascending node longitude;
is
the ascending node longitude; ![]() are the limb darkening
coefficients, respectively for the primary and the secondary;
are the limb darkening
coefficients, respectively for the primary and the secondary;
![]() is the standard deviation;
is the standard deviation; ![]() are the
luminosities, respectively of the primary, secondary, and third
light in units of the total luminosity of the system;
are the
luminosities, respectively of the primary, secondary, and third
light in units of the total luminosity of the system; ![]() are the radii of the primary and secondary in units of the
semi-major axis of the system.
are the radii of the primary and secondary in units of the
semi-major axis of the system.
| Parameter | "2019" | "2020" | "2022" | "2024" | ZTF |
| 323.65 |
323.81 |
324.56 |
324.83 |
323.15 |
|
| JD 2458776.01 | 2458970.66 | 2459867.60 | 2460404.71 | 2457816.02 |
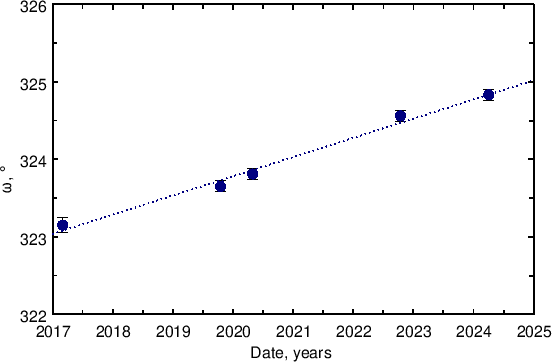 |
Fig. 2. The periastron longitude versus time. The first (2017) data point corresponds to results derived from ZTF light curves, the other data points are results derived from TESS light curves. See Table 2. |
For subsequent calculations, we assumed that radii and
luminosities of the stars and the orbital inclination had not
changed during TESS observations. This supposition made it
possible to find the periastron longitude for different epochs and
to determine the apsidal motion rate from these calculations.
Table 2 shows the periastron longitude computed with all other
parameters fixed (using the solution for the 2019 light curve,
Table 1). In Table 2, ![]() is the average epoch of the values of
is the average epoch of the values of
![]() in corresponding sets of observations.
in corresponding sets of observations.
Figure 2 shows the dependence of the periastron longitude on time for solutions that correspond to TESS light curves in 2019, 2020, 2022, 2024 (Table 2) and to the ZTF observations. The linear dependence can be seen, the least square method gives the solution with 10% uncertainty:
| (3) |
| Min I | (O-C) |
(O-C) |
Min II | (O-C) |
(O-C) |
| BJD | days | days | BJD | days | days |
| 2458768.0013 | -0.0007 | 0.0001 | 2458770.1787 | 0.0008 | 0.0001 |
| 2458771.3446 | -0.0011 | -0.0003 | 2458773.5213 | -0.0002 | -0.0010 |
| 2458774.6886 | -0.0008 | 0.0000 | 2458780.2101 | 0.0012 | 0.0004 |
| 2458778.0313 | -0.0017 | -0.0009 | 2458783.5526 | -0.0017 | -0.0009 |
| 2458781.3761 | -0.0006 | 0.0002 | 2458786.8972 | 0.0009 | 0.0001 |
| 2458784.7195 | -0.0009 | -0.0001 | 2458960.7704 | 0.0015 | 0.0003 |
| 2458788.0636 | -0.0005 | 0.0003 | 2458964.1141 | 0.0015 | 0.0003 |
| 2458958.5920 | -0.0010 | 0.0002 | 2458967.4577 | 0.0014 | 0.0002 |
| 2458961.9357 | -0.0010 | 0.0002 | 2458970.8020 | 0.0020 | 0.0008 |
| 2458965.2793 | -0.0011 | 0.0001 | 2458974.1450 | 0.0013 | 0.0001 |
| 2458971.9666 | -0.0012 | 0.0000 | 2458977.4889 | 0.0014 | 0.0002 |
| 2458975.3103 | -0.0012 | 0.0000 | 2458980.8319 | 0.0007 | -0.0005 |
| 2458978.6542 | -0.0010 | 0.0002 | 2459853.5410 | 0.0033 | 0.0002 |
| 2458981.9973 | -0.0016 | -0.0004 | 2459856.8840 | 0.0026 | -0.0005 |
| 2459854.7025 | -0.0030 | 0.0001 | 2459860.2288 | 0.0037 | 0.0006 |
| 2459858.0460 | -0.0032 | -0.0001 | 2459866.9155 | 0.0030 | -0.0001 |
| 2459861.3891 | -0.0038 | -0.0007 | 2459870.2591 | 0.0029 | -0.0002 |
| 2459868.0775 | -0.0028 | 0.0004 | 2459873.6034 | 0.0035 | 0.0004 |
| 2459871.4208 | -0.0032 | 0.0000 | 2459876.9462 | 0.0026 | -0.0005 |
| 2459878.1082 | -0.0032 | -0.0001 | 2459880.2902 | 0.0029 | -0.0002 |
| 2459881.4520 | -0.0032 | 0.0000 | 2460398.5656 | 0.00432 | 0.00012 |
| 2460396.3815 | -0.0039 | 0.0004 | 2460401.9103 | 0.00528 | 0.00108 |
| 2460399.7255 | -0.0036 | 0.0007 | 2460405.2525 | 0.00383 | -0.00038 |
| 2460403.0691 | -0.0037 | 0.0006 | 2460418.6288 | 0.00528 | 0.00104 |
| 2460406.4131 | -0.0034 | 0.0009 | 2460421.9726 | 0.00538 | 0.00113 |
| 2460419.7878 | -0.0035 | 0.0008 | |||
| 2460423.1318 | -0.0032 | 0.0011 |
Times of minima derived from TESS observations are collected in
Table 3. The time of the primary minimum is one of the parameters
that can be found in free search in a light curve solution along
with other parameters. The time of the secondary minimum is
obtained in the mode of search for only this parameter with the
remaining parameters fixed at the values derived for the free
search option. The differences between observed (O) and calculated
(C) times for primary (I, (O-C)![]() ) and secondary (II,
(O-C)
) and secondary (II,
(O-C)![]() ) minima (Table 3) were calculated using the
ephemerides:
) minima (Table 3) were calculated using the
ephemerides:
| (4) |
| (5) |
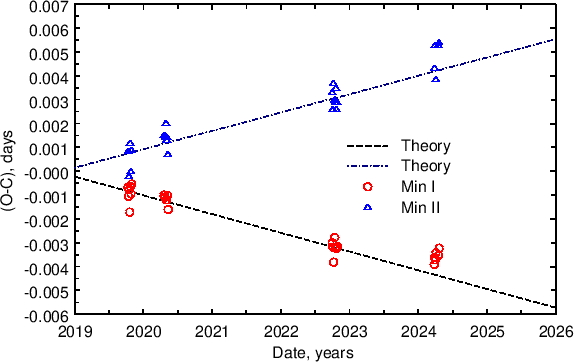
The displacement of (O-C) deviations of the primary and secondary minima with respect to each other (Fig. 3) usually can be explained with apsidal motion. Due to this motion, periods of primary and secondary minima are different. A short time interval of observations in comparison with the period of apsidal motion and a lucky orientation of the periastron with respect to the observer make it possible to describe (O-C) with a linear formula. New ephemerides calculated using the least square method are as follows:
| (6) |
| (7) |
The difference between the periods for secondary and primary
minima is
![]() s. The equation by Rudkjøbing
(1959) relates the difference between periods of primary and
secondary mimina to the apsidal motion rate:
s. The equation by Rudkjøbing
(1959) relates the difference between periods of primary and
secondary mimina to the apsidal motion rate:
| (8) |
For the difference between periods for primary and secondary
minima ![]() s, the corresponding apsidal motion rate is:
s, the corresponding apsidal motion rate is:
This rate is in a satisfactory agreement with that calculated above (Eq. 2).
To compare theoretical and observational values of the apsidal
motion rate, it is necessary to know parameters of the stars. The
most important parameters are masses and temperatures of the
components. If the temperature of the primary is assumed to be
8500 K, then (taking into account the ratio of surface
brightnesses of the stars), the temperature of the secondary,
according to the Stephan-Boltzmann law, should be 5880 K (see
above). Masses of main sequence stars with such temperatures
should be ![]() and
and ![]() , respectively (see
Fig. 9 in Eker et al. 2018). Using these input parameters, we
estimated theoretical values of the stellar internal structure
coefficients
, respectively (see
Fig. 9 in Eker et al. 2018). Using these input parameters, we
estimated theoretical values of the stellar internal structure
coefficients ![]() (Sterne, 1939) from tables by Claret & Gimenez
(1989). The apsidal motion rate obtained from theory and from
observations is the same inside its uncertainty interval, the
values of
(Sterne, 1939) from tables by Claret & Gimenez
(1989). The apsidal motion rate obtained from theory and from
observations is the same inside its uncertainty interval, the
values of ![]() are as follows:
are as follows:
![]() ,
,
![]() . These quantities can be obtained for the effective
temperature of the primary star 8500 K; for another temperature,
the result can be different.
. These quantities can be obtained for the effective
temperature of the primary star 8500 K; for another temperature,
the result can be different.
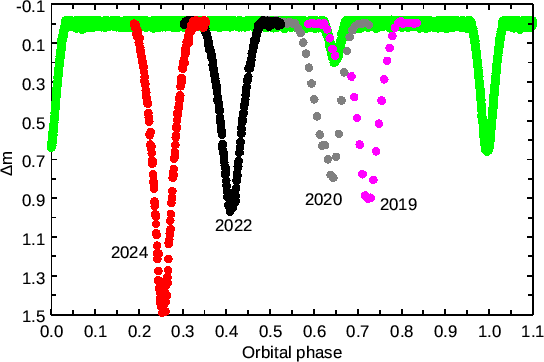
The system has an interesting peculiarity in its TESS light
curves. In each set of TESS observations (2019, 2020, 2022, 2024),
there is one extremely deep minimum at different phases. Such
extreme minima are deeper than the primary minimum by more than
0![]() 25, and their widths are also larger by a factor of
25, and their widths are also larger by a factor of ![]() (see Table 4 and Fig, 4). The orbital phases of the binary
are plotted along the abscissa of Fig. 4. The shape of extremely
deep minima in 2019, 2022, and 2024 is almost symmetric. The shape
of minimum in 2020 is non-symmetric, its position in the light
curve coincides with the secondary minimum of the system. Times of
minima in 2019, 2022, and 2024 supposedly have a period
(see Table 4 and Fig, 4). The orbital phases of the binary
are plotted along the abscissa of Fig. 4. The shape of extremely
deep minima in 2019, 2022, and 2024 is almost symmetric. The shape
of minimum in 2020 is non-symmetric, its position in the light
curve coincides with the secondary minimum of the system. Times of
minima in 2019, 2022, and 2024 supposedly have a period
![]() . With this period, the deep minimum of
2020 should happen 8 hours later than it was observed. Probably,
both stars can be eclipsed by a dark body (e.g., a comet, a disk
around a planet/brown dwarf). Alternatively, these minima can
arise from TESS hardware noise. At least, earlier we did not see
anything similar in other light curves of other eclipsing binary
stars (including TESS light curves, e.g., the light curves of
FL Lyr, Kozyreva et al. 2023).
. With this period, the deep minimum of
2020 should happen 8 hours later than it was observed. Probably,
both stars can be eclipsed by a dark body (e.g., a comet, a disk
around a planet/brown dwarf). Alternatively, these minima can
arise from TESS hardware noise. At least, earlier we did not see
anything similar in other light curves of other eclipsing binary
stars (including TESS light curves, e.g., the light curves of
FL Lyr, Kozyreva et al. 2023).
Acknowledgments
This research has made use of the SIMBAD database (operated at CDS, Strasbourg, France) and of NASA's Astrophysics Data System. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST).
References:
Bai, Y., Liu, J., Bai, Z. et al. 2019, Astron. J., 158, No. 2, id. 93
Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, Publ. Astron. Soc. Pacific, 131, 018002
Claret, A. & Gimenez, A., 1989, Astron. & Astrophys., Suppl. Ser., 81, No. 1, 37
Eker, Z., Bakis, V., Bilir, S., et al. 2018, Monthly Notices Roy. Astron. Soc., 479, 5491
Kazarovets, E. V., 2021, Perem. Zvezdy Prilozh. / Var. Stars Suppl., 21, No. 2
Kazarovets, E. V., Samus, N. N., Durlevich, O. V., et al. 2023, Perem. Zvezdy / Var. Stars, 43, No. 9, 101
Khaliullina, A. I. & Khaliullin, K. F. 1984, Soviet Astron., 28, No. 2, 228
Kozyreva, V. S., Bogomazov, A. I., Demkov, B. P. et al. 2023, Astron. Rep., 67, No. 5, 483
Kozyreva, V. S. & Zakharov, A. I. 2006, Astron. Lett., 32, No. 5, 313
Nielsen, A. V. 1936, Astron. Nachr., 261, 7
Pickles, A. J. 1998, Publ. Astron. Soc. Pacific, 110, 863
Rudkjøbing, M. 1959, Ann. d'Astrophys., 22, No. 2, 111
Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, Astron. J., 158, No. 4, id. 138
Sterne, T. E. 1939, Monthly Notices Roy. Astron. Soc., 99, 662
Tonry, J. L., Denneau, L., Flewelling, H., et al. 2018, Astrophys. J., 867, No. 2, id. 105
van Hamme, W. 1993, Astron. J., 106, No. 5, 2096