 |
Астронет: В.Ю. Протасов Геометрия звездного неба http://www.astronet.ru/db/msg/1249137 |

Геометрия звёздного неба
В.Ю. Протасов
Московский Государственный Университет, Механико-математический факультет, Воробьевы Горы, Москва, 119992, e-mail: v-protassov@yandex.ru
Небо над головой - самый древний учебник геометрии. Первые
понятия, такие как точка и круг - оттуда. Скорее даже не учебник,
а задачник. В котором отсутствует страничка с ответами. Два круга
одинакового размера - Солнце и Луна, движутся по небу, каждый со
своей скоростью. Остальные объекты - светящиеся точки, движутся
все вместе, словно они прикреплены к сфере, вращающейся со
скоростью 1 оборот в 24 часа. Правда, среди них есть исключения -
5 точек движутся как им вздумается. Для них подобрали особое слово
- "планета", по-гречески - "бродяга". Сколько человечество
существует, оно пытается разгадать законы этого вечного движения.
Первый прорыв произошел в 3 веке до н.э., когда греческие ученые,
взяв на вооружение молодую науку - геометрию, смогли получить
первые результаты об устройстве Вселенной. Об этом и пойдет речь.
Чтобы иметь некоторое представление о сложности задачи, рассмотрим
такой пример. Представим себе светящийся шар диаметром 10 см.,
неподвижно висящий в пространстве. Назовём его ![]() . Вокруг него на
расстоянии чуть больше 10 метров обращатся маленький шарик
. Вокруг него на
расстоянии чуть больше 10 метров обращатся маленький шарик ![]() диаметром 1 миллиметр, а вокруг
диаметром 1 миллиметр, а вокруг ![]() на расстоянии
на расстоянии ![]() см.
обращается совсем крохотный шарик
см.
обращается совсем крохотный шарик ![]() , его диаметр - четверть
миллиметра. На поверхности среднего шарика
, его диаметр - четверть
миллиметра. На поверхности среднего шарика ![]() живут
микроскопичекие существа. Они обладают неким разумом, но покидать
пределы своего шарика не могут. Все что они могут - смотреть на
два других шара -
живут
микроскопичекие существа. Они обладают неким разумом, но покидать
пределы своего шарика не могут. Все что они могут - смотреть на
два других шара - ![]() и
и ![]() . Спрашивается, могут ли они узнать
диаметры этих шаров, и измерить расстояния до них ? Сколько ни
думай, дело, казалось бы, безнадёжное. Мы нарисовали сильно
уменьшенную модель Солнечной системы (
. Спрашивается, могут ли они узнать
диаметры этих шаров, и измерить расстояния до них ? Сколько ни
думай, дело, казалось бы, безнадёжное. Мы нарисовали сильно
уменьшенную модель Солнечной системы (![]() - Солнце,
- Солнце, ![]() - Земля,
- Земля,
![]() - Луна). Вот такая задача стояла перед древними астрономами.
И они её решили ! Более 22 веков назад, не пользуясь ничем, кроме
с самой элементарной геометрии, на уровне 8 класса (свойства
прямой и окружности, подобные треугольники и теорема Пифагора). И,
конечно, наблюдая за Луной и за Солнцем. Над решением трудились
несколько учёных. Мы выделим двух. Это математик Эратосфен,
измеривший радиус земного шара, и астроном Аристарх, вычисливший
размеры Луны, Солнца и расстояния до них. Как они это сделали ?
- Луна). Вот такая задача стояла перед древними астрономами.
И они её решили ! Более 22 веков назад, не пользуясь ничем, кроме
с самой элементарной геометрии, на уровне 8 класса (свойства
прямой и окружности, подобные треугольники и теорема Пифагора). И,
конечно, наблюдая за Луной и за Солнцем. Над решением трудились
несколько учёных. Мы выделим двух. Это математик Эратосфен,
измеривший радиус земного шара, и астроном Аристарх, вычисливший
размеры Луны, Солнца и расстояния до них. Как они это сделали ?
 Е.Н.Конева, М.В.Перепухов. Через терниии к звездам |
 Рис. 1. |
Для современников Эратосфен был знаменит как крупнейший
учёный-энциклопедист, занимавшийся не только математикой, но и
географией, картографией и астрономией. Он долгое время возглавлял
Александрийскую библиотеку - центр мировой науки того времени.
Работая над составлением первого атласа Земли (речь, конечно, шла
об известной к тому времени её части), он задумал провести точное
измерение земного шара. Идея была такова. В Александрии все
знали, что на юге, в городе Сиена (современный Асуан) один день в
году, в полдень, Солнце достигает зенита. Исчезает тень от
вертикального шеста, на несколько минут освещается дно колодца.
Происходит это в день летнего солнцестояния, 22 июня - день
наивысшего положения Солнца на небе. Эратосфен направляет своих
помощников2
в Сиену, и те устанавливают, что ровно в полдень (по солнечным часам)
Солнце находится точно в зените. Одновременно (как написано в
первоисточнике: "в тот же час"), т.е., в полдень по солнечным
часам, Эратосфен измеряет длину тени от вертикального шеста в
Александрии. Получился треугольник ![]() (
(![]() - шест,
- шест, ![]() -
тень, рис.2).
-
тень, рис.2).
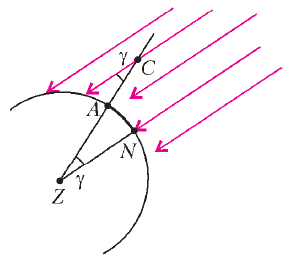 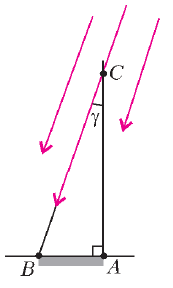 Рис. 2. |
Итак, солнечный луч в Сиене перпендикулярен
поверхности Земли, а значит проходит через её центр - точку ![]() .
Параллельный ему луч в Александрии составляет угол
.
Параллельный ему луч в Александрии составляет угол
![]() с вертикалью. Пользуясь равенством накрестлежащих
углов при параллельных, заключаем, что
с вертикалью. Пользуясь равенством накрестлежащих
углов при параллельных, заключаем, что
![]() . Если обозначить через через
. Если обозначить через через ![]() длину окружности, а
через
длину окружности, а
через ![]() длину её дуги
длину её дуги ![]() , то получаем пропорцию
, то получаем пропорцию
![]() . Угол
. Угол ![]() в
треугольнике
в
треугольнике ![]() Эратосфен измерил, получилось
Эратосфен измерил, получилось ![]() .
Величина
.
Величина ![]() - не что иное, как длина пути от Александрии до
Сиены, примерно
- не что иное, как длина пути от Александрии до
Сиены, примерно ![]() км. Её Эратосфен аккуратно вычисляет, исходя
из среднего времени движения верблюжьих караванов, регулярно
ходивших между двумя городами, а также, используя данные
бематистов - людей специальной профессии, измерявших расстояния
шагами. Теперь осталось решить пропорцию
км. Её Эратосфен аккуратно вычисляет, исходя
из среднего времени движения верблюжьих караванов, регулярно
ходивших между двумя городами, а также, используя данные
бематистов - людей специальной профессии, измерявших расстояния
шагами. Теперь осталось решить пропорцию
![]() , получив длину окружности (т.е., длину
земного мередиана)
, получив длину окружности (т.е., длину
земного мередиана)
![]() км. Тогда радиус Земли
км. Тогда радиус Земли ![]() равен
равен
![]() , это примерно
, это примерно ![]() км. То, что длина земного мередиана
выражается столь круглым числом в
км. То, что длина земного мередиана
выражается столь круглым числом в ![]() км., не удивительно,
если вспомнить, что единица длины в 1 метр и была введена (во
Франции в конце 18 века), как одна сорокамиллионная часть
окружности Земли (по определению !). Эратосфен, конечно,
использовал другую единицу измерения - стадий (около 200
м). Стадиев было несколько: египетский, греческий, вавилонский, и
каким из них пользовался Эратосфен - неизвестно. Поэтому трудно
судить наверняка о точности его измерения. Кроме того, неизбежная
ошибка возникала в силу географического положения двух городов.
Эратосфен рассуждал так: если города находятся на одном мередиане
(т.е., Александрия расположена в точности к северу от Сиены), то
полдень в них наступает одновременно. Поэтому, сделав измерения во
время наивысшего положения Солнца в каждом городе, мы должны
получить правильный результат. Но на самом деле Александрия и
Сиена - далеко не на одном мередиане. Сейчас в этом легко
убедиться, взглянув на карту, но у Эратосфена такой возможности не
было, он как раз и работал над составлением первых карт. Поэтому
его метод (абсолютно верный !) привёл к ошибке в определении
радиуса Земли. Тем не менее, многие исследователи уверены, что
точность измерения Эратосфена была высока, и что он ошибся менее,
чем на
км., не удивительно,
если вспомнить, что единица длины в 1 метр и была введена (во
Франции в конце 18 века), как одна сорокамиллионная часть
окружности Земли (по определению !). Эратосфен, конечно,
использовал другую единицу измерения - стадий (около 200
м). Стадиев было несколько: египетский, греческий, вавилонский, и
каким из них пользовался Эратосфен - неизвестно. Поэтому трудно
судить наверняка о точности его измерения. Кроме того, неизбежная
ошибка возникала в силу географического положения двух городов.
Эратосфен рассуждал так: если города находятся на одном мередиане
(т.е., Александрия расположена в точности к северу от Сиены), то
полдень в них наступает одновременно. Поэтому, сделав измерения во
время наивысшего положения Солнца в каждом городе, мы должны
получить правильный результат. Но на самом деле Александрия и
Сиена - далеко не на одном мередиане. Сейчас в этом легко
убедиться, взглянув на карту, но у Эратосфена такой возможности не
было, он как раз и работал над составлением первых карт. Поэтому
его метод (абсолютно верный !) привёл к ошибке в определении
радиуса Земли. Тем не менее, многие исследователи уверены, что
точность измерения Эратосфена была высока, и что он ошибся менее,
чем на ![]() . Если это так, то улучшить этот результат
человечество смогло только через 2 тысячи лет, в середине 19 века.
Над этим трудилась группа учёных во Франции и экспедиция
В.Я.Струве в России. Даже в эпоху великих географических открытий,
в 16 веке, люди не смогли достичь результата Эратосфена, и
пользовались неверным значением длины земной окружности в 37.000
км. Ни Колумб, ни Магеллан не знали, каковы истинные размеры
Земли, и какие расстояния им придётся преодолевать. Они-то
считали, что длина экватора на 3 тысячи км. меньше, чем на самом
деле. Знали бы - может и не поплыли бы.
. Если это так, то улучшить этот результат
человечество смогло только через 2 тысячи лет, в середине 19 века.
Над этим трудилась группа учёных во Франции и экспедиция
В.Я.Струве в России. Даже в эпоху великих географических открытий,
в 16 веке, люди не смогли достичь результата Эратосфена, и
пользовались неверным значением длины земной окружности в 37.000
км. Ни Колумб, ни Магеллан не знали, каковы истинные размеры
Земли, и какие расстояния им придётся преодолевать. Они-то
считали, что длина экватора на 3 тысячи км. меньше, чем на самом
деле. Знали бы - может и не поплыли бы.
В чем причина столь высокой
точности метода Эратосфена (конечно, если он пользовался нужным
стадием) ?
До него измерения были локальными, на расстояниях, обозримых
человеческим глазом, т.е., не более 100 км. Таковы, например,
способы в упражнениях 1 и 2. При этом неизбежны ошибки
из-за рельефа местности, атмосферных явлений, и т.д.
Чтобы добиться большей точности, нужно проводить измерения
глобально, на расстояниях, сравнимых с радиусом Земли. Расстояние
в ![]() км. между Александрией и Сиеной оказалось вполне
достаточным.
км. между Александрией и Сиеной оказалось вполне
достаточным.
Упражнение 1. Как вычислить радиус Земли по следующим данным: с горы высотой 500 м. просматриваются окрестности на расстоянии 80 км.?
Упражнение 2. Как вычислить радиус Земли по следующим данным: корабль высотой 20 м., отплыв от берега на 16 км., полностью исчезает из вида ?.
Упражнение 3. Два друга - один в Москве, другой - в Туле,
берут по метровому шесту и ставят их вертикально. В момент, в
течение дня, когда тень от шеста достигает наименьшей длины,
каждый из них измеряет длину тени. В Москве получилось ![]() см., а
в Туле -
см., а
в Туле - ![]() см. Выразите радиус Земли через
см. Выразите радиус Земли через ![]() и
и ![]() . Города
расположены на одном меридиане на расстоянии 185 км.
. Города
расположены на одном меридиане на расстоянии 185 км.
Как видно из упражнения 3, опыт Эратосфена можно проделать и в наших широтах, где Солнце никогда не бывает в зените. Правда, для этого нужны две точки обязательно на одном мередиане. Если же повторить опыт Эратосфена для Александрии и Сиены, и при этом сделать измерения в этих городах одновременно (сейчас для этого есть технические возможности), то мы получим верный ответ, при этом будет не важно, на каком мередиане находится Сиена (почему ?).
 Памятник Аристарху-Самосскому в Салониках |
Вычисление Аристарха можно условно разбить на три шага. Каждый шаг
сводится к простой геометрической задаче. Первые два шага совсем
элементарны, третий - чуть посложнее. В геометрических
построениях мы будем обозначать через ![]() и
и ![]() центы Земли,
Солнца и Луны соответственно, а через
центы Земли,
Солнца и Луны соответственно, а через
![]() и
и ![]() -
их радиусы. Все небесные тела будем считать шарами, а их орбиты -
окружностями, как и считал сам Аристарх (хотя, как мы теперь
знаем, это не совсем так). Мы начинаем с первого шага, и для этого
немного понаблюдаем за Луной.
-
их радиусы. Все небесные тела будем считать шарами, а их орбиты -
окружностями, как и считал сам Аристарх (хотя, как мы теперь
знаем, это не совсем так). Мы начинаем с первого шага, и для этого
немного понаблюдаем за Луной.
Шаг 1. Во сколько раз Солнце дальше, чем Луна ?
Как известно, Луна светит отражённым солнечным светом. Если взять шар, и посветить на него со стороны большим прожектором, то в любом положении освещенной окажется ровно половина поверхности шара. Граница освещённой полусферы - окружность, лежащая в плоскости, перпендикулярной лучам света. Таким образом, Солнце всегда освещает ровно половину поверхности Луны. Видимая нам форма Луны зависит от того, как расположена эта освещённая половина. При новолунии, когда Луна вовсе не видна на небе, Солнце освещает её обратную сторону. Затем освещенная полусфера постепенно поворачивается в сторону Земли. Мы начинаем видеть тонкий серп, затем - месяц ("растущая Луна"), далее - полукруг (эта фаза Луны называется "квадратурой"). Затем день ото дня (вернее, ночь от ночи) полукруг дорастает до полной Луны. Потом начинается обратный процесс: освещённая полусфера от нас отворачивается. Луна "стареет", постепенно превращаясь в месяц, повёрнутый к нам левой стороной, подобно букве "C", и, наконец, в ночь новолуния исчезает. Период от одного новолуния до другого длится примерно четыре недели. За это время Луна совершает полный оборот вокруг Земли. От новолуния до половины Луны проходит четверть периода, отсюда и название "квадратура".
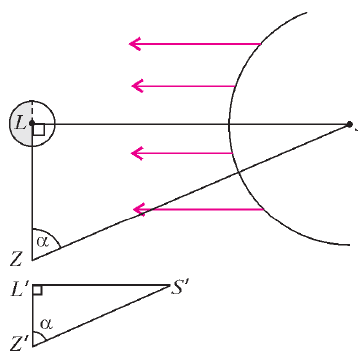 Рис. 3. |
Итак, измерив угол ![]() между лучами
между лучами ![]() и
и ![]() во время
квадратуры, Аристарх вычисляет отношение расстояний до Луны и до
Солнца. Как одновременно застать Солнце и Луну на небосводе ? Это
можно сделать ранним утром, когда в ясную погоду видны оба
небесных тела. Сложность возникает по другому, неожиданному,
поводу. Во времена Аристарха не было косинусов. Первые понятия
тригонометрии появятся позже, в работах Аполлония и Архимеда. Но
Аристарх знал, что такое подобные треугольники, и этого было
достаточно. Начертив маленький прямоугольный треугольник
во время
квадратуры, Аристарх вычисляет отношение расстояний до Луны и до
Солнца. Как одновременно застать Солнце и Луну на небосводе ? Это
можно сделать ранним утром, когда в ясную погоду видны оба
небесных тела. Сложность возникает по другому, неожиданному,
поводу. Во времена Аристарха не было косинусов. Первые понятия
тригонометрии появятся позже, в работах Аполлония и Архимеда. Но
Аристарх знал, что такое подобные треугольники, и этого было
достаточно. Начертив маленький прямоугольный треугольник ![]() с тем же острым углов
с тем же острым углов
![]() , и
измерив его стороны, получаем, что
, и
измерив его стороны, получаем, что
![]() , и это отношение примерно равно
, и это отношение примерно равно
![]() . Получается, что Солнце в 400 раз дальше от Земли,
чем Луна. Эту константу - отношение расстояний от Земли до Солнца
и от Земли до Луны, мы
мы будем обозначать буквой
. Получается, что Солнце в 400 раз дальше от Земли,
чем Луна. Эту константу - отношение расстояний от Земли до Солнца
и от Земли до Луны, мы
мы будем обозначать буквой ![]() . Итак, мы нашли, что
. Итак, мы нашли, что
![]() .
.
Шаг 2. Во сколько раз Солнце больше Луны ?
Для того, чтобы найти отношение радиусов Солнца и Луны, Аристарх привлекает Солнечные затмения (рис.4). Они происходят, когда Луна загораживает Солнце. При частичном, или как говорят астрономы, частном затмении Луна лишь проходит по диску Солнца, не закрывая его полностью. Порой такое затмение даже нельзя разглядеть невооружённым глазом, Солнце светит как в обычный день. Лишь сквозь сильное затемнение, например, закопчёное стекло, видно, как часть солнечного диска закрыта чёрным кругом.
 Рис. 4. |
Гораздо реже происходит полное затмение, когда Луна на несколько
минут полностью закрывает солнечный диск. В это время становится
темно, на небе появляются звёзды. Затмения наводили ужас на
древних людей, считались предвестниками трагедий. Солнечное
затмение наблюдается по-разному в разных частях Земли. Во время
полного затмения на поверхности Земли возникает тень от Луны -
круг, диаметр которого не превосходит 270 км. Лишь в тех районах
земного шара, по которым проходит эта тень, можно наблюдать полное
затмение. Поэтому в одном и том же месте полное затмение
происходит крайне редко - в среднем раз в 200-300 лет. Аристарху
повезло - он смог наблюдать полное солнечное затмение
собственными глазами. На безоблачном небе Солнце постепенно начало
тускнеть и уменьшаться в размерах, установились сумерки. На
несколько мгновений Солнце исчезло. Потом проглянул первый луч
света, солнечный диск стал расти, и вскоре Солнце засветило в
полную силу. Почему затмение длится столь короткое время ?
Аристарх отвечает на этот вопрос: причина в том, что Луна имеет те
же видимые размеры на небе, что и Солнце. Что это значит ?
Проведём плоскость через центры Земли, Солнца и Луны. Получившееся
сечение изображено на рисунке 5 (а). Угол между касательными,
проведёными из точки ![]() к окружности Луны называется
угловым размером Луны, или её угловым диаметром. Так же
определяется угловой размер Солнца. Если угловые диаметры Солнца и
Луны совпадают, то они имеют одинаковые видимые размеры на небе,
а
при затмении Луна действительно полностью
загораживает Солнце (рис. 5 (б)), но лишь на мгновение, когда
совпадут лучи
к окружности Луны называется
угловым размером Луны, или её угловым диаметром. Так же
определяется угловой размер Солнца. Если угловые диаметры Солнца и
Луны совпадают, то они имеют одинаковые видимые размеры на небе,
а
при затмении Луна действительно полностью
загораживает Солнце (рис. 5 (б)), но лишь на мгновение, когда
совпадут лучи ![]() и
и ![]() . На фотографии полного солнечного
затмения (см. рис. 4) ясно видно равенство размеров.
. На фотографии полного солнечного
затмения (см. рис. 4) ясно видно равенство размеров.
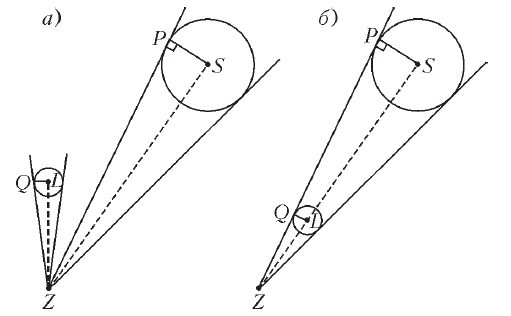 Рис. 5. |
Вывод Аристарха оказался поразительно точен ! В реальности средние
угловые диаметры Солнца и Луны отличаются всего на ![]() . Мы
вынуждены говорить о средних диаметрах, поскольку они меняются в
течение года, так как планеты движутся не по окружностям, а по
эллипсам.
. Мы
вынуждены говорить о средних диаметрах, поскольку они меняются в
течение года, так как планеты движутся не по окружностям, а по
эллипсам.
Соединив центр Земли ![]() с центрами Солнца
с центрами Солнца ![]() и Луны
и Луны ![]() , а также
c точками касания
, а также
c точками касания ![]() и
и ![]() , получим два прямоугольных
треугольника
, получим два прямоугольных
треугольника ![]() и
и ![]() (рис. 5 (а)). Они подобны, поскольку у
них есть пара равных острых углов
(рис. 5 (а)). Они подобны, поскольку у
них есть пара равных острых углов
![]() .
Следовательно,
.
Следовательно,
![]() . Таким образом, отношение радиусов Солнца и
Луны равно отношению расстояний от их центров до центра Земли.
Итак,
. Таким образом, отношение радиусов Солнца и
Луны равно отношению расстояний от их центров до центра Земли.
Итак,
![]() . Несмотря
на то, что их видимые размеры равны, Солнце оказалось больше Луны
в
. Несмотря
на то, что их видимые размеры равны, Солнце оказалось больше Луны
в ![]() раз !
раз !
Равенство угловых размеров Луны и Солнца - счастливое совпадение. Оно не вытекает из законов механики. У многих планет Солнечной системы есть спутники: у Марса их два, у Юпитера - четыре (и еще несколько десятков мелких), и все они имеют разные угловые размеры, не совпадающие с солнечным.
Теперь мы приступаем к решающему и самому сложному шагу.
Шаг 3. Вычисление размеров Солнца и Луны и расстояний до них.
Итак, нам известно отношение размеров Солнца и Луны, и отношение
их расстояний до Земли. Эта информация относительна: она
восстанавливает картину окружающего мира лишь с точностью до
подобия. Можно удалить Луну и Солнце от Земли в 10 раз, увеличив
во столько же раз их размеры, и видимая с Земли картина останется
такой же. Чтобы найти реальные размеры небесных тел, надо
соотнести их с каким-то известным размером.
Но из всех астрономических величин Аристарху пока
известен только радиус земного шара3 ![]() км.
Поможет ли это ? Хоть в
каком-то из видимых явлений, происходящих на небе, появляется
радиус Земли ? Не случайно говорят "небо и земля", имея в виду
две несовместные вещи. И всё же, такое явление есть. Это - лунное
затмение. С его помощью, применив довольно хитроумное
геометрическое построение, Аристарх вычисляет отношение радиуса
Солнца к радиусу Земли, и цепь замыкается: теперь мы одновременно
находим радиус Луны, радиус Солнца, а заодно и расстояния от Луны
и от Солнца до Земли.
км.
Поможет ли это ? Хоть в
каком-то из видимых явлений, происходящих на небе, появляется
радиус Земли ? Не случайно говорят "небо и земля", имея в виду
две несовместные вещи. И всё же, такое явление есть. Это - лунное
затмение. С его помощью, применив довольно хитроумное
геометрическое построение, Аристарх вычисляет отношение радиуса
Солнца к радиусу Земли, и цепь замыкается: теперь мы одновременно
находим радиус Луны, радиус Солнца, а заодно и расстояния от Луны
и от Солнца до Земли.
 Рис. 6. |
Упражнение 4. На плоскости дана дуга окружности. С помощью циркуля и линейки постройте отрезок, равный её радиусу.
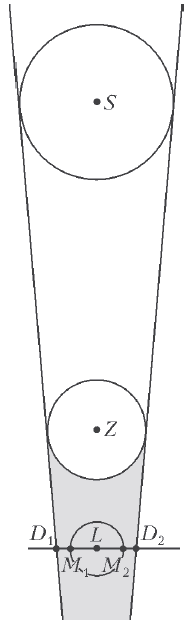 Рис. 7. |
Задача 1. Даны три окружности с центрами
![]() и
и ![]() , лежащими на одной прямой. Отрезок
, лежащими на одной прямой. Отрезок ![]() ,
проходящий через
,
проходящий через ![]() , перпендикулярен прямой
, перпендикулярен прямой ![]() , а его концы
лежат на общих внешних касательных к первой и второй окружностям.
Известно, что отношение отрезка
, а его концы
лежат на общих внешних касательных к первой и второй окружностям.
Известно, что отношение отрезка ![]() к диаметру третьей
окружности равно
к диаметру третьей
окружности равно ![]() , а отношение диаметров первой и третьей
окружности равно
, а отношение диаметров первой и третьей
окружности равно
![]() . Найти отношение
диаметров первой и второй окружности.
. Найти отношение
диаметров первой и второй окружности.
Если решить эту задачу, то будет найдено отношение радиусов Солнца
и Земли. Значит, будет найден радиус Солнца, а с ним и Луны. Но
решить её не удастся. Можете попробовать - в задаче не достаёт
одного данного. Например, угла между общими внешними касательными
к первым двум окружностям. Но даже если этот угол был бы известен,
решение будет использовать тригонометрию, которую Аристарх не
знал
(мы формулируем соответствующую задачу в упражнении 6).
Он находит более простой выход. Проведём диаметр ![]() первой
окружности и диаметр
первой
окружности и диаметр ![]() второй, оба - параллельные отрезку
второй, оба - параллельные отрезку
![]() . Пусть
. Пусть ![]() и
и ![]() - точки пересечения отрезка
- точки пересечения отрезка
![]() с прямыми
с прямыми ![]() и
и ![]() соответственно (рис. 8).
соответственно (рис. 8).
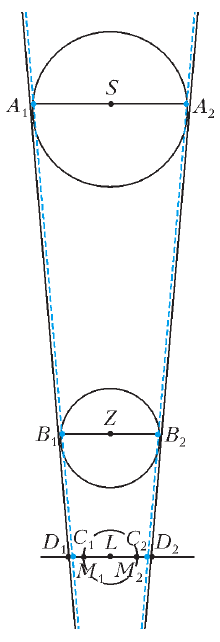 Рис. 8. |
Задача 1'. На боковых сторонах ![]() и
и
![]() трапеции
трапеции
![]() взяты точки
взяты точки ![]() и
и ![]() так,
что отрезок
так,
что отрезок ![]() параллелен основаниям. Пусть
параллелен основаниям. Пусть ![]() и
и ![]() -
середины отрезков
-
середины отрезков
![]() и
и ![]() соответственно. На
основании
соответственно. На
основании ![]() лежит отрезок
лежит отрезок ![]() с серединой
с серединой ![]() .
Известно, что
.
Известно, что
![]() и
и
![]() . Найти
. Найти
![]() .
.
Решение. Так как
![]() , то
, то
![]() ,
а значит треугольники
,
а значит треугольники ![]() и
и ![]() подобны с коэффициентом
подобны с коэффициентом
![]() . Следовательно,
. Следовательно,
![]() , и поэтому точка
, и поэтому точка ![]() лежит на отрезке
лежит на отрезке
![]() . Аналогично,
. Аналогично, ![]() лежит на отрезке
лежит на отрезке ![]() (рис. 9). Так
как
(рис. 9). Так
как
![]() и
и
![]() , то
, то
![]() .
.
Далее, треугольники ![]() и
и ![]() подобны. Их
коэффициент подобия равен
подобны. Их
коэффициент подобия равен
![]() . Следовательно,
. Следовательно,
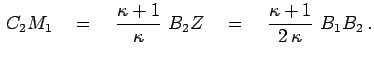
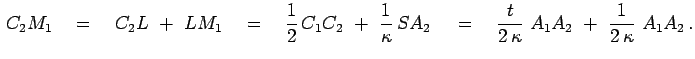
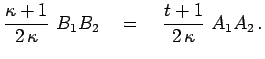
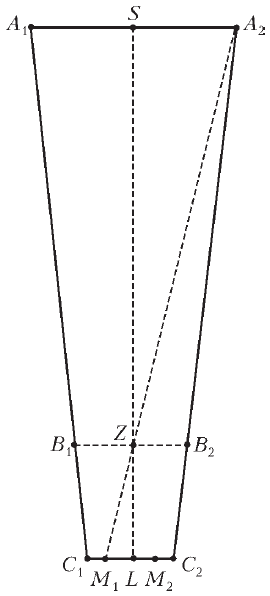 Рис. 9. |
Теперь расстояния от Земли до Луны и до Солнца вычисляются в один
шаг, это может быть сделано с помощью углового диаметра. Угловой
диаметр ![]() Солнца и Луны равен примерно полградуса (если
быть совсем точным,
Солнца и Луны равен примерно полградуса (если
быть совсем точным, ![]() ). Как древние астрономы его
измеряли, об этом речь впереди. Опустив касательную
). Как древние астрономы его
измеряли, об этом речь впереди. Опустив касательную ![]() на
окружность Луны, получаем прямоугольный треугольник
на
окружность Луны, получаем прямоугольный треугольник ![]() с острым
углом
с острым
углом
![]() (рис. 10).
(рис. 10).
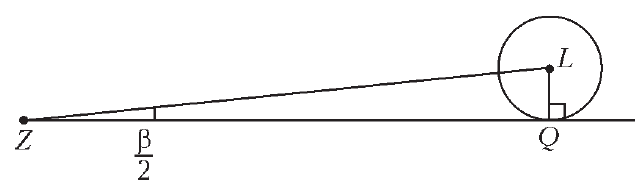 Рис. 10. |
Из него находим
![]() , что примерно равно
, что примерно равно
![]() , или
, или ![]() . Аналогично, расстояние до Солнца равно
. Аналогично, расстояние до Солнца равно
![]() .
.
Всё. Размеры Солнца и Луны и расстояния да них найдены.
Упражнение 5. Докажите, что прямые
![]() и две общие
внешние касательные к первой и второй окружностям (рис. 8)
пересекаются в одной точке.
и две общие
внешние касательные к первой и второй окружностям (рис. 8)
пересекаются в одной точке.
Упражнение 6. Решите задачу 1, если дополнительно известен угол между касательными между первой и второй окружностью.
Упражнение 7. Солнечное затмение может наблюдаться в одних частях земного шара и не наблюдаться других. А лунное затмение ?
Упражнение 8. Докажите, что солнечное затмение может наблюдаться только во время новолуния, а лунное затмение - только во время полнолуния.
Упражнение 9. Что происходит на Луне, когда на Земле происходит лунное затмение ?
На самом деле всё было несколько сложнее.
Геометрия только формировалась, и многие привычные для нас, ещё с восьмого класса школы,
вещи были в то время совсем не очевидны. Аристарху потребовалось написать целую книгу,
чтобы изложить то, что мы изложили на трёх страницах. И с экспериментальными
измерениями тоже всё было непросто. Во-первых, Аристарх ошибся с
измерением диаметра земной тени во время лунного затмения, получив отношение ![]() , вместо
, вместо
![]() . Кроме того, он, вроде бы, исходил из неверного
значения угла
. Кроме того, он, вроде бы, исходил из неверного
значения угла ![]() - углового диаметра Солнца, считая его равным
- углового диаметра Солнца, считая его равным ![]() .
Но эта версия спорная: Архимед в своём трактате "Псаммит"
пишет, что, напротив, Аристарх пользовался почти правильным
значением в
.
Но эта версия спорная: Архимед в своём трактате "Псаммит"
пишет, что, напротив, Аристарх пользовался почти правильным
значением в ![]() . Однако, самая ужасная ошибка произошла на
первом шаге, при вычислении параметра
. Однако, самая ужасная ошибка произошла на
первом шаге, при вычислении параметра ![]() - отношения
расстояний от Земли до Солнца и до Луны. Вместо
- отношения
расстояний от Земли до Солнца и до Луны. Вместо
![]() у
Аристарха получилось
у
Аристарха получилось
![]() . Как можно было ошибиться
более, чем в 20 раз ? Обратимся еще раз к шагу 1, рис 3. Для того,
чтобы найти отношение
. Как можно было ошибиться
более, чем в 20 раз ? Обратимся еще раз к шагу 1, рис 3. Для того,
чтобы найти отношение
![]() Аристарх
измерил угол
Аристарх
измерил угол
![]() , и тогда
, и тогда
![]() . Например, если угол
. Например, если угол ![]() был
бы равен
был
бы равен ![]() , то мы получили бы
, то мы получили бы ![]() , и Солнце было бы
вдвое дальше от Земли, чем Луна. Но результат измерения оказался
неожиданным: угол
, и Солнце было бы
вдвое дальше от Земли, чем Луна. Но результат измерения оказался
неожиданным: угол ![]() получался почти прямым. Это означало,
что катет
получался почти прямым. Это означало,
что катет ![]() во много раз превосходит
во много раз превосходит ![]() . У Аристарха
получилось
. У Аристарха
получилось
![]() , и тогда
, и тогда
![]() (напомним, что все вычисления у нас -
приближённые). Истинное значение угла
(напомним, что все вычисления у нас -
приближённые). Истинное значение угла
![]() , и
, и
![]() . Так
погрешность измерения менее, чем в
. Так
погрешность измерения менее, чем в ![]() , привела к ошибке в
, привела к ошибке в ![]() раз ! Завершив вычисления, Аристарх приходит к выводу, что радиус
Солнца равен
раз ! Завершив вычисления, Аристарх приходит к выводу, что радиус
Солнца равен ![]() радиусов Земли (вместо
радиусов Земли (вместо ![]() ).
).
Ошибки были неизбежны, учитывая несовершенные измерительные
приборы того времени. Важнее то, что метод оказался правильным.
Вскоре (по историческим меркам, т.е., примерно через 100 лет)
выдающийся астроном античности Гиппарх (190 - ок. 120 до н. э.)
устранит все неточности и, следуя методу Аристарха, вычислит
правильные размеры Солнца и Луны. Возможно, ошибка Аристарха
оказалась в результате даже полезной. До него господствовало
мнение, что Солнце и Луна либо вовсе имеют одинаковые размеры (как
и кажется земному налюдателю), либо отличаются несильно. Даже
отличие в ![]() раз удивило современников. Поэтому, не исключено,
что, найди Аристарх правильное отношение
раз удивило современников. Поэтому, не исключено,
что, найди Аристарх правильное отношение
![]() ,
в это никто бы не поверил, а может быть, и сам учёный отказался
бы от своего метода, сочтя результат несуразным. Известный принцип
гласит, что
геометрия - это искусство хорошо рассуждать на плохо выполненных чертежах.
Перефразируя, можно сказать, что наука в целом - это искусство делать верные выводы из
неточных, или даже ошибочных, наблюдений. И Аристарх такой вывод сделал !
За 17 веков до Коперника он понял, что в центре мира находится не
Земля, а Солнце. Так впервые появилась гелиоцентрическая модель и
понятие Солнечной системы.
,
в это никто бы не поверил, а может быть, и сам учёный отказался
бы от своего метода, сочтя результат несуразным. Известный принцип
гласит, что
геометрия - это искусство хорошо рассуждать на плохо выполненных чертежах.
Перефразируя, можно сказать, что наука в целом - это искусство делать верные выводы из
неточных, или даже ошибочных, наблюдений. И Аристарх такой вывод сделал !
За 17 веков до Коперника он понял, что в центре мира находится не
Земля, а Солнце. Так впервые появилась гелиоцентрическая модель и
понятие Солнечной системы.
Господствовавшее в Древнем Мире представление об устройстве
Вселенной, знакомое нам по урокам истории, заключалось в том, что
в центре мира - неподвижная Земля, вокруг неё по круговым орбитам
вращаются 7 планет, включая Луну и Солнце (которое тоже
считалось планетой). Завершается все небесной сферой с
прикреплёнными к ней звёздами. Сфера
вращается вокруг Земли, делая полный оборот за 24 часа. Со временем в эту модель многократно
вносились исправления. Так, стали считать, что небесная сфера
неподвижна, а Земля вращается вокруг своей оси. Затем стали
исправлять траектории движения планет: круги заменили циклоидами,
т.е., линиями, которые описывают точки окружности при её движении
по другой окружности (об этих замечательных линиях можно прочитать
в
книгах Г.Н.Бермана "Циклоида",
А.И.Маркушевича "Замечательные кривые", а также в "Кванте":
статья С.Верова "Тайны циклоиды" N8, 1975, и статья
С.Г.Гиндикина "Звездный век циклоиды", N6,1985). Циклоиды лучше
согласовывались с результатами наблюдений, в частности, объясняли
"попятные" движения планет. Это - геоцентрическая
система мира, в центре которой - Земля ("гео"). Во II в. н.э.
она приняла окончательный вид в книге "Альмагест" Клавдия
Птолемея (87-165 н.э.), выдающегося греческого астронома, однофамильца
египетских царей. Со временем некоторые циклоиды усложнялись,
добавлялись всё новые промежуточные окружности. Но в целом
система Птолемея господствовала около полутора тысячелетий, до XVI
века, до открытий Коперника и Кеплера. Поначалу геоцентрической
модели придерживался и Аристарх. Однако, вычислив, что радиус
Солнца в ![]() раз больше радиуса Земли, он задал простой вопрос:
почему такое большое Солнце должно вращаться вокруг такой
маленькой Земли ? Ведь если радиус Солнца больше в
раз больше радиуса Земли, он задал простой вопрос:
почему такое большое Солнце должно вращаться вокруг такой
маленькой Земли ? Ведь если радиус Солнца больше в ![]() раз, то
его объём больше почти в
раз, то
его объём больше почти в ![]() раз ! Значит, в центре мира должно
находиться Солнце. Вокруг него вращаются 6 планет, включая
Землю.4 А седьмая планета, Луна, вращается вокруг Земли.
Так впервые появилась гелиоцентрическая
система мира ("гелиос" - Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение
планет по круговым орбитам, лучше согласуется с результатами
наблюдений. Но её не приняли ни учёные, ни официальные власти.
Аристарх был обвинён в безбожии и подвергся преследованиям. Из
всех астрономов античности, только Селевк стал сторонником новой
модели. Больше её не принял никто, по крайней мере, у историков
нет твёрдых сведений на этот счёт. Даже Архимед и Гиппарх,
почитавшие Аристарха и развившие многие его идеи, не решились
поставить Солнце в центр мира. Почему ?
раз ! Значит, в центре мира должно
находиться Солнце. Вокруг него вращаются 6 планет, включая
Землю.4 А седьмая планета, Луна, вращается вокруг Земли.
Так впервые появилась гелиоцентрическая
система мира ("гелиос" - Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение
планет по круговым орбитам, лучше согласуется с результатами
наблюдений. Но её не приняли ни учёные, ни официальные власти.
Аристарх был обвинён в безбожии и подвергся преследованиям. Из
всех астрономов античности, только Селевк стал сторонником новой
модели. Больше её не принял никто, по крайней мере, у историков
нет твёрдых сведений на этот счёт. Даже Архимед и Гиппарх,
почитавшие Аристарха и развившие многие его идеи, не решились
поставить Солнце в центр мира. Почему ?
Как же получилось, что в течении 17 веков учёные не принимали
простой и логичной системы мира, предложенной Аристархом ? И это
несмотря на то, что официально признанная геоцентрическая система
Птолемея часто давала сбои, не согласуясь с результатами
наблюдений за планетами и за звёздами. Приходилось добавлять всё
новые окружности (так называемые, вложенные циклы) для
"правильного" описания движения планет. Самого Птолемея
трудности не пугали, он писал: "К чему удивляться сложному
движению небесных тел, если их сущность нам неизвестна ?" Однако,
уже к XIII веку этих окружностей накопилось 75 ! Модель стала
столь громоздкой, что начали раздаваться осторожные возражения:
неужели мир в самом деле устроен так сложно ? Широко известен
случай с Альфонсом X (1226-1284), королем Кастильи и Леона,
государства, занимавшего часть современной Испании. Он,
покровитель наук и искусств, собравший при своём дворе пятьдесят
лучших астрономов мира, на одной из научных бесед обмолвился, что
"если бы при сотворении мира Господь оказал мне честь и спросил
моего совета, многое было бы устроено проще." Подобная дерзость
не прощалась даже королям: Альфонс был низложен и отправлен в
монастырь.5 Но
сомнения остались. Часть из них можно было бы разрешить, поставив
Солнце в центр Вселенной и приняв систему Аристарха. Его труды
были хорошо известны. Однако, ещё много веков никто из учёных не
решался на такой шаг. Причины были не только в страхе перед
властями и официальной церковью, которая считала теорию Птолемея
единственно верной. И не только в инертности человеческого
мышления: не так-то просто признать, что наша Земля - не центр
мира, а лишь рядовая планета. Всё-таки, для настоящего учёного ни
страх ни стереотипы - не препятствия на пути к истине.
Гелиоцентическая система отвергалась по вполне научным, можно даже
сказать, геометрическим причинам. Если допустить, что Земля
вращается вокруг Солнца, то, её траектория - окружность с
радиусом равным расстоянию от Земли до Солнца. Как мы знаем, это
расстояние равно 23455 радиусов Земли, т.е., более 150 миллионов
километров.
Значит, Земля в течение полугода перемещается на 300 миллионов километров. Гигантская величина !
Но картина звёздного неба для земного наблюдателя при этом
остаётся такой же. Земля то приближается, то удаляется от звёзд на
300 миллионов километров, но
ни видимые расстояния между звёздами (например, форма созвездий),
ни их яркость не меняются. Это означает, что расстояния до звёзд
должны быть ещё в несколько тысяч раз больше. То есть, небесная
сфера должна иметь совершенно невообразимые размеры ! Это, между
прочим, осознавал и сам Аристарх, который писал в своей книге:
"Объём сферы неподвижных звёзд во столько раз больше объёма сферы
с радиусом Земля-Солнце, во сколько раз объём последней больше
объёма земного шара". Т.е., по Аристарху выходило, что
расстояния до звёзд равно
![]() , это более 3.5 триллионов
километров (в реальности расстояние от Солнца до ближайшей звезды
ещё примерно в 11 раз больше. В модели, которую мы представили в
самом начале, когда расстояние от Земли до Солнца равно 10 м.,
расстояние до
ближайшей звезды равно ... 2700 километров !).
Вместо компактного и уютного мира, в центре которого находится
Земля, и который помещается внутри относительно небольшой
небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала
всех.
, это более 3.5 триллионов
километров (в реальности расстояние от Солнца до ближайшей звезды
ещё примерно в 11 раз больше. В модели, которую мы представили в
самом начале, когда расстояние от Земли до Солнца равно 10 м.,
расстояние до
ближайшей звезды равно ... 2700 километров !).
Вместо компактного и уютного мира, в центре которого находится
Земля, и который помещается внутри относительно небольшой
небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала
всех.
Между тем, невозможность геоцентрической системы мира, с круговыми движениями всех планет вокруг Земли, может быть установлена с помощью простой геометрической задачи.
Задача 2. На плоскости даны две окружности
с общим центром ![]() , по ним равномерно движутся две точки:
точка
, по ним равномерно движутся две точки:
точка ![]() по одной окружности, и точка
по одной окружности, и точка ![]() по другой. Докажите,
что либо они двигаются в одном направлении с одинаковой угловой
скоростью, либо в некоторый момент времени угол
по другой. Докажите,
что либо они двигаются в одном направлении с одинаковой угловой
скоростью, либо в некоторый момент времени угол
![]() тупой.
тупой.
Решение. Если точки движутся в одном
направлении с разными скоростями, то через некоторое время лучи
![]() и
и ![]() окажутся сонаправленными. Далее угол
окажутся сонаправленными. Далее угол
![]() начинает монотонно возрастать до следующего совпадения, т.е., до
начинает монотонно возрастать до следующего совпадения, т.е., до
![]() . Следовательно, в некоторый момент он равен
. Следовательно, в некоторый момент он равен ![]() .
Случай, когда точки движутся в разных направлениях рассматривается
так же.
.
Случай, когда точки движутся в разных направлениях рассматривается
так же.
Теорема 1. Ситуация, при которой все планеты Солнечной системы равномерно вращаются вокруг Земли по круговым орбитам, невозможна.
Доказательство. Пусть ![]() - центр Земли,
- центр Земли, ![]() - центр Меркурия, а
- центр Меркурия, а ![]() - центр Венеры. Согласно многолетним
наблюдениям, у Меркурия и Венеры разные периоды обращения, а
угол
- центр Венеры. Согласно многолетним
наблюдениям, у Меркурия и Венеры разные периоды обращения, а
угол
![]() никогда не превосходит
никогда не превосходит ![]() . В силу
результата задачи 2, теорема доказана.
. В силу
результата задачи 2, теорема доказана.
Конечно, древние греки неоднократно встречались с подобными парадоксами. Именно поэтому, чтобы спасти геоцентрическую модель мира, они заставили планеты двигаться не по окружностям, а по циклоидам.
Доказательство теоремы 1 не совсем честно, поскольку Меркурий и
Венера вращаются не в одной плоскости, как в задаче 2, а в разных.
Хотя, плоскости их орбит почти совпадают: угол между ними - всего
несколько градусов. В упражнении 10 мы предлагаем Вам устранить
этот недостаток и решить аналог задачи 2 для точек, вращающихся в
разных плоскостях. Другое возражение: может быть угол ![]() бывает
тупым, но мы этого не видим, поскольку на земле в это время день ?
Принимаем и это. В упражнении 11 нужно доказать, что для
трёх вращающихся радиусов
всегда настанет момент времени, когда
они будут образовывать друг с другом тупые углы. Если на концах
радиусов - Меркурий, Венера и Солнце, то в этот момент времени
Меркурий и Венера будут видны на небе, а Солнце - нет, то есть на
земле будет ночь. Но должны предупредить: упражнения 10 и 11
значительно сложнее задачи 2.
Наконец, в упражнении 12 мы предлагаем Вам, ни много ни мало, вычислить расстояние от
Венеры до Солнца и от Меркурия до Солнца (они, конечно, вращаются вокруг Солнца, а не вокруг Земли).
Убедитесь сами, насколько это просто, после того, как мы узнали
метод Аристарха.
бывает
тупым, но мы этого не видим, поскольку на земле в это время день ?
Принимаем и это. В упражнении 11 нужно доказать, что для
трёх вращающихся радиусов
всегда настанет момент времени, когда
они будут образовывать друг с другом тупые углы. Если на концах
радиусов - Меркурий, Венера и Солнце, то в этот момент времени
Меркурий и Венера будут видны на небе, а Солнце - нет, то есть на
земле будет ночь. Но должны предупредить: упражнения 10 и 11
значительно сложнее задачи 2.
Наконец, в упражнении 12 мы предлагаем Вам, ни много ни мало, вычислить расстояние от
Венеры до Солнца и от Меркурия до Солнца (они, конечно, вращаются вокруг Солнца, а не вокруг Земли).
Убедитесь сами, насколько это просто, после того, как мы узнали
метод Аристарха.
Упражнение 10. В пространстве даны две окружности с общим
центром ![]() , по ним равномерно, с разными угловыми скоростями,
движутся две точки: точка
, по ним равномерно, с разными угловыми скоростями,
движутся две точки: точка ![]() по одной окружности, и точка
по одной окружности, и точка ![]() по
другой. Докажите, что
в некоторый момент
угол
по
другой. Докажите, что
в некоторый момент
угол
![]() тупой.
тупой.
Упражнение 11. На плоскости даны три окружности с общим
центром ![]() , по ним равномерно, с разными угловыми скоростями,
движутся три точки. Докажите, что в некоторый момент все три
угла между лучами с вершиной
, по ним равномерно, с разными угловыми скоростями,
движутся три точки. Докажите, что в некоторый момент все три
угла между лучами с вершиной ![]() , направленными в данные точки,
тупые.
, направленными в данные точки,
тупые.
Упражнение 12. Известно, что максимальное угловое расстояние
между Венерой и Солнцем, т.е., максимальный угол между лучами,
направленными с Земли к центрам Венеры и Солнца,
равно ![]() .
Найдите радиус орбиты Венеры. То же - для Меркурия, если
известно, что максимальное угловое расстояние между Меркурием и
Солнцем равно
.
Найдите радиус орбиты Венеры. То же - для Меркурия, если
известно, что максимальное угловое расстояние между Меркурием и
Солнцем равно ![]() .
.
Следуя шаг за шагом рассуждениям Аристарха, мы упустили лишь один
аспект: как измерялся угловой диаметр Солнца ? Сам Аристарх этого
не делал, пользуясь измерениями других астрономов (по-видимому, не
совсем верными). Напомним, что радиусы Солнца и Луны он смог
вычислить, не привлекая их угловые диаметры. Посмотрите ещё раз на
шаги 1, 2 и 3: нигде значение углового диаметра не используется !
Он нужен только для вычисления расстояний до Солнца и до Луны.
Попытка определить угловой размер "на глазок" успеха не
приносит. Если попросить несколько человек оценить угловой
диаметр Луны, большинство назовут угол от 3 до 5 градусов, что в
разы больше истинного значения. Сказывается обман зрения:
ярко-белая Луна на фоне тёмного неба кажется массивной. Первым,
кто провёл математически строгое измерение углового диаметра
Солнца и Луны, был
Архимед (287 - 212 до н. э.) Он изложил свой метод в книге "Псаммит" ("Исчисление песчинок").
Сложность задачи он осознавал:
"Получить точное значение этого угла - дело нелегкое, потому что
ни глаз, ни руки, ни приборы, при помощи которых производится
отсчет, не обеспечивают достаточной точности." Поэтому Архимед не
берётся вычислить точное значение углового диаметра Солнца, он
лишь оценивает его сверху и снизу. Он помещает круглый цилиндр на
конце длинной линейки, напротив глаза наблюдателя. Линейка
направляется на Солнце, и цилиндр придвигается к глазу до тех пор,
пока он не заслонит собой Солнце полностью. Затем наблюдатель
уходит, а на конце линейки отмечается отрезок ![]() , равный размеру
человеческого зрачка (рис. 11).
, равный размеру
человеческого зрачка (рис. 11).
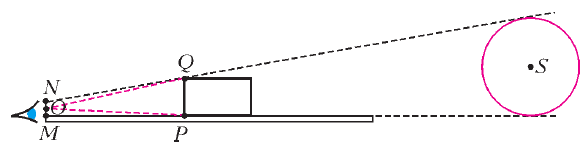 Рис. 11. |
Тогда угол ![]() между
прямыми
между
прямыми ![]() и
и ![]() меньше углового диаметра Солнца, а угол
меньше углового диаметра Солнца, а угол
![]() - больше. Мы обозначили через
- больше. Мы обозначили через
![]() диаметр основания цилиндра, а через
диаметр основания цилиндра, а через ![]() - середину
отрезка
- середину
отрезка ![]() . Итак,
. Итак,
![]() (докажите это в
упражнении 13). Так Архимед находит, что угловой диаметр Солнца
заключён в пределах от
(докажите это в
упражнении 13). Так Архимед находит, что угловой диаметр Солнца
заключён в пределах от ![]() до
до ![]() . Неясным остаётся,
почему Архимед измеряет Солнце, а не Луну. Он был хорошо знаком с
книгой Аристарха, и знал что угловые диаметры Солнца и Луны
одинаковы. Луну же измерять гораздо удобнее: она не слепит глаза,
и границы её видны отчётливее.
. Неясным остаётся,
почему Архимед измеряет Солнце, а не Луну. Он был хорошо знаком с
книгой Аристарха, и знал что угловые диаметры Солнца и Луны
одинаковы. Луну же измерять гораздо удобнее: она не слепит глаза,
и границы её видны отчётливее.
Некоторые древние астрономы измеряли угловой диаметр Солнца,
исходя из продолжительности солнечного или лунного затмения.
Попробуйте восстановить этот способ в упражнении 14. А можно
сделать то же, не дожидаясь затмений, а просто наблюдая закат
Солнца. Выберем для этого день весеннего равноденствия 22 марта,
когда Солнце восходит точно на востоке а заходит точно на западе.
Это означает, что точки восхода ![]() и заката
и заката ![]() диаметрально
противоположны. Для земного наблюдателя Солнце движется по
окружности с диаметром
диаметрально
противоположны. Для земного наблюдателя Солнце движется по
окружности с диаметром ![]() .
.
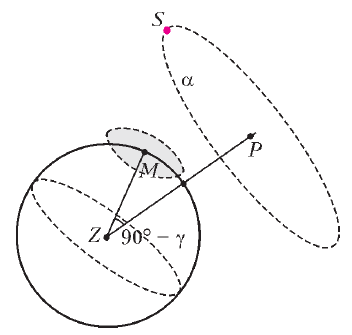 Рис. 12. |
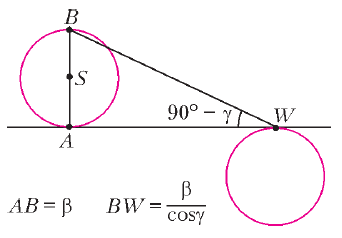 Рис. 13. |
Упражнение 13. Докажите, что угол ![]() между прямыми
между прямыми ![]() и
и
![]() (рис. 12.) меньше углового диаметра Солнца, а угол
(рис. 12.) меньше углового диаметра Солнца, а угол
![]() - больше.
- больше.
Упражнение 14. Предложите способ измерения угловых размеров Луны во время лунного затмения.