Астронет: А. В. Локтин, В. А. Марсаков Звездная астрономия в лекциях http://variable-stars.ru/db/msg/1245721/lec.9.3.html

9.3 Распределение Шварцшильда

Лекция 9. Движение Солнца в пространстве и остаточные скорости звёзд

9.3 Распределение Шварцшильда

Как известно из статистической механики, полное описание системы взаимодействующих частиц можно дать, если знать распределение частиц по координатам и скоростям - так называемую функцию фазовой плотности. Если проинтегрировать такую функцию по скоростям, то получим пространственное распределение частиц. Пространственное распределение звёзд и газовых облаков в Галактике мы рассмотрели в предыдущих лекциях. Если проинтегрировать функцию фазовой плотности по координатам, мы получим распределение скоростей частиц, а исключив потоковые движения - например вращение Галактики и движение Солнца в пространстве, мы получим распределение остаточных скоростей, которое можно исследовать на основе наблюдательных данных. Некоторые сведения о дисперсии скоростей мы уже получили в предыдущих параграфах. Рассмотрим распределение остаточных скоростей звёзд в Галактике более подробно.

Чтобы исследовать распределение остаточных скоростей звёзд введем функцию распределения векторов скоростей В таком случае где dN есть число звёзд, векторы остаточных скоростей которых заключены между и Если бы распределение векторов скоростей было случайным и для каждой звезды являлось следствием многих взаимодействий, изменяющих скорость, то выражалась бы трехмерным нормальным распределением:

где A есть так называемая ковариационная матрица, содержащая дисперсии и ковариации величин u, v и w, а во внутренних скобках под знаком экспоненты стоит полная квадратичная форма от компонентов скорости звезды:

Линейные члены здесь не приведены, так как по определению остаточной скорости они равны нулю. Отметим также, что в общем случае, если рассматривать распределение скоростей в Галактике в целом, коэффициенты, входящие в выражение (9-6), есть функции координат. Если рассматривать только ближайшие окрестности Солнца, то коэффициенты можно считать константами.

Если приравнять показатель степени в выражении (9 -5) константе, то получим уровневую поверхность, описывающую форму распределения. В частности, такие поверхности для трехмерного нормального распределения являются трехосными эллипсоидами. Впервые описание распределения остаточных скоростей звёзд с помощью такой плотности распределения предложил в начале ХХ-го века Шварцшильд. В более простом случае, когда направления осей эллипсоида скоростей совпадают с осями координат, ковариации (множители при произведениях разных компонентов) равны нулю и параметрами распределения оказываются только дисперсии скоростей по трем координатам - дисперсии компонентов вектора остаточной пространственной скорости. Распределение Шварцшильда при этом принимает следующий вид: где σ_u, σ_v, σ_w обозначают соответствующие дисперсии остаточных скоростей. Как известно, квадратичную форму можно привести к нормальному виду методами линейной алгебры, так что из наблюдательных данных мы можем получить не только дисперсии скоростей, но и остальные константы выражения (9-5), значит можно оценить не только величины дисперсии скоростей, но и ориентацию эллипсоида скоростей в пространстве.

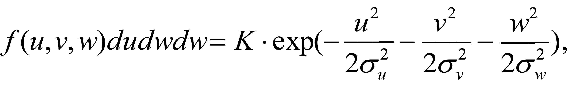
В течение ХХ-го века много усилия было затрачено на определение параметров эллипсоидов скоростей, так как эти параметры тесно связаны с динамикой Галактики. Изучались как дисперсии скоростей, так и ориентация эллипсоида скоростей в пространстве. Кстати, направление большой оси эллипсоида скоростей называется направлением вертекса, это название пришло из так называемой теории двух потоков - одной из попыток описания остаточных скоростей, имеющей в настоящее время лишь исторический интерес. Получить параметры эллипсоида скоростей из наблюдательных данных достаточно легко. Для этого можно использовать или лучевые скорости, или собственные движения и расстояния до исследуемых объектов. Особенно легко получить их из компонентов полной пространственной скорости. Для этого надо к выражению (9-5) добавить еще одно неизвестное - константу, а для выборки наблюдаемых пространственных остаточных скоростей использовать (9-6) как условные уравнения, находя параметры методом наименьших квадратов. Этот метод впервые был предложен в начале ХХ века Дзевульским. Использование отдельно лучевых скоростей или собственных движений более трудоемко, при этом результаты сильно зависят от распределения используемых звёзд по небу - оно должно быть по возможности равномерным, чего добиться достаточно трудно.

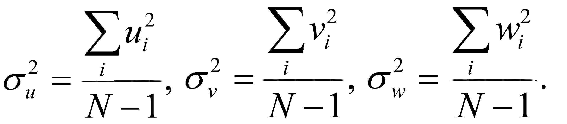
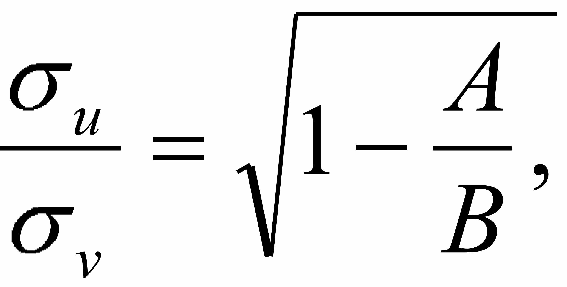
Еще легче получить по пространственным скоростям параметры выражения (9-7). Для этого надо просто вычислить соответствующие дисперсии компонентов остаточной скорости: В § 15.3 мы рассмотрим связь дисперсий скоростей с динамическими свойствами Галактики на примере модели стационарной Галактики. Стационарность при этом означает неизменность функции фазовой плотности со временем. Отметим только, что эта модель приводит к совершенно определенным соотношениям между дисперсиями компонентов остаточных скоростей. А именно, в этом случае две большие и равные по величине полуоси должны быть направлены на центр Галактики и перпендикулярно плоскости диска (в направлении оси z). Малая полуось должна быть направлена в сторону галактического вращения. А отношение малой полуоси к большой при этом определяется только кривой круговых скоростей вращения Галактики и для малой окрестности Солнца должно выполняться соотношение: где А и В есть так называемые постоянные Оорта, также определяемые из наблюдений. Отметим, что этот результат получается даже при более общих предположениях о форме распределения остаточных скоростей, чем задаваемое эллипсоидом Шварцшильда (9-7), так как здесь достаточно, чтобы плотность распределения скоростей имела вид f = f(Q) где Q есть полная квадратичная форма от компонент остаточной скорости, а функция f не обязательно являлась экспоненциальной. Также отметим, что при стандартных значениях постоянных Оорта (А = 15 км/с/кпк и В = -10 км/с/кпк) мы получаем отношение дисперсий Эту величину можно сравнить с результатами обработки наблюдательных данных.