 |
Астронет: А. В. Локтин, В. А. Марсаков Звездная астрономия в лекциях http://www.astronet.ru/db/msg/1245721/lec.3.1.html |
Определение расстояний до звёздных объектов
3.1 Геометрические методы определения расстояний до небесных тел
Рассмотрим способы оценки расстояний до объектов, не связанные с анализом электромагнитного излучения этих объектов. Разнообразие чисто геометрических методов определения расстояний является следствием разнообразия изучаемых космических объектов. Здесь мы не будем рассматривать определение расстояний до относительно близких объектов, таких как ИСЗ или планеты, где используются методы радио и оптической локации, и остановимся на определении расстояний до звёзд, которое является основой для определения галактических и внегалактических расстояний.
Первым из таких методов рассмотрим метод тригонометрических параллаксов. Расстояния до звёзд неизмеримо больше их диаметров, поэтому звёзды обычно рассматриваются как точечные объекты. При этом на протяжении десятков и сотен лет их движение относительно Солнца с большой степенью точности можно рассматривать как равномерное и прямолинейное. Если перенести систему координат в центр Земли, то в наблюдаемое движение звезды войдут движение Земли относительно Солнца и собственное движение звезды. В первом приближении движение Земли вокруг Солнца рассматривается как движение по кругу радиусом 1 а.е. с периодом T = 1 год. Таким образом, мы наблюдаем два движения - равномерное прямолинейное движение за счёт собственного движения и движение по кругу в плоскости, параллельной плоскости эклиптики.
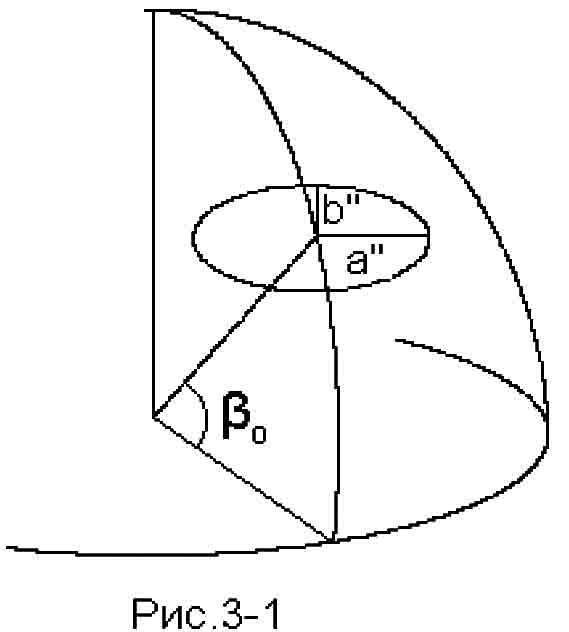
Проецируя движение звезды на плоскость, касательную к небесной сфере в точке, являющейся проекцией положения звезды (см. рис. 3-1), получим движение по эллипсу, большая ось которого равна a″, а малая - b″ = a″ sin β0(здесь β0 - эклиптическая широта звезды), и прямолинейное движение центра эллипса. Вследствие этого в эклиптической системе координат рассматриваемое движение представляется выражениями:
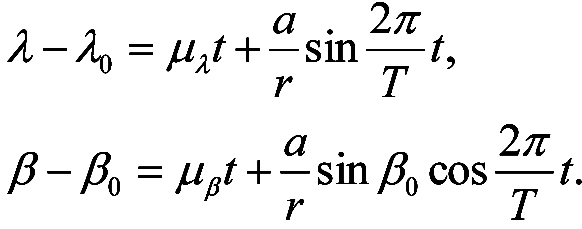
|
Здесь r - расстояние до звезды, 2π/Т - угловая скорость движения Земли по орбите вокруг Солнца, μ - соответствующая компонента собственного движения, выраженного в радианах, λ0 и β0 - эклиптические координаты центра эллипса.
Выражение a/r есть синус угла, под которым со звезды виден радиус земной орбиты. Этот угол, выраженный в секундах дуги, называется годичным параллаксом звезды, т.е. π = a/r. Часто сейчас вместо термина <годичный параллакс> используют словосочетание тригонометрический параллакс, чтобы резче подчеркнуть отличие тригонометрического метода определения расстояний от фотометрических и спектральных. Если расстояние выражено в астрономических единицах, то имеем r = 206265/π если же за единицу расстояния взять 206265 а.е., то имеем r = 1/π, такая единица измерения расстояния называется парсек, т.е. π = a/r. Это расстояние, с которого радиус земной орбиты виден под углом в одну угловую секунду. Умножив число секунд в радиане на величину астрономической единицы в километрах, получим, что 1 парсек равен приблизительно 3.1× 1013 км.
Выражения (3-1) можно использовать для определения тригонометрических параллаксов звёзд. На практике определяют большое число положений звёзд в течение достаточно большого промежутка времени (порядка года и больше), например фотографическим методом, и используют первое из выражений (3-1), чаще всего переписанное для экваториальных координат, получая значение тригонометрического параллакса методом наименьших квадратов. При этом обычно используются относительные определения, когда определяются смещения координат измеряемых звёзд относительно группы слабых звёзд, для которых тригонометрические параллаксы можно считать близкими к нулю. В таблице 3-1 приведены наземные определения тригонометрических параллаксов нескольких ярких звёзд. Из таблицы видно, что даже самые близкие к Солнцу звёзды имеют тригонометрические параллаксы менее одной угловой секунды. Обратим внимание, что среди самых визуально ярких звёзд некоторые оказываются весьма далекими от нас.
Таблица 3-1
| Звезда | π″ | Звезда | π″ | |||
| α CMa (Сириус) | 0.375 | α CMi (Процион) | 0.288 | |||
| α Boo (Арктур) | 0.090 | α Ori (Бетельгейзе) | 0.005 | |||
| α Lyr (Вега) | 0.123 | α Proxima Cen | 0.762 | |||
| α Aur (Капелла) | 0.073 | α Cen A | 0.754 | |||
| β Ori (Ригель) | 0.001 | α Звезда Барнарда | 0.552 | |||
Следующим важнейшим геометрическим методом определения расстояний является метод движущегося скопления. Среди близких к Солнцу рассеянных скоплений и звёздных групп имеется несколько так называемых движущихся, т.е. имеющих заметное общее для звёзд группировки собственное движение, что говорит о не очень большом расстоянии группировки от Солнца. Направления собственных движений звёзд, принадлежащих таким группам, пересекаются в точке радианта. Этот эффект является следствием известного из теории перспективы схождения параллельных линий, который очень четко показывают метеоры, принадлежащие одному потоку.
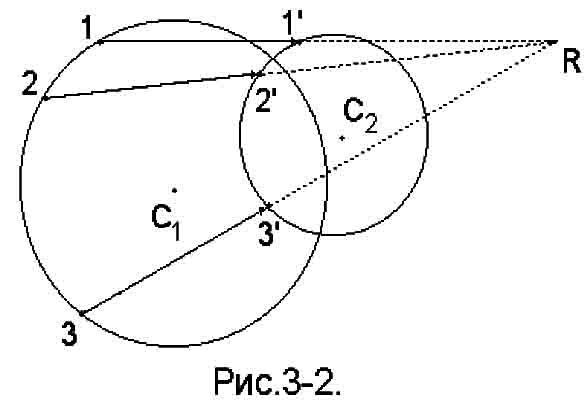 В нашем случае радиант есть точка пересечения больших кругов, проведенных через звёзды в направлении их собственных движений. Этот эффект поясняется рисунком 3-2. На рисунке большой окружностью схематически показано звёздное скопление в проекции на небесную сферу в некоторый момент в прошлом, а меньшей окружностью - то же скопление, удалившееся от нас за некоторое время, что привело к уменьшению его угловых размеров и смещению его центра за счёт собственного движения скопления в целом. Ясно, что мы выбрали пример, когда лучевая скорость скопления положительна. Точками 1, 2, 3 изображены три звезды и смещение этих звёзд в точки 1', 2', 3' за счёт собственного движения. Буквой R обозначено положение радианта.
В нашем случае радиант есть точка пересечения больших кругов, проведенных через звёзды в направлении их собственных движений. Этот эффект поясняется рисунком 3-2. На рисунке большой окружностью схематически показано звёздное скопление в проекции на небесную сферу в некоторый момент в прошлом, а меньшей окружностью - то же скопление, удалившееся от нас за некоторое время, что привело к уменьшению его угловых размеров и смещению его центра за счёт собственного движения скопления в целом. Ясно, что мы выбрали пример, когда лучевая скорость скопления положительна. Точками 1, 2, 3 изображены три звезды и смещение этих звёзд в точки 1', 2', 3' за счёт собственного движения. Буквой R обозначено положение радианта.
Если известны координаты радианта и лучевые скорости хотя бы для нескольких звёзд скопления, можно надежно определить индивидуальные параллаксы звёзд - членов движущегося скопления. Зная прямое восхождение A и склонение D радианта, легко определить угловое расстояние каждой звезды - члена скопления от радианта (на рис.3-2 это отрезки 1'- R, 2'- R, 3' - R) по формуле:
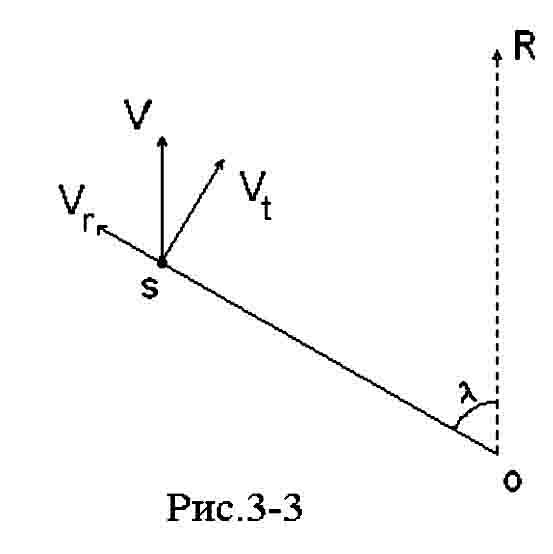 Из рис.3-3, на котором в точке О находится наблюдатель, R обозначает направление на радиант, а в точке S находится наблюдаемая звезда, видно, что Vr = V cos λ, где V есть пространственная скорость скопления. Измерив лучевую скорость для нескольких звёзд скопления, можно получить оценку средней пространственной скорости скопления . Тангенциальная скорость звезды есть:
Из рис.3-3, на котором в точке О находится наблюдатель, R обозначает направление на радиант, а в точке S находится наблюдаемая звезда, видно, что Vr = V cos λ, где V есть пространственная скорость скопления. Измерив лучевую скорость для нескольких звёзд скопления, можно получить оценку средней пространственной скорости скопления . Тангенциальная скорость звезды есть:
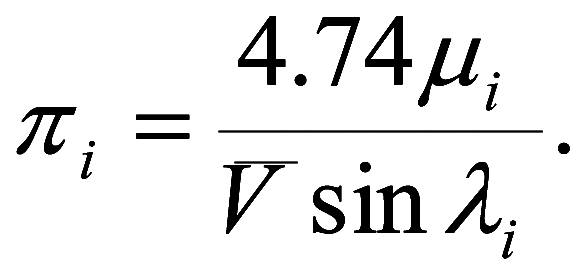
|
| r = d ctga |
M¤