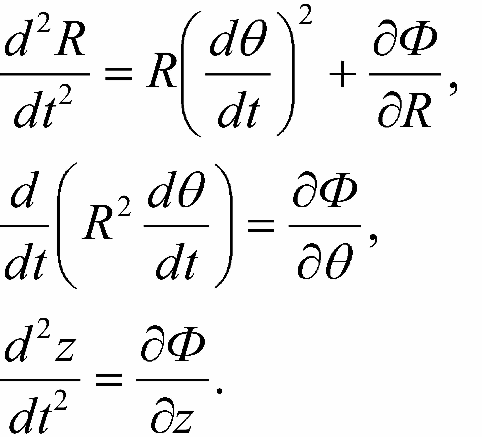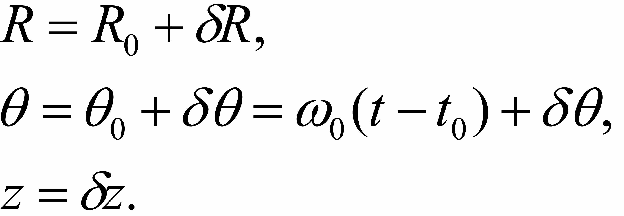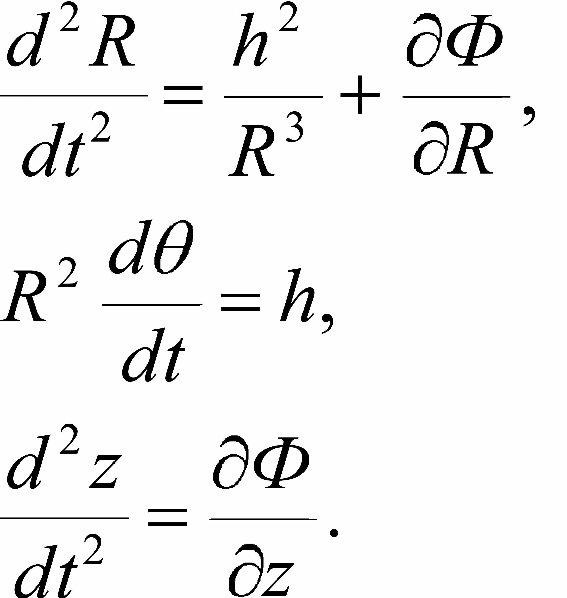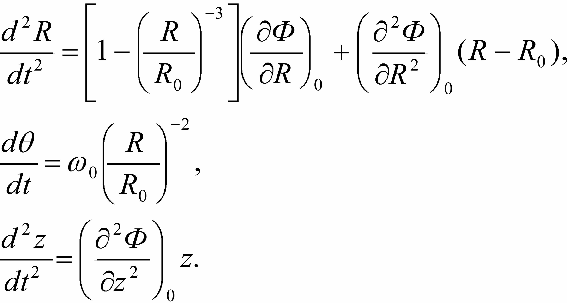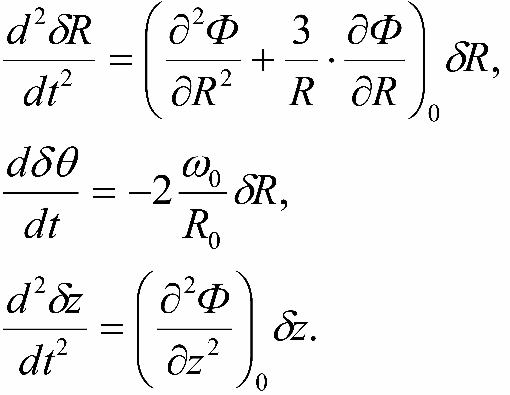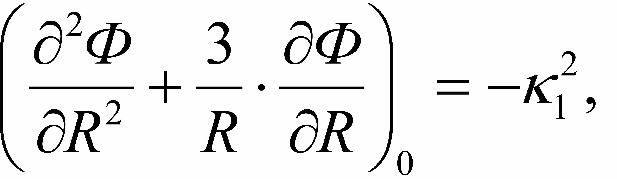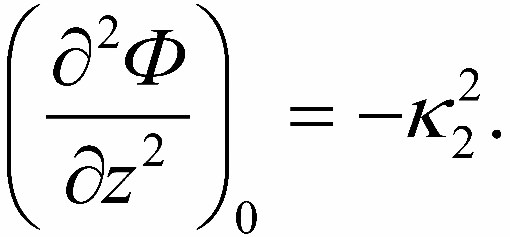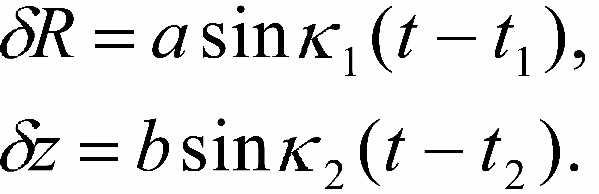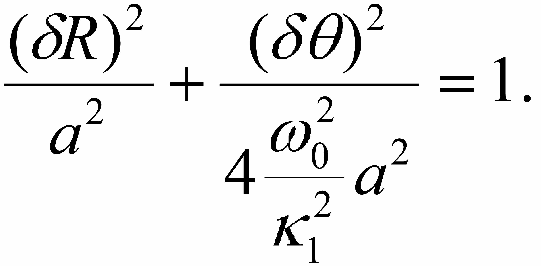16.1 Эпициклическое приближение
Изучение движений звёзд удобно проводить, используя аппарат исследования галактических орбит, так как орбиты связывают наблюдаемые движения звёзд со свойствами гравитационного потенциала Галактики. При этом результаты исследований выражаются в более наглядной форме, чем, например, при использовании дисперсий скоростей. Изучение галактических орбит используется при исследовании устойчивости звёздных группировок, например движущихся эггеновских групп. Понятно, что галактические орбиты всех объектов ограничены в пространстве, иначе Галактика слилась бы с фоном. Так как даже галактический диск имеет ненулевую толщину, орбиты трехмерны и в общем случае незамкнуты.
Ранее мы уже сделали вывод, что орбиты звезды диска должны быть близки к круговым, поскольку их остаточные скорости существенно меньше скорости вращения Галактики. В этом случае мы можем линеаризовать уравнения движения и получить интегрируемую систему дифференциальных уравнений. Уравнения движения звезды в цилиндрической системе координат, подходящей для нашей осесимметричной Галактики, имеют вид:
В этих выражениях
Ф = Ф(R,Θ, z) есть гравитационный потенциал Галактики. Задав значения пространственных координат и компоненты скорости звезды в некоторый начальный момент времени, можно вычислить положение объекта в любой последующий момент, решив систему (16-1).
Пусть гравитационный потенциал Галактики имеет цилиндрическую симметрию: Ф = Ф(R,z) . Тогда второе уравнение (16-1) интегрируется и дает так называемый интеграл площадей:
Уравнения (16-1) - (16-2) решаются аналитически только в отдельных, мало интересных частных случаях, например, для кеплеровских орбит, когда вся масса, создающая поле тяготения, сосредоточена в точке. Однако даже для таких простых форм потенциала, как потенциал Паренаго, аналитических решений не существует. Поэтому для исследования свойств галактических орбит приходится искать упрощающие предположения.
Движение по орбите, близкой к круговой, можно представить как сумму двух движений: движения по круговой орбите и небольшие отклонения от этого движения. Запишем пространственные координаты звезды в виде координат точки, движущейся по круговой орбите и малых поправок:
Здесь R
0 = const - радиус некоторой круговой орбиты, соответствующей заданной кинетической энергии звезды, и целиком лежащей в плоскости Галактики, а Θ
0 - азимутальный галактоцентрический угол, соответствующий движению по этой орбите. Назовем, для краткости, рассматриваемую орбиту варьированной. Определим R
0 так, чтобы постоянная площадей h для соответствующей круговой орбиты равнялась значению этой постоянной для рассматриваемой варьированной орбиты. Перепишем уравнения (16-1) с помощью интеграла площадей в виде:
Определим частоту вращения Галактики на расстоянии R
0 от оси ее вращения из интеграла площадей как
ω0 = h / R02. В этом случае из первого уравнения системы (16-1) можно получить:
где нулевой индекс означает взятие производной в точке R
0. Разлагая с использованием этого выражения потенциал
Ф = Ф(R,z) в ряд по степеням малых величин
(R - R0) и z и оставляя в выражениях первые степени координат, получаем:
Теперь подставим в эту систему выражения (16-4), пренебрегая вторыми и более высокими степенями вариаций переменных. Получим систему:
Легко увидеть, что выражения в скобках первого и третьего уравнений отрицательны. Поэтому можно ввести обозначения:
Теперь хорошо видно, что первое и третье уравнения представляют собой уравнения малых колебаний и легко интегрируются. Получаем:
Здесь a, b, t
1, t
2 - постоянные интегрирования. Подставляя первое из выражений (16-11) во второе уравнение (16-8) получаем:
Таким образом, в плоскости Галактики точка, движущаяся по почти круговой орбите, описывает эллипс относительно точки, движущейся по соответствующей круговой орбите. По координате z точка при этом совершает гармонические колебания. Так как частоты колебаний в плоскости Галактики и z-направлении не совпадают, орбита получается не замкнутой, не лежит в плоскости и при движении объекта она заполняет симметричную относительно плоскости Галактики трехмерную торообразную фигуру вращения.
Исключая время из первого выражения (16-10) и выражения (16-11), получаем уравнение эллипса:
Движение по эллипсу в рассмотренном приближении напоминает движение по эпициклу, поэтому это приближение называется
эпициклическим приближением, а величину называют эпициклической частотой. Величину при этом можно назвать эпициклической амплитудой. Легко показать, используя выражение (16-9), что эпициклическая частота может быть оценена через постоянные Оорта:
Для принятых нами в качестве стандартных значений А = 15 км/с/кпк и В = -10 км/с/кпк, получаем для эпициклической частоты величину 31.6 км/с/кпк. Это означает, что период эпициклических колебаний составляет около 80% от периода вращения Галактики на солнечном галактоцентрическом расстоянии.
Величину к22 - квадрат частоты колебаний в направлении оси z, называют динамическим параметром, и обозначают C2. В звёздной динамике выводится выражение, связывающее эту частоту с дисперсией скоростей в z-направлении и градиентом плотности вещества в плоскости Галактики:
где
ρ - плотность вещества - функция, зависящая от координат. Величины в правой части выражения (16-14) можно найти из наблюдений и оказывается, что в окрестностях Солнца
период колебаний в z-направлении составляет около 45% от периода вращения диска Галактики. Для получения величины логарифмического градиента плотности, входящей в выражение (16-14), достаточно взять звёзды одного типа, например красные гиганты, и провести звёздные подсчёты.
Рассмотрим, наконец, как получаются динамические оценки плотности вещества Галактики в окрестностях Солнца. Запишем уравнение Пуассона в цилиндрической системе координат:
Можно показать, что первые два слагаемых выражаются через постоянные Оорта:
Третье слагаемое в левой части (16-16) есть определенный нами выше динамический параметр. В результате для определения плотности вещества в окрестностях Солнца получаем:
Именно это выражение использовалось для получения приведенного ранее (см.
12.1) значения плотности вещества в окрестностях Солнца. В привычных единицах принятые нами значения постоянных Оорта и величина C = 70 км/с/кпк приводит к значению
ρ ≈ 6 • 10-24 г/см3 .