Координаты в звёздной астрономии
Оглавление
Изучение астрономических объектов естественно начинать с фиксации положений этих объектов в какой-либо системе координат. Главной системой координат, используемой в звёздной астрономии, является галактическая система координат. Экваториальная система координат, которую обычно астрономы используют для определения положений и движений небесных объектов, никак не связана с положениями и движением этих объектов в Галактике. То же можно сказать и об эклиптической системе координат. Галактическая система координат непосредственно связана с существованием в нашей Галактике сильной концентрации многих объектов к плоскости Млечного Пути. Для этой системы координат основной плоскостью является плоскость симметрии нашей Галактики. Отметим, что Солнце не лежит в плоскости Галактики, его положение смещено приблизительно на 10 парсек в сторону северного галактического полюса. Северный полюс Галактики находится в созвездии Волосы Вероники и для него в настоящее время приняты следующие значения экваториальных координат AG = 192њ.85948, DG = +27њ.12825 на равноденствие 2000.0 (до недавнего времени принимали AG = 12h49m = 192њ.25, DG = +27њ.4 на равноденствие 1950.0). Южный полюс Галактики находится в созвездии Скульптора. Галактическая долгота l отсчитывается от направления на центр Галактики против часовой стрелки, если смотреть с ее северного полюса. Галактическая широта b отсчитывается от плоскости Галактики в направлении ее полюса, прочем широта cчитается положительной по направлению к северному полюсу Галактики, и отрицательной - к южному. Галактические координаты не меняются со временем, как меняются экваториальные координаты вследствие прецессии земной оси, так как с Землей они не связаны.
Рассмотрим переход от экваториальных координат к галактическим. Ранее для этого широко использовались таблицы, которые приводились в любом руководстве по звёздной астрономии. В настоящее время используют соответствующие программы. На рис.1-1 показана небесная сфера, на которой указаны северный полюс мира (Pm), северный полюс Галактики (Pg) и объект S. Для полярного треугольника легко записать формулы, связывающие экваториальные и галактические координаты:
|
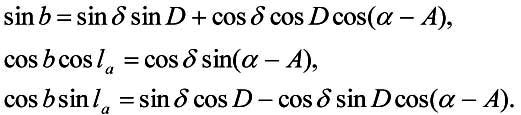
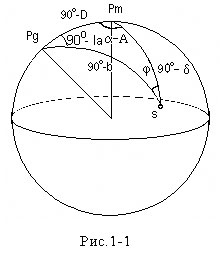Указанная на рис.1-1 и в формулах (1-1) величина la отсчитывается от точки пересечения небесного и галактического экваторов (величина галактической долготы восходящего узла галактического экватора в настоящее время принята равной 32њ.93192), а не от направления на центр Галактики. Поэтому, чтобы получить значения галактических долгот, отсчитываемых от центра Галактики, необходимо добавить к величинам , получаемым из выражений (1-1), поправку, равную галактической долготе северного полюса мира - 122њ.93192.. (Отметим, что поскольку галактическая долгота изменяется в диапазоне (0њ - 360њ), для ее правильного определения необходимы два уравнения.)
До 1970г. иногда использовалась старая (так называемая - первая) система галактических координат, где долгота как раз и отсчитывалась от точки пересечения небесного и галактического экваторов. В старой галактической системе, обозначавшейся верхним индексом I, координаты центра Галактики были равны l1=327њ.69 и b1=-1њ.40 В старых работах и в некоторых каталогах новые галактические координаты (вторая система) обозначались индексом II. Вторая система галактических координат изначально была основана на радионаблюдениях нейтрального водорода, но после запуска искусственного спутника Hipparcos были уточнены координаты Северного полюса Галактики. В настоящее время последние уточнения утверждены съездом МАС.
Формулы для пересчёта собственных движений из экваториальной системы координат в галактическую легко получить дифференцированием выражений (1-1) по времени, считая экваториальные координаты функциями времени, так как собственные движения представляют собой изменения со временем угловых координат объектов. Можно поступить и по другому. Чтобы получить вектор с компонентами (µ l, µb ) из вектора ( µl, µb ) , необходимо осуществить поворот системы координат, связанной с объектом S на угол, составляемый на небесной сфере большими кругами, проходящими через объект и полюс мира, объект и полюс Галактики (см. рис.1-1). В этом случае:
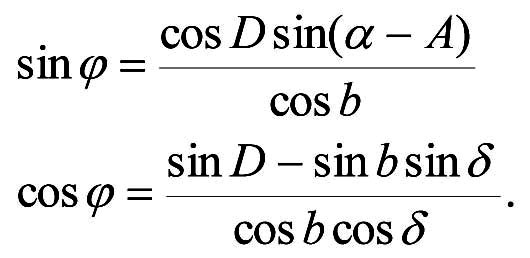
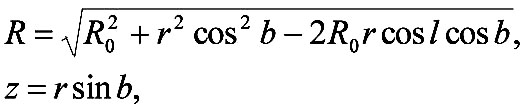
Выражения для тригонометрических функций угла φ легко получить, рассматривая полярный треугольник на рис. 1-1 (приводятся окончательные выражения):
Еще одной системой координат, часто используемой при анализе структуры, кинематики и динамики Галактики, является цилиндрическая галактоцентрическая система координат (R, Θ,z). Здесь R есть расстояние объекта от оси вращения Галактики, z - расстояние объекта от плоскости Галактики, - угол между направлениями на объект и на Солнце из центра Галактики. Система координат задается галактической плоскостью и перпендикулярной к этой плоскости осью, пересекающей плоскость в центре Галактики и совпадающей с ее осью вращения. Для перехода от галактической системы координат
(r,l,b) , где r - расстояние объекта от Солнца, к системе (R,Θ,z) следует использовать формулы:
где R
0 есть расстояние Солнца от центра Галактики, а угол между линией Солнце-центр Галактики и линией объект-центр Галактики (галактоцентрический угол) легко найти, еще раз применив теорему косинусов:
Дифференцируя формулы (1-4) - (1-5) по времени, можно получить формулы перехода от лучевых скоростей v
r и компонент собственного движения (µ
l, µ
b ) к компонентам скорости в цилиндрической галактоцентрической системе координат (v
R, v
Θ,v
Z ), вычисляя компоненты тангенциальной скорости через собственные движения
и
и поворачивая систему координат на угол Θ (помня при этом, что R
0 =const). Величина постоянной k равна частному от деления количества километров в астрономической единице на число секунд в тропическом году k = 4.74064 км/с, обычно в звёздноасторомических задачах достаточно округленной величины 4.74.
