Астронет > Лекции о формировании и ранней эволюции планетных систем

Астронет: Филип Армитедж, Виктория Воробьева Лекции о формировании и ранней эволюции планетных систем
http://variable-stars.ru/db/msg/1223087/part2.html

II. Протопланетные диски

А. Окружение формирующихся звезд

Звезды и сегодня образуются в Галактике из газа, сосредоточенного в небольших и плотных ядрах молекулярных облаков. Молекулярные облака наблюдаются в одной или нескольких молекулярных линиях (например, в линиях СО, ¹³СО и NH₃), каждая из которых может быть использована как для исследования областей с различной плотностью, так и для получения информации о движении газа (такого, как вращение, сжатие и т.п.). Наблюдения плотных, маленьких по размерам ядер молекулярных облаков (с размерами порядка 0.1 пк), которые являются непосредственными предшественниками формирующихся звезд, показывают градиенты скорости, равные по порядку величины 1 км/с на 1 пк. Даже если весь этот градиент приписать вращению, параметр

$\beta\equiv\frac{E_{\mathrm{rot}}}{|E_{\mathrm{grav}}|}$ (9)

оказывается маленьким: часто по порядку величины он равен 0.01. Следовательно, вращение не является особенно важным на ранних стадиях коллапса. С другой стороны, угловой момент ядра молекулярного облака оказывается большим, по порядку величины равным J_core ~ 10⁵⁴ г см²/сек. Этот угловой момент гораздо больше углового момента Солнечной системы, не говоря уж про Солнце – несоответствие, которое названо "проблемой углового момента при формировании звезд". Полное решение этой проблемы заключается в возможности формирования двойной звездной системы, потере углового момента при истечении вещества и формировании диска. Для наших целей достаточно отметить, что характерный угловой момент газа в ядре молекулярного облака соответствует характерному угловому моменту газа на кеплеровской орбите вокруг звезды солнечной массы с орбитальным расстоянием 10–100 а.е.

Подведя черту, отметим, что наблюдаемые свойства ядер молекулярных облаков совместимы с формированием больших дисков – размером с Солнечную систему и больше – вокруг недавно сформировавшихся звезд. Сразу после своего формирования эти диски могут быть весьма массивны.

Рисунок 7. Схематическая иллюстрация распределения энергии в спектре молодой звезды, окруженной диском. Существование диска выводится из инфракрасного избытка в спектре (относительно ожидаемых величин, вычисленных из знания температуры фотосферы молодой звезды) на длинах волн порядка 1 мм. Часто наблюдается также ультрафиолетовый избыток, который является признаком аккреции газа на поверхность звезды, приводящей к появлению горячих пятен.

Молодые звездные объекты классифицируются по форме их спектров в инфракрасном диапазоне. Как показывает Рисунок 7, молодые звездные объекты часто демонстрируют:

Инфракрасный избыток в спектре как признак наличия горячей пыли в околозвездном диске.
Ультрафиолетовый избыток в спектре, который говорит о наличии на поверхности звезды областей с высокой температурой (горячих пятнах), где аккумулируется газ из диска.

Чтобы определить величину инфракрасного избытка в спектре, полезно ввести меру наклона спектра между ближним ИК–диапазоном (2.2 мкм) и средним ИК–диапазоном (10 мкм):

$\alpha_{\mathrm{IR}}=\frac{\Delta\log(\lambda F_\lambda)}{\Delta\log\lambda}$ (10)

Мы будем классифицировать молодые звездные объекты как:

Объекты нулевого класса: спектр имеет максимум в дальнем ИК или миллиметровом диапазоне (~100 мкм).
Объекты первого класса: плоский спектр или спектр, возрастающий к среднему ИК–диапазону (a_ir > 0).
Объекты второго класса: спектр, падающий к среднему ИК–диапазону (–1.5 < a_ir < 0). К этому классу относятся классические звезды типа Т Тельца.
Объекты третьего класса: звезды, почти достигшие главной последовательности с небольшим или отсутствующим инфракрасным избытком. Они называются "звезды типа Т Тельца со слабой линией H" (заметим, что хотя эти объекты определены через эквивалентную ширину линии Нα, наличие линии является признаком аккреции, который хорошо коррелирует с наличием инфракрасного избытка).

Эта схема классификации объектов, основанная на наблюдениях, получила и теоретическую интерпретацию, отчасти как эволюционная последовательность (Adams, Lada & Shu, 1987). В частности, ранние объекты нулевого класса, теряя свои диски, становятся объектами второго класса и, в конечном счете, становятся объектами третьего класса. Угол наклона системы к лучу зрения тоже играет важную роль: в зависимости от него объект может выглядеть как объект первого или второго класса.

Б. Пассивные околозвездные диски

Существует важное физическое различие между пассивными околозвездными дисками, которые только переизлучают свет звезды, и активными дисками, которые перерабатывают потенциальную гравитационную энергию газа в энергию газовых потоков. Для диска с приростом массы $\dot М$ , вращающимся вокруг звезды со светимостью L и радиусом R, равным двум солнечным радиусам, критическая скорость аккреции, ниже которой энергией аккреции можно пренебречь, может быть оценена как:

$\frac{1}{4}L_\odot=\frac{GM_*\dot M}{2R_*}\,,$ (11)

где учитывается, как будет показано ниже, что диск перехватывает примерно четверть светового потока от звезды. Численно

$\dot M \approx 3\times10^{-8}M_\odot/\textrm{год}\,.$ (12)

Скорость аккреции, измеренная у классических звезд типа Т Тельца, меняется по порядку величины от значения выше критической до значений на два порядка ниже. Таким образом, нельзя считать, что протопланетные диски являются или всегда пассивными, или всегда активными. Скорее, тепловая структура дисков на ранних стадиях больше напоминает структуру активного диска с выделением тепла из–за аккреции, а на поздних стадиях преобладает простое переизлучение света звезды.

1. Вертикальная структура

Вертикальная структура геометрически тонкого диска (не важно, активного или пассивного) определяется рассмотрением вертикального гидростатического равновесия (Рисунок 8):

$\frac{dP}{dz}=-\rho g_z\,,$ (13)

где ρ – плотность газа. Игнорируя гравитационное влияние диска (обычно это оправданно), получим, что вертикальный компонент силы притяжения, действующий на цилиндрический объем газа с радиусом r и высотой над усредненной плоскостью диска z, равен:

$g_z=\frac{GM_*}{d^2}\sin\theta=\frac{GM_*}{d^3}z\,.$ (14)

Для тонкого диска z<<r, и

$g_z\simeq \Omega^2z\,,$ (15)

где Ω=(GM_*/r³)^1/2 – кеплеровская угловая скорость. Если мы для простоты предположим, что диск является вертикально изотермическим (что является хорошим приближением для пассивного диска и не очень хорошим для активного диска), тогда уравнение состояния будет: Р=ρс_s², где с_s – скорость звука. Уравнение гидростатического равновесия (формула 13) тогда может быть переписана как:

$c_s^2\frac{d\rho}{dz}=-\Omega^2\rho z\,.$ (16)

Это уравнение имеет решение:

$\rho=\rho(z=0)e^{-z^2/h^2}\,,$ (17)

где h – вертикальный масштаб уменьшения плотности,

$h=\sqrt{2\,}\frac{c_s}{\Omega}\,.$ (18)

Сравнивая толщину диска с его радиусом, получим:

$\frac{h}{r} \approx \frac{c_s}{v_\phi}\,,$ (19)

где vφ – локальная орбитальная скорость. Мы видим, что толщина диска h/r пропорциональна числу Маха газового потока.

Рисунок 8. График для вычисления вертикального гидростатического равновесия в околозвездном диске.

Рисунок 9. График для вычисления температурного профиля плоского пассивного диска. Мы рассматриваем поверхность единичной площади в плоскости диска на расстоянии r от звезды радиуса R_*. Ось сферических полярных координат – линия между поверхностью и центром звезды, причем угол φ=0 в направлении на полюс звезды.

Форма диска зависит от отношения h(r)/r. Если мы параметризуем изменения радиальной скорости звука как

$c_s \propto r^{-\beta}\,,$ (20)

тогда зависимость толщины диска от радиуса будет

$\frac{h}{r}\propto r^{-\beta+1/2}\,.$ (21)

Диск будет толстым (т.е. h/r будет увеличиваться с увеличением радиуса, делая диск похожим на шар), если β < 1/2. Для этого требуется, чтобы температурный профиль T(r)~r^-1 или более пологий. Как мы коротко покажем, толстые диски – нормальное явление, особенно близко от звезды.

2. Радиальный температурный профиль

Физика вычислений радиального температурного профиля пассивного диска была описана в работах Adams & Shu (1986), Kenyon & Hartmann (1987) и Chiang & Goldreich (1997). Мы начнем рассмотрение с простейшей модели тонкого плоского диска, в экваториальной плоскости которого поглощается все попавшее на него звездное излучение и переизлучается по закону черного тела в соответствии с локальной температурой. Нагревом звезды диском пренебрегаем.

Рассмотрим поверхность в плоскости диска на расстоянии r от звезды радиуса R. Звезда представлена сферой с постоянной яркостью I. Введя сферические полярные координаты, как это показано на Рисунке 9, мы получим, что поток звездного света, проходящий через эту поверхность, равен:

$F=\int I_*\sin\theta\cos\phi d\Omega\,.$ (22)

Мы учитываем только поток, приходящий от верхней половины звезды, и излучение только верхней половины диска. Тогда пределы интегрирования будут:

$-\pi/2 < \phi \leq \pi/2\,,$
$0 < \theta < \sin^{-1} \left(\frac{R_*}{r}\right)\,.$ (23)

Подставляя dΩ = sin θ dθ dφ, получим интеграл для излучения:

$F=\int_{-\pi/2}^{\pi/2} \cos\phi d\phi \int_0^{\sin^{-1}(R_*/r)}\sin^2\theta d\theta\,,$ (24)

который равен

$F=I_* \left[ \sin^{-1}\left(\frac{R_*}{r}\right) -\left(\frac{R_*}{r}\right) \sqrt{1-\left(\frac{R_*}{r}\right)^2\,} \right]\,.$ (25)

Для звезды с эффективной температурой Т яркость I_*=(1/π)σT_*⁴, здесь σ – постоянная Стефана-Больцмана. Приравнивая F к излучению одной стороны диска σТ_диска⁴, мы получим радиальный температурный профиль:
$\left(\frac{T_{\mathrm{disk}}}{T_*}\right) = \frac{1}{\pi} \left[\sin^{-1}\left(\frac{R_*}{r}\right) -\left(\frac{R_*}{r}\right) \sqrt{1-\left({R_*}{r}\right)^2\,} \right]\,.$ (26)

Интегрируя по радиусу, мы получим полную яркость диска:

$F=2\times\int_{R_*}^\infty 2\pi r\sigma T_{\mathrm{disk}}^4 dr = \frac{1}{4} F_*\,.$ (27)

Мы пришли к выводу, что плоский пассивный диск, охватывающий звездный экватор, перехватывает четверть звездного излучения. Отношение наблюдаемой болометрической яркости такого диска к яркости звезды будет меняться в зависимости от угла наклона системы к лучу зрения, но в любом случае яркость диска всегда меньше яркости звезды. Форма температурного профиля, полученная из выражения (26), не слишком очевидна. Разлагая правую часть уравнения по Тейлору (и считая R << r, т.е. речь идет о диске достаточно далеко от звездной поверхности), получим:

$T_{\mathrm{disk}} \propto r^{-3/4}\,,$ (28)

как предельный температурный профиль тонкого, плоского, пассивного диска. Для газа с постоянной молекулярной массой mu это приводит к профилю скорости звука

$c_s \propto r^{-3/8}\,.$ (29)

Считая диск вертикально изотермичным, мы получим и выражение для толщины диска:

$\frac{h}{r} \propto r^{1/8}\,,$ (30)

и предсказываем, что диск должен немного расширяться с ростом расстояния до звезды. Если это действительно происходит, то внешние части диска перехватывают большую долю звездного света и нагреваются до более высоких температур. Следовательно, температурный профиль T_disk ∝ r^-3/4 – самый крутой профиль, который можно получить для пассивного диска.

Рисунок 10. Здесь схематически показан спектр диска. На коротких волнах мы видим экспоненциальное спадание, соответствующее высокотемпературному кольцу диска (обычно на внутреннем краю). На длинных волнах расположен "хвост" Рэлея–Джинса, отражающий излучение холодного материала во внешней части диска. На средних волнах находится плоская часть спектра, так как полный спектр отражает излучение протяженного черного тела.

3. Распределение энергии в спектре

Предположим, что каждое кольцо в диске излучает как абсолютно черное тело с локальной температурой Т_disk(r). Если диск простирается от rin до rout, спектр диска является суммой спектров таких тел:

$F_\lambda \propto \int_{r_{in}}^{r_{out}} 2\pi r B_\lambda[Е(r)] dr\,,$ (31)

где B_λ – функция Планка:

$B_\lambda(T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{hc/\lambda kT}-1}\,,$ (32)

Поведение спектра, выраженного выражением (31), легко представить. На длинных волнах (λ >> hc/kT(r_out)) мы возвращаемся к формуле Рэлея-Джинса:

$\lambda F_\lambda \propto \lambda^{-3}\,,$ (33)

тогда как для коротких волн (λ << hc/kT(r_in)) наблюдается экспоненциальное спадание энергии в спектре, что соответствует самому горячему краю диска:

$\lambda F_\lambda \propto \lambda^{-4} e^{-hc/\lambda kT(r_{in})}\,.$ (34)

Для промежуточных длин волн

$\frac{hc}{kT(r_{in})} \ll \lambda \ll \frac{hc}{kT(t_{out})}$ (35)

формируется спектр, который может быть найден подстановкой

$x\equiv \frac{hc}{\lambda kT(r_{in})} \left(\frac{r}{r_{in}}\right)^{3/4}$ (36)

в уравнение (31). Мы имеем тогда, приблизительно,

$F_\lambda \propto \lambda^{-7/3} \int_0^\infty \frac{x^{5/3}dx}{e^x-1} \propto \lambda^{-7/3}$ (37)

$\lambda F_\lambda \propto \lambda^{-4/3}\,.$ (38)

Общий вид спектра, схематически показанный на Рисунке 10, является спектром "протяженного" черного тела (Lynden-Bell, 1969).

Распределение энергии в спектре, предсказанное этой простой моделью, демонстрирует инфракрасный избыток, но с понижением в области средних инфракрасных волн. Это слишком круто, чтобы соответствовать наблюдениям даже источников второго класса.

4. Эскиз более полных моделей

Для вычисления детального вида спектра пассивного плоского диска необходимо учитывать еще два обстоятельства. Первое, как было показано выше, заключается в том, что диск расширяется с ростом r, и, как следствие, поглощает и перерабатывает большую долю звездного света. Для больших r Kenyon & Hartmann (1987) нашли, что расширяющиеся по мере удаления от звезды дисковые модели приводят к температурному профилю

$T_{\mathrm{disk}} \propto r^{-1/2}\,,$ (39)

который более плоский, чем профиль, полученный выше. Второе обстоятельство заключается в том, что предположение о чернотельном характере излучения диска оказывается слишком простым. Фактически пыль в поверхностном слое диска излучает как более нагретое тело, потому что она гораздо эффективнее поглощает звездный свет на более коротких волнах, чем излучает в среднем инфракрасном диапазоне (Shlosman & Begelman, 1989). Частицы пыли размером а эффективно поглощают свет с длиной волны λ < 2πa, но плохо поглощают и излучают волны с длиной волны λ > 2πa. В результате диск поглощает звездный свет вблизи своей поверхности (где оптическая глубина порядка единицы), но в этой области оптическая глубина на излучение в дальнем инфракрасном диапазоне оказывается много меньше единицы. Излучение, приходящее из поверхностного слоя диска, оказывается более горячим, чем это было предсказано в модели "протяженного черного тела".

Chiang & Goldreich (1997) показали, что относительно простая дисковая модель, включающая в себя:

Горячий поверхностный слой пыли, который непосредственно переизлучает половину звездного света, и
Более холодную внутреннюю часть диска, которая перерабатывает вторую половину звездного света в тепловое излучение,

с учетом расширения диска по краям, может прекрасно воспроизводить большинство наблюдаемых спектров. Обзор недавних работ по моделированию дисков сделан Dullemond et al. (2007).

Приведенные выкладки в принципе достаточны для того, чтобы понять структуру и форму спектра источников второго класса. Однако для источников первого класса возможно наличие оболочки (состоящей из газа и пыли, продолжающих падать на протозвезду с протопланетным диском), что также нуждается в рассмотрении. Направляем читателя к Eisner et al. (2005) для изучения одного из примеров моделирования таких систем.

В. Активные аккреционные диски

Радиальный баланс сил в пассивном диске включает в себя вклад гравитации, центробежной силы и радиального градиента давления. Запишем соответствующее уравнение:

$\frac{v_\phi^2}{r} = \frac{GM_*}{r^2} + \frac{1}{\rho}\frac{dP}{dr}\,,$ (40)

где vφ – радиальная скорость газа, Р – давление.

Чтобы оценить величину градиента давления, заметим, что

$\frac{1}{\rho}\frac{dP}{dr} \sim -\frac{1}{\rho}\frac{P}{r} \sim -\frac{1}{\rho}\frac{\rho c_s^2}{r} \sim -\frac{GM_*}{r^2} \left(\frac{h}{r}\right)^2\,,$ (41)

где на последнем шаге мы сделали подстановку h ~ c_s/Ω. Если v_K – кеплеровская скорость на расстоянии r от звезды, то мы имеем:

$v_\phi^2 = v_{K}^2 \left[ 1-{\cal O}\left(\frac{h}{r}\right)^2 \right]\,,$ (42)

т.е. в случае тонкого (h << r)^*** диска градиентом газового давления можно пренебречь по сравнению с кривой вращения газа.

^***[Однако это не означает, что градиент давления вообще не важен. Как мы увидим дальше, небольшая разница между v и vk приобретает огромное значение для динамики небольших камешков в диске.]

С очень небольшой погрешностью можно сказать, что угловой момент газа в диске равен угловому моменту движения по соответствующей кеплеровской орбите:

$\ell = r^2\Omega = \sqrt{GM_*r\,}\,,$ (43)

который является возрастающей функцией r. Падая на звезду, газ в диске должен утратить угловой момент:

Через перераспределение углового момента в диске (обычно описываемое как "вязкость", хотя это не совсем точный термин),
Через утрату углового момента из системы звезда+диск, например, путем истечения намагниченного дискового ветра.

Модели второго класса – есть хорошо известный пример, в котором решение для дискового ветра было получено Blandford & Payne (1982) – широко не обсуждаются (возможно, незаслуженно) – в частности, потому, что в нескольких белых карликах, окруженных аккреционными дисками, наблюдаются неблагоприятные (disfavor) модели ветра, хотя там нет ограничений, существующих для протопланетных дисков. Здесь мы получим уравнения для времени эволюции поверхностной плотности тонкого вязкого диска (Lynden–Bell & Pringle, 1974; Shakura & Sunyaev, 1973). Хороший обзор фундаментальных теорий дисковой аккреции можно найти у Pringle (1981) и Frank, King & Raine (2002).

1. Диффузионное уравнение эволюции

Пусть диск имеет поверхностную плотность S(r,t) и радиальную скорость v_r(r,t), причем v_r < 0 соответствует приближению к звезде. Потенциал установлен так, что угловая скорость зависит только от расстояния до звезды: Ω = &Omega(r). В цилиндрических координатах уравнение непрерывности для осесимметричного потока (см., например, Pringle (1981)):

$r\frac{\partial\Sigma}{\partial t} = \frac{\partial}{\partial r}(r\Sigma v_r)=0\,.$ (44)

Аналогично, сохранение углового момента дает:

$r\frac{\partial\Sigma r^2\Omega}{\partial t} = \frac{\partial}{\partial r}(r\Sigma v_r \cdot r^2\Omega) = \frac{1}{2\pi} \frac{\partial G}{\partial r}\,,$ (45)

где член в правой части уравнения соответствует вращательному моменту, действующему на поток вследствие сил вязкости. Как известно из гидродинамики (Pringle, 1981), G дается в терминах кинематической вязкости ν согласно выражению:

$G=2\pi r \nu\Sigma r \frac{d\Omega}{dr} \cdot r\,,$ (46)

где правая сторона уравнения есть результат произведения длины окружности, силы вязкости на единицу длины и длину плеча r. Если мы заменяем G, исключаем из уравнения v_r с помощью уравнений (44) и (45) и ограничиваемся кеплеровским потенциалом с Ω ~ r_-3/2, мы получим эволюционное уравнение для поверхностной плотности тонкого аккреционного диска в его нормальной форме:

$\frac{\partial\Sigma}{\partial t} = \frac{3}{r} \frac{\partial}{\partial r} \left[ r^{1/2} \frac{\partial}{\partial r}(\nu\Sigma r^{1/2})\right]\,.$ (47)

Это частное дифференциальное уравнение для эволюции поверхностной плотности S имеет форму уравнения диффузии. Чтобы сделать это явным, совершим подстановку:

$X \equiv 2r^{1/2}\,,$
$f \equiv \frac{3}{2} \Sigma X\,.$ (48)

Для постоянной кинематической вязкости ν уравнение (47) тогда принимает типичную форму уравнения диффузии:

$\frac{\partial f}{\partial t} = D \frac{\partial^2 f}{\partial X^2}$ (49)

с коэффициентом диффузии

$В = \frac{12\nu}{X^2}\,.$ (50)

Характерное время диффузии, полученное из уравнения (49), равно X²/D. Возвращаясь обратно к физическим переменным, мы обнаружим, что характерное время эволюции диска на расстоянии r от звезды с кинематической вязкостью ν равно:

$\tau \simeq \frac{r^2}{\nu}\,.$ (51)

Наблюдения эволюции диска (например, определение характерного времени векового уменьшения скорости аккреции) вместе с оценками размеров диска могут помочь определить эффективную вязкость диска (Hartmann et al., 1998).

2. Решения

В общем случае вязкость является функцией местных условий в диске (таких, как поверхностная плотность, расстояние до звезды, температура, степень ионизации и т.д.) Если вязкость ν зависит от поверхностной плотности S, тогда уравнение (47) становится нелинейным уравнением, которое не имеет аналитических решений (кроме нескольких особых случаев). Если есть более сложная зависимость от местных условий, тогда уравнение эволюции поверхностной плотности должно быть решено одновременно с уравнением эволюции центральной температуры (Pringle, Verbunt & Wade, 1986). Однако аналитическое решение возможно, если u может быть записано как степенная функция r (Lynden–Bell & Pringle, 1974), и этого достаточно для иллюстрации основного поведения решения уравнения (47).

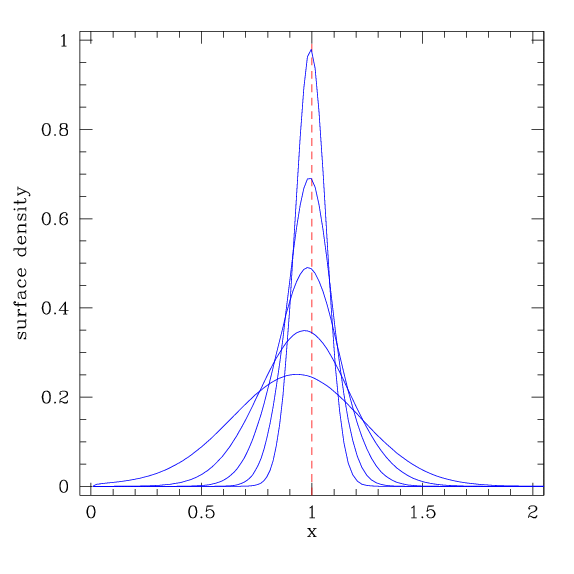
Сначала мы опишем решение для функции Грина для случая ν=const. Предположим, что в момент времени t=0 весь газ сосредоточен в тонком кольце массой m и радиусом r₀:

$\Sigma(r,t=0) = \frac{m}{2\pi r_0}\delta(r-r_0)\,.$ (52)

Легко показать, что его решение:

$\Sigma(x,\tau)=\frac{m}{2\pi r_0} \frac{1}{\tau} x^{-1/4} e^{-(1+x^2)/\tau} I_{1/4}\left(\frac{2x}{\tau}\right)\,,$ (53)

где мы записали решение в безразмерных переменных x=r/r₀, τ=12νt/r₀², I_1/4 – модифицированная функция Бесселя первого рода.

Если Вы не водите близкое знакомство с функциями Бесселя, решение для функции Грина не покажется Вам особенно ясным и прозрачным. Эволюция, подразумеваемая этим решением, представлена на Рисунке 11. Наиболее важные свойства решения, при t, стремящемся к бесконечности – это:

Поток массы к r = 0, и
Угловой момент, уносимый небольшой долей массы, течет к r = бесконечности.

Рисунок 11. Численное решение уравнения эволюции диска для случая ν=const, вычерченное для значений безразмерного времени τ, равного 0.01, 0.02, 0.04, 0.08 и 0.16. Начальное состояние представляет собой узкое кольцо с массой m при x = 1. Для x = 0.01 было применено граничное условие: равный нулю угловой момент. Заметим, что из-за этого граничного условия решение уравнения на более поздних временах немного отличается от аналитического решения, данного в тексте.

Это разделение массы и углового момента – генетическая особенность эволюции вязкого диска, и она явно важна для решения проблемы углового момента при формировании звезд.

Большую практическую пользу принесло самоподобное решение, также полученное Lynden–Bell & Pringle (1974). Рассмотрим диск, в котором вязкость меняется как степенная функция расстояния до звезды:

$\nu \propto r^\gamma\,.$ (54)

Предположим, что диск в момент времени, равный нулю, имеет профиль поверхностной плотности, соответствующий устойчивому, установившемуся решению состояния (с этим законом изменения вязкости) до r = r₁ с экспоненциальным снижением плотности для больших r. Как мы кратко покажем ниже, начальная поверхностная плотность в этом случае имеет форму:

$\Sigma(t=0)=\frac{C}{3\pi\nu_1 \widetilde{r}\gamma} e^{-\widetilde{r}(2-\gamma)}\,,$ (55)

где С – константа, . Автомодельное решение тогда:

$\Sigma(\widetilde{r},T)=\frac{C}{3\pi\nu_1\widetilde{r}\gamma} T^{-(5/2-\gamma)(2-\gamma)} e^{-\widetilde{r}(2-\gamma)/T}\,,$ (56)

где

$T \equiv \frac{t}{t_s} + 1\,,$
$t_s \equiv \frac{1}{3(2-\gamma)^2} \frac{r_1^2}{\nu_1}\,.$ (57)

Это решение показано на Рисунке 12.

Рисунок 12. Автомодельное решение уравнения эволюции диска для случая γ = 1, вычерченное для величин безразмерного времени T, равных 1, 2, 4 и 8. Величина поверхностной плотности по оси y произвольна.

В течение долгого времени масса диска уменьшается, в то время как характерный масштаб диска (изначально равный r₁) увеличивается с сохранением углового момента. Это решение весьма полезно как для аналитического изучения эволюции дисков, так и для сравнения наблюдаемых масс и размеров дисков и скорости аккреции с теорией (Hartmann et al., 1998).

Стационарное решение для зависимости поверхностной плотности диска от радиуса может быть выведено из условия $\partial/\partial t = 0$ и интегрирования уравнения (45) с условием сохранения углового момента:

$\Sigma r^3\Omega v_r = \nu\Sigma r^3 \frac{d\Omega}{dr} + \textrm{const}\,.$ (58)

Заметив, что скорость аккреции $\dot M=-2\pi r \Sigma v_r$ , мы имеем:

$-\frac{\dot M}{2\pi} r^2\Omega = \nu\Sigma r^3 \frac{d\Omega}{dr} + \textrm{const}\,.$ (59)

Для определения константы интегрирования отметим, что вращательный момент диска исчезает, если dΩ/dr = 0. В этом случае константа может быть оценена, она будет пропорциональна локальному потоку углового момента:

$\textrm{const} \propto \dot M r^2 \Omega\,.$ (60)

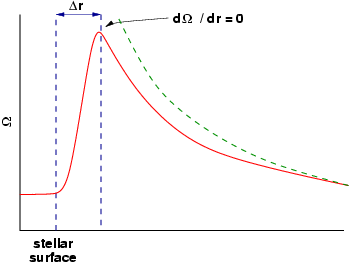
Обычно он определяется на внутренней границе диска. Особенно простой пример – это случай диска, который простирается от экватора медленно вращающейся звезды. Этот случай проиллюстрирован на Рисунке 13.

Рисунок 13. Схематический график зависимости угловой скорости Ω(r) для медленно вращающейся звезды, окруженной тонким аккреционным диском, распространяющимся от звездного экватора. При больших радиусах в диске угловая скорость меняется по нормальному кеплеровскому закону, показанному пунктирной зеленой линией. Чтобы гладко перейти на вращение экватора звезды, угловая скорость должна повернуть (начать уменьшаться) на малых расстояниях от звезды в переходной зоне, известной как граничный слой. Существование граничного слоя предполагает, что на некотором расстоянии от звезды dΩ/dr = 0, и в этой точке вязкое напряжение исчезает.

В зоне перехода между кеплеровским профилем угловой скорости в диске и намного меньшей угловой скоростью на поверхности звезды должен быть максимум в угловой скорости газа Ω на некотором радиусе r_*+Δr. Элементарные аргументы (Pringle, 1977) – которые, однако, могут быть неприменимы при очень высоких скоростях аккреции объектов типа FU Ориона (т.н. фуоров) (Popham et al., 1993), но верны во всех прочих случаях – говорят о том, что Δr<<r, так что этот переход происходит в узком пограничном слое вблизи поверхности звезды_***.

_***[Физика самого граничного слоя представляется весьма интересным приложением, так как граничный слой – область сильных сдвигов, которые устойчивы в противоположность магнитовращательной неустойчивости, которая, как мы обсудим позже, является критической для переноса углового момента в диск. Pringle (1989), Armitage (2002) и Pessah, Chan & Psaltis (2006) изучали роль магнитных полей в переходном слое.]

Константа из уравнения (59) тогда может быть вычислена как:

$\textrm{const} \approx -\frac{\dot M}{2\pi} r_*^2 \sqrt{\frac{GM_*}{r_*^3}\,}\,,$ (61)

и уравнение (59) становится

$\nu\Sigma = \frac{\dot M}{3\pi} \left(1-\sqrt{\frac{r_*}{r}\,}\right)\,.$ (62)

Учитывая вязкость, это уравнение определяет стационарное состояние профиля поверхностной плотности диска со скоростью аккреции $\dot M$ . Вдали от границы S(r) ~ ν^-1.

Внутренние граничные условия, которые приводят к уравнению (62), описаны как граничное условие нулевого момента. Как уже было замечено, условие нулевого углового момента физически реализуется, когда существует граничный слой между звездой и ее диском. Этого нет, однако, в случае классических звезд типа Т Тельца. Наблюдательные данные (Bouvier et al., 2007) говорят о том, что при аккреции на звезды типа Т Тельца звездная магнитосфера разрушает внутренний аккреционный диск, приводя к магнитосферному типу аккреции, при котором газ "приклеевается" к линиям звездного магнитного поля и баллистически падает на поверхность звезды (Königl, 1991). Магнитное сцепление между звездой и ее диском вводит поправку в обмен угловым моментом, изменяет стационарный профиль поверхностной плотности вблизи внутреннего радиуса усечения и может заставить звезду вращаться медленнее, чем в ином случае (Armitage & Clarke, 1996; Collier Cameron & Campbell, 1993). Регулирует ли такой "захват диска" реальное вращение молодых звезд, остается предметом дискуссий (Herbst & Mundt, 2005; Matt & Pudritz, 2005; Rebull et al., 2006).

3. Температурный профиль

Пользуясь методом Frank, King & Raine (2002), мы получим радиальную зависимость эффективной температуры активного аккреционного диска, рассматривая чистый вращательный момент кольца шириной Δr. Этот момент – $(\partial G/\partial r)\Delta r$ :

$\Omega \frac{\partial G}{\partial r} \Delta r \equiv \left[ \frac{\partial}{\partial r}(G\Omega) - G\Omega^\prime \right] \Delta r\,.$ (63)

Записав это выражение, мы заметим, что, если рассматривать весь диск (интегрируя по r), то первый член выражения в правой части уравнения определен исключительно граничными величинами G Sigma. Следовательно, мы отождествляем этот член с переносом энергии, связанным с моментом вязкости, текущим сквозь кольцо. С другой стороны, второй член выражения представляет собой скорость потери энергии газом. Мы предполагаем, что эта энергия в конечном итоге превратилась в тепло и была излучена, так что скорость диссипации в единице поверхности диска (учитывая, что диск имеет две стороны), есть:

$D(r) = \frac{G\Omega^\prime}{4\pi r} = \frac{9}{8} \nu\Sigma\Omega^2\,,$ (64)

где мы предполагаем кеплеровский профиль угловой скорости. Для излучения абсолютно черного тела D(r) = σТ_диска⁴. Делая подстановку для Sigma и используя для u S стационарное решение, полученное из уравнения (62), получим:

$T_{\mathrm{disk}}^4 = \frac{3GM_*\dot M}{8\pi\sigma r^3} \left( 1-\sqrt{\frac{r_*}{r}\,}\right)\,.$ (65)

Заметим, что

Вдали от граничного слоя (r>>r_*) температурный профиль активного аккреционного диска Т_диска ∝ r^-3/4. Т.е. он имеет ту же форму, что и для пассивного аккреционного диска, даваемую уравнением (28)
Температурный профиль не зависит от вязкости. Это является привлекательной особенностью теории при данной неопределенности происхождения и неизвестной эффективности переноса углового момента диска, хотя, с другой стороны, это лишает нас множества возможных путей изучения основной физики путем наблюдения стационарных дисков.

Для скорости аккреции, равной , мы получим для звезды солнечной массы на расстоянии 1 а.е. эффективную температуру диска, равную 150К. Это – поверхностная температура. Как мы покажем ниже, центральная температура должна быть существенно выше.

4. Причина переноса углового момента

В протопланетном диске можно пренебречь молекулярной вязкостью. Для газа, в котором длина свободного пробега молекул есть lambda, вязкость

$\nu \sim \lambda c_s\,,$ (66)

где с_s – скорость звука. Длина свободного пробега определяется как λ = 1/nσ, где n – концентрация молекул газа, σ – сечение их взаимодействия. Эти величины легко вычисляются. Например, рассмотрим протопланетный диск с поверхностной плотностью Σ=1000 г/см², h/r=0.05 для 1 а.е. Плотность в середине (в центральной плоскости) диска по порядку величины равна n ~ Σ/ (2 mH h) = 4 x 10¹⁴ см^-3, тогда как скорость звука связанная с h/r равна 1.5 км/сек. Считая сечение взаимодействия близким к площади молекулы водорода (σ ~ 10^-15 см²), получим:

$\lambda \sim 2.5~\textrm{см,}$
$\nu \sim 4\times10^5 \textrm{см}^2/\textrm{с.}$ (67)

Связанное с этими величинами характерное время эволюции диска, равное τ = r²/ν, составляет по порядку величины 10¹³ лет, что в 10⁶ раз больше наблюдаемого времени эволюции дисков.

В своей классической работе Шакура и Сюняев (1973) отметили, что турбулентность в диске может обеспечить эффективную вязкость, которая будет гораздо больше молекулярной вязкости. Для изотропной турбулентности максимальный размер ячейки турбулентности в диске по порядку величины будет равен толщине диска h, тогда как максимальная скорость турбулентного движения будет сравнима со скоростью звука c (еще большая скорость привела бы к появлению ударных волн и быстрому рассеянию кинетической энергии турбулентных движений в виде тепла). Мотивируясь этими соображениями, Шакура и Сюняев (1973) предложили параметризацию:

$\nu = \alpha c_s h\,,$ (68)

где α – безразмерный параметр, который показывает, насколько эффективно турбулентность приводит к переносу углового момента. Заметим, что существование турбуленции в диске априори не дает гарантию, что произойдет перенос углового момента наружу.

В стандартной теории так называемых "альфа-дисков" параметр α считается константой. Если это так, становится возможным аналитическое решение для вертикальной структуры активного аккреционного диска и выведение ν как функции r, Σ и α. Детали этого процесса можно найти у Frank, King & Raine (2002) Комбинируя известную форму функции для ν с уравнением эволюции диска (47), можно получить полную теорию для предсказания времени эволюции диска, с единственным неизвестным, являющимся соответствующей величиной α. Все это очень хорошо, но нет физических причин полагать α константой, а если вместо этого считать ее свободной функцией, то большая часть заманчивой простоты теории утрачивается. Модели "альфа-дисков" должны рассматриваться скорее как иллюстрации, нежели прямые предсказания эволюции дисков.

Чтобы прямо оценить, как велика альфа, нужно учесть наблюдаемую эволюцию протопланетных дисков. Предположим, например, что шкала времени эволюции на 50 а.е. составляет 1 миллион лет. Тогда начиная действовать по альфа-рецепту (уравнение 68) и заметив, что c_s~ hΩ, получим выражение для времени эволюции:

$\tau = \frac{r^2}{\nu} = \left(\frac{h}{r}\right)^{-2} \frac{1}{\alpha\Omega}\,.$ (69)

Сделав подстановку для tau и r и снова допуская, что h/r ~ 0.05, получим оценку для α = 0.02. Эта величина достаточно типична – попытки наблюдательно ограничить альфу на крупных масштабах в протопланетных дисках (ни одна из этих попыток не является намного более сложной, чем наши сырые оценки) приводят к оценкам ~10^-2 (Hartmann et al., 1998)^***. Эти значения по порядку величины меньше, чем значение α, полученное при моделировании вспышек карликовых новых, которые происходят в аккреционном диске вокруг белого карлика (Cannizzo, 1993).

^***[Важным исключением является моделирование мощных взрывных событий, известных как вспышки объектов типа FU Ориона (фуоров), которые (если их интерпретировать как саморегулирующуюся тепловую неустойчивость) требуют меньших значений альфа, равных по порядку величины 10^-3 и меньше (Bell & Lin, 1994).]

Несмотря на реальный прогресс, сохраняются определенные сомнения относительно физической причины и свойств переноса углового момента в протопланетном диске. Число Рейнолдса для течения в диске:

$\textrm{Re} \equiv \frac{UL}{\nu}\,,$ (70)

где U – характерная скорость и L – характерный размер, чрезмерно велико (по порядку величины равно 10¹⁴, если брать те же параметры, что мы использовали, рассчитывая величину молекулярной вязкости). На Земле течение становится турбулентным при критическом числе Рейнольдса, по порядку величины равном 10⁴, так что интуиция подсказывает, что течения в протопланетном диске должны быть сильно турбулентны чисто из гидродинамических эффектов. Детальное изучение, однако, не подтверждает этот вывод. Для начала заметим, что условие для линейной гидродинамической устойчивости в дифференциально вращающемся потоке (критерий Рэлея) – увеличение собственного углового момента при движении наружу:

$\frac{d}{dr}(r^2\Omega) > 0\,.$ (71)

В кеплеровском диске r²Ω ∝ r^1/2, так что поток всегда линейно устойчив.

Существует огромное количество литературы, в которой исследовалась возможность нелинейной неустойчивости, которая может привести к турбуленции в аккреционном диске. На данный момент нет никакого безусловного свидетельства того, что такая неустойчивость существует, и численные эксперименты показали, что гидродинамические возмущения в потоке кеплеровского диска – которые могут при некоторых обстоятельствах показать существенный временный рост (Afshordi, Mukhopadhyay & Narayan, 2005; Ioannou & Kakouris, 2001) – в конечном итоге распадаются (Balbus & Hawley, 2006; Balbus, Hawley & Stone, 1996; Shen, Stone & Gardiner, 2006). Эксперименты приводят к похожим выводам (Ji et al., 2006). Подобные вихри, которые в строго двумерных моделях диска являются долговечными и способны переносить угловой момент (Godon & Livio, 1999; Johnson & Gammie, 2005), в трехмерных моделях становятся подвержены разрушительной неустойчивости (по крайней мере около центральной плоскости диска, для больших z ситуация более благоприятна) (Barranco & Marcus, 2005; Shen, Stone & Gardiner, 2006). И, наконец, конвекция, которая может существовать в некоторых областях протопланетного диска, переносит угловой момент внутрь – и в результате не может быть самоподдерживающейся в отсутствии других источников переноса (Ryu & Goodman, 1992; Stone & Balbus, 1996).

Самогравитация дает противоядие к этому унылому перечню отрицательных результатов. Достаточно массивный диск неустойчив (Toomre, 1964) к развитию спиральных рукавов, которые переносят угловой момент наружу. Мы обсудим физику, лежащую в основе этой неустойчивости, позже, когда будем обсуждать модель дисковой неустойчивости для формирования планет–гигантов, но сейчас отметим, что неустойчивость возникает, когда

$\frac{M_{\mathrm{disk}}}{M_*} > \frac{h}{r}\,.$ (72)

Самогравитация может играть роль в протопланетном диске на ранних этапах, когда диск достаточно массивен, но она не важна впоследствии, когда М_диска<< М_star.

Возвращаясь к несамогравитирующим дискам, заметим, что условия гидродинамической устойчивости, данные в уравнении (71), драматически меняются в присутствии даже слабого магнитного поля. Принимая во внимание, что гидродинамический поток устойчив, только когда собственный угловой момент увеличивается наружу, магнитогидродинамический поток для устойчивости нуждается в том, чтобы угловая скорость сама была возрастающей функцией радиуса (Balbus & Hawley, 1991; Chandrasekhar, 1961; Velikhov, 1959)^***:

$\frac{d}{dr}(\Omega^2) > 0\,,$ (73)

^***[Значение результата Чандрасекара для происхождения турбуленции в протопланетном диске было высоко оценено Сафроновым (1969), который заметил, что критерий магнитогидродинамической устойчивости не переходит в критерий Рэлея при магнитном поле, стремящемся к нулю, и что "для слабого магнитного поля облако должно быть менее устойчиво, чем мы нашли ранее в отсутствии поля". Важность магниторотационной неустойчивости для аккреционных дисков была оценена по достоинству лишь спустя 20 лет Балбусом и Холли (Balbus & Hawley).]

Условие (73) в кеплеровском диске не выполняется. Как следствие, в идеале (коэффициент диффузии, равный нулю) магнитогидродинамики при произвольно слабом магнитном поле достаточно, чтобы привнести в кеплеровский диск линейную неустойчивость, с возмущениями, экспоненциально растущими за динамическое время. Всесторонний обзор физики этой неустойчивости – называемой магниторотационной – или неустойчивостью Балбуса–Холли был выполнен Balbus & Hawley (1998). Магниторотационная неустойчивость является линейной и приводит к самоподдерживающейся турбуленции в хорошо ионизованном аккреционном диске (Brandenburg et al., 1995; Stone et al., 1996). Она переносит угловой момент наружу, массу потока – внутрь, и освобождает гравитационную потенциальную энергию. Магниторотационная неустойчивость не всегда действует подобно "альфа–вязкости" (Pessah, Chan & Psaltis, 2006), но, согласно численному моделированию, грубо эквивалентна ей и обычно приводит к эффективности переноса порядка α ~ 10^-2 – подобно величинам, выведенным для протопланетных дисков, но меньше, чем они же, предполагаемые для дисков вокруг белых карликов (вспышки карликовых новых звезд).

5. Слоистые диски

Как полагает большинство, магниторотационная неустойчивость – самая важная (а возможно, и единственная) причина переноса углового момента в аккреционных дисках вокруг белых карликов, нейтронных звезд и черных дыр. Однако в протопланетных дисках возникает интересное осложнение, связанное с тем, что низкая степень ионизации газа приводит к конечной проводимости. Удельное сопротивление (или другие отклонения от идеальной магнитогидродинамики, такие как амбиполярная диффузия или эффект Холла) может тогда потенциально заглушить магниторотационную неустойчивость, подавить турбулентность и связанный с нею перенос углового момента. Линейная физика в этом режиме была проанализирована в многочисленных работах, включая работы Blaes & Balbus (1994), Desch (2004) and Salmeron & Wardle (2005), к которым мы и направляем читателей. Здесь я обрисую более широкую картину, основанную на простой физике, которая была предложена Gammie (1996) как модель, для которой магниторотационная неустойчивость могла бы работать в протопланетных дисках. Я подчеркиваю, что в отличие от предыдущего обсуждения основных принципов магниторотационной неустойчивости, это применение к протопланетным дискам остается несколько умозрительным.

Следуя Гамми (Gammie), мы начнем с замечания, что в присутствии удельного сопротивления (предполагая, что именно оно является самым главным эффектом неидеальности, нарушающим магниторотационную неустойчивость), магнитное поле подчиняется обычному уравнению индукции:

$\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) - \nabla \times (\eta\nabla \times \mathbf{B})\,,$ (74)

где η – магнитный коэффициент диффузии. С другой стороны, η может быть записана в терминах степени ионизации x = n_e/n_H:

$\eta = 6.5 \times 10^{-3} x^{-1} \textrm{см}^2/\textrm{с.}$ (75)

Наша цель состоит в определении минимального значения x, для которого магниторотационная неустойчивость еще будет работать, несмотря на затухание, вызванное удельным сопротивлением. Делая это, мы заметим, что удельное сопротивление легче всего подавляет магниторотационную неустойчивость на малых масштабах. Поэтому мы рассмотрим в диске элементы наибольших размеров l = h, и приравняем характерное время роста возмущений вследствие магнитогидродинамической неустойчивости (Balbus & Hawley, 1998):

$\tau_{\mathrm{MRI}} \sim \frac{h}{v_A}\,,$ (76)

где v_A = (B²/4πρ)^1/2 – скорость альвеновских волн, к характерному времени затухания:

$\tau_{\mathrm{затух}} \sim \frac{h^2}{\eta}\,.$ (77)

Таким образом, мы получим простой критерий для срабатывания магниторотационной неустойчивости:

$\eta < h v_A\,.$ (78)

Остается оценить соответствующие величины h и v_A. Для грубой оценки мы можем предположить, что при 1 а.е. h = 10¹² см и v_A ~ c ~ 10⁵ см/сек (более точно v_A ~ α^1/2c_s, где α – коэффициент магнитогидродинамической турбуленции, аналогичный альфе Шакуры–Сюняева). В этом случае предел магнитного коэффициента диффузии η < 10¹⁷ см²/сек, который соответствует минимальной степени ионизации

$x > 10^{-13}\,,$ (79)

которая более менее совпадает с величиной, полученной из более строгого анализа (Balbus & Hawley, 1998; Gammie 1996).

Стоит отметить очень важную вещь – эта степень ионизации является очень маленькой! Линейный рост возмущений вследствие магниторотационной неустойчивости оказывается настолько быстрым, что даже крошечная степень ионизации достаточно хорошо "приклеивает" газ к магнитному полю и преодолевает стабилизирующее действие удельного сопротивления.

Хотя для работы магниторотационной неустойчивости требуется совсем малая степень ионизации, в протопланетном диске могут быть области, где и такая степень ионизации может быть не достигнута. Нужно рассмотреть два источника ионизации:

Ионизация при столкновениях. Вычисления Umebayashi (1983) показали, что ионизация щелочных металлов достаточна для поддержания x > 10^-13. Это происходит при температурах порядка 1000К и выше. Область самой внутренней части диска – в пределах нескольких десятых а.е. от звезды – должна быть в состоянии поддерживать магниторотационную неустойчивость в результате просто тепловой ионизации.
Ионизация космическими лучами. Космические лучи поглощаются слоем вещества с поверхностной плотностью 100 г/см². (Umebayashi & Nakano, 1981). Они ионизируют всю толщу диска достаточно хорошо, чтобы магниторотационная неустойчивость заработала на больших расстояниях от звезды, где поверхностная плотность газа меньше двух критических, и ионизуют поверхностный слой с плотностью, равной критической, на меньших расстояниях.

Рисунок 14. Схематический рисунок модели слоистого диска, представленный Gammie (1996). В этой модели внутренняя часть диска достаточно горяча, чтобы тепловая ионизация "приклеила" газ к магнитному полю и допустила развитие магниторотационной неустойчивости. На больших расстояниях от звезды космические лучи проникают на всю толщину диска и обеспечивают необходимую ионизацию. Вероятно, что на средних (промежуточных) расстояниях аккреция происходит в активном поверхностном слое с плотностью ~100 г/см², который ионизован космическими лучами. Внутри этого слоя расположена неактивная "мертвая зона", в которой развитие магниторотационной неустойчивости подавлено и почти нет турбулентности.

Если нет других источников ионизации, то на расстояниях, где диск достаточно прохладен, чтобы не ионизироваться при столкновениях атомов и молекул газа, и достаточно плотен, чтобы в него не проникали космические лучи, мы могли бы ожидать новую структуру ("мертвую зону"), в которой диск вблизи своей центральной плоскости был бы неподвижным, и только поверхностный слой был бы магнитно активным и поддерживал аккрецию (Gammie, 1996). Модель такого слоистого диска представлена на Рисунке 14.

Модели слоистых дисков качественно отличаются от обычных полностью вязких дисков в двух важных аспектах. Во-первых, поток массы через активный слой есть функция (по аналогии с уравнением 62) вязкости и глубины колонки ν_слояΣ_слоя активного слоя, которая не зависит от полной поверхностной плотности диска на этом расстоянии от звезды. Можно предсказать, что количество массы, которую активный слой может пропустить через себя, является падающей функцией расстояния до звезды, таким образом, газ, втекающий внутрь из внешних слоев диска, выбывает из потока и накапливается в мертвой зоне. В этом случае узкое место ("бутылочное горлышко") при аккреции на звезду находится на внутреннем крае слоистой части диска. Поток массы через эту область оценивается по порядку величины в 10_-8 масс Солнца в год, что согласуется с наблюдениями звезд типа Т Тельца солнечной массы (Gammie, 1996). Однако предсказанный поток массы должен быть примерно константой и не зависеть от массы звезды, что не согласуется (Alexander & Armitage, 2006) с очевидным увеличением средней скорости аккреции в зависимости от массы звезды:

$\dot M \propto M_*^2\,,$ (80)

что было выведено из наблюдений как звездных, так и субзвездных объектов (Mohanty, Jayawardhana & Basri, 2005).

Во-вторых, слоистые модели предсказывают, что область вблизи центральной плоскости диска должна быть неподвижна в точности на тех расстояниях от звезды, которые представляют наибольший интерес с точки зрения формирования планет. Это имеет важное значение для оседания пыли, для последующего роста планетезималей и для миграции маломассивных планет (Matsumura & Pudritz, 2005). Возможна также причастность слоистой модели к объяснению переменности молодых звезд, так как растущая мертвая зона обеспечивает резервуар газа на малых расстояниях от звезды, где он в принципе может быть нагрет и ионизирован, приводя к вспышкам аккреции (Armitage, Livio & Pringle, 2001).

Слоистые диски дают нам интересные возможности, однако существуют ли они в действительности? В настоящее время существует несколько наблюдательных ограничений на их существование, хотя теоретически идея остается возможной. Численное моделирование (Sano & Stone, 2002) подтвердило, что, когда магнитное число Рейнолдса (оцененное в подходящем масштабе диска):

$\textrm{Re}_M \equiv \frac{v_A^2}{\eta\Omega}$ (81)

падает ниже критического значения, лежащего в области между 1 и 30, турбуленция, возникающая из развития магниторотационной неустойчивости, оказывается подавленной. Это широко согласуется с простыми аргументами, приведенными выше, и приводит к той же критической степени ионизации. Однако необходимо крайне мало энергии для того, чтобы поддерживать достаточный уровень ионизации для развития магниторотационной неустойчивости, и было предложено, что энергии турбуленции достаточно для поддержания ионизации и магниторотационной неустойчивости активного диска (Inutsuka & Sano, 2005). Другая возможность, подтвержденная недавним численным моделированием Turner, Sano & Dziourkevitch (2006), заключается в том, что турбулентное перемешивание способно перенести достаточно зарядов из поверхностного слоя к центральной плоскости диска и обеспечить там не равный нулю перенос вещества. Учитывая эти теоретические сомнения, вопрос, имеют ли протопланетные диски структуру, подобную указанной на Рисунке 14, остается открытым. Критический вопрос – существуют ли в достаточных количествах маленькие зерна (пылинки), смешанные с газом, чтобы эффективно поглощать свободные электроны.

6. Рассеяние диска

Утрата газовой компоненты протопланетных дисков накладывает временной предел на завершение процесса формирования планет–гигантов и меняет окружающую среду при формировании планет земного типа. Самоподобное решение уравнения эволюции вязких дисков (формула 57) предсказывает, что поверхностная плотность и скорость аккреции уменьшаются на поздних временах по степенному закону, и, следовательно, переход между диском и бездисковым состоянием должен быть постепенным. Однако этого не наблюдается. Молодые звезды со свойствами, промежуточными между "классическими звездами типа Т Тельца" и "обнаженными звездами типа Т Тельца", относительно редки и составляют примерно 10% от полной популяции звезд, которые демонстрируют, по крайней мере, один признак околозвездного диска. Согласно этой статистике, можно сделать вывод, что характерное время рассеяния диска невелико и составляет ~10⁵ лет (Simon & Prato, 1995; Wolk & Walter, 1996).

Ключевой механизм, который может приводить к рассеянию диска, был обнаружен с помощью наблюдений космическим телескопом им. Хаббла маломассивных звезд, освещенных сильным ионизирующим излучением, испускаемым массивными звездами в ядре Туманности Ориона в скоплении Трапеция (O'Dell, Wen & Hu, 1993). Изображения показывают туманности в форме головастика, окружающие молодые звезды с околозвездными дисками, которые интерпретируются как фотоиспарение и улетучивание газа из диска в результате освещения внешним ионизирующим излучением (Johnstone, Hollenbach & Bally, 1998). Основная физика этого процесса относительно проста (Bally & Scoville, 1982; Hollenbach et al., 1994; Shu, Johnstone & Hollenbach, 1993) и тесно связана с хорошо изученной проблемой ветров, нагретых комптоновским излучением, в аккреционных дисках активных ядер галактик (Begelman, McKee & Shields, 1983). Жесткие ультрафиолетовые кванты^*** с энергией >13.6 эВ ионизируют и нагревают поверхностный слой диска, повышая его температуру до 10⁴ К, характерную для HII областей.

^*** [Ультрафиолетовые кванты с энергией 6 эВ < E <13.6 эВ также могут играть важную роль. Ультрафиолетовое излучение, достаточное для диссоциации молекул водорода, также может приводить к утеканию газа во внешних частях диска, где скорость вращения меньше. Детальная физика таких потоков – которые больше напоминают области фотодиссоциации, нежели области HII – тяжела для вычислений, потому что температура горячего газа определяется балансом между фотоэлектрическим нагревом и охлаждением путем излучения атомных и молекулярных линий. Адамс и др. (2006) рассмотрел потерю массы дисков из-за внешнего ультрафиолетового излучения в своих моделях эволюции дисков в скоплениях, однако это ветры, вызванные излучением дальнего ультрафиолета, которые более важны для эффективного и быстрого рассеяния диска в конце фазы "классической звезды типа Т Тельца".]

Скорость звука в фотоионизированном газе составляет c_s ~ 10 км/сек. За пределами критического радиуса, определенного как

$r_g = \frac{GM_*}{c_s^2}\,,$ (82)

скорость звука в горячем газе превышает локальную кеплеровскую скорость. В этом случае газ становится несвязанным и вытекает из диска как тепловой ветер. Для звезды солнечной массы критический радиус оценивается в 9 а.е.

Этот же самый процесс может произойти независимо от того, приходит ли ультрафиолетовое излучение из внешнего источника, такого как массивная звезда в скоплении, или непосредственно от центральной звезды. Однако в типичной области звездообразования (Lada & Lada, 2003) большинство маломассивных звезд получает слишком мало ультрафиолетового излучения из внешних источников для того, чтобы их диски разрушились (Adams et al., 2006). Поэтому вероятнее, что фотоиспарение произойдет из–за излучения центральной звезды. В этом режиме Hollenbach et al. (1994) получил оценку скорости потери массы путем фотоиспарения:

$\dot M_{\mathrm{wind}} \simeq 4\times10^{-10} \left(\frac{\Phi}{10^{41}\,\textrm{c}^{-1}}\right)^{1/2} \left(\frac{M_*}{M_\odot}\right)^{1/2} M_\odot/\textrm{год,}$ (83)

где Φ – поток звездного света, способного ионизировать газ. Было предсказано, что большая часть потери массы через ветер произойдет вблизи r_g, с радиальной зависимостью темпа потери массы: $\dot\Sigma \propto r^{-5/2}$ . Гидродинамическое численное моделирование, проведенное Font et al. (2004), в значительной степени подтверждает эту основную картину, хотя в деталях было найдено, что потеря массы происходит и при расстояниях от звезды, меньших критического радиуса, а полный темп потери массы несколько меньше предсказанного уравнением (83).

Сочетание фотоиспарительного ветра и эволюции вязкого диска приводит к быстрому рассеянию диска (Clarke, Gendrin & Sotomayor, 2001). Вычисления Alexander, Clarke & Pringle (2006) предлагают трехступенчатый сценарий, схематически представленный на Рисунке 15:

Сначала . Потеря массы через "дисковый ветер" оказывает незначительное влияние на диск, который эволюционирует как в обычных вязких моделях. Скорость аккреции и поверхностная плотность постепенно понижаются в вязкой шкале времени всего диска (определенной на больших расстояниях от звезды), которая по порядку величины равна миллиону лет.
Через несколько миллионов лет скорость аккреции уменьшается так, что . Дисковый ветер становится тогда достаточно сильным, чтобы определять эволюцию поверхностной плотности диска вблизи критического радиуса, привести к появлению промежутка (щели) в диске и отключить внутренний диск от пополнения газом из внешних, удаленных от звезды областей диска.
Как только внутренний диск оказывается лишен газа, оставшийся газ во внешней части диска становится непосредственно освещен ультрафиолетовым светом звезды (а перед этим он освещался в основном светом, рассеянным газом на более тесных орбитах). Этот свет быстро нагревает и рассеивает весь оставшийся газ.

Главный источник неопределенности в этих моделях – происхождение и величина потока звездного ионизирующего излучения. Есть немного ограничений на величину потока для звезд типа Т Тельца солнечной массы, и почти нет информации для звезд других масс.

Рисунок 15. Схематическая иллюстрация того, как фотоиспарение, вызванное центральным источником ультрафиолетового излучения, рассеивает протопланетный диск. В начальный момент ультрафиолетовое излучение (показанное красными стрелками) ионизирует поверхность диска, приводя к вертикальному расширению связанной атмосферы диска при r < r_g, и потере массы путем теплового "дискового" ветра при i>r > r_g. Поток ионизирующего излучения, который заставляет испарятся внешний диск, возникает путем рассеяния фотонов звездного излучения диском на малых расстояниях от звезды ("диффузное поле"). Через несколько миллионов лет темп аккреции в диске падает до величин, сравнимых со скоростью потери массы через "дисковый ветер". В этот момент ветер приводит к появлению в диске промежутка (щели) вблизи критического радиуса, отрезающего внутренний диск от пополнения запасов вещества из внешних слоев диска. Внутренний диск тогда быстро стекает на звезду – приводя к появлению "внутренней дыры" – и прямое ультрафиолетовое излучение звезды быстро рассеивает внешние области диска.

Г. Последовательность конденсаций

В активном аккреционном диске должен существовать температурный градиент по вертикальной оси z для энергии, которая переносится от плотной центральной плоскости диска к фотосфере, где она освобождается и излучается (заметим, что для тонкого диска с h/r << 1 градиент по z будет доминировать над радиальным градиентом, которым можно пренебречь). Простое применение теории переноса излучения в плоскопараллельном случае (Rybicki & Lightman, 1979) позволяет нам получить отношение между центральной температурой диска Tc и эффективной температурой диска T_disk.

Продолжая, определим оптическую толщину в центральной плоскости диска

$\tau = \frac{1}{2} \kappa_R \Sigma\,,$ (84)

где k_R – средняя непрозрачность Росселанда, Σ – поверхностная плотность диска. Вертикальный профиль плотности диска есть ρ(z). Если вертикальный перенос энергии происходит путем диффузии излучения (в некоторых областях также может быть важна конвекция), тогда для τ >> 1 вертикальный поток энергии дается уравнением диффузии излучения:

$F(z)= -\frac{16\sigma T^3}{3\kappa_R\rho} \frac{dT}{dz}\,.$ (85)

Давайте предположим для простоты, что вся диссипация энергии происходит при z=0. ^***

^*** [Отмечу, что для дисков, в которых активна магниторотационная неустойчивость, численное моделирование, проведенное Miller & Stone (2000), предлагает, что значительная доля освобожденной энергии переносится к большим z и рассеивается в областях с намного меньшей оптической глубиной, возможно, формируя горячую корону.]

В этом случае F(z) = σТ_диска⁴ не меняется с высотой (остается константой). Интегрируем, предполагая, что непрозрачность остается константой:

$-\frac{16\sigma}{3\kappa_R} \int_{T_c}^{T_{disk}} T^3dT = \sigma T_{\mathrm{disk}}^4 \int_0^z \rho(z')dz'$
$-\frac{16\sigma}{3\kappa_R} \left[\frac{T^4}{4}\right]_{T_c}^{T_{disk}} = T_{\mathrm{disk}}^4 \frac{\Sigma}{2}\,,$ (86)

где при выводе финального уравнения мы использовали тот факт, что при &taul>>1 практически весь газ диска лежит ниже фотосферы. Для больших τ мы ожидаем, что Т_c⁴>> Т_диска⁴, и уравнение упрощается до:

$\frac{T_c^4}{T_{\mathrm{disk}}^4} \simeq \frac{3}{4}\tau\,.$ (87)

Значение этого результата заключается в том, что активные диски с большой оптической глубиной являются гораздо более горячими вблизи центральной плоскости, нежели на поверхности. Например, если τ~100, для теплового излучения, испускаемого диском на некотором радиусе Т_c~ 3 Т_диска. Это важно, т.к. центральная температура определяет скорость звука, а та определяет вязкость (уравнение 68), а еще центральная температура определяет, какие льды и минералы могут там существовать. Таким образом, относительно скромные уровни аккреции могут существенно изменить тепловую структуру диска.

И для формирования планет земного типа, и для формирования планет-гигантов (если их формирование происходит путем аккреции на ядро) представляют большой интерес примесь твердого компонента в диске. Газ, формирующий протопланетный диск, будет включать в себя межзвездные пылевые гранулы, состоящие из смеси силикатов, графита и полициклических ароматических углеводородов (ПАУ). Измерение зависимости поглощения света в межзвездной среде от длины волны привело к предположению, что количество пылевых гранул распределяется по степенному закону в зависимости от их размеров (Mathis, Rumpl & Nordsieck, 1977):

$n(a) \propto a^{-3.5}\,,$ (88)

где а – размер гранул (в предположении их сферичности), а распределение охватывает пылинки размером от 0.005 до 1 мкм. Это распределение обычно является отправной точкой для дальнейшей эволюции в условиях большей плотности, преобладающих в диске. В наиболее горячих внутренних областях диска центральная температура может быть достаточно высока для разрушения гранул (от 1000К до 2000К в зависимости от того, из графита или силикатов сделаны пылинки). Отсутствие пыли очень близко от звезды является одним из главных аргументов против образования горячих юпитеров "на месте", но радиус разрушения пыли достаточно мал (обычно гораздо меньше 1 а.е.), чтобы изредка приводить к образованию планеты земного типа или планеты–гиганта. Однако с наблюдательной точки зрения важно, что разрушение пыли приводит к резкому уменьшению непрозрачности газа. Поэтому во внутренней части диска будет наблюдаться дыра, отверстие, даже если газ будет там присутствовать.

Если газ, составляющий протопланетный диск, имеет известный элементный состав (например, как у Солнца), то это хорошая задача для химика – вычислить наиболее термодинамически устойчивую смесь химических веществ при данных давлении и температуре. Изобилие различных минералов и льдов в диске будет вытекать из этой последовательности конденсаций при условии, что есть достаточно времени для достижения равновесия химических реакций – это разумное предположение для горячего внутреннего диска, но в прохладных внешних частях диска возможны отклонения вследствие замедления химических реакций и радиального дрейфа газа и пыли. Состав равновесной смеси больше зависит от температуры, нежели от давления, таким образом, мы можем примерно нанести на карту последовательность конденсаций и предсказать изменение состава диска в зависимости от радиуса. Таблица II, адаптированная Лоддером Lodders (2003), перечисляет различные температуры, ниже которых должны доминировать различные льды и минералы. Из них, безусловно, самая важная – температура, ниже которой может существовать водный лед – это 180К при давлении 10^-4 бар (хотя в условиях протопланетного диска лед конденсируется при температуре 150К). Для смеси солнечного состава поверхностная плотность сконденсировавшихся материалов драматически растет с формированием водяного льда:

Σ(льда и камня) $\simeq$ 4Σ(камня), (89)

хотя это отношение зависит от еще неуверенного знания точного солнечного состава Lodders (2003). Это заставляет нас связывать изменения в эффективности формирования планет (в частности, разделение между планетами земного типа и планетами–гигантами в Солнечной системе) со значительным изменением предсказанной поверхностной плотности твердых частиц на данном расстоянии от звезды.

Радиус протопланетного диска, вне которого может существовать водяной лед, называется снеговой линией. В Солнечной системе астероиды, богатые льдом, были найдены только во внешней части пояса астероидов (Morbidelli et al., 2000), что говорит о том, что снеговая линия в протосолнечной туманности располагалась около 3 а.е. Для пассивных протопланетных дисков вычисленное расположение снеговой линии оказывается гораздо ближе к звезде – в ряде случаев порядка 1 а.е. – однако увеличение скорости аккреции до значений, соответствующих классическим звездам типа Т Тельца, достаточно для переноса снеговой линии до 3 а.е.