 |
Астронет: Л. Л. Соколов, К. В. Холшевников/Коуровка Задача N тел и проблема интегрируемости http://variable-stars.ru/db/msg/1210340/node8.html |
4.1. Основная теорема о существовании интегралов
Пусть
- непустые области пространства
.
Рассмотрим задачу Коши с начальными данными из 
:
где
- функция гладкости 
.
Решение (
) обозначим
.
Теорема 5.
Пусть решения системы (47) определены при всех
и не выходят из 
;
существует функция
гладкости и постоянная 
такие, что
где
.
Тогда существует инвариантная область
,
в которой существует набор 
независимых автономных интегралов
гладкости .
Суть условия (48) сводится к следующему. Хотя отдельная траектория системы (47) не имеет самопересечений, сколь угодно узкая трубка траекторий самопересекаться может. А это - препятствие к интегрируемости [9]. Условие (48) говорит о том, что по крайней мере в одном направлении трубка движется без возвращений назад и поэтому избегает самопересечений.
Доказательство. Обозначим
- инвариантная относительно потока системы (47)
область, причем
- отображение
гладкости области
на ; 
-
отображение гладкости области
на 
,
причем (48) справедливо для всех
.
Запишем групповое свойство отображения 
:
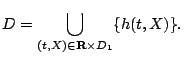
В частности,
В силу (48) уравнение
имеет относительно
единственное решение
при любых
.
По теореме о неявной функции 
имеет гладкость .
По определению и согласно (50)
, что в сопоставлении с
(51) и (52) дает
.
Подставляя в (50),
получим
Итак, при любом фиксированном 
правая часть (53) не
меняется вдоль решений (47). Как уже отмечалось,
- отображение на . Поэтому отображение
:
есть интеграл системы (47) гладкости
.
Мы построили набор скалярных интегралов - 
компонент
отображения 
. Осталось доказать, что среди них ровно
независимых. Это следует из очевидного свойства функции
(54): есть отображение орбит, т. е.
тогда и только тогда, когда существует такое
, что
.
Теорема доказана.
Всякая орбита по общей теории диффеоморфна точке, окружности
или прямой. В силу (52) время однозначно определяется положением,
поэтому каждая орбита уравнений (47) в
диффеоморфна прямой. Концы ее отделены друг от друга в силу (48).
<< 4. Интегрируемость | Оглавление | 4.2. Региональная интегрируемость задачи >>