 |
Астронет: А. А. Токовинин/ESO Пособие по адаптивной оптике обсерватории Серро-Тололо http://www.astronet.ru/db/msg/1205112/part3/wfs.html |
ВВЕРХ: Введение
ДАЛЕЕ: Лазерные опорные звезды
3. Датчики волнового фронта
- 3.1. Требования к датчикам волнового фронта
- 3.2. Датчики волнового фронта Шэка-Гартмана
- 3.3. Датчики искривления
- 3.4. Другие датчики волнового фронта
- 3.5. Восстановление волнового фронта
3.1. Требования к датчикам волнового фронта
Задача измерения искажений волнового фронта часто встречается в оптике (например, при изготовлении и испытании зеркал для телескопов), и обычно решается с помощью интерферометров. Почему бы не использовать стандартные лазерные интерферометры в датчиках волнового фронта (WFS) для адаптивной оптики?
Во-первых, система адаптивной оптики должна использовать свет звезд, проходящий сквозь турбулентную атмосферу, чтобы измерять волновые фронты, и следовательно, использовать некогерентные (а часто и неточечные) источники. Даже лазерные опорные звезды недостаточно когерентны, чтобы работать в обычных интерферометрах. WFS должны работать с некогерентными источниками белого света.
Во-вторых, интерференционные узоры хроматичны. Мы не можем позволить пропускать свет звезд через фильтр, так как мы хотим использовать слабые звезды. WFS должны очень эффективно использовать фотоны.
В-третьих, интерферометры определяют фазу с неопределенностью в
![]() ,
в то время как атмосферные искажения фазы обычно превосходят
,
в то время как атмосферные искажения фазы обычно превосходят
![]() .
WFS должны обладать линейностью во всем диапазоне атмосферных
искажений.
Существуют алгоритмы для "развертывания" фазы, позволяющие
устранить эту неопределенность, но они работают медленно,
а атмосферная турбулентность изменяется быстро, с характерным
временем в миллисекунды: WFS должны быть быстрыми.
.
WFS должны обладать линейностью во всем диапазоне атмосферных
искажений.
Существуют алгоритмы для "развертывания" фазы, позволяющие
устранить эту неопределенность, но они работают медленно,
а атмосферная турбулентность изменяется быстро, с характерным
временем в миллисекунды: WFS должны быть быстрыми.
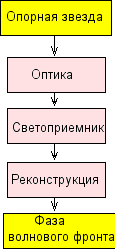
Этим требованиям удовлетворяют несколько существующих принципов устройства WFS. Каждый WFS состоит из следующих основных компонентов:
|
- Оптическое устройство,
которое преобразует аберрации в изменение интенсивности света
(в отличие от радиоволн, фазу оптических волн невозможно измерить
прямо по весьма фундаментальным физическим причинам, связанным
с квантовой природой света). Оптическая часть определяет линейность и
реакцию WFS.
- Детектор
преобразует интенсивность света в электрический сигнал.
Сигнал имеет шум благодаря фотонной природе света, но может
содержать также вклад от шума детектора. Накопление света
в детекторе приводит к задержке в цикле управления, которая
ограничивает ширину полосы сервоустройства.
- Реконструктор необходим для превращения сигналов в фазовые аберрации. Вычисления должны быть достаточно быстрыми, на практике это означает, что могут использоваться только линейные реконструкторы. Линейный реконструктор обычно производит умножение матриц.
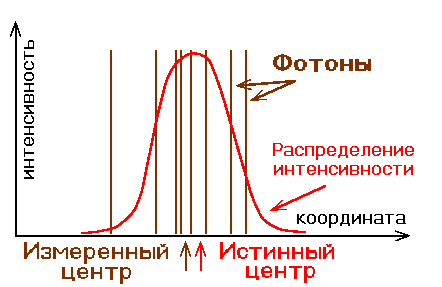
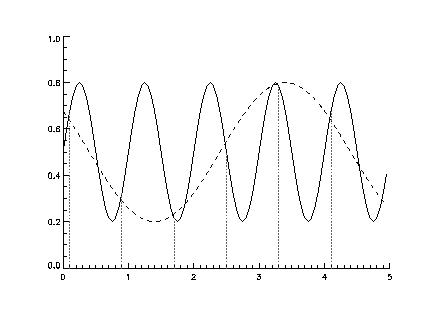 Не стоит говорить, что любой реальный WFS имеет конечное пространственное
разрешение, которое должно соответствовать размеру корректирующих
элементов (то есть расстоянию между актуаторами в деформируемом
зеркале). Искажения волнового фронта с меньшими размерами не должны
восприниматься. Однако, они влияют на сигнал WFS, вызывая так
называемую ошибку совмещения (подобно ошибке совмещения
во временных сигналах с конечной дискретизацией, смотри рисунок).
Спектр турбулентности уменьшается к высоким пространственным частотам,
поэтому ошибка совмещения часто мала по сравнению с другими
ошибками адаптивной оптики, в частности с ошибкой аппроксимации.
Не стоит говорить, что любой реальный WFS имеет конечное пространственное
разрешение, которое должно соответствовать размеру корректирующих
элементов (то есть расстоянию между актуаторами в деформируемом
зеркале). Искажения волнового фронта с меньшими размерами не должны
восприниматься. Однако, они влияют на сигнал WFS, вызывая так
называемую ошибку совмещения (подобно ошибке совмещения
во временных сигналах с конечной дискретизацией, смотри рисунок).
Спектр турбулентности уменьшается к высоким пространственным частотам,
поэтому ошибка совмещения часто мала по сравнению с другими
ошибками адаптивной оптики, в частности с ошибкой аппроксимации.
3.2. Датчики волнового фронта Шэка-Гартмана
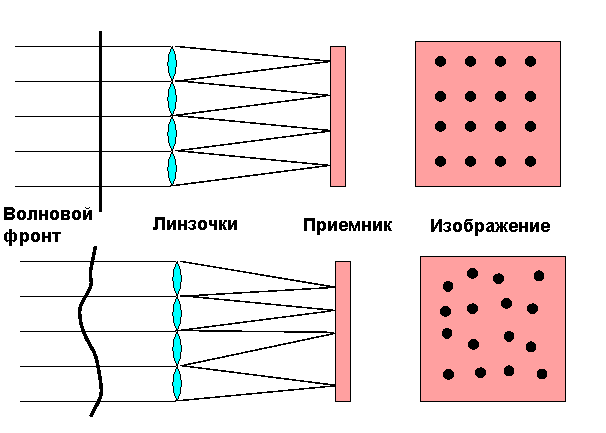
Хорошо известный тест Гартмана, первоначально разработанный для испытания оптики телескопов, был применен в адаптивной оптике в наиболее распространенном типе WFS. Изображение выходного зрачка проектируется на массив линз - двумерную решетку из маленьких одинаковых линз. Каждая линза занимает малую часть апертуры, называемую субзрачком, и строит изображение источника. Все изображения строятся на одном детекторе, обычно на ПЗС.
Когда входящий волновой фронт плоский, все изображения расположены
в правильном порядке, определяемом геометрией массива линз.
Когда волновой фронт искажается, изображения смещаются от своих
заданных положений. Смещение центроида изображения в двух
перпендикулярных направлениях
![]() пропорциональны средним наклонам волнового фронта по
пропорциональны средним наклонам волнового фронта по
![]() в субапертурах. Таким образом, WFS Шэка-Гартмана (S-H WFS)
измеряет наклоны волнового фронта.
Сам волновой фронт восстанавливается по массиву измеренных
наклонов, с точностью до постоянной, которая не играет роли при
построении изображения. Разрешение S-H WFS равно размеру субапертуры.
в субапертурах. Таким образом, WFS Шэка-Гартмана (S-H WFS)
измеряет наклоны волнового фронта.
Сам волновой фронт восстанавливается по массиву измеренных
наклонов, с точностью до постоянной, которая не играет роли при
построении изображения. Разрешение S-H WFS равно размеру субапертуры.
Вопрос:
Каков максимальный угловой размер источника, при котором начнут
перекрываться изображения от соседних субапертур? Возьмите размер
линзы 0.5 мм и фокальное расстояние 50 мм. Подходит ли такой
массив линз для системы адаптивной оптики с размером субапертуры
![]() =1 м?
=1 м?
Вопрос:
Оцените среднеквадратичные наклоны волновых фронтов на субапертурах
как функцию размера субапертуры
![]() и
и ![]() (используйте
коэффициенты атмосферных наклонов из раздела 1.10).
Вычислите для
(используйте
коэффициенты атмосферных наклонов из раздела 1.10).
Вычислите для
![]() =1 м
и качества изображения 1 секунда.
=1 м
и качества изображения 1 секунда.
Преимущество S-H WFS в том, что он полностью ахроматичен,
наклоны не зависят от длины волны. Он также может работать с
неточечными (протяженными) источниками. Если
![]() - это фаза волнового фронта, то наклон по
x, измеряемый S-H WFS, вычисляется как
- это фаза волнового фронта, то наклон по
x, измеряемый S-H WFS, вычисляется как
 |
(1) |
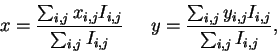 |
(2) |
 Теперь можно оценить ошибку определения наклона из-за фотонного шума.
Пусть
Теперь можно оценить ошибку определения наклона из-за фотонного шума.
Пусть
![]() радианов - это радиус изображения, формируемого каждой субапертурой.
Для протяженных источников
радианов - это радиус изображения, формируемого каждой субапертурой.
Для протяженных источников
![]() равно размеру источника (точнее, дисперсии распределения интенсивности
вокруг центра). Для точечных источников
равно размеру источника (точнее, дисперсии распределения интенсивности
вокруг центра). Для точечных источников
![]() если субапертуры меньше, чем
если субапертуры меньше, чем ![]() (изображения, ограниченные дифракцией), или
(изображения, ограниченные дифракцией), или
![]() для больших субапертур (размер изображения определяется атмосферным
дрожанием). Распределение интенсивности в изображении можно рассматривать
как распределение плотности вероятности приходящих фотонов.
Следовательно, каждый приходящий фотон позволяет определить положение
изображения с ошибкой
для больших субапертур (размер изображения определяется атмосферным
дрожанием). Распределение интенсивности в изображении можно рассматривать
как распределение плотности вероятности приходящих фотонов.
Следовательно, каждый приходящий фотон позволяет определить положение
изображения с ошибкой
![]() . Если
. Если ![]() фотонов зарегистрированы за время экспозиции,
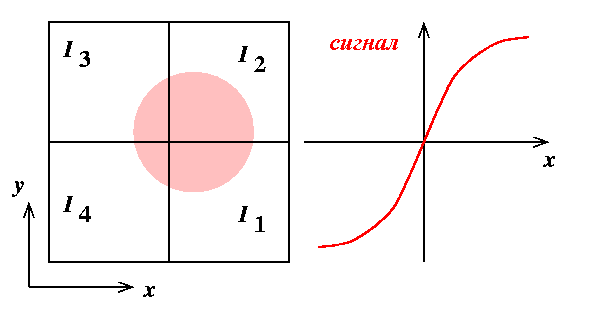
фотонная ошибка положения центроида (т.е. наклона) будет равна
фотонов зарегистрированы за время экспозиции,
фотонная ошибка положения центроида (т.е. наклона) будет равна
![]() ,
как после повторения измерения
,
как после повторения измерения
![]() раз.
раз.
В фотометрическом диапазоне R (длина волны около 600 нм), где
чувствительность современных детекторов максимальна, звезда
0 величины дает поток в 8000 фотонов в секунду на квадратный сантиметр
на нанометр полосы пропускания (эффективная полоса пропускания может
для хорошего ПЗС достигать 300 нм). Для звезды величины m
поток уменьшится в
![]() раз. При вычислении потока, доступного детектору WFS, необходимо
принять во внимание оптическое пропускание.
раз. При вычислении потока, доступного детектору WFS, необходимо
принять во внимание оптическое пропускание.
Вопрос: Вычислите количество фотонов, зарегистрированных за экспозицию в 1 мс в субапертуре 1 м от звезды 15-й величины. Принять полное пропускание 0.3 и квантовую эффективность 0.6.
Общепринято выражать все ошибки волнового фронта в радианах.
Мы умножим ошибку наклона на
![]() ,
чтобы получить дисперсию различия фазы между краями субапертуры в
квадратных радианах:
,
чтобы получить дисперсию различия фазы между краями субапертуры в
квадратных радианах:
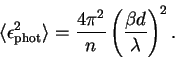 |
(3) |
Вопрос:
Сколько фотонов необходимо накопить, чтобы добиться фотонной
ошибки в 1 радиан в S-H WFS с
![]() ?
Принять, что получение изображения и исследование волнового фронта
осуществляются на одной длине волны.
?
Принять, что получение изображения и исследование волнового фронта
осуществляются на одной длине волны.
Ошибка восстановления волновых фронтов пропорциональна
![]() с коэффициентом, называемым распространение шума.
Известно, что для S-H WFS распространение шума порядка единицы
и лишь немного увеличивается с количеством элементов (наклоны
интегрируются реконструктором, поэтому шум не усиливается).
с коэффициентом, называемым распространение шума.
Известно, что для S-H WFS распространение шума порядка единицы
и лишь немного увеличивается с количеством элементов (наклоны
интегрируются реконструктором, поэтому шум не усиливается).
Фотонный шум пропорционален квадрату размера субапертуры
![]() .
Это означает, что для данного
.
Это означает, что для данного
![]() ,
фотонная ошибка S-H WFS не зависит от размера его субапертуры.
Этот вывод верен только для идеального детектора; в реальных системах
с ПЗС (например,
NAOS на VLT)
для более слабых опорных звезд используются большие субапертуры.
,
фотонная ошибка S-H WFS не зависит от размера его субапертуры.
Этот вывод верен только для идеального детектора; в реальных системах
с ПЗС (например,
NAOS на VLT)
для более слабых опорных звезд используются большие субапертуры.
 Сколько пикселов в детекторе должно быть отведено на каждую
субапертуру? Чтобы точно вычислить положение центроидов, каждое
индивидуальное изображение должно строиться достаточно детально,
и на каждую субапертуру необходимо более 4х4 пикселов. Однако
каждый пиксел ПЗС приемника дает шум считывания, который для
слабых опорных звезд доминирует в фотонном шуме. Поэтому в
некоторых конструкциях (например,
Altair для Джемини-Север)
на каждую субапертуру приходится только 2х2 пиксела. В этом случае
каждый элемент работает как квадратная ячейка, и
наклоны по x,y вычисляются из отношений интенсивности:
Сколько пикселов в детекторе должно быть отведено на каждую
субапертуру? Чтобы точно вычислить положение центроидов, каждое
индивидуальное изображение должно строиться достаточно детально,
и на каждую субапертуру необходимо более 4х4 пикселов. Однако
каждый пиксел ПЗС приемника дает шум считывания, который для
слабых опорных звезд доминирует в фотонном шуме. Поэтому в
некоторых конструкциях (например,
Altair для Джемини-Север)
на каждую субапертуру приходится только 2х2 пиксела. В этом случае
каждый элемент работает как квадратная ячейка, и
наклоны по x,y вычисляются из отношений интенсивности:
| (4) |
Реакция детектора наклона с квадратной ячейкой линейна только для
наклонов меньших, чем
![]() ,
коэффициент реакции пропорционален
,
коэффициент реакции пропорционален
![]() (и поэтому может изменяться, в зависимости от качества изображения
или размера объекта). Это цена, которую нужно заплатить за
увеличение чувствительности, которая имеет первостепенное
значение для астрономов.
(и поэтому может изменяться, в зависимости от качества изображения
или размера объекта). Это цена, которую нужно заплатить за
увеличение чувствительности, которая имеет первостепенное
значение для астрономов.
Вопрос: Какой должна быть форма изображения опорной звезды, чтобы добиться в точности линейной кривой реакции квадратной ячейки?
S-H WFS широко распространены, так как они основаны на проверенной технологии и богатом опыте, компактны и стабильны. Эти WFS требуют калибровки номинального положения пятна, которая производится при получении изображения искусственного точечного источника.
3.3. Датчики искривления
Метод измерения искривления волнового фронта разрабатывался Ф.Роддиером с 1988 г. Его идея состояла в непосредственном соединении биморфного зеркала с датчиком искривления (CS), при котором отпадет необходимость в промежуточных вычислениях (хотя это так и не было осуществлено).
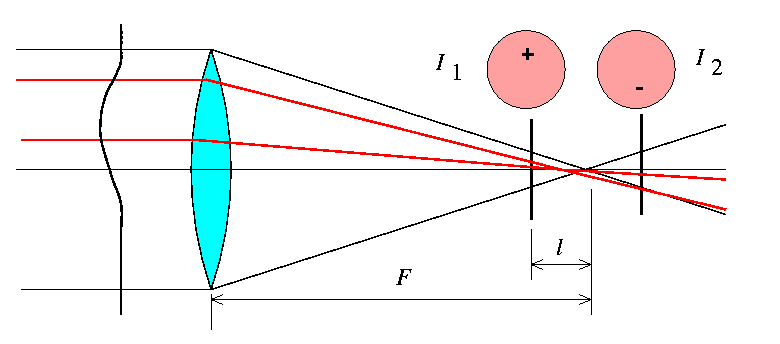
Пусть ![]() - распределение интенсивности света в предфокальном изображении звезды,
расфокусированном на некоторое расстояние
- распределение интенсивности света в предфокальном изображении звезды,
расфокусированном на некоторое расстояние
![]() , а
, а
![]() -
соответствующее распределение интенсивности в зафокальном изображении.
Здесь
-
соответствующее распределение интенсивности в зафокальном изображении.
Здесь
![]() - координата в плоскости изображения
и
- координата в плоскости изображения
и ![]() -
фокусное расстояние телескопа. Два этих изображения - как бы
изображения зрачка, уменьшенные с фактором
-
фокусное расстояние телескопа. Два этих изображения - как бы
изображения зрачка, уменьшенные с фактором
![]() .
В приближении геометрической оптики местные искривления волнового фронта
делают одно изображение ярче, а другое слабее; нормализованную
разницу интенсивностей можно записать как
.
В приближении геометрической оптики местные искривления волнового фронта
делают одно изображение ярче, а другое слабее; нормализованную
разницу интенсивностей можно записать как
![\begin{displaymath}
\frac{I_1(\vec{r}) -I_2(\vec{r})}{I_1(\vec{r}) +I_2(\vec{r})...
...triangledown^2 \phi \left( \frac{F \vec{r}}{l}\right) \right].
\end{displaymath}](http://images.astronet.ru/pubd/2005/04/08/0001205125/part3/img29.gif) |
(5) |
Вопрос: Нарисуйте пары пред- и зафокальных изображений для аберраций Зернике от 2 до 6.
Для источника с конечным угловым размером
![]() пред- и зафокальные изображения размыты на величину
пред- и зафокальные изображения размыты на величину
![]() .
Размытие должно быть меньше проекции размера субапертуры
.
Размытие должно быть меньше проекции размера субапертуры
![]() :
:
| (6) |
| (7) |
Для измерения волнового фронта с большим разрешением требуется большая расфокусировка, соответственно уменьшается чувствительность CS. Это означает, что CS может испытывать трудности с измерением аберраций высокого порядка.
Для точечных источников и больших субапертур (случай, представляющий
практический интерес) размытие
![]() определяется атмосферными аберрациями,
определяется атмосферными аберрациями,
![]() ,
как и для S-H WFS. Если система адаптивной оптики работает по
замкнутому циклу и остаточные аберрации (на длине волны работы WFS)
становятся малы, размытие уменьшается до
,
как и для S-H WFS. Если система адаптивной оптики работает по
замкнутому циклу и остаточные аберрации (на длине волны работы WFS)
становятся малы, размытие уменьшается до
![]() ,
позволяя уменьшить расфокусировку и увеличить чувствительность.
Это свойство до некоторых пределов действительно используется
в реальных системах адаптивной оптики: расфокусировка уменьшается,
когда цикл замыкается.
,
позволяя уменьшить расфокусировку и увеличить чувствительность.
Это свойство до некоторых пределов действительно используется
в реальных системах адаптивной оптики: расфокусировка уменьшается,
когда цикл замыкается.
Искажения волнового фронта с высокой частотой (меньше, чем размер
субапертуры) имеют спектр мощности (дисперсию амплитуд Фурье),
пропорциональный
![]() , но их спектр
кривизны пропорционален
, но их спектр
кривизны пропорционален ![]() и может вызвать большую ошибку совмещения. Чтобы не допустить
этого, сигнал должен быть сглажен перед разделением на субапертуры.
Сглаживание осуществляется уменьшением расфокусировки
и может вызвать большую ошибку совмещения. Чтобы не допустить
этого, сигнал должен быть сглажен перед разделением на субапертуры.
Сглаживание осуществляется уменьшением расфокусировки
![]() ,
которая также увеличивает чувствительность. В общем, выбор
,
которая также увеличивает чувствительность. В общем, выбор
![]() весьма критичен для CS, его необходимо подстраивать при изменении
качества изображения. Сигнал CS - это только более или менее
грубое приближение действительной кривизны волнового фронта...
весьма критичен для CS, его необходимо подстраивать при изменении
качества изображения. Сигнал CS - это только более или менее
грубое приближение действительной кривизны волнового фронта...
Мы приведем без вывода формулу для дисперсии фазы из-за фотонного
шума в CS, когда расфокусировка подстроена до оптимального значения:
 |
(8) |
 Масштаб пред- и зафокальных изображений зависит от расфокусировки
Масштаб пред- и зафокальных изображений зависит от расфокусировки
![]() которую необходимо изменять во время работы.
Это неудобно; в действительности сигнал кривизны регистрируется
в изображении зрачка с фиксированным масштабом, в то время как
величина расфокусировки подстраивается с помошью специального
оптического устройства (смотри ниже). Внешние субапертуры
проектируются на границу зрачка, их сигнал дает информацию о
радиальных градиентах фазы, включая общие наклоны (смотри рисунок).
которую необходимо изменять во время работы.
Это неудобно; в действительности сигнал кривизны регистрируется
в изображении зрачка с фиксированным масштабом, в то время как
величина расфокусировки подстраивается с помошью специального
оптического устройства (смотри ниже). Внешние субапертуры
проектируются на границу зрачка, их сигнал дает информацию о
радиальных градиентах фазы, включая общие наклоны (смотри рисунок).
Датчики искривления в действующих системых адаптивной оптики (например, в
PUEO и
Hokupa'a )
используют в качестве светоприемников лавинные фотодиоды (APD).
Это, как и фотоумножители - одноканальные устройства. Индивидуальные
фотоны детектируются и превращаются в электрические импульсы
без шума считывания и с малым темновым током, максимальная квантовая
эффективность около 60%. Индивидуальные сегменты зрачка выделяются
решеткой из линз (которая обычно соответствует радиальной геометрии
биморфного деформируемого зеркала), затем свет от каждого сегмента
фокусируется и передается на соответствующий фотодиод по
стекловолокну. Количество фотодиодов равно числу сегментов.
Внешние сегменты отслеживают края апертуры, и их сигналы пропорциональны
градиентам волнового фронта вдоль нормали.

Лавинные фотодиоды - большие и дорогие, поэтому эта конструкция
пригодна только для систем низкого порядка. Для того, чтобы на каждый
пиксел приходился один детектор, пред- и зафокальные изображения
попеременно подаются на один фотодиод, затем сигнал демодулируется
в компьютере волнового фронта. Модуляция фокусного расстояния
осуществляется с помощью колеблющегося мембранного зеркала,
помещенного в фокальной плоскости (типичная частота 2 КГц).
Расфокусировка
![]() обратно пропорциональна амплитуде колебаний мембраны, которая
подстраивается к изменяющемуся качеству изображений и может быть
уменьшена, когда цикл управления адаптивной оптикой замыкается,
увеличивая чувствительность детектора искривления. Полезная
компенсация турбулентности была достигнута даже с таким низким
сигналом, как 1 фотон на субапертуру за один цикл управления!
обратно пропорциональна амплитуде колебаний мембраны, которая
подстраивается к изменяющемуся качеству изображений и может быть
уменьшена, когда цикл управления адаптивной оптикой замыкается,
увеличивая чувствительность детектора искривления. Полезная
компенсация турбулентности была достигнута даже с таким низким
сигналом, как 1 фотон на субапертуру за один цикл управления!
Альтернативным решением может быть использование ПЗС как светоприемников в CS. Это обсуждается уже долгое время, однако в действующих системах пока не осуществлено. Недостаток ПЗС - шум считывания, который при низком уровне световых потоков становится доминирующим шумом. В Европейской Южной обсерватории были разработаны специальные ПЗС, которые позволяют осуществить несколько циклов модуляции за одно считывание.
Вопрос:
Предположим, что ПЗС с шумом считывания 5 электронов используется в
WFS. Каким должно быть число зарегистрированных фотонов
![]() ,
чтобы шум считывания стал меньше фотонного шума?
,
чтобы шум считывания стал меньше фотонного шума?
3.4. Другие датчики волнового фронта
 Трудности интерферометрических измерений волнового фронта можно
преодолеть, если интерферирующие лучи представляют собой волновые
фронты с небольшим боковым сдвигом
Трудности интерферометрических измерений волнового фронта можно
преодолеть, если интерферирующие лучи представляют собой волновые
фронты с небольшим боковым сдвигом
![]() (это называется интерферометром сдвига). Если сдвиг
меньше
(это называется интерферометром сдвига). Если сдвиг
меньше
![]() ,
различие фазы меньше одной длины волны, и отсутствует
неопределенность в
,
различие фазы меньше одной длины волны, и отсутствует
неопределенность в
![]() .
Интенсивность света в интерферограмме
будет равна
.
Интенсивность света в интерферограмме
будет равна
![\begin{displaymath}
I(\vec{r}) = \vert e^{i \phi(\vec{r})} + e^{i \phi(\vec{r}+\...
...t[ \rho \frac{\partial \phi(\vec{r})}{\partial \rho} \right].
\end{displaymath}](http://images.astronet.ru/pubd/2005/04/08/0001205125/part3/img41.gif) |
(9) |
Для малых сдвигов различие фазы пропорционально первой производной (наклону), следовательно, сигнал интерферометра сдвига похож на сигнал S-H WFS. Два сдвига в перпендикулярных направлениях необходимы, чтобы измерить наклоны x,y. В первой удачной системе адаптивной оптики (RTAC) использовался датчик волнового фронта, основанный на интерферометре сдвига, но теперь этот метод полностью оставлен в пользу S-H WFS.
Вопрос:
Оцените максимальный сдвиг
![]() ,
чтобы сохранить линейную реакцию интерферометра сдвига при данном
качестве изображения
(задано
,
чтобы сохранить линейную реакцию интерферометра сдвига при данном
качестве изображения
(задано ![]() ).
).
Другие типы интерферометров были предложены для использования в детекторах волнового фронта. Некоторые могут давать сигналы, прямо пропорциональные фазе (таким образом отпадает необходимость в реконструкторе), хотя и в ограниченном динамическом диапазоне. Некоторые решения могут представлять интерес для исправления остаточных аберраций высокого порядка (т.е. в системах адаптивной оптики с очень высокой степенью компенсации, необходимых для обнаружения экстрасолнечных планет).

Пирамидальный датчик волнового фронта (P-WFS) разрабатывается итальянскими астрономами. Прозрачная пирамида помещена в фокальной плоскости и рассекает изображение звезды на четыре части. Каждый пучок преломляется, и лучи формируют четыре изображения зрачка телескопа на одной ПЗС-матрице. Таким образом, каждая субапертура регистрируется четырьмя пикселами ПЗС. Оптическая схема похожа на испытание с помощью ножа Фуко.
Предположим, что источник света протяженный, и будем использовать
геометрическую оптику. Наклон волнового фронта в какой-либо субапертуре
изменяет положение источника на пирамиде, следовательно изменяется
световой поток, регистрируемый четырьмя пикселами, который в другом
случае был бы одинаковым. Вычисляя нормализованные разности
интенсивностей, мы получим два сигнала, пропорциональные наклонам
волнового фронта в двух направлениях. Чувствительность P-WFS зависит от
размера источника
![]() .
P-WFS можно рассматривать как массив квадратных ячеек, он похож на
S-H WFS.
.
P-WFS можно рассматривать как массив квадратных ячеек, он похож на
S-H WFS.
Что происходит, когда используется точечный источник (звезда) и
принимается во внимание влияние дифракции? Распределение интенсивности
в четырех изображениях зрачка становится сложной нелинейной функцией
формы волнового фронта, P-WFS больше не измеряет наклоны.
В случае слабых аберраций (амплитуда много меньше
![]() )
форму волнового фронта все же можно восстановить, хотя и более сложным
способом. Для того, чтобы восстановить линейность, звезда быстро
движется над вершиной пирамиды (например, по кругу), создавая
кольцеобразный источник. Это не модуляция (как в CS), а просто размазывание
точечного источника, так как сигнал интегрируется по одному или
нескольким циклам дрожания.
)
форму волнового фронта все же можно восстановить, хотя и более сложным
способом. Для того, чтобы восстановить линейность, звезда быстро
движется над вершиной пирамиды (например, по кругу), создавая
кольцеобразный источник. Это не модуляция (как в CS), а просто размазывание
точечного источника, так как сигнал интегрируется по одному или
нескольким циклам дрожания.
Вопрос: Нарисуйте изображения четырех зрачков в P-WFS для случая расфокусировки (мода Зернике номер 6).
Каковы преимущества P-WFS? Во-первых,отсутствует решетка из линз, субапертуры определяются пикселами детектора. Это означает, что для слабых звезд число субапертур можно уменьшить просто бинированием ПЗС. Во-вторых, амплитуду дрожания звезды можно подстраивать для наилучшего компромисса между чувствительностью (меньшее дрожание) и линейностью (большее дрожание). Для малых амплитуд чувствительность P-WFS может быть выше, чем S-H WFS (см. Astron. Astrophys. V. 369, P. L9, 2001). Наконец, возможно (по крайней мере в принципе) поместить несколько пирамид в фокальной плоскости, чтобы объединить свет нескольких слабых опорных звезд на одном детекторе. Несмотря на интерес к P-WFS, пока нет работающих систем адаптивной оптики с WFS такого типа.
Фаза может быть определена из анализа двух одновременных изображений звезды, одно в фокусе и другое расфокусированное (или, в общем, с какой-либо известной аберрацией). Этот подход называется фазовое различие. Алгоритм нелинейный (и поэтому медленный?), преимущества его применения в адаптивной оптике пока не ясны.
"Идеальный" датчик волнового фронта еще не изобретен. Не существует общей теоремы, которая бы установила абсолютный предел чувствительности любого WFS из-за фотонного шума. Вместо этого, у нас есть несколько эмпирических решений, возможность оптимизировать их параметры и выбирать лучшие среди имеющихся вариантов.
3.5. Восстановление волнового фронта
В этом разделе проблема вычисления формы волнового фронта на основании данных WFS рассматривается в общем виде.
Измерения (данные WFS) можно представить как вектор
![]() (
его длина равна удвоенному числу субапертур N для S-H WFS,
так как измеряются наклоны в двух направлениях, и равна N
для CS). Неизвестные (волновой фронт) - это вектор
(
его длина равна удвоенному числу субапертур N для S-H WFS,
так как измеряются наклоны в двух направлениях, и равна N
для CS). Неизвестные (волновой фронт) - это вектор
![]() ,
который может определен как значения фазы на координатной
сетке или, чаще, как
коэффициенты
Зернике.
Предполагается, что соотношение между измерениями и неизвестными
линейное, по крайней мере в первом приближении. Самая общая форма
линейного соотношения задается произведением матриц,
,
который может определен как значения фазы на координатной
сетке или, чаще, как
коэффициенты
Зернике.
Предполагается, что соотношение между измерениями и неизвестными
линейное, по крайней мере в первом приближении. Самая общая форма
линейного соотношения задается произведением матриц,
| (10) |
Матрица реконструктора B осуществляет обратную
операцию, определяя вектор волнового фронта из измерений:
| (11) |
Вопрос: Для данного количества субапертур N, оцените число арифметических операций, необходимых для восстановления фазы. Как оно зависит от длины волны, на которой получается изображение (для данного числа Штреля)?
Количество измерений обычно больше числа неизвестных, поэтому
применимо решение методом наименьших квадратов. В приближении
наименьших квадратов мы ищем такой фазовый вектор
![]() ,
который наилучшим образом описывает данные. Полученный в результате
реконструктор -
,
который наилучшим образом описывает данные. Полученный в результате
реконструктор -
| (12) |
Почти во всех случаях обращение матрицы вызывает затруднения, так как
матрица
![]() -
сингулярная.
Это означает, что на некоторые параметры (или комбинации параметров)
данные не накладывают ограничений. Например, мы не можем определить
первую моду
Зернике (поршень)
из измерений наклона. На практике обращение матрицы осуществляется
с удалением неопределенных (или плохо определнных)
параметров с помощью алгоритма разложения вырожденных значений.
В системах Шэка-Гартмана с квадратной геометрией, плохо определяемые
моды обычно включают квазипериодические деформации с частотой
решетки актуаторов.
-
сингулярная.
Это означает, что на некоторые параметры (или комбинации параметров)
данные не накладывают ограничений. Например, мы не можем определить
первую моду
Зернике (поршень)
из измерений наклона. На практике обращение матрицы осуществляется
с удалением неопределенных (или плохо определнных)
параметров с помощью алгоритма разложения вырожденных значений.
В системах Шэка-Гартмана с квадратной геометрией, плохо определяемые
моды обычно включают квазипериодические деформации с частотой
решетки актуаторов.
Сколько мод
Зернике
можно восстановить с помощью S-H WFS, имеющего
![]() субапертур? На первый взгляд, до
2
субапертур? На первый взгляд, до
2![]() .
На самом деле, только
.
На самом деле, только
![]() ,
потому что наклоны x,y не полностью независимы, они избыточны.
Для CS максимальное число мод также равно
,
потому что наклоны x,y не полностью независимы, они избыточны.
Для CS максимальное число мод также равно
![]() .
.
Реконструктор, использующий метод наименьших квадратов, не является лучшим. Из руководств по статистике известно, что лучшее восстановление может быть достигнуто с использованием априорной информации о свойствах сигнала. В случае адаптивной оптики такой информацией является статистика возмущений волнового фронта (например, ковариация мод Зернике) и статистика шума WFS. Стараясь найти решение, которое дает минимальную ожидаемую остаточную фазовую дисперсию (следовательно, максимальное число Штреля), мы получим матрицу реконструктора, которая похожа на фильтр Винера.
В случае одномерных сигналов фильтр Винера в пространстве частот
записывается как
 |
(13) |
Вопрос:
Пространственный спектр мощности ошибок наклона белый
(не зависит от частоты f) и спектр мощности
атмосферных наклонов пропорционален
![]() .
Как максимальная частота скомпенсированных аберраций зависит от
уровня шума
.
Как максимальная частота скомпенсированных аберраций зависит от
уровня шума
![]() ?
?
В системах адаптивной оптики выражения для минимальной дисперсии реконструктора включают матрицу взаимодействия и матрицы ковариации шума и атмосферных возмущений. Сходные результаты получаются с использованием других статистических подходов (максимум правдоподобия или максимальная постериорная вероятность).
Для любого реконструктора B, шум восстановленной фазы
![]() равен
равен
| (14) |
Выводы. Датчик волнового фронта - это ключевая часть астрономических систем адаптивной оптики, так как опорные звезды часто слабые, что ограничивает достижимую степень исправления турбулентности. Рассмотрены два ниболее распространенных принципа устройства датчиков волового фронта - Шэка-Гартмана и искривления. Для обеих мы можем вычислить фотонную ошибку и оценить ошибки восстановления волнового фронта как функцию величины опроной звезды и параметров системы. Основные принципы реконструкции волнового фронта были введены без углубления в подробности.
ВВЕРХ: Введение
ДАЛЕЕ: Лазерные опорные звезды