Astronet Астронет: Л. А. Вайнштейн, С. А. Каплан,  "Физика Космоса", 1986 Тепловое излучение
http://variable-stars.ru/db/msg/1202772

Тепловое излучение

 - эл.-магн. излучение, генерируемое за счет энергии теплового движения частиц излучающего тела. Т.и. тел удовлетворяет осн. закону Кирхгофа - отношение излучающей способности тела к его поглощающей способности есть универсальная функция температуры, не зависящая от физ. и геометрич. структуры тела. Т.и. в основном генерируется электронами. Характерной особенностью Т.и. явл. экспоненциальный спад интенсивности на больших частотах $\nu$:
$I_\nu \sim e^{-h\nu/kT} , h \nu\gg kT$ . (1)

Чернотельное излучение.

Важным частным случаем Т.и. явл. излучение абсолютно черного тела (чернотельное излучение), для к-рого коэфф. поглощения $\alpha^T_\nu=1$ на всех частотах. Интенсивность такого излучения $B_\nu$ определяется Планка законом излучения:
$B_\nu (T) = {2h\nu^3\over {c^2}} {1\over {e^{h\nu/kT} -1}}$ . (2)
При $h \nu\gg kT$ это выражение переходит в ф-лу Вина: $B_\nu (T) = {2h\nu^3\over {c^2}} \exp(-h\nu/kT)$, а при $h \nu\ll kT$ - в Рэлея-Джинса закон излучения. Если коэфф. поглощения тела $\alpha^T_\nu <1$, но не зависит от частоты, то интенсивность излучения равна $aB_\nu (T)$, где постоянная a < 1. Этот случай наз. излучение серого тела.

Если источником излучения явл. плазма, в к-рой электроны и тяжелые частицы (атомы, ионы) характеризуются различной температурой, то в ф-ле (2) под T надо понимать электронную температуру.

В случае неоднородного источника выходящее из него излучение явл. интегралом (суммой) по областям с различными темп-рами. Обычно в узкой спектральной области такое излучение можно описать ф-лой (2) с некоторой эффективной темп-рой.

Спектр чернотельного излучения не зависит от хим. состава тела и от природы физ. процессов в ищлучающем объеме. Более того, это излучение зависит не от объема тела, а лишь от величины его поверхности. Чернотельное излучение имеет место при термодинамическом равновесии излучения с веществом. Для равновесия необходимо, чтобы полная система - вещество и излучение - была замкнута, т.е. выход излучения должен составлять пренебрежимо малую часть от его количества в объеме системы. Это возможно лишь в том случае, когда фотон успевает многократно поглотится и переизлучитсья, прежде чем достигнет поверхности тела, т.е. на любой частоте $\tau=\alpha_\nu l$. Здесь l - характерный размер тела, $\alpha_\nu$ - коэфф. поглощения на ед. длины; величина $\tau$ наз. оптич. глубиной (оптической толщей) тела (на частоте $\nu$). Поскольку $\alpha_\nu$ пропорционален плотности или квадрату плотности, условие $\tau\gg 1$ выполняется при очень больших плотностях или размерах излучающих тел.

Спектр Т.и. даже однородного оптически толстого ($\tau\gg 1$) слоя плазмы может существенно отличатсья от чернотельного, если в переносе излучения существенную роль играет рассеяние излучения, т.к. в этом случае фотонам с разной энергией соответствует разная вероятность выхода из слоя.

Излучение оптически тонкой плазмы (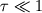$\tau\ll 1$).

Другим предельным случаем Т.и. явл. излучение плазмы, вещещство к-рой находится прибл. в термодинамич. равновесии, но излучение свободно из нее выходит. Это соответствует оптически тонкой ($\tau\ll 1$) плазме в локальном термодинамич. равновесии (ЛТР). В отличие от чернотельного излучения интенсивность и спектр излучения оптически тонкой плазмы существенным образом зависит от ее состава и ионизац. состояния, а также от вероятностей (сечений) конкретных процессов генерации излучения. При ЛТР распределение электронов и др. частиц описывается Максвелла распределением , а распределение атомов и ионов по возбужденным состояниям икратностям ионизации - Больцмана распределением и Саха формулой. Т.и. помимо непрерывного спектра включает спектральные линии (см. также Линейчатое излучение).

Общим св-вом любого механизма Т.и. явл. экспоненциальный спад на больших частотах (ф-ла 1). Однако множитель перед экспонентой для различных механизмов существенно различен. Непрерывный спектр Т.и. оптически тонкой горячей плазмы обусловлен гл. обр. тормозным излучением и фоторекомбинацией (см. Рекомбинация) электронов на положит. ионах. В холодной плазме при kT <0,5 эВ играют роль тормозное излучение на нейтральных атомах и отрицат. ионах и фотозахват электрона с образованием отриц. иона. Для оценки интенсивности непрерывного излучения электронов в поле положит. ионов часто используется т.н. приближение Крамерса, в к-ром поле иона предполагается чисто кулоновским (т.е. полем точечного заряда), а задача об излучении решается методом классич. электродинамики с использованием принципа соответствия. В приближении Крамерса электрон с энергией E в поле иона испускает излучение (в интервале энергий фотонов от 0 до E), интенсивность к-рого не зависит от частоты. С учетом максвелловского распределения по энергиям интенсивность тормозного излучения $I_{\nu t}$ на ионах с зарядом Z из ед. объема плазмы с темп-рой T в интервале 1 Гц и ед. телесного угла:
$I_{\nu t}=I_0 e^{-h\nu/kT}$ ,
$I_0=N_e N_Z {32 \sqrt{\pi} a_0^3 Ry Z^2 \over {3\sqrt{3} \cdot 137^3}} \left( {Ry\over {kT}} \right)^{1/2}$ , (3)
где $a_0=\hbar^2/m_e e^2$ - первый боровский радиус, $Ry=e^2/2a_0=13,6$ эВ - энергия ионизации атома водорода (постоянная Ридберга), $1/137=e^2/\hbar c$ - постоянная тонкой структуры.

При фоторекомбинации на n-й уровень положительного иона испускается фотон с энергией $h\nu=E+h\nu_n$, где $h\nu_n = E_n$ - энергия уровня (отсчитанная от границы ионизации). При $\nu > \nu_n$ интенсивность убывает как $\exp[-h(\nu - \nu_n)]$. Т.о., спектр рекомбинац. излучения представляет собой совокупность "зубцов", каждый из к-рых имеет резкий край и примыкает к границе соответствующей спектральной серии линейчатого спектра. Вероятность рекомбинации на n-й уровень (т.е. высота зубца) с ростом n убывает (~ 1/n), зубцы сгущаются и, наконец, сливаются.

Суммарная интенсивность тормозного и рекомбинац. излучения электронов с темп-рой T на ионах с зарядом Z в приближении Крамерса дается ф-лой:
$I_{\nu t}=I_0\; e^{-h\nu/kT} \left[ 1+\sum\limits_n {2 Q E_n^{3/2} e^{E_n/kT}\over {ZRy^{1/2} kT}} \right]$ . (4)
Здесь сумма берется по уровням n иона с зарядом Z-1, для к-рых $E_n \le h\nu$; фактор Q=1 для возбужденных уровней и для осн. состояния атомов с одним электроном на незаполненной оболочке, а для остальных зависит от числа электронов и электронной конфигурации. При $h\nu = E_n$ в $I_\nu$ начинает давать вклад новый уровень - появляется зубец, высота к-рого $\sim E_n^{3/2} / Z\sim Z^2/n^2$ . С ростом темп-ры зубцы сглаживаются и, вообще, роль рекомбинац. излучения падает. Но при этом может "включаться" рекомбинация на ионы с более высоким значением Z.

В космич. плазме непрерывный спектр включает тормозное и рекомбинац. излучение на ионах различных элементов. Тормозное излучение связано только с ионами H+ и He2+, вклад более тяжелых элементов мал. Рекомбинац. излучение на тяжелых элементах может быть существенным, если kT< IZ,a, где IZ,a - энергия ионизации иона Z элемента a.

К Т.и. оптически тонкой плазмы в ЛТР относятся оптич. излучение и радиоизлучение корон Солнца и звезд, межзвездного газа в областях HI и HII, поскольку оно обусловлено тепловыми электронами.

Излучение оптически толстой плазмы (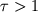$\tau > 1$).

С увеличением оптич. толщи излучающего объема происходит переход от излучения оптически тонкой плазмы в ЛТР к чернотельному излучению. При этом происходит своего рода насыщение. Интенсивность излучения при $\tau > 1$ перестает расти с увеличением плотности и объема V (для оптически тонкой плазмы интенсивность непрерывного спектра пропорциональна $N_e^2 l$, где Ne - концентрация электронов). Этот переход происходит неравномерно по спектру. Коэфф. поглощения в линиях намного больше, чем в непрерывном спектре, так что переход к чернотельному излучению начинается в линиях. Когда оптич. толща в центре линии $\tau_L$ достигает 1, интенсивность в этой точке спектра становится близкой к чернотельной при данной темп-ре. При дальнейшем росте $\tau_L$ интенсивность в центре линии практически не меняется, но линия становится шире (см. Кривая роста). Когда оптич. толща в континууме $\tau_c$ приближается к 1, $\tau_L$ уже настолько велика, что линия практически сливается с континуумом. При $\tau_c >1$ излучение во всем спектре становится чернотельным.

В реальных условиях, если оптич. толща $\tau \gg 1$, излучение выходит из слоя, оптич. глубина к-рого $\Delta\tau\sim 1$. Характеристики излучения (напр., эффективная темп-ра) являются нек-рым средним по слою. При этом геометрич. толщина слоя оказывается существенно больше для непрерывного спектра, чем для линий. Другими словами, излучение в непрерывном спектре выходит из б'ольших глубин и соответствует большей эффективной темп-ре, чем в линии.

В недрах звезд вещество и излучение находятся практически в термодинамическом равновесии, т.к. отток энергии наружу мал по сравнению с полным количеством лучистой энергии, испускаемой и поглощаемой веществом звезды. Во внеш. слоях выход излучения становится существенным. Излучение, выходящее из слоя $\Delta\tau\sim 1$, фактически не явл. чернотельным, но в первом приближении можно полагать $\alpha_\nu=$const, т.е. оно представляет собой излучение серого тела с нек-рой эффективной темп-рой.

Во многих астрофизических объектах первостепенную роль играют механизмы нетеплового излучения, в частности синхротронное излучение и обратный эффект Комптона (см. Комптоновское рассеяние).

(Л.А. Вайнштейн, С.А. Каплан)


Глоссарий Astronet.ru

Rambler's Top100 Яндекс цитирования