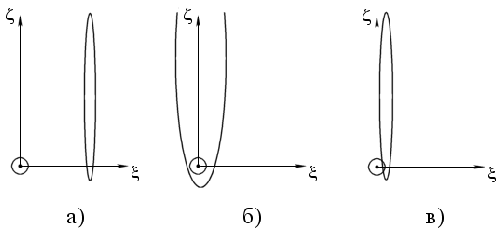|
Астронет: Н. Б. Железнов/Коуровка Астероидно-кометная опасность: современное состояние проблемы http://www.astronet.ru/db/msg/1202522/node4.html |
3. Поиск потенциально опасных сближений астероидов с Землей и оценка вероятности столкновений
Рассмотрим некоторые используемые в решении проблемы астероидной опасности величины и определения.
Минимальное расстояние между орбитами - параметр MOID.
Величина минимального расстояния между орбитой АСЗ и орбитой Земли
(параметр ![]() - Minimum Orbital Intersection Distance) служит
критерием для выделения потенциально опасных астероидов из числа
всех АСЗ.
- Minimum Orbital Intersection Distance) служит
критерием для выделения потенциально опасных астероидов из числа
всех АСЗ.
Минимальное расстояние между двумя орбитами достигается вдоль некоторой прямой, которая перпендикулярна к орбитам обоих тел, то есть перпендикулярна к касательным, проведенным к орбитам в точках, находящихся на минимальном для данных орбит расстоянии. Точки двух софокусных орбит, находящиеся на минимальном расстоянии, и величина самого расстояния могут быть найдены аналитически или численным способом. В общем случае задача сводится к решению тригонометрического уравнения восьмой степени (Kholshevnikov and Vassiliev, 1999).
Скорость соударения тела с Землей.
Обозначим вектор гелиоцентрической скорости астероида
в момент столкновения как v с компонентами ![]() ,
, ![]() ,
, ![]() ,
а вектор гелиоцентрической скорости Земли в этот момент как
,
а вектор гелиоцентрической скорости Земли в этот момент как
![]() . В таком случае скорость тела
относительно Земли без учета ее притяжения равна
. В таком случае скорость тела
относительно Земли без учета ее притяжения равна
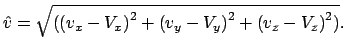
Эту скорость относительно Земли, еще не измененную ее притяжением, часто называют гиперболическим избытком скорости. Полная скорость соударения с Землей находится по формуле
|
|
(1) |
где
![]() - параболическая скорость
относительно Земли, то есть скорость, которую приобретает тело,
падающее на Землю «из бесконечности», где его скорость
относительно Земли равна нулю. Параболическая скорость
относительно Земли приближенно равна 11.18 км/с.
- параболическая скорость
относительно Земли, то есть скорость, которую приобретает тело,
падающее на Землю «из бесконечности», где его скорость
относительно Земли равна нулю. Параболическая скорость
относительно Земли приближенно равна 11.18 км/с.
Отметим, что средние скорости столкновения АСЗ с Землей (с учетом притяжения Земли) составляют около 20 км/с (Kholshevnikov and Shor, 1995; 1996; Gladman et al., 2000).
Энергия столкновения. При столкновении космического тела с Землей его кинетическая энергия является главным разрушительным фактором. Поэтому оценка кинетической энергии является едва ли не первейшей задачей при обнаружении тела на орбите, приводящей к столкновению с Землей.
Кинетическая энергия ![]() выражается формулой
выражается формулой
![]() , в которой
, в которой ![]() - масса тела, а
- масса тела, а
![]() - его скорость относительно Земли с учетом
притяжения Земли, рассчитанная по формуле (1).
- его скорость относительно Земли с учетом
притяжения Земли, рассчитанная по формуле (1).
Скорость тела относительно Земли всегда может быть вычислена достаточно точно для ориентировочных расчетов, а массу, за отсутствием других возможностей, в подавляющем числе случаев массу можно оценить по фотометрическому диаметру тела и его предполагаемой плотности.
Величину кинетической энергии, приносимой падающим на Землю телом,
принято выражать в мегатоннах тринитротолуолового эквивалента. При
этом
![]()
Плоскость цели.
Плоскость цели - это плоскость, проходящая через центр
планеты-мишени перпендикулярно к невозмущенному
вектору скорости тела-снаряда относительно планеты-мишени ![]() .
.
Прицельное расстояние и радиус захвата. Относительная
скорость астероида ![]() на входе в сферу действия равна
разности гелиоцентрических скоростей астероида и Земли. По
направлению она близка к асимптоте гиперболы, описываемой телом в
сфере действия планеты. Обогнув Землю, на выходе из сферы действия
астероид имеет ту же самую по величине относительную скорость
на входе в сферу действия равна
разности гелиоцентрических скоростей астероида и Земли. По
направлению она близка к асимптоте гиперболы, описываемой телом в
сфере действия планеты. Обогнув Землю, на выходе из сферы действия
астероид имеет ту же самую по величине относительную скорость
![]() , но ее направление изменяется на некоторый угол.
Расстояние от центра Земли до этой асимптоты называется прицельным
расстоянием (
, но ее направление изменяется на некоторый угол.
Расстояние от центра Земли до этой асимптоты называется прицельным
расстоянием (![]() ). Прицельное расстояние связано с минимальное
расстоянием гиперболы от центра Земли (
). Прицельное расстояние связано с минимальное
расстоянием гиперболы от центра Земли (![]() ) следующим
соотношением:
) следующим
соотношением:
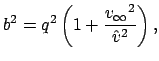
|
(2) |
где

есть параболическая скорость относительно Земли. В этой
формуле ![]() - гравитационная постоянная,
- гравитационная постоянная, ![]() - масса
Земли, а
- масса
Земли, а ![]() - ее экваториальный радиус. Если в формулу
(2) подставить
- ее экваториальный радиус. Если в формулу
(2) подставить ![]() , равное
, равное ![]() , то
, то ![]() будет равно
прицельному расстоянию, при котором траектория астероида коснется
поверхности Земли. Соответствующее значение прицельного расстояния
называется радиусом захвата. При решении вопроса о реальности
столкновения следует использовать не радиус Земли, а ее радиус
захвата.
будет равно
прицельному расстоянию, при котором траектория астероида коснется
поверхности Земли. Соответствующее значение прицельного расстояния
называется радиусом захвата. При решении вопроса о реальности
столкновения следует использовать не радиус Земли, а ее радиус
захвата.
На первом этапе решения задачи об оценке вероятности
столкновения АСЗ с Землей строится номинальная орбита астероида,
полученная путем улучшения предварительной орбиты из наблюдений с
помощью метода наименьших квадратов (МНК). При этом элементы
номинальной орбиты определяются со среднеквадратичными ошибками
![]() . Таким образом, в пространстве элементов орбит
номинальная орбита окружена областью возможных орбит. Эта
область может быть квалифицирована как область неопределенности
начальных условий движения. Фактическая орбита тела, которая
нам неизвестна, находится где-то внутри области
неопределенности. Эллипсоид с центром в точке на номинальной
орбите и полуосями, равными
. Таким образом, в пространстве элементов орбит
номинальная орбита окружена областью возможных орбит. Эта
область может быть квалифицирована как область неопределенности
начальных условий движения. Фактическая орбита тела, которая
нам неизвестна, находится где-то внутри области
неопределенности. Эллипсоид с центром в точке на номинальной
орбите и полуосями, равными ![]() , ограничивает область, в
которой сосредоточены практически все совместимые с наблюдениями
начальные условия. Мы будем называть такой эллипсоид
доверительным, а ограничиваемую им область начальных условий -
доверительной областью. Тело на возможной орбите мы будем называть
виртуальным (возможным) астероидом (Milani et al., 2000).
, ограничивает область, в
которой сосредоточены практически все совместимые с наблюдениями
начальные условия. Мы будем называть такой эллипсоид
доверительным, а ограничиваемую им область начальных условий -
доверительной областью. Тело на возможной орбите мы будем называть
виртуальным (возможным) астероидом (Milani et al., 2000).
На втором этапе будем предполагать, что задача имеет линейный характер. Это равносильно предположению, что область пространства, занятая виртуальными астероидами в окрестности сближения астероида, соответствующего номинальному решению, с Землей, представляет собой эллипсоид.
Рассмотрим систему координат, связанную с плоскостью цели.
Ось ![]() направлена параллельно скорости астероида относительно Земли на
границе сферы действия (
направлена параллельно скорости астероида относительно Земли на
границе сферы действия (![]() ), ось
), ось ![]() вдоль кратчайшего расстояния
между орбитами, ось
вдоль кратчайшего расстояния
между орбитами, ось ![]() перпендикулярна осям
перпендикулярна осям ![]() и
и ![]() и
направлена так, что вместе с ними образует правую систему координат.
и
направлена так, что вместе с ними образует правую систему координат.
Цепочка виртуальных астероидов, вытянувшихся вдоль номинальной
орбиты, проектируется на плоскость цели в прямую, параллельную оси
![]() , причем виртуальный астероид, соответствующий центру
доверительного эллипсоида в момент
, причем виртуальный астероид, соответствующий центру
доверительного эллипсоида в момент ![]() , пересекает плоскость
цели в точке, расположенной, вообще говоря, выше или ниже оси
, пересекает плоскость
цели в точке, расположенной, вообще говоря, выше или ниже оси
![]() . Область вокруг этой точки на плоскости
. Область вокруг этой точки на плоскости ![]() ,
, ![]() является отображением области возможных начальных условий движения
на плоскость цели. Поскольку мы предполагаем линейный характер
задачи, можно утверждать, что область начальных значений,
ограниченная в момент
является отображением области возможных начальных условий движения
на плоскость цели. Поскольку мы предполагаем линейный характер
задачи, можно утверждать, что область начальных значений,
ограниченная в момент ![]() доверительным эллипсоидом, отобразится
на плоскость
доверительным эллипсоидом, отобразится
на плоскость ![]() ,
, ![]() в часть плоскости, ограниченную
эллипсом с центром в точке, соответствующей центру доверительного
эллипсоида. Задача сводится к тому, чтобы найти
координаты центра эллипса на плоскости
в часть плоскости, ограниченную
эллипсом с центром в точке, соответствующей центру доверительного
эллипсоида. Задача сводится к тому, чтобы найти
координаты центра эллипса на плоскости ![]() ,
, ![]() и его
полуоси и оценить расположение эллипса относительно изображения
Земли.
и его
полуоси и оценить расположение эллипса относительно изображения
Земли.
Возможны следующие три случая взаимного расположения Земли и эллипса на плоскости цели:
- эллипс расположен на некотором расстоянии от окружности с радиусом, равным радиусу захвата Земли (рис. 2,а), что практически исключает возможность столкновения астероида с Землей;
- кружок с радиусом, равным радиусу захвата, находится внутри эллипса (рис. 2,б). Вероятность столкновения может быть рассчитана, исходя из отношения площади кружка к площади, ограниченной эллипсом. Для повышения точности прогноза можно учесть неодинаковую вероятность попадания виртуальных астероидов в различные точки области, ограниченной эллипсом;
- площадь, ограниченная эллипсом, частично покрывает область захвата Земли (рис. 2,в). Этот случай практически не отличается от предыдущего. Вероятность столкновения рассчитывается с учетом отношения перекрывающейся области ко всей площади, ограниченной эллипсом.
Нелинейный характер задача может иметь место по многим причинам.
Доверительный эллипсоид уже в момент ![]() может недостаточно
хорошо описывать область возможных начальных условий, поскольку
само распределение ошибок наблюдений может не подчиняться закону
Гаусса. Проекция доверительного эллипсоида на плоскость цели в
момент
может недостаточно
хорошо описывать область возможных начальных условий, поскольку
само распределение ошибок наблюдений может не подчиняться закону
Гаусса. Проекция доверительного эллипсоида на плоскость цели в
момент ![]() сближения с Землей, отдаленный от
сближения с Землей, отдаленный от ![]() на десятилетия,
вытягивается в очень узкую область, которая к тому же искривляется
в соответствии с кривизной земной орбиты. По всем этим причинам
линейный анализ задачи становится неадекватным, и требуется
применение более тонких методов анализа. К настоящему времени
предложено два таких метода: метод Монте-Карло и метод линии
вариации.
на десятилетия,
вытягивается в очень узкую область, которая к тому же искривляется
в соответствии с кривизной земной орбиты. По всем этим причинам
линейный анализ задачи становится неадекватным, и требуется
применение более тонких методов анализа. К настоящему времени
предложено два таких метода: метод Монте-Карло и метод линии
вариации.
Получение оценки вероятности столкновения АСЗ с Землей в случае нелинейной задачи имеет свои особенности, которые, ввиду их сложности, приводить здесь не будем.
<< 2. Астероиды, сближающиеся с | Оглавление | 4. Туринская и Палермская >>