Astronet Астронет: Р. А. Сюняев,  "Физика Космоса", 1986 Комптоновское рассеяние
http://variable-stars.ru/db/msg/1202008

Комптоновское рассеяние

 - упругое рассеяние фотона на свободном электроне. К. р. определяет непрозрачность вещества для жёстких (высокоэнергичных) рентгеновских и гамма-лучей. Оно играет важную роль в атмосферах нейтронных звёзд, в рентг. источниках, в недрах звёзд. Частным случаем К. р. в пределе низкочастотных фотонов и малоэнергичных электронов явл. томсоновское рассеяние. Рассеяние фотона на покоящемся электроне в силу законов сохранения энергии и количества движения сопровождается уменьшением энергии фотона и передачей её электрону. Это явление было экспериментально открыто в 1922 г. амер. физиком А. Комптоном, исследовавшим рассеяние рентг. лучей в графите, и известно как эффект Комптона (комптон-эффект), или эффект отдачи. Рассеяние низкочастотных фотонов на ультрарелятивистских электронах приводит к увеличению (во много раз) энергии фотонов - т.н. обратный комптон-эффект. Обратный комптон-эффект явл. одним из важнейших механизмов формирования спектров рентгеновского и гамма-излучения астрономич. объектов.

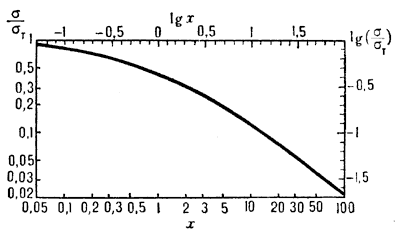
Рис. 1. Зависимость сечения комптоновского
рассеяния $\sigma$ от параметра
$x=(2h\nu/m_ec^2)\cdot \gamma(1-\mu v/c)$.
Сечение нормировано на $\sigma_T$.
Сечение К. р. (сечение Клейна-Нишины-Тамма) зависит от параметра $x=(2h\nu/m_ec^2)\cdot \gamma(1-\mu v/c)$, где $\nu$ - частота фотона до рассеяния, ($\mu$ - косинус угла $\Theta$ между направлениями распространения фотона и электрона до рассеяния, v - скорость электрона до рассеяния, $\gamma=[1-(v/c)^2]^{-1/2}$ - лоренц-фактор электрона. Эта зависимость приведена на рис. 1. В случае рассеяния на покоящемся электроне $x=2h\nu/m_ec^2$. В нерелятивистском пределе (при $x\ll 1$) сечение $\sigma$ медленно уменьшается: $\sigma=\sigma_T(1-x)$. В ультрарелятивистском пределе ($x\gg 1$) оно быстро убывает с ростом х: $\sigma=(3/4)\sigma_T\cdot x^{-1}(\ln x+1/2)$. Т. о., для низкочастотных фотонов сечение рассеяния равно сечению томсоновского рассеяния $\sigma_T=(8\pi/3)(e^2/m_ec^2)= 6,65\cdot 10^{-25} \mbox{см}^2$. При рассеянии на покоящихся электронах индикатриса рассеяния низкочастотных фотонов рэлеевская (см. Рэлеевское рассеяние). При $h\nu\ge m_ec^2$ увеличивается вероятность рассеяния вперёд, т.е. в направлении распространения фотона (см. рис. 1 в ст. Взаимодействие излучения с веществом).

Как и томсоновское рассеяние, К. р. может приводить к заметным поляризац. эффектам.

В процессе К. р. изменяются частота фотона и энергия электрона. Частота фотона после рассеяния
$\nu'=\nu\;{1-\mu {v\over c}\over {1-\mu'{v\over c} + {h\nu\over {\gamma m_ec^2}}(1-\cos\alpha)}}$ , (1)
где $\mu'$ - косинус угла $\Theta'$ между направлениями распространения фотона после рассеяния и электрона до рассеяния, $\alpha$ - угол рассеяния (угол между направлениями распространения фотона до и oпосле рассеяния, рис. 2). При рассеянии на покоящемся электроне (эффект Комптона)
$\nu'=\nu\;{1\over {1 + {h\nu\over {m_ec^2}}(1-\cos\alpha)}}$
или
$\lambda'=\lambda + {h\over {m_ec}}(1-\cos\alpha)$ , (2)
т. е. длина волны фотона $\lambda$ при рассеянии увеличивается, это увеличение (пропорциональное h и, следовательно, имеющее квантовую природу) зависит лишь от угла рассеяния. Величина $\lambda_C=h/m_ec=0,024 $\AA наз. комптоновской длиной волны. Из (2) видно, что изменение длины волны фотона при рассеянии на неподвижном электроне не превышает $\lambda$ и, т.о., существенно лишь для достаточно коротковолнового излучения.

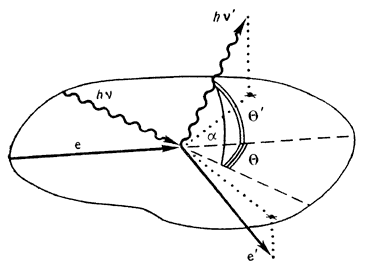
Рис. 2. Геометрия комптоновского рассеяния.
Сплошные стрелки - направления движения
электрона до и после рассеяния,
волнистые - то же для фотона.
При К. р. жесткого фотона $\gamma_1$ с энергией $h\nu_1$ на электроне имеется малая вероятность рождения низкочастотного фотона $\gamma_2$ с энергией $h\nu_2 < h\nu_1$: $\gamma_1+{\rm e \to e} +\gamma_1+\gamma_2$. Этот процесс наз. двойным комптон-эффектом. Рождение низкочастотных фотонов вследствие двойного комптон-эффекта может конкурировать с тормозным процессом e+p$\to$e+p+$\gamma_т$ (см. Тормозное излучение) лишь в экстремально разреженной и горячей плазме на ранних стадиях расширения Вселенной, в рентгеновских и гамма-источниках.

Комптон-эффект ограничивает пробег жёстких фотонов в веществе. В результате многократных рассеяний жёсткий фотон уменьшает свою энергию (отдавая её электронам), переходит в др. область спектра и поглощается вследствие фотоионизации атомов. К. р. определяет длину пробега жёстких рентг. фотонов (10 кэВ < $h\nu$ < 3 МэВ) в разреженной астрофизич. плазме. Рассеяние жёстких фотонов с $h\nu > 3$ кэВ на электроне в атоме водорода (или др. атома) происходит с тем же сечением, что и на свободном электроне. Это связано с тем, что энергия, сообщаемая электрону в силу эффекта отдачи, превышает энергию связи электрона в атоме водорода.

При рассеянии низкочастотных фотонов на ультрарелятивистских электронах (обратный комптон-эффект) максимальна вероятность рассеяния фотонов в направлении движения электрона ($\mu'\sim 1$). Если $h\nu/\gamma m_ec^2\ll 1$ то, как следует из (1), изменение частоты фотона описывается ф-лой:
$\nu'=\nu\;{1-\mu {v\over c}\over {1-\mu'{v\over c}}}$ . (3)
Т. о., при рассеянии низкочастотных фотонов на ультрарелятивистских электронах изменение частоты происходит только из-за Доплера эффекта (так же, как при отражении от движущейся стенки), а сечение рассеяния равно томсоновскому (мала величина х). Это легко понять, поскольку в этом случае в системе покоя электрона происходит классич. томсоновское рассеяние. Следовательно, обратный комптон-эффект, в отличие от комптон-эффекта, явл. чисто классич. эффектом (изменение частоты не зависит от h). Из (3) также следует, что при рассеянии в направлении движения электрона ($\mu'\sim 1$) происходит значит. увеличение частоты фотона $\nu\sim\gamma^2\nu$. Частота фотонов при рассеянии на изотропно распределённых релятивистских электронах в среднем должна увеличиваться в $(4/3)\gamma^2$ раз. Такое же ср. увеличение имеет место, если фотоны изотропного поля излучения рассеиваются на пучке ультрарелятивистских электронов. Если электроны имеют степенное распределение по энергиям $dN_e=K\varepsilon_e^{-\beta}\;d\varepsilon_e$ (dNe - концентрация релятивистских электронов в интервале энергий от $\varepsilon_e$, до $\varepsilon_e+d\varepsilon_e$, то спектр жёсткого излучения, формирующегося в результате обратного комптон-эффекта низкочастотных фотонов, также оказывается степенным. Его интенсивность $I_\nu=B\nu^{-s}$ (K и B - константы), где спектр. индекс $s=(\beta-1)/2$. При очень высоких энергиях электронов, когда параметр х становится большим, уменьшается сечение рассеяния, прирост энергии фотонов при рассеянии становится меньше, чем $\sim\gamma^2\nu$. Это приводит к отклонению спектра жёсткого излучения от степенного закона. Асимптотически интенсивность $I_\nu\sim\nu^{-\beta}\ln(h\nu kT_r/m_e^2c^4)$, где Tr - темп-ра низкочастотных фотонов.

Обратный комптон-эффект часто считают осн. механизмом формирования жёстких степенных спектров излучения в квазарах и ядрах галактик. Этот процесс явл. осн. причиной потерь энергии релятивистскими электронами в изотропном поле низкочастотного излучения (напр., в поле микроволнового фонового излучения, заполняющего Вселенную) или в поле излучения компактных объектов. Характерное время потерь энергии в таком поле излучения $t\approx (3/4)m_e c/\sigma_T \varepsilon_r \gamma$, т.е. тем меньше, чем выше энергия электрона ($\sim\gamma$) и плотность энергии излучения $\varepsilon_r$. При $\varepsilon_r>H^2/8\pi$, где Н - напряжённость магн. поля, потери энергии на обратный комптон-эффект превышают потери на синхротронное излучение.

К. р. может происходить не только на электронах, но и на любых др. заряженных частицах (напр., протонах). Но поскольку сечение К. р. обратно пропорционально квадрату массы, К. р. на тяжёлых частицах существенно менее эффективно.

(Р.А. Сюняев)


Глоссарий Astronet.ru

Rambler's Top100 Яндекс цитирования