1.

Окажись на месте котенка Сабрины популярная певица Сабрина, или кто другой из людей, не сносить бы бедняжке головы. Чем не истина.

Дело в том, что люди и кошки падают по-разному, как показано на рисунке:

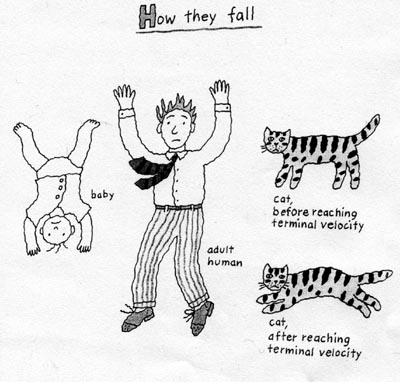
У кошки исключительно эффективный вестибулярный аппарат, что позволяет ей быстро ориентироваться в пространстве при падении. Кошка, изогнувшись, очень быстро оказывается лапами вниз в самом начале падения. В результате удар распределяется на все четыре лапы. Взрослые люди, если они не акробаты, при падении кувыркаются беспорядочно и чаще всего приземляются на ноги и менее часто - на голову. Дети падают головой вниз, так как у них голова относительно большая, что смещает центр тяжести тела. При этом они инстинктивно вытягивают руки. Поэтому характерные травмы у упавших с высоты людей и кошек разные. Люди чаще ломают ноги (взрослые) или руки (дети), а также разбивают черепа. Тогда как кошки с равной вероятностью ломают все свой четыре лапы [2], [3].

2.

Если человек падает с 9-го этажа, у него меньше шансов выжить, чем если бы он упал с 4-го.

Как ни странно, у кошек все наоборот. Статистический материал, собранный Нью-Йоркскими ветеринарами показывает, что погибли только 5 процентов кошек, упавших с высоты 7-32-го этажа, в то время как 10 процентов - при падении с высоты 2-6-го этажа. Вот истина достойная удивления. Графически она показана ниже (смертность людей и кошек при падении с разных высот):

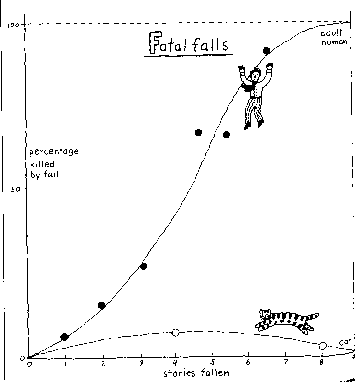
Существование предельной скорости падения объясняет этот удивительный феномен [2], [3].

3.

При падении скорость тела не растет все время, а стремится к некоторому предельному значению.

Это легко понять: сопротивление воздуха увеличивается со скоростью, и в конце концов уравновешивает силу тяжести. С этого момента скорость тела перестает расти, если форма тела не меняется.

Сопротивление воздуха тем больше, чем больше поперечное сечение тела. А сила тяжести определяется массой тела. Отношение поперечного сечения к массе у кошек больше, чем у людей. Поэтому предельная скорость падения у кошки (около 100 км/ч) примерно два раза меньше, чем у людей, и, соответственно, у нее больше шансов выжить. Но это еще не все.

4.

Вполне вероятно, что форма кошки до достижения предельной скорости и после ее достижения разные.

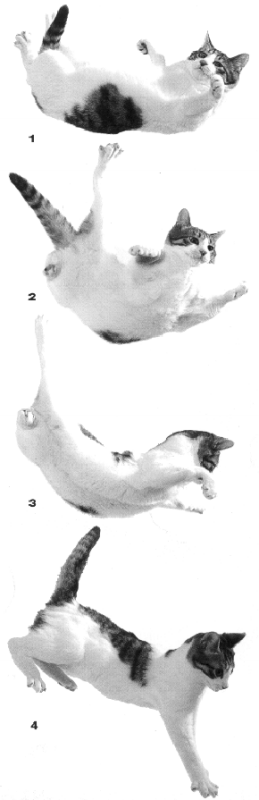
Пока кошка чувствует ускорение падения, она инстинктивно напрягается, выгибает спину и вытягивает лапы вниз. Упав в этой позе, кошка может сломать лапы. Хотя опять-таки у нее меньше шансов это сделать, чем у нетренированных людей после парашютного прыжка. Дело в том, что кошка падает на согнутые лапы, смягчая удар при падении. У человека такого инстинкта нет. Только длительные тренировки, такие как у парашютистов или у гимнастов, могут его научить приземлятся на согнутые ноги, подобно кошке. После достижения предельной скорости ускорение пропадает, кошка инстинктивно расслабляется и принимает форму белки-летяги, раскинув лапы горизонтально. Это увеличивает поперечное сечение и уменьшает предельную скорость падения. Кроме того в такой позе у кошки меньше шансов сломать лапы при ударе о землю, так как сила удара распределяется на всю площадь и диссипируется через мягкие ткани. Интересно, что лапы были сломаны у большинства кошек, свалившихся с 7-8-го этажа, и лишь у каждой тринадцатой из упавших с девятого этажа и выше [2].

Теперь вернемся к удивительной способности кошек менять ориентацию своего тела во время падения. Это роднит их с бароном Мюнхаузеном, который сам вытащил себя из болота, схватившись за свои волосы.

5.

Но, в отличие от барона Мюнхаузена, кошки при этом не нарушают законов физики. Наоборот, они умело этими законами пользуются.

Чтобы понять это, присмотримся пристальнее к падающим кошкам на рисунках внизу:

6.

Кошка в первую очередь бросает злобный взгляд на экспериментатора, который в доску ее замучил.

Потом резко поворачивает переднюю часть тела вниз. Согласно закону сохранения момента импульса, задняя часть тела при этом поворачивается в противоположную сторону. Но кошка прижимает передние лапы и вытягивает задние, а также оперирует хвостом, если он у нее есть (некоторые эксперименты с котом без хвоста показали, что наличие хвоста в этом деле не принципиально [4]). Цель этих манипуляций состоит в том, чтобы уменьшить момент инерции передней части тела и увеличить момент инерции задней части. Момент импульса равен произведению момента инерции на угловую скорость, поэтому несмотря на то, что момент импульса передней части тела в точности равен моменту импульса задней части, у передней части угловая скорость будет больше и, следовательно, в результате она повернется больше, чем повернется задняя часть тела в обратную сторону. После этого кошка повторяет трюк в обратном направлении. Только на сей раз прижимает задние лапы и вытягивает передние. Вследствие чего угол поворота задней части тела на этот раз будет больше, чем передней части. В итоге, когда оба этапа завершены, кошка восстанавливает свою форму и оказывается повернутой на нужный угол [5],[6].

7.

Эта нехитрая наука изменения ориентации тела в пространстве с помощью изменения формы была понятна людям уже лет сто назад [7].

А кошкам, надо полагать, это было известно с незапамятных времен. Но, оказывается, несравненно глубокие истины ждали своего часа и вдумчивого наблюдателя за полетом падающей кошки, который задался бы вопросом: каким образом кошка должна менять свою форму, чтобы проделать свой поворот наиболее экономным образом (а вы можете не сомневаться, что она делает это именно так)?

8.

Оказывается, для этого кошка должна решить почти такое же уравнение, которое описывает движение кварков в цветовом поле! [8],[9].

Каждая разновидность, или аромат кварков (а их всего шесть, по крайнее мере известных на сегодняшний день) может находиться в трех разных состояниях. Физики эти состояния условно называют цветом. Скажем, кварк может быть красным, зеленым или синим. Причем все эти цвета совершенно равноправны. И то, что определенные состояния кварка мы назвали красным, зеленым и синим,- это всего лишь условное соглашение. Любые другие три линейно независимые комбинации из этих состояний мы с таким же успехом могли бы назвать красным, зеленым и синим. Причем наше соглашение о том, что мы называем красным, зеленым и синим, может меняться от точки к точке в пространстве-времени. Физика от этого соглашения не должна зависеть, так как это всего лишь условность. Математически переход от одного соглашения (базиса) к другому задается комплексной унитарной матрицей три на три. Множество таких матриц составляет так называемую SU(3) неабелеву группу (если вам эти слова не понятны, а вы тем не менее хотите знать, как устроена природа, нет другого пути, кроме изучения математики, прислушиваясь к Дираку: "Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой... Почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе. Мы должны просто принять это как данное. Ситуацию, вероятно, можно было бы описать, сказав, что Бог является математиком очень высокого ранга, и что он при построении Вселенной использовал математику высшего уровня" [10]). Но "кинетическая" энергия кварков содержит производные по пространственно-временным координатам, и, если матрицы перехода от одного базиса к другому зависят от этих координат, при изменении наших соглашений возникнут дополнительные члены, содержащие производные этих матриц. Чтобы эти члены исчезли (ведь реальность не может зависеть от наших соглашений) надо обычные производные заменить на ковариантные производные, которые содержат компенсирующие калибровочные поля (глюоны в случае кварков). Все это является обобщением принципа минимального взаимодействия классической электродинамики и, вкупе с квантовыми представлениями, приводит к квантовой хромодинамике - современной теорий сильных взаимодействий.

В случае падающей кошки, роль пространства-времени в вышеописанной конструкции играет многообразие всевозможных форм кошки в ее системе центра масс. Чтобы сравнить ориентацию разных форм кошки, надо с каждой формой жестко связать оси координат. Но это можно сделать бесконечно многими способами, так как любой поворот системы осей тоже дает допустимую реперную конфигурацию. Физика (угол поворота кошки при последовательном изменении ее формы) не должна зависеть от произвольных соглашений о том, как прикрепить реперные оси к каждой форме. Поэтому опять появляются калибровочные поля, и возникает задача, математически подобная хромодинамической проблеме описания движения кварков во внешнем цветовом поле. Только на этот раз калибровочной группой является не SU(3), а SO(3) - группа трехмерных поворотов. Эта последняя, кстати, тоже неабелева группа, и чудесным образом падающая кошка оказывается связанной с теорией полей Янга-Миллса - одной из основных несущих конструкций Стандартной Модели элементарных частиц.

9.

Кошки не единственные существа, "знающие" теорию калибровочных полей. Как ни странно, эта наука очень важна для микроорганизмов.

Например, движение сперматозоидов тоже можно описать с помощью калибровочных потенциалов, и, следовательно, без этой, казалось бы, весьма абстрактной математической теории нам с вами не появиться на белом свете.

Дело в том, что движение микроорганизмов происходит при очень маленьких числах Рейнольдса. Число Рейнольдса показывает относительную важность сил инерции и сил вязкости при движении в газе или в жидкости. Когда человек движется через воздух, число Рейнольдса больше миллиона. При плавании в воде оно уменьшается до десяти тысяч. Все равно это очень много, чтобы составить интуитивное понимание того, что происходит в мире микроорганизмов, где число Рейнольдса много меньше единицы. Следующий пример даст более образное понимание этого. Чтобы человек плавал при тех же числах Рейнольдса, как, скажем, его собственный сперматозоид, надо его поместить в густое болото и запретить двигать любой частью своего тела со скоростью больше, чем один сантиметр в минуту [11].

При очень малых числах Рейнольдса силы вязкости преобладают, и инерцией можно пренебречь. Тогда в этом странном мире плавающих микроорганизмов реализуется вариант механики Аристотеля: тело перестает двигаться, как только перестают толкать его. С пренебрежением инерцией проблема движения становится по существу чисто геометрической проблемой. Величины перемещения и поворота вследствие последовательности изменений формы не зависят от того, насколько быстро эти изменения происходили, а зависят только от их геометрии, и опять подходящим математическим языком для описания такой ситуации оказывается теория калибровочных полей [8].

10. 

"Непостижимая эффективность математики в естественных науках ... это чудесный дар, который мы не понимаем и которого не заслуживаем" [12].

Эти слова Вигнера невольно вспоминаешь, видя, как переплелись между собой с помощью математики падающая кошка, кварки и плавающие инфузории. Вот еще один пример такого же рода. У пчел есть весьма сложный символьный язык танца с помощью которого пчела сообщает своим сородичам расстояние и направление до источника пищи [13]. Существование такого языка у пчел - факт сам по себе таинственный и достойный восхищения. Но вот математик Барбара Щипман (Barbara Shipman) заметила [14] в фигурах этого танца проявления шестимерного флагового многообразия, эзотерической математической конструкции, которую используют физики при изучении квантовой хромодинамики. И то не все, а только математически очень продвинутые.

Что это, случайное совпадение или очередное проявление "непостижимой эффективности математики" - пока неизвестно.

Но вернемся к падающей кошке. Несмотря на совершенство кошачьей акробатики, различные повреждения все равно вероятны при падении с большой высоты. Поэтому можно предположить, что эволюция выработала у кошек некий механизм исцеления.

11.

Как ни странно, ученые подозревают, что мурлыканье кошки и есть этот самый механизм [15],[16]!

Возможно, низкочастотные вибрации той частоты и той интенсивности, которую создают кошки при мурлыкании, обладают терапевтическим эффектом [16].

Но это уже одиннадцатая истина, тогда как для спокойного сна требовалось всего лишь десять. Но грядут и другие дни, и ваша душа снова станет искать истины, например каков молекулярный механизм эволюции, которая наделила кошек столь совершенными свойствами [17]. Ибо "все давно уже сказано, но так как никто не слушает, приходится постоянно возвращаться назад и повторять все сначала" [18].