Astronet Астронет: И. В. Чилингарян/Физический факультет МГУ Классификация объектов по распределению энергии в спектре
http://variable-stars.ru/db/msg/1191305/node2.html
<< Введение | Оглавление | 2. Библиотека template-спектров >>

Разделы

1. Математический аппарат классификации

Математический и статистический подход к классификации объектов по фотометрическим данным можно разделить на три уровня. Под первым уровнем будем понимать способ использования фотометрических данных, под вторым - алгоритм, применяемый для работы с данными, а под третьим - дополнительную коррекцию результатов, проводимую за счет привлечения дополнительных сведений. Выбор верного пути по этим уровням в значительной мере определяет успех классификации.

1.1. Первый уровень обработки фотометрических данных - способы представления данных

Данные, получаемые в результате обработки наблюдений, представляют из себя потоки излучения от объектов в каждом фильтре. Существует несколько вариантов представления этих данных для дальнейшей обработки.

  1. Первый вариант - вычисление показателей цвета объектов, то есть разностей звездных величин, получаемых из потоков в каждом фильтре. Общепринятым в настоящее время является использование так называемых AB-величин, предложенных Oke [19]. В этом случае применяются $F_{\nu}$-потоки. Звездная величина в фильтре вычисляется по формуле:
    \begin{displaymath} AB=-2.5 \lg{\frac{\int F_{\nu}(\nu)D(\nu)d\nu}{\int D(\nu)d\nu}}-48.61 \end{displaymath} (1.1)

    где $F_{\nu}$ выражено в $erg \cdot cm^{-2} s^{-1} Hz^{-1}$, а $D(\nu)$ - кривая пропускания фильтра.

    Группа немецких исследователей из института им.Макса Планка (обзор CADIS), которая работает с показателям цветов объектов, использует звездные величины, получаемые из потоков от объектов, выраженных в $\gamma \cdot m^{-2} s^{-1}$$^{-1}$, как принято в рентгеновской астрономии.

    Далее можно строить двуцветные диаграммы для различных комбинаций показателей цвета и пытаться разделять различные типы объектов по областям локализации на этих диаграммах. Такие работы проводятся с начала 60-х годов. Сейчас этот подход развивает вышеупомянутая группа немецких исследователей. Он же используется при выборе объектов для спектроскопии в обзоре SDSS. Как показано в работах [6,7], при помощи анализа значений показателей цвета в ситуации с большим числом фильтров, становится возможным довольно точное определение красного смещения для внегалактических объектов (ошибка в определении 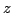$z$ меньше 0.1).

    В настоящее время в связи с мощным и быстрым развитием вычислительных средств становится возможным строить классификацию объектов в многомерном пространстве цветов при помощи методов кластерного анализа, когда каждому типу объектов соответствуют свои области связности.

    Серьезным недостатком подхода, использующего показатели цвета, можно считать увеличение ошибок при их нахождении за счет того, что обе звездные величины, используемые в расчетах, известны с ошибками, соответственно взятие их разности увеличивает абсолютную и относительную ошибки значения показателя цвета.

  2. Второй вариант, который в настоящее время активно используется значительной частью научных коллективов, работающих по данной тематике, заключается в построении зависимостей потока (AB-величины, показателя цвета) от длины волны или частоты, и дальнейшем анализе этой зависимости. В случае использования потоков данная зависимость называется распределением энергии в спектре объекта (Spectral Energy Distribution, SED) и представляет собой, по сути, низкодисперсионный спектр объекта. После этого производится сравнение SED классифицируемых объектов с SED объектов известного типа и красного смещения, либо с модельными данными. Первым исследователем, применивших этот метод для поиска внегалактических объектов, был Баум в 1962 году (см гл. 1).

    Теперь можно рассмотреть, в каком виде лучше представлять данные при работе с распределениями энергии в спектрах:

    1. Первый способ - представление данных в виде потоков в фильтрах, то есть непосредственное использование выходных данных фотометрии прямых изображений. В этом случае при сравнении распределений энергии в спектрах для объектов разной яркости необходимо найти нормировочный коэффициент, который достаточно просто определяется при использовании метода минимизации $\chi^2$ или максимального правдоподобия (см. ниже). При этом данный способ наиболее удобен с точки зрения расчетов.
    2. Второй способ - представление потоков от объектов в звездных величинах. В этом случае, в связи с логарифмическим характером звездных величин, коэффициент нормировки превращается в аддитивную константу. В этом случае упрощаются расчеты в случае использования многомерного полиномиального приближения модельных данных, но появляются проблемы, связанные со слабыми объектами, когда поток близок к нулю и соответственно звездная величина будет иметь большие ошибки, либо вовсе не будет определена в случае отрицательного значения потока. Выход из этой ситуации заключается в использовании так называемых asinh-величин [20].
    3. Третий способ - использование показателей цвета от объектов, в данном случае - разностей звездных величин в соседних фильтрах. По сути это численное дифференцирование SED, полученного вторым способом. В этом случае зависимости показателей цвета от длины волны для объектов с различной яркостью, но одинаковым видом спектра, будут совпадать с точностью до ошибок определения показателей цвета. Тогда мощные эмиссионные/абсорбционные детали в спектре будут приводить к скачкам показателей цвета в соседних точках через ноль. Основной недостаток такого представления, уже отмеченный выше - это увеличение ошибок при определении показателей цвета для слабых объектов.
    В целом с математической точки зрения все три способа были бы идентичны при высоком отношении сигнал/шум, но на практике в случае предельно слабых объектов (малое отношение сигнал/шум) лучше использовать первый способ представления, при средних отношениях сигнал/шум возможно использование второго способа, а при высоких - третьего. В данной работе используется первый способ, то есть работа с распределениями энергии в спектрах ведется в терминах потоков ($F_{\lambda}$). Это позволяет работать во всем диапазоне отношений сигнал/шум, что необходимо для успешной классификации объектов в глубоких полях.

1.2. Второй уровень обработки фотометрических данных - математический и статистический аппарат

Данный раздел содержит описание математических и статистических алгоритмов, предназначенных для второго варианта представления фотометрических данных. Все математические выкладки для методов аппроксимации распределений энергии в спектрах будут приведены для представления данных в виде потоков ($F_{\lambda}$). Они могут быть достаточно просто преобразованы к виду, использующему данные в любой из двух оставшихся форм.

1.2.1. Методы минимизации и максимального правдоподобия

В качестве входных данных мы имеем значения потоков от объекта в N фильтрах, их ошибки, шаблонный (template) спектр и кривые пропускания используемых светофильтров. Обозначим наблюдаемые потоки как $F_{i}$, их ошибки как $\Delta F_{i}$, кривые пропускания фильтров как $D_{i}(\lambda )$, распределение энергии в template-спектре как $S(\lambda )$, модельные потоки как $T_{i}$. Предполагается, что наблюдаемые потоки исправлены за спектральную чувствительность приемника.

Тогда

\begin{displaymath} T_{i}=\int\limits_{0}S(\lambda )D_{i}(\lambda )d\lambda \end{displaymath} (1.2)

Критерий $\chi ^{2}$ вычисляется следующим образом:

\begin{displaymath} \chi ^{2}=\sum_{i=1}^{N}\frac{(\alpha T_{i}-F_{i})^{2}}{\Delta F_{i}^{2}} \end{displaymath} (1.3)

Где нормировочный множитель $\alpha $ можно вычислить, исходя из соображений о минимуме $\chi ^{2}$, при фиксированных значениях потоков, продифференцировав выражение для $\chi ^{2}$ по $\alpha $ и приравняв значение производной 0, откуда получаем:

\begin{displaymath} \alpha =\frac{\sum\limits_{i=1}^{N}{\frac{T_{i}F_{i}}{\Delta... ...}{% \sum\limits_{i=1}^{N}{\frac{T_{i}^{2}}{\Delta F_{i}^{2}}}} \end{displaymath} (1.4)

Вычислив значение $\chi ^{2}$ легко вычислить критерий значимости:

\begin{displaymath} P(\chi ^{2})=\frac{\int\limits_{\chi ^{2}}e^{-t}t^{\frac{N}{2}-1}dt}{% \int\limits_{0}e^{-t}t^{\frac{N}{2}-1}dt} \end{displaymath} (1.5)

В качестве наиболее простого примера рассмотрим попытку проклассифицировать объект как звезду. Для этого необходимо построить модельные потоки для звезд из какой-либо библиотеки звездных спектров, например Pickles, взятых в определенной последовательности, скажем по спектральным классам. Тогда после вычисления значения $\chi^2$ для каждого типа спектра будет получена зависимость критерия значимости каждого такого определения от спектрального класса и класса светимости, что позволит сделать вывод, что, к примеру, объект N классифицируется как звезда K4V с погрешностью 1 спектральный подкласс с вероятностью 70%.

Входные данные для метода максимального правдоподобия такие же, как и в предыдущем случае, но вместо минимизации $\chi^2$ вычисляется значение и производится максимизация так называемой функции правдоподобия $L$:

\begin{displaymath} -\ln{L}+const=\sum\limits_{i=1}^{N}\frac{(\alpha T_{i}-F_{i})^{2}}{2 \Delta F_{i}^{2}} \end{displaymath} (1.6)

С математической точки зрения данная процедура абсолютно идентична минимизации $\chi^2$, различие заключается лишь в обозначениях.

1.2.2. Методы многомерной полиномиальной аппроксимации

Принципиально другим является подход к фотометрической классификации объектов, использующий так называемые тренировочные наборы данных, то есть фотометрические данные для объектов известного типа (в частном случае красного смещения) в тех же фильтрах. В качестве тренировочного набора данных можно брать результаты моделирования. Вначале неким образом производится параметризация распределений энергии в спектрах объектов из тренировочного набора. Затем производится аппроксимация зависимости искомых параметров объекта (типа объекта, красного смещения, спектрального класса и т.п.) от этих распределений, обычно с помощью многомерного полиномиального фиттинга. В результате можно определить искомые параметры для неизвестного объекта, подставив параметризацию его SED в аппроксимацию данной зависимости.

Математически данная задача довольно сложна, и в настоящее время один из наиболее популярных подходов к ее решению заключается в использовании искусственных нейронных сетей [23,24].

Нейронные сети неоднократно успешно использовались в астрономии, в частности, для морфологической классификации галактик [25], для морфологического разделения звезд и галактик [21,22] и спектральной классификации звезд [26,27,28]. С математической точки зрения нейронная сеть представляет собой нелинейный оператор, действуя которым на входные данные, можно получить результат определенного вида на выходе. Обычно нейронные сети для наглядности представляют как совокупность нескольких уровней - входного, одного или более скрытых и выходного. При этом каждый узел сети соединен со всеми узлами предыдущего уровня и со всеми узлами следующего уровня. Архитектура нейронной сети может быть описана соотношением $N_{in}:N_1:N_2:\ldots:N_{out}$, где $N_{in}$ - число входных узлов, $N_{i}$ - число узлов на $i$-м скрытом уровне и $N_{out}$ - число выходов. Каждая связь между узлами имеет вес и все они для каждого из уровней образуют вектор весовых коэффициентов.

Рассмотрим процесс поиска красного смещения для внегалактических объектов. На вход нейронной сети подаются потоки или $AB$-величины в каждом из фильтров, на выходе получается значение красного смещения. Перед использованием нейронных сетей для получения корректных результатов необходимо провести так называемый процесс тренировки сети. Для этого на вход подаются данные их тренировочного набора, а на выход - известное $z$. Тогда в процессе тренировки нейронной сети производится ее оптимизация при помощи минимизации остаточной функции:

\begin{displaymath} E = \frac{1}{2}\sum\limits_{k}[z_k-F(w,x_k)]^2 \end{displaymath} (1.7)

где функция $F(w,x_k)$ задается сетью. Передаточная функция $g_p$, заданная в каждом узле $p$, берет в качестве аргумента
\begin{displaymath} u_p=\sum\limits_{j}w_j x_j \end{displaymath} (1.8)

где сумма берется по всем входным узлам для узла $p$. Она обычно выбирается таким образом, чтобы входной аргумент мог принимать произвольные значения, а выходные значения лежали бы в строго ограниченном диапазоне. По аналогии с биологией в качестве передаточной функции обычно используют какую-либо из сигмоидных функций, к примеру $g_p(u_p)=1/[1+\exp{(-u_p)}]$, то есть функцию, график которой похож на букву $S$. Комбинация $g_p$ по всей сети формирует функцию $F(w,x_k)$. В процессе тренировки нейронной сети необходимо делать проверку работоспособности с помощью выборки данных из тренировочного набора, имеющих те же статистические характеристики, что и данные, используемые для тренировки; при этом веса связей замораживаются [24].

Как показано в работах [23,24] применение нейронных сетей для метода, использующего тренировочные наборы данных, дает результаты не хуже методов минимизации $\chi^2$, а зачастую намного лучше.

Если необходимо производить вероятностные оценки, то есть, например, получить плотность вероятности от красного смещения, необходимо построить нейронную сеть с большим количеством выходов, каждый из которых будет соответствовать шагу по $z$. Во время тренировки необходимо задавать "1" только на выходе, соответствующем правильному красному смещению, а на всех остальных "0". Тогда в результате применения нейронной сети к входным данным на каждом из выходов будет получаться соответствующее значение плотности вероятности.

У метода использующего нейронные сети есть один достаточно большой недостаток - даже при использовании современных вычислительных средств время, затрачиваемое на тренировку нейронной сети, достигает нескольких часов, в отличие от метода минимизации $\chi^2$, при правильной реализации которого несколько тысяч объектов будут обработаны меньше, чем за минуту.

1.3. Третий уровень обработки фотометрических данных - использование дополнительных сведений

После проведения второго этапа обработки может оказаться, что часть объектов примерно равновероятно классифицируется по различным типам и/или красным смещениям. При этом в ряде случаев некоторые варианты можно отбросить, если привлечь дополнительные сведения.

Например, если объект 18-й звездной величины равновероятно классифицируется как квазар с красным смещением 4.0 и эллиптическая галактика с красным смещением 3.9, то второй вариант физически не реализуем, если принять во внимание расстояние, определяемое по значению z, и диапазон светимостей квазаров и галактик. Здесь дополнительной информацией служат функции светимости соответствующих типов объектов.

Другим видом дополнительной информации является морфология объекта. Если объект на прямом снимке имеет протяженный вид, а классифицируется либо как звезда спектрального класса К, либо как галактика с небольшим красным смещением, то первый вариант отбрасывается, так как звезда должна быть точечным объектом, то есть ее форма не может сильно отличаться от средней PSF по полю.

Наиболее неоднозначной является ситуация, когда слабый объект классифицируется как звезда и как квазар либо галактика с большим красным смещением. Здесь морфологический критерий не работает, функции светимости далеких объектов известны не очень хорошо. Но в случае если наблюдается поле на высоких галактических широтах, можно наложить ограничения на яркость звезд поля, принимая во внимание звездное население, которое присутствует на данных направлениях в Галактике. Здесь приводится таблица 1.1, в которой содержится информация о различных типах звезд, которые можно встретить на высоких галактических широтах. В первой колонке содержится информация о спектральном классе и классе светимости звезд, во второй - диапазон абсолютных звездных величин в фильтре V, в третьей - максимальное расстояние, на котором можно встретить данные звезды, и в четвертой - минимальную яркость, которую они могут иметь.


Таблица 1.1. Нижние пределы на яркость звезд, наблюдаемых на высоких галактических широтах
Sp, Lum M R, kpc $m_{lim}$ Sp, Lum M R, kpc $m_{lim}$
OI-V -4..-9 0.5 4 FV-VI 5..1 0.5 13
BI-V 0..-8 0.5 8 GV-VI 7..3 25 24
AI-IV -1..-8 0.5 7 KV-VI 9..5 25 26
FI-IV 0..-7 25 17 MV-VI 17..8 25 $>$30
GI-IV 2..-7 25 19 LV $>$17 25 $>$30
KI-IV 4..-7 25 21 WD 16..8 25 $>$30
MI-IV 4..-7 25 21 PLN* 8..0 25 25
AV-VI 3..-1 0.5 11        

Используя данные из таблицы, в некоторых случаях можно уверенно отделить звезды от далеких галактик и квазаров. К примеру, если объект классифицируется примерно равновероятно как далекий объект и как звезда, и при этом его яркость существенно слабее значения из третьей колонки таблицы, то предпочтение отдается первому варианту классификации.


<< Введение | Оглавление | 2. Библиотека template-спектров >>

Rambler's Top100 Яндекс цитирования