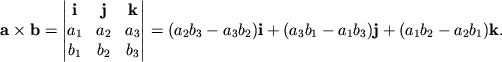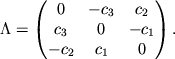 |
Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия http://www.variable-stars.ru/db/msg/1190817/node8.html |
2.2. Скаляры, векторы, тензоры и системы
координат
Прежде чем выводить основные формулы сферической геометрии, рассмотрим более общий вопрос: об определении скалярных, векторных величин, тензоров в математике и физике и их связи с системами координат.
Многие физические законы в векторной форме имеют вид:
т.е. вектор
Введем систему координат с началом в точке ![]() и осями
и осями
![]() . Направления осей задаются векторами
. Направления осей задаются векторами
![]() , соответственно, причем длина каждого вектора
считается равной единице. Поэтому они называются единичными
векторами. Система координат
, соответственно, причем длина каждого вектора
считается равной единице. Поэтому они называются единичными
векторами. Система координат ![]() является прямоугольной
(декартовой), если векторы
является прямоугольной
(декартовой), если векторы
![]() взаимно перпендикулярны.
взаимно перпендикулярны.
Скалярное произведение векторов обозначается точкой ![]() и
является скаляром, т.е. величиной, каждое значение которой может
быть выражено числом. Скалярами, например, являются масса,
температура, давление, длина и т.д.
и
является скаляром, т.е. величиной, каждое значение которой может
быть выражено числом. Скалярами, например, являются масса,
температура, давление, длина и т.д.
Пусть в системе ![]() векторы
векторы
![]() ,
,
![]() имеют
компоненты (декартовы координаты)
имеют
компоненты (декартовы координаты)
![]() и
и
![]() , причем
, причем ![]() -- это проекции векторов на ось
-- это проекции векторов на ось ![]() ,
, ![]() -- на ось
-- на ось ![]() ,
,
![]() -- на ось
-- на ось ![]() . Тогда модули векторов
. Тогда модули векторов ![]() и
и ![]() равны
равны
Из свойств скалярного произведения выделим следующие:
где
Из определения скалярного произведения следует, что оно равно
произведению модуля одного вектора на величину проекции другого
вектора на первый. Пусть
![]() -- углы
между вектором и осями системы координат (единичными векторами
-- углы
между вектором и осями системы координат (единичными векторами
![]() ), соответственно. Используя
определение скалярного произведения, находим, что проекции
вектора
), соответственно. Используя
определение скалярного произведения, находим, что проекции
вектора ![]() на оси системы координат
на оси системы координат ![]() равны
равны
Если в формуле (2.2)
![]() , то
, то ![]() . Значит два
вектора перпендикулярны тогда и только тогда, когда их скалярное
произведение равно нулю. Используя это свойство, получим:
. Значит два
вектора перпендикулярны тогда и только тогда, когда их скалярное
произведение равно нулю. Используя это свойство, получим:
Так как векторы
![]() имеют
единичную длину, то
имеют
единичную длину, то
Вектор ![]() может быть выражен через компоненты
может быть выражен через компоненты
![]() следующим образом:
следующим образом:
В линейной алгебре выражение (2.5) называется разложением вектора
Так как в дальнейшем мы будем использовать матричные методы
вычислений, то следует использовать более общее определение
скалярного произведения. Определим матрицу ![]() как
таблицу
как
таблицу
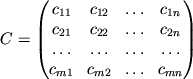
Согласно определению, произведение матрицы ![]() размера
размера ![]() на матрицу
на матрицу ![]() размера
размера ![]() есть матрица
есть матрица ![]() размера
размера
![]() , причем элементы матрицы
, причем элементы матрицы ![]() определяются формулой:
определяются формулой:
Исходя из этого определения получим, что скалярное произведение равно произведению вектор-строки на вектор-столбец, и (2.6) можно записать в виде:
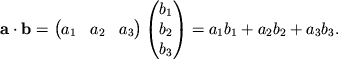
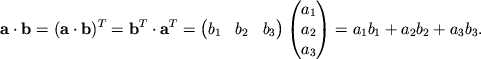
Вернемся к свойству (2.1). В более общем виде его можно записать в виде:
где
причем
В декартовой системе координат ![]() компоненты векторов
компоненты векторов ![]() и
и ![]() строго пропорциональны:
строго пропорциональны:
В общем виде, когда диагональные элементы
![]() не равны друг другу или недиагональные элементы
не равны друг другу или недиагональные элементы
![]() отличны от нуля, зависимость компонент вектора
отличны от нуля, зависимость компонент вектора ![]() от компонент вектора
от компонент вектора ![]() выражается вместо (2.9) системой
уравнений:
выражается вместо (2.9) системой
уравнений:
Это означает, что физический закон не может быть описан простым уравнением вида (2.1). Компоненты вектора
Пусть модуль вектора ![]() равен 2, вектор лежит в плоскости
равен 2, вектор лежит в плоскости
![]() , и угол между вектором и осью
, и угол между вектором и осью ![]() равен
равен ![]() . Тогда
проекции
. Тогда
проекции ![]() на оси
на оси ![]() равны:
равны:
Используя правила умножения матрицы на столбец, найдем компоненты
вектора
![]() по формуле:
по формуле:
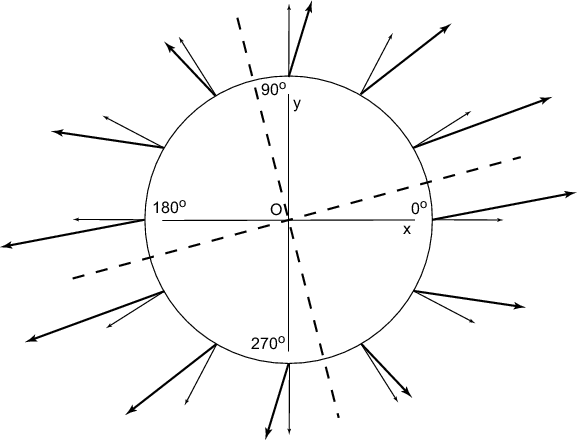 |
Рис. 2.4.
К определению тензора |
Определим теперь эти направления следующим образом.
Требование пропорциональности векторов, накладываемое физическим законом, приводит к уравнению:
Параметры
Очевидно, что система (2.11) имеет решение ![]() , которое
не дает нам никакой информации. Чтобы система (2.11) имела
нетривиальное решение, детерминант матрицы
, которое
не дает нам никакой информации. Чтобы система (2.11) имела
нетривиальное решение, детерминант матрицы
![]() должен равняться нулю:
должен равняться нулю:
Уравнение (2.12) является полиномом относительно параметра
Если собственные значения найдены (обозначим их как ![]() ),
то имеем:
),
то имеем:
Каждому собственному значению
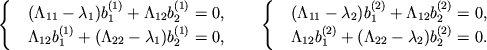
Так как
![]() , то, как говорят, строки матрицы
, то, как говорят, строки матрицы ![]() линейно зависимы. Поэтому компоненты собственных векторов можно
найти лишь с точностью до произвольной постоянной. Из первых
уравнений этих систем получим:
линейно зависимы. Поэтому компоненты собственных векторов можно
найти лишь с точностью до произвольной постоянной. Из первых
уравнений этих систем получим:
Умножим первое уравнение скалярно на вектор-строку
![]() , а второе -- на вектор-строку
, а второе -- на вектор-строку
![]() ,
и затем вычтем одно из другого. Получим
,
и затем вычтем одно из другого. Получим
Легко проверить, что если матрица
Так как
В трехмерном пространстве три собственных вектора определяют три
взаимно-перпендикулярных направления, которые можно выбрать в
качестве осей декартовой системы координат. Они называются
главными осями тензора ![]() . Вдоль главных осей векторы
. Вдоль главных осей векторы ![]() и
и ![]() параллельны.
Диагональные элементы тензора в системе главных осей называются
главными моментами тензора, и применительно к каждой конкретной задаче имеют особое
значение.
параллельны.
Диагональные элементы тензора в системе главных осей называются
главными моментами тензора, и применительно к каждой конкретной задаче имеют особое
значение.
На рис. 2.4 главные оси тензора ![]() показаны
пунктирной линией. В системе главных осей недиагональные
компоненты тензора равны нулю. Это легко показать, используя
пример, рассмотренный выше. Собственные значения матрицы
показаны
пунктирной линией. В системе главных осей недиагональные
компоненты тензора равны нулю. Это легко показать, используя
пример, рассмотренный выше. Собственные значения матрицы
![]() равны
равны
![]() . Компоненты
собственных векторов могут быть найдены с точностью до
произвольной постоянной:
. Компоненты
собственных векторов могут быть найдены с точностью до
произвольной постоянной:
![]() ,
,
![]() . Отсюда получим, что угол
. Отсюда получим, что угол ![]() между вектором
между вектором
![]() и осью
и осью ![]() равен
равен
![]() , а
между вектором
, а
между вектором
![]() и осью
и осью ![]() равен
равен
![]() .
Определим теперь оси новой системы координат
.
Определим теперь оси новой системы координат ![]() ,
, ![]() ,
направив их вдоль векторов
,
направив их вдоль векторов
![]() ,
,
![]() ,
соответственно. Преобразование от координат
,
соответственно. Преобразование от координат ![]() к
координатам
к
координатам ![]() , как будет показано ниже, можно записать в виде
матричного уравнения:
, как будет показано ниже, можно записать в виде
матричного уравнения:
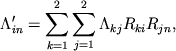
В главе 4 мы рассмотрим системы координат, связанные с Землей. Особое значение имеет система координат, определяемая главными моментами инерции Земли или осями фигуры Земли.
Условие равенства нулю скалярного произведения определяет
перпендикулярность векторов, но не зависит от их взаимной
ориентации. Так, если единичные векторы
![]() декартовой системы координат лежат в плоскости страницы, то
третий вектор
декартовой системы координат лежат в плоскости страницы, то
третий вектор ![]() , перпендикулярный и
, перпендикулярный и ![]() , и
, и ![]() ,
может быть направлен либо вверх, либо вниз. В зависимости от
направления
,
может быть направлен либо вверх, либо вниз. В зависимости от
направления ![]() система координат называется левой или правой.
система координат называется левой или правой.
Выбрать ту или иную систему координат можно с помощью векторного произведения векторов.
а его направление совпадает с направлением движения правого винта при его повороте от
Непосредственной подстановкой можно убедиться, что
которая часто будет использоваться в дальнейшем изложении курса.
С помощью определения векторного произведения можно однозначно определить ориентацию базисной тройки векторов. Мы будем использовать только правые системы координат (исключением является горизонтальная система).
Вернемся теперь к закону (2.7):
Тогда
Так как в (2.19)
![]() , то матрица
, то матрица
![]() называется антисимметричной. Соответственно,
тензор, изображаемый матрицей (2.19), называется
антисимметричным.
называется антисимметричной. Соответственно,
тензор, изображаемый матрицей (2.19), называется
антисимметричным.
Суммируем вышесказанное. Определение системы координат означает выбор тройки базисных векторов, которые: описывают 1) ориентацию системы в пространстве, а также позволяют 2) однозначно определить положение объекта относительно осей системы.
Можно определить разные системы координат в зависимости от
решаемой задачи. Выбор в качестве системы координат декартовой
системы определяется следующими свойствами этой системы: оси,
задаваемые тройкой базисных векторов
![]() ,
являются взаимно-перпендикулярными, направление осей неизменно
для любой точки пространства, оси являются прямыми линиями.
,
являются взаимно-перпендикулярными, направление осей неизменно
для любой точки пространства, оси являются прямыми линиями.
В декартовой системе координат закон пропорциональности между
двумя векторами, записанный в виде (2.7):
![]() , упрощается, так как тензор
, упрощается, так как тензор ![]() является квадратной
матрицей с особыми свойствами. Если матрица
является квадратной
матрицей с особыми свойствами. Если матрица ![]() симметрична, то существуют выделенные в пространстве направления,
в которых векторы
симметрична, то существуют выделенные в пространстве направления,
в которых векторы ![]() и
и ![]() параллельны. Подчеркнем, что
это -- математическая интерпретация закона (2.7). С
физической точки зрения и векторы
параллельны. Подчеркнем, что
это -- математическая интерпретация закона (2.7). С
физической точки зрения и векторы ![]() ,
, ![]() , и тензор
, и тензор
![]() отражают вполне определенные свойства физического тела,
и, следовательно, существование главных осей тензора отражает
физические характеристики тела.
отражают вполне определенные свойства физического тела,
и, следовательно, существование главных осей тензора отражает
физические характеристики тела.
Если матрица ![]() антисимметрична, то это означает, что
векторы
антисимметрична, то это означает, что
векторы ![]() и
и ![]() всегда перпендикулярны, и с
математической точки зрения действие такого тензора эквивалентно
векторному произведению.
всегда перпендикулярны, и с
математической точки зрения действие такого тензора эквивалентно
векторному произведению.
<< 2.1. Основные понятия | Оглавление | 2.3. Сферическая система координат >>