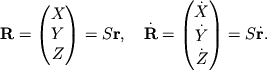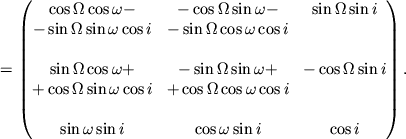|
Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия http://www.astronet.ru/db/msg/1190817/node23.html |
3.10.2. Параметры и аномалии кеплеровской орбиты
При рассмотрении движения планет можно ограничиться только случаем эллиптического движения. Орбита планеты в этом случае характеризуется шестью параметрами.
Определим систему координат ![]() , связанную с орбитой планеты.
Точка орбиты, ближайшая к Солнцу, называется
перигелием, а наиболее удаленная от Солнца --
афелием. Ось
, связанную с орбитой планеты.
Точка орбиты, ближайшая к Солнцу, называется
перигелием, а наиболее удаленная от Солнца --
афелием. Ось ![]() направим в перигелий,
ось
направим в перигелий,
ось ![]() -- перпендикулярно плоскости орбиты. Точки пересечения
плоскости орбиты планеты и эклиптики называются узлами
орбиты, причем восходящим узлом называется тот, который планета
проходит, переходя из области отрицательных широт в область
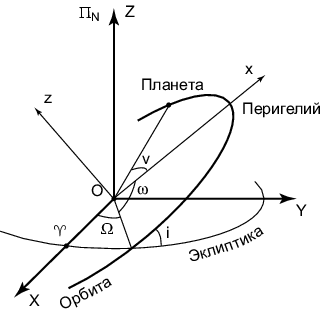
положительных широт. Графическое
представление и параметры кеплеровской орбиты показаны на
рис. 3.14.
-- перпендикулярно плоскости орбиты. Точки пересечения
плоскости орбиты планеты и эклиптики называются узлами
орбиты, причем восходящим узлом называется тот, который планета
проходит, переходя из области отрицательных широт в область
положительных широт. Графическое
представление и параметры кеплеровской орбиты показаны на
рис. 3.14.
Ориентация орбиты в пространстве (ориентация системы координат
![]() относительно гелиоцентрической системы
относительно гелиоцентрической системы ![]() )
описывается тремя углами. Угол между направлением на точку
весеннего равноденствия и точку восходящего узла называется
долготой восходящего узла и обозначается
)
описывается тремя углами. Угол между направлением на точку
весеннего равноденствия и точку восходящего узла называется
долготой восходящего узла и обозначается
![]() . Двугранный угол между
плоскостями орбиты и эклиптики называется наклонением
орбиты и обозначается как
. Двугранный угол между
плоскостями орбиты и эклиптики называется наклонением
орбиты и обозначается как ![]() . Третьим
углом, который обозначается
. Третьим
углом, который обозначается ![]() и называется
аргументом перигелия, является угол между
направлениями на восходящий узел и перигелий. Так как угол
и называется
аргументом перигелия, является угол между
направлениями на восходящий узел и перигелий. Так как угол ![]() постоянен, то это означает
неизменность положения оси
постоянен, то это означает
неизменность положения оси ![]() и в плоскости орбиты, и в
пространстве.
и в плоскости орбиты, и в
пространстве.
Следующие два параметра: большая полуось ![]() и эксцентриситет
и эксцентриситет ![]() определяют размеры и форму
орбиты. И, наконец,
положение тела на орбите в начальный момент определяется
эпохой прохождения через перигелий
--
определяют размеры и форму
орбиты. И, наконец,
положение тела на орбите в начальный момент определяется
эпохой прохождения через перигелий
-- ![]() .
.
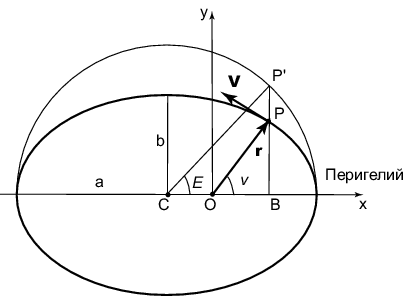
Мгновенное положение планеты на момент ![]() определяется углом
определяется углом
![]() , который называется истинной
аномалией (рис. 3.15).
, который называется истинной
аномалией (рис. 3.15).
Помимо истинной аномалии в небесной механике используются
эксцентрическая ![]() и
средняя
и
средняя ![]() аномалии. Построим
окружность радиуса
аномалии. Построим
окружность радиуса ![]() , равным большой полуоси эллипса, с
центром, который совпадает с центром эллипса
, равным большой полуоси эллипса, с
центром, который совпадает с центром эллипса ![]() . Опустим
перпендикуляр
. Опустим
перпендикуляр ![]() на ось
на ось ![]() ; тогда его продолжение пересечет
окружность в точке
; тогда его продолжение пересечет
окружность в точке ![]() . Угол
. Угол
![]() называется
эксцентрической аномалией. Угол, равный средней аномалии,
определяется средним движением и равен
называется
эксцентрической аномалией. Угол, равный средней аномалии,
определяется средним движением и равен
Часто в небесной механике и астрометрии используется величина, определяемая формулой
и называемая средней долготой.
Так как движение планеты при кеплеровском движении происходит в
плоскости, то положение планеты определяется проекциями
радиус-вектора
![]() , которые равны
, которые равны ![]() . Проекция
. Проекция
![]() на ось
на ось ![]() равна нулю:
равна нулю:
![]() . Из рис. 3.15
очевидно, что
. Из рис. 3.15
очевидно, что
Также, используя рис. 3.15, находим, что
Так как
Из выражений (3.56), (3.57) и формулы тангенса половинного угла получим выражение, связывающее истинную и эксцентрическую аномалии:
Углы
Теперь вернемся к уравнению (3.42). Так как
![]() , то уравнение (3.42) можно переписать в
виде:
, то уравнение (3.42) можно переписать в
виде:
Заменяя
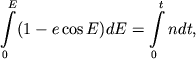
где
Найдем теперь вектор скорости
![]() . Заметим, что
. Заметим, что
![]() . Вектор скорости лежит в
плоскости орбиты, следовательно, его проекция на ось
. Вектор скорости лежит в
плоскости орбиты, следовательно, его проекция на ось ![]() равна
нулю. Из (3.56) находим проекции
равна
нулю. Из (3.56) находим проекции
![]() :
:
и квадрат скорости
Дифференцируя по времени вектор скорости (3.62) и учитывая,
что
![]() , найдем вектор ускорения тела при
движении по кеплеровской орбите, который также лежит в плоскости
орбиты:
, найдем вектор ускорения тела при
движении по кеплеровской орбите, который также лежит в плоскости
орбиты:
Для вычисления прямоугольных координат и проекций скорости тела в
гелиоцентрической системе координат достаточно найти матрицу
поворота ![]() системы
системы ![]() . Если матрица
. Если матрица ![]() известна, то
преобразование записывается в виде матричных уравнений:
известна, то
преобразование записывается в виде матричных уравнений:
Матрица ![]() вычисляется следующим образом (см. рис. 3.14):
сначала выполняем поворот относительно оси
вычисляется следующим образом (см. рис. 3.14):
сначала выполняем поворот относительно оси ![]() на угол
на угол ![]() до совмещения оси
до совмещения оси ![]() с линией узлов, затем -- поворот
относительно линии узлов на угол
с линией узлов, затем -- поворот
относительно линии узлов на угол ![]() и, наконец, поворот
относительно оси
и, наконец, поворот
относительно оси ![]() на угол
на угол ![]() :
:
Если элементы орбиты тела известны, то его положение и скорость в
эклиптической системе координат в любой момент времени ![]() определяются следующей последовательностью вычислений: 1) сначала
находится средняя аномалия
определяются следующей последовательностью вычислений: 1) сначала
находится средняя аномалия ![]() по формуле (3.53); 2) решая
уравнение Кеплера (3.61), находим эксцентрическую аномалию
по формуле (3.53); 2) решая
уравнение Кеплера (3.61), находим эксцентрическую аномалию
![]() ; 3) зная
; 3) зная ![]() , получим радиус-вектор тела
, получим радиус-вектор тела
![]() (3.57) и его проекции
(3.57) и его проекции ![]() в орбитальной системе
координат (3.56); 4) и, используя уравнения (3.65) и
матрицу (3.66), получим прямоугольные эклиптические координаты
и проекции скорости тела.
в орбитальной системе
координат (3.56); 4) и, используя уравнения (3.65) и
матрицу (3.66), получим прямоугольные эклиптические координаты
и проекции скорости тела.
Если эксцентриситет орбиты мал, то удобным методом решения
уравнения Кеплера является метод итераций. На первом шаге
предполагается, что ![]() . Тогда процесс итераций
. Тогда процесс итераций
Выразим теперь в виде ряда по степеням экцентриситета ![]() истинную аномалию
истинную аномалию ![]() как функцию средней аномалии
как функцию средней аномалии ![]() . Для этого
умножим сначала первое уравнение (3.56) на
. Для этого
умножим сначала первое уравнение (3.56) на ![]() , второе
-- на
, второе
-- на ![]() и сложим результат. После приведения подобных
членов получим:
и сложим результат. После приведения подобных
членов получим:
Выразим теперь
![$\displaystyle \sin E=\sin(M+e\sin M+\frac{e^2}{2}\sin 2M) \approx \sin
M\Bigl[1-\frac{(e\sin M)^2}{2}\Bigr]+\frac{e}{2}\sin
2M+\frac{e^2}{2}\cos M\sin 2M.
$](http://images.astronet.ru/pubd/2003/06/11/0001190894/tex/formula912.gif)
Аналогично находим, что
В заключение этого раздела рассмотрим движение Земли по орбите.
1) Центр тяжести Земли движется относительно центра масс системы
Земля+Луна. Последний находится на линии, соединяющей центры масс
Земли и Луны, на расстоянии, равном
![]() км от центра тяжести Земли, где
км от центра тяжести Земли, где ![]() -- расстояние между Землей и Луной, массы которых равны
-- расстояние между Землей и Луной, массы которых равны
![]() .
.
2) Центр тяжести системы Земля+Луна движется вокруг Солнца по
орбите, элементы которой не являются постоянными, а являются
функциями времени. Орбита близка к круговой; эксцентриситет
орбиты равен
![]() . Орбита центра тяжести системы
Земля+Луна является возмущенной вследствие притяжения
Земли, Луны и Солнца планетами. Из-за возмущений движение центра
тяжести системы Земля+Луна отличается от кеплеровского движения,
однако это отличие не превышает в долготе
. Орбита центра тяжести системы
Земля+Луна является возмущенной вследствие притяжения
Земли, Луны и Солнца планетами. Из-за возмущений движение центра
тяжести системы Земля+Луна отличается от кеплеровского движения,
однако это отличие не превышает в долготе
![]() , в широте
, в широте
![]() .
.
3) Центр Солнца движется относительно центра тяжести солнечной
системы -- барицентра. Движение центра Солнца
относительно барицентра солнечной системы определяется, главным
образом, двумя наиболее массивными планетами -- Юпитером и
Сатурном и представляется двумя почти круговыми движениями с
периодами обращения этих планет (![]() и
и ![]() лет).
Радиус круговых движений центра Солнца относительно барицентра
равен примерно
лет).
Радиус круговых движений центра Солнца относительно барицентра
равен примерно
![]() для Юпитера и
для Юпитера и
![]() для Сатурна (
для Сатурна (![]() и
и ![]() --
отношения массы Солнца к массам Юпитера и Сатурна)
(рис. 3.16).
--
отношения массы Солнца к массам Юпитера и Сатурна)
(рис. 3.16).
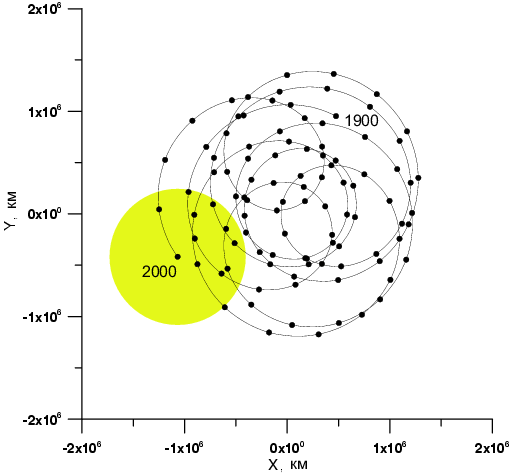 |
Рис. 3.16. Движение Солнца относительно барицентра солнечной системы в эклиптической системе координат на интервале времени 1900 -- 2000 гг. Промежуток между точками равен одному году. |
Орбитальные скорости движения Юпитера и Сатурна равны примерно 13
км/с и 9,5 км/с, соответственно компоненты скорости движения
центра Солнца, вызываемые этими планетами, составляют
![]() ,
,
![]() .
.
<< 3.10.1. Законы Кеплера | Оглавление | 4. Системы координат на >>