Астронет > Сферическая астрономия

Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия
http://www.variable-stars.ru/db/msg/1190817/node17.html

<< 3.5. Преобразование координат из | Оглавление | 3.7. Восход и заход >>

3.6. Суточное вращение небесной сферы

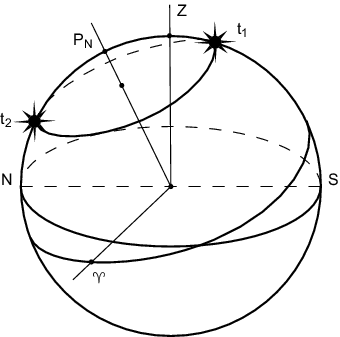
Из-за вращения Земли вокруг своей оси кажется, что небесная сфера вращается вокруг оси мира, которая параллельна оси вращения Земли. В результате этого через небесный меридиан периодически проходят звезды, Солнце и другие светила.

Определение 3.6.1 Момент прохождения звезды через меридиан называется кульминацией звезды.

Та из двух кульминаций, которая происходит ближе к зениту, называется верхней, вторая -- нижней. Для наблюдателя в северном полушарии верхняя кульминация происходит к югу от северного полюса мира (момент $t_{1}$ ), а нижняя -- к северу от точки $P_{N}$ (момент $t_{2}$ ) (рис. 3.9).

Рис. 3.9. Верхняя и нижняя кульминации звезды для наблюдателя в северном полушарии

Очевидно, что промежуток времени между $t_{1}$ и $t_{2}$ равен $12^h$ (или $180^\circ$ в угловой мере).

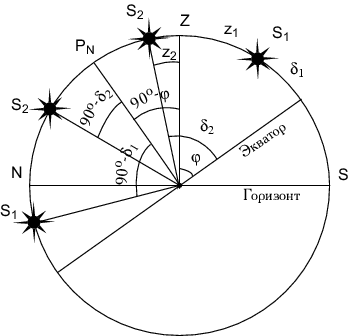
Из рис. 3.10 ясно, что для звезды $S_1$ , кульминирующей к югу от зенита, $\varphi =z_1+\delta_1$ , тогда как для звезды $S_2$ , кульминирующей к северу от зенита, справедливо равенство $\varphi =\delta_2 -z_2$ .

Рис. 3.10. Заходящие и незаходящие звезды

Таким образом в верхней кульминации имеем:

$\displaystyle \textrm{для}\ S_1:\qquad z_u=\varphi -\delta,\ \textrm{ если}\ \varphi\gt \delta;$

(3.24)

$\displaystyle \textrm{для}\ S_2:\qquad z_u=\delta -\varphi,\ \textrm{если}\ \varphi \lt \delta.$

(3.25)

Для нижней кульминации получим:

$\displaystyle z_l=(90^\circ-\varphi)+(90^\circ-\delta)=180^\circ-(\varphi+\delta).$

(3.26)

Зенитное расстояние звезды в верхней (нижней) кульминации является минимальным (максимальным) зенитным расстоянием. В зависимости от величин $z_u$ и $z_l$ звезды можно разделить на незаходящие, невосходящие, восходящие и заходящие. Если в нижней кульминации $z_l\lt 90^\circ$ , то звезда всегда находится над горизонтом. Из (3.24) следует: что

$\displaystyle z_l=180^\circ-(\varphi +\delta )\lt 90^\circ .$

Для незаходящих звезд в северном полушарии выполняется соотношение:

$\displaystyle \delta \gt 90^\circ-\varphi.$

Для невосходящих звезд зенитное расстояние в верхней кульминации $z_u\gt 90^\circ$ ,т.е. $\varphi -\delta \gt 90^\circ$ или $\delta \lt -(90^\circ-\varphi)$ . Таким образом, если склонение звезды $\delta$ удовлетворяет условию

$\displaystyle -(90^\circ-\varphi)\lt \delta \lt 90^\circ-\varphi,$

то звезда периодически восходит и заходит.

Часто наблюдения звезды в верхней и нижней кульминациях используется для определения широты места или склонения звезды. Если при помощи наблюдений получены $z_u$ и $z_l$ , то, складывая (3.23) и (3.24), получим:

$\displaystyle \varphi =90^\circ-\frac{z_u+z_l}{2}.$

В этом случае не требуется знать склонение звезды. Обратно, склонение звезды может быть найдено, если неизвестна широта места из уравнения:

$\displaystyle \delta =90^\circ+\frac{z_u-z_l}{2}.$

<< 3.5. Преобразование координат из | Оглавление | 3.7. Восход и заход >>