Астронет > Сферическая астрономия

Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия
http://variable-stars.ru/db/msg/1190817/node15.html

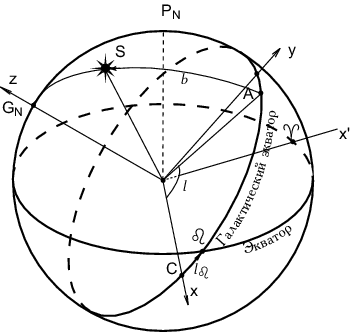
<< 3.3. Эклиптическая система координат | Оглавление | 3.5. Преобразование координат из >>

3.4. Галактическая система координат

Еще одной, часто используемой, особенно в звездной динамике, системой координат является галактическая система.

Наша Галактика, или Млечный Путь, классифицируется как спиральная галактика. Основными составляющими Галактики являются плоский диск диаметром более 100000 световых лет, ядро и гало. Большая часть звезд и газопылевых облаков сосредоточены в галактическом диске. Структура диска неоднородна; известны несколько спиральных рукавов, в которых плотность звезд и газа значительно выше средней. Значительная часть звезд концентрируется к центральной части, или к галактическому ядру, и образует в центре Галактики утолщение. И, наконец, третьей составляющей Галактики является гало, которое состоит из старых звезд и шаровых скоплений. Гало имеет практически сферическую форму.

Солнце находится на периферии Галактики (на расстоянии примерно 28000 световых лет от ее центра) и является одной из звезд, составляющих ее диск. Так как мы смотрим на Галактику изнутри, находясь в ее диске, то последний проецируется на небесную сферу как полоса звезд, или Млечный Путь. Вместе с ближайшими к нему звездами Солнце движется со скоростью примерно 250 км/с в направлении созвездия Лебедя. Это движение объясняется вращением галактического диска. Солнце делает полный оборот вокруг центра Галактики за период $\sim 200$ млн. лет.

Для изучения движения звезд в Галактике за основную плоскость галактической системы координат естественно принять плоскость диска. Положение основной плоскости в экваториальной системе задается координатами одного из полюсов галактической системы.

При обработке результатов проекта HIPPARCOS галактическая система координат была определена следующим образом^3.5. Обозначим точку, экваториальные координаты которой на эпоху J2000.0 равны

$\displaystyle \alpha$	$\displaystyle =192\hbox{$^{\circ}$\kern-.15cm{,}\kern.04cm}85948,$
$\displaystyle \delta$	$\displaystyle =27\hbox{$^{\circ}$\kern-.15cm{,}\kern.04cm}12825,$

как $G_N$ и назовем ее северным галактическим полюсом, а диаметрально противоположную точку -- южным. Большой круг, перпендикулярный линии, соединяющей полюсы, назовем галактическим экватором (рис. 3.5).

Рис. 3.5. Галактическая система координат

Определение 3.4.1 Большой круг, проходящий через звезду $S$ и полюсы Галактики, называется кругом галактической широты.

Если точка $A$ является точкой пересечения круга широты и галактического экватора, то дуга $\widehat{AS}$ называется галактической широтой звезды: $\widehat {AS}=b$ . Галактические широты положительны в северном и отрицательны в южном полушарии: $-90^\circ\le b \le 90^\circ$ . Раньше галактические долготы $l$ отсчитывались от восходящего узла $\ascnode$ , то есть точки пересечения галактического и небесного экваторов, прямое восхождение которой равнялось $\sim 18^h40^m$ . Сейчас начало отсчета долгот (точка $C$ на рис. 3.5 -- направление на центр Галактики) определяется галактической долготой восходящего узла $\ascnode$ , которая равна $l_{\ascnode} =32\hbox{$^{\circ}$\kern-.15cm{,}\kern.04cm}93192$ . Галактические долготы отсчитываются от $0^\circ$ до $360^\circ$ против часовой стрелки, если смотреть с северного полюса Галактики.

Единичный вектор в направлении северного полюса Галактики обозначим как ${\bf k}_g$ , а вектор, направленный в центр Галактики -- как ${\bf i}_g$ . Ось $Ox$ галактической системы направим вдоль вектора ${\bf i}_g$ , ось $Oz$ -- вдоль ${\bf k}_g$ . Ось $Oy$ определяется единичным вектором ${\bf j}_g$ , который равен ${\bf j}_g= {\bf k}_g\times {\bf i}_g$ .

Аналогичным образом (заданием тройки базисных векторов) могут быть определены любые другие системы координат.

После определения основных сферических систем координат рассмотрим методы, используемые для преобразования координат из одной системы в другую.

<< 3.3. Эклиптическая система координат | Оглавление | 3.5. Преобразование координат из >>