|
Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия http://www.astronet.ru/db/msg/1190817/node13.html |
3.2. Экваториальная система координат
Направление оси вращения Земли является вторым выбранным направлением для наблюдателя, находящегося на поверхности Земли. С направлением оси вращения Земли связана вторая широко используемая в астрономии система координат -- экваториальная.
Допустим пока, что центр небесной сферы совпадает с центром масс Земли. Если продолжить ось вращения Земли до пересечения с небесной сферой, то точки пересечения называются полюсами мира, а сама ось -- осью мира.
В настоящее время северный полюс мира располагается вблизи (на
расстоянии менее ![]() ) от Полярной звезды (
) от Полярной звезды (![]() Малой
Медведицы). Поэтому Полярная звезда практически неподвижна. Если
наблюдатель находится в северном полушарии Земли и будет смотреть
на нее длительное время, то увидит, что остальные звезды совершают
круговое движение вокруг Полярной звезды. Кажущееся вращение
небесной сферы относительно Полярной звезды (точнее вокруг оси
мира) происходит против часовой стрелки и является отражением
вращения Земли. Если встать лицом по направлению к Полярной
звезде и провести большой круг через нее (точнее через северный
полюс мира) и зенит, то пересечение этого круга с плоскостью
горизонта определит точку севера.
Малой
Медведицы). Поэтому Полярная звезда практически неподвижна. Если
наблюдатель находится в северном полушарии Земли и будет смотреть
на нее длительное время, то увидит, что остальные звезды совершают
круговое движение вокруг Полярной звезды. Кажущееся вращение
небесной сферы относительно Полярной звезды (точнее вокруг оси
мира) происходит против часовой стрелки и является отражением
вращения Земли. Если встать лицом по направлению к Полярной
звезде и провести большой круг через нее (точнее через северный
полюс мира) и зенит, то пересечение этого круга с плоскостью
горизонта определит точку севера.
В дальнейшем изложении будем считать, что на небесную сферу мы смотрим снаружи. Это аналогично взгляду на глобус Земли. Координаты звезд в экваториальной системе в этом случае определяются аналогично широте и долготе на поверхности Земли. Заметим, что при взгляде на небесную сферу снаружи расположение звезд зеркально отличается от того, что видит наблюдатель с поверхности Земли.
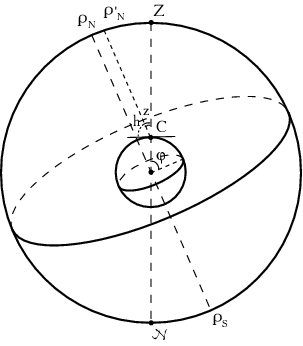
Отметим на рис. 3.2 северный (![]() ) и южный (
) и южный (![]() ) полюсы
мира, а также зенит
) полюсы
мира, а также зенит ![]() и надир
и надир ![]() наблюдателя, расположенного
в точке
наблюдателя, расположенного
в точке ![]() на поверхности Земли.
на поверхности Земли.
Проведем через точку
Парадокс, суть которого заключается в том, что с одной стороны радиус
небесной сферы равен единице, а с другой, что точки ![]() и
и ![]() расположены на бесконечном расстоянии, решается достаточно просто:
радиус Земли пренебрежимо мал по сравнению с расстоянием до ближайших
звезд.
расположены на бесконечном расстоянии, решается достаточно просто:
радиус Земли пренебрежимо мал по сравнению с расстоянием до ближайших
звезд.
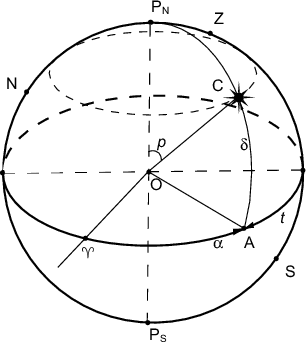
Пусть ![]() -- звезда на небесной сфере (рис. 3.3).
-- звезда на небесной сфере (рис. 3.3).
Второй координатой в экваториальной системе координат является
прямое восхождение ![]() .
Никакого особого (выделенного) направления в плоскости экватора
нет. Поэтому выбор начала отсчета прямых восхождений произволен.
.
Никакого особого (выделенного) направления в плоскости экватора
нет. Поэтому выбор начала отсчета прямых восхождений произволен.
До 1998 года эта точка определялась в момент пересечения центром Солнца небесного экватора, когда Солнце двигается из южного полушария в северное. Это происходит примерно 21 марта каждого года, и точка называется точкой весеннего равноденствия. Противоположная точка на экваторе называется точкой осеннего равноденствия. Эту точку Солнце проходит примерно 23 сентября.
Видимое движение Солнца есть не что иное, как отражение движения Земли вокруг Солнца. Плоскость земной орбиты назовем плоскостью эклиптики, которая определяет эклиптическую систему координат. Поэтому, согласно определению, принятому до 1998 г., точки весеннего и осеннего равноденствий лежали на линии пересечения небесного экватора и эклиптики. Так как координаты Земли и Солнца находятся на основе решения уравнений динамики, то плоскость эклиптики определяется на основе динамического метода. Точки весеннего и осеннего равноденствий, определяемые пересечением экватора и эклиптики, называются динамическими, а сам момент пересечения центром Солнца динамической точки весеннего равноденствия -- динамическим равноденствием.
С 1998 г. Международным астрономическим союзом (МАС) в качестве
реализации небесной системы координат принят каталог
внегалактических радиоисточников. МАС рекомендует, чтобы начало
прямых восхождений новой небесной системы координат было близким
к динамическому равноденствию J2000.03.4. Для этого начало системы отсчета прямых
восхождений с 1998 г. по решению МАС было определено следующим
образом. Из разных каталогов были выбраны 23 радиоисточника,
среди которых был и квазар 3C273, и вычислены средние значения
прямого восхождения каждого из них. Затем координаты источников
были исправлены таким образом, чтобы прямое восхождение квазара
3C273 было согласовано со значением в системе фундаментального
каталога FK5 (
![]() J2000.0), т.е.
разница между этим значением и средним прямым восхождением
3C273 была добавлена к прямым восхождениям остальных 22
источников. При таком определении точка весеннего равноденствия
уже не привязывается к эклиптике.
J2000.0), т.е.
разница между этим значением и средним прямым восхождением
3C273 была добавлена к прямым восхождениям остальных 22
источников. При таком определении точка весеннего равноденствия
уже не привязывается к эклиптике.
В настоящее время точка весеннего равноденствия находится в
созвездии Рыб, точка осеннего равноденствия -- в созвездии Девы.
Принятое обозначение точек -- ![]() и
и ![]() для весеннего
и осеннего равноденствий, соответственно, относятся к знакам Овна
и Весов. Причиной смещения точек весеннего и осеннего
равноденствия является прецессия, о которой мы расскажем
позже. В результате прецессии плоскость
небесного экватора не сохраняет свое положение в пространстве, а
полюсы мира описывают на небесной сфере окружность приблизительно
за 26000 лет. Примерно 4500 лет назад северный полюс мира
находился около звезды
для весеннего
и осеннего равноденствий, соответственно, относятся к знакам Овна
и Весов. Причиной смещения точек весеннего и осеннего
равноденствия является прецессия, о которой мы расскажем
позже. В результате прецессии плоскость
небесного экватора не сохраняет свое положение в пространстве, а
полюсы мира описывают на небесной сфере окружность приблизительно
за 26000 лет. Примерно 4500 лет назад северный полюс мира
находился около звезды ![]() Дракона (Тубан), которая была в
то время полярной. Через 2000 лет полярной будет звезда
Дракона (Тубан), которая была в
то время полярной. Через 2000 лет полярной будет звезда ![]() Цефея (Альран), а через 14000 лет -- Вега (созвездие Лира).
Цефея (Альран), а через 14000 лет -- Вега (созвездие Лира).
Если при вычислении положения небесного экватора на определенный момент времени учитывается только явление прецессии (нутация не принимается во внимание), то экватор называется средним. Международный астрономический союз рекомендует относить координаты звезд или радиоисточников к среднему экватору для выбранных моментов времени, так называемым стандартным эпохам. В настоящее время стандартной эпохой считается дата: январь 1,5 2000 г. Момент времени определяется для геоцентрической системы отсчета в шкале земного времени (Terrestrial Time, TT) (см. §5.5.2).
Если точка весеннего равноденствия ![]() определена, то дуга
экватора
определена, то дуга
экватора
![]() от точки весеннего равноденствия до
круга склонений звезды называется прямым
восхождением:
от точки весеннего равноденствия до
круга склонений звезды называется прямым
восхождением:
Если ![]() -- зенит наблюдателя,
-- зенит наблюдателя, ![]() и
и ![]() -- точки севера и юга на плоскости горизонта (на рис. 3.3
горизонт не показан), то, как было сказано раньше, плоскость
-- точки севера и юга на плоскости горизонта (на рис. 3.3
горизонт не показан), то, как было сказано раньше, плоскость
![]() является плоскостью небесного меридиана. Двугранный
угол между плоскостью небесного меридиана и кругом склонения
называется часовым углом
является плоскостью небесного меридиана. Двугранный
угол между плоскостью небесного меридиана и кругом склонения
называется часовым углом ![]() светила.
Часовые углы отсчитываются от высшей точки экватора по часовой
стрелке, если смотреть с северного полюса мира, от
светила.
Часовые углы отсчитываются от высшей точки экватора по часовой
стрелке, если смотреть с северного полюса мира, от ![]() до
до
![]() или от
или от ![]() до
до ![]() . Заметим, что система
координат
. Заметим, что система
координат
![]() , задаваемая часовым углом и склонением,
является левой.
, задаваемая часовым углом и склонением,
является левой.
Малый круг, параллельный экватору и проходящий через звезду ![]() ,
называется параллелью (показан пунктирной линией на
рис. 3.3).
,
называется параллелью (показан пунктирной линией на
рис. 3.3).
В экваториальной системе координат основными кругами являются: экватор, от которого отсчитываются склонения, небесный меридиан, круг склонений. Основные точки -- это полюсы мира, точка весеннего равноденствия -- начало отсчета прямых восхождений -- и высшая точка экватора -- начало отсчета часовых углов.
Базисную тройку векторов, определяющих экваториальную систему
координат, обозначим как
![]() , причем вектор
, причем вектор
![]() направлен в северный полюс мира
направлен в северный полюс мира ![]() и определяет ось
и определяет ось
![]() декартовой системы координат, вектор
декартовой системы координат, вектор ![]() направлен в
точку весеннего равноденствия
направлен в
точку весеннего равноденствия ![]() и определяет ось
и определяет ось ![]() , а
вектор
, а
вектор ![]() равен:
равен:
![]() и задает
ось
и задает
ось ![]() , так что
, так что
![]() составляют правую
тройку векторов.
составляют правую
тройку векторов.
<< 3.1. Горизонтальная система координат | Оглавление | 3.3. Эклиптическая система координат >>