Звездная динамика

При таком подходе описание системы звёзд подобно описанию газа. Наиболее велико сходство между звёздным скоплением и плазмой - ионизованным газом, состоящим из ионов и электронов. Подобно звёздам в скоплении, электроны и ионы плазмы взаимодействуют между собой с силой, убывающей с расстоянием по закону обратных квадратов. Однако в характере взаимодействий имеется и существенное различие, связанное с тем, что звёзды между собой всегда притягиваются, а в плазме частицы как притягиваются, так и отталкиваются в зависимости от знака зарядов. Вследствие этого плазму всегда можно считать нейтральной, а звёздное скопление всегда "заряжено" и должно иметь спец. строение, чтобы находиться в равновесии.

Ур-ние для ф-ции f наз. кинетическим, оно учитывает изменение f при регулярном движении звёзд, а также при их столкновениях. При взаимодействии звёзд по закону обратных квадратов сила, действующая на звезду, определяется в основном гравитац. полем, создаваемым далёкими звёздами, а не столкновениями звёзд. Т.о., чтобы найти f для звёзд, нужно знать создаваемое ими гравитац. поле, т.е. совместно с кинетич. ур-нием решать и ур-ние для гравитационного потенциала . Система ур-ний для описания бесстолкновительных звёздных систем была получена в 1915 г. англ. физиком и астрофизиком Дж. Джинсом. Аналогичная система ур-ний для описания бесстолкновительной плазмы с учётом электрич. и магн. сил была в 1938 г. получена советским физиком А.А. Власовым.

Помимо усреднённого гравитац. поля на движение каждой звезды оказывают влияние случайные близкие пролёты др. звёзд (столкновения). Столкновения звёзд приводят к изменению их траекторий, представляющих собой криволинейное движение в усреднённом поле. Эти изменения описываются столкновительным членом, входящим в ур-ние для f. В равновесной звёздной системе, согласно вириала теореме, кинетич. энергия звезды в среднем равна половине потенциальной: , где - масса и средний квадрат скорости звезды, M, R - масса и характерный размер системы. В этом состоит существенное отличие звёздной системы от газа и плазмы, где кинетич. энергия частицы много больше потенциальной (частица между столкновениями практически свободна), и поэтому траектории частиц до и после столкновения почти прямолинейны. Это приводит к тому, что в газе и плазме столкновительный член явл. локальным (изменение траекторий происходит лишь в области достаточно тесного сближения частиц), а в звёздной системе он в каждой точке зависит от распределения звёзд во всей системе, что делает его намного более сложным.

Бесстолкновительная звёздная система (характерное время между столкновениями много больше времени существования системы) может прийти в стационарное состояние и находиться в нём неограниченно долго. Переход системы в стационарное состояние (релаксация системы) происходит за счёт перемешивания траекторий звёзд при их движении в общем гравитац. поле. Процесс бесстолкновительной релаксации звёздных систем был впервые рассмотрен англ. астрономом Д. Линден-Беллом в 1967 г. и назван им бурной релаксацией (violent relaxation). Стационарное состояние достигается за характерное время t_h, определяемое неск. пролётами звездой радиуса системы R: . Это время для звёздных скоплений и галактик меньше космологического лет (возраст Вселенной). Для Галактики лет. Т. о., большинство звёздных систем во Вселенной находятся в стационарном состоянии, к-рое может быть описано решением бесстолкновительного кинетич. ур-ния. Характерной чертой стационарного состояния, достигаемого в результате бурной релаксации, явл. выравнивание ср. скоростей у звёзд различной массы. В этом её принципиальное отличие от истинной релаксации (столкновительной), приводящей к выравниванию ср. энергий звёзд различной массы и достижению локального термодинамического равновесия.

Рис. 1. Различные типы галактик: вверху - спиральная галактика М81 (слева) и бароспиральная галактика (справа); внизу - иррегулярная галактика (слева) и эллиптическая галактика М87 (справа).

Наблюдаемое разнообразие галактик (рис. 1) в значит. степени связано с различием начальных условий при их образовании. В системе без столкновений стационарное решение для ф-ции распределения звёзд имеет большой произвол, нужно лишь, чтобы оно зависело только от интегралов движения звезды (величин, не изменяющих своего значения в процессе движения). Очевидными интегралами явл. энергия звезды и при наличии аксиальной симметрии - её вращательный момент. Из анализа распределения звёзд в Галактике следует вывод о существовании, по крайней мере, ещё одного интеграла движения, не имеющего столь очевидного физ. смысла.

Роль парных столкновений в звёздных системах зависит от плотности звёзд (числа звёзд в ед. объёма) и в достаточно плотных скоплениях может быть существенной. В отличие от бесстолкновительного случая столкновения ведут к образованию единой ф-ции распределения, соответствующей термодинамич. равновесию - Максвелла распределению:

Здесь Т - темп-ра скопления в энергетич. единицах, характеризующая ср. кинетич. энергию звезды в системе. Универсальность ф-ции распределения приводит к сглаживанию различия между такими системами и установлению универсального распределения плотности. Системы могут отличаться только сплюснутостью, обусловленной их вращением. Характерное время установления равновесного распределения
(лет),
где N - полное число звёзд в системе, R - размер системы (в см). Для галактики это время , но для шаровых скоплений и ядерных областей галактик , т.е. система успевает релаксировать за время существования галактики, чем объясняется правильная форма этих звёздных систем (рис. 2).

Испарение звёзд и эволюция звёздных систем.
Столкновения приводят к установлению максвелловского распределения, в котором имеются звёзды всех энергий. Однако гравитационный потенциал на поверхности скопления конечен, поэтому звёзды, обладающие достаточно большой энергией, покидают систему (испаряются). Т.о., столкновения приводят к испарению звёзд из системы. Чтобы испариться, звезда должна приобрести скорость , что в 2 раза больше среднеквадратичной скорости . За характерное время количество улетевших звёзд примерно соответствует числу звёзд в максвелловском распределении с v>v_исп, что равно . Испарение звёзд из системы в результате столкновений впервые было исследовано советским астрофизиком В.А. Амбарцумяном в 1938 г. и независимо от него амер. астрономом Л. Спитцером в 1940 г.

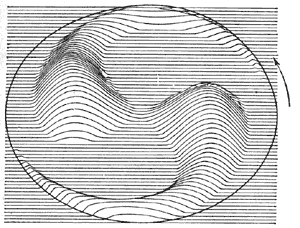
Рис. 2. Столкновительные системы: вверху - шаровое скопление, внизу - ядро галактики М31 (приведено распределение яркости по наблюдениям с баллонного телескопа "Стратоскоп II"; по оси ординат - поверхностная яркость в звёздных величинах на квадратную секунду дуги, масштаб 1"-4пк).

Наибольшую роль в испарении звёзд играют столкновения со звёздами, пролетающими далеко от данной звезды и передающими ей малые порции энергии. Это приводит к тому, что лишь небольшая доля звёзд (~ 1/ln N) улетает с большой скоростью, а осн. масса их медленно расплывается и образует разрежённое гало звёздного скопления. Одновременно оставшаяся масса звёзд, теряющих энергию, сжимается, образуя уплотняющееся ядро. Изолированная звёздная система (при учёте только парных столкновений) должна закончить своё существование испарением большинства звёзд системы и релятивистским гравитационным коллапсом остатка. В реальном звёздном скоплении, входящем в состав галактики, коллапсирующее ядро может не возникнуть, если масса остатка окажется слишком малой (). В этом случае образуется массивная норм. звезда либо двойная система, судьба к-рой определяется её ядерной эволюцией и такова же, как и у др. звёзд Галактики, не входивших в плотные скопления. Оценки показывают, что итогом эволюции ядер шаровых звёздных скоплений с числом звёзд ~ 10⁵-10⁶ вряд ли могут явиться коллапсирующие объекты - черные дыры. В ядрах галактик и в квазарах, в к-рых число звёзд может достигать ~ 10⁸-10¹¹, в результате эволюции и испарения звёзд в конце может произойти релятивистский коллапс и возникнуть чёрная дыра с массой . Приведённые оценки сделаны без учёта вращения, к-рое уменьшает массу коллапсирующего остатка.

Помимо парных столкновений в плотных звёздных скоплениях могут происходить лобовые столкновения звёзд, приводящие к их частичному слиянию, сбросу массы, образованию ударных волн. Оценки показывают, что лобовые столкновения могут играть заметную роль в эволюции только самых плотных ядер галактики квазаров с N ~ 10¹⁰ внутри объёма с R = 10¹⁷ см. В шаровых и рассеянных скоплениях, входящих в состав Галактики, лобовые столкновения весьма маловероятны.

Неустойчивости и спиральная структура галактик.
Итак, за исключением плотных центральных областей и шаровых скоплений, основная часть звёзд, входящих в галактики, не испытывает столкновений и движется в её усреднённом гравитационном поле. Важной характерной чертой бесстолкновительной звёздной системы явл. возможность развития в ней неустойчивостей различных типов. Главным стимулом для изучения этих неустойчивостей явилась попытка объяснить природу возникновения спиральной структуры галактик. Спиральные рукава представляют собой волны - спиральные уплотнения, распространяющиеся по веществу галактики и сохраняющие почти неизменной свою форму. Рассматриваются различные причины возникновения таких волн. Согласно одной точке зрения, спиральная волна связана с существованием в центре галактики асимметричного образования - вращающегося бара (от англ. bar - брусок, полоса), являющегося генератором волны. Действительно, в нек-рых галактиках видны вращающиеся вытянутые образования, от к-рых отходят спиральные рукава (рис. 1). Однако во многих спиральных галактиках бары не видны, поэтому, согласно др. точке зрения, причиной возникновения спиральной волны явл. неустойчивости.

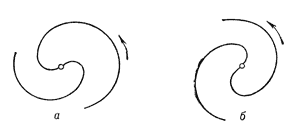
Рис. 3. Формы спиралей: а - отстающая, б - лидирующая (стрелками указано направление вращения).

В звёздной системе возможно развитие гравитационных неустойчивостей, а также кинетич. неустойчивостей, связанных, как и в плазме, с видом ф-ции распределения. Невращающиеся системы - эллиптич. галактики, шаровые скопления - устойчивы относительно всех типов возмущений, что позволяет им сохранять правильную форму даже в отсутствие столкновений. По мере увеличения вращения и приобретения галактикой формы диска возрастает число неустойчивых мод (видов) собственных колебаний. Наиболее важной явл. джинсовская неустойчивость тонкого диска. При образовании уплотнения в тонком диске возрастают гравитац. силы, стремящиеся увеличить плотность. Центробежные силы и давление препятствуют росту плотности. Центробежные силы приводят к стабилизации самых крупномасштабных возмущений, связанных со сжатием или расширением диска как целого. Изотропное давление в диске стабилизирует мелкомасштабные возмущения с длиной волны порядка или меньше толщины диска. Возмущения промежуточных масштабов в тонком диске оказываются неустойчивыми, и результатом их развития может оказаться спиральная структура. Численные расчёты развития неустойчивостей в тонком диске в гидродинамич. приближении показывают, что наиболее быстро растёт двухрукавная спиральная мода, соответствующая отстающей спирали (с закручивающимися ветвями). Различие между лидирующей и отстающей спиральными волнами показано на рис. 3.

Рис. 4. Расчёты спиральной структуры на ЭВМ - неустойчивая двухрукавная отстающая спираль.

На рис. 4 приведена форма спиральной волны, полученная в численных расчётах собственных колебаний диска. Эти результаты находятся в соответствии с наблюдениями галактик, к-рые показывают, что осн. типом спиралей явл. двухрукавные и отстающие.

Кинетические неустойчивости.
Впервые неустойчивости подобного типа были изучены в плазме (см. Неустойчивости плазмы). Эти неустойчивости обусловлены взаимодействием волн с частицами. Неустойчивость возникает, когда частицы передают волне больше энергии, чем отнимают от неё. Для этого необходимо, чтобы ф-ция распределения была далека от равновесной. Т.н. пучковая неустойчивость развивается, когда ф-ция распределения f имеет локальный максимум в области больших скоростей (т.е. имеется пучок частиц с большими скоростями). Циклотронная неустойчивость может развиваться в быстровращающейся звёздной системе. Дрейфовая, или градиентная, неустойчивость развивается в неоднородной звёздной системе при наличии градиентов плотности или темп-ры. Роль кинетич. неустойчивостей в галактиках ещё не совсем понятна. Скорость нарастания обусловленных этими неустойчивостями возмущений обычно меньше, чем у гравитационной неустойчивости. В спиральных галактиках имеется сферич. подсистема, скорость вращения к-рой много меньше, чем у диска. В этих условиях будут развиваться пучковая, а также две другие кинетич. неустойчивости, чем можно объяснить нек-рые особенности структуры спиральных галактик. При наличии резких градиентов скорости в Галактике возможно развитие неустойчивости, связанной со скачками тангенциальной скорости.

Бароподобная неустойчивость, массивные короны галактик.
Аксиально-симметричная форма вращающегося самогравитирующего тела становится неустойчивой при достаточно быстром вращении. В результате развития этой неустойчивости образуется трёхосная фигура (бар), из-за чего данная неустойчивость названа бароподобной. Она изучена ещё в 19 в. при рассмотрении самогравитирующих конфигураций несжимаемой жидкости и носит универсальный характер, в т.ч. имеет место и в звёздных системах. Момент вращения у дисков в спиральных галактиках столь велик, что должно было бы существовать большое количество эллиптич. дисков. Однако наблюдения не позволяют отличить эллиптич. диск от эллиптич. проекции кругового диска на небесную сферу. Обычно считается, что галактич. диски явл. круговыми, поэтому для их устойчивости необходимо наличие массивной сферич. составляющей с массой, превышающей массу светящегося вещества. Анализ распределения скоростей галактик - спутников нашей Галактики - показывает, что эта масса может быть распределена в обширной короне, окружающей Галактику, и масса короны может на порядок превышать массу Галактики. Предполагается наличие аналогичных корон и у др. галактик, однако их существование ещё не явл. твердо установленным наблюдательным фактом.

Численные расчёты в звёздной динамике.

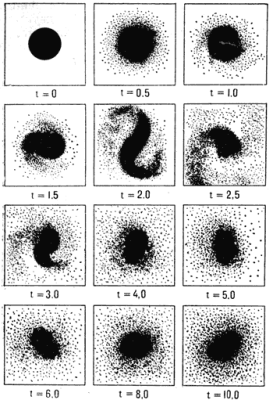
Рис. 5. Эволюция однородно вращающегося диска из 105 точечных масс. Время указано в единицах периода вращения диска. Начальные хаотические скорости имеют нормальное распределение. Хорошо видно развитие двухрукавной спиральной структуры, которая постепенно размывается в результате релаксации системы.

С развитием вычислительной техники стало возможным изучать звёздные системы, не прибегая к кинетическому уравнению, а решая непосредственно уравнения движения отдельных тяготеющих масс. Количество рассматриваемых тяготеющих масс ограничено возможностями ЭВМ и составляет неск. тысяч при учёте тяготения каждой массы в отдельности и неск. сотен тысяч при учёте только усреднённого потенциала звёзд. Расчёты подтверждают появление и развитие спиральных структур (рис. 5), испарение отдельных точечных масс. В системах с неск. тысячами звёзд (при реальном учёте тяготения каждой звезды) эволюция ведёт к образованию большого числа связанных пар. Выделяющаяся при образовании таких пар потенциальная энергия (см. Энергия связи) приводит к полному разлёту скопления в конце эволюции. Подобные расчёты могут применяться для описания последних стадий эволюции ядра шарового скопления и указывают на то, что черные дыры при этом не образуются. Численные расчёты с успехом применяются при исследовании скоплений галактик, где число членов сравнительно невелико.

Численные расчёты позволяют исследовать столкновения галактик, к-рые моделируются неск. сотнями или тысячами точек. Получается, что после достаточно близкого пролёта одной галактики мимо другой в диске возбуждаются спиральные волны. Это может происходить в богатых скоплениях галактик, где близкие пролёты галактик достаточно вероятны.

Лит.:
Чандрасекар С., Принципы звездной динамики, пер. с англ., М., 1948; Огородников К.Ф., Динамика звездных систем, М., 1958; Динамика и эволюция звездных систем, [Сб. ст.], М.- Л., 1975; Поляченко В.Л., Фридман А.М., Равновесие и устойчивость гравитирующих систем, М., 1976.

(Г.С. Бисноватый-Коган)