 |
Астронет: С. А. Жевакин, А. А. Памятных, "Физика Космоса", 1986 Пульсации звезд http://www.astronet.ru/db/msg/1188567 |
Пульсации звезд
собственные колебания колебания звезд, проявляющиеся в их периодическом сжатии и расширении. Простейший вид собств. колебаний звезды - радиальные сферически-симметричные пульсации, при к-рых она периодически расширяется и сжимается, сохраняя при этом форму шара (в общем случае нерадиальных колебаний меняется и форма звезды, напр., звезда периодически принимает форму то вытянутого, то сплюснутого эллипсоида).
По совр. представлениям, переменность цефеид, звезд
типов RV Тельца, RR Лиры, ![]() Щита,
Щита, ![]() Цефея, ZZ
Кита
(белых карликов) и некоторых др. типов физ.
переменных звезд обусловлена их П.
Цефея, ZZ
Кита
(белых карликов) и некоторых др. типов физ.
переменных звезд обусловлена их П.
|
|
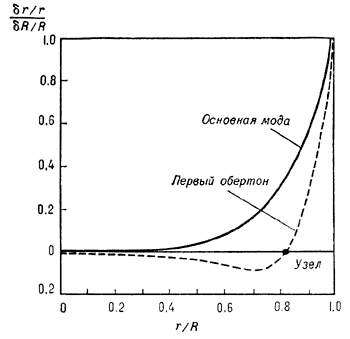
Рис. 1. Поведение относительной амплитуды малых радиальных колебаний в пульсирующей звезде-гиганте ( на расстоянии r от центра звезды, в единицах относительной амплитуды звезды, R - радиус звезды). Сплошная линия - колебания на основной частоте, штриховая - на частоте первого обертона. Колебания на частоте первого обертона имеют узел при |
Период P собств. колебаний звезды при том или ином типе колебаний (для к.-л.
моды) определяется в основном ср. плотностью вещества звезды ![]() (т.е.
в конечном счете ее полной массой
(т.е.
в конечном счете ее полной массой ![]() и радиусом R).
Это теоретич. соотношение имеет вид
и радиусом R).
Это теоретич. соотношение имеет вид ![]() = const, где "постоянная"
различна для разных мод, и, кроме того, она немного зависит от внутр. строения звезды
(в частности, чем больше концентрация вещества к центру, тем меньше период осн. моды
при заданных
= const, где "постоянная"
различна для разных мод, и, кроме того, она немного зависит от внутр. строения звезды
(в частности, чем больше концентрация вещества к центру, тем меньше период осн. моды
при заданных ![]() и R). Периоды большинства переменных
звезд согласуются с гипотезой радиальных колебаний в осн. моде, но у нек-рых звезд
наблюдается,
по-видимому, П. в обертонах или даже одновременно в неск. модах (в т.ч. и нерадиальных).
Для звезд конкретного типа переменности, напр., типа RR Лиры, имеющих сходное строение,
соотношение
и R). Периоды большинства переменных
звезд согласуются с гипотезой радиальных колебаний в осн. моде, но у нек-рых звезд
наблюдается,
по-видимому, П. в обертонах или даже одновременно в неск. модах (в т.ч. и нерадиальных).
Для звезд конкретного типа переменности, напр., типа RR Лиры, имеющих сходное строение,
соотношение ![]() =const хорошо выполняется.
=const хорошо выполняется.
В пульсирующей звезде, за исключением ее самых внешних областей, колебания происходят почти адиабатически (см. Адиабатический процесс), в том смысле, что в течение цикла колебаний любой выделенный в звезде слой никак не изменяет проходящий через него поток излучения и пульсирует как бы в условиях полной теплоизоляции, без теплообмена с окружающими слоями. Анализ адиабатич. П. не может дать никакой информации о пульсационной устойчивости звезды, т.е. о том, будут ли малые колебания нарастать или затухать с течением времени. Однако такой анализ обычно дает хорошее описание механич. св-в звезды, в частности весьма точные значения периодов и правильное представление о распределении амплитуды П. вдоль радиуса.
Хотя неадиабатич. эффекты и малы, они приводят к медленному изменению амплитуды П. Очевидно, если в момент наибольшего сжатия выделенный в звезде слой получает нек-рое количество теплоты, то последующее расширение будет происходить при большем давлении, чем произошло сжатие. В результате работа, совершенная слоем за цикл колебаний, будет положительной, т.е., как и в любой тепловой машине, будет иметь место превращение тепловой энергии в механическую. Такой слой будет вносить вклад в возбуждение (раскачку) колебаний. Если же в момент наибольшего сжатия слой теряет теплоту, то он вносит вклад в затухание колебаний. Если суммарная работа всех слоев в звезде за цикл колебаний положительна, то звезда пульсационно неустойчива (колебания нарастают), в противоположном случае - устойчива (колебания затухают).
|
|
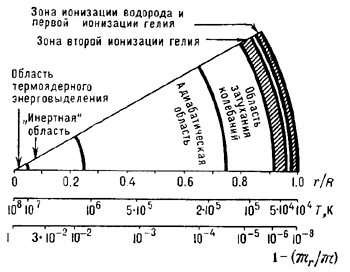
Рис. 2. Схематическое расположение областей, определяющих основные особенности пульсаций модели переменной звезды типа RR Лиры. Нижняя шкала указывает доли звездной массы, отсчитываемой от поверхности ("инертная" область в объеме от центра содержит свыше 99% массы звезды а масса зон ионизации всего лишь |
|
|
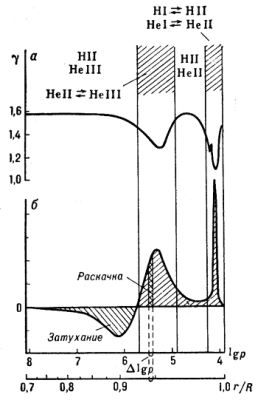
Рис. 3. а - Изменение показателя адиабаты в звезде типа RR Лиры с глубиной (общее строение звезды показано на рис. 2). Заштрихованы области частичной ионизации. б - Вклад различных слоев звезды в возбуждение или затухание малых колебаний. Слой толщиной работу, измеряемую площадью с двойной штриховкой. Зона HeII пульсаций. Суммарная работа всех слоев (заштрихованная площадь с учетом знака работы) положительна, поэтому звезда пульсационно неустойчива. |
Раскачавающее действие зон частичной ионизации основано на том, что при сжатии они
способны несколько задерживать проходящий через них поток излучения, а при расширении
-
наоборот, усиленно терять энергию, отдавая ее внешним слоям. Действительно, в зоне
частичной ионизации энергия, выделяющаяся при сжатии, идет не только на нагрев газа,
но
и на его ионизацию. Это препятствует сильному повышению темпратуры при сжатии. [Относительные
изменения плотности ![]() связаны с относительными изменениями
темп-ры
связаны с относительными изменениями
темп-ры ![]() соотношением
соотношением ![]() ,
строго выполняющимся лишь при адиабатич. колебаниях.] В зоне второй
ионизации гелия
,
строго выполняющимся лишь при адиабатич. колебаниях.] В зоне второй
ионизации гелия ![]() (рис. 3) вместо обычного значения
(рис. 3) вместо обычного значения
![]() для идеального одноатомного газа, т.е. при сжатии
повышение темп-ры в зоне ионизации оказывается меньшим, чем в прилегающих более глубоких
слоях. Для заданного коэфф. непрозрачности поток излучения пропорционален T4,
а поэтому при сжатии в зоне ионизации произойдет задержка потока излучения, идущего
изнутри. Данный эффект, связанный с прямым влиянием изменений темп-ры на поток излучения,
наз.
для идеального одноатомного газа, т.е. при сжатии
повышение темп-ры в зоне ионизации оказывается меньшим, чем в прилегающих более глубоких
слоях. Для заданного коэфф. непрозрачности поток излучения пропорционален T4,
а поэтому при сжатии в зоне ионизации произойдет задержка потока излучения, идущего
изнутри. Данный эффект, связанный с прямым влиянием изменений темп-ры на поток излучения,
наз. ![]() -механизмом. Значительную, если не осн. роль играют и изменения
непрозрачности. Коэффициент непрозрачности
-механизмом. Значительную, если не осн. роль играют и изменения
непрозрачности. Коэффициент непрозрачности ![]() зависит от T
и
зависит от T
и ![]() по закону
по закону ![]() (
(![]() - постоянная величина для вещества данного хим. состава,
- постоянная величина для вещества данного хим. состава, ![]() ,
, ![]() ). Из-за малых вариаций темп-ры в зоне ионизации
при П. изменения плотности становятся определяющими в законе непрозрачности, т.е.
при сжатии непрозрачность будет увеличиваться (в др. областях звезды она уменьшается
из-за сильного повышения темп-ры). Поток излучения обратно пропорционален коэфф.
). Из-за малых вариаций темп-ры в зоне ионизации
при П. изменения плотности становятся определяющими в законе непрозрачности, т.е.
при сжатии непрозрачность будет увеличиваться (в др. областях звезды она уменьшается
из-за сильного повышения темп-ры). Поток излучения обратно пропорционален коэфф.
![]() ,
поэтому из-за увеличения
,
поэтому из-за увеличения ![]() в зоне ионизации при сжатии (рис.
4) также произойдет задержка излучения. Кроме того, в зоне ионизации водорода поакзатель
s становится малым или даже отрицательным, что способствует еще большему увеличению
в зоне ионизации при сжатии (рис.
4) также произойдет задержка излучения. Кроме того, в зоне ионизации водорода поакзатель
s становится малым или даже отрицательным, что способствует еще большему увеличению
![]() при сжатии. В целом эффект, связанный с прямым влиянием изменений
непрозрачности на поток излучения наз.
при сжатии. В целом эффект, связанный с прямым влиянием изменений
непрозрачности на поток излучения наз. ![]() -механизмом. Следует
отметить, что
-механизмом. Следует
отметить, что ![]() -механизм и
-механизм и ![]() -механизм не явл.
независимыми,
их разделение несколько искусственное.
-механизм не явл.
независимыми,
их разделение несколько искусственное.
Рассмотренные эффекты изменений темп-ры и непрозрачности сами по себе еще недостаточны
для обеспечения раскачки П. Во внутр. частях зоны ионизации, где ![]() уменьшается в направлении от центра (достигая минимума ок. середины зоны), происходит
задержка потока излучения при сжатии; во внеш. же частях этой зоны, где
уменьшается в направлении от центра (достигая минимума ок. середины зоны), происходит
задержка потока излучения при сжатии; во внеш. же частях этой зоны, где ![]() увеличивается в направлении от центра, при сжатии может происходить усиленный отток
теплотыЮ и тогда эта внеш. часть будет вносить вклад в затухание П. Затухание будет
иметь
место в области над зоной ионизации, где показатель
увеличивается в направлении от центра, при сжатии может происходить усиленный отток
теплотыЮ и тогда эта внеш. часть будет вносить вклад в затухание П. Затухание будет
иметь
место в области над зоной ионизации, где показатель ![]() приблизительно
постоянен, а коэфф.
приблизительно
постоянен, а коэфф. ![]() при сжатии уменьшается. При этом суммарный
раскачивающий эффект зоны ионизации может оказаться малым или вообще отсутствовать,
особенно при негомологичности колебаний (в данном случае при больших изменениях физ.
параметров
в ходе П. во внеш. части зоны по сравнению с внутр. областью).
при сжатии уменьшается. При этом суммарный
раскачивающий эффект зоны ионизации может оказаться малым или вообще отсутствовать,
особенно при негомологичности колебаний (в данном случае при больших изменениях физ.
параметров
в ходе П. во внеш. части зоны по сравнению с внутр. областью).
Однако из-за очень низкой плотности самых внеш. слоев их П. характеризуются сильной неадиабатичностью (сильным теплообменом между отдельными слоями), и оказывается, что такие разреженные слои неспособны эффективно задерживать проходящий через них поток излучения: в любой момент времени выделенный слой теряет через свою внеш. границу столько же энергии, сколько получает ее изнутри. Т.о., самые внешние слои не вносят никакого вклада в возбуждение или затухание П.
|
|
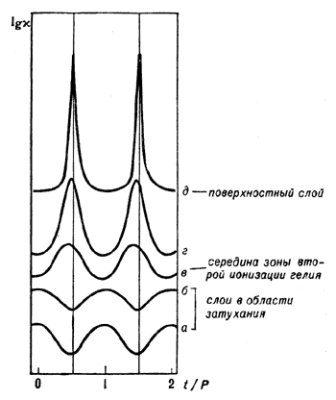
Рис. 4. Изменение коэффициента непрозрачности во внешних слоях модели классической цефеиды с течением времени t (охвачены два периода P установившихся пульсаций). Вертикальные линии отмечают моменты ниабольшего сжатия. В эти моменты значения в зонах частичной ионизации водорода и гелия (слои в-д) и к минимальному (слои а-б). (По данным Дж. Кокса) |
Аналогично зоне второй ионизации гелия могут действовать зоны ионизации водорода
и первой ионизации гелия, поскольку и в них показатель адиабаты ![]() мал (рис.
3, а), а коэффициент непрозрачности при сжатии сильно возрастает (рис. 4, пик в поверхностном
слое). Но вклад этих зон в возбуждение П. невелик, поскольку они располагаются
обычно в разреженных поверхностных слоях. Лишь для относительно холодных звезд ионизация
водорода происходит в достаточно плотных слоях, и тогда эта зона частичной ионизации
может вносить существенный вклад в раскачку П. Однако в оболочках холодных звезд
перенос энергии осуществляется преимущественно конвекцией,
к-рая, по-видимому, препятствует возбуждению П. Почти несомненно, что именно появление
эффективной конвекции во внеш. слоях звезд и определяет положение низкотемпературной
границы полосы неустойчивости на диаграмме Герцшпрунга-Ресселла.
мал (рис.
3, а), а коэффициент непрозрачности при сжатии сильно возрастает (рис. 4, пик в поверхностном
слое). Но вклад этих зон в возбуждение П. невелик, поскольку они располагаются
обычно в разреженных поверхностных слоях. Лишь для относительно холодных звезд ионизация
водорода происходит в достаточно плотных слоях, и тогда эта зона частичной ионизации
может вносить существенный вклад в раскачку П. Однако в оболочках холодных звезд
перенос энергии осуществляется преимущественно конвекцией,
к-рая, по-видимому, препятствует возбуждению П. Почти несомненно, что именно появление
эффективной конвекции во внеш. слоях звезд и определяет положение низкотемпературной
границы полосы неустойчивости на диаграмме Герцшпрунга-Ресселла.
Анализ пульсационной устойчивости звезды относительно малых возмущений (т.н. линейный анализ устойчивости) еще не дает представления об амплитуде усатновившихся П. (а также о форме кривых блеска и лучевой скорости), он лишь указывает на возможность экспоненциального роста или затухания колебаний. Зависимость эффективности механизмов возбуждения
Теория радиальных колебаний, возбуждаемых ионизационными механизмами, хорошо объясняет
осн. особенности П.з. в полосе неустойчивости (цефеиды, переменные типа RR Лиры,
![]() Щита), хотя ряд вопросов еще не решен. П. долгопериодических, полуправильных и неправильных
переменных изучены значительно хуже, отчасти из-за трудностей, связанных с необходимостью
учета взаимодействия П. с конвекцией, очень эффективной в оболочках этих звезд. Переменность
белых карликов и нек-рых звезд типа
Щита), хотя ряд вопросов еще не решен. П. долгопериодических, полуправильных и неправильных
переменных изучены значительно хуже, отчасти из-за трудностей, связанных с необходимостью
учета взаимодействия П. с конвекцией, очень эффективной в оболочках этих звезд. Переменность
белых карликов и нек-рых звезд типа ![]() Цефея связана, вероятно,
с их нерадиальными колебаниями, однако механизмы возбуждения П. этих звезд пока неизвестны.
Солнце также явл., по-видимому, пульсирующей звездой, испытывающей различные виды
радиальных и нерадиальных колебаний с периодами от нескольких минут до нескольких
часов (см. Колебания и волны на
Солнце).
Цефея связана, вероятно,
с их нерадиальными колебаниями, однако механизмы возбуждения П. этих звезд пока неизвестны.
Солнце также явл., по-видимому, пульсирующей звездой, испытывающей различные виды
радиальных и нерадиальных колебаний с периодами от нескольких минут до нескольких
часов (см. Колебания и волны на
Солнце).
Лит.:
Жевакин С.А., Теория звездных пульсаций, в кн.: Пульсирующие звезды, М., 1970; Кокс
Дж., Теория звездных пульсаций, пер. с англ., М., 1983.
(С.А. Жевакин, А.А. Памятных)
С. А. Жевакин, А. А. Памятных, "Физика Космоса", 1986
Глоссарий Astronet.ru