Астронет > Линейчатое излучение (излучение в линиях)

Астронет: Л. А. Вайнштейн, "Физика Космоса", 1986 Линейчатое излучение (излучение в линиях)
http://variable-stars.ru/db/msg/1188392

Линейчатое излучение (излучение в линиях)

1. Введение
2. Локальное термодинамическое равновесие
3. Корональный предел
4. Промежуточный случай
5. Спектральная диагностика
6. Сателлиты

1. Введение

Линейчатое излучение - излучение нагретого газа (плазмы) на определённых частотах, наблюдаемое в форме дискретных спектральных линий. Л. и. образуется во внеш. частях атмосфер звёзд (хромосфере, короне), межзвёздной и межгалактич. среде, аккрецирующем газе рентгеновских источников и др. Фотоны Л. и. испускаются отдельными атомами (ионами, молекулами), оказавшимися в возбуждённом состоянии, при переходах в них электрона на более низкий уровень энергии (в частности, в осн. энергетич. состояние). Испущенный атомом фотон может либо выйти из объёма плазмы и достичь наблюдателя, либо поглотиться одним из окружающих атомов. В последнем случае атом, поглотивший фотон, оказывается в возбуждённом состоянии и может вновь испустить фотон с энергией $\varepsilon=h\nu$ , но, вообще говоря, уже др. частоты (см. Взаимодействие излучения с веществом). Если излучение и поглощение происходят многократно, спектр. линия сильно уширяется. Действительно, фотон с частотой, близкой к частоте центра линии, с большой вероятностью поглощается вновь, а фотон с частотой, далёкой от центра линии, легко выходит из объёма. Поэтому вероятность выхода фотона в "крыльях" линии эффективно возрастает, т.е. линия уширяется. В пределе линия исчезает - сливается с непрерывным спектром. Поэтому Л. и. сохраняется лишь в случае не слишком большой плотности и размеров излучающей среды.

Л. и. несёт важную информацию о состоянии и физ. процессах в излучающей среде (см. ниже раздел Спектральная диагностика). Наиболее проста спектр. диагностика плазмы в случае, когда вероятность вторичного поглощения испущенного в любой точке фотона мала, т.е. излучение свободно выходит из объёма. Такой случай наз. оптически тонкой плазмой. Ниже рассматривается именно этот случай. О формировании спектр. линий в условиях существенного поглощения фотонов (оптически толстая плазма) см. в ст. Атмосферы звезд.

Рассмотрим испускание фотона к.-л. спектр. линии при переходе электрона в ионе X_z с уровня k (с энергией $\varepsilon_k$ ) на уровень k' ( $\varepsilon_{k'}$ ). Здесь Х - к.-л. элемент, а z - спектроскопич. символ иона, к-рый на 1 больше кратности иона, т.е. Х_z = Х^(z-1)+ (см. Ионизация).

Частота испущенного фотона tex>(\varepsilon_k-\varepsilon_{k'})/h зависит от квантовых чисел k и k' уровней энергии и, кроме того, быстро растёт (~ z²) с ростом z. Соответственно фотон может оказаться в различных областях спектра - от радио- до рентгеновской. Так, в хромосферах звёзд, где T ~ 10⁴ К, образуются гл. обр. линии нейтральных атомов и первых ионов (с z = 2) в УФ- и видимой областях. Осн. часть Л. и. солнечной короны, где $T\approx 2\cdot 10^6$ K, приходится на резонансные линии ионов с z = 8-12, лежащие в рентг. области (10-40 $\AA$ ) и дальней УФ-области (100-300 $\AA$ ). Наконец, хорошо известны рекомбинационные радиолинии, связанные с переходами между высоковозбуждёнными уровнями с главным квантовым числом n ~ 100 или с переходами между компонентами сверхтонкой структуры уровней энергии (напр., радиолиния водорода 21 см).

Светимость L_kk' излучающего объёма V плазмы в спектр. линии $k\to k'$ равна:
$L_{kk'}=VN_k(X,z) A_{kk'}\varepsilon_{kk'}$ , (1)
где A_kk' - вероятность перехода $k\to k'$ (т.е. число переходов в ед. времени на один атом), а N_k(X,z) - концентрация ионов Х_z, находящихся на возбуждённом уровне k. Удобно выразить N_k(X,z) через относительную концентрацию n_z=N_k(X,z)/N(X) ионов Х_z и населённость уровня k: n_k=N_k(X,z)/N(X,z). Кроме того, в астрофизике принято выражать количество атомов в ед. объёма, т.е. концентрацию атомов N(X) через обилие $\alpha$ элемента Х относительно водорода: $\alpha$ (Х)= N(X)/N_H. Поэтому ф-лу (1) можно представить в виде:
$L_{kk'}=VN_{\rm H}\alpha({\rm X}) n_z n_k A_{kk'}\varepsilon_{kk'}$ . (2)

Относительная концентрация ионов n_k определяется ионизационным равновесием в плазме, т.е. динамич. равновесием процессов ионизации и рекомбинации. Очень важно при этом, что при столкновении электрона с ионом вероятность ионизации намного больше, чем вероятность рекомбинации. Поэтому максимум функции n_k(T) достигается уже при сравнительно низкой темп-ре T, когда $kT\ll\chi_z$ ( $\chi_z$ - энергия ионизации иона Х_z) и, следовательно, ещё мала доля электронов, имеющих достаточную энергию, чтобы ионизовать атом. Для большинства уровней энергия возбуждения уровня из осн. состояния E_k0 порядка $\chi_z$ . Т.о., в области максимума относительной концентрации n_k(T)
$\varepsilon_{k0},\chi_z\gg kT$ . (3)
Отметим, что с ростом z отношение $\chi_z/kT$ становится меньше. Необходимые для поддержания ионизац. равновесия возбуждение и ионизация атомов осуществляются электронами с энергией $\varepsilon>kT$ , т.е. относительно небольшим числом электронов с высокой энергией, образующих "хвост" Максвелла распределения.

2. Локальное термодинамическое равновесие

Населённости уровней n_k и, следовательно, характеристики спектра Л. и. оказываются существенно различными в случаях плотной и разреженной плазмы. Физически это определяется конкуренцией процессов излучательного перехода (т.е. спонтанного испускания фотона) и безызлучательного перехода при столкновении возбуждённого атома со свободным электроном (т.н. тушащее столкновение с передачей избытка энергии свободному электрону). Ниже будут рассмотрены предельные случаи: локальное термодинамич. равновесие (большая плотность плазмы) и корональный предел (низкая плотность).

Частота тушащих столкновений пропорциональна концентрации электронов. При достаточно большой концентрации она намного превышает число излучательных переходов. Поэтому излучение практически не влияет на населённости возбуждённых уровней, и, следовательно, населённости определяются законами термодинамики, т.е. даются Больцмана распределением:
$n_k=n_0\;\left({g_k\over {g_0}}\right)\;e^{-\beta_{k0}}$ , где $\beta_{k0}={\varepsilon_k-\varepsilon_0\over{kT}}$ . (4)
В ф-ле (4) индекс 0 соответствует осн. состоянию, g_k и g₀ - статистические веса (они определяют число состояний с данной энергией - степень вырождения уровня), $\varepsilon_k$ и $\varepsilon_0$ - энергии уровней. Следовательно, n_k зависит только от Т и $\varepsilon_k$ , а интенсивность линии, согласно (2), пропорциональна вероятности перехода A_kk'.

Согласно неравенству (3), населённости возбуждённых состояний, как правило, малы и почти все атомы (ионы) находятся в осн. состоянии, т.е. $n_0\approx 1$ .

Вероятности переходов A_kk' удовлетворяют определённым правилам отбора, накладывающим ограничения на возможные изменения квантовых чисел при переходах. Состояние атома характеризуется набором квантовых чисел $k=\{\gamma, n, l, L, S, J\}$ , где n и l - главное и орбитальное квантовые числа электрона, совершающего переход (т.н. оптич. электрона), $\gamma$ - совокупность квантовых чисел, описывающих прочие электроны атома, a L, S, J - орбитальный, спиновый и полный моменты атома в целом. При переходе $k\to k'$ изменяется чётность состояния (т.е. $\Delta l=\pm 1$ ), спин не меняется ( $\Delta S=0$ ), моменты L и J изменяются не более чем на единицу. Переходы, не удовлетворяющие этим правилам отбора, наз. запрещёнными.

В действительности по ряду причин вероятность запрещённых переходов $A_{kk'}\ne 0$ , но она на неск. порядков меньше, чем для разрешённых переходов. Поскольку интенсивность Л. и. пропорциональна A_kk', запрещённые линии оказываются чрезвычайно слабыми. С ростом z степень запрета убывает.

Подобные условия часто наз. локальным термодинамическим равновесием (ЛТР), имея в виду термодинамическое равновесие по отношению к населённости возбуждённых состояний и ионизац. состоянию атомов и ионов. Если, однако, излучающий объём явл. оптически тонким (как предполагалось выше), то само излучение далеко от термодинамически равновесного, к-рое даётся Планка законом излучения.

ЛТР имеет место, напр., в хромосферах Солнца и звёзд, правда, оптическая толща там не всегда мала. В условиях ЛТР распределение атомов по возбуждённым уровням определяется ф-лой Больцмана (4), распределение по состояниям ионизации - Саха формулой, а распределение свободных частиц по энергии - ф-лой Максвелла. При нарушении термодинамич. равновесия (напр., при низких плотностях, см. ниже) распределения Больцмана и Саха не имеют места. Однако распределение Максвелла имеет гораздо более широкую применимость и сохраняется даже при предельно низких плотностях.

3. Корональный предел

Предел, противоположный термодинамическому, соответствует низкой плотности и часто наз. корональным пределом (КП), т.к. хорошо реализуется в условиях солнечной короны, где низка электронная концентрация (N_e ~ 10⁸-10⁹ см^-3). Поскольку частота тушащих столкновений пропорциональна N_e, столкновениями можно пренебречь. Поэтому населённости уровней соответствуют равновесию между возбуждением электронными ударами и излучательными спонтанными переходами. Т.к. эти два процесса разной природы (в отличие от процессов возбуждения и тушения электронами), условия далеки от термодинамических.

При низких плотностях, вообще говоря, повышается роль возможных внеш. источников излучения. При этом населённости уровней и св-ва Л. и. существенно отличаются от условий КП. Примером могут служить зоны НII, квазары и др., где ионизац. равновесие определяется излучением центрального горячего тела и, следовательно, большую роль играет рекомбинац. заселение уровней.

При максвелловском распределении электронов по скоростям, принятом и для КП, число электронов с энергией $\varepsilon>\varepsilon_{k0}$ , т.е. достаточной для возбуждения уровня k, $\sim \exp(-\varepsilon_{k0}/kT)$ . Поэтому частоту столкновений, приводящих к возбуждению, можно записать в виде: $N_e q_{k0} \exp(-\varepsilon_{k0}/kT)$ , где коэфф. q_k0 определяется сечением возбуждения. Населённость уровней n_k в данном случае определяется балансом возбуждения ударами электронов и излучательных переходов:
$n_k=N_e\;\left({q_{0k}\over {A_k}}\right)\;e^{-\beta_{k0}}$ , (5)
где $A_k\sum\limits_{k'}A_{kk'}$ - полная вероятность излучательного распада уровня k (т.е. всех возможных излучательных переходов на нижележащие уровни). Как видно, осн. зависимость n_k от темп-ры в КП, как и в ЛТР, даётся экспоненциальным фактором $\exp(-\beta_{k0})$ . Однако, в отличие от (4), населённости оказываются теперь пропорциональными N_e и зависят от скоростей элементарных процессов q_k0 и A_k. Поскольку N_e предполагается малой, $N_e q_{0k}/A_k\ll 1$ , т.е. $n_k (k\ne 0)$ много меньше, чем в условиях термодинамич. равновесия, возбуждение ударами электронов осуществляется только из осн. состояния.

Ф-ла для светимости в линии L_kk' получается при подстановке выражения (5) в ф-лу (2):
$L_{kk'}=VN_{\rm H}N_e\alpha({\rm X}) n_z q_{0k} \left({A_{kk'}\over {A_k}} \right) \varepsilon_{kk'}\;e^{-\beta_{k0}}$ . (6)
Отношение A_kk' /A_k наз. фактором ветвления. Для первых возбуждённых состояний возможен лишь один переход с уровня k и фактор ветвления равен 1. При этом L_kk' не зависит от вероятности перехода, т.е. светимости для разрешённых и запрещённых переходов оказываются одного порядка. Это легко понять: ввиду отсутствия тушащих столкновений атом, возбуждённый на уровень k, остаётся на нём, пока не произойдёт излучательный переход. Строго говоря, указанное св-во относится лишь к метастабильным уровням, для к-рых нет конкурирующих разрешённых переходов на другой уровень, т.е. ветвление отсутствует (A_kk'=A_k). Наличие в спектре ярких запрещённых линий является главным отличием КП от ЛТР, где L_kk'~ A_kk' , т.е. запрещённые линии чрезвычайно слабы.

В качестве примера можно привести характерную тройку линий гелиеподобных ионов в рентг. спектрах солнечной короны: резонансную, интеркомбинационную (переход с изменением спина) и запрещённую. Наблюдаемые интенсивности этих линий относятся приблизительно как 1:0, 3:0,8, хотя степень запрета последней чрезвычайно велика - достигает 10⁹ при z = 10 (с ростом z степень запрета ослабевает). Помимо возбуждения ударами электронов заселение уровня k возможно также за счёт излучательных каскадных переходов с более высоких уровней энергии и при рекомбинации на возбуждённые уровни. Для "сильных" линий (напр., резонансных) роль каскадных процессов и рекомбинац. заселения уровней, как правило, мала - не превосходит 20%. Однако для уровней с малой вероятностью прямого возбуждения роль этих процессов может быть существенной. В частности, диэлектронная рекомбинация может играть определяющую роль для заселения высоких уровней с главным квантовым числом $n\gg 1$ .

Другим важным св-вом КП явл. зависимость [см. (6)]:
$L_{kk'}\sim N_{\rm H}N_eV\sim N_e^2 V$ . (7)
Величина $N_e^2 V=$ ME наз. объёмной мерой эмиссии. Т.о., в КП светимость L_kk' ~ ME, в то время как в условиях ЛТР, согласно (4) и (2), L_kk' ~ N_HV, т.е. пропорциональна числу излучающих атомов.

4. Промежуточный случай

В общем случае, когда физ. состояние плазмы не отвечает ни условиям ЛТР, ни условиям КП, населённости определяются балансом всех процессов заселения и распада уровней, включая тушащие столкновения и ступенчатое возбуждение, к-рые в КП не играли роли. Для нахождения n_k (а следовательно, и интенсивностей спектр. линий) приходится решать весьма громоздкую систему алгебраич. ур-ний баланса. Решение этих ур-ний позволяет сделать следующие выводы. При низкой плотности плазмы (т.е. при КП) и фиксированном числе атомов N_HV светимость L_kk' ~ N_e. С ростом плотности "включаются" тушащие столкновения, рост L_kk' замедляется и в пределе ЛТР L_kk' уже не зависит от концентрации электронов N_e. Однако рост L_kk' с увеличением N_e может прекратиться значительно раньше установления ЛТР. Обозначим $N_e^*$ электронную концентрацию, при к-рой тушащие столкновения начинают сказываться на населённости уровня k и, следовательно, нарушать условия КП. Приближённо
$N^*_e\approx {A_k\over {q_k}}, q_k= \sum\limits_{j\ne k} q_{jk}$ , (8)
где q_k - суммарная скорость тушащих столкновений. Для запрещённых линий A_k мало и условия КП нарушаются при значительно меньшей концентрации N_e, чем для разрешённых. Другими словами, рост L_kk' с увеличением концентрации электронов для запрещённых линий прекращается значительно раньше, т.е. на более низком уровне, чем для разрешённых линий.

Скорость тушащих столкновений q_kj растёт с уменьшением расстояния между уровнями | $\varepsilon_k-\varepsilon_j$ |. Поэтому они переводят атом с уровня k не в осн. состояние, а на ближайший уровень, с к-рого возможен излучательный переход. Это означает, что при $N_e > N_e^*(k)$ светимость сначала "перекачивается" из запрещённых линий в разрешённые. Лишь затем, с ростом N_e, наступают условия ЛТР для всех линий.

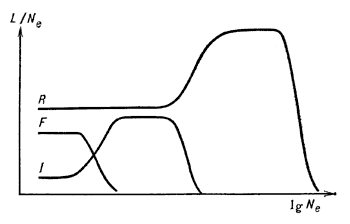
Рис. 1. Зависимость от электронной концентрации
интенсивности резонансной (R),
интеркомбинационной (I) и запрещённой (F) линий
гелиеподобного иона. Масштаб по оси абсцисс
зависит от заряда иона.

На рис. 1 показано изменение с N_e светимости трёх типов линий гелиеподобного иона: запрещённой (F), интеркомбинационной (I) и резонансной (R). Степень запрета линии F на неск. порядков сильнее, чем линии I. Для удобства по вертикальной оси отложена величина L/N_e.

Значение q_kj, как уже отмечалось, растёт с уменьшением расстояния между уровнями. Вероятность излучательных переходов между такими уровнями, наоборот, убывает. Из этого вытекают два важных следствия.

1. Для высоких уровней энергии атомов (когда квантовое число n велико) расстояние между уровнями уменьшается, и, следовательно, $N_e^*$ уменьшается. Поэтому имеется тенденция к термодинамически равновесному распределению населённостей между высокими уровнями. При этом распределение населённостей просто следует статистич. весу (экспоненц. фактор для близких уровней одинаков), а интенсивность линий пропорциональна A_kk'.

2. Для ионов энергии уровней растут ~ Z₂, a $N_e^*$ растёт как Z₆ или Z₇ для разрешённых переходов и ещё быстрее для запрещённых. Поэтому для многозарядных ионов (т.е. при высоких темп-рах) $N_e^*$ велико, влияние тушащих столкновений незначительно и КП имеет место практически при всех плотностях, встречающихся в астрофизич. условиях.

5. Спектральная диагностика

Л. и. может использоваться для определения темп-ры T и электронной концентрации N_e плазмы. Как уже отмечалось, температурная зависимость интенсивности линий в условиях ЛТР и КП аналогична ( $L_{kk'}\sim e^{-\beta_{k0}}$ ). Темп-ра может быть определена по спектр. линиям как ионов одного типа, так и ионов различных типов. Очень удобны для определения T линии-сателлиты в спектрах многозарядных ионов (см. ниже).

Соотношение (8) явл. основой спектр. диагностики плотности плазмы (при малых и умеренных плотностях). При этом наиболее удобно сравнивать интенсивности запрещённой и разрешённой линий, полагая, что для последней КП выполняется (одновременно может выполняться КП по одним линиям и ЛТР по другим). Если отношение интенсивностей отличается от вычисленного с помощью ф-л (5) или (7), то $N_e\ge N_e^*(k)$ для соответствующей запрещённой линии. Величина $N_e^*$ определяется по известным значениям A_k и q_k с помощью (слегка уточнённого) соотношения (8). Используя различные запрещённые линии, можно оценивать N_e в различных диапазонах (ср. рис. 1).

В нек-рых случаях оказывается удобным использовать для определения N_e абс. светимости
$L_{kk'}\sim N^2_e V$ (КП),
$L_{kk'}\sim N_{\rm H} V$ (ЛТР).(9)

В условиях, далёких от термодинамич. равновесия, Л. и. даёт возможность определить T, N_e и обилие элементов $\alpha$ (Х), а также получить детальную информацию о процессах в плазме. С ростом плотности плазмы число одновременно происходящих микропроцессов увеличивается и получить детальную информацию об отдельных процессах оказывается уже невозможным. В условиях ЛТР информация об отдельных микропроцессах полностью утрачивается и оказывается возможным определять лишь макрохарактеристики: $T, N_e, \alpha$ (X); причём для определения N_e необходимы абс. измерения либо линии разных ионов (пользуются ф-лой Саха). Наконец, в оптически толстой плазме при полном термодинамич. равновесии частиц и излучения последнее имеет планковскую зависимость интенсивности от частоты. При этом теряется информация как о N_e, так и о $\alpha$ (Х), т.е. по характеру распределения энергии в спектре можно определить лишь темп-ру плазмы.

6. Сателлиты

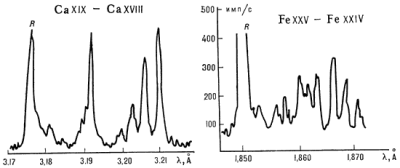
Рис. 2. Сателлитная структура около резонансной линии (R)
гелиеподобного иона: слева - лазерная плазма; справа -
солнечная корона.

Особую категорию линий в спектре многозарядных ионов Х_z составляют сателлиты резонансной и др. линий. Сателлиты возникают при переходах между теми же уровнями, что и осн. линия, но оказываются несколько смещёнными по частоте из-за присутствия одного (или нескольких) дополнительных электронов на возбуждённом уровне nl. Наличие дополнительного nl-электрона обусловлено, как правило, рекомбинац. захватом (диэлектронная рекомбинация - осн. механизм образования сателлитов). Возбуждённый ион может испустить либо электрон (и вернуться в исходное состояние), либо фотон с частотой, близкой к частоте осн. линии (сателлит). При n = 2 или 3 сателлиты хорошо разрешаются от осн. линии, а при $n\ge 4$ обычно сливаются с ней.

Отношение интенсивностей сателлита и осн. линии мало при Z < 10 и быстро растёт (~ Z⁴) с ростом Z. При $Z\ge 20$ интенсивность сателлитов становится порядка интенсивности осн. линии и далее почти не меняется с увеличением Z. Отношение интенсивностей зависит от темп-ры. Действительно, возбуждение сателлита сопровождается захватом электрона на уровень с отрицат. энергией $-\delta\varepsilon$ . Поэтому на возбуждение сателлита требуется меньше энергии, чем на возбуждение осн. линии. Отношение интенсивностей сателлита и осн. линии $\sim\delta\beta\exp(\delta\beta)$ , где $\delta\beta=\delta\varepsilon/kT$ . Из ф-лы видно, что с ростом темп-ры сателлиты становятся относительно слабее. Поскольку сателлиты расположены весьма близко к осн. линии и возбуждаются из того же осн. состояния, они весьма удобны для определения темп-ры. На рис. 2 показана сателлитная структура в области резонансной линии ионов CaXIX (лазерная плазма) п FeXXV (солнечная корона, вспышка). В последнем случае структура относительно слабее ввиду большей температуры.

Лит.:
Вайнштейн Л.А., Собельман И.И., Юков Е.А., Возбуждение атомов и уширение спектральных линий, М., 1979; Каплан С.А., Пикельнер С.Б., Физика межзвездной среды, М., 1979.

(Л.А. Вайнштейн)

Л. А. Вайнштейн, "Физика Космоса", 1986
Глоссарий Astronet.ru