Астронет > Координаты астрономические

Астронет: В. В. Нестеров, "Физика Космоса", 1986 Координаты астрономические
http://variable-stars.ru/db/msg/1188359

Координаты астрономические

Подавляющее большинство координатных систем в астрономии явл. сферическими и основываются на понятии небесной сферы, в качестве к-рой выбирается сфера произвольного радиуса (обычно условно принимаемого равным единице) с центром, совпадающим с началом заданной системы отсчёта. В соответствии с решаемой задачей используются топоцентрич. небесная сфера (центр - в точке наблюдения), геоцентрич. небесная сфера (центр её совпадает с центром масс Земли), гелиоцентрическая, планетоцентрическая и др. небесные сферы. Изменение К. а. небесного тела при переходе между системами координат с различными центрами определяется соответствующим параллаксом. Напр., при переходе от геоцентрич. к гелиоцентрич. К. а. учитывается годичный параллакс небесного тела. Однако для далёких объектов (звёзды, за исключением самых близких, галактики и т.п.) изменение К. а., связанное с изменением положения центра небесной сферы в пределах Солнечной системы, пренебрежимо мало.

Рис. 1. Важнейшие точки и круги
на небесной сфере.

Изображение небесной сферы, а также важнейших кругов и точек на ней приводится на рис. 1. Сечения небесной сферы плоскостями, проходящими через её центр, образуют на сфере большие круги, остальными плоскостями - малые круги. Прямая, проведённая параллельно местной отвесной линии через центр небесной сферы, пересекает сферу в точках зенита (Z) и надира (Na). Большой круг, плоскость к-рого перпендикулярна этой прямой, наз. математич. или астрономич. горизонтом (линия WSEN). Прямая, проходящая через центр сферы параллельно оси вращения Земли, наз. осью мира и пересекает сферу в полюсах мира (P_N и P_S). Большой круг небесной сферы, плоскость к-рого перпендикулярна оси мира, наз. небесным экватором (AEA'W), a большой круг, проходящий через полюсы мира и зенит, - небесным меридианом (Q_NZP_S). На рис. также показана эклиптика (QQ'), плоскость к-рой параллельна плоскости орбиты Земли. Эклиптика пересекается с небесным экватором в т.н. точках весеннего () и осеннего () равноденствия.

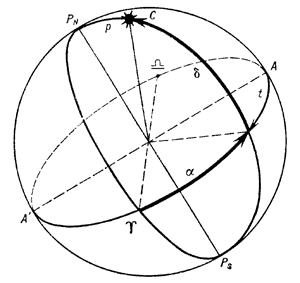
Рис. 2. Экваториальная система координат.
- небесный экватор.

Выбор системы координат на небесной сфере фиксируется: избранной точкой (полюсом системы); большим кругом, задаваемым пересечением небесной сферы с плоскостью, перпендикулярной проходящему через полюс диаметру сферы; точкой на этом большом круге, от к-рой начинается отсчёт дуг вдоль этого круга. В установленной т.о. системе координатами объекта являются, во-первых, отрезок дуги большого круга, проходящего через объект и полюс системы (он измеряется от осн. большого круга до объекта), и, во-вторых, дуга осн. большого круга, заключённая между начальной отсчётной точкой и точкой пересечения с большим кругом, проходящим через объект и полюс. Если не оговорено особо, то первая координата измеряется в градусной мере в обе стороны от осн. большого круга (т.е. от 0 до $\pm$ 90^o), вторая же координата измеряется в градусной или часовой мере (от 0 до 360^o или от 0 до 24 ч) от начальной отсчётной точки до пересечения осн. большого круга с большим кругом, проходящим через полюс и объект. При этом отсчёт ведётся против часовой стрелки, если смотреть с северного полюса данной координатной системы.

Наиболее часто применяются следующие системы К. а.

Горизонтальная система.
Полюс её - точка зенита, осн. круг - линия астрономич. горизонта, на к-рой фиксируется начало отсчёта (обычно точка юга S). Координатами объекта в горизонтальной системе явл. его высота h (или зенитное расстояние z, равное дополнению высоты до 90^o) и азимут а, отсчитываемый от точки юга на запад вдоль горизонта.

Экваториальная система (рис. 2).
Полюс её - северный полюс мира (P_N), осн. круг системы - небесный экватор. В качестве отсчётной точки фиксируется точка весеннего равноденствия . Координаты объекта С - его склонение $\delta$ (или полярное расстояние p, дополняющее склонение до 90^o) и прямое восхождение $\alpha$ . В другом, часто используемом варианте экваториальной системы второй координатой явл. часовой угол объекта t - двугранный угол между плоскостью небесного меридиана и плоскостью, в к-рой находится круг склонений (т.е. большой круг, проходящий через полюс мира и объект). Часовой угол обычно отсчитывается в часовой мере в обе стороны от точки A (от 0 до $\pm$ 12 ч).

Эклиптическая система.
Полюс её - одна из точек пересечения небесной сферы с перпендикуляром к плоскости орбиты Земли (северный полюс эклиптики). Осн. круг - эклиптика. Координаты объекта - эклиптическая широта $\beta$ и эклиптическая долгота $\lambda$ , отсчитываемая от точки .

Галактическая система.
Полюс её - точка на небесной сфере, имеющая экваториальные координаты: $\alpha_0$ = 12ч 49 мин, $\delta= 27,4^\circ$ (направление нормали к плоскости Галактики). Осн. круг системы - пересечение плоскости Галактики с небесной сферой - галактич. экватор. Координаты объектов - галактическая широта b и галактическая долгота l, отсчитываемая от направления на центр Галактики вдоль галактического экватора в сторону возрастания прямых восхождений.

Координаты объекта, заданные в одной системе координат, могут быть пересчитаны в др. систему с помощью простых формул сферич. тригонометрии. Напр., переход от экваториальной системы координат к эклиптической осуществляется по следующим ф-лам:
$\cos\beta \cdot\cos\lambda=\cos\delta\cdot\cos\alpha$
$\cos\beta\cdot\sin\lambda=\cos\delta\cdot\sin\alpha\cdot\cos\varepsilon+\sin\delta\cdot\sin\varepsilon$
$\sin\beta =-\cos\delta\cdot\sin\alpha\cdot\sin\varepsilon+\sin\delta\cdot\cos\varepsilon$

(В.В. Нестеров)

В. В. Нестеров, "Физика Космоса", 1986
Глоссарий Astronet.ru