Астронет > Ядерные реакции

Астронет: В. С. Имшенник, Д. К. Надежин, "Физика Космоса", 1986 Ядерные реакции
http://variable-stars.ru/db/msg/1188318/text

Ядерные реакции

1. Введение
2. Способы записи ядерных реакций
3. Энергетический выход ядерной реакции
4. Сечение и скорость ядерной реакции
5. Радиус действия ядерных сил, кулоновский и центробежный энергетические барьеры
6. Механизмы ядерных реакций. Термоядерные реакции
7. Статически равновесные ядерные реакции
8. Термоядерная эволюция звезд
9. Заключение

1. Введение

Я.р. называются процессы превращения атомных ядер (Я) при взаимодействии их между собой и с элементарными частицами.

В астрофизике Я.р. рассматриваются в основном в двух аспектах - как источник энергии звезд и как причина образования и изменений содержания хим. элементов во Вселенной в целом и в отдельных ее структурных элементах (галактиках, звездах, межзвездной среде и т.д.). Огромные запасы внутриядерной энергии постепенно освобождаются посредством Я.р. в недрах звезд и обеспечивают их длительное существование в виде почти не меняющихся со временем (стационарных) гидростатически равновесных тел. Я.р. играют определяющую роль и на нестационарных стадиях эволюции звезд, в т.ч. при вспышках новых и сверхновых звезд. На всех этих стадиях звездной эволюции посредством Я.р. синтезируется большинство встречающихся в природе тяжелых элементов.

Исходные данные о Я.р. астрофизика берет из экспериментальной и теоретической ядерной физики. Я.р. определяются тремя из известных четырех фундаментальных взаимодействий - сильным, эл.-магн. и слабым (лишь гравитац. взаимодействие не имеет непосредственного отношения к Я.р.). С этим связано громадное разнообразие Я.р.

Наибольший интерес для астрофизики представляют реакции (Р) слияния Я, иначе говоря, синтез тяжелых Я из более легких Я и элементарных частиц. В процессах синтеза выделение энергии происходит вплоть до образования ядер Fe и Ni, к-рые имеют наибольшую энергию связи в расчете на один нуклон. Появление на определенных стадиях эволюции звезд свободных нейтронов и захват их Я элементов группы железа приводит к синтезуу еще более тяжелых атомных Я, вплоть до Я трансурановых элементов.

На заключительных стадиях эволюции достаточно массивных звезд, когда темп-ра в их недрах становится очень высокой, скорости Я.р. увеличиваются настолько, что почти каждому элементарному акту синтеза к.-л. Я соответствует обратный акт расщепления этого Я на исходные составляющие. В результате устанавливаюся вполне определенное концентрации Я, не зависящие от скоростей Я.р. Такое состояние звездного вещества принято наз. ядерным статистич. равновесием или NSE (от англ. nuclear statistical equilibrium). Состояние NSE поддерживается быстрыми и многочисленными прямыми и обратными Я.р. Установление NSE в недрах звезд - одна из двух главных причин потери механич. устойчивости звезд и перехода их в состояние гравитац. коллапса на конеч. стадиях эволюции, вторая причина - нейтронизация звездного вещества (см. Гравитационный коллапс).

Особое место в ядерной астрофизике занимают вызываемые слабым взаимодействием Р электронов и позитронов с Я. В этих Р участвуют также нейтрино. Позитронные бета-распады (см. Бета-процессы) явл. непременным звеном в цепочках Р синтеза хим. элементов из водорода (см. Водородный цикл и Углеродный цикл). Электроннные бета-распады вместе с Р захвата нейтронов делают возможным образование в природе наиболее тяжелых хим. элементов. Захват электронов Я, сопровождаемый интенсивным нейтринным излучением, оказывает решающее влияние на св-ва звездного вещества на конечных стадиях эволюции звезд (при нейтронизации и гравитац. коллапсе). Поглощение и излучение нейтрино в Р электронов и позитронов с нейтронами, протонами и Я играет важную роль в гидродинамич. картине образования нейтронных звезд (и, возможно, Черные дыр). Оно также определяет характеристики сопровождающих гравитац. коллапс всплесков нейтринного излучения, теоретич. предсказание к-рых имеет большое значение для реализации на нейтринных обсерваториях программ детектирования гравитационных колапсов. Из этого краткого перечисления видно, насколько важны для астрофизики Я.р., обусловленные слабым взаимодействием.

Др. область астрофизики, в к-рой св-ва Я.р. играют определяющую роль, относится к взаимодействию высокоэнергичных частиц (ускоренных Я) с межзвездной средой и веществом разреженных звездных атмосфер и околозвездных оболочек. Высокоэнергичные частицы могут появляться в результате эл.-магн. ускорения при вспышках на звездах и в магнитосферах пульсаров, а также вследствие прямого гидродинамич. ускорения в ударных волнах. Если вызываемые такими частицами Я.р. сопровождаются отщеплением от реагирующих ядер легких фрагментов - протонов (p), нейтронов (n), $\alpha$ -частиц и т.д., то их наз. реакциями скалывания. Я.п. скалывания позволяют объяснить ряд особенностей состава космических лучей и отчасти происхождение легких элементов - Li, Be и B. Частицы достаточно больших энергий могут также приводить к образованию мезонов и др. адронов помимо нейтронов и протонов.

Я.р. лежат в основе строения и эволюции вещества Вселенной, поскольку представляют собой те элементарные процессы, посредством к-рых становится возможным проявление микроскопических св-в Я в огромных масштабах космоса.

2. Способы записи ядерных реакций

Употребляется два способа зариси Я.р. Один из них аналогичен обычным хим. ур-ниям, напр.:
¹³C + $\alpha$ = ¹⁶O + n + 2,22 МэВ , (1)
причем вместо знака равенства чаще пишется стрелка, чтобы подчеркнуть, в каком направлении идет Я.р. В правой части может быть указан энегетический выход реакции Q (в МэВ). Положительное значение Q соответствует выделению, а отрицательное - поглощению энергии в Я.р.

Во втором (сокращенном) способе записи выделяются тяжелые Я (мишень и продукты реакции), а бомбардирующая и и выбрасываемая (или выбрасываемые) более легкие частицы пишутся в скобках и разделяются запятой. Указанная выше Р записывается при этом как ¹³C( $\alpha$ , n)¹⁶O, а все Р такого типа наз. реакциями ( $\alpha$ , n). Большое значение в астрофизике имеют также реакции (p, $\gamma$ ), (n, $\gamma$ ), (p, n), (p, 2n), ( $\alpha, \gamma$ ) и др. В число Я.р. включают и определяемые слабым взаимодействием бета-процессы. Распад трития можно записать как ³H(e^-, $\tilde{\nu}$ )³He, а захват протоном электрона - элементарный акт нейтронизации - как ¹H(e^-, $\nu$ )n. В сокращенной записи вне скобок стараются по возможности использовать хим. символы элементов (напр., ¹H вместо p и ³H вместо трития t). Кроме того, дейтерий ²H иногда обозначают как ²D, а тритий ³H как ³T.

3. Энергетический выход ядерной реакции

В Я.р. строго выполняются законы сохранения импульса и энергии. Однако нек-рая часть икнетич. энергии может переходить в энергию покоя (см. Масса покоя) и, наоборот, энергия покоя может освобождаться в виде кинетич. энергии [как в реакции (1)], к-рая передается др. частицам при последующих столкновениях или уносится такими элементарными частицами, как фотоны и нейтрино. Энергетическим выходом реакции Q наз. разность между суммарными энергиями покоя всех частиц до и после Я.р. Если Q >0, то суммарная энергия покоя уменьшается в процессе Я.р. Такие Я.р. наз. экзоэнергетическими или беспороговыми. В принципе они могут протекать при сколь угодно малой начальной кинетич. энергии частиц. Наоборот, при Q <0 часть исходной кинетич. энергии частиц превращается в энергию покоя. Такие Я.р. наз. эндоэнергетическими или пороговыми. Для их протекания необходимо, чтобы кинетич. энергия частиц превышала нек-рую величину (порог реакции).

Закон сохранения импульса накладывает ограничение на величину кинетич. энергии, к-рая может перейти в энергию покоя. Вся кинетич. энергия может перейти в энергию покоя лишь в том случае, когда полный импульс реагирующих частиц равен нулю. Поэтому Я.р. удобно рассматривать в системе координат, в к-рой центр инерции (ц.и.) взаимодействующих частиц покоится, т.е. полный импульс равен нулю по определению. Далее, если особо не оговорено, под энергией взаимодействия будет подразумеваться кинетич. энергия частиц в системе ц.и. В случае двух нерелятивистских ат. Я энергия взаимодействия определяется по ф-ле
$\varepsilon=Mv^2/2$ , (2)
где $v=|v_1-v_2|$ - относительная скорость частиц, а M - приведенная масса
$M=m_u {A_1 A_2\over {A_1+A_2}}$ , (3)
причем A¹ и A² - массы Я, измеренные в а.е.м. (A¹u).

Условие протекания эндоэнергетических Я.р. можно записать в виде $\varepsilon > |Q|$ . Из этого неравенства с помощью (2) можно получить в лабораторной системе координат, где, напр., частица с массой m² покоится, а частица с массой m¹ налетает на нее с кинетич. энергией $\varepsilon_1$ , необходимое условие для протекания эндоэнергетической реакции:
$\varepsilon_1 > |Q| \cdot \left(\ 1+ {m_1\over {m_2}} \right)$ . (4)
Такое возрастание порога реакции в лабораторной системе координат объясняется тем, что часть кинетич. энергии, связанная с движением центра масс, остается бесполезной для Я.р.

4. Сечение и скорость ядерной реакции

Рассмотрим реакцию между частицами двух типов (1 и 2). Предположим для простоты, что частицы 1 покоятся, а частицы 2 налетают на них со скоростью v. Тогда скорость реакции P₁₂, т.е. число реакций в ед. времени в ед. объема, будет пропорциональна произведению n₁ j, где j=n₂v - число частиц 2, проходящих через ед. площади в ед. времени (поток частиц 2), а n₁ и n₂ - числа частиц 1 и 2 в ед. объема. Коэффициент пропорциональности $\sigma$ имеет размерность площади и наз. сечением Я.р. Выражение $P_{12}=n_1 n_2 \sigma v$ остается справедливым и в том случае, когда движутся оба типа частиц (тогда v - скорость взаимного сближения частиц, т.е. их относительная скорость). Сечения Я.р., вообще говоря, зависят от скорости (кинетич. энергии) реагирующих частиц. Кроме того, в астрофизич. объектах (напр., в звездном веществе) обычно представлены частицы с различными скоростями. Поэтому для нахождения полного числа Я.р. в ед. объема необходимо усреднить приведенное выше выражение для P₁₂ по распределению относит. скоростей частиц
$P_{12}={n_1 n_2 \over {1+\delta_{12}}}\;<\sigma v>$ , (5)
где угловыми скобками обозначено ср. значение и введена величина $\delta_{12}$ , равная 0 или 1 в зависимости от того, различны или тождественны частицы 1 и 2. Введение величины $\delta_{12}$ связано с тем, что в описанном выше способе подсчета числа реакций в случае тождественных частиц участие каждой частицы в реакции учитывается дважды: один раз, когда эта частица рассматривается как мишень, а в другой раз как бомбардирующая частица.

Скорость выделения энергии $\varepsilon$ , рассчитанная на единицу массы, вещества с плотностью $\rho$ находится из соотношения
$\varepsilon=Q\cdot P_{12}/\rho$ . (6)
Теория ядерных взаимодействий вместе с данными экспериментальной ядерной физики позволяет рассчитать сечения Я.р., а с ними и две осн. используемые в астрофизике характеристики Я.д. - P₁₂ и $\varepsilon$ .

5. Радиус действия ядерных сил, кулоновский и центробежный энергетические барьеры

Ядерные силы явл. короткодействующими. Поэтому для эффективного протекания Я.р. частицы должны подойти достаточно близко друг к другу. Характерное расстояние R, в пределах к-рого ядерные силы оказываются существенными (его наз. радиусом ядерного взаимодействия), определяется соотношением
$R\approx R_0\left(A_1^{1/3}+A_2^{1/3}\right)$ , (7)
где A₁ и A₂ - массовые числа реагирующих Я, а $R_0\approx 1,5\cdot 10^{-13}$ см.

В цепочке ядерных превращений, к-рая заканчивается синтезом в звездах Я тяжелых элементов из первичных водорода и гелия, ключевыми звеньями оказываются Р протонов и $\alpha$ -частиц между собой и с более тяжелыми Я, а также нек-рых Я с ядрами того же сорта и с подобными Я. В таких Я.р. сближению частиц на малые расстояния R препятствуют силы электростатич. отталкивания, и поэтому реагирующие частицы должны преодолеть кулоновский энергетический барьер.

Зависимость кулоновской потенциальной энергии V_c от расстояния между частицами r имеет вид
V_c(r)=e² Z₁ Z₂/r , (8)
где Z₁ и Z₂ - заряды частиц в ед. заряда электрона e. Высота кулоновского энергетического барьера $\varepsilon_c$ получается при подстановке r=R в (8): $\varepsilon_c=V_c(R)$ (рис. 1).

На б'ольших расстояниях ( $r\ge R$ ) взаимодействие заряженных частиц определяется кулоновским потенциалом (8). Обалсть ядерного взаимодействия (r < R) приближенно можно описать некоторым эффективным потенциалом. Для многих целей оказывается достаточным считать, что потенциал имеет вид прямоугольной ямы с глубиной V₀=-40 МэВ. Крутые края такой ямы описывают интенсивное прияжение между ат. Я на расстоянии $r\approx R$ .

Рис. 1. Кулоновский энергетический барьер $\varepsilon_c$ ;
V_C(r) - потенциал взаимодействия,
R - радиус ядерного взаимодействия,
V₀ - потенциал ядерного взаимодействия,
$\varepsilon$ - энергия относительного движения частиц
(энергия взаимодействия). Подбарьерный
переход показан штриховой линией.

В общем случае относительное движение частиц характеризуется моментом импульса, к-рый, согласно квантовой механике, может принимать лишь дискретные значения $\hbar\sqrt{l(l+1)}$ , определяемые орбитальным квантовым числом l=0, 1, 2, ..., l_макс, где $l_{макс}=R/\bar{\lambda}$ $\bar{\lambda}=\hbar/Mv$ . При l=0 момент импульса равен нулю., что соответствует лобовому столкновению частиц. Когда частицы подходят близко друг к другу с сохранением момента импульса, кинетич. энергия их относительного вращения быстро возрастает. Поэтому для попадания в область действия ядерных сил заряженным частицам необходимо преодолеть не только кулоновский, но в случае l>0 еще и центробежный энергетический барьер: $\varepsilon_R=l(l+1)\hbar^2/2MR^2$ . При взаимодействии нейтронов с Я кулоновский барьер отсутствует и остается только центробежный барьер (для l>0). Существенно, что в случае l=0 центробежный барьер отсутствует. Кроме того, для нейтронов даже при l=1 высота центробежного барьера оказывается большой по сравнению с энергией, к-рую они могут иметь в звездном веществе [с увеличением l высота центробежного барьера растет как l(l+1)].

Поэтому нейтроны эффективно реагируют с Я лишь при лобовых столкновениях в отсутствии центробежного барьера (при l=0). При взаимодействии Я друг с другом высота центробежного барьера может уже не быть столь большой (велико MR²). Однако в этом случае значительно более важную роль играет кулоновский энергетический барьер. Именно он определяет зависимость сечения Я.р. от энергии взаимодействия частиц, тогда как суммарный вклад центробежных барьеров при различных $l \ge 1$ сводится лишь к умножению сечения Я.р. при l=0 на слабо зависящий от энергии коэффициент, к-рый входит в общий множитель, обычно определяемый из данных эксперимента. Т.о., при характерных для звездного вещества энергиях взаимодействия центробежный энергетический барьер имеет второстепенное значение.

В классической механике попадание частиц в область r < R возможно лишь при условия, что энергия взаимодействия (2) превышает высоту энергетич. барьера, т.е. когда $\varepsilon>\varepsilon_c$ для заряженных частиц. Однако в квантовой механике существует конечная вероятность сближения частиц до расстояний r < R даже в случае $\varepsilon\ll\varepsilon_c$ (туннельный эффект). Такой подбарьерный переход не означает нарушения закона сохранения энергии, полная энергия системы после перехода в точности равна энергии до перехода. Именно этот случай реализуется в звездах: они светят миллиарды лет благодаря освобождениюзапасов ядерной энергии при постепенном "просачивании" Я сквозь энергетич. барьер .Расчет вероятности подбарьерного перехода показывает, что она резко понижается как с увеличением высоты потенциального барьера, так и с уменьшением энергии взаимодействия при фиксированной высоте барьера. Именно этим объясняется сильная зависимость сечений Я.р. между заряженными частицами от энергии (и в конечном счете скоростей Я.р. от темп-ры), а также от зарядов Z реагирующих Я.

Следует отметить важное обстоятельство: вероятность подбарьерного перехода не зависит от направления движения частицы, т.е. от того, преодолевает ли частица энергетич. барьер, проникая в Я, или, наоборот, стремится с такой же энергией покинуть Я.

6. Механизмы ядерных реакций. Термоядерные реакции

Попадание частиц в область действия ядерных сил явл. необходимым, но, вообще говоря, недостаточным условием протекания данной Я.р. С той или иной вероятностью Я.р. может закончиться разными путями, т.е. пойти по различным каналам. Рещультат Я.р. во многом зависит от механизма ее протекания. По механизму Я.р. подразделяются на две осн. группы: прямые Я.р. и Я.р., протекающие через составное ядро. (В этом разделе, как и в разделе 5, не рассматриваются обусловленные слабым взаимодействием реакции электронов, позитронов и нейтрино с Я.) В прямых Я.р. энергия частиц передается за короткое ядерное время ~ 10²² с (время прохождения реагирующими частицами расстояния, равного размеру ядра) непосредственно одному или группе из неск. нуклонов, к-рые и образуют продукты Р. Примером могут служить (p, n)- (n, p)-реакции при энергиях порядка неск. десятков МэВ.

Внутри звезд характерные энергии частиц значительно меньше ( $\le 1$ МэВ). При таких энергиях большинство Я.р. идет через составное Я. В процессе взаимодействия энергия постепенно распределяется между всеми имеющимися нуклонами реагирующих частиц, к-рые объединяются на промежуточной стадии Р в одно сравнительно долгоживущее (до 10^-14 с) составное Я. На заключительной стадии Р составное Я с определеннной вероятностью распадается на продукты Р по одному из возможных каналов, напр.:
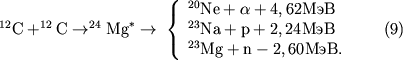
$^{12}\rm{C}+^{12}\rm{C}\to^{24}\rm{Mg}^*\to \;\left\{ \begin{array}{l} ^{20}\rm{Ne}+\alpha+4,62 \mbox{МэВ}\\ ^{23}\rm{Na+p}+2,24 \mbox{МэВ} \quad\quad\quad(9)\\ ^{23}\rm{Mg+n}-2,60 \mbox{МэВ} .\\ \end{array} \right.$

Составное Я - возбужденное ядро ²⁴Mg* - распадается по неск. возможным каналам, число к-рых тем больше, чем сильнее возбуждение. В (9) указаны три осн. способа распада, соответствующих энергиям частиц внутри звезд. Каналы с испусканием $\alpha$ -частиц и протонов примерно равновероятны, поскольку выделяемые энергии сравнимы с высотой кулоновских барьеров для вылетающих частиц. Канал с испусканием нейтрона сильно эндоэнерггетичен и поэтому обладает небольшой вероятностью (она достигает неск. % лишь при взрывном горении углерода на конечных стадиях звездной эволюции, когда темп-ра превышает $3\cdot 10^9$ К). Вероятности распада составного ядра зависят лшь от энергии возбуждения и не зависят от способа его образования, т.к. составное Я слишком долго "живет" в ядерных масштабах времени и поэтому "забывает" историю своего происхождения.

Р, идущие через составное ядро, делятся в свою очередь на резонансные и нерезонансные. Составное ядро, как и всякая квантовая система, может находится только в состояниях, характеризуемых дискретными значениями энергии (уровнями энергии). Если энергия реагирующих частиц такова, что энергия возбуждения составного ядра оказывается близкой в к.-л. его изолированному энергетическому уровню, то вероятность образования составного ядра, а следовательно и сечения Р, резко возрастают (резонанс). В этом случае скорость Р определяется теми частицами, к-рые взаимодействуют с энергией $\varepsilon$ , близкой к энергии $\varepsilon_r$ , соответствующей возникновению резонанса. Однако с ростом энергии возбуждения, а также с увеличением массовых чисел реагирующих Я резко возрастает число уровней и расстояния (по энергии) между уровнями становятся сравнимыми с их шириной. Уровни перекрываются, и зависимость сечения образования составного Я от энергии уже не имеет вид далеко отстоящих резких максимумов, а представляет собой, хотя и волнообразную, но в сремнем плавно меняющуюся функцию. В таких условиях в полную скорость Я.р. вносят вклад частицы в широком интервале энергий, Я.р. протекает нерезонансным образом. Кроме того, резонансная энергия может оказаться трудно достижимой в Я.р. Напр., ближайший изолированный уровень составного Я может располагаться столь высоко, что в звездном веществе практически не будет частиц с нужной высокой энергией. В случае экзоэнергетических Р составное Я может, наоборот, иметь минимальную энергию возбуждения (т.е. энергию возбуждения при энергии взаимодействия $\varepsilon$ =0), превышающую энергию изолированного уровня. В обоих случаях Я.р. тем не менее может идти с нек-рой скоростью, поскольку при отличии энергии Р от резонансной все-таки имеется не равная нулю вероятность образования составного Я. Зависимость сечения такой Р от энергии плавная. Говорят, что Р идет на крыльях резонанса, но нерезонансным образом.

Прямые Я.р. также носят нерезонансный характер.

Расчет сечения нерезонансных экзоэнергетических Я.р. между заряженными частицами приводит к следующему результату:
$\sigma(\varepsilon)=(C/\sqrt{\varepsilon})[\sqrt{\varepsilon_G/\varepsilon}\cdot\exp(-\sqrt{\varepsilon_G/\varepsilon})]=(S/\varepsilon)\cdot\exp(-\sqrt{\varepsilon_G/\varepsilon})$ , (10)
где $\varepsilon_G=(M/2)(2\pi e^2 Z_1 Z_2/\hbar)^2$ - т.н. энергия Гамова, а C и S - паарметры, к-рые слабо зависят от $\varepsilon$ . Множитель в квадратных скобках в (10) описывает вероятность прохождения частицы сквозь кулоновский энергетический барьер и наз. проницаемостью барьера. Множитель $C/\sqrt{\varepsilon}$ в первом приближении можно представить как произведение геометрич. сечения столкновения, пропорционального R², на вероятность осуществления Я.р., когда частицы находятся в пределах действия ядерных сил, т.е. на расстояниях r < R. Эта последняя равна произведению вероятности образования составного Я, к-рая пропорциональна времени пребывания частиц в области r < R, т.е. величине $R/v\sim 1/\sqrt{\varepsilon}$ , и вероятности распада составного Я по интересующему нас каналу, слабо зависящей от $\varepsilon$ .

Прия Я.р. с участием во входном канале нейтральных частиц (нейтронов, фотонов) сближение частиц не затруднено кулоновским энергетическим барьером. Для теории происхождения хим. элементов важна Р радиационного захвата нейтрона (n, $\gamma$ ). Интересны также реакции (n, p) и (n, $\alpha$ ), но скорость их обычно меньше, чем (n, $\gamma$ ), особенно на тяжелых Я, поскольку вылетающим протонам и $\alpha$ -частицам приходится преодолевать кулоновский барьер. Однако в нек-рых экзоэнергетических Р нейтронов с легкими и средними Я кулоновский барьер для вылетающих частиц не очень высок, а энерговыделение в Р столь велико, что энергии протонов и $\alpha$ -частиц оказываются сравнимыми с высотой кулоновского барьера. Такие Р могут поэтому идти с довольно большой скоростью. Напр., реакция ¹⁴N(n, p)¹⁴C + 0,63 МэВ играет роль сильного поглотителя нейтронов на стадии горения водорода в звездах. Высокой скоростью и особенно большим энерговыделением обладают реакция (n, p) на неустойчивых к позитронному распаду Я:
¹¹C(n, p)¹¹B + 2,77 МэВ,
²⁶Al(n, p)²⁶Mg + 4,79 МэВ и др.

Даже при очень малых энергиях интенсивно протекают нек-рые (n, $\alpha$ )-реакции, например, ⁶Li(n, $\alpha$ )³H + 4,78 МэВ, ¹⁰B(n, $\alpha$ )⁷Li + 2,79 МэВ, а также ¹¹C + n $\to \;3\alpha$ + 11,4 МэВ.

При низких энергиях сечение нерезонансного поглощения нейтронов в экзоэнергетических реакциях (n, $\gamma$ ), (p, $\gamma$ ), (n, $\alpha$ ) и др. подчиняются знаменитому (подтвержденному многочисленными экспериментами и теоретическими оценками) "закону 1/v", т.е. сечение обратно пропорционально относительной скорости нейтронов и Я или корню квадратному из энергии взаимодействия
$\sigma(\varepsilon)=C_1/v=C/\sqrt{\varepsilon}$ , (11)
где коэфф. C несколько изменяется с энергией нейтронов.

Экзоэнергетические нерезонансные Р между заряженными частицами отличаются от Р между Я и нейтронами в основном наличием в сечении дополнительного множителя, учитывающего проницаемость кулоновского барьера: величина $C/\sqrt{\varepsilon}$ в (11) имеет тот же физ. смысл, что и в (10).

В резонансных Р плавные зависимости (10) и (11) сечения от $\varepsilon$ нарушаются появлением резких максимумов (резонансов) значений коэфф. S и C при таких значениях $\varepsilon=\varepsilon_r$ , для к-рых энергия возбуждения составного Я равна энергии к.-л. его изолированного энергетич. уровня. Зависимость сечения от энергии вблизи изолированного резонанса описывается как для нейтральных, так и для заряженных частиц ф-лой Брейта-Вигнера (она приводится в учебниках по ядерной физике).

Энергию, необходимую для протекания Я.р., частицы звездного вещества приобретают в результате столкновений в процессе хаотического теплового движения. Я.р., эффективные лишь при достаточно высокой темп-ре вещества, наз. термоядерными реакциями. Для определения скорости термоядерной Р (число актов за ед. времени в ед. объема) необходимо усреднить произведение $\sigma v$ с учетом распределения частиц по относительным скоростям v, к-рое получается из распределения Максвелла заменой массы первой или второй частиц на приведенную массу M. С учетом того, что v² связано с $\varepsilon$ в системе ц.и. соотношением (2), вклад $\Delta P_{12}$ всех частиц 1 и 2, имеющих энергию относительного движения между $\varepsilon$ и $\varepsilon + \Delta\varepsilon$ , в полную скорость Р [в соответствии с (5)] равен
$\Delta P_{12}={n_1 n_2\over{1+\delta_{12}}}\cdot{2\over{kT}}\cdot\sqrt{{2\over{\pi M kT}}}\cdot\left[\sigma(\varepsilon)\cdot \varepsilon\cdot e^{-\varepsilon/kT}\right]\cdot\Delta\varepsilon$ . (12)
Полная скорость реакции P₁₂ находится суммированием всех $\Delta P_{12}$ [интегрированием (12) по всем значениям $\varepsilon$ от 0 до $\infty$ ]. Сравнение полученного таким путем P₁₂ с (5) дает искомое выражение для $<\sigma v>$ .

Рис. 2. Вид барьерного пика для главной
реакции углеродного цикла ¹⁴N(p, $\gamma$ )¹⁵O.
По вертикальной оси отложены значения функций,
обозначенных на рисунке цифрами:
1 - $10^8 \cdot\exp(-\varepsilon/kT)$ ;
2 - $10^{16} \cdot\exp(-\sqrt{\varepsilon_G/\varepsilon})$ при $T=2\cdot 10^7$ К;
3 - $10^{25} \cdot\exp(-\sqrt{\varepsilon_G/\varepsilon}-\varepsilon/kT)$ ; $\varepsilon_0/kT=18,7; \; \Delta\varepsilon_0/kT\approx 10$ .

Скорость термоядерной Р между заряженными частицами очень мала как при низких энергиях частиц $\varepsilon\le kT$ (вследствие трудности преодоления кулоновского энергетического барьера), так и при высоких энергиях $\varepsilon\gg kT$ (благодаря малому числу частиц с такими энергиями в случае максвелловского распределения частиц по скоростям). Поэтому существует определенный интервал энергий, в к-ром частицы взаимодействуют достаточно эффективно. Зависящая от энергии часть ф-лы (12) (выделена квадратными скобками) представляет собой с учетом (10) произведение двух экспонент - увеличивающейся с ростом $\varepsilon$ , барьерной, и уменьшающейся, максвелловской (рис. 2). При нек-рой энергии $\varepsilon_0$ это произведение достигает максимума [слабая зависимость $S(\varepsilon)$ не меняет существа дела], к-рый наз. барьерным пиком. Осн. вклад в полную скорость Р вносят частицы с энергиями в интервале $\varepsilon \pm \Delta\varepsilon_0$ . Согласно вычислениям
$\varepsilon_0=kT (\varepsilon_G/4kT)^{1/3}; \quad \Delta\varepsilon_0=4kT\sqrt{\varepsilon_0/3kT}$ . (13)

Структура барьерного пика такова, что интегрированием (12) т.н. методом "перевала" удается получить для $<\sigma v>$ аппрксимационную ф-лу высокой точности:
$<\sigma v>=4\sqrt{{2\varepsilon_0\over{3M}}}\cdot{S_э\over{kT}}\cdot e^{-3\varepsilon_0/kT}\sim T^{-2/3}\cdot \exp(-C/T^{1/3})$ , (14)
где S_э - эффективное значение слабо меняющейся ф-ции $S(\varepsilon)$ .

Особенность барьерного пика в том, что при характерных для недр звезд физ. условиях он располагается в области энергий, значительно превышающих ср. тепловую энергию частиц ( $\varepsilon \ge 10 kT$ ), и явл. довольно широким, поскольку $\Delta\varepsilon_0$ сравнимо по величине с $\varepsilon_0$ .

В случае нерезонансного взаимодействия нейтронов с Я выражение в квадратных скобках в (12) с учетом (11) достигает максимума при $\varepsilon=kT/2$ . Ширина этого максимума $\Delta\varepsilon\approx 2kT$ . Поэтому наиболее интенсивно реагируют нейтроны с энергиями, близкими к характерной тепловой энергии kT.

При взаимодействии заряженных частиц вклад резонансов в скорость термоядерной Р особенно существен тогда, когда их энергии попадают в интервал $\Delta\varepsilon_0$ (вблизи $\varepsilon_0$ ), в то время как при взаимодействии нейтронов наиболее эффективны резонансы с энергиями, близкими к kT.

При больших плотностях звездного вещества, достигаемых в процессе эволюции звезд, скорости Я.р. увеличиваются за счет экранирования положительного заряда Я отрицательно заряженными электронами. Электронное экранирование приводит к эффективному снижению кулоновского барьера и тем самым облегчает сближение Я. Этот эффект особенно значителен при плотностях $\rho\ge 10^6 \mbox{г/см}^3$ , когда в недрах звезд, несмотря на высокую темп-ру, электронный газ становится вырожденным (сильное экранирование). При отсутствии вырождения экранирование не столь эффективно (слабое экранирование). В случае очень больших плотностей эффект экранирования оказывается столь значительным, что Я.р. идут уже в основном не за счет высокой темп-ры, а благодаря снижению кулоновского барьера. Такие реакции иногда наз. пикноядерными.

7. Статически равновесные ядерные реакции

В недрах обычных звезд экзоэнергетические Я.р. - источники звездной энергии - протекают при темп-рах, для к-рых ср. энергия теплового движения частиц ниже как энергетического выхода Р, так и высоты кулоновского барьера ( $kT\ll Q, \varepsilon_c$ ). Поэтому скорость обратных пороговых Р ничтожно мала - в звездном веществе практически отсутствуют частицы с энергиями больше Q. Однако на заключительных стадиях эволюции достаточно массивных звезд, а также в процессе гравитац. коллапса звездных ядер темп-ра достигает значений $T> (3-6)\cdot 10^9$ К, при к-рых в веществе имеется уже довольно много частиц с энергиями, необходимыми для быстрого протекания как прямых, так и обратных реакций. Особенно интенсивно идут реакции (p, $\gamma$ ), (n, $\gamma$ ), ( $\alpha, \gamma$ ) и обратные им реакции фотоотщепления нуклонов и $\alpha$ -частиц от Я. Достаточно эффективными оказываются также прямые и обратные Р типа (p, n), (n, $\alpha$ ), (p, $\alpha$ ) и др. Путем последовательных фотоотщеплений нуклонов и $\alpha$ -частиц, а также обратных радиационных захватов Я с одними значениями (A, Z) превращаются в Я с другими (A, Z), и наоборот. В веществе появляются практически отсутствовавшие при более низких темп-рах свободные нейтроны, протоны и $\alpha$ -частицы. Устанавливаются вполне определенные равновесные концентрации различных Я (NSE). В условиях NSE массовая концентрация X_{A, Z} [ ${\rm X}_{A,Z}\equiv A n_{A,Z} m_u /\rho$ , где n_A,Z - число Я (A, Z) в ед. объема] Я любого вида связана с концентрациями свободных нейтронов X_n и протонов X_p соотношением, аналогичным известной формуле Саха для определения равновесной ионизации компонентов газа
${\rm X}_{A,Z}=\omega_{A,Z} A^{5/2} \cdot {1\over {2^A}}\cdot \left( {2\pi\hbar^2\over{m_u kT}}\right)^{{3\over 2} (A-1)}\cdot \left( {\rho\over{m_u}}\right)^{A-1} {\rm X}^{A-Z}_n {\rm X}^Z_p\exp\left({Q_{A,Z}\over {kT}}\right)$ , (15)
Здесь A - массовое число (число нуклонов в Я). Через Q_A,Z обозначена абс. величина связи атомного ядра (A, Z), а через $\omega_{A,Z}$ - его статистич. вес:
$\omega_{A,Z} =(2I_0+1)+\Sigma_r(2I_r+1) \exp\left(-\varepsilon_r /kT\right)$ , (16)
где I₀ - cпин осн. состояния, а суммирование производится по возбужденным состояниям с энергиями возбуждения $\varepsilon_r$ . Концентрация атомных ядер (A, Z), находящихся в к.-л. определенном возбужденном состоянии ${\rm X}_{A,Z}^r$ , задается ф-лой (15) с заменой $\omega_{A,Z}$ на $(2I_r+1) \exp\left(-\varepsilon_r /kT\right)$ (для осн. состояния r=0 и $\varepsilon_0=0$ ). Еще до установления NSE (на более ранних стадиях эволюции звезд) возникают такие условия, когда не все, а лишь нек-рые Я.р. уравновешиваются обратными реакциями. Иначе говоря, осуществляется частичное равновесие по Я.р. Примером может служить предшествующий NSE $\alpha$ -процесс (см. следующий раздел), а также Я.р. синтеза углерода из гелия. Если к.-л. Я.р. в точности уравновешивается обратной ей Я.р., то концентрации частиц, вступающих в Р, и частиц - продуктов Р оказываются связанными определенным соотношением, к-рое можно получить с помощью (15). Именно такое соотношение используется при расчете скорости синтеза углерода, осуществляющегося в две стадии:
3 ⁴He $\rightleftharpoons$ ¹²C* - 0,379 МэВ , (17)
¹²C* $\to$ ¹²C + 7,654 МэВ . (18)

В Р (17) из трех $\alpha$ -частиц образуется возбужденное Я углерода ¹²C* (I_r=0 $\varepsilon_r=7,654$ МэВ). Эта Р фактически явл. результатом двух последовательных резонансных Я.р., в к-рых возникает неустойчивое ядро ⁸Be: 2 ⁴He $\rightleftharpoons$ ⁸Be и ⁴He + ⁸Be $\rightleftharpoons$ ¹²C*. В подавляющем большинстве случаев ¹²C* распадается (через ⁸Be) на исходные $\alpha$ -частицы. Лишь в одном из 2500 случаев после испускания $\gamma$ -фотонов и электрон-позитронных пар ¹²C* переходит в конечный продукт гелиевых реакций - ядро ¹²C в осн. состоянии. Поэтому с большой точностью можно считать реакцию (17) равновесной и воспользоваться (15) для нахождения $n^*_{12}$ - числа ядер ¹²C* в ед. объема:
$n^*_{12}\equiv {\rm X}^*_{12}\cdot {\rho\over {12 m_u}} = 3^{3/2}\cdot \left( {\pi\hbar^2\over {m_u kT}} \cdot {{\rm X_{He}}\rho\over {8m_u}} \right)^3 \cdot e^{Q/kT}$ , (19)
где Q=-0,379 МэВ, а X_He - концентрация исходного гелия.

8. Термоядерная эволюция звезд

Термоядерные Р в звездах приводят к постепенному изменению хим. состава звездного вещества, что вызывает перестройку звезды и ее продвижение по эволюционному пути. Первый этап эволюции заканчивается истощением водорода в центральных областях звезды. Затем после повышения темп-ры, вызванного сжатием центральных слоев звезды, лишенных источников энергии, становятся эффективными термоядерные Р горения гелия, к-рые сменяются Р горения C, O, Si и последующих элементов - вплоть до Fe и Ni. Вследствие сильной зависимости подбарьерных термоядерных Р от темп-ры, на каждом очередном этапе гоерния темп-ра звездного вещества остается примерно постоянной. После источщения очередного ядерного горючего происходит повышение темп-ры и плотности до тех пор, пока не включаются новые термоядерные Р между Я - продуктами предыдущего этапа эволюции. Следовательно, каждому этапу звездной эволюции соответствуют определенные термоядерные Р. Первыми в цепи таких Я.р. стоят водородные термоядерные Р. Они протекают двумя путями в зависимости от начальной темп-ры T_c в центре звезды, к-рая связана с ее массой ${\mathfrak M}$ в момент достижения главной последовательности. При $T_c<1,7\cdot 10^6$ К ( ${\mathfrak M}\le 1,2 {\mathfrak M}_\odot$ ) основной оказывается цепочка реакций водородного цикла, тогда как при более высоких темп-рах преобладают Р углеродного цикла. Наиболее медленную Р каждого цикла (точнее, имеющую наименьшее значение $<\sigma v>$ ) наз. главной реакцией, поскольку именно она определяет темп горения водорода и связанного с ним энерговыделения. От скоростей остальных, более быстрых Р зависят лишь значения устанавливающихся квазистационарных концентраций участвующих в них Я, а также характеристики сопутствующего нейтринного излучения. Главная Р водородного цикла - первичная Р:
¹H + ¹H $\to$ ²D + e⁺ + $\nu$ , (20)
в к-рой происходит позитронный распад одного из протонов в момент сближения двух протонов на расстояние действия ядерных сил. Сечение этой Р определяется лишь теоретич. путем, т.к. из-за ее крайне малой вероятности невозможно выполнить соответствующие измерения в лаборатории. Для грубой оценки сечения этого сложного процесса можно воспользоваться ф-лой, имеющей ясный физ. смысл:
$\sigma\approx(4\pi b^2)\cdot \left( \sqrt{{\varepsilon_G\over{\varepsilon}}} \cdot e^{-\sqrt{\varepsilon_G/\varepsilon}} \right) \left( {2b\over v}\cdot {\ln 2\over{t_{1/2}}}\right)$ , (21)
где первый сомножитель равен сечению соударения ( $b=4,3\cdot 10^{-13}$ см - радиус дейтрона), второй описывает вероятность подбарьерного перехода, а третий - вероятность бета-процесса, к-рая равна произведению времени соударения 2b/v на вероятность бета-процесса за ед. времени ln2/t_1/2 (t_1/2 - время полураспада нейтрона). Третий сомножитель чрезвычайно мал: ~ 10^-23 при t_1/2= 630 с и v=10⁸ см/с. С учетом того, что $v\sim \sqrt{\varepsilon}$ , ф-лу (21) можно записать в стандартном виде (10).

В связи с проблемой солнечных нейтрино сечение Р (20) вычислялось самым тщательным образом с учетом различных поправок (радиационных, мезонных и др.). Для Р (20)
$<\sigma v>_{1,1}=6,33\cdot 10^{-39} \cdot T_9^{-2/3}\cdot e^{-3,38/T_9^{1/3}}\times\\ \times (1+0,123\;T_9^{1/3}+1,09\;T_9^{2/3}+0,938\;T_9)\;\mbox{см}^3/с$ , (22)
где $T_9=T/10^9$ К. Выражение в скобках учитывает слабую зависимость $S(\varepsilon)$ . Приближенное выражение (21) дает примерно в 3 раза большее значение $<\sigma v>_{1,1}$ по сравнению с (22), что позволяет пользоваться (21) при грубых оценках.

Синтез гелия из водорода в Р углеродного цикла протекает при участии катализаторов, роль к-рых играют малые примеси изотопов C, N и O в первоначальном звездном веществе. Главная Р в этом случае ¹⁴N(p, $\gamma$ )¹⁵O настолько медленнее остальных Р с участием C и O, что все первоначально имевшиеся изотопы C и O успевают быстро (по сравнению с характерным временем эволюции звезды) превратится в ¹⁴N. При темп-рах $(20-40)\cdot 10^6$ К, типичных для звезд главной последовательности, реакция ¹⁴N(p, $\gamma$ )¹⁵O идет нерезонансным образом (рис. 2).

Общий результат водородного или углеродного цикла можно записать в виде
4 ¹H $\to$ ⁴He +2v +26,73 МэВ ( $6,4\cdot 10^{18}$ эрг/г) . (23)
Часть освобождающейся в Р (23) энергии уносят нейтрино: $\approx$ 0,6 МэВ в водородном цикле и $\approx$ 1,7 МэВ в углеродном цикле на один образовавшийся атом гелия. Остальная энергия постепенно просачивается к поверхности звезды и поддерживает ее свечение многие миллионы и миллиарды лет.

Последующий синтез хим. элементов из гелия и возможной в звездных условиях примеси к нему водорода сильно затруднен. Дело в том, что в природе не существует ядра ⁵Li и поэтому столкновения между протонами и $\alpha$ -частицами к синтезу ядер не приводят.

Хим. элементы тяжелее ⁴He начинают синтезироваться лишь после полного выгорания водорода в центральной области звезды, когда темп-ра поднимается до $(2-3)\cdot 10^8$ К, а плотность увеличивается на 2-3 порядка и достигает 10³-10⁴ г/см³. В таких условиях становятся эффективными Р (17) и (18), итог к-рых можно представить в виде
3 ⁴He $\to$ ¹²C + 7,28 МэВ ( $5,85\cdot 10^{17}$ эрг/г) . (24)

В астрофизической литературе этот процесс принято называть 3 $\alpha$ -реакцией. Его скорость, т.е. число актов в ед. объема в ед. времени, равна отношению равновесной концентрации n*₁₂ из (19) к определенному из эксперимента времени жизни $\tau^*=1,8\cdot 10^{-13}$ с ядра ¹²C* по отношению к распаду (18):
$P_{3\alpha}=n^*_{12}/\tau^*=4,37\cdot 10^{13} \cdot\left({X_{He}\rho\over {T_9}}\right)^3\cdot e^{-4,4/T_9} \;[\mbox{актов/(см}^3 \cdot с)]$ . (25)

Одновременно с 3 $\alpha$ -реакцией в звездах может идти Р
⁴He + ¹²C $\to$ ¹⁶O + $\gamma$ + 7,16 МэВ . (26)
Ее скорость определяется нерезонансным вкладом уровней 7,12 и 6,92 МэВ составного ядра ¹⁶O. Соотношение между ¹²C и ¹⁶O - продуктами горения ⁴He - зависит от соотношений скоростей процессов (24) и (26). В наиболее массивных звездах ( ${\mathfrak M}\ge 40 {\mathfrak M}_\odot$ ) горение гелия происходит при относительно низкой плотности и более высокой темп-ре (по сравнению с менее массивными звездами), поэтому в таких звездах скорость Р (26) относительно велика. В этом случае за 3 $\alpha$ -реакцией всегда следует Р (26) и весь синтезированный в 3 $\alpha$ -реакции углерод превращается в кислород:
4 ⁴He $\to$ ¹⁶O + 14,44 МэВ ( $8,7\cdot 10^{17}$ эрг/г) . (27)
В результате в массивной звезде образуется кислородная сердцевина (кислородное звездное ядро). В синтезированном кислороде возможна небольшая примесь ²⁰Ne и ²⁴Mg, появляющихся в реакциях ¹⁶O( $\alpha, \gamma$ )²⁰Ne и ²⁰Ne( $\alpha, \gamma$ )²⁴Mg. В звездах средних масс ( $(10-30) {\mathfrak M}_\odot$ ) скорость Р (26) не так велика, чтобы весь углерод успел превратиться в кислород - к моменту исчерпания гелия концентрации ¹²C и ¹⁶O сравнимы. Внутри таких звезд образуются углеродно-кислородные (CO-) звездные ядра. В звездах малых масс ( $< 10 {\mathfrak M}_\odot$ ) Р (26) малоэффективна, и гелий превращается преимущественно в углерод.

Дальнейший ход термоядерной эволюции связан с реакциями горения углерода и кислорода. Электронный газ с CO-ядрах звезд малых масс сильно вырожден, и поэтому горение углерода в Я.р. (9) обладает рядом особенностей. Во-первых, эффект сиьлного электронного экранирования способствует значительному увеличению скорости Р, во-вторых, термоядерная Р протекает в веществе с малой теплоемкостью и, в-третьих, давление вещества слабо зависит от темп-ры. Два последних обстоятельства приводят к тому, что после того как при T~10⁹ К начинается выделение энергии в Я.р. (9), темп-ра быстро поднимается (до ~10¹⁰ К), скорость Р резко увеличивается, а их продукты начинают взаимодействовать между собой и с исходными ¹²C и ¹⁶O - горение углерода приобретает взрывной характер. Инициированная реакцией (9) разветвленная цепь термоядерных Р заканчивается образованием наиболее сильно связанных Я группы железа (см. Энергия связи) с выделением энергии ~ 10¹⁸ эрг/г. Горение углерода в вырожденных звездных ядрах считается наиболее вероятным механизмом взрывов по крайней мере части сверхновых звезд. В массивных звездах горение углерода происходит в невырожденном (или слабовырожденном) веществе, темп-ра к-рого стабилизируется условиями гидростатического равновесия на уровне $(5-7)\cdot 10^8$ К. Появляющиеся в Я.р. (9) $\alpha$ -частицы и протоны сразу же вступают в термоядерные Р с ¹²C, ¹⁶O, ²⁰Ne, ²³Na и продуктами этих Р. В конечном счете ядра ¹²C превращаются преимущественно в ²⁴Mg с примесью ¹⁶O, ²⁰Ne, ²⁸Si и нек-рых др. изотопов. Итог углеродных Р можно грубо представить в виде
2 ¹²C $\to$ ²⁴Mg + 13,93 МэВ ( $5,6\cdot 10^{17}$ эрг/г) . (28)
Последующее горение кислорода начинается при темп-ре $T\approx 2\cdot 10^9$ К реакциями
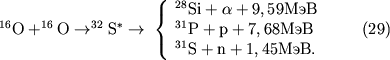
$^{16}\rm{O}+^{16}\rm{O}\to^{32}\rm{S}^*\to \;\left\{ \begin{array}{l} ^{28}\rm{Si}+\alpha+9,59 \mbox{МэВ}\\ ^{31}\rm{P+p}+7,68 \mbox{МэВ} \quad\quad\quad (29)\\ ^{31}\rm{S+n}+1,45 \mbox{МэВ} .\\ \end{array} \right.$
Нек-рый вклад могут вносить также др. каналы распада составного ядра ³²S*, напр. ³²S* $\to$ ³⁰Si + 2p, ²⁴Mg + 2 $\alpha$ . Цепочка вызванных процессом (29) ядерных превращений заканчивается образованием серы ³²S с примесью ²⁸Si и ³⁶Ar. Конечный результат можно приближенно записать в виде
2 ¹⁶O $\to$ ³²S + 16,54 МэВ ( $4,99\cdot 10^{17}$ эрг/г) . (30)

После того как горение кислорода заканчивается и темп-ра поднимается до $3\cdot 10^9$ К, начинается заключительный этап термоядерной эволюции. Из-за большого кулоновского барьера между двумя ядрами ³²S их взаимодействие оказывается неэффективным. Однако при таких темп-рах $\gamma$ -фотоны уже достаточно быстро (в звездном масштабе времени) отщепляют от ³²S и др. изотопов нйетроны, протоны и $\alpha$ -частицы, к-рые снова захватываются Я. Вскоре после начала фоторасщепления серы в заметной концентрации в звездном веществе остается наиболее устойчивый по отношению к фоторасщеплению изотоп ²⁸Si. Все остальные изотопы оказываются распределенными в широком интервале массовых чисел A вплоть до элементов группы железа, причем их концентрации уменьшаются с ростом A. Характерное время термоядерной эволюции на этом этапе определяется скоростью фоторасщепления кремния. В звездном веществе устанавливается состояние промежуточного равновесия (квазиравновесия) по Я.р.: имеющиеся в небольших концентрациях протоны, нейтроны и $\alpha$ -частицы интенсивно реагируют с различными изотопами в Р типа (p, $\gamma$ ), (n, $\gamma$ ), ( $\alpha, \gamma$ ), (p, n), (p, $\alpha$ ), (n, $\alpha$ ), причем каждая из Р такого типа с участием к.-л. изотопа (кроме ²⁸Si) приблизительно компенсируется обратной Р. В результате при заданной концентрации ²⁸Si концентрации др. изотопов оказываются связанными с концентрациями n, p и $\alpha$ -частиц определенными соотношениями (см. раздел 7).

По мере фоторасщепления ²⁸Si продолжается выделение энергии, темп-ра возрастает и в квазиравновесии все большее значение приобретают изотопы группы железа. Этот процесс наз. обычно $\alpha$ -процессом, поскольку наибольшие концентрации в условиях квазиравновесия имеют $\alpha$ -частичные изотопы, такие, как ²⁸Si, ³²S, ³⁶Ar, ⁴⁰Ca, ⁵⁶Ni и др., и в первом приближении его можно представить как перераспределение $\alpha$ -частиц между различными изотопами.

К концу $\alpha$ -процесса темп-ра поднимается до $(4-5)\cdot 10^9$ К и наступает конечное состояние термоядерной эволюции массивных звезд - ядерное статистич. равновесие (NSE). Суммарное энерговыделение при переходе от ³²S к NSE составляет $\approx 2,5\cdot 10^{17}$ эрг/г.

Внутри массивных звезд образуются железные звездные ядра, к-рые в конце концов теряют устойчивость и переходят в состояние гравитац. коллапса, заканчивающегося образованием нейтронных звезд и, возможно, черных дыр. Первостепенную роль при этом начинают играть управляемые слабым взаимодействием Я.р. электронов, позитронов и нейтрино с Я, нейтронами и протонами. Такие Я.р. описываются теорией слабых взаимодействий. На св-ва звездного начинают существенно влиять два обстоятельства: вырождение электронного газа и присутствие Я в различных возбужденных состояниях. Эти обстоятельства учитываются при решении таких астрофизич. проблем, как, напр., происхождение хим. элементов, нейтронизация звездного вещества и нейтринное излучение звезд.

9. Заключение

Термодинамические Р, происходящие в глубоких недрах звезд, обусловливают их эволюцию от стадии звездообразования до конечных стадий взрыва и коллапса. Но существуют и др. физ. условия, в к-рых Я.р. могут быть также источником энергии и причиной многих космич. явлений. К таким явлениям относятся, напр., вспышки новых a000">барстеры. Их объясняют align="absmiddle" width="43" height="15" > К. Несмотря на усложнение картины термоядерного существенно

Кинетич. энергия частиц, необходимая для осуществления Я.р., конечно, не обязательно связана с тепловым движением частиц. Тем более не обязательно равновесное (максвелловское) распределение частиц по скоростям. Если не ограничиваться рассмотрением только глубоких звездных недр, то в определенных астрофиз. условиях, в особенности в разреженных оболочках и атмосферах звезд, могут действовать неравновесные газодинамические и электродинамические процессы "холодного" ускорения Я и элементарных частиц. С приобретением достаточно больших энергий ускоренные частицы могут осуществить Я.р. синтеза не термоядерного характера. Не исключены в астрофизических условиях также Я.р. деления. Процессы деления Я играют, по-видимому, существенную роль при выбросе вещества из глубоких слоев нейтронных звезд на определенных стадиях их эволюции. Это связано с тем, что вещество внутри нейтронных звезд состоит, по всей вероятности, из свободных нейтронов, сильно нейтронизованных ядер (с очень большими значениями массовых чисел A) и релятивистских вырожденных электронов. Попав при выбросе в разреженное вещество, эти Я после неск. последовательных бета-распадов оказываются неустойчивыми по отношению к Я.р. деления. Такой процесс может быть существенным в природе гамма-барстеров, а также в нуклеосинтезе самых тяжелых из существующих атомных Я. В синтезе тяжелых элементов, расположенных за железным пиком (см. Распространенность элементов), очень важную роль играют Я.р. с нейтронами.

Лит.:
Широков Ю.М., Юдин Н.П., Ядерная физика, 2 изд., М., 1980; Внутреннее строение звезд, под ред.Л. Аллера и Д.Б. Мак-Лафлина, пер. с англ., М., 1970; Фаулер У., Хойл Ф., Нейтринные процессы и образование пар в массивных звездах и сверхновых, пер. с англ., М., 1967; Тейлер Р.Дж., Происхождение химических элементов, пер. с англ., М., 1975; Essays in nuclear astrophysics, ed. by C.A. Barnes, D.D. Clayton, D.N. Schramm, Camb., 1982; Fowler W.A., Caughlan G.R., Zimmerman B.A., Thermonuclear reaction rates. 2, "Annual review of astronomy and astrophysics", 1975, v. 13, p. 69.

(В.С. Имшенник, Д.К. Надежин)

В. С. Имшенник, Д. К. Надежин, "Физика Космоса", 1986
Глоссарий Astronet.ru