 |
Астронет: Н. Г. Бочкарев, "Физика Космоса", 1986 Ионизация http://www.astronet.ru/db/msg/1188296 |
Ионизация
- отрыв от атомов, молекул, атомных или молекулярных ионов электрона (электронов) или заменяющих его частиц, напр. в мезоатомах и мезомолекулах - мезонов.Обычно ионизуемые системы находятся в состояниях с отрицат. полной энергией, В этом случае на отрыв частицы требуется затратить энергию. Как правило, И. происходит либо вследствие поглощения фотона (фотоионизация), либо под действием ударов частиц. Кроме того, атом может быть ионизован в результате того, что центральная часть его резко меняет свою скорость, так что внешние, слабо связанные с атомным остатком электроны "не успевают" за этим движением и "стряхиваются" (эффект стряхивания). Такой процесс возможен, напр., если ядро атома испытало радиоактивный распад или взаимодействовало с энергичной частицей, передавшей ядру значит. импульс.
Иногда ионизуемые системы могут находиться в неустойчивом состоянии с положит. полной энергией (автоионизационные состояния). В этом случае возможна самопроизвольная ионизация - автоионизация - выброс одного или неск. электронов.
В многоэлектронных системах при И. может быть оторван любой электрон. Обычно до ионизации
либо все электроны находятся в состояниях с наименьшими возможными энергиями (основное
состояние системы), либо один из электронов находится на более высоком уровне энергии (одноэлектронное возбуждённое состояние или просто
возбуждённое состояние). Миним. энергия, необходимая в этом случае для И., наз. энергией
связи уровня. Для атома водорода энергия связи уровня n равна: ![]() эВ. Энергия связи осн. уровня наз. потенциалом И. Потенциалы И. атомов колеблются
от 3,89 эВ для цезия до 24,59 эВ для гелия. Для ионов они больше, чем для атомов.
Потенциалы
И. молекул, как правило, не превышают потенциалов И. составляющих их атомов.
эВ. Энергия связи осн. уровня наз. потенциалом И. Потенциалы И. атомов колеблются
от 3,89 эВ для цезия до 24,59 эВ для гелия. Для ионов они больше, чем для атомов.
Потенциалы
И. молекул, как правило, не превышают потенциалов И. составляющих их атомов.
Если от ионизуемой системы отрывается не самый внешний электрон, а внутренний, обладающий
большей энергией связи, то на И. затрачивается больше энергии. Самую большую энергию
приходится затратить на отрыв электрона с самого внутреннего, ближайшего к ядру электронного
слоя. называемого К-слоем. Напр., для нейтрального кислорода (OI) потенциал И.
К-слоя ![]() = 553 эВ, а для железа (FeI)
= 553 эВ, а для железа (FeI) ![]() = 6,4 кэВ.
= 6,4 кэВ.
После И. атома или иона с одного из внутр. слоев (К- или для сложных атомов L-, Х-слоёв) ион оказывается в автоионизац. состоянии. Образовавшаяся вакансия может заполниться либо при испускании фотона, называемого характеристическим и попадающего обычно в рентг. область спектра, либо безызлучательным способом, когда избыток энергии передается одному или нескольким электронам и они выбрасываются из иона (автоионизация).
Процесс безызлучательного заполнения вакансий во внутр. электронных слоях атомов и ионов наз. эффектом Оже. В результате эффекта Оже и за счёт эффекта стряхивания внеш. электронов из атома часто выбрасывается не один, а много электронов. Характеристич. фотоны испускаются с большей вероятностью после И. внутр. слоев элементов второй половины периодич. системы Менделеева, а эффект Оже преобладает для более лёгких элементов.
Автоионизац. состояния и автоионизация возникают также в случае, если на достаточно высоких уровнях энергии атома (иона) одновременно находится более одного электрона, возбуждённого из внеш. слоя (валентные электроны атома или иона). В космич. условиях такого типа дважды возбуждённые автоионизац. состояния возникают гл. обр. в процессе диэлектронной рекомбинации, а в лабораторной плазме - при облучении среды мощными лазерными пучками света.

|
|
Рис. 1. а - зависимость от энергии электронов с основного уровня ударами электронов, потенциал ионизации водорода. Сечение выражено в величинах площади первой боровской орбиты б - зависимость сечения фотоионизации основном состоянии, от длины волны фотона Указаны порог ионизации невозбуждённого атома внутренних L- и K-слоев ( |
Эффективность И. частицей с энергией ![]() или фотоном
с
или фотоном
с ![]() , как и эффективность др. элементарных процессов,
характеризуется
эффективным поперечным сечением
, как и эффективность др. элементарных процессов,
характеризуется
эффективным поперечным сечением ![]() этого процесса,
имеющим размерность площади. Значение
этого процесса,
имеющим размерность площади. Значение ![]() равно нулю при
равно нулю при ![]() и
и ![]() при
при ![]() для
соответствующего электрона. В случае И. частицами (электронами, атомами, ионами)
для
соответствующего электрона. В случае И. частицами (электронами, атомами, ионами)
![]() максимально для отрыва внеш. валентных электронов и мало для внутр. электронов. Причём
сечение И. наибольшее (И. происходит наиболее эффективно) обычно при скоростях ионизующей
частицы, близких к орбитальной скорости ионизуемого электрона в модели атома Бора.
Это приводит к тому, что И. электронами эффективна при энергиях 1,5-10
максимально для отрыва внеш. валентных электронов и мало для внутр. электронов. Причём
сечение И. наибольшее (И. происходит наиболее эффективно) обычно при скоростях ионизующей
частицы, близких к орбитальной скорости ионизуемого электрона в модели атома Бора.
Это приводит к тому, что И. электронами эффективна при энергиях 1,5-10![]() (рис.
1,а), а тяжёлыми частицами - при много больших энергиях. В результате И. частицей
от ионизуемой системы может быть оторвано более одного электрона (даже без эффекта
Оже) -
многоэлектронная И., но вероятность этого мала (обычно меньше 1% от вероятности одноэлектронной
И.).
(рис.
1,а), а тяжёлыми частицами - при много больших энергиях. В результате И. частицей
от ионизуемой системы может быть оторвано более одного электрона (даже без эффекта
Оже) -
многоэлектронная И., но вероятность этого мала (обычно меньше 1% от вероятности одноэлектронной
И.).
Частота парных столкновений частиц двух сортов, т.е. число столкновений в 1 см3
в 1 с, пропорциональна концентрации (количеству в 1 см3)
частиц каждого сорта, их относительной скорости и размерам сталкивающихся частиц.
Частота парных столкновений, приводящих к И., пропорциональна не размерам частиц,
а сечению
И. ![]() . Если оба сорта сталкивающихся частиц принимают участие в
тепловых движениях (напр., столкновения электронов с атомами или ионами среды, но
не столкновения
частиц космических лучей с частицами среды),
то распределение скоростей их движения v, как правило, описывается Максвелла распределением. Тогда скорость И. атомов, молекул или
ионов с концентрацией Ni, электронами с концентрацией
Ne
равна
. Если оба сорта сталкивающихся частиц принимают участие в
тепловых движениях (напр., столкновения электронов с атомами или ионами среды, но
не столкновения
частиц космических лучей с частицами среды),
то распределение скоростей их движения v, как правило, описывается Максвелла распределением. Тогда скорость И. атомов, молекул или
ионов с концентрацией Ni, электронами с концентрацией
Ne
равна
NiNeqi(T),
(1)
где коэффициент И. qi (см3/с)
явл. усреднённым по максвелловскому распределению скоростей произведением ![]() . Для самого распространённого во Вселенной элемента - водорода при И. с
осн. уровня электронами
. Для самого распространённого во Вселенной элемента - водорода при И. с
осн. уровня электронами
![]() , (2)
, (2)
![]() , (3)
, (3)
где ![]() - потенциал И. водорода, Т - темп-ра в Кельвинах. Численные
значения qi приведены в таблице.
- потенциал И. водорода, Т - темп-ра в Кельвинах. Численные
значения qi приведены в таблице.
В случае И. фотонами ![]() часто имеет наибольшее значение
у порога И.
часто имеет наибольшее значение
у порога И. ![]() и далее падает с ростом
и далее падает с ростом ![]() .
Однако фотоны эффективно ионизуют атомы и ионы не только с внеш., но и с внутр. слоев
(если, конечно, достаточна энергия фотона). В результате этого полная эффективность
И.
возрастает скачками (рис. 1,6) при увеличении
.
Однако фотоны эффективно ионизуют атомы и ионы не только с внеш., но и с внутр. слоев
(если, конечно, достаточна энергия фотона). В результате этого полная эффективность
И.
возрастает скачками (рис. 1,6) при увеличении ![]() до потенциалов
И. внутр. электронов, т.е. до
до потенциалов
И. внутр. электронов, т.е. до ![]() и т.д.
и т.д.
Зависимость от температуры Т коэффициента ионизации qi (см3/с) атомов водорода с основного уровня энергии (ударами электронов).
|
|
Поскольку хим. состав космич. вещества везде, за исключением нек-рых звёзд, почти
одинаков, можно найти эффективное сечение ![]() поглощения УФ-
и рентг.
излучения в неионизованной космич. среде со средним хим. составом в расчёте на один
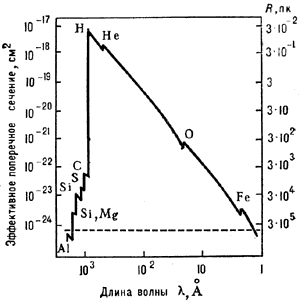
атом водорода (рис. 2):
поглощения УФ-
и рентг.
излучения в неионизованной космич. среде со средним хим. составом в расчёте на один
атом водорода (рис. 2):
![]() , (4)
, (4)
где Z - номер элемента в периодич. системе элементов Менделеева, ![]() - сечение фотоионизации атома этого элемента с осн. уровня фотонами
с энергией
- сечение фотоионизации атома этого элемента с осн. уровня фотонами
с энергией ![]() - обилие
элемента Z (отношение его концентрации к концентрации атомов водорода).
- обилие
элемента Z (отношение его концентрации к концентрации атомов водорода). ![]() и т.д. Несмотря на малое обилие элементов тяжелее гелия
(для каждого из них AZ < 0,001), они, как видно
из рис. 2,
дают значит. вклад в поглощение рентг. лучей. Связано это с очень высокой эффективностью
фотоионизации K-слоев атомов. Поэтому
и т.д. Несмотря на малое обилие элементов тяжелее гелия
(для каждого из них AZ < 0,001), они, как видно
из рис. 2,
дают значит. вклад в поглощение рентг. лучей. Связано это с очень высокой эффективностью
фотоионизации K-слоев атомов. Поэтому ![]() испытывает заметные
скачки при значениях
испытывает заметные
скачки при значениях ![]() для ряда элементов, указанных на
рис. 2. Знание
для ряда элементов, указанных на
рис. 2. Знание ![]() позволяет определить, какое расстояние способны
пройти
в среде фотоны с разными длинами волн до момента их поглощения. Напр., оказывается,
что фотоны с длинами волн от неск. десятков
позволяет определить, какое расстояние способны
пройти
в среде фотоны с разными длинами волн до момента их поглощения. Напр., оказывается,
что фотоны с длинами волн от неск. десятков ![]() до 912
до 912 ![]() столь
интенсивно ионизуют межзвёздный газ, что не могут пройти даже поперёк галактич. газового
диска.
столь
интенсивно ионизуют межзвёздный газ, что не могут пройти даже поперёк галактич. газового
диска.
|
|
Рис. 2. Эффективное поперечное сечение фотоионизации нейтрального межзвёздного газа усреднённого галактического состава, излучения. R - расстояние, соответствующее оптической толще Штриховой линией отмечено значение томсоновского сечения. |
Из сказанного выше следует, что атомы, а иногда и молекулы, имеющие много электронов,
в результате одного акта И. или при последовательных актах И. могут оказаться в разных
состояниях И., характеризуемых зарядом иона в единицах заряда протона. Состояние
И. указывается либо величиной и знаком заряда, напр. О+,
О3+,
О2-, Fe+24, H![]() ,
Н2О-, либо, в случае положительно
заряженных
ионов, в виде спектроскопич. символа, напр. для указанных выше ионов кислорода и
железа - ОII, OIV, FeXXV. Здесь римской цифрой указывается число, на единицу большее
заряда
иона. Цифра I соответствует нейтральному атому.
,
Н2О-, либо, в случае положительно
заряженных
ионов, в виде спектроскопич. символа, напр. для указанных выше ионов кислорода и
железа - ОII, OIV, FeXXV. Здесь римской цифрой указывается число, на единицу большее
заряда
иона. Цифра I соответствует нейтральному атому.
Атомы могут быть ионизованы до голых ядер. Молекулы не бывают сильно заряженными, т.к. в этом случае они становятся неустойчивыми и распадаются (диссоциируют). Максимально возможный отрицат. заряд иона определяется сродством к электрону и ни в каких случаях не превышает трёх электронных зарядов.
В условиях, близких к термодинамическому равновесию, напр. внутри звёзд и в фотосферах нормальных звёзд, степень И. атомов определяется Саха формулой, согласно к-рой степень И. любого атома растёт с увеличением темп-ры и падает с ростом плотности газа (точнее, с ростом концентрации электронов).
В космич. условиях нередки случаи, когда степень И. газа определяется И. электронами и радиационной плюс диэлектронной рекомбинациями. Такая ситуация возникает в достаточно разреженной горячей среде вне мощных полей жёсткого эл.-магн. излучения (УФ- и рентг. лучей) и при отсутствии сильных потоков космич. лучей. Такие условия характерны, напр., для солнечной хромосферы и солнечной короны и вообще верхних атмосфер звёзд многих типов, а также для оболочек сверхновых звёзд, межгалактич. газа в скоплениях галактик (см. Ионизационное равновесие). В этих условиях степень И. среды зависит только от её темп-ры Т (увеличиваясь с ростом Т), но не зависит от плотности среды.
В космич. условиях наибольшая степень И. встречается в недрах звёзд, в остатках сверхновых звёзд, в горячих областях межзвёздного газа с Т ~ 1 млн. К, в межгалактич. газе скоплений галактик, где Т ~ 100 млн. К, а также в газовых оболочках ряда рентг. источников и на внутр. краях аккреционных газовых дисков вокруг нейтронных звезд и чёрных дыр.
Лит.:
Мартынов Д.Я., Курс общей астрофизики, 3 изд., М., 1979; Каплан С.А., Пикельнер С.Б.,
физика межзвездной среды, М., 1979; Соболев В. В., Курс теоретической астрофизики,
2
изд., М., 1975.
(Н.Г. Бочкарев)
Н. Г. Бочкарев, "Физика Космоса", 1986
Глоссарий Astronet.ru