Астронет > Что померил WMAP

Астронет: С. А. Павлюченко/ГАИШ Что померил WMAP
http://variable-stars.ru/db/msg/1187213/wmap.html

Что измерил WMAP.

В середине февраля 2003-го года были опубликованы обработанные результаты, полученные в результате работы спутника WMAP (Wilkinson Microwave Anisotropy Probe). Эти работы были прокомментированы (на русском языке тут и тут), теперь же попытаемся разобраться в том, какие космологические параметры можно определить, используя данные WMAP'а, и что они означают. На самом деле, при определении космологических параметров используют не только данные WMAP'а, но также данные других экспериментов -- как по реликтовому излучению (вернее, по его анизотропии), так и иных -- по сверхновым, крупномасштабной структуре, ...

На самом деле космологические параметры приводятся для конкретной взятой космологической модели. Простейшей моделью, рассмотренной при анализе данных WMAP'а, была плоская Вселенная, заполненная излучением, барионами, холодной темной материей и в которой присутствует космологическая постоянная. Такая модель прекрасно описывается шестью космологическими параметрами: постоянной Хаббла h (в величинах 100 км/с/Мпк, то есть, если H= 70 км/с/Мпк, то h=0.7), плотностью материи $\Omega_m h^2$ и барионов $\Omega_b h^2$ , оптической толщей до сферы последнего рассеяния $\tau$ , скалярным спектральным индексом $n_S$ и нормировочным множителем для перехода от величин, в которых работает программа CMBFAST, с помощью которой строились рассчетные кривые к наблюдаемым. Метод определения космологических параметров таков: имея наблюдаемую картину, строим с помощью CMBFAST различные кривые и смотрим, при каких значениях параметров наблюдается наилучшее согласие теории и эксперимента. Для описанной выше модели эти параметры таковы:

Параметр Обозначение
Величина

плотность барионов
$\Omega_b h^2$
$0.024 \pm 0.001$

плотность материи
$\Omega_m h^2$
$0.14 \pm 0.02$

постоянная Хаббла
h
$0.72 \pm 0.05$

оптическая толща
$\tau$
$0.166^{+0.076}_{-0.071}$

спектральный индекс
$n_S$
$0.99 \pm 0.04$

нормиров. множитель
A
$0.9 \pm 0.1$

Ниже приведен расширенный набор космологических параметров, который получается из предыдущего после некоторых вычислений.

Параметр
Величина

амплитуда флуктуаций плотности
$\sigma_8 = 0.9 \pm 0.1$

амплитуда флуктуаций скоростей $\sigma_8 \Omega_m^{0.6} = 0.44 \pm 0.10$

плотность барионов / крит. плотность
$\Omega_b = 0.047 \pm 0.006$

плотность материи / крит. плотность $\Omega_m = 0.29 \pm 0.07$

возраст Вселенной
$t_0 = 13.4 \pm 0.3$ млрд. лет

красной смещение на момент рекомбинации $z_{dec} = 1088^{+1}_{-2}$

возраст Вселенной на момент рекомбинации $t_{dec} = 372 \pm 14$ тыс. лет

отношение числа фотонов к числу барионов
$\eta = (6.5^{+0.4}_{-0.3}) \times 10^{-10}$

Ниже приведен график с данными WMAP'а и рассчитанным спектром анизотропии РИ, наилучшим образом согласующимся с наблюдениями.

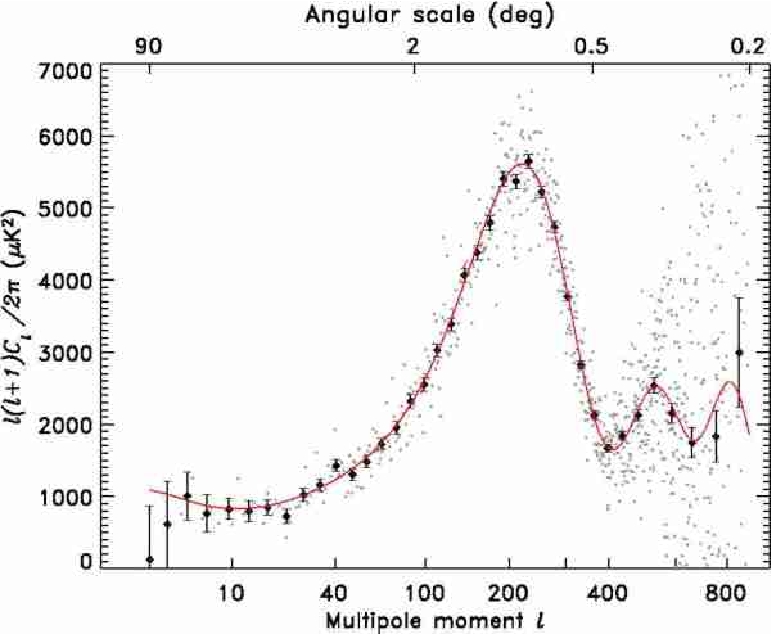
Прокомментируем некоторые из этих параметров.

Постоянная Хаббла

Пожалуй, самый известный космологический параметр, определяющий скорость расширения Вселенной в наши дни. Величина, полученная WMAP'ом ( $0.72 \pm 0.05$ ), находится в хорошем согласии с данными других экспериментов по определению постоянной Хаббла (в основном, Hubble Key Project).

Амплитуды флуктуаций

Величины $\sigma_8$ , $\sigma_8 \Omega_m^{0.6}$ ( $\sigma_8 \Omega_m^{0.5}$ ) описывают соответственно амплитуды флуктуаций плотности и скоростей галактик (их скоплений) в радиусе 8 Мпк от нас. Измерения эффектов слабого линзирования и пекулярных скоростей оказываются чуствительны к величине $\sigma_8 \Omega_m^{0.6}$ , а "обильность" скоплений галактик на малых z -- к очень близкой велчине $\sigma_8 \Omega_m^{0.5}$ .
Сама велчина $\sigma$ определяется следующим образом:
$\sigma (R) \frac{\delta M}{M} (R) = \int\limits_{\Omega} \frac{\delta \rho}{\rho} (\vec r) d^3 r$ ,
где $\delta M$ - флуктуации массы, а $\delta \rho$ - флуктуации плотности. Далее, определяя величину
$\vec {\cal P} = \frac{3 a}{4 \pi} \int \frac{\delta \rho}{\rho} (r,\theta,\varphi) d^3r \frac{\vec r}{r^3}$ ,
можно определить флуктуацию скоростей
$\vec V = \vec {\cal P} \cdot H \cdot \frac{1}{3} f(\Omega_m)$ .
Кстати говоря, с ее помощью можно определить $\Omega_m$ из данных по крупномасштабной структуре Вселенной -- данные показывают, что можно считать, что $f(\Omega_m) \approx \Omega_m^{\alpha}$ , где $\alpha = 0.56$ (при этом предполагается, что $\Omega_m \geqslant 0.1$ ). Но при этом важно понимать, что это только подгонка под такую степенную зависимость, а не какое-то фундаментальное свойство природы.

Обилие барионов

Величина, очень жестко определяемая из первичного нуклеосинтеза. Кроме того, очень сильно влияет на высоту первого пика в угловом спектре анизотропии реликтового излучения. Так что эта величина, определяемая довольно точно. Ее же можно получить из анализа $L_{\alpha}$ -леса, а также из наблюдений далеких квазаров и галактик (по их спектрам).

Возраст Вселенной

Интересная вещь -- возраст Вселенной все уменьшается и уменьшается, как это не парадоксально ! Действительно, сразу после открытия ускоренного расширения Вселенной из анализа данных по сверхновым типа Ia только по ним оценки возраста были $14.9 \pm 0.9$ млрд. лет; после недавнего эксперимента ARCHEOPS по данным как ARCHEOPS'а, так и других экспериментов по РИ, сверхновым, крупномасштабной структуре, линзированию, ... он составлял уже ~13.7 млрд. лет; сейчас же, по данным WMAP'а он составляет $13.4 \pm 0.3$ млрд. лет. При этом интересны другие оценки возраста Вселенной, сделанные по возрастам различных объектов (они дают минимально возможный возраст Вселенной, ведь не могут же звезды быть старше Вселенной !). Так вот, по возрастам белых карликов возраст Вселенной не должен быть меньше $12.7 \pm 0.7$ млрд. лет, по возрастам шаровых звездных скоплений (ШЗС) -- не менее 11 - 16 млрд. лет, по распаду радиоактивных веществ -- не менее 9.5 - 20 млрд. лет. Но два последних метода жутко неточные, так что на то, что по их данным Вселенная должна быть старше, можно не обращать внимания.

Спектральный индекс

Величина, характеризующая спектр возмущений. Инфляционная теория предсказывает плоский спектр $n_S = 1$ -- так называемый спектр Харрисона-Зельдовича (на самом деле не точно 1, но можно так считать). Так что отличие ее от 1 если не ставит под удар инфляционную теорию, то по крайней мере требует объяснить сей феномен. Чуть ниже мы еще вернемся к этому. Если же мы примем во внимание не только данные WMAP'а, но и другие космологические тесты, то получим следующую картину:

только WMAP
WMAP+CBI+ACBAR
то же +2dFGRS
то же + $L_{\alpha}$ -лес

$n_S$ $0.99 \pm 0.04$
$0.97 \pm 0.03$
$0.97 \pm 0.03$ $0.96 \pm 0.02$

$\tau$ ${0.166}^{+0.076}_{-0.071}$
${0.143}^{+0.071}_{-0.062}$
${0.148}^{+0.073}_{-0.071}$ ${0.117}^{+0.057}_{-0.053}$

h
$0.72 +/- 0.05$
$0.73 +/- 0.03$
$0.73 +/- 0.03$ $0.72 +/- 0.03$

$\Omega_m h^2$ $0.14 +/- 0.02$
$0.13 +/- 0.01$
$0.134 +/- 0.006$
$0.133 +/- 0.006$

$\Omega_b h^2$ $0.024 +/- 0.001$
$0.023 +/- 0.001$ $0.023 +/- 0.001$ $0.0226 +/- 0.0008$

Видно, что другие эксперименты "корректируют" значения космологических параметров, получаемых из данных WMAP'а. При этом из последнего столбика видно, что при добавлении данных по $L_{\alpha}$ -лесу у нас серьезно меняется индекс спектра скалярных возмущений. Это было одним из открытий WMAP'а, пока его не "закрыли". Дело в том, что данные по $L_{\alpha}$ -лесу крайне неточны, и комбинирование их с довольно точными данными экспериментов по РИ, в первую очередь, самого WMAP'а, не приведет ни к чему хорошему. Именно этим -- крайней неточностью данных по $L_{\alpha}$ -лесу и вызвано это "открытие".
Вторым открытием WMAP'а (на этот раз уже настоящем) стало то, что оптическая толща до сферы последнего рассеяния не равна 0! Это означает, что в нашей Вселенной была вторичная ионизация (первичная -- это та, которая была до рекомбинации). В последнее время появилось немало работ, посвященных этой теме, и подавляющее большинство авторов сходятся на том, что вторичная ионизация обусловлена звездами III поколения. Это первые звезды во Вселенной, образовывавшиеся на z ~ 20 (для примера -- галактики начали образовываться на z ~ 6, именно поэтому мы и не видим более далеких объектов), когда еще никаких галактик не было и в помине. Так что данные о том, что оптическая толща до сферы последнего рассеяния не равна 0 можно считать свидетельством существования звезд III поколения.

Вот такие результаты принес нам WMAP -- более точные космологические параметры, одно несостоявшееся и одно вполне состоявшееся открытия.

Параметр	Обозначение	Величина
плотность барионов	$\Omega_b h^2$	$0.024 \pm 0.001$
плотность материи	$\Omega_m h^2$	$0.14 \pm 0.02$
постоянная Хаббла	h	$0.72 \pm 0.05$
оптическая толща	$\tau$	$0.166^{+0.076}_{-0.071}$
спектральный индекс	$n_S$	$0.99 \pm 0.04$
нормиров. множитель	A	$0.9 \pm 0.1$

Параметр	Величина
амплитуда флуктуаций плотности	$\sigma_8 = 0.9 \pm 0.1$
амплитуда флуктуаций скоростей	$\sigma_8 \Omega_m^{0.6} = 0.44 \pm 0.10$
плотность барионов / крит. плотность	$\Omega_b = 0.047 \pm 0.006$
плотность материи / крит. плотность	$\Omega_m = 0.29 \pm 0.07$
возраст Вселенной	$t_0 = 13.4 \pm 0.3$ млрд. лет
красной смещение на момент рекомбинации	$z_{dec} = 1088^{+1}_{-2}$
возраст Вселенной на момент рекомбинации	$t_{dec} = 372 \pm 14$ тыс. лет
отношение числа фотонов к числу барионов	$\eta = (6.5^{+0.4}_{-0.3}) \times 10^{-10}$

	только WMAP	WMAP+CBI+ACBAR	то же +2dFGRS	то же + $L_{\alpha}$ -лес
$n_S$	$0.99 \pm 0.04$	$0.97 \pm 0.03$	$0.97 \pm 0.03$	$0.96 \pm 0.02$
$\tau$	${0.166}^{+0.076}_{-0.071}$	${0.143}^{+0.071}_{-0.062}$	${0.148}^{+0.073}_{-0.071}$	${0.117}^{+0.057}_{-0.053}$
h	$0.72 +/- 0.05$	$0.73 +/- 0.03$	$0.73 +/- 0.03$	$0.72 +/- 0.03$
$\Omega_m h^2$	$0.14 +/- 0.02$	$0.13 +/- 0.01$	$0.134 +/- 0.006$	$0.133 +/- 0.006$
$\Omega_b h^2$	$0.024 +/- 0.001$	$0.023 +/- 0.001$	$0.023 +/- 0.001$	$0.0226 +/- 0.0008$