 |
Астронет: Р. З. Дурлевич, "Физика Космоса", 1986 Альвеновские волны http://www.astronet.ru/db/msg/1186368 |
Альвеновские волны
АЛЬВЕНОВСКИЕ ВОЛНЫ - поперечные магнитогидродинамические волны, распространяющиеся вдоль силовых линий магн. поля. Названы в честь швед. астрофизика X. Альвена, предсказавшего в 1942 г. их существование. В А. в. в колебаниях участвует не только эл.-магн. поле, но и частицы проводящей среды, т. е. А. в. возможны лишь при наличии магн. поля и проводящей среды, ведущей себя как единая жидкость или газ. Последнее условие нарушается, если частота колебаний среды ω становится сравнимой или превосходит ионную циклотронную частоту ωHi, т. к. при таких частотах поведение ионов и свободных электронов среды оказывается различным. Т. о., частоты А. в. ограничены сверху значением ωHi, и в этом смысле их можно назвать низкочастотными.
Для того чтобы магн. поле А. в. не очень
быстро затухало, среда должна обладать
достаточно высокой проводимостью σ.
Характерное время затухания магн. поля в
масштабах порядка длины волны λ,
равное t0 = 4πσλ2/с2
(см. Магнитогидродинамика),
должно быть много больше периода колебаний
Р = 2π/ω = λ/vA
(vA - скорость А. в.). При этом магн.
силовые линии колеблются вместе со средой
("вмороженность" силовых линий).
Колебания среды также должны затухать не
очень быстро. Для этого её кинематическая
вязкость v должна быть достаточно малой
(время вязкого затухания колебаний с
масштабом ~λ порядка λ2/v).
Условие малости затухания А. в. за счёт этих
двух эффектов можно записать в виде ![]() или
или
![]() , где vM= с2/4πσ
- т. н.
магнитная вязкость.
Видно, что неравенство лучше выполняется
для низких частот (больших длин волн), и по
этой причине оно легче реализуется в космич.
масштабах, чем в лабораторных условиях.
, где vM= с2/4πσ
- т. н.
магнитная вязкость.
Видно, что неравенство лучше выполняется
для низких частот (больших длин волн), и по
этой причине оно легче реализуется в космич.
масштабах, чем в лабораторных условиях.
Для иллюстрации сущности А. в. часто
прибегают к аналогии между вмороженными в
среду силовыми линиями маги. поля Н и
натянутыми струнами или резиновыми жгутами.
Вдоль силовой линии поля, так же как и вдоль струны,
может распространяться поперечная волна.
Скорость v распространения волн по струне с
натяжением T и плотностью ρ определяется
соотношением ![]() . Поскольку натяжение Т
силовых линий пропорционально квадрату
напряжённости магн. поля, Т = H2/4π, скорость
распространения А. в.
. Поскольку натяжение Т
силовых линий пропорционально квадрату
напряжённости магн. поля, Т = H2/4π, скорость
распространения А. в. ![]() (т. н.
альвеновская скорость), где ρ - плотность колеблющейся
среды.
(т. н.
альвеновская скорость), где ρ - плотность колеблющейся
среды.
 |
|
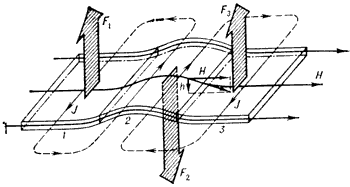
Поля, токи и силы, возникающие при
смещении |
А. в. можно рассматривать как замедленные
поперечные эл.-магн. волны. Учёт токов
смещения приводит к следующему выражению
для скорости А. в.: ![]() , что при
достаточно больших ρ совпадает с
, что при
достаточно больших ρ совпадает с
![]() . При
очень малых ρ А. в. плавно переходят в
обычные эл.-магн. волны в вакууме. При этом
их скорость, как видно из приведённого
выражения, становится равной скорости
света с.
. При
очень малых ρ А. в. плавно переходят в
обычные эл.-магн. волны в вакууме. При этом
их скорость, как видно из приведённого
выражения, становится равной скорости
света с.
Возникнув в результате, напр., конвективных движений проводящей среды в нек-рой области и затухая в др. месте, А. в. способны осуществлять обмен энергией между удаленными областями космич. пространства. При определённых условиях энергия А. и. может переходить в др. виды энергии, напр. в тепловую (вязкое затухание, джоулева диссипация), в энергию ускоренных частиц (Ландау затухание), в энергию др. видов волн. Особый интерес для астрофизики представляет тот факт, что собственное поле волны h может значительно превосходить исходное поле Н. Т. о., А. в. способны усиливать магн. поле и переносить его на большие расстояния. По совр. представлениям, А. в. играют значит. роль в процессах, происходящих в магнитосферах Земли н планет, межпланетной плазме, явлениях на Солнце, в радиогалактиках и др.
Лит.:
Альвен Г., Фельтхаммар К.
- Г.,
Космическая электродинамика, пер. с англ., 2 изд., М.,
1967
Пикельнер С. Б., Основы
космической электродинамики, 2 изд., М., 1966
(Р.3. Дурлевич)
Р. З. Дурлевич, "Физика Космоса", 1986
Глоссарий Astronet.ru