 |
Астронет: J. M. Pierre/Interwoven Inc., San Francisco Введение в суперструны http://variable-stars.ru/db/msg/1185844/basics.html |
Основы струнной теории
Мы привыкли думать об элементарных частицах (типа электрона) как о точечных 0-мерных объектах. Несколько более общим является понятие фундаментальных струн как 1-мерных объектов. Они бесконечно тонкие, а длина их порядка
. Но это просто ничтожно мало по
сравнению с длинами, с которыми мы обычно имеем дело, так что можно считать, что они практически
точечные. Но, как мы увидим, их струнная природа довольно важна.
Струны бывают открытыми и замкнутыми. Двигаясь в пространстве-времени, они покрывают поверхность, называемую мировым листом.
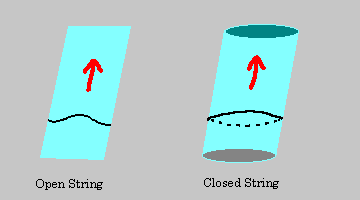
Эти струны имеют определенные колебательные моды, которые определяют присущие частице квантовые числа, такие, как масса, спин, и т.д.. Основная идея состоит в том, что каждая мода несет в себе набор квантовых чисел, отвечающих определенному типу частиц. Это и есть окончательное объединение - все частицы могут быть описаны через один объект - струну !
В качестве примера рассмотрим замкнутую струну, которая выглядит так:
Такая струна отвечает безмассовому гравитону со спином 2 - частице, переносящей гравитационное взаимодействие. Кстати, это одна из особенностей струнной теории - она естественно и неизбежно включает в себя гравитацию как одно из фундаментальных взаимодействий.
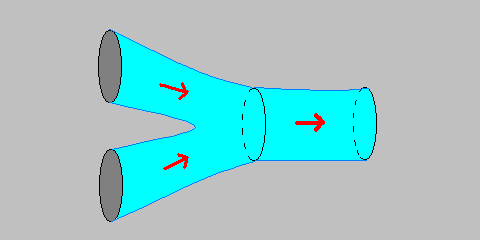
Струны взаимодействуют путем деления и слияния. Например, аннигиляция двух замкнутых струн в одну замкнутую выглядит следующим образом:
Отметим, что поверхность мирового листа - гладкая поверхность. Из этого следует еще одно "хорошее" свойство струнной теории - в ней нет ряда расходимостей, присущих квантовой теории поля с точечными частицами. Фейнмановская диаграмма для такого же процесса
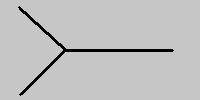
содержит топологическую сингулярность в точке взаимодействия.
Если мы "склеим" два простейших струнных взаимодействия между собой, то получим процесс, в
котором две замкнутые струны взаимодействуют через объединение в промежуточную замкнутую струну,
которая потом опять распадается на две:
Этот основной вклад в процесс взаимодействия называется древесным приближением. Для того,
чтобы вычислить квантовомеханические амплитуды процессов используя теорию возмущений,
добавляют вклады от квантовых процессов высших порядков. Теория возмущений дает хорошие результаты,
так как вклады становятся все меньше и меньше, когда мы используем все более высшие порядки. Даже
если вычислить лишь первые несколько диаграмм, то можно получить достаточно точные результаты. В струнной
теории высшие порядки отвечают большему числу дыр (или "ручек") на мировых листах.
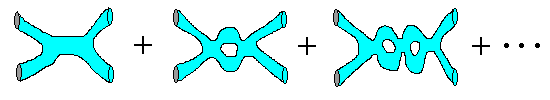
Хорошо в этом подходе то, что каждому порядку теории возмущения соответствует только одна диаграмма (например, в теории поля с точечными частицами число диаграмм растет экспоненциально в высших порядках). Плохо же то, что точные расчеты диаграмм с более чем двумя дырами очень сложны по причине сложности математического аппарата, используемого при работе с подобными поверхностями. Теория возмущений очень полезна при исследовании процессов со слабой связью, и большая часть открытий в области физики элементарных частиц и струнной теории связана именно с ней. Однако, все это еще далеко от завершения. Ответы на самые глубокие вопросы теории можно будет получить лишь после того, как будет завершено точное описание этой теории.
<< Почему именно струнная теория ? | Оглавление | D-браны >>