"...Задача эта, которую мы можем назвать "ограниченной проблемой в широком смысле", не совпадает с общей задачей о трех телах. Определение "ограниченной проблемы" введено впервые в небесную механику Пуанкаре ввиду практической необходимости как-то ограничить общую задачу о трех телах... Одна из конечных масс у Пуанкаре предполагалась очень малой по сравнению с другой. В копенгагенсткой задаче обе конечные массы были приняты равными."
"Метод, лежащий в основе наших исследований, есть метод числового интегрирования дифференциальных уравнений движения... В процессе работы мы варьировали начальные условия движения, чтобы исчерпать область возможных движений во всех желательных направлениях."
На рисунках вращающающая вместе с массами m1 и m2 система координат выбрана таким образом, чтобы прямая, соединяющая эти массы, служила осью x (это не относится к рис. 13).
"Представлены чертежи, сопровождаемые некоторыми пояснениями, представляют общий очерк простых периодических и наиболее элементарных асимптотических движений в ограниченной проблеме и почти исчерпывают разнообразие форм движения при избранном соотношении масс конечных тел."
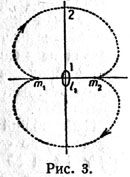
 | | Две равных массы движутся по круговым орбитам вокруг общего центра тяжести под действием взаимного притяжения. |
|
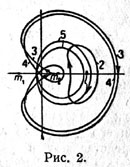 | Обратные периодические орбиты вокруг L2.Орбиты начинаются с точки
либрации L2, переходят в бесконечно малое движение, далее в конечные периодические орбиты. После прохождения через массу m2 переходит в орбиту с петлей. Далее в обратном порядке. |
|
 | | Обратные периодические орбиты вокруг L1. Движение начинается точкой покоя L1, затем следует бесконечно малое движение, затем конечные орбиты либрационного типа, затем переход к двойной орбите выбрасывания. Далее могут быть развиты орбиты с петлями вокруг масс m1 и m2 |
|
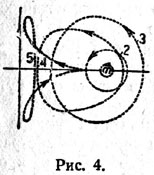 | | Прямые периодические орбиты вокруг m2. Представлен ход развития бесконечно малых круговых орбит с бесконечной скоростью движения в орбиты выбрасывания из m2. |
|
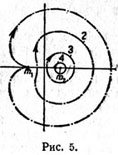 | | Обратные периодические орбиты вокруг m2. Орбиты развиваются от бесконечно малых круговых около m2 с бесконечной скоростью движения в орбиты выбрасывания из m1. |
|
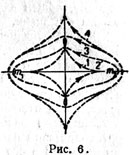 | | Прямые периодические орбиты вокруг обеих масс. Орбиты развиваются от орбит выбрасывания к орбитам со спиралевидными траекториями, асимптотически приближающимися к точкам L4 и L5. Скорость вблизи точек либрации делается бесконечно малой. Орбиты с петлями вокруг m1 и m2 также асимптотически завершаются около L4 и L5 |
|
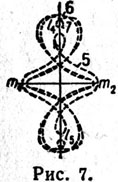 | | то же, что для рис. 6. |
|
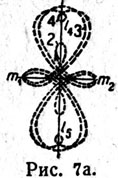 | | то же, что для рис. 6. |
|
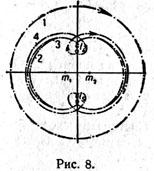 | | Вдали от масс орбиты круговые с малыми скоростями движения. При приближении к массам орбиты как бы сплющиваются. Последовательно орбиты превращаются в асимптотическое движение около точек L4 и L5. |
|
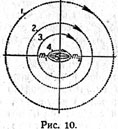
 | | Показано развитие форм движения от периодических орбит путем образования ряда петель к орбитам асимптотическим (рис. 6, 7, 8). |
|
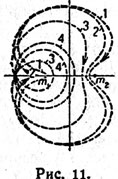
 | | Обратные периодические орбиты вокруг обеих масс с обратным движением в абсолютных осях: круговая орбита бесконечно большого радиуса с ьесконечно медленным движением; сплющивание при непрерывном возрастании скорости движения. В конце: прямолинейное колебательное движение между обеими конечными массами с бесконечно большой скоростью. |
|
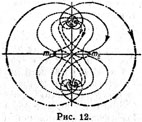
 | | Обратные, подобные либрационным, периодические орбиты, асиметричные относительно оси ординат. Показана эволюция форм движения, включая орбиты выбрасывания. |
|
 | | Показана система периодических орбит, которые одновременно являются асимптотическими по отношению к L4 и L5. |
|
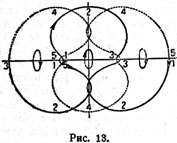 | | Движение трех тел с соотношением масс 1:2:1 по орбитам, соответствующим трем либрациям около точек L3, L1, L2. |
|
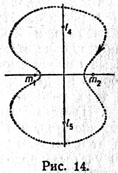 | | Обратные, подобные либрационным, периодические орбиты. |
|
<< Назад















