Астронет > Инфляция, квантовая космология и антропный принцип. Хаотическая инфляция

Астронет: А. Д. Линде Инфляция, квантовая космология и антропный принцип
http://variable-stars.ru/db/msg/1181084/node2.html

<< Введение|Оглавление|Квантовые флуктуации на инфляционной стадии >>

Хаотическая инфляция

Инфляционная теория формулировалась во множестве вариантов, начиная с моделей, основанных на квантовой гравитации (Starobinsky, 1980) и теории высокотемпературных фазовых переходов со сверхохлаждением (supercooling) и экспоненциальным расширением в состоянии ложного вакуума (Guth, 1981; Linde, 1982a; Albrecht and Steinhardt, 1982). Однако, с появлением сценария хаотической инфляции (Linde, 1983b) было понято, что основные принципы инфляции очень просты, и что для нее вовсе не обязательны термодинамическое равновесие, сверхохлаждение и расширение в состоянии ложного вакуума.

Для объяснения основной идеи хаотической инфляции рассмотрим простейшую модель скалярного поля $\phi$ с массой $m$ и плотностью потенциальной энергии $V(\phi) = {m^2\over 2} \phi^2$ (см. рис. 1). Так как эта функция имеет минимум при $\phi = 0$ , можно было бы ожидать осцилляций скалярного поля $\phi$ вблизи этого минимума. Это действительно имеет место, если вселенная не расширяется. Однако, можно показать, что в быстро расширяющейся вселенной скалярное поле скатывается вниз очень медленно, подобно шарику в вязкой жидкости, причем эффективная вязкость оказывается пропорциональной скорости расширения.

Эволюция однородного скалярного поля в нашей модели описывается двумя уравнениями - уравнением для поля

$\ddot\phi + 3H\dot\phi = -m^2\phi \ ,$

и уравнением Эйнштейна

$H^2 +{k\over a^2} ={8\pi \over 3M_p^2}\, \left( {1\over 2}\dot \phi^2+V(\phi) \right) \ .$

Здесь $H = \dot a/a$ - постоянная Хаббла для вселенной с масштабным фактором $a(t)$ (размер вселенной), $k = -1, 0, 1$ соответственно для открытой, плоской и закрытой моделей, $M_p$ - планковская масса, $M_p^{-2} = G$ , где $G$ - гравитационная постоянная. Первое уравнение похоже на уравнение движения гармонического осциллятора, где вместо $x(t)$ мы имеем $\phi(t)$ . Член $3H\dot\phi$ аналогичен описывающему вязкость в уравнении для гармонического осциллятора.

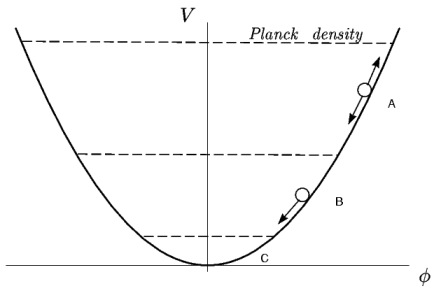
Рис. 1. Движение скалярного поля в теории с $V(\phi) = {m^2\over 2} \phi^2$ . Возможны несколько различных режимов в зависимости от величины поля $\phi$ Если плотность потенциальной энергии поля превышает планковское значение $\rho \sim M_p^4 \sim 10^{94}$ г/см $^3$ , квантовые флуктуации пространства-времени настолько сильны, что их уже нельзя описать в обычных терминах. Это состояние называется пространственно-временной пеной. На чуть меньших энергиях (область A: $m M_p^3 < V(\phi) < M_p^4$ ) квантовые флуктуации пространства-времени малы, но флуктуации скалярного поля $\phi$ могут быть значительными. Скачки скалярного поля, вызванные квантовыми флуктуациями, приводят к вечному самовоспроизведению инфляционной вселенной (что мы обсудим ниже). При еще меньших величинах $V(\phi)$ (область B: $m^2 M_p^2 < V(\phi) < m M_p^3$ ) флуктуации скалярного поля малы, оно медленно скатывается подобно шарику в вязкой жидкости. Инфляция имеет место как в области A, так и в области B. Наконец, вблизи минимума $V(\phi)$ (область C) скалярное поле быстро осциллирует, рождая пары элементарных частиц, и вселенная становится горячей.

Если скалярное поле $\phi$ изначально было большим, постоянная Хаббла $H$ также была велика, в соответствии со вторым уравнением. Это означает, что вязкий член был очень большим, и скалярное поле двигалось очень медленно, подобно шарику в вязкой жидкости. Потому на этой стадии плотность энергии скалярного поля, в отличие от подобной величины для обычной материи, оставалась практически постоянной, и расширение вселенной продолжалось с гораздо большей скоростью, чем в старой космологической теории. Благодаря быстрому росту размеров вселенной и медленности движения поля $\phi$ , вскоре после начала данной стадии мы имеем $\ddot\phi \ll 3H\dot\phi$ , $H^2 \gg {k\over a^2}$ , $\dot \phi^2\ll m^2\phi^2$ , так что можно упростить систему уравнений:

$3{\dot a \over a}\dot\phi = -{m^2\phi} \ ,$ $H ={\dot a \over a} ={2 m\phi\over M_p}\, \sqrt { \pi \over 3} \ .$

Последнее уравнение показывает, что размер вселенной $a(t)$ на данной стадии растет примерно как $e^{Ht}$ , где $H = {2 m\phi\over M_p}\, \sqrt { \pi \over 3}\,$ .

Эта стадия экспоненциально-быстрого расширения называется инфляцией. В реалистичных версиях инфляционной теории ее длительность может быть достаточно малой, вплоть до $10^{-35}$ секунд. Как только поле $\phi$ становится достаточно малым, вязкость также уменьшается, инфляция кончается, и скалярное поле начинает осциллировать вблизи минимума $V(\phi)$ . Как любое быстро осциллирующее классическое поле, оно теряет энергию за счет рождения пар частиц. Эти частицы, взаимодействуя между собой, приходят в тепловое равновесие с некой температурой $T$ . С этого момента соответствующая часть вселенной может быть описана стандартной теорией горячей вселенной.

Главное отличие инфляционной теории от старой космологии становится очевидным, если посчитать размер типичной инфляционной области в конце инфляции. Даже если начальный размер инфляционной вселенной был очень мал (порядка планковского длины $l_P \sim 10^{-33}$ см.), после $10^{-35}$ секунды инфляции вселенная достигает огромных размеров - $l \sim 10^{10^{12}}$ см. Это приводит к тому, что вселенная становится практически плоской и однородной на больших масштабах, так как все неоднородности растягиваются в $10^{10^{12}}$ раз.

Этот фактор является модельно-зависимым, однако во всех реалистичных моделях вселенная после инфляции оказывается на много порядков больше масштаба той части вселенной, которую мы можем видеть ( $$l \sim 10^{28}$ cm$ ). Это сразу же решает большинство проблем классической космологии (Linde, 1990a).

Рассмотрим вселенную, изначально состоящую из многих областей со случайным образом распределенным скалярным полем $\phi$ (или же ансамбль вселенных с различными величинами поля). В тех частях, где скалярное поле слишком мало, инфляция никогда не начинается, потому они не вносят существенного вклада в объем вселенной. Основную же ее часть занимают те области, в которых скалярное поле изначально было большим. Инфляция таких областей формирует огромные "острова" в первичном хаосе, размер каждого такого "острова" существенно превышает размер наблюдаемой части вселенной. Именно поэтому я называю этот сценарий хаотической инфляцией

Есть существенное отличие данного сценария от старой идеи создания всей вселенной в некий момент времени (Большой Взрыв) практически однородной и нагретой до бесконечно больших температур. В новой модели более не требуются условия изначальной однородности и термодинамического равновесия. Каждая часть вселенной может иметь сингулярное начало (см. в работе (Borde et al, 2001) обсуждение современного состояния вопроса). Однако, в контексте хаотической инфляции это не означает, что вся вселенная как целое возникла из сингулярности. Различные части вселенной могли возникать в разные моменты времени, и потом разрастаться до размеров, значительно превышающих размер вселенной. Наличие начальной сингулярности (или сингулярностей) не означает, что вселенная была создана как целое в результате единственного Большого взрыва. Это означает, что бы более не вправе говорить, что вся вселенная родилась в некий момент времени $t=0$ , до которого ее не существовало. Это справедливо для всех вариантов теории хаотической инфляции, даже если не принимать во внимание процесс самовоспроизведения вселенной, обсуждающийся в разделе 4.

Возможность того, что наша однородная часть вселенной возникла из начального хаотического состояния, имеет важное значение для антропного принципа. До сих пор мы рассматривали простейшую инфляционную модель с всего одним скалярным полем. Реалистичные модели элементарных частиц, однако, вводят множество других скалярных полей. Например, в соответствии со стандартной теорией электрослабого взаимодействия, массы всех элементарных частиц зависят от величины хиггсовского скалярного поля $\varphi$ в нашей вселенной. Эта величина определяется положением минимума эффективного потенциала $V(\varphi)$ . В простейших моделях $V(\varphi)$ имеет только один минимум. Однако в общем случае этот потенциал может иметь множество различных минимумов. Так, в простейшей суперсимметричной теории, объединяющей слабое, сильное и электромагнитное взаимодействия, эффективный потенциал имеет несколько различных минимумов равной глубины по отношению к двум скалярным полям, $\Phi$ и $\varphi$ . Если эти скалярные поля скатываются в различные минимумы в разных частях вселенной (этот процесс называют спонтанным нарушением симметрии), массы элементарных частиц и законы взаимодействий в них будут различными. Каждая из этих частей может стать экспоненциально большой в результате инфляции. В некоторых из этих частей не будет разницы между сильным, слабым и электромагнитным взаимодействиями, и жизнь нашего типа будет невозможна. Другие же части будут похожи на ту, в которой живем мы (Linde, 1983c).

Это значит, что даже если мы и найдем последнюю Теорию Всего (TOE, Theory of Everything), мы все равно будем не в состоянии однозначно предсказать свойства элементарных частиц в нашей вселенной; вселенная может состоять из различных экспоненциально больших частей с различными свойствами элементарны частиц. Это - важный шаг на пути к доказательству антропного принципа. Следующий же шаг может быть сделан, если мы примем во внимание квантовые флуктуации в процессе инфляции.

<< Введение|Оглавление|Квантовые флуктуации на инфляционной стадии >>