Астронет: Н. В. Никитин/НИИЯФ МГУ Физика элементарных частиц и t-кварк http://variable-stars.ru/db/msg/1179679/node3.html

<< Открытие t-кварка | Оглавление | Литература >>

Комментарии переводчика

Покажем, как получаются формулы (2) и (3) методами квантовой теории поля.

Везде далее будем предполагать, что имеет место следующий процесс: фермион с 4-импульсом и антифермион с 4-импульсом аннигилируют в фотон или глюон с 4-импульсом , из которого рождается пара фермион-антифермион с 4-импульсами и соответственно. Фермионы в начальном и конечном состояниях считаются ультрарелятивистскими, то есть . Обозначим .

а) Рассмотрим реакцию (рис. 2 (a)). Примем, что и . Тогда, согласно правилам Фейнмана, получаем для матричного элемента

Усредняя квадрат модуля матричного элемента по спинам начальных фермионов и суммируя по спинам конечных, находим

где , и -спинорные индексы, -лоренцовский индекс. В системе центра масс 4-импульсы фермионов имеют вид

где , -угол между направлениями движения частиц и . Можно проверить, что для скалярных произведений 4-векторов справедливы следующие формулы

Тогда

Используя выражение для двухчастичного фазового объема в случае безмассовых частиц , запишем дифференциальное сечение реакции в виде

Интегрируя по от -1 до 1, получаем окончательное выражение для полного сечения

которое совпадает с формулой (2).

б) Рассмотрим несколько более сложную реакцию . Введем цветовые индексы кварков и . Очевидно, что . Матричный элемент реакции имеет вид

где - заряд кварка в единицах . Учитывая, что , после усреднения по спинам начальных лептонов и суммированию по спину и цвету конечных кварков находим:

Для суммирования по спину и цвету кварков использовалась матрица плотности вида
. Сечение реакции равно

в) Теперь рассмотрим реакцию вида , где -виртуальный глюон (рис. 2 (b)). Пусть , где - набор из восьми матриц Гелл-Манна размерности , а - цветовой индекс глюонов. Поясним, почему глюоны имеют восемь цветовых индексов. Каждый глюон несет на себе два цветовых индекса: один - кварка, другой - антикварка. Например, синий-антизеленый или красный-антикрасный. Как легко видеть, всего таких комбинаций девять. Но комбинация "красный-антикрасный синий-антисиний зеленый-антизеленый" бесцветна и не участвует в сильном взаимодействии. Таким образом, на девять комбинаций кварковых индексов существует одно условие, что ведет к восьми независимым комбинациям. Конечно, подобное рассуждение не является строгим. Математически строго восемь глюонных цветовых индексов получается, если использовать теорию групп (подробнее см., например, книгу [10]) Для -матриц верны следующие соотношения (см. [10]): и при . Примем, что и что . Тогда для матричного элемента процесса можно записать

Усредняя по спинам и цветам начальных кварков и суммируя по спинам и цветам конечных, получаем выражение

поскольку

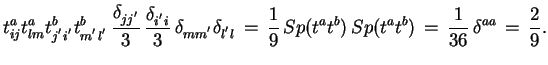Таким образом, для сечения процесса получаем формулу

которая воспроизводит выражение (3).

Задача. Покажите, что сечение процесса равно

г) Кратко остановимся на реакции . В отличии от хорошо известной из КЭД реакции , вычисление сечения аннигиляции кварков в глюоны на порядок более сложно даже в случае безмассовых кварков. Это связано с тем, что в КХД к двум аннигиляционным диаграммам, известным из КЭД, добавляется третья от трехглюонной вершины. Без вывода приведем окончательный ответ для дифференциального сечения аннигиляции кварков в глюоны в СЦМ сталкивающихся частиц в пределе нулевых масс кварков:

Расходимость при возникла из-за пренебрежения массами сталкивающихся кварков.

Задача. Данных, приведенных в пунктах б)-г), вполне достаточно, чтобы написать выражение для . Подскажем, что при написании формулы (6) проводились усреднения по начальным поляризациям и цветам кварков и суммирования по конечным поляризациям и цветам глюонов. В случае реакции нужно просуммировать по начальным поляризациям и цветам глюонов и усреднить по конечным поляризациям и цветам кварков.

д) Наконец, скажем несколько слов о возможных каналах распадов -кварка. Абсолютно доминирующим является канал . Ширина распада, в пренебрежении массами -бозона и -кварка, дается формулой

где -матричный элемент матрицы Кабаяши-Маскава (КМ-матрицы). Поскольку КМ-матричные элементы кварковых переходов и равны соответственно и , то распады по каналам и составляют примерно 0,2% и 0,01% от общего числа всех распадов -кварка. Таким образом, полная ширина распада -кварка практически совпадает с парциальной шириной распада по каналу .

Как уже было отмечено Дональдом Перкинсом, top-кварк распадается быстрее, чем успевает образовать связанное состояние. Его время жизни сравнимо с временем жизни -бозонов. Поэтому формально можно утверждать, что с обнаружением -кварка увенчались успехом поиски свободных кварков. Более того, аргумент противников кварковой модели, заключающийся в том, что кварки лишь удобный формализм для описания адронов, но сами они не существуют, поскольку свободные кварки не наблюдаемы, оказался опровергнутым экспериментально.

Поскольку -кварк настолько тяжел, что , то возможен распад . Однако он сильно подавлен по фазовому объему, и поэтому идет примерно в миллион раз реже, чем распад . Данный распад интересен тем, что его ширина чрезвычайно чувствительна к массе top-кварка. При изменении на 10 ГэВ, ширина распад изменяется более чем в три раза. На протон-протонном коллайдере LHC точные измерения массы -кварка планируется произвести, используя именно канал . Возможны редкие распады -кварка , идущие в рамках Стандартной Модели только за счет однопетлевых "пингвинных" диаграмм. Но их вероятность пренебрежимо мала, так что ни на одном из действующих и планирующихся к постройке ускорителей они не могут быть найдены.

До тех пор, пока считалось, что масса нейтрального бозона Хиггса находится в районе 90 ГэВ, планировалось изучение канала распада . Следующее из экспериментов на LEP-е ограничение ГэВ закрыло столь интересный канал.

Протон-антипротонный коллайдер Tevatron, который работает в настоящее время в Фермилабе, может изучать только основной канал распада -кварка . На строящемся в CERN-e протон-протонном коллайдере LHC будет возможно изучать распады и, вероятно, распад . Остальные каналы не будут доступны экспериментальному наблюдению в ближайшие десятилетия, если только верна современная теория взаимодействия элементарных частиц. В противном случае следует ждать любых сюрпризов. И это особенно интересно!

Получим формулу (7) с учетом ненулевой массы -бозона. Пусть 4-импульс -кварка равен , а 4-импульсы -кварка и -бозона и соответственно. Поскольку и , то можно принять, что , , . Тогда для скалярных произведений

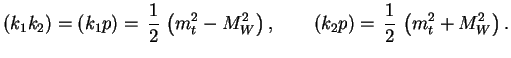Константа слабого взаимодействия удовлетворяет следующему условию . Согласно правилам Фейнмана для матричного элемента распада

Суммируя по спинам конечных частиц и усредняя по спину начальной частицы, получаем

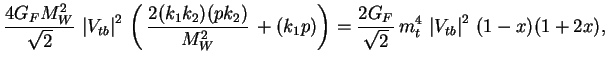где . Квадрат матричного элемента не зависит от углов и модулей конечных импульсов, а потому можно сразу записать, что

Учтя формулу для двухчастичного фазоваго объема, когда одна из частиц безмассовая , получаем окончательный ответ

При формула (8) переходит в формулу (7). Поправка на массу дает ГэВ, что достаточно хорошо согласуется с грубой оценкой, приведенной Д.Перкинсом.

Задача. Если в конечном состоянии находятся две частицы с 4-импульсами и , то элемент двухчастичного фазового объема определяется как

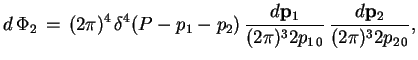где -полный 4-импульс системы, . Проверить, что верны следующие выражения для двухчастичного фазоваго объема в случае
а) безмассовых частиц: ;
б) одной массивной (), одной безмассовой частиц: , если ;
в) двух массивных частиц с массами и : , где , если .

Автор благодарит Константина Томса за оказание технической помощи при подготовке иллюстраций к статье.

---

<< Открытие t-кварка | Оглавление | Литература >>